振动力学课程设计题目
振动力学ch1习题题目

习题 1.8 不计质量的等截面悬臂梁长为 L,抗弯刚度为 EI,自由端有集中质量 m1 和 m2。梁静止时突 然释放质量 m1。试求 m2 的自由振动。
长为 l 的均匀杆及弹簧 K、 阻尼器 C 组成。 习题 1. 9 图示系统由一质量为 m, 试以杆的偏角为广义坐标建立系统的动力学方程,给出存在自由振动的条件。若 在弹簧原长处立即释手, 试求杆的最大振幅和发生时间、 最大角速度和发生时间。 是否发生在过平衡位置时?
习题 1.10 质量 m 2000 kg ,以匀速度 v 0.03m / s 运动,与弹簧 K、阻尼器 C 相撞后 一起作自由振动,如图所示。已知 K 48020N / m , C 1960N s / m 。问质 量 m 在相撞后多少时间达到最大振幅?最大振幅是多大?
1. 11 求图示系统的动力学方程, 并给出存在往复运动的条件。 设 t=0 时质量的位移为 x0, 速度为 v0测某液体的粘度系数 。一等厚薄板质量为 M,面
积为 A,悬挂于弹簧 K 上。先使系统在空气中自由振 动,测得周期为 T1 , (空气阻力忽略不计) 。然后放入被 已知薄板受到的 测液体中作衰减振动, 测得周期为 T2 。 阻尼力 F
2 Av , ( v 为相对速度) ,试证明
习题 1.1 质量为 m 的质点由长度为 l、质量为 m1 的均质细杆约束 在铅垂平面内做微幅摆动,求系统的固有频率。
习题 1.2 质量为 m、半径为 R 的均质柱体在水平面上作无滑 动的微幅滚动,在 CA=a 的 A 点系有两根刚度系数为 k 的水平 弹簧,求系统的固有频率。
习题 1.3 转动惯量为 J 的圆盘由三段抗扭刚度分别为 k1,k2 和 k3 的轴约束, 求系统的固有 频率。
习题 1.4 在图示系统中,已知 ki(i=1,2,3) ,m,a 和 b, 横杆质量不计, 求系统的固有频率。
《振动力学》习题集(含答案)
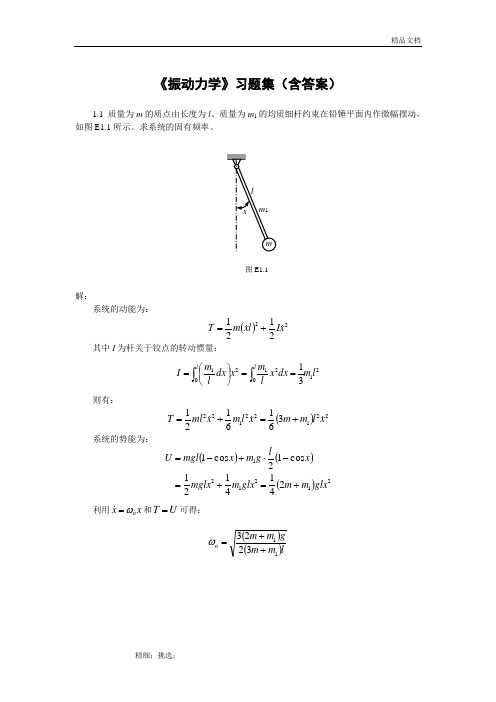
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解: 系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
振动力学课程设计报告材料(2)

振动力学课程设计报告课设题目:电磁振动给料机的振动分析与隔振设计单位:专业/班级:姓名:指导教师:一、前言1、课题目的或意义通过对结构进行振动分析或参数设计,进一步巩固和加深振动力学课程中的基本理论知识,初步掌握实际结构中对振动问题分析、计算的步骤和方法,培养和提高独立分析问题和运用所学理论知识解决实际问题的能力。
2、课题背景:1、结构:本设计中,料槽底板采用16mm厚钢板焊接而成,再用筋板加强。
料槽衬板采用20mm厚钢板。
料槽材料全部采用镇静钢,能承受工作过程中由于振动产生的交变载荷,焊缝不易开裂。
2、工程应用前景:振动给料机用于把物料从贮料仓或其它贮料设备中均匀或定量的供给到受料设备中,是实行流水作业自动化的必备设备分敞开型和封闭型两种,本设计中电磁振动给料为双质体系统,结构简单,操作方便,不需润化,耗电量小;可以均匀地调节给料量为了减小惯性力,在保证强度和刚度的前提下,应尽可能减轻振动槽体的质量。
从而使其在实际工程应用中会有非常广泛的前景。
二、振动(力学)模型建立1、结构(系统)模型简介123123k k k c c c 、为隔振弹簧,为主振弹簧,、、分别为隔振和主振弹簧的阻尼4k 、4c 分别为尼龙连接板得等效刚度和阻尼。
0m 为偏心块质量,1m 为给料槽体质量,2m 激振器的振动质量。
R m —输送槽体(包括激振器)的质量,1500kg ;即012R m m m m ++=G m —槽内物料的结合质量。
在实际中系统为离散的,而建立模型后将质量进行集中从而该系统可视为为连续系统,通过上网搜索资料以及书中知识总结并设计出如上所示电磁振动给料机力学模型,其组成为料槽、电磁激振器、减振器、电源控制箱等组成。
2、系统模型参数(包括系统所必需的几何、质量、等效刚、激励等)根据实际应用情况假设个几何参数为:外形尺寸(长x 宽x 高):4057 x 2100 x 1730mm1l =390mm 2l =1140mm 3l =650mm质量参数:150018753375R G m m m kg =+=+=0587m Kg = 1456m Kg = 2457m Kg =等效刚度:由公式得24055(1)()79e k K N c k μλγλ=-∆++1k =875641N/m 2k =854213N/m 3k =2126284N/m 4k =458256 N/m激振力矩阵:三、振动分析1、振动方程建立由于系统做微抛物运动,因此系统有两个自由度,所以其振动微分方程如下:MX CX KX F++=其中; 。
振动力学课程设计报告--垂直振动输送机的机械振动与隔振分析

振动力学课程设计报告课设题目:垂直振动输送机的机械振动与隔振分析单位:理学院专业/班级:工程力学09-1姓名:指导教师:2011-12-18一、前言1、课题目的或意义主要研究双质体垂直振动输送机输送原理及设计理论,根据参数对其进行运动分析和隔振分析。
通过对结构进行振动分析或参数设计,进一步巩固和加深振动力学课程中的基础理论知识,初步掌握实际结构中对振动问题分析、计算的步骤和方法,培养和提高独立分析问题和运用所学理论知识解决实际问题的能力。
2、课题背景:垂直振动输送机主要应用于箱式元件的提升输送,按照进料口出料口的方向分为Z型垂直提升机和C型垂直提升机两种提升输送机。
垂直振动提升机主要应用于矿山、冶金、化工、轻工、建材、机械、粮食等各行业垂直输送50毫米以下的粉状、颗粒状、块状物料,在连续供料条件下也可用于输送具有滚动性的团状物料,可以代斗式提升机、倾斜使用皮带输送机等。
惯性自同步垂直振动提升机由于应用了机械振动学的自同步原理具有结构简单,技术参数先进,安装调整方便,维修量小,占地面积小及对基础无特殊要求等特点,而且设备费用和运送费用较低。
在有特殊要求时可同时完成冷却、干燥等多种工艺过程,是一种理想的物料垂直提升设备。
ZC系列垂直振动输送机的工作原理:ZC系列垂直振动输送机的驱动装置振动安装在输送塔下部,两台振动电机堆成交叉安装,输送塔由管体和焊接在管体周围的螺旋输送槽组成,输送塔座于减振装置上,减振装置有底座和隔振弹簧组成。
当垂直输送机工作时,根据双振电机自同步原理,由振动电机产生激振力,强迫整个输送塔体作水平圆运动和向上垂直运动的空间复合振动,螺旋槽内的物料则受输送槽的作用,做匀速抛掷圆运动,沿输送槽体向上运动,从而完成物料的向上(或向下)输送作业。
二、振动(力学)模型建立1、结构(系统)模型简介此系统为双质体垂直振动输送机,为离散体。
此结构由螺旋槽体、底座、隔振弹簧、激振电动机和底架组成,底架固结于地面上,两台振动电机堆成交叉安装,输送塔由管体和焊接在管体周围的螺旋输送槽组成,输送塔座于减振装置上,减振装置有底座和隔振弹簧组成。
振动力学习题集含答案

解:
,
动量守恒:
,
平衡位置:
,
,
故:
故:
2.4在图E2.4所示系统中,已知m, , , 和 ,初始时物块静止且两弹簧均为原长。求物块运动规律。
图E2.4答案图E2.4
解:
取坐标轴 和 ,对连接点A列平衡方程:
即:
(1)
对m列运动微分方程:
即:
(2)
由(1),(2)消去 得:
图E2.7
解:
,
s=1时共振,振幅为:
(1)
远离共振点时,振幅为:
(2)
由(2)
由(1)
, ,
故:
2.7求图T 2-7中系统的固有频率,悬臂梁端点的刚度分别是 及 ,悬臂梁的质量忽略不计。
图T 2-7答案图T 2-7
解:
和 为串联,等效刚度为: 。(因为总变形为求和)
和 为并联(因为 的变形等于 的变形),则:
图E1.9答案图E1.9
解:
利用动量矩定理得:
,
,
,
,
1.12面积为S、质量为m的薄板连接于弹簧下端,在粘性流体中振动,如图E1.12所示。作用于薄板的阻尼力为 ,2S为薄板总面积,v为速度。若测得薄板无阻尼自由振动的周期为 ,在粘性流体中自由振动的周期为 。求系数 。
图E1.12
解:
平面在液体中上下振动时:
和 为串联(因为总变形为求和),故:
故:
2.9如图T 2-9所示,一质量m连接在一刚性杆上,杆的质量忽略不计,求下列情况系统作垂直振动的固有频率:
(1)振动过程中杆被约束保持水平位置;
(2)杆可以在铅锤平面内微幅转动;
(3)比较上述两种情况中哪种的固有频率较高,并说明理由。
振动力学第三版课程设计

振动力学第三版课程设计一、前言振动力学是一门重要的工程学科,是研究振动现象、振动特性和振动控制等方面的学科。
本次课程设计旨在通过理论分析和计算实例,深入理解振动力学的基本理论和应用,全面提高学生的振动力学知识。
二、课程设计目的1.了解振动力学的基本概念及其基本理论;2.掌握振动系统的自由振动和强制振动的计算方法;3.熟悉振动系统的动力响应分析方法;4.掌握振动系统的非线性振动特性;5.掌握振动控制的基本方法;6.具备一定的综合应用能力。
三、课程设计内容1. 振动系统的自由振动和强制振动•振动系统的基本元件与模型•振动系统的自由振动•单自由度体系的阻尼简谐振动•单自由度体系的非阻尼简谐振动•振动系统的强制振动•简谐强迫振动的响应分析方法•非简谐强迫振动的响应分析方法2. 振动系统的动力响应分析方法•随机振动分析方法•有限元方法•能量法•非线性动力学分析方法3. 振动系统的非线性振动特性•不同非线性系统的基本行为•非线性振动分析方法•非线性动力学控制4. 振动控制的基本方法•振动控制的基本原理•主动控制与被动控制•最优控制与稳定性分析四、课程设计要求1.在掌握基本理论的前提下,学生需要独立完成两个以上的计算分析实例;2.要求对实例的分析过程进行详细记录,并说明所采取的计算方法和理论分析方法;3.提交实验报告,每个实例的报告应包括实验目的、实验原理、实验步骤、实验结果分析和结论等部分;4.要求各组学生相互合作,共同讨论、探讨,不得抄袭或抄袭他人的报告。
五、课程设计参考资料1.高清愿、骆仲毅. 振动力学[M]. 机械工业出版社, 2014.2.邬建国、冯海燕. 振动力学[M]. 电子工业出版社, 2015.3.石晓宝. 振动理论与应用[M]. 东南大学出版社, 2013.4.张强. 振动控制技术[M]. 科学出版社, 2015.本次课程设计的参考资料仅供学生扩展和延伸知识使用,学生应在课程设计过程中根据实际需要选择参考资料。
《振动力学》习题集[含答案]
![《振动力学》习题集[含答案]](https://img.taocdn.com/s3/m/bf1e364afad6195f302ba63b.png)
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解:系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得:()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得:()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解:系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
《振动力学》习题集(含答案)

《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解: 系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
振动力学课程设计题目采用MATLAB 对所选的问题进行数值计算和作图,采用高于MATLAB7.4(2007)版本所编写的程序需转换为文本(.txt )文件, 早于MATLAB7.4(2007)版本所编写的程序可直接采用M 文件传送至QQ :296637844。
题目如下,其中1,2,3题为必做题,4-38选二题(第一轮:一班01号为第4题, 一班02号为第5题…一班28号为第25题, 二班01号为第26题,…二班17号为第38题, 二班18号为第4题,…二班27号为第13题;第二轮:一班01号为第14题…)。
文件名采用自己的姓名。
考核时间暂定于12月30日。
题目: 1. 编写MA TLAB 程序,根据书本公式(3.1-10)、(3.1-10)作出单自由度系统强迫振动的幅频特性曲线、相频特性曲线。
0.1,0.2,0.3,0.5,0.7,1.0,1.2ς=。
2. 根据书本图4.5-3,分析有阻尼动力减振器的特性。
包括在不同的质量比,频率比,阻尼比条件下结构的响应。
3. 对于图2所示体系,用矩阵迭代法计算其固有频率及振型。
1231,2m m m ===,1230c c c ===,1231,5,8k k k ===,1230,0,0F F F ===,1231,1,1ωωω===。
4. 采用中心差分法计算单自由度体系10105sin(/2)x cx x t ++= ,当c=3和c=20,000,0x x== 前10s 内的位移,作出其时间位移曲线图。
5. 采用Houbolt 法计算单自由度体系10105sin(/2)x cx x t ++= ,当c=3和c=20,000,0x x== 前10s 内的位移,作出其时间位移曲线图。
6. 采用Wilson-θ法计算单自由度体系10105sin(/2)x cxx t ++= ,当c=3和c=20,000,0x x== 前10s 内的位移,作出其时间位移曲线图。
7. 采用Newmark-β法计算单自由度体系10105sin(/2)x cx x t ++= ,当c=3和c=20,000,0x x== 前10s 内的位移,作出其时间位移曲线图。
8. 采用中心差分法计算10105sin(/2)2sin()sin(2)x cx x t t t ++=++ ,当c=3和c=20,000,0x x== 前10s 内的位移,作出其时间位移曲线图。
9. 采用Houbolt 法计算10105sin(/2)2sin()sin(2)x cxx t t t ++=++ ,当c=3和c=20,000,0x x== 前10s 内的位移,作出其时间位移曲线图。
10. 采用Wilson-θ法计算10105sin(/2)2sin()sin(2)x cxx t t t ++=++ ,当c=3和c=20,000,0x x== 前10s 内的位移,作出其时间位移曲线图。
11. 采用Newmark-β法计算10105s in (/2)2s in ()s in (2x c x x t t t ++=++ ,当c=3和c=20,000,0x x== 前10s 内的位移,作出其时间位移曲线图。
12. 采用卷积积分法计算单自由度体系m=10kg ,c=3Ns/m ,k=10N/s ,分别在()5(),5(),5sin(2)(),(02)F t N t N t N t s =≤≤作用下前10s 内的时间位移曲线。
13. 采用中心差分法计算单自由度体系m=10kg ,c=3Ns/m ,k=10N/s ,分别在()5(),5(),5sin(2)(),(02)F t N t N t N t s =≤≤作用下前10s 内的时间位移曲线。
14. 采用Houbolt 法计算单自由度体系m=10kg ,c=3Ns/m ,k=10N/s ,分别在()5(),5(),5sin(2)(),(02)F t N t N t N t s =≤≤作用下前10s 内的时间位移曲线。
15. 采用Wilson-θ法计算单自由度体系m=10kg ,c=3Ns/m ,k=10N/s ,分别在()5(),5(),5sin(2)(),(02)F t N t N t N t s =≤≤作用下前10s 内的时间位移曲线。
16. 采用Newmark-β法计算单自由度体系m=10kg ,c=3Ns/m ,k=10N/s ,分别在()5(),5(),5sin(2)(),(02)F t N t N t N t s =≤≤作用下前10s 内的时间位移曲线。
17. 采用卷积积分法计算单自由度体系m=10kg ,c=3Ns/m ,k=10N/s ,在5(),(01)()105(),(12)t N t s F t t N t s ≤≤⎧=⎨-≤≤⎩作用下前10s 内的时间位移曲线。
18. 采用中心差分法计算单自由度体系m=10kg ,c=3Ns/m ,k=10N/s ,在5(),(01)()105(),(12)t N t s F t t N t s ≤≤⎧=⎨-≤≤⎩作用下前10s 内的时间位移曲线。
19. 采用Houbolt 法计算单自由度体系m=10kg ,c=3Ns/m ,k=10N/s ,在5(),(01)()105(),(12)t N t s F t t N t s ≤≤⎧=⎨-≤≤⎩作用下前10s 内的时间位移曲线。
20. 采用Wilson-θ法计算单自由度体系m=10kg ,c=3Ns/m ,k=10N/s ,在5(),(01)()105(),(12)t N t s F t t N t s ≤≤⎧=⎨-≤≤⎩作用下前10s 内的时间位移曲线。
21. 采用Newmark-β法计算单自由度体系m=10kg ,c=3Ns/m ,k=10N/s ,在5(),(01)()105(),(12)t N t s F t t N t s ≤≤⎧=⎨-≤≤⎩作用下前10s 内的时间位移曲线。
22. 求1tan ββ=的前4个解,要求误差小于0.0123. 对于图1所示体系,采用中心差分法计算其位移响应,并作出前10s 内每个质点的时间位移曲线。
121m m ==,121c c ==,121,5k k ==,120,1F F ==,121,1ωω==,11220x xx x ==== 。
图124. 对于图1所示体系,采用Houbolt 法计算其位移响应,并作出前10s 内每个质点的时间位移曲线。
121m m ==,121c c ==,121,5k k ==,120,1F F ==,121,1ωω==,11220x xx x ==== 。
25. 对于图1所示体系,采用Wilson-θ法计算其位移响应,并作出前10s 内每个质点的时间位移曲线。
121m m ==,121c c ==,121,5k k ==,120,1F F ==,121,1ωω==,11220x xx x ==== 。
26. 对于图1所示体系,采用Newmark-β法计算其位移响应,并作出前10s 内每个质点的时间位移曲线。
121m m ==,121c c ==,121,5k k ==,120,1F F ==,121,1ωω==,11220x xx x ==== 。
27. 对于图1所示体系,采用中心差分法计算其位移响应,并作出前10s 内每个质点的时间位移曲线。
121m m ==,121c c ==,121,5k k ==,121,1F F ==,121,2ωω==,11220x xx x ==== 。
28. 对于图1所示体系,采用Houbolt 法计算其位移响应,并作出前10s 内每个质点的时间位移曲线。
121m m ==,121c c ==,121,5k k ==,121,1F F ==,121,2ωω==,11220x xx x ==== 。
29. 对于图1所示体系,采用Wilson-θ法计算其位移响应,并作出前10s 内每个质点的时间位移曲线。
121m m ==,121c c ==,121,5k k ==,121,1F F ==,121,2ωω==,11220x xx x ==== 。
30. 对于图1所示体系,采用Newmark-β法计算其位移响应,并作出前10s 内每个质点的时间位移曲线。
121m m ==,121c c ==,121,5k k ==,121,1F F ==,121,2ωω==,11220x xx x ==== 。
31. 对于图2所示体系,采用中心差分法计算其位移响应,并作出前10s 内每个质点的时间位移曲线。
1231,2m m m ===,1231c c c ===,1231,5,8k k k ===,1230,1,0F F F ===,1231,1,1ωωω===,1122330x xx x x x ====== 。
图232. 对于图2所示体系,采用Houbolt 法计算其位移响应,并作出前10s 内每个质点的时间位移曲线。
1231,2m m m ===,1231c c c ===,1231,5,8k k k ===,1230,1,0F F F ===,1231,1,1ωωω===,1122330x xx x x x ====== 。
33. 对于图2所示体系,采用Wilson-θ法计算其位移响应,并作出前10s 内每个质点的时间位移曲线。
1231,2m m m ===,1231c c c ===,1231,5,8k k k ===,1230,1,0F F F ===,1231,1,1ωωω===,1122330x xx x x x ====== 。
34. 对于图2所示体系,采用Newmark-β法计算其位移响应,并作出前10s 内每个质点的时间位移曲线。
1231,2m m m ===,1231c c c ===,1231,5,8k k k ===,1230,1,0F F F ===,1231,1,1ωωω===,1122330x xx x x x ====== 。
35. 对于图2所示体系,采用中心差分法计算其位移响应,并作出前10s 内每个质点的时间位移曲线。
1231,2m m m ===,1231c c c ===,1231,5,8k k k ===,1232,1,1F F F ===,1231,1,2ωωω===,1122330x xx x x x ====== 。
36. 对于图2所示体系,采用Houbolt 法计算其位移响应,并作出前10s 内每个质点的时间位移曲线。
1231,2m m m ===,1231c c c ===,1231,5,8k k k ===,1232,1,1F F F ===,1231,1,2ωωω===,1122330x xx x x x ====== 。
