轴向受载铁木辛柯梁的弯曲研究
铁木辛柯梁理论

铁木辛柯梁理论
简称为“六理”的铁木辛柯梁理论是20世纪著名哲学家和历史
学家铁木辛柯、梁公开提出的一种“系统性社会理论”,旨在实施
“自由、平等、法治”的人权概念,以及在未来实现民主社会和新型
国家的建立。
铁木辛柯梁理论的一个关键思想是,一个强大的国家可以通过保
障人权来获得发展与繁荣,因此,铁木辛柯和梁提出,在未来的社会
发展中保护人权应成为国家最重要的任务。
此外,国家只有保护宪法
中规定的权利,改善人民的物质生活和持续发展,才能实现所谓的自
权安全。
此外,铁木辛柯梁理论还详细说明了每一个国家社会发展的未来
蓝图,把成长和发展过程定位到国家对民众权力的责任上。
理论的核
心就是人的自由、平等和尊严的维护,因为,只有当国民获得自由和
平等待遇时,会有社会新进展,把人类带到自由平等的社会。
另外,铁木辛柯梁理论还认为,法治的实施是社会发展不可或缺
的前提,它使国家能够有效管理国家和社会关系,并将国家的行动和
价值观以及国家标准配备于一身。
将法治作为社会进步的神经,它能
够完美融合社会所有组成部分,形成一个完整而和谐的国家机构系统。
从上述,我们可以明确看到,“铁木辛柯梁理论”作为一个“系
统性社会理论”,它提供了一种以自由、平等和法治为核心的社会理论,确保每个国家実施人权和法治的统一主体,有利于建立一个安全
而平等的社会。
铁木辛柯梁

铁木辛柯梁(Timoshenko beam)就是能考虑剪切变形的梁。
具体地说,它的位移和截面转角是独立插值的,而不是由位移的导数来求得。
就是对于梁的高度较大,铁木辛柯梁是考虑剪切的梁,欧拉梁(Euler–Bernoulli beam)是材料力学里讲的梁,忽略剪切作用。
铁木辛柯梁主要考虑剪切变形,而且位移和转角是独立的,不是通过位移导数求得。
欧拉梁基于平截面假定,弯曲是主要变形,忽略剪切变形的影响,其计算公式通过平衡微分方程得到,而非变形协调方程。
The model takes into account shear deformation and rotational inertia effects, making it suitable for describing the behavior of short beams, sandwich composite beams or beams subject to high-frequency excitation when the wavelength approaches the thickness of the beam.Example of simply support beam in Timoshenko beam theoryand the free end is at . If a point load is applied to the middle of beam in the positive direction there are some equation:Therefore, from the expressions for the bending moment and shear force, we haveIntegration of the first equation, and application of the boundarycondition at , leads toThe second equation can then be written asIntegration and application of the boundary condition at givesThe axial stress is given by。
沿轴向指数分布的功能梯度Timoshenko梁的频率精确解

沿轴向指数分布的功能梯度Timoshenko梁的频率精确解邓昊;程伟【摘要】Based on the state space variable replacement,the transfer matrix equation of a Timoshenko beam with axially exponential distributed functional gradation was derived.The exact solution of natural frequencies of the structure with multiple boundary conditions was obtained by the transfer matrix method and compared with the available analytical solution.The results show that the relation curve between the frequency and the gradient of the material is continuous and smooth,and there is no jumping phenomenon.Meanwhile the finite element method was used to verify the results.The effects of shear stiffness and moment of inertia on the natural frequencies of the structure were analyzed by comparing the results according to different beam theories.The calculation results show that the method presented is clear in physical concept and can reduce the computational complexity and the amount of computation.%通过对状态空间变量进行变量替换,求得了沿轴向指数分布的功能梯度Timoshenko梁的状态空间传递矩阵方程.通过传递矩阵法计算了多种边界条件下结构固有频率的精确解,并与解析解进行对比.通过分析梯度参数对结构固有频率与模态振型的影响,该计算结果表明频率与材料梯度变量之间的关系曲线是连续光滑的,并未出现部分文献中的跳跃现象,并且采用有限元法该计算结果进行验证.通过对比不同梁理论的计算结果,定量的分析了剪切刚度和转动惯量对结构固有频率的影响.计算结果表明,该方法物理概念清晰,降低问题求解难度的同时可以减少计算量.【期刊名称】《振动与冲击》【年(卷),期】2017(036)006【总页数】7页(P91-96,113)【关键词】状态空间变量;传递矩阵法;固有频率;功能梯度材料;指数梯度【作者】邓昊;程伟【作者单位】北京航空航天大学航空科学与工程学院,北京100191;北京航空航天大学航空科学与工程学院,北京100191【正文语种】中文【中图分类】TV312工程中存在着大量的多相材料,为了使材料的性质从一相过渡到另一相,通常在两相材料之间使用沿轴向变化的功能梯度材料。
铁木辛柯材料力学

铁木辛柯材料力学铁木辛柯(Tm1-xCoxFe2)是一种具有潜在应用前景的磁性材料,其具有优异的磁性能和力学性能,因此在磁记录、传感器、磁存储器件等领域具有广泛的应用前景。
本文将对铁木辛柯材料的力学性能进行详细介绍和分析。
首先,铁木辛柯材料的力学性能主要包括硬度、弹性模量、屈服强度、断裂韧性等指标。
硬度是材料抵抗外界压力的能力,通常用洛氏硬度或维氏硬度来表示;弹性模量是材料在弹性阶段内的应力和应变关系的斜率,是衡量材料抗弹性变形能力的重要参数;屈服强度是材料在拉伸或压缩过程中开始发生塑性变形的应力值;断裂韧性是材料抗断裂能力的指标,通常用冲击韧性和断裂韧性来表示。
这些力学性能指标对于铁木辛柯材料的工程应用具有重要意义。
其次,铁木辛柯材料的力学性能受多种因素影响,包括晶体结构、晶粒大小、杂质含量、热处理工艺等。
晶体结构是决定材料硬度和弹性模量的重要因素,晶粒大小对材料的塑性变形和断裂韧性具有显著影响,杂质含量会影响材料的强度和韧性,热处理工艺可以改善材料的力学性能。
因此,通过合理设计材料的组织结构和优化工艺参数,可以有效提高铁木辛柯材料的力学性能。
最后,针对铁木辛柯材料的力学性能优化,可以采取一系列方法进行改进。
例如,可以通过合金化、晶粒细化、热处理强化等手段来提高材料的硬度和强度;可以通过合理设计材料的组织结构和形貌,来提高材料的断裂韧性和抗疲劳性能;还可以通过表面处理、涂层改性等手段来改善材料的耐磨性和耐蚀性能。
这些方法可以有效地提高铁木辛柯材料的力学性能,拓展其在工程领域的应用范围。
综上所述,铁木辛柯材料具有优异的磁性能和力学性能,在磁记录、传感器、磁存储器件等领域具有广泛的应用前景。
通过对其力学性能的深入研究和优化,可以进一步提高其在工程应用中的性能表现,推动其在材料科学和工程技术领域的发展和应用。
铁木辛柯梁
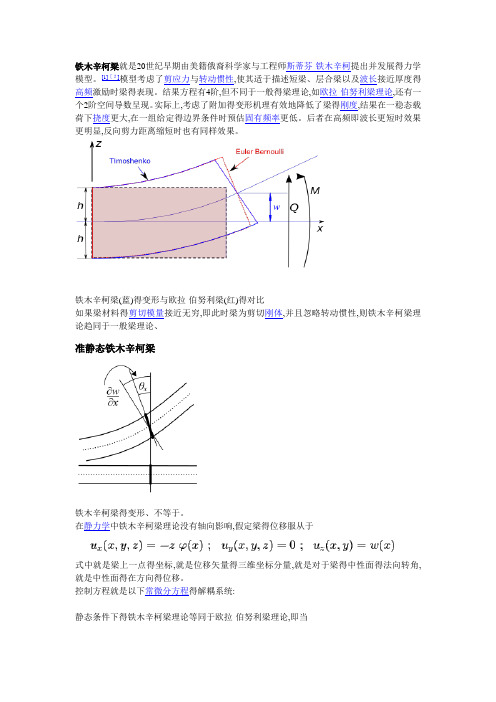
铁木辛柯梁就是20世纪早期由美籍俄裔科学家与工程师斯蒂芬·铁木辛柯提出并发展得力学模型。
[1][2]模型考虑了剪应力与转动惯性,使其适于描述短梁、层合梁以及波长接近厚度得高频激励时梁得表现。
结果方程有4阶,但不同于一般得梁理论,如欧拉-伯努利梁理论,还有一个2阶空间导数呈现。
实际上,考虑了附加得变形机理有效地降低了梁得刚度,结果在一稳态载荷下挠度更大,在一组给定得边界条件时预估固有频率更低。
后者在高频即波长更短时效果更明显,反向剪力距离缩短时也有同样效果。
铁木辛柯梁(蓝)得变形与欧拉-伯努利梁(红)得对比如果梁材料得剪切模量接近无穷,即此时梁为剪切刚体,并且忽略转动惯性,则铁木辛柯梁理论趋同于一般梁理论、准静态铁木辛柯梁铁木辛柯梁得变形、不等于。
在静力学中铁木辛柯梁理论没有轴向影响,假定梁得位移服从于式中就是梁上一点得坐标,就是位移矢量得三维坐标分量,就是对于梁得中性面得法向转角,就是中性面得在方向得位移。
控制方程就是以下常微分方程得解耦系统:静态条件下得铁木辛柯梁理论等同于欧拉-伯努利梁理论,即当可忽略上面控制方程得最后一项,得到有效得近似,式中就是梁得长度。
对于等截面均匀梁,合并以上两个方程,动态铁木辛柯梁在铁木辛柯梁理论中若不考虑轴向影响,则给出梁得位移式中就是梁内一点得坐标,就是位移矢量得三维坐标分量,就是对于梁得中性面得法向转角,就是中性面方向得位移。
从以上假设,铁木辛柯梁,考虑到振动,要用线性耦合偏微分方程描述:[3]其中因变量就是梁得平移位移与转角位移。
注意不同于欧拉-伯努利梁理论,转角位移就是另一个变量而非挠度斜率得近似。
此外,•就是梁材料得密度(而非线密度);•就是截面面积;•就是弹性模量;•就是剪切模量;•就是轴惯性矩;•,称作铁木辛柯剪切系数,由形状确定,通常矩形截面;•就是载荷分布(单位长度上得力);••这些参数不一定就是常数。
对于各向同性得线弹性均匀等截面梁,以上两个方程可合并成[4][5]轴向影响如果梁得位移由下式给出其中就是方向得附加位移,则铁木辛柯梁得控制方程成为其中,就是外加轴向力。
梁的有限元分析原理 - 考虑剪切变形影响的梁单元

代人
比较:弯曲梁 单元中的单刚
得到:
等截面梁单元有限元分析
8
长沙理工大学
小结
剪切变形的影响通过系数b反映在刚度矩阵中,使刚度减弱。 对矩形截面:
,当l >>h,b趋于0,可以忽略剪力变形的影响。
等截面梁单元有限元分析
9
长沙理工大学
Timoshenko梁单元
铁木辛柯梁单元——采用两个独立变量 挠度 w
几何关系,曲率
对比
等截面梁单元有限元分析
3
最小势能原理
长沙理工大学
k为截面剪切校正因子
1.经典梁单元 2.铁木辛柯梁单元
——C1型单元 ——C0型单元
等截面梁单元有限元分析
4
长沙理工大学
在经典梁单元基础上引入剪切变形的影响. 挠度叠加
结点位移
其中
采用不考虑剪切变形梁单元的w相同的Hermite插值; 采用2结点的Lagrange插值,即线性插值。
解决方法
假设剪切应变
代替插值函数
计算泛函的剪切应变能时,θ采用低一 阶,和dw/dx同阶插值函数代替原插值 函数
18
等截面梁单元有限元分析
长沙理工大学
等截面梁单元有限元分析
——考虑剪切变形的梁单元
2014.4.13
1
长沙理工大学
介绍.
轴力构件 axial elements 杆单元
受弯构件 flexural elements 梁单元
考虑剪切变形的梁单元
等截面梁单元有限元分析
2
长沙理工大学 假设:梁内的横向剪切力Q所产生的剪切变形将引起梁的附加挠度, 并使原来垂直于中面的截面变形后不再和中面垂直,而且发生翘曲。 考虑剪切变形的梁单元 但在这里,假设原来垂直于中面的截面变形后仍保持为平面。 几何描述
曲线梁桥的受力特点和分析方法

曲线梁桥的受力特点和分析方法摘要:由于在经济和审美上的优势,曲线梁桥被广泛应用于现代公路立交系统。
曲线梁的竖曲和扭转耦合,由于结构上的特点,相对于直梁桥而言,曲线梁的分析更为复杂。
本文对弯道梁桥的受力特点进行了介绍,并总结了分析弯道梁桥的有关理论。
关键词:曲线梁桥;弯扭耦合;支承体系;有限元法引言曲线梁桥是指主梁本身为弧形的弯曲桥梁。
由于其独特的线形,曲线梁桥突破了多种地形的限制,同时在高速公路、山地公路、城市桥梁等方面,由于其优美的曲线造型而得到了更快的发展。
曲线梁桥具有现实意义,发展前景非常看好,无论从几何角度、美学角度,还是从经济角度,都是如此。
1曲线桥梁受力特性1.1弯扭耦合作用由于受弯曲率的影响,当竖向弯曲时,曲线梁截面必然会产生扭转,而这种扭转又会导致梁的挠曲变形,这种挠曲变形被称为“弯扭耦合作用”。
对于弯道梁桥的设计,相对于直线型梁桥来说,要特别注意,因为弯道扭力耦合作用所产生的附加扭力,会使梁体结构产生较不利的受力条件,从而增加结构的挠曲变形。
值得注意的是,由于自重在使用荷载下占绝大多数,对于混凝土曲线箱梁桥而言,也会导致更明显的弯扭耦合。
由于弯道梁桥沿弯梁的线形布置支承不成直线,因此由于弯道外侧较重,导致桥体恒载重心相对于形心向外偏移。
曲线梁在自重的作用下,也会产生扭转和扭曲的变形,从而使曲线桥发生翻转,出现匍匐的现象,这就是曲线梁在自重的作用下产生的变形[1]。
1.2曲线梁内外侧受力不均匀曲线桥因弯曲和扭动耦合作用,变形大于同跨径的直线桥,且曲率半径越小、桥越宽,因此其简支曲线梁外缘的挠度比内缘大,这种变化趋势是显而易见的。
曲线梁桥体具有向外扭转的较大扭力、弯曲扭力耦合和偏载作用的可能。
扭转作用会越来越明显,曲率半径越小、跨度越大的曲线梁桥甚至会引起抗扭支座内侧支座产生空心现象,这种情况在抗扭转支座的内部支座上会产生空心现象,这种情况的发生曲线桥的支点反力与直线桥相比,有一种倾向,它的外侧会变大、内侧会变小,甚至在内侧产生负反力。
铁木辛柯梁

运动平衡 平衡 本构模型
Material Laws Strains Kinematic equations Displacements Stresses Equilibrium Forces
1.2 Kinematic equations
Remember the equations for EulerBernoulli beams……
4.1 Solving problem
The process
Formulation FEM
Implementation Discretisation
Methods on implementation Methods on discretisation
4.2 High Order functions
Displacement
= 0 when parameter reaches
infinity
Locking
3.1 Locking behaviour exhibits slow converging rate
Converging behaviour of FE solution
1.2 1 Relative displacemen 0.8 0.6 0.4 0.2 0 0 5 10 15 Number of elements Euler Bernoulli (Analytical) Timoshenko (FE approximation) 20 25 30
Material Laws
M = EIκ Q = αGAγ
1.6 Boundary conditions
Displacement / Essential / Dirichlet
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
轴向受载铁木辛柯梁的弯曲研究WANG Xuhong;LI Xiangyu【摘要】轴向受载的铁木辛柯梁的弯曲问题.在新近提出的一种铁木辛柯梁模型中,引入了一个反映变形过程中轴力方向的跃迁系数,基于此模型,解析地获得了多种边界条件下梁挠度的封闭形式的表达式.此外,采用数值计算验证当前结果的正确性,并探讨了跃迁系数对梁弯曲行为的影响.【期刊名称】《成都大学学报(自然科学版)》【年(卷),期】2019(038)002【总页数】4页(P187-189,205)【关键词】跃迁系数;铁木辛柯梁;弯曲行为【作者】WANG Xuhong;LI Xiangyu【作者单位】;【正文语种】中文【中图分类】TB123;TU3110 引言轴向受载的梁由于其能够提升抗拉和抗弯强度而被广泛应用于工程建设中.例如,在宏观尺度上,轴向受载梁经常被用在桥梁、铁路和隧道等基础设施建设和航空工业中的关键部位[1-2];而在微纳米尺度,轴向受到压力的纳米线常被埋在PDMS 基体中构成结构的一部分[3-5].因此,轴向受载的梁的变形行为是一个很重要的研究课题.例如,Simsek等[6-7]基于铁木辛柯梁理论,采用修正的偶应力理论和高阶梁理论研究了功能梯度纳米梁的弯曲问题;Ansari等[8]为了修正铁木辛柯梁理论,采用应力梯度弹性理论考察了横向剪切变形的影响;Li等[9]采用拉格朗日运动关系研究了考虑摩擦影响的棱柱铁木辛柯梁的大变形问题;Tuna等[10]基于初始积分模型,研究了欧拉—伯努利梁和铁木辛柯梁的静力弯曲行为并得到了解析解.事实上,对于铁木辛柯梁轴向力在变形时的方向有两种不同的假设:一种认为,轴力的方向沿着中性轴的方向[11-13],另一种认为,轴力的方向垂直于变形后的横截面[14-15].对此,Chen等[16]通过引入跃迁系数建立了一个统一的铁木辛柯梁模型,并研究了梁的强迫振动.但随着跃迁系数的引入,有许多典型的问题需要解决,比如新近提出的梁模型的静态响应问题.对此,本研究主要分析了跃迁系数对轴向受载铁木辛柯梁弯曲行为的影响:首先,推导出了控制方程,再通过拉普拉斯变换对其进行处理,得到了方程的解析解;其次,展开数值计算验证当前解的正确性并考察了跃迁系数对铁木辛柯梁弯曲行为的影响.1 问题描述和解决1.1 问题描述在笛卡尔坐标系Oxy中,考虑一个长为L、高为h,在轴向和横向分别受力为T 和P的梁(见图2).梁的材料参数为:杨氏模量为E,剪切模量为G,密度为ρ,横截面面积为A,惯性矩为I.图1 铁木辛柯梁模型示意图由文献[16]可得轴向受载铁木辛柯梁的控制方程为,EIφ″+(κGA+αT)(w′-φ)=0(κGA+αT)(w″-φ′)-Tw″=P(1)式中,w和φ分别表示挠度和转角,α表示轴力方向的跃迁系数.在本研究中,α在0到1之间变化,当α=0时,对应轴力的方向沿着中性轴的方向,当α=1时,对应轴力的方向垂直于变形后的横截面,压力(或拉力)被假定为正(或负).将(1)式表述为挠度的方程,可以得到,w″″+a2w″=f(x)(2)其中,(3)a1=κGA-(1-α)T,a2=κGA+αT(4)式中,κ为剪切修正系数.假定在梁上任意点x0处受到一个大小为P的集中力,则方程为,(5)式中,δ()为狄拉克函数.式(5)的解是数学上的格林函数解,对于解决很多相关的问题十分重要.例如,在梁上施加一个分布力P(x),可通过叠加原理得到相应的挠度,W(x)=P(x0)w(x;x0)dx0(6)1.2 拉普拉斯变换根据已经给出的控制方程,对式(5)关于坐标x进行拉普拉斯变换,可以得到,(7)式中,w(0)、w′(0)、w″(0)、w‴(0)是待定常数,s是拉普拉斯复数.对式(7)进行拉普拉斯逆变换可以得到,w(x;x0)=H(x-x0)Ψ1(x-x0)+w(0)Ψ2(x)+w′(0)Ψ3(x)+w″(0)Ψ4(x)+w‴(0)Ψ5(x)(8)式中,H(x)是单位阶跃函数.方程Ψi(x)的定义如下,(9)通过拉普拉斯变换可得到式(5)的通解,而式(8)中的待定常数可以通过边界条件进行确定.1.3 待定常数的确定通过边界条件可确定相应条件下显式表达式所需的待定常数.在确定这些常数之前,先得到转角φ、弯矩M和剪力V确切的表达式如下所示,(10)由式(8)可得,(11)本研究中考虑4种常见的边界条件,即简支梁、固支梁、悬臂梁、一端简支一段固支的梁.其中,对于简支梁,w(0)=0,M(0)=0,w(L)=0,m(L)=0;对于固支—简支,w(0)=0,φ(0)=0,w(L)=0,M(L)=0;对于固支梁,w(0)=0,φ(0)=0,w(L)=0,φ(L)=0;对于悬臂梁,w(0)=0,φ(0)=0,M(L)=0,V(L)=0.如此,可以通过边界条件确定相应的待定常数,将其代回(8)式中,便可以得到多种边界条件下挠度的显式表达式.2 数值分析考虑两种类型的力,即集中力和分布力,将其施加在一个特定参数的铁木辛柯梁上.材料具体参数如下,E=7.0×1010N/m2,G=2.61×1010 N/m2,L=0.5m,κ=0.87,ρ=2 778 kg/m3,横截面是高为h的正方形.为了方便计算,引入以下的无量纲参数,式中,nH和nC为无量纲化的轴向压力,η表示高跨比.简支梁和固支梁的临界屈曲力分别是,(12)2.1 解的有效性为了验证当前结果的有效性,本研究对解析解和有限元(FEM)结果进行对比,考虑以下两种情形:其一,在梁的中点处施加单位大小的集中力;其二,在梁表面施加集度为单位力的分布力.这两种情形下,梁的高跨比均为0.2,且都在轴向受到一个单位大小的力.在数值模拟计算中,采用商业有限元软件ANSYS 15.0,并用BEAM 188梁单元划分网格.在模拟中,设有1 000个单元和2 002个节点.无量纲化挠度随无量纲化坐标x/L变化的曲线如图2所示,其中是简支梁在梁中点处受到集中力P时的最大挠度,为PL3/(48EI).由图2可以看出,解析结果和有限元结果较为吻合,这在一定程度上证明了结果的有效性.2.2 跃迁系数对挠度的影响在梁的中点处施加一个单位大小的集中力,并在轴向施加不同等级的轴力,来观察梁挠度的变化.图2 高跨比为0.2,简支梁和固支梁无量纲化挠度随无量纲化坐标x/L的变化为了量化跃迁系数α对静挠度的影响,定义相对误差为,式中,和分别表示当α=0和α=1时发生在简支梁和固支梁中点处的最大挠度.为了符合工程中梁的实际情况,高跨比的取值不大于0.3.相对误差随高跨比和轴向压力的变化趋势如图3所示.图3 简支梁和固支梁相对误差随高跨比和轴向压力的变化由图3可以看出,相对误差RDdef随着高跨比和轴向压力的增大而增大.当轴力为高跨比为0.3时,α对梁挠度的影响接近50%,表明跃迁系数α对梁挠度具有重要的影响.3 结论本研究基于统一铁木辛柯梁模型分析了梁的弯曲问题,并通过拉普拉斯变换得到了多种边界条件下梁挠度和转角的解析表达式.首先,通过理论推导和数值分析验证了结果的有效性.其次,相比简支梁,跃迁系数α对固支梁的影响随着高跨比的增大而增大,当轴力为高跨比为0.3时,跃迁系数对梁挠度的影响接近50%,此证明了跃迁系数对工程实际的重要性.参考文献:【相关文献】[1]Lin T Y,Burns N H.Design of prestressed concrete structures[M].New York,NY,USA:John Wiley Sons Inc,1981.[2]Aslam M,Shafigh P,Jumaat M Z,et al.Strengthening of RC beams using prestressed fiber reinforced polymers:A review[J].Constr Build Mater,2015,82(1):235-256.[3]Ahn J H,Je J H.Stretchable electronics:Materials,architectures and integrations[J].J PhysD Appl Phys,2012,45(10):103001.[4]Xu F,Lu W,Zhu Y.Controlled 3D buckling of silicon nanowires for stretchable electronics[J].ACS Nano,2010,5(1):672-678.[5]Ryu S Y,Xiao J,Park W I,et teral buckling mechanics in silicon nanowires on elastomeric substrates[J].Nano Lett,2009,9(9):3214-3219.[6]Simsek M,Yurtcu H H.Analytical solutions for bending and buckling of functionally graded nanobeams based on the nonlocal Timoshenko beam theory[J].Compos Struct,2013,97(1):378-386.[7]Simsek M,Reddy J N.Bending and vibration of functionally graded microbeams using a new higher order beam theory and the modified couple stress theory[J].Int J Eng Sci,2013,64(1):37-53.[8]Ansari R,Gholami R,Shojaei MF,et al.Size-dependent bending,buckling and free vibration of functionally graded Timoshenko microbeams based on the most general strain gradient theory[J].Compos Struct,2013,100(1):385-397.[9]Li D K,Li X rge deflection and rotation of Timoshenko beams with frictional end supports under three-point bending[J].CR Mécan,2016,344(8):556-568.[10]Tuna M,Kirca M.Exact solution of Eringen’s nonlocal integral model for bending of Euler-Bernoulli and Timoshenko beams[J].Int J Eng Sci,2016,105(1):80-92.[11]Viola E,Ricci P,Aliabadi M H.Free vibration analysis of axially loaded cracked Timoshenko beam structures using the dynamics tiffness method[J].J Sound Vib,2007,304(1/2):124-53.[12]Mei C,Karpenko Y,Moody S,et al.Analytical approach to free and forced vibrations of axially loaded cracked Timoshenko beams[J].J Sound Vib,2006,291(3/5):1041-1060. [13] P.Forced transverse vibration of rayleigh and Timoshenko double-beam system with effect of compressive axial load[J].Int J Mech Sci,2012,60(1):59-71.[14]Saito H,Otomi K.Vibration and stability of elastically supported beams carrying an attached mass under axial and tangential loads[J].J Sound Vib,1979,62(2):257-266. [15]Kounadis A,Katsikadelis J T.Shear and ro tatory inertia effect on Beck’s column[J].J Sound Vib,1976,49(2):171-178.[16]Chen T,Su G Y,Shen Y S,et al.Unified Green’s functions of forced vibration of axially loaded Timoshenko beam:Transition parameter[J].Int J Mech Sci,2016,113(1):211-220.。
