应变梯度理论
第三章应变理论课件

Venant)1797年生于法国,
1886年逝世。1825年毕业于
巴黎桥梁公路学校,后从事
工程设计工作,1837年回该
校任教,1868年当选为法国
科学院院士。在弹性力学、
塑性力学、流体力学等方面
做出了贡献。他的力作用的
局部思想被称为“圣维南原 理”。
圣维南
(A.J.Saint-Venant)
§3-5 变形协调方程
§3-3 转动张量
如图4设过点 从物体中任意取出
一微元线段 。若令点 的坐标
为
,则点 的坐标为
变形后, 变成 的位移为
。令点 的位移为
于是
图4
, 则点
§3-3 转动张量
§3-3 转动张量
其中
若令
则
表示位移矢量 的旋度,
则分别表示物体
内微元体绕相应的坐标轴的旋转分量,而
则代
表微元体的刚性转角。
§3-3 转动张量
应变协调方程的物理意义: ➢ 物体变形后每一单元体都发生形状改变,如变形不满
足一定的关系,变形后的单元体将不能重新组合成连 续体,其间将产生缝隙或出现相互嵌入现象。 ➢ 为使变形后的物体保持连续体,应变分量必须满足一 定的关系。 注:应变协调方程是变形连续的必要和充分条件!
例题
例1. 设物体变形时产生的应变分量为
在略去二阶及更高阶的微量以后简化为 线段 的正应变是
(3)
§3-2 小应变张量(几何方程)
由于位移是微小的, 方向的位移所引起的线段 的伸缩,是更高一阶微小的,略去不计。同样线段
的正应变是 (4)
求出线段 与 之间的直角改变,也就是剪应 变 ,用位移分量来表示。
§3-2 小应变张量(几何方程)
应变梯度理论有限元c0-1分片检...

第44卷第4期2004年7月大连理工大学学报JOurnal Of Dalian University Of TechnOlOgyVOl .44,NO .4Jul =================================================================.2004文章编号:1000-8608(2004)04-0474-04收稿日期:2003-04-15;修回日期:2004-01-15.基金项目:国家自然科学基金资助项目(10172023).作者简介:陈万吉 (1941-),男,教授,博士生导师.应变梯度理论有限元:C 0-1分片检验及其变分基础陈万吉(大连理工大学工业装备结构分析国家重点实验室,辽宁大连116024)摘要:基于细观有限元弹性应变梯度理论,首次提出应变梯度有限元的C 0-1分片检验条件及其变分基础和一种构造应变梯度单元的方法.与常规的C 0分片检验和C 1分片检验不同,C 0-1分片检验要求检验函数为满足平衡方程的二次函数,并同时通过线性平面应力C 0分片检验和应变梯度常曲率的C 1分片检验.进一步提出一个平面18-D0F 三角形应变梯度单元(RCT9+RT9),算例表明该单元通过C 0-1分片检验,无伪零能模式,并有较高的精度.关键词:弹性应变梯度理论;平面18-D0F;三角形应变梯度单元;C 0-1分片检验中图分类号:0242.21文献标识码:A引言传统的弹性力学不考虑材料的微/细观结构,按均匀化假定,将材料从宏观假定开始一直延伸到微/细观乃至无限小并保持不变,这种理论被成功地用于宏观结构力学性能包括变形和应力的分析.事实上,材料的微/细观结构总是不均匀的,含有夹杂~缺欠~微裂纹或晶格存在,材料的不均匀性产生的尺度效应和与材料的破坏有关的变形局部化现象是传统的连续体力学不能解释和无法解决的问题.按连续统方法建立的细观材料偶应力/应变梯度理论,可显现材料的细观性能,反映材料的不均匀性产生的尺度效应和变形局部化现象,并可以与传统的弹性力学保持自然的衔接.偶应力/应变梯度理论不仅与材料的宏观参数有关,而且与材料新的细观参数有关.早在1909年COsserat 就建立了偶应力理论[1];后来,TOupin [2]~KOiter [3]和Mindlin [4]在本构方程中引入应变梯度,提出一种广义理论或称应变梯度理论;Aifantis [5]~Fleck 等[6]发展了塑性应变梯度理论.塑性应变梯度理论更能反映细观材料的尺度和变形局部化效应,近来,塑性应变梯度理论的研究很受重视.偶应力/应变梯度理论较传统的弹性力学更为复杂,有限元法仍然是有效的求解方法,而现有的有限元程序还不能求解这类问题.细观有限元模型可以分为偶应力型和应变梯度型,偶应力型单元的节点参数是线位移和旋转位移,应变梯度型是位移及其一阶导数,前者的节点参数少,有可能降低协调要求.细观有限元研究还有待深入,不仅是工程应用的需要,而且在对材料长度常数的识别中也要用到有限元分析,这对有限元的计算精度有很高的要求.1应变梯度理论基本方程几何方程:E zj =12(~z,j +~j,z )(1)本构方程:6zj =C zjkl (E kl -/2e2E kl )(2)式中:~z ~E zj ~6zj 分别为位移~应变~应力,2=82/8z 2+82/832+82/8z 2,C zjkl 为常规弹性常数,/e 为材料长度常数.记6(0)zj =C zjkl E kl ,m kzj =C zjmn /2e E mn,k ,m kzj,k =C zjkl /2e2E kl ,则平衡方程:(6(0)zj -m kzj,k ),j =0(3)边界力:t z=O(0)zj n j-n j m kzj,ku z=m kzj n k(4)偶应力理论是在本构方程中引入旋转变量E~zj= 12(M z,j-M j,z),即O zj=C zjkl(E kl-A2e2E~kl).2增强型C0-1分片检验对于含刚体模式而无多余零能模式的单元,由分片检验函数M=c0+c1x+c2y+c3x2+ c4xy+c5y2和U=Z0+Z1x+Z2y+Z3x2+Z4xy +Z5y2(c z~Z z为给定的常数,但是这个分片检验函数在单元内应预先满足齐次平衡方程),限定至少包含一个内点的由有限元分割的任意一小片的边界位移,由此求得的小片有限元解为检验函数的精确解,则称通过增强型C0-1分片检验.收敛的单元函数还要包含刚体模式而无伪零能模式和一定的连续性条件(下面的单体条件).对梯度应变部分,满足常梯度应变C1连续条件必然包含位移的二次项,这个检验函数求得的单元节点位移参数或小片边界位移参数,同时产生膜应力的线性应力,要求膜应力部分满足线性应力C0分片检验.C0-1分片检验与常规有限元法的C0分片检验及C1分片检验不同,C0-1分片检验是耦合型的分片检验.分别通过C0分片检验及C1分片检验的细观应变梯度有限元不一定能通过C0-1分片检验.3增强型C0-1分片检验的变分依据由单元内的分部积分公式,有V e (O(0)zj-m kzj,k),j M z dU=8V e(t z M z+u z n k M z,k)ds-V e(O(0)zj E zj+m kzj E zj,k)dU(5)式中:Mz为单元位移,可以是协调位移,也可以是不协调位移,对于不协调元需要在边界上用单元边界公共位移M~z 代替Mz;O0zj~m kzj为单元内的应力;t z~u z为对应O0zj~m kzj的单元边界力.对于基于位移法的有限元模型,为了能表达式(5)中的应变能,单元位移最低阶应当是二次,如果由此确定的单元内的应力满足平衡,即V e (O(0)zj-m kzj,k),j M z dU=0,则8V e(t z M z+u z n k M z,k)ds=V e(O(0)zj E zj+m kzj E zj,k)dU(6)由此,可以对分片检验条件C0-1给出一种力学解释:一个单元体内位移(协调/不协调)产生的应变与满足域内平衡的任意应力所做的内功等于单元边界上对应的边界力与单元边界公共位移所做的功.这是单元的内功和外功相等的条件,但单元的内位移和边界位移可以是不一致的.这也可以称为C0-1单体检验条件.显然,当式(5)中不含应变梯度项时,对应式(5)的单元位移最低阶是线性并应力自动满足平衡,得常规C0分片检验条件.418-DOF的梯度应变平面三角形单元(RCT9+RT9)建立一个通过C0-1分片检验的18-DOF梯度应变平面三角形的单元位移函数是很困难的.本文建议用2套函数分别考虑通过C0线性应力分片检验和通过C1常应力的分片检验,建立通过C0-1分片检验的18-DOF的平面梯度应变三角形单元.该单元函数将涉及3个三角形薄板单元函数(BCIZ~RT9和CT9单元),其中RT9单元函数用于计算应变梯度部分,由BCIZ和CT9组合的RCT9单元函数用于计算膜应力部分.4.19-DOF三角形薄板单元BCIZ单元函数具体公式为I0=Fg(7)其中,形函数F见文献7 .4.29-DOF三角形薄板单元RT9单元函数8具体公式为I0=I0+12(x2y2xy)(B c-B0)g(8)式中:B0=1A VeBdxdy,B是由I0求得的薄板单元的位移-应变矩阵;Bc g=R T c u~ds,R Tc=A2-Amm2Am2Am A2-m J2,u~=8I~8n8I~J8s,A~m是边界的法线方向余弦.8I~/8n按线性函数插值,8I~/8s按二次函数插值,经积分求得B c1=574第4期陈万吉:应变梯度理论有限元:C0-1分片检验及其变分基础/1m 1-/3m 31Z(/Z1y Z 1+/Z 3y 13)1Z(/Z 111Z +/Z 3131)/3m 3-/1m 11Z (m Z 1y Z 1+m Z 3y 13)1Z(m Z 111Z +m Z 3131)Z(m Z 1-m Z 3)/Z 111Z +/Z3131m Z 1y Z 1+m Z3y L J 13(9)式中:/z ~m z 是第z 边界的法线方向余弦;1zj =1z-1j ,y zj =y z -y j ,1z 和y z 是节点z 的坐标.边界位移的另一种选择是 w ~/ 1和 w ~/ 均按线性函数插值,得B %c1=1Zy Z 3 13Z 13Z y LJZ 3(1 )最后,由B c 和B %c 组合求得B c ,B c =B c +O(B c -B %c ).本文经过比较选O =-.Z 5(注意:用于求解薄板问题的原薄板单元RT9时O = .Z 5).经节点参数按w z -U z ,Uz 的转换求得用于计算应变梯度部分的RT9单元函数U 和U.4.39-DOF 三角形薄板单元CT9单元函数先假定w ^=3z=1N zwz+6j=4N jw j,其中Nz是用面积坐标L z 表示的形函数,例如,N 1=(ZL 1-1)L 1,N 4=4L 1L Z .单元边界位移按三次梁函数表示,消去边中点的位移,得单元函数w ^=Ng(11)其中N =(N 1N ZN 3),N j =(R j R 1jR yj );j =1,Z ,3(1Z )R 1= .5(m 1N 4/S 1-m 3N 6/S 3)+L 1R 11=- .1Z 5(m Z1N 4+m Z 3N 6)(13)R y1= .1Z 5(/1m 1N 4+/3m 3N 6)RCT9单元函数w 采用BCIZ 和CT9的组合,即w=w ^ +B(w -w ^ ).其中,w ~w ^分别为BCIZ 和CT9的单元函数,本文经过算例比较选择B =- .Z 5.经节点参数按w z -U z ,Uz 的转换求得RCT9单元函数U 和U.5算例5.1C 0-1分片检验计算结果表明,本文建立的18-DOF 单元(RCT9+RT9)通过C -1分片检验,无伪零能模式.能通过线性应力C 分片检验的单元还有LST,与RT9结合建立的单元可以通过C -1分片检验,但有7个伪零能模式.5.z孔边应力集中问题这是一个偶应力问题,可以用来检验尺度效应与单元精度.无限大弹性平板含半径为a 的圆孔,远处作用1方向的均匀分布力p.TUZ 4L4单元是Z 4-DOF 六节点三角形单元[9],其中,角节点参数为位移及其一阶导数,边中点为位移参数,单元内有4个内部参数,文献[9]仅对TUZ 4L4单元进行了C 分片检验(不是C -1分片检验),而且没有做特征值检验.计算结果见图1和表 1.TUZ 4L4单元计算的网格用了144 个单元,Z 983个节点.本文计算网格仅用了96个单元,117个节点,节点个数减少到原来的1/Z 5,可见本文的单元(RCT9+RT9)比TUZ 4L4单元精度高,而且也高于单元(BCIZ +RT9).孔的邻域内的应力分布也有改变,当/e /a = 1. ,u = .Z 5时,剪应力z 1y 经典弹性理论和偶应力的有限元结果见图Z.图1带圆孔方板孔边应力集中系数k 6(u = )Fig.1The st r ess c On ce n t ra ti On fa ct Or k 6On the bOundary Of the ci r c ular h Ol e (u = )表1带圆孔方板孔边应力集中系数k 6的计算结果(u = )T ab .1Num e r ic al r es ul ts Of the st r ess c On ce n t ra ti On fa ct Or k 6On the bOundary Of the ci r c ular h Ol e (u = )/e /a TUZ 4L4BCIZ +RT9RCT9+RT9EXA CT . 13. 3.197 3. 85 3. .1 Z.9 Z 3. 41Z.918Z.878 .1Z 5Z.849Z.977Z.84 Z.8Z 4 .167Z.758Z.834Z.7Z 3Z.7Z 9 .Z 5 Z.577Z.646Z.51 Z.545 .333Z.4Z Z Z.461Z.345Z.389 .5 Z.Z 1Z.Z 3Z.1Z 7Z.1691.1.91Z1.8991.8751.889674大连理工大学学报第44卷(a)经典理论的有限元结果(b)偶应力理论的有限元结果图2孔的邻域剪应力T :y (T :y S T y:)的分布(/e /a =1.0,u =0.25)Fig.2Results of the shear stress T :y (T :y S T y:)distribution in the vicinity of the hole (/e /a = 1.0,u =0.25)参考文献:[1]COSSERAT E,COSSERAT F.Theorie des CorpsDef ormables [M].Paris:Hermann et Fils,1909.[2]TOUPIN R A.Elastic materials With couple stresses[]].Arch Rational Mech Anal,1962,ll:385-414.[3]KOITER W T.Couple stresses in the theory ofelasticity,I andII[A].Proceedings of the KoninkliskeNederlandseAkademieVanW etenschappen (B )[C].[s l]:[s n],1964.17-44.[4]MIN DL IN R D .Microstructure in linear elasticity[]].Arch Rational Mech Anal,1964,l 6:51-78.[5]AIFANTIS E C.On the microstructural origin ofcertain inelastic models []].Trans A S M E J E ng Mater Tech,1984,l 06:326-330.[6]F L ECKNA,HUTCHINSON]W.Aphenomenological theory for strain gradient effects inplasticity []].J Mech Ph y s S olids,1993,4l:1825-1857.[7]B A Z E L E Y G P,CHEUN G Y K,IRONS B M,eta l .Triangular elements in bending conforming and non-conformingsolution[A].ProceedingsofConf erence Matri x Methods in S tr u ct u ral Mechanics [C].Ohio:Air Force Institute Technology,1965.547-576.[8]CHEUN GYK,CHENWan-j i.Refinednine-parameter triangular thin plate bending element by using refined direct stiffness method []].I nt J N u mer Methods E ng,1995,38(2):283-298.[9]SHU ]Y ,KIN G W E,F L ECK N A.Finiteelements for materials With strain gradient effects []].I nt J N u mer Methods E ng,1999,44(3):373-391.F inite element methods in strain gradient theor y :C 0-1patch test and its Variational basicCHENan -j i(State k ey lab .Of Str uct .An al .fOr l n d .Egu i p .,Dal i an Un i v .Of tech n Ol .,Dal i an 116024,Ch i n a )Abstract :B ased on finite element formulations for the theory in strain gradient elasticity ofmicrostructures,a convergence criterion for the C 0-1patch test and its variational basic are first introduced.The element displacement function should pass the C 1constant curvature patch test and the C 0linear stress patch test.The test displacement function for C 0-1patch test should be a complete second-order polynomial that satisfies the e g uilibrium e g uation.A neW approach to devising strain gradient finite elements that can pass the C 0-1patch test is proposed.18-D OF plane strain gradient triangular element (RCT9-RT9),Which can pass the C 0-1patch test and has no spurious Z ero energy modes,is proposed.Numerical e X amples are employed to e X amine the performances of the proposed element by carrying out the C 0-1patch test.The proposed element possesses higher accuracy compared With other strain gradient elements.Ke y W ords:theory of strain gradient elasticity ;plane 18-D OF ;triangular strain gradient element ;C 0-1patch test774第4期陈万吉:应变梯度理论有限元:C 0-1分片检验及其变分基础。
第三章 应变理论

位移梯度张量 对称张量 反对称张量
ui, j 分解
T = Tji ij
Tij = −Tji
1 1 ui , j = (ui , j +u j ,i ) + (ui , j −u j ,i ) 2 2 =D+ R 1 D = (u , j +u j ,i ) 变形张量 i 2 1 转动张量 R= (u , j −u j ,i ) i 2
o
x2
定义角应变(工程应变) 定义角应变(工程应变)
γ
γ12
同理有
∂u2 ∂u1 =α + β = + = 2ε12 ∂x1 ∂x2
γ 23
∂u3 ∂u2 = + = 2ε23 ∂x2 ∂x3
∂u1 ∂u3 γ 31 = + = 2ε31 ∂x3 ∂x 1
应变分量
∂u1 ε11 = ∂x1 ∂u2 ε22 = ∂x2 ∂u3 ε33 = ∂x3
" '
∂u β= 1 ∂x2
x1
o x3
A
α
dx1
∂u2 dx1 ∂x1
∂u2 α= ∂x 1
x1
x1 x 2
平面内的转动位移
21
即绕 x 3 轴的转动位移 ω x2
C
D''
C
''
β
ωZ
D
1 ∂u2 ∂u1 ω21 = ω3 = ( − ) 2 ∂x1 ∂x2
B
B
''
oA
x3
α
x1
同理有绕 x 1 x 2 轴的转动位移ω 32
u1, j u2 , j u3, j 称为位移梯度。 称为位移梯度 位移梯度。
abaqus2用户单元子程序

20 ABAQUS用户单元子程序(UEL)在这一章中将列举两个在这些年里发展过的ABAQUS/Standard用户单元子程序(UEL)。
第一个例子是一个非线性的索单元,我们的目的是通过这个比较简单的例子让读者了解用户单元子程序的基本开发过程;第二个例子是一个用于计算应变梯度理论的单元,应变梯度是当今比较热点的一个科研前沿问题,有各种理论,我们为了验证新的理论,需要数值结果与实验对照来进行评价,整个例子的目的是通过它说明用户子单元可以求解的问题范围很广,但是由于内容比较艰深,程序也很长,所以这个例子我们并没有给出最后的全部程序。
另外,到目前为止,ABAQUS还只有隐式求解器ABAQUS/Standard支持用户自定义单元,而显式求解器ABAQUS/Explicit中还不支持这一功能。
20.1 非线性索单元20.1.1 背景钢索斜拉桥和斜拉索结构广泛应用于土木工程建筑上。
索力的计算分析是设计和施工的关键环节。
清华大学工程力学系在采用ABAQUS进行荆沙长江斜拉桥的计算机仿真分析(这个项目我们已在第15章“ABAQUS在土木工程中的应用(一)——荆州长江大桥南汊斜拉桥结构三维仿真分析”中讨论过)时,也曾进行了自行建立索单元的尝试。
本节介绍的就是这方面的工作。
香港理工大学土木与结构工程系采用ABAQUS有限元软件进行计算,完成了香港Ting Kau斜拉桥和Tsing Ma悬索桥的结构计算和分析。
对于钢索计算,他们采用梁单元进行模拟。
由于梁单元含有弯曲刚度,计算的高阶频率值偏高,周期较低。
一般假设索是单向受拉力的构件。
随着应变的非线性增加,索力呈非线性增加。
尽管ABAQUS单元库中有500个以上的单元类型,但是,还没有索单元。
本文发展了三维非线性索单元模型,形成ABAQUS的用户单元子程序,可以利用ABAQUS输入文件调入到具体的分析中。
通过静态和动态例题的计算比较,索单元工作良好。
20.1.2 基本公式在三维索单元计算中,如图20-1所示,坐标x 和位移u 的变量表达式为:ij ji i j ji u u u x x x -=-= (x,y,z) (u,v,w) (20-1)应变的公式为:()⎥⎦⎤⎢⎣⎡+++++=222211ji ji ji ji ji ji ji ji ji w v u w z v y u x L ε (20-2)公式(20-2)中,L 为索的长度,索的张力为:0N AE N +=ε(20-3)在公式(20-3)中,A 为截面面积,E 为弹性模量,N 0为初始张力。
基于能量非局部模型的应变梯度理论的开题报告

基于能量非局部模型的应变梯度理论的开题报告一、研究背景及意义在材料力学领域,塑性应变梯度理论已经成为了一个热门的研究方向。
应变梯度理论致力于研究结构界面和表面等处的应变梯度对材料力学性能的影响,对于理解由小尺寸效应引起的材料行为的变化、探索纳米机械行为、研究薄膜和纳米器件的可靠性以及研制高性能材料等都具有一定的促进作用。
然而,传统的线性玻璃力学理论无法很好地描述小尺寸效应下的材料行为,需要特殊的力学模型来预测和分析这些行为。
能量非局部模型是一种重要的材料力学模型,它在应变梯度理论的基础上加入了能量非局部效应,可以更好地描述小尺寸效应下的材料行为,如力学性质、变形、断裂等。
因此,本文提出了一种基于能量非局部模型的应变梯度理论,探究小尺寸效应对材料力学性能的影响。
二、研究方法和预期结果本文将从以下三个方面展开研究:1. 建立基于能量非局部模型的应变梯度理论在传统应变梯度理论的基础上,引入能量非局部效应,建立一种基于能量非局部模型的应变梯度理论,分析材料在小尺寸效应下的变形和断裂行为。
具体方法为,利用能量非局部效应建立适合小尺寸结构的势函数,同时引入能量积分的概念,根据能量变化设计新的应变梯度模型,最终建立基于能量非局部模型的应变梯度理论。
2. 分析小尺寸效应对材料力学性能的影响利用所建立的基于能量非局部模型的应变梯度理论,探究小尺寸效应下材料的变形和断裂行为。
通过仿真模拟和数值计算,分析材料纳米级别下的力学性质、变形等,提高对小尺寸效应下材料力学性能的理解。
3. 验证理论的可行性针对所建立的基于能量非局部模型的应变梯度理论,设计相应的实验验证方法。
通过实验测试,比较理论计算值和实验数据的差异,验证理论的可行性,并为理论在实践中的应用提供一定的参考。
预期结果为,建立一种基于能量非局部模型的应变梯度理论,分析小尺寸效应对材料力学性能的影响。
通过实验验证,比较理论计算值和实验数据,验证理论的可行性。
研究成果将为理解材料行为的变化提供一定的理论基础,并为研制高性能材料提供指导建议。
弹性力学课件第三章应变理论

有限差分法
01
有限差分法是一种基于离散化的数值分析方法,通过将连续的时间或 空间离散化为有限个差分,建立差分方程进行求解。
02
在弹性力学中,有限差分法常用于求解波动问题和热传导问题等偏微 分方程。
03
有限差分法的优点在于简单直观,易于编程实现,特别适合处理规则 区域的问题。
应变分析在断裂力学中的应用对于评估材料的安全性和可靠性具有重要意义,特别是在 航空航天、石油化工和核能等领域的高强度材料中尤为重要。
流体力学中的应变分析
01
流体力学是研究流体运动规律和流体与固体相互作用的一门学科。 在流体力学中,应变分析是研究流体流动状态和流体机械性能的 基础。
02
应变分析在流体力学中主要关注流体在不同压力、温度和 剪切力等条件下的流动行为。通过测量流体的应变响应, 可以评估流体的流动特性和机械性能,为流体机械的设计 和优化提供依据。
应变理论在处理大变形和塑性变形时存在困难,需要 引入更复杂的模型和理论。
应变理论在处理多相材料和复合材料时,难以准确描 述材料的复杂行为。
应变理论的新发展
发展了高阶应变理论,以更准确地描述材料的复杂 变形行为。
引入了有限变形理论,对应变和应力进行更全面的 描述。
结合数值计算方法,如有限元法,对应变进行数值 模拟和分析。
弹性力学课件第三章应变理论
目
CONTENCT
录
• 应变理论概述 • 应变理论基础 • 应变分析方法 • 应变理论应用 • 应变理论发展前景
01
应变理论概述
应变定义与测量
应变定义
物体在外力作用下发生的形状和尺寸 的相对变化。
位错密度晶体塑性模型及在微成形模拟中的应用

Evers等人、 Cheong 和 Busso、Ma等人采用高阶位错密度晶体塑性模型,分别研究了晶格 错配引起的GNDs强化效应、Hall-Petch效应以及宏观非均匀塑性变形过程中梯度强化效应
据本文所知: 当前尚未报道可同时描述塑性微成形工艺一阶尺度效应和二阶尺度效应的研究成果
上海交通大学工学博士论文答辩
1
选题意义及背景
1
微成形研究现状 课题研究现状 拟解决的关键问题和技术
1
1
1
1
选题意义及背景
微成形工艺的应用
塑性微成形的优点: 大批量、低成本、 高精度、高效率、 短周期、无污染、 净成形
微型硬盘(Toshiba)
微型齿轮传动器(Sandia)
微挤压集成电路引脚(LFT)
微拉深电子枪圆杯(Philip)
● FCC晶体有12个滑移系
● 每个滑移系由滑移面的 法线 和滑移方向
组成
位错滑移引起的分切应变张量
Schmid张量
上海交通大学工学博士论文答辩
2-2
有限变形晶体塑性理论
现象学晶体塑性流动模型和硬化模型
● 塑性功等效原理
● 滑移系分切应力 ● 现象学率相关流动方程
● 现象学硬化方程
滑移系交互系数
(自硬化、潜硬化)
上海交通大学工学博士论文答辩 2-4
基于超弹性框架的准隐式积分算法
次弹性晶体塑性模型数值缺点
● 需要考虑增量客观性,晶粒相对于材料的旋转 ● 需要逐步更新晶粒取向、滑移系矢量、Schmid张量
本文准隐式积分算法的特点
● 对流动方程进行一阶Taylor展开,提高数值稳定性 ● 基于超弹性框架,在晶粒未发生旋转的中间构型进行本构计算,无需更考虑 晶粒相对于材料的旋转和增量客观性 ● 无需逐步更新晶粒取向、滑移系矢量和Schmid张量 ● 便于在主流的动力显式有限元软件中实现
第四章变形梯度与应变(徐春晖、李明瑞)
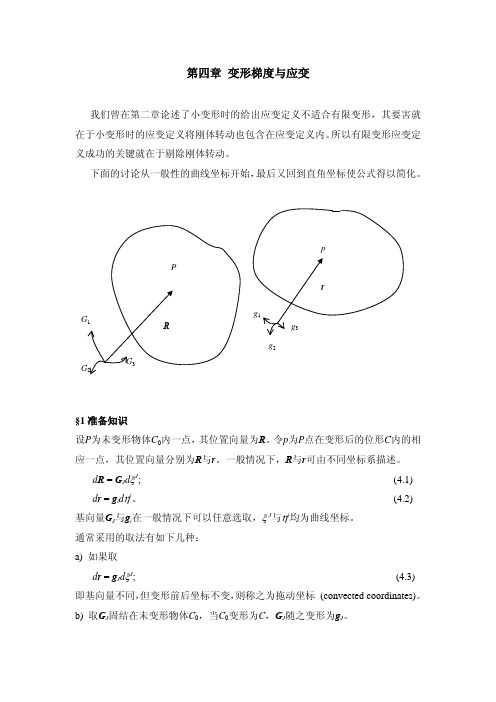
第四章 变形梯度与应变我们曾在第二章论述了小变形时的给出应变定义不适合有限变形,其要害就在于小变形时的应变定义将刚体转动也包含在应变定义内。
所以有限变形应变定义成功的关键就在于剔除刚体转动。
下面的讨论从一般性的曲线坐标开始,最后又回到直角坐标使公式得以简化。
§1准备知识设P为未变形物体C0内一点,其位置向量为R。
令p为P点在变形后的位形C内的相应一点,其位置向量分别为R与r。
一般情况下,R与r可由不同坐标系描述。
d R = G J dξJ;(4.1)d r = g i dηi。
(4.2) 基向量G J与g i在一般情况下可以任意选取,ξ J与ηi均为曲线坐标。
通常采用的取法有如下几种:a) 如果取d r = g J dξJ; (4.3) 即基向量不同,但变形前后坐标不变,则称之为拖动坐标 (convected coordinates)。
b) 取G J固结在未变形物体C0,当C0变形为C,G J随之变形为g J。
c) 取g J固结在已变形物体C,G J为相应的未变形前的,按照同一变形规律变过来的基向量。
d) G J与g i取为固定空间中的基向量,不随物体的变形而变,二者可以相同,也可不同,特别是二者均取之为同一的直角坐标系。
在变形前微线段的弧长向量平方为d R⋅d R = dξI dξJ G I⋅ G JG I⋅ G J = G IJ是基向量G I的度量张量。
变形后的弧长向量平方为d r⋅d r= dηi dηj g i⋅ g jg i⋅ g j = g ij是基向量g i的度量张量。
变形前后弧长平方的改变量为:d r⋅d r -d R⋅d R = dηi dηj g i⋅ g j- dξI dξJ G I⋅ G J。
如果将变形后的坐标看作是以变形前的坐标为自变量的函数,η = η(ξ),则有dηi dηj= ∂ηi/∂ξM∂ηj/∂ξK dξM dξK变换张量的求和指标(一般称为哑标,可以用任意字母表示),有d r⋅d r - d R⋅d R= ∂ηm/∂ξI∂ηk/∂ξJ dξI dξJ g m⋅ g k - dξI dξJ G I⋅ G J=( g mk∂ηm/∂ξI∂ηk/∂ξJ- G IJ) dξI dξJ = 2E IJ dξI dξJ (4.4) 张量E IJ为Green-Lagrange应变张量,也有称之为Green应变张量或Lagrange应变张量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应变梯度理论应变梯度理论是近解释材料在微米尺度下的尺寸效应现象而发展起来的一种新理论。
Fleek等⑹于1994年在细铜丝的扭转实验中观测到微尺度下应变梯度的硬化,其中直径12」m的无量纲扭转硬化约为直径170 ^m的三倍。
通过对1251 m、25」m和50 ^m三种厚度纯镍薄片的弯曲测试,Stolken和Evanslv[7]于1998年发现镍的无量纲弯曲硬化随着薄片厚度的减小而明显增大,然而在拉伸试验中并未发现这种微尺度现象。
Chong和Lam[8]于1999年通过压痕实验观察到热固性环氧树脂和热塑性聚碳酸酷的无量纲硬化与应变梯度有关,材料的塑性具有微尺度效应。
McFarland和Colton[9J于2005年通过对不同厚度聚丙烯悬臂微梁的弯曲测试,同样观测到无量纲弯曲刚度随梁厚减小而增大。
与宏观尺度相比,微尺度下结构的力学特性及行为研究主要考虑到以下两个方面(1) 尺度效应。
材料不是无限可分。
因此材料颗粒的固有属性将影响到微结构的力学特性。
(2) 表面和界面效应。
一些在宏观尺度下常被忽略的力和现象,在微尺度下起着重要的作用;而一些在宏观领域作用显著的力和现象,在微尺度下作用微小,甚至可以忽略。
例如,微尺度下,与特征尺寸L的高次方成比例的惯性力、电磁力(L3)等的作用相对减小,而与尺寸的低次方成比例的粘性力、弹性力(L2)、表面张力(LI)、静电力(L0)等的作用相对增大。
随着尺寸的减小,表面积(L2)与体积(L3)之比相对增大,表面力学和物理效应将起主导作用。
理论模型建立(1)偶应力理论早在一个多世纪前,voigt[12]便提出了体力偶和面力偶的概念,并建议构建考虑作用在材料微粒表面或边界上的力偶的连续模型。
随后Cosserat兄弟[14]根据的假设建立了相关的Cosserat理论,对应的运动方程中出现了偶应力。
直到20世纪60年代左右,一些学者才开始尝试Cosserat理论的改进扩展工作,他们对Cosserat连续体物质点的旋转施加一定约束,并逐渐发展了一种更为普遍的理论一偶应力理论。
相比其它非经典连续介质理论,偶应力理论是一种相对简单的理论。
如应变梯度理论考虑旋转梯度、拉伸和膨胀梯度的影响,而偶应力理论仅考虑了旋转梯度(与偶应力共轭)。
Ashby[22]指出几何必需位错和统计储存位错是材料的塑性硬化来源,而几何必需位错产生于塑性剪切应变梯度。
据此,Fleek和Hutchinson [23]及Fleek等⑹在偶应力理论框架上发展了一种应变梯度塑性理论(通常称为CS应变梯度塑性理论),它是经典的J2形变或J2流动理论的推广。
在理论中为了考虑旋转梯度的影响,引入了偶应力,并且服从二阶变形梯度本构率的Clausius-Duhem热力学限制条件[24]。
这种理论不仅在模拟裂纹扩展时能消除裂纹尖端的应力奇异性[25],还能成功预测微结构力学行为中的微尺度效应。
例如,Fleck等⑹铜丝的扭转实验中证实了应变梯度硬化的存在,并应用提出的CS应变梯度塑性理论成功解释了这种微尺度现象。
经典牛顿力学框架下,连续变形体的材料颗粒仅在力的作用下作平动;在TouPin和Min diin等学者[18-21健立的传统偶应力弹性理论中,材料颗粒不仅在力的作用下作平动,还在力偶的作用下作转动。
因此,偶应力理论中的系统能量包括应力对应变和偶应力对旋转形变做的功,其中旋转形变是二阶变形梯度的反对称部分,含有8个独立分量。
对于各向同性线弹性材料而言,系统本构方程中除了两个经典的拉梅系数外,还包含两个与材料微结构有关的附加常数。
在上述偶应力理论构建中,仅用到传统的力和力矩的平衡关系,对力偶并没有施加约束。
Yang等[28]从引入高阶平衡关系角度出发,提出一种修正偶应力理论。
在添加力偶矩平衡关系后,偶应力张量被约束成对称量,它对与之共轭张量的曲率张量的对称部分做功,并与应力对应变做的功一起转变为系统能量。
这种理论下的本构方程仅包含一个附加常数,从而大大降低了非经典常数的确定难度。
Park和Gao[29]曾使用这种新理论计算Bemoulli-Euler微梁的弯曲,发现微梁厚度与材料内察长度相当时,呈现出明显的尺度效应,所求得的无量纲弯曲刚度与弯曲实验测量值[28]吻合得较好。
(2)应变梯度理论应变梯度理论的基本思想是通过将高阶应变梯度和/ 或位错密度纳入支配材料行为的本构或演化方程,来引入尺度对结构或系统的弹、塑性变形和位错运动等力学行为的影响。
这种理论最早由Mindlin[30] 提出,他将弹性体的应变能密度视为应变和它的第一、二阶导数的函数。
同时,他也给出了一种更常用的仅包含应变和其一阶导数的简化理论,简化后的附加变形包含了二阶变形梯度的所有18 个独立分量。
比较而言,偶应力理论仅包含了二阶变形梯度中的8 个独立分量,而应变梯度理论是一个完整的二阶梯度理论。
Mindlin 为非经典连续介质力学研究提供了一种新的思路,后人针对各种应用对其理论进行了改进和扩充。
除了弹性材料外,不少学者致力建立了塑性[31-33] 、弹塑性[34]、热弹性135]等材料的应变梯度模型。
例如,通过使用等效应变的一次和二次拉普拉斯算子表示附加的应变梯度,Aifantis 等[32] 建立了应变梯度塑性理论。
Fleek等[31]和Gao等[331则发展了另一种基于几何必需位错的应变梯度塑性理论。
Aifantis 为应变梯度理论的发展和应用做出了卓越的贡献。
他和他的合作者们建立并逐步发展了模拟物体弹性、塑性和位错动力行为的各种应变梯度理论,并就相关理论的发展、应用及数学表述给出了综述[36]。
另外,黄克智等[37]也在他们的综述性文章中综合介绍了偶应力和应变梯度塑性理论。
除了用于描述位错组态、材料软化和裂纹尖端附近的变形场等问题外[36],应变梯度理论也广泛应用在微尺度效应研究中。
例如,Aifantis[38] 讨论了应变梯度弹性、塑性理论在解释不常见微结构的标准尺寸试件或普通微结构的小尺寸试件的扭转和弯曲中的微尺度现象上的能力。
在Mindlin[30]建立的传统应变梯度弹性理论中,附加变形即引入的二阶变形梯度,它包括了8个独立分量的反对称部分和10个独立分量的对称部分在内的所有18 个独立分量。
对于各向同性材料而言,二阶变形梯度对应有七个线性弹性常数,即两个拉梅系数和五个与材料微结构有关的非经典常数。
应用虚功原理得到的控制方程和边界条件也包含五个附加常数,从而能捕捉到微结构中的尺度效应。
后来,Fleck 和Hutchinson[31 ,39]重新表述了Mindlin 的应变梯度理论,他们将二阶变形梯度张量分解成两个独立部分,即拉伸梯度张量和旋转梯度张量。
与Min diin的工作类似,Fleck和Hutchi nson 仅使用了传统平衡关系—力和力矩平衡来支配高阶应力行为。
受Yang 等[28]的工作启发,Lam 等[40]尝试将新的高阶平衡关系应用在本构关系及控制方程的推导中。
在施加附加的力偶矩平衡关系后,Lam 等重新定义了高阶应变张量及与之共扼的高阶应力张量,并推导了相应的本构关系和应变能表述。
由于高阶平衡关系的引入,旋转梯度的反对称部分不出现在变形能中,与微结构有关的附加材料常数的个数由五个减少到三个。
基于所提出的新理论,Lam 等[40]研究了微悬臂梁的弯曲问题,发现微梁的无量纲刚度与梁厚呈二次方反比关系,这与微梁的弯曲实验观测结果相吻合。
(3) 微态理论微态理论是由连续介质力学大师Erin gen建立。
在1964年,Erin ge n[41]、Eri ngen和Suhubi[42]分别提出了简单微流体和简单微弹性体理论,他们的模型中分别考虑了微流体的局部微运动和微固体的微变形和微旋转,并推导了对应的基本场方程、边界条件和本构方程。
到1966年,Eringen[43]综合阐述了这类理论,并将之正式命名为微态连续统力学。
这种理论把材料体看作无数变形物质点的连续集合,每个物质点都具有有限的尺寸和内部结构。
除了经典的三个平动自由度外,每个材料物质点还具有独立的拉伸和旋转自由度,即允许物质点作刚体运动和发生变形。
因此,微态连续体的变形会同时产生宏观应变和微观内部应变。
后来的学者发展和拓宽了该理论,建立了弹粘塑性材料[44]、考虑热存储效应[45]、热磁祸合弹性体[46] 等一系列理论模型。
Chen和Lee[47]建立了基于微态理论的所有瞬时力学变量和原子坐标及速度的联系,并通过统计系综平均后得到连续场量,从而将微态理论和分子动力学结合起来。
微态理论已经应用于微尺度结构与材料的模拟中。
例如,Dinard[48]使用基于微态理论的各向异性可压缩塑性模型,探讨了含孔洞泡沫镍板的尺度效应,成功预测了孔洞周围的应变集中随孔洞尺寸减小而减弱的变化趋势。
微极理论微极理论实质是微态理论的一种特例。
微极理论中,每个材料物质点除了经典的三个平动自由度外,仅添加了独立的旋转自由度,即意味着物质点可以作刚体运动,但不允许变形。
Eringen[491于1965年首次提出微极连续统理论,并在同年[50]和1967年[51]分别构建了基于微极理论的流体和弹性体模型。
相一比经典力学理论,由于附加独立自由度的引入,微极材料会有旋转惯性矩、体力偶和表面力偶的作用产生。
微极理论的后续研究重心在于该理论的扩展和推广。
Erin gen、de Borst、Tauchert等学者在该领域作了大量的工作,提出了用于粘弹性[52]、塑性[53]、热弹性[54]等材料的微极理论。
微极理论同样可以描述微结构中的尺度效应。
例如,McFarland和CoIton[9]使用微极弹性连续理论探讨了微结构对悬臂微梁的弯曲刚度的影响,计算结果预测到梁的弯曲刚度随梁厚减小而增大,这与文中实验所观测到的微尺度现象是吻合的。
上述理论对每个物质点均引入了附加自由度或高阶变形,与之不同的另一种理论则考虑了表面效应的影响。
由于微尺度结构具有急剧增大的表面/体积比,表面效应的重要性显著提高。
为了引入表面效应,Gurtin和Murdoch[55]提出了一种表面弹性理论,将表面看作和体不同性质、无滑移地勃附在体上的二维弹性膜,表面应力的出现导致了非经典的边界条件,它和表面经典的弹性方程共同组成场方程。
对于特征尺寸大于100nm的结构,表面/体积比可以忽略,因此表面弹性理论目前仅运用在纳米结构中。
Wang和Feng [56-58]基于Bemoulli-Euler梁和Timoshenko梁理论,建立了一种考虑表面效应的理论模型,有力预测了纳米梁在振动和屈曲行为中的微尺度效应。
实验研究方法微尺度材料的力学性能测试主要包括弹性模量、泊松比、残余应力屈服强度、疲劳强度和断裂强度等参数,常用的测量方法有拉伸测试法、弯曲测试法、纳米压入法、鼓膜法和共振频率测试法等[59]拉伸试验法(I)拉伸测试法拉伸测试是测量弹性模量、泊松比、屈服强度和断裂强度等参数的最直接的方法。
