湖南大学机械振动习题课
湖南大学研究生机械振动_习题第一章
某一数值附近反复变化。
一、振动工程的重要性
• 1. 大型回转机械动态失稳造成事故 • 2. 桥梁由于共振、风激振动倒塌 • 3. 产品包装 • 4. 汽车舒适性，航天工程 • 5. 机床加工质量 • 6. 夯士、振动检测
国家重点工程:长江三峡水利 枢纽工程,135米蓄水前中孔 闸门振动试验现场(2003年4 月应用锤击模态法)
st
m
d2x dt 2
P
k ( st
x)
mg k st
O x
F
m
d2x dt 2
kx
x
P
表明，物体偏离平衡位置于坐标x处，受到与偏离距离成正 比而与偏离方向相反的合力，称此力为恢复力。
在恢复力作用下维持的振动称为无阻尼自由振动。
重力加在振动系统上只改变其平衡位置，只要将坐标原点取 在平衡位置，可得到如上形式的运动微分方程。
无阻尼自由振动是简谐振动，是一种周期振动，任何瞬时t，其 运动规律x（t）总可以写为: x（t）= x（t+T）
T为常数，称为周期，单位符号为s。 这种振动经过时间T后又重复原来的运动。
考虑无阻尼自由振动微分方程
d2x dt 2
2 n
x
0
解为：
x Asin(nt )
角度周期为2π，则有:
[n (t T ) ] (nt ) 2
武汉大桥局桥科院、北方交通大学进行 的“秦-沈线中华之星高速列车通过桥梁 振动及结构应变试验” 。 中华之星高速 列车设计时速260Km/h，实际测试时速 321.5 Km / h 。大桥为 28 孔双线后张 法 预应力混凝土简支箱梁桥 ， 梁顶宽 12.4m，梁高2.2m，梁跨长24.6m。
机械振动基础课后习题解答_第3章习题
m
0
0 m
u1 u2
3k k
k 3k
u1 u2
2ku0
sin 0
t
K
2M
3k
2m
k
k
3k 2m
H11 ( )
3k 2m ()
H 21 ( )
k ()
u1(t) u2 (t)
H11 ( ) H21()
2ku0
sin
t
3k 为反共振频率 m
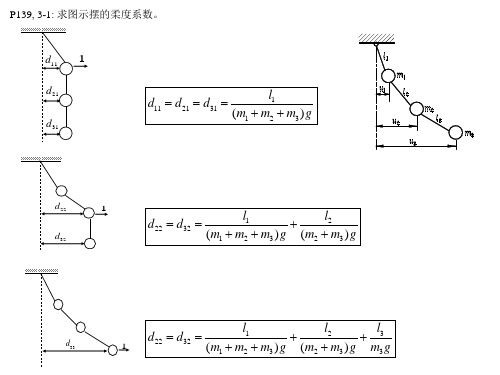
P140,3-9: 图示系统初始静止，求左端基础产生阶跃位移u0后系统的响应。
ml2 1 0 M 3 0 7 /16
K
l2k 16
9 9
9
13
| K 2M | 0
1 0.65
k m
2 2.62
k m
P139,3-3: 建立图示系统的运动微分方程，并求当ki k,i 1, 6, m1 m, m2 2m, m3 m时的固有 频率和固有振型。
m1
M
m2
u2
c
3c
2c
u2
k
3k
2k
u2
0
m u3 0 2c 2c u3 0 2k 2k u3 f0
1 0,2
k m
, 3
2k m
1 1 1
φ1
1 , φ2
0
, φ3
1
1
1/ 2
1
u1 1
u2
1
u3 1
1 0 1/ 2
1 q1
1
q2
1 q3
)d
u0 2
(1 cos1t)
q2
(t)
u0 2
(1
cos 2t )
机械振动_机械波课后习题
机械振动_机械波课后习题(2) 弹簧振子在光滑水平面上作简谐振动时，弹性力在半个周期内所作的功为(B)k A 72 (3) 谐振动过程中，动能和势能相等的位置的位移等于(A) _A4 (D)5.2填空题(1) 一质点在X 轴上作简谐振动，振幅 A= 4cm,周期T= 2s,其平衡位置取作坐标原点。
若t = 0时质点第一次通过x = — 2cm 处且向X 轴负方向运动，则质点第二次通过 x = — 2cm 处的时刻为 ____ s 。
(2) 一水平弹簧简谐振子的振动曲线如题 5.2(2)图所示。
振子在位移为零，速度为一：A 、加速度为零和弹性力为零的状态，对应于曲线上的____________ 点。
振子处在位移的绝对值为 A 、速度为零、加速度为-？2A 和弹性力为一KA 的状态，则对应曲线上的点。
题5.2(2) 图⑶一质点沿x 轴作简谐振动，振动范围的中心点为x 轴的原点，已知周 5.1选择题 (1) 一物体作简谐振动, 时刻的动能与t 二T/8 (A)1 : 4 (B) 1: 习题5 ?机械振动振动方程为-Acos( t -),则该物体在"0 (T 为振动周期)时刻的动能之比为:2 (C) 1: 1 (D) 2 : 1 (A)kA 2 (C) kA 7/4(D)0(B)期为T,振幅为A(a)若t=0时质点过x=0处且朝x轴正方向运动，则振动方程为X= ____________________ 0(b)若t=0时质点过x=A/2处且朝x轴负方向运动，则振动方程为X= __________________ 05.3 符合什么规律的运动才是谐振动？分别分析下列运动是不是谐振动：(1)拍皮球时球的运动；(2)如题5.3图所示，一小球在一个半径很大的光滑凹球面内滚动(设小球所经过的弧线很短).题5.3图题5.3图(b)5.4弹簧振子的振幅增大到原振幅的两倍时，其振动周期、振动能量、最大速度和最大加速度等物理量将如何变化？5.5单摆的周期受哪些因素影响？把某一单摆由赤道拿到北极去，它的周期是否变化？5.6简谐振动的速度和加速度在什么情况下是同号的？在什么情况下是异号的？加速度为正值时，振动质点的速率是否一定在增大？5.7质量为10 10°kg的小球与轻弹簧组成的系统，按x =0.1cos(8t三)(SI)的3规律作谐振动，求：(1)振动的周期、振幅和初位相及速度与加速度的最大值；(2)最大的回复力、振动能量、平均动能和平均势能，在哪些位置上动能与势能相⑶t2 =5s与t1 =1s两个时刻的位相差;5.8—个沿x轴作简谐振动的弹簧振子，振幅为A，周期为T ,其振动方程用余弦函数表示.如果t=0时质点的状态分别是：(1)xo = -A ；(2)过平衡位置向正向运动；(3)过处向负向运动；2(4)过x二- A处向正向运动.J2试求出相应的初位相，并写出振动方程.5.9一质量为10 10"kg的物体作谐振动，振幅为24cm，周期为4.0s，当t = 0时位移为24cm .求:(1)t =0.5s时，物体所在的位置及此时所受力的大小和方向；(2)由起始位置运动到x =12cm处所需的最短时间；⑶在x =12cm处物体的总能量.5.10有一轻弹簧，下面悬挂质量为1.0g的物体时，伸长为4.9cm .用这个弹簧和一个质量为8.0g的小球构成弹簧振子，将小球由平衡位置向下拉幵1.0cm后，给予向上的初速度V0 =5.0cm/s，求振动周期和振动表达式.5.11题5.11图为两个谐振动的x-t曲线，试分别写出其谐振动方程.题5.11图5.12一轻弹簧的倔强系数为k，其下端悬有一质量为M的盘子.现有一质量为m 的物体从离盘底h高度处自由下落到盘中并和盘子粘在一起，于是盘子幵始振动.(1)此时的振动周期与空盘子作振动时的周期有何不同？(2)此时的振动振幅多大？⑶ 取平衡位置为原点，位移以向下为正，并以弹簧幵始振动时作为计时起点，求初位相并写出物体与盘子的振动方程.5.13 有一单摆，摆长I =1.0m ，摆球质量m=10 10 Jkg ，当摆球处在平衡位置时，若给小球一水平向右的冲量 F ：t 二1.0 10-kg m/ s ，取打击时刻为计时起点(t =0)，求振动的初位相和角振幅，并写出小球的振动方程.5.14 有两个同方向、同频率的简谐振动，其合成振动的振幅为0.20m ，位相与第一振动的位相差为一，已知第一振动的振幅为0.173m ，求第二个振动的振幅以及第6一、第二两振动的位相差.题5.14图5.15 试用最简单的方法求出下列两组谐振动合成后所得合振动的振幅:5.16 一质点同时参与两个在同一直线上的简谐振动，振动方程为试分别用旋转矢量法和振动合成法求合振动的振动幅和初相，并写出谐振方程。
机械振动习题集
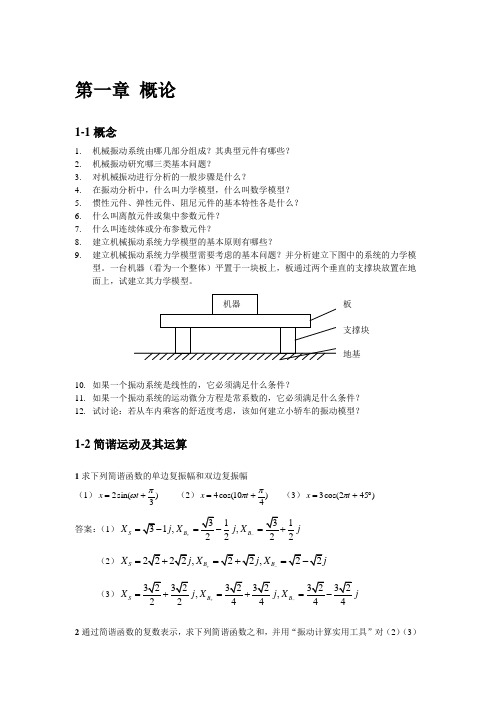
第一章 概论1-1概念1. 机械振动系统由哪几部分组成？其典型元件有哪些？2. 机械振动研究哪三类基本问题？3. 对机械振动进行分析的一般步骤是什么？4. 在振动分析中，什么叫力学模型，什么叫数学模型？5. 惯性元件、弹性元件、阻尼元件的基本特性各是什么？6. 什么叫离散元件或集中参数元件？7. 什么叫连续体或分布参数元件？8. 建立机械振动系统力学模型的基本原则有哪些？9.建立机械振动系统力学模型需要考虑的基本问题？并分析建立下图中的系统的力学模型。
一台机器（看为一个整体）平置于一块板上，板通过两个垂直的支撑块放置在地面上，试建立其力学模型。
10. 如果一个振动系统是线性的，它必须满足什么条件？11. 如果一个振动系统的运动微分方程是常系数的，它必须满足什么条件？ 12. 试讨论：若从车内乘客的舒适度考虑，该如何建立小轿车的振动模型？1-2简谐运动及其运算1求下列简谐函数的单边复振幅和双边复振幅 （1）)3sin(2πω+=t x （2）)410cos(4ππ+=t x （3）)452cos(3︒+=t x π答案：（1）111,,2222S B B X j X j X j +-==-=+ （2）,,S B B X X X +-== （3）,,224444S B B X j X j X j +-=+=+=-2通过简谐函数的复数表示，求下列简谐函数之和，并用“振动计算实用工具”对（2）（3）进行校核（1）)3sin(21πω+=t x )32s i n (32πω+=t x （2）t x π10sin 51=)410cos(42ππ+=t x（3）)302sin(41︒+=t x π )602sin(52︒+=t x π)452cos(33︒+=t x π)382cos(74︒+=t x π )722cos(25︒+=t x π答案：（1）)6.6cos(359.412︒+=t x ω （2）)52.4710cos(566.312︒-=t x π （3）)22.92cos(776.1412345︒+=t x π3试计算题1中)(t x 的一阶导数和二阶导数对应的复振幅，并给出它们的时间历程4设)(t x 、)(t f 为同频简谐函数，并且满足)(t f cx x b x a =++ 。
机械振动学习题解答(二)
于是
k 800 103 r 2 2.504rad/s 3 m 2500 10 / 9.8
2.504 60 =23.9r/min 故最大转速为 2 FT ②力传递率 20% r 2.57 F 4.55 60 k =43.5r/min 4.551rad/s 转速 于是 r 2 m
解：系统的微分方程为 mx k0ei 2 x F0eit
设系统的稳态响应 x Xeit ，代入上式得
m 2 X k0ei 2 X F0
k0 cos 2 m 2 ik0 sin 2 X F0
解得 其中
X
X X ei
而活塞的运动为
4－2 如图所示，质量可忽略的直角刚性杆可绕铰链O自由转 动，弹簧一端有简谐位移扰动 A cos ωt 。试导出系统的振动 微分方程，并求系统的稳态响应。
A cos ωt m mg L
xB 解：设刚性杆向顺时针方向转动θ角， B 则图中B点的位移和速度分别为 xB a sin a , xB a cos a
X
F02 4 N /
2
k m
2 2
要使运动能继续，X不能为虚数，所以
F02 4 N / 0
2
N
F0
4
4－5 带结构阻尼的单自由度系统，若刚度和阻尼的作用可用 i 2 复数形式 k k0e 表示，系统的等效质量为 m，求系统在简谐 激励下的响应。
2 v k L W v L k 2 W
4－8 图示系统中，集中质量 m = 20 kg，弹簧刚度 k = 3.5 kN/m，阻尼器的黏性阻尼系数为c = 0.2 kN· s/m，凸轮的转速 为60r/min，行程为0.01m。试求系统的稳态响应。
机械振动_机械波课后习题
习题5 •机械振动5.1选择题(1) 一物体作简谐振动，振动方程为x=Acos(，t )，则该物体在t=0时刻2的动能与t二T/8(T为振动周期)时刻的动能之比为：(A) 1: 4 ( B) 1：2 (C) 1：1 (D) 2：1(2) 弹簧振子在光滑水平面上作简谐振动时，弹性力在半个周期内所作的功为(A)kA2(B) kA2/2(C) kA2//4(D)0(3)谐振动过程中，动能和势能相等的位置的位移等于(A)，4(C) 一3A2(B)冷(D) - 2A5.2填空题(1) 一质点在X轴上作简谐振动，振幅A = 4cm,周期T = 2s,其平衡位置取作坐标原点。
若t= 0时质点第一次通过x = —2cm处且向X轴负方向运动，则质点第二次通过x= —2cm处的时刻为___ So(2) —水平弹簧简谐振子的振动曲线如题 5.2(2图所示。
振子在位移为零，速度为—呱、加速度为零和弹性力为零的状态，对应于曲线上的______________ 点。
振子处在位移的绝对值为A、速度为零、加速度为--2A和弹性力为-KA的状态，则对应曲线上的_____________ 点。
题5.2(2)图(3) —质点沿x轴作简谐振动，振动范围的中心点为x轴的原点，已知周期为T，振幅为A。
(a) 若t=0时质点过x=0处且朝x轴正方向运动，则振动方程为x= __________________ 。
(b) 若t=0时质点过x=A/2处且朝x轴负方向运动，则振动方程为x= ________________ 。
5.3符合什么规律的运动才是谐振动？分别分析下列运动是不是谐振动：⑴拍皮球时球的运动；(2)如题5.3图所示，一小球在一个半径很大的光滑凹球面内滚动(设小球所经过的弧线很短).题5.3图题5.3图(b)5.4弹簧振子的振幅增大到原振幅的两倍时，其振动周期、振动能量、最大速度和最大加速度等物理量将如何变化？5.5单摆的周期受哪些因素影响？把某一单摆由赤道拿到北极去，它的周期是否变化？5.6简谐振动的速度和加速度在什么情况下是同号的？在什么情况下是异号的？加速度为正值时，振动质点的速率是否一定在增大？5.7质量为10 10：kg的小球与轻弹簧组成的系统，按x = 0.1cos(8t，空)(SI)的规律3作谐振动，求：(1) 振动的周期、振幅和初位相及速度与加速度的最大值；(2) 最大的回复力、振动能量、平均动能和平均势能，在哪些位置上动能与势能相等？⑶t2 =5S与t1 =1s两个时刻的位相差；5.8 一个沿x轴作简谐振动的弹簧振子，振幅为A，周期为T，其振动方程用余弦函数表示•如果t =0时质点的状态分别是:(1) x o = -A ；(2) 过平衡位置向正向运动；A(3) 过x二一处向负向运动；2A(4) 过x A处向正向运动.V2试求出相应的初位相，并写出振动方程.5.9 —质量为10 10^kg的物体作谐振动，振幅为24cm，周期为4.0s，当t =0时位移为24cm .求：(1) t =0.5s时，物体所在的位置及此时所受力的大小和方向；(2) 由起始位置运动到x = 12cm处所需的最短时间；(3) 在x =12cm处物体的总能量.5.10有一轻弹簧，下面悬挂质量为1.0g的物体时，伸长为4.9cm .用这个弹簧和一个质量为8.0g的小球构成弹簧振子，将小球由平衡位置向下拉开 1.0cm后，给予向上的初速度V。
湖南大学机械振动习题课
2 n 1 tan 2 1 n
等效激励：旋转部件偏心质量引起的振动
M
me m t u x
M
2
sin t u x
e
2
k c
a
2
k
k
c
b
The rotating unbalance system can be equated to a SDOF system as shown above. 由动量定理（theorem of momentum）
Therefore, solve to get: B = 0 and A = 0.0353. Hence, x 0.0353e
n t
sin d t
For maximum displacement: velocity x
0
dx x 0.0353e nt (n sin d t d cos d t ) 0 dt n sin d t d cos d t 0
振幅： A u (
n
0 u
)
2
n
v0
v0
m k
最大张力： T mg kA mg v0 mk 1000 9.8 0.5 1000 4 105 1.98 104 (N)
此题基本理论：单自由度自由振动 Free vibration of SDOF
( 2 1)n t ( 2 1)n t
k c 0 2m m
2
2
Over-damped ( 1 )
x(t ) a1e
Critically Damped ( 1 )
a2e
机械振动一章习题解答
T = 2π
所以应当选择答案(C)。
m ( k1 + k 2 ) m = 2π k k1 k 2
习题 12—4
一质点作简谐振动，周期为 T，当它由平衡位置向 X 轴正方向运动 ］
时，从二分之一最大位移处到最大位移处这段路程所需要的时间为： ［ (A) T/4。 (B) T/12。 (C) T/6。 (D) T/8。
解： 单摆的振动满足角谐振动方程， 这里所给的 θ 是初始角位移，显然是从最大角位移处计时。由 旋转矢量法容易判断该单摆振动的初位相为 “0” ， 因此，应当选择答案(C) 。 −θm
题解 12―1 图
习题 12—2
轻弹簧上端固定，下端系一质量为 m1 的物体，稳定后在 m1 下边又
系一质量为 m2 的物体，于是弹簧又伸长了 ∆x ，若将 m2 移去，并令其振动，则 振动周期为： ［ (A) T = 2π ］
位相 ϕ = π 2 ，故振动方程为
x = 0.02 cos(1.5t +
π ) 2
(SI)
习题 12─17
两个同方向的简谐振动的振动方程分别为
1 ， x 2 = 3 × 10 − 2 cos 2π (t + ) 4
1 x1 = 4 × 10 − 2 cos 2π (t + ) 8
(SI)
求：合振动方程。 解：设合振动方程为
X
习题 12─12
一质点作简谐振动，振动图
线如图所示，根据此图，它的周期
4 O –2
2
t (s)
T=
ϕ=
，用余玄函数描述时的初位相
习题 12―12 图
。 解：根据振动图线可画出旋转矢量图，可得
t=2
∴ ∴
机械振动习题和答案解析
《机械振动噪声学》习题集1－1 阐明下列概念，必要时可用插图。
(a) 振动；(b) 周期振动和周期；(c) 简谐振动。
振幅、频率和相位角。
1－2 一简谐运动，振幅为0.20 cm，周期为0.15 s，求最大的速度和加速度。
1－3 一加速度计指示结构谐振在82 Hz 时具有最大加速度50 g，求其振动的振幅。
1－4 一简谐振动频率为10 Hz，最大速度为4.57 m/s，求其振幅、周期和最大加速度。
1－5 证明两个同频率但不同相位角的简谐运动的合成仍是同频率的简谐运动。
即：A cos ωn t +B cos (ωn t + φ) =C cos (ωn t + φ' )，并讨论φ＝0、π/2 和π三种特例。
1－6 一台面以一定频率作垂直正弦运动，如要求台面上的物体保持与台面接触，则台面的最大振幅可有多大？1－7 计算两简谐运动x1 = X1 cos ω t和x2 = X2 cos (ω + ε ) t之和。
其中ε << ω。
如发生拍的现象，求其振幅和拍频。
1－8 将下列复数写成指数A e i θ形式：(a) 1 + i3(b) -2 (c) 3 / (3- i ) (d) 5 i (e) 3 / (3- i )2(f) (3+ i ) (3 + 4 i ) (g) (3- i ) (3 - 4 i ) (h) [ ( 2 i ) 2 + 3 i + 8]2－1 钢结构桌子的周期τ＝0.4 s，今在桌子上放W = 30 N 的重物，如图2－1所示。
已知周期的变化∆τ＝0.1 s。
求：( a ) 放重物后桌子的周期；( b )桌子的质量和刚度。
2－2 如图2－2所示，长度为L、质量为m 的均质刚性杆由两根刚度为k 的弹簧系住，求杆绕O点微幅振动的微分方程。
2－3 如图2－3所示，质量为m、半径为r的圆柱体，可沿水平面作纯滚动，它的圆心O用刚度为k的弹簧相连，求系统的振动微分方程。
图2－1 图2－2 图2－32－4 如图2－4所示，质量为m、半径为R的圆柱体，可沿水平面作纯滚动，与圆心O 距离为a 处用两根刚度为k的弹簧相连，求系统作微振动的微分方程。
机械振动基础经典习题
(ω ) = k 3kω m + ω m
2 2 4
2
解法2: 解法 :
m 0 u1 2k 运动方程: 0 m u + k 2
m 0 2k 0 m u + k
k u1 f1 sin ωt = k u2 f 2 cos ωt
用 复数 激振力 的实部 表示真 实的激 振力
k i f1 jωt e u = k f2
-1
u = ue jωt
2k u(t ) = k
真实
k 0 i f1 iωt 2 m e ω 0 m k f2
-1 k m 0 i f1 iωt ω2 e k 0 m f2
T T T
2m 0 q1 2k 0 2m q + 0 2
0 q1 f 0δ (t ) q = f δ (t ) 6k 2 0
f0 f0 q1 (t ) = sin ω1t, q2 (t ) = sin ω2t 2mω1 2mω2
f0 f0 u1 (t ) = sin ω1t sin ω2t 2mω1 2mω2
P90,2-19: 求图示系统在零初始条件下的脉冲响应.
m 0
0 u1 2k u + k m 2
k u1 0 u = f δ (t ) 2k 2 0
1 1 k 3k φ1 = , φ2 = ω1 = , ω2 = m Re k
f1 sin ωt (ω) = k2 3kω2m+ω4m2 k 1 k ω 2m * u (t ) = 2 (ω ) k 2k ω m f 2 cos ωt
P89,2-10: 建立图示双单摆的微振动微分方程,并求固有频率和固有振型.
P89,2-18: 若要使图示系统中左边质量块的稳态振幅取最小值,激振力的频率应为多少? 并求出 此时右 边质量块 的稳态 响应.
机械振动 课后习题和答案 第三章 习题和答案
3.1 如图所示扭转系统。
设12122;t t I I k k ==1．写出系统的刚度矩阵和质量矩阵；2．写出系统的频率方程并求出固有频率和振型，画出振型图。
解：1)以静平衡位置为原点，设12,I I 的转角12,θθ为广义坐标，画出12,I I 隔离体，根据牛顿第二定律得到运动微分方程：111121222221()0()0t t t I k k I k θθθθθθθ⎧++-=⎪⎨+-=⎪⎩ ，即：1112122222122()00t t t t t I k k k I k k θθθθθθ⎧++-=⎪⎨-+=⎪⎩所以：[][]12212220,0t t t t t k k k I M K k k I +-⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦系统运动微分方程可写为：[][]11220M K θθθθ⎧⎫⎧⎫⎪⎪+=⎨⎬⎨⎬⎪⎪⎩⎭⎩⎭………… (a)或者采用能量法：系统的动能和势能分别为θθ=+2211221122T E I I θθθθθθθ=+-=++-222211212121221121111()()2222t t t t t t U k k k k k k求偏导也可以得到[][],M K由于12122;t t I I k k ==，所以[][]212021,0111t M I K k -⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦2)设系统固有振动的解为： 1122cos u t u θωθ⎧⎫⎧⎫=⎨⎬⎨⎬⎩⎭⎩⎭，代入（a ）可得：[][]122()0u K M u ω⎧⎫-=⎨⎬⎩⎭………… (b)得到频率方程：22121211222()0t t t t k I k k k I ωωω--==--即：224222121()240t t I k I k ωωω=-+=解得：21,222ω==所以：1ω=2ω= ………… (c)将（c ）代入（b ）可得：112121211122(22220(22t t t t t t k k I k I u u k k k I I ⎡⎤±--⎢⎥⎧⎫⎢⎥=⎨⎬⎢⎥⎩⎭⎢⎥--⎢⎥⎣⎦解得：11212u u =-；12222u u =令21u ，得到系统的振型为：-0.70710.70713.2 求图所示系统的固有频率和振型。
(完整版)大学机械振动课后习题和答案(1~4章总汇)
1.1 试举出振动设计、系统识别和环境预测的实例。
1.2 如果把双轴汽车的质量分别离散到前、后轴上去，在考虑悬架质量和非悬架质量两个离散质量的情况下，画出前轴或后轴垂直振动的振动模型简图，并指出在这种化简情况下，汽车振动有几个自由度?1.3 设有两个刚度分别为1k ，2k 的线性弹簧如图T —1.3所示，试证明：1)它们并联时的总刚度eq k 为：21k k k eq +=2)它们串联时的总刚度eq k 满足：21111k k k eq +=解：1)对系统施加力P ，则两个弹簧的变形相同为x ，但受力不同，分别为：1122P k xP k x=⎧⎨=⎩由力的平衡有：1212()P P P k k x =+=+故等效刚度为：12eq Pk k k x ==+2)对系统施加力P ，则两个弹簧的变形为： 1122Px k Px k ⎧=⎪⎪⎨⎪=⎪⎩，弹簧的总变形为：121211()x x x P k k =+=+故等效刚度为：122112111eq k k P k x k k k k ===++1.4 求图所示扭转系统的总刚度。
两个串联的轴的扭转刚度分别为1t k ，2t k 。
解：对系统施加扭矩T ，则两轴的转角为： 1122t t Tk T k θθ⎧=⎪⎪⎨⎪=⎪⎩系统的总转角为：121211()t t T k k θθθ=+=+，12111()eq t t k T k k θ==+故等效刚度为：12111eq t t k k k =+1.5 两只减振器的粘性阻尼系数分别为1c ，2c ，试计算总粘性阻尼系数eq c1)在两只减振器并联时，2)在两只减振器串联时。
解：1)对系统施加力P ，则两个减振器的速度同为x &，受力分别为：1122P c x P c x =⎧⎨=⎩&& 由力的平衡有：1212()P P P c c x =+=+&故等效刚度为：12eq P c c c x ==+& 2)对系统施加力P ，则两个减振器的速度为： 1122P x c P x c ⎧=⎪⎪⎨⎪=⎪⎩&&，系统的总速度为：121211()x x x P c c =+=+&&& 故等效刚度为：1211eq P c x c c ==+&1.6 一简谐运动，振幅为0.5cm，周期为0.15s，求最大速度和加速度。
机械振动基础课后习题解答_第2章习题
0.5
1
1
1
1 1/ 3
u1 (t ) u2 (t)
8 4
/ /
9 9
cos(
k 2m
)t
1/9 1/ 9
cos(
2k )t m
(3) 求结构的稳态响应
m1u1(t) k1(u1(t) u2 (t)) m2u2 (t) k1(u1(t) u2 (t)) k2 (u2 (t) v(t))
0 0
(K 2M)φ 0
1
1
2 2
k J
,
2
1
2k 2 J
1 1
φ1
1/
2
,
φ2
1/
2
P88,2-6: 不计刚杆质量，按图示坐标建立运动微分方程，并求出固有频率和固有振型。
系统动能：T
1 2
mu12
1 2
2mu22
系统势能：U
1 2
k (2u1
u2 )2
1 2
k (2u2
P87,2-1: 图示用于风洞试验的翼型剖面由拉伸弹簧k1和扭转弹簧k2支承着，剖面重心G到支承点 的距离为e, 剖面绕重心的转动惯量为J0,试建立系统运动微分方程。
动能：T
1 2
m(h e )2
1 2
J0 2
势能：U
1 2
k1h2
1 2
k2 2
m me
J0
me me2
h
k1
0
(e 0)
)
Re
2k k
k k
2
m
0
0 m
－1
i
f1
f2
eit
u* (t )
1
大学物理第五章机械振动习题解答和分析
5-1有一弹簧振子，振幅 A 2.0 10 2m ，周期T 1.0s ，初相 3 / 4.试写出它的振 动位移、速度和加速度方程。
分析根据振动的标准形式得出振动方程，通过求导即可求解速度和加速度方程。
一 2解：振动方程为： x Acos[ t ] Acos[ t ] 一 3代入有关数据得： x 0.02 cos[2 t ]（ SI ） 4振子的速度和加速度分别是：3 v dx/dt 0.04 sin[2 t ]（SI ） 4a d 2x/dt 20.08 2 cos[2 t —]（SI ）45-2若简谐振动方程为 x 0.1cos[20 t /4]m ，求： （1） 振幅、频率、角频率、周期和初相； （2） t=2s 时的位移、速度和加速度.分析 通过与简谐振动标准方程对比，得出特征参量。
解：（1）可用比较法求解.根据x Acos[ t ]0.1cos[20 t /4]（1）t=0时，作用于质点的力的大小；（2 ）作用于质点的力的最大值和此时质点的位置分析 根据振动的动力学特征和已知的简谐振动方程求解，位移最大时受力最大。
得：振幅A 0.1m ，角频率20 rad / s ，频率/2 10s 1，周期T 1/0.1s ，/4rad(2) t 2s 时，振动相位为20 t/4(40/ 4) rad 由 x A cos ，A sin ，a A 2 cos2x 得x 0.0707m, 4.44m/s,a279m/s 25-3质量为2 kg 的质点，按方程x0.2sin[5t ( /6)](SI)沿着 x 轴振动.求:解：（1）跟据f ma m 2x，x 0.2sin[5t （ /6）]将t 0代入上式中，得：f 5.0N（2）由f m 2x可知，当x A 0.2m时，质点受力最大，为f 10.0N5-4为了测得一物体的质量 m 将其挂到一弹簧上并让其自由振动，测得振动频率1.0Hz ；而当将另一已知质量为 m'的物体单独挂到该弹簧上时，测得频率为22.0Hz .设振动均在弹簧的弹性限度内进行，求被测物体的质量分析根据简谐振动频率公式比较即可。
机械振动学习题解答1ppt课件
解：
2 x x 2c X o s (t ) c o s ( t )
1 2
当ε<< ω时，
x x 2 X c o s (t ) c o s t
1 2
2
2
f 拍振的振幅为2X，拍频为 （不是 ） 2 4 例 ： 当 = 8 0 ， = 4 ， X 5 时 ， x x 1 0 c o s ( 2 t ) c o s ( 8 0 t ) 1 2
能量法 1）设系统相对于平衡位置发生了广义位移x（或θ）； 2）写出系统势能U（包括重力势能mgh和弹簧弹性势 1 1 2 1 2 dP 2 2 m x J c x k x 能 ），动能V= 2 （或 2 ），耗散能P： d t 2 d ( UVP ) 0列方程。 3）由能量守恒原理 d t
2－5 求图示弹簧－质量－滑轮系统的振动微分方程。 解：（力法）静平衡时有： mg k （Δ为弹簧的伸长量）
M, r F F k x mg
假设弹簧相对于平衡位置伸长x，则圆 盘沿逆时针方向转过x/r角
质量m 圆盘M
m x m g F
2 M r x F r k ( x ) r 2 r
F 2k sin 2
i
θ
F
T 由动量矩定理 J i
得
m L L L Fc o s m g s i n 3 2 2
sin , cos 1
2
mg
又由于
上式可化简为
m mg k 0 3 2 L 2
（能量法）设系统处于静平衡位置时势能为0。当 杆顺时针偏转θ角时 势能 动能
2 1 L L U 2 k mg 1 cos sin 2 2 2 2 1 1 mL 2 2 V J 2 2 3
机械振动基础课后习题答案
N
m
mg
P57.1-3: 求简谐位移u1 (t ) = 5e j (ωt +30 )与u2 (t ) = 7e j (ωt +90 )的合成运动u (t ), 并求u (t )与u1 (t )的相位差。
20周阻尼器消耗的能量 = = 1 1 mg 2 2 2 k ( A02 − An ) = ( A0 − An ) 2 2 δs 10 × 9.8 ((6.4 × 10−3 ) 2 − (1.6 × 10−3 ) 2 ) = 0.19(NM) 2 × 0.01
P58.1-15: 图示系统的刚杆质量不计，m = 1kg，k = 224N/m, c = 48Ns/m, l1 = l = 0.49m, l2 = l / 2, l3 = l / 4。 求系统固有频率及阻尼比。
系统固有频率： n = ω k m
ɺ 初始条件： (0) = 0, u (0) = v0 u
ɺ u0 v0 m k
2 振幅： = u0 + ( a
ωn
)2 =
ωn
= v0
最大张力： = mg + ka T = mg + v0 mk = 1000 × 9.8 + 0.5 1000 × 4 ×105 = 1.98 ×104 (N)
Bd = f 0 /( k − mω 2 ) = 0.01
响应： 响应：
u (t ) = a1 cos ω n t + a2 sin ω n t + 0.01sin(ω t − ϕ )
机械振动 课后习题和答案 第四章 习题和答案
4.1 按定义求如图所示三自由度弹簧质量系统的刚度矩阵，并用能量法检验。
求系统的固有频率和振型。
（设132142356;2;;2;3;m m m m m k k k k k k k k k =========）解：1)以静平衡位置为原点，设123,,m m m 的位移123,,x x x 为广义坐标，画出123,,m m m 隔离体，根据牛顿第二定律得到运动微分方程：11112122222132352623333243()0()()0()0m x k x k x x m x k x x k x x k x k x m x k x x k x ++-=⎧⎪+-+-++=⎨⎪+-+=⎩所以：[][]1231222235633340010000020;01032021020023m M m m m k k k K k k k k k k k k k k ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦+--⎡⎤⎡⎤⎢⎥⎢⎥=-+++-=--⎢⎥⎢⎥⎢⎥⎢⎥-+-⎣⎦⎣⎦系统运动微分方程可写为：[][]11220x x M K x x ⎧⎫⎧⎫+=⎨⎬⎨⎬⎩⎭⎩⎭…… (a)或者采用能量法：系统的动能和势能分别为=++ 222112233111222T E m xm xm x=+-+-+++22222112123234356211111()()()22222U k x k x x k x x k x k k x=+++++++--22212123562343212323111()()()222U k k x k k k k x k k x k x x k x x求偏导也可以得到[][],M K2)设系统固有振动的解为： 112233cos x u x u t x u ω⎧⎫⎧⎫⎪⎪⎪⎪=⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎩⎭，代入（a ）得：[][]1223()0u K M u u ω⎧⎫⎪⎪-=⎨⎬⎪⎪⎩⎭…… (b)得到频率方程：2222320()21022023k mk k k mk kk mωωωω--=---=--即：222422()(3)(21622)0k m m km k ωωωω=--+=解得：2(4k mω=±和23k mω=所以：123ωωω=<=<=………… (c)将（c）代入（b）可得：1233(4202102(420023(4kk m km ukk k m k umukk k mm⎡⎤-±-⎢⎥⎧⎫⎢⎥⎪⎪⎢⎥--±-=⎨⎬⎢⎥⎪⎪⎢⎥⎩⎭⎢⎥--±⎢⎥⎣⎦和123332021023200233kk m km ukk k m k umukk k mm⎡⎤--⎢⎥⎧⎫⎢⎥⎪⎪⎢⎥---=⎨⎬⎢⎥⎪⎪⎢⎥⎩⎭⎢⎥--⎢⎥⎣⎦解得：112131::1:2u u u≈；122232::1:0:1u u u≈-；132333::1:2u u u≈；令31u=，得到系统的振型为：0 1-1 0.618 111.6181 14.2 按定义求如图T—4.2所示三自由度扭转系统的刚度矩阵和质量矩阵。
机械振动习题讲解
机械振动1、按激励的情况振动可分为哪几类（至少五类）。
（5）绪论答：（答出5个）固有振动：无激励时系统所有可能的运动集合.固有振动不是现实的振动,它仅反映系统的固有属性自由振动：系统在初始激励下或原有的激励消失后的振动。
强迫振动：系统在持续的外界激励作用下产生的振动自激振动：系统受到由其自身运动诱发出来的激励作用而产生和维持的振动.参数振动：激励因素以系统本身的参数随时间变化的形式出现的振动随机振动：系统在非确定性的随机激励下所作的振动2、振动中两个简谐振动的合成分几种情况，简单阐述其性质。
（9）第一章答：1、两个相同频率的简谐振动的合成仍然是简谐振动，并且保振原来的频率2、频率不同的两个简谐振动的合成不再是简谐振动，振动比为有理数时，合成为周期振动；频率比为无理数时，合成为非周期振动。
3、频率很接近的两个简谐振动的合成会出现“拍”的现象3、阐述等效刚度和等效质量的概念。
（6）第二章答：使系统在选定的坐标上产生单位位移而需要在此坐标方向上施加的力,叫做系统在这个坐标上的等效刚度使系统在选定的坐标上产生单位加速度而需要在此坐标方向上施加的力,叫做系统在这个坐标上的等效质量二、计算题：1、质量弹簧系统，W= 150N，= 1cm，= 0.8cm，= 0.16cm。
求阻尼系数c。
(10)第二章过阻尼例3解：由于ζ很小，2、橡皮金属减振器在额定重量下静位移为1.6mm，用作航空仪表隔振。
飞机振动范围20～200Hz；求：(1)最低隔振效率？(2)当隔振效率为50％时，对应的频率是多少？（15）第三章第二类隔振例1解：这是第二类隔振问题（1）仪表隔振系统的固有频率为：求用λ，由~λ曲线可见，当λ>1以后λ越大（激励频率越高），隔振效果提高；因此最低隔振效率发生在f=20Hz处。
忽略阻尼，则：（2）若 , 则由，得：；则：3、建立右图系统的运动微分方程（15）解：受力分析：4、图示三个数学摆串联,，摆长，求：系统作微幅摆动时的运动微分方程。
湖南大学-理论力学-第十章机械振动基础
(2)双面与单面约束
双面: 约束方程为等式。
单面: 约束方程为不等式。
8-1 约束与位形
第四页，共70页。
8-1-1 约束及其分类
(3)完整与非完整约束
约束方程不包含质点速度，或包含速度但是可
积分的约束，称为完整约束。
包含质点速度且不可积分成完整约束的，称为
非完整约束。
8-1 约束与位形
第五页，共70页。
1)几何法: 用求实位移的方法，而实位移与速度成正比，故可
用类似速度分析的方法确定各点的虚位移的关系。
rAcos ψ 90 rB cos
rAsin ψ rB cos y
亦可 rA Cv A cos rB CvB sin( ) O
若给相反方向虚位移，结果如何?
Cv
rA
WF Fi ri 0
虚功方程
或
Fxi δxi Fyi δyi Fzi δzi 0
8-2 虚位移与虚位移原理
第二十一页，共70页。
8-2-3 虚位移原理
① 适用于任意约束质点系，包括刚体与变形体，
但对变形体需计入内力虚功。
② 平衡的充要条件。(几何静力学对变形体非充分)
③针对静止平衡系统。
设n个质点，受m个完整约束和l个非完整约束。
k =3n-m-l
空间刚体系 k =6n-s, s =m+l
平面机构
k =3n-s
1. k=?
A
B
O1
O2
8-1 约束与位形
k=2n-s =2× 3-5=1 k=3n-s=3× 4-(2× 5+1)=1 C k=3× 5-(2× 6+2)=1
第七页，共70页。
8-1-2 质点系的位形