中心复合试验设计概述
(3)中心复合设计表分析
255
254
253
Y 252
251
2
250
1
0C
-2
-1
-1
B
0
1
-2 2
Hold values: A: 0.0000000000002
第三步: 在
所示:
第四步: 在出现的
第五步: 点击“
选“Target”因为我们希 望输出变量的值在设计中
Surface Plot of Y
Surface Plot of Y
254
253
252
251
Y 250
249
248
2
247
1
0C
-2
-1
-1
A
0
1
-2
2
Hold values: B: 0.0000000000002
从(A、 C从、(YB)、 C(、AY、)B 、中Y,)A因图 素表被 面固图定形 近c:似 参为数平优 化,用优
Linear Square Residual Lack-ofPure Total
分析上表 可知:因
A、B、C均为 显著影响因素 A2项为显著影 响因素
线性项和二 次项为显著 影响因素
显著非线 性影响,
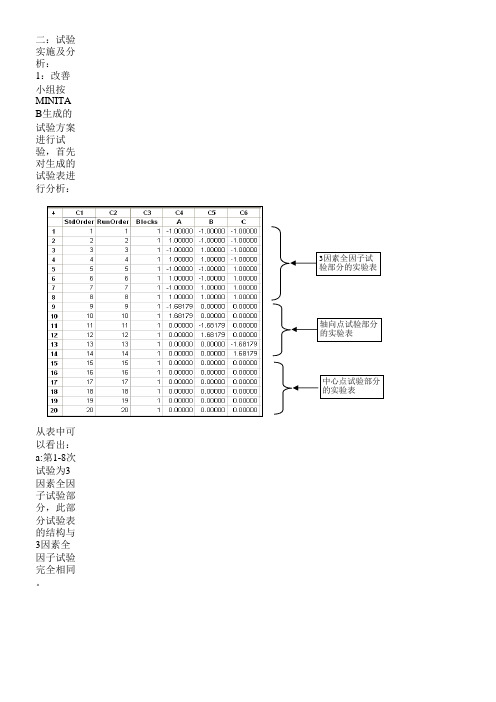
3a::取进得行的 数据如下
b:用 M(a)I:N在ITA MINITA
StdOrder 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
C -1 -1 -1 -1 1 1 1 1 0 0 0 0 -1.68179 1.68179 0 0 0 0 0 0
中心复合设计详解

中心复合设计详解中心复合设计(Central Composite Design,CCD)是实验设计中常用的一种方法,它结合了全因子设计和部分因子设计的优点,通过添加中心点和轴向点来评估响应面的曲率,从而更准确地预测最优解。
以下是中心复合设计的详细解释:基本概念:中心点:所有因子的中间水平组合,用于估计纯误差。
轴向点:在因子空间中沿着坐标轴方向取点,用于估计响应面的曲率。
立方体点:全因子设计或部分因子设计的角点,用于估计主效应和交互效应。
设计构造:选择需要考察的因子和水平。
确定全因子或部分因子的角点(立方体点)。
添加中心点,通常重复多次以更好地估计实验误差。
添加轴向点,这些点位于因子空间的坐标轴上,距离中心点的距离(α值)是事先确定的,通常是为了使设计旋转或正交。
设计特点:能够评估非线性关系:通过轴向点和中心点,可以检测响应面是否存在曲率,从而判断因子与响应之间是否存在非线性关系。
高效性:相比于全因子设计,中心复合设计需要的实验次数较少。
灵活性:可以通过调整α值来平衡设计的旋转性和正交性。
可扩展性:容易添加额外的中心点或轴向点以增加设计的精度。
实验步骤:根据实验目的确定因子和水平。
构造中心复合设计,确定实验点。
进行实验并记录响应数据。
使用统计软件(如Minitab、Design-Expert等)拟合响应面模型。
分析模型的有效性,包括残差分析、模型显著性检验等。
利用模型预测最优解并进行验证实验。
应用领域:中心复合设计广泛应用于各种需要优化多个因子影响的过程,如化工、制药、食品科学、机械工程等领域。
它特别适用于当对因子的主效应、交互效应以及二次效应感兴趣时,且预期响应面可能存在曲率的情况。
注意事项:在选择α值时需谨慎,以确保设计的旋转性或正交性符合实验需求。
中心点的重复次数应根据实验误差的预期大小来确定。
在分析响应面模型时,应注意检查模型的假设条件是否满足,如正态性、同方差性等。
Mintab_DOE操作说明(中心复合设计)

2
中心複合設計
試驗目的: 本试验的目标为确定塑胶件注塑工序的射出压力、保持压力和射出时间与零件关键尺寸之 间的关系,并对三种因素的水平设置进行优化。。 确定测量指标: 小组确定以该零件的关键尺寸“252+2mm”作为测量指标。 确定影响因素XS 本例影响因素为 1、射出压力 2、保持压力 确定试验因素水平表
15
中心複合設計
18: 添加軸向點分析結果如下:
射出壓力,保持壓力及射出時 間的P值均小於0.05,故其均為 顯著因子
A B C
A*A項,其P值亦小於0.05,故 其也為顯著因子
線性項和二次項的P值亦小於 0.05,故其也為顯著因子
16
中心複合設計
19: 建立回歸方程:
前四項為顯著因子,故回歸方 程中列入果如下:
射出壓力,保持壓力及射出時 間的P值均小於0.05,故其均為 顯著因子
A B C
A*A項,其P值亦小於0.05,故 其也為顯著因子
線性項和二次項的P值亦小於 0.05,故其也為顯著因子
分析上表可知:因素A、B、C及A因素的平方项为输出变量的显著影响因素,说明本例存在 显著非线性影响,需继续进行轴向点试验以测试各因素与输出间的真正关系。
目標達成率
23
中心複合設計
22: 試驗結論: 1.因素射出压力、保持压力、射出时间均队对零件关键尺寸有显著影响。其中因素A的影响 存在2次影响(非先线性影响)。 2.将各试验因素设置在如下水平时零件尺寸最优(252):
因子
最優參數
A.射出壓力(PSI)
1468.18
B.保持壓力(PSI)
回歸方程式: Y= 252.5+1.08A+0.72B-0.69C-0.54A*A ---A: 射出壓力 ---B: 保持壓力 ---C: 射出時間
中心复合设计的中心点数量

中心复合设计的中心点数量1.引言1.1 概述概述部分的内容:中心复合设计是一种重要的实验设计方法,广泛应用于许多科学研究领域。
它是一种在实验设计中使用的统计方法,用于研究多个因素对实验结果的影响。
该方法通过确定合适的中心点数量来实现实验因素的最优配置,以达到更准确的实验结果。
中心复合设计的基本思想是在原始因素水平的基础上添加一组中心点,再围绕这些中心点随机设置一组试验因素水平,以此来研究因素对结果的影响。
通过多次重复实验,可以统计分析各个因素的作用程度,从而找出最优的实验条件。
中心复合设计的应用领域非常广泛。
在工程领域,它可以用于优化生产工艺、提高产品质量和性能,以及减少资源浪费。
在药物研发领域,它可以用于优化药物配方、减少副作用和提高疗效。
在农业领域,它可以用于优化农作物种植方式和施肥方案,提高产量和品质。
中心点数量是中心复合设计中一个非常关键的参数。
它的选择会直接影响实验结果的准确性和可靠性。
如果中心点数量过少,可能会导致因素间的相互作用无法准确评估,结果产生偏差。
而如果中心点数量过多,就会增加实验的复杂性和成本。
因此,在进行中心复合设计时,需要根据实际情况合理选择中心点数量。
一般来说,根据因素数量和实验条件的复杂程度,可以通过经验或者计算方法确定合适的中心点数量。
总之,中心复合设计是一种非常有用的实验设计方法,可以帮助研究人员在有限的实验条件下,获取更准确和可靠的实验结果。
选择合适的中心点数量是保证实验设计质量和结果有效性的重要因素。
在接下来的文章中,我们将详细介绍中心复合设计的概念、应用领域以及中心点数量对实验结果的影响。
1.2 文章结构文章结构部分的内容如下:文章结构:本文将按照以下结构进行讨论:引言、正文和结论。
2.1 引言部分将概述中心复合设计的概念,并介绍本文的主要目的。
2.2 正文部分将详细探讨中心复合设计的概念和应用领域。
首先,将对中心复合设计的概念进行阐述,包括其基本原理和相关概念。
中心复合设计

中心复合设计
这就是最常用的响应曲面试验设计。
中心复合设计由包含中心点的因子设计或部分因子设计组成,并用一组轴点(或星点)进行了增强,以便对弯曲进行估计。
使用中心复合设计可以:
·有效估计一次与二次项
·通过向以前运行的因子设计添加中心点与轴点,为带有弯曲的响应变量建模。
中心复合设计在顺序试验中尤为有用,因为经常可以通过添加轴点与中心点来基于以前的因子试验进行构建工作。
例如,您要确定对塑料部件进行注塑成型的最佳条件。
首先运行一个因子试验并确定显著因子:温度(水平设在 190°与 210°)与压力(水平设在 50MPa 与100MPa)。
可以使用响应曲面设计试验确定每个因子的最优设置。
下面就是此试验的设计点:
(设计中心点为 200°,75MPa)
如果可能,中心复合设计可以具有所希望的正交区组与可旋转属性。
·正交区组–通常,中心复合设计会在多个区组中运行。
中心复合设计能够以正交方式划分区组,从而可以独立估计模型项与区组效应并最大限度地减少回归系数的变异。
·可旋转–可旋转的设计提供了所希望的属性,即距设计中心等距离的所有点处的预测方差就是恒定的。
表面中心设计就是一种 alpha 为 1 的中心复合设计类型。
在此设计中,轴点或“星”点位于因子空间的每个面的中心,因此水平 = + 1。
这种设计变形要求每个因子有 3 个水平。
使用适当星点来增强现有因子设计或分辨率 V 设计也会生成此设计。
Mintab-DOE操作说明(中心复合设计)

05
结论与展望
中心复合设计在DOE中的优势与局限性
要点一
高效
要点二
全面
中心复合设计能够快速有效地找到关键因素及其交互作用 ,减少实验次数。
能够考虑多个因素及其交互作用,提供更全面的实验设计 。
中心复合设计在DOE中的优势与局限性
• 精确:能够估计因素之间的交互作用,提 高实验的精确度。
因子选择
根据实验目的选择关键因子,并确定其水平范围和变化类型 。
确定实验设计类型与规格
设计类型
根据实验目的和因子数量选择适合的中心复合设计类型,如中心复合面设计、中心复合轴设计等。
设计规格
确定实验设计的具体规格,包括重复实验次数、因子水平数目等。
生成中心复合设计表
设计软件
使用专业的实验设计软件(如Mintab) 生成中心复合设计表。
响应曲面法
响应曲面法是一种通过构建数学模型来描述实验因素与响应变量之间关系的统计方 法。
通过中心复合设计,可以获得多个实验点,并利用这些数据拟合出响应曲面模型。
响应曲面法可以用于预测不同实验因素水平下的响应变量值,并确定最优的实验条 件。
多元线性回归分析
1
多元线性回归分析是一种统计方法,用于研究多 个自变量与因变量之间的线性关系。
感谢观看
THANKS
中心复合设计的概念与应用
概念
中心复合设计是一种实验设计方法,它允许研究者同时研究多个因素及其交互作 用,以确定最佳的参数组合。
应用
中心复合设计广泛应用于各种领域,如化学、生物、工程和制药等,用于优化产 品或过程,提高性能和效率。
02
中心复合设计的基本步骤
中心复合设计

中心复合设计-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
中心复合设计
这是最常用的响应曲面试验设计。
中心复合设计由包含中心点的因子设计或部分因子设计组成,并用一组轴点(或星点)进行了增强,以便对弯曲进行估计。
使用中心复合设计可以:
·有效估计一次和二次项
·通过向以前运行的因子设计添加中心点和轴点,为带有弯曲的响应变量建模。
中心复合设计在顺序试验中尤为有用,因为经常可以通过添加轴点和中心点来基于以前的因子试验进行构建工作。
例如,您要确定对塑料部件进行注塑成型的最佳条件。
首先运行一个因子试验并确定显著因子:温度(水平设在 190°和 210°)和压力(水平设在 50MPa 和100MPa)。
可以使用响应曲面设计试验确定每个因子的最优设置。
下面是此试验的设计点:
(设计中心点为 200°,75MPa)
如果可能,中心复合设计可以具有所希望的正交区组和可旋转属性。
·正交区组–通常,中心复合设计会在多个区组中运行。
中心复合设计能够以正交方式划分区组,从而可以独立估计模型项和区组效应并最大限度地减少回归系数的变异。
·可旋转–可旋转的设计提供了所希望的属性,即距设计中心等距离的所有点处的预测方差是恒定的。
表面中心设计是一种 alpha 为 1 的中心复合设计类型。
在此设计中,轴点或“星”点位于因子空间的每个面的中心,因此水平 = + 1。
这种设计变形要求每个因子有 3 个水平。
使用适当星点来增强现有因子设计或分辨率 V 设计也会生成此设计。
中心复合设计原理

中心复合设计原理(Central Composite Design,简称CCD)是一种用于实验设计的统计方法。
它是响应面分析设计中常用的一种方法,用于确定多个因素对某个响应变量的最佳组合。
中心复合设计原理包括两个主要的设计因素:中心点和星点。
中心点是在每个因素的水平范围内选择中间值,用于确定对响应变量的基本影响。
而星点则是在每个因素的水平范围外选择几个点,用于评估因素对响应变量的非线性影响。
中心复合设计原理的步骤如下:
1. 确定需要研究的因素和响应变量:确定对响应变量有潜在影响的因素,并定义响应变量。
2. 选择因素的水平:确定每个因素的水平范围,通常选择低水平、高水平和中心水平。
3. 构建试验设计表:根据因素的水平和中心点与星点的数量,构建一个试验设计表。
这个表将列出每个因素在每个水平上的设置。
4. 进行试验:按照试验设计表进行实际试验,并记录响应变量的观测结果。
5. 进行数据分析:使用统计方法分析试验结果,建立响应面模型,评估因素对响应变量的影响。
6. 进行优化:基于建立的响应面模型,确定使响应变量达到最佳水平的因素组合。
中心复合设计原理的优点是可以同时研究多个因素,并且考虑了线性和非线性的影响。
它可以帮助研究人员确定最佳的因素组合以优化响应变量,从而提高产品或工艺的性能。
然而,中心复合设计原理也有一些限制,如对因素间相互作用的假设较强,样本容量要求较高等。
在实际应用中,需要根据具体情况和实验要求来选择合适的设计方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中心复合试验中的立方点、轴向点和中心点
中心复合试验设计由立方点、轴向点和中心点试验三 部分组成,下面以2因子中心复合试验设计为例分别对 三种点加以说明。 立方点 立方点即全因子设计或分部试验设计中的2水平对应的 “-1”和“+1”点,表示如下图:
确定试验因素水平表 水平 A:射出压力 B:保持压力 C:射出时间 1200 700 1.2 + 1400 800 fFactory Pro" 试用版本创建
试验方案确定
改善小组确信三个因素的交互作用对输出有重要影 响,并怀疑非线性影响也是重要影响。因为全因子设 计可测试因素间的相互作用,中心复合设计可以测试 因素的非线性影响,小组决定选择中心复合设计进行 试验。 改善上组确信三个因素的交互作用对输出有重要影 响,并怀疑非线性影响也是重要影响。因为全因子设 计可测试因素间的相互作用,中心复合设计可以测试 因素的非线性影响,小组决定选择中心复合设计进行 试验。
(0,0)
PDF 文件使用 "pdfFactory Pro" 试用版本创建
中心复合设计例
中心复合设计常用于在确信怀疑试验因素对试验指 标存在非线性影响时对因素与指标间的关系进行试验 分析,本节将以3因素中心复合设计为例来讲述中心复 合设计的流程及策略。 某公司生产塑胶零件,长期以来该公司生产的一种 主要产品,销往国外一跨国公司的激光头用滑动底架 的某个关键尺寸难于有效控制,该公司决定成立改善 小组对此进行研究改善。经认真调查分析,小组认为 此尺寸偏差过大的原因是由于零件变形引起,于是小 组将目光聚焦在零件注塑成型工序,经过前期分析和 经验判断,小组确定注塑时引起零件变形的关键因素 为射出压力、保持压力和射出时间。小组决定通过试 验设计来确定以上因素与零件尺寸之间的关系以进行 改善。
(+1)
B+
(-1) B-
A(-1)
A+ (+1)
PDF 文件使用 "pdfFactory Pro" 试用版本创建
轴向点 轴向点又叫始点,分布在轴向上,记为(+a,0)、(a,0)、(0, +a)、(0, -a),如下图表示。
(0,+a)
(-a,0)
(+a,0)
中心复合试 验设计概述
主讲:张驰 中国质量协会六西格玛专家组成员 中国质量协会六西格玛黑带注册导师
PDF 文件使用 "pdfFactory Pro" 试用版本创建
中心复合试验设计概述
中心复合设计是在2水平全因子和分部试验设计的基础 上发展出来的一种试验设计方法,它是2水平全因子和 分部试验设计的拓展。通过对2水平试验增加一个设计 点(相当于增加了一个水平),从而可以对评价指标 (输出变量)和因素间的非线性关系进行评估。它常 用于在需要对因素的非线性影响进行测试的试验。
PDF 文件使用 "pdfFactory Pro" 试用版本创建
建立试验目标 本试验的目标为确定塑胶件注塑工序的射出压力、保 持压力和射出时间与零件关键尺寸之间的关系,并对 三种因素的水平设置进行优化。 作出试验设计计划表 DOE试验计划表 项目负责人:刘军 部门:工程部 项目名:塑胶件成型过程改善 日期:2002年4月10日 DOE目标:确定注胶成型过程的射出压力、保持压力 和射出时间与零件关键尺寸之间的关系,并对三种因 素的水平设置进行优化 关键特性 零件关键 尺寸 输出特性指标 测量什么/如何测量 卡尺 规格 是否用于DOE 252+2mm 是
PDF 文件使用 "pdfFactory Pro" 试用版本创建
试验策划
PDF 文件使用 "pdfFactory Pro" 试用版本创建
确定测量指标 小组确定以该零件的关键尺寸“252+2mm”作为测量指 标。 确定影响因素XS 本例影响因素为 1、射出压力 2、保持压力 3、射出时间
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
中心复合设计的特点
1、可以进行因素数在2—6个范围内的试验。 2、试验次数一般为14—90次:2因素12次,3因素20次, 4因素30次,5因素54次,6因素90次。 3、可以评估因素的非线性影响。 4、适用于所有试验因素均为计量值数末尾的试验。 5、在使用时,一般按三个步骤进行试验。 (1)先进行2水平全因子或分部试验设计。 (2)再加上中心点进行非线性测试。 (3)如果发现非线性影响为显著影响,则加上轴向点 进行补充试验以得到非线性预测方程。 6、中心复合试验也可一次进行完毕,(在确信有非线性 影响的情况下)。
(0,-a)
PDF 文件使用 "pdfFactory Pro" 试用版本创建
中心点 中心点亦即设计中心,在坐标轴上表示为(0,0), 表示在上图中,即(0,0)点。 将三种点集成在一个图上表示如下: (0,+a)
(-1,+1) (-a,0) (-1,-1) (0,-a) (+1,+1) (+a,0) (+1,-1)
