并行计算课程设计报告
并行计算课程报告

并行计算课程报告1.学习总结1.1并行计算简介并行计算是相对于串行计算来说的。
它是一种一次可执行多个指令的算法,目的是提高计算速度,及通过扩大问题求解规模,解决大型而复杂的计算问题。
所谓并行计算可分为时间上的并行和空间上的并行。
时间上的并行就是指流水线技术,而空间上的并行则是指用多个处理器并发的执行计算。
1.2并行计算机分类和并行机体系结构的特征按内存访问模型、微处理器和互联网络的不同,当前流行的并行机可分为对称多处理共享存储并行机(SMP:Symmetric Multi-Processing)、分布共享存储并行机(DSM:Distributed Shared Memory)、机群(cluster)、星群(constellation)和大规模并行机(MPP:Massively Parallel Processing)等五类。
SMP并行机有如下主要特征:对称共享存储、单一的操作系统映像、局部高速缓存cache 及其数据一致性、低通信延迟、共享总线带宽、支持消息传递、共享存储并行程序设计。
SMP 并行机具有如下缺点:欠可靠、可扩展性(scalability)较差。
DSM 并行机具有如下主要特征:并行机以结点为单位,每个结点包含一个或多个CPU,每个CPU 拥有自己的局部cache,并共享局部存储器和I/O设备,所有结点通过高性能互联网络相互连接;物理上分布存储;单一的内存地址空间;非一致内存访问(NUMA)模式;单一的操作系统映像;基于cache 的数据一致性;低通信延迟与高通信带宽;DSM 并行机可扩展到数百个结点,能提供每秒数千亿次的浮点运算性能;支持消息传递、共享存储并行程序设计。
机群(cluster)有三个明显的特征:①系统由商用结点构成,每个结点包含2-4 个商用微处理器,结点内部共享存储。
②采用商用机群交换机连接结点,结点间分布存储。
③在各个结点上,采用机群Linux 操作系统、GNU 编译系统和作业管理系统。
并行计算结构算法编程课程设计

并行计算结构算法编程课程设计一、课程背景高性能计算(High Performance Computing,HPC)已经成为科技竞争的重要战场之一。
各大科研机构、高校都在日益加大对高性能计算的投入和重视。
在为科学研究提供强有力的支撑的同时,也在很大程度上推动了信息技术的进步和发展。
并行计算结构算法编程课程是计算机科学与技术专业的一门重要的课程,重点讲解并行计算系统的结构、算法设计与编程方法。
二、课程目标本课程旨在介绍并行计算结构和基本的并行算法设计与优化方法,通过学习课程,达到以下目标:1.掌握并行计算系统的结构,包括传统的并行计算系统和云计算系统。
2.熟悉并行算法的设计与优化,掌握传统的并行算法和新兴的并行算法。
3.掌握并行程序的编写方法,能够使用现代工具和技术编写高效的并行程序。
4.具备一定的实验设计和实验分析能力,能够独立完成并行计算相关的实验与项目。
三、课程内容1. 并行计算系统的结构1.1 什么是并行计算系统1.2 传统式并行计算系统1.3 云式并行计算系统2. 并行计算算法设计2.1 并行计算中的任务划分2.2 并行计算中的数据划分2.3 并行计算中的任务调度2.4 并行计算中的数据通信3. 并行程序的编写3.1 编写并行程序的基本原则3.2 选用适合的编程语言3.3 选择美国能源部国家科学院NNSA的ASC黄金标准测试用例4. 课程设计4.1 课程设计项目的内容和要求4.2 怎么设计一个并行计算程序4.3 基于MPI的分散式矩阵-向量乘法运算的实现4.4 基于OpenMP的PDE求解器的实现四、实验环境本课程的实验环境为台式机或服务器,由学生自行摆放,安装MATLAB和MPI 等软件。
五、参考资料1.Peter Pacheco, An Introduction to Parallel Programming,Elsevier, 2011.2.Arora Jaswinder Pal Singh, Anindya Das, Practical ParallelProgramming, PHI Learning Private Limited, 2012.3.Tim Mattson, Beverly Sanders, Berna Massingill, Patterns forParallel Programming, Addison-Wesley Professional, 2004.本文档主要让读者了解并行计算结构算法编程课程设计的内容,以及课程的目的和参考资料。
矩阵并行计算课程设计

矩阵并行计算课程设计一、课程目标知识目标:1. 理解矩阵并行计算的基本概念,掌握并行计算中矩阵运算的核心算法。
2. 能够运用所学的矩阵并行计算方法,解决高中数学及物理中相关问题。
3. 了解矩阵并行计算在科学研究和实际工程中的应用。
技能目标:1. 培养学生熟练运用计算工具(如计算器、编程软件等)进行矩阵并行计算的能力。
2. 培养学生分析问题、设计并行算法解决问题的能力。
3. 提高学生的团队协作和沟通能力,能在小组讨论中分享和交流矩阵并行计算的方法和技巧。
情感态度价值观目标:1. 激发学生对矩阵并行计算的兴趣,培养其主动探索科学问题的精神。
2. 培养学生严谨、务实的科学态度,使其认识到矩阵并行计算在解决实际问题中的价值。
3. 增强学生的国家荣誉感和使命感,认识到我国在并行计算领域的发展优势和潜力。
课程性质:本课程为高中信息技术选修课程,以矩阵并行计算为核心,结合数学、物理等学科知识,培养学生的计算思维和实际操作能力。
学生特点:高中年级学生具备一定的数学基础和编程能力,对科学计算有浓厚兴趣,善于探索和解决问题。
教学要求:注重理论与实践相结合,通过案例分析、小组讨论、上机实践等方式,使学生掌握矩阵并行计算的基本方法和技能。
同时,关注学生的个体差异,因材施教,提高学生的综合素养。
二、教学内容1. 矩阵并行计算的基本概念与原理:介绍矩阵并行计算的定义、发展历程,分析其优缺点,讲解并行计算的基本原理。
相关教材章节:第二章 并行计算基础2. 矩阵并行算法:讲解矩阵乘法、矩阵求逆等核心算法的并行化方法,分析算法性能,讨论优化策略。
相关教材章节:第三章 矩阵并行算法3. 并行计算工具与平台:介绍常用的并行计算工具和平台,如MATLAB、CUDA等,指导学生如何使用这些工具进行矩阵并行计算。
相关教材章节:第四章 并行计算工具与平台4. 矩阵并行计算案例分析:分析实际案例,如图像处理、物理模拟等,使学生了解矩阵并行计算在具体问题中的应用。
《并行计算导论》课程报告
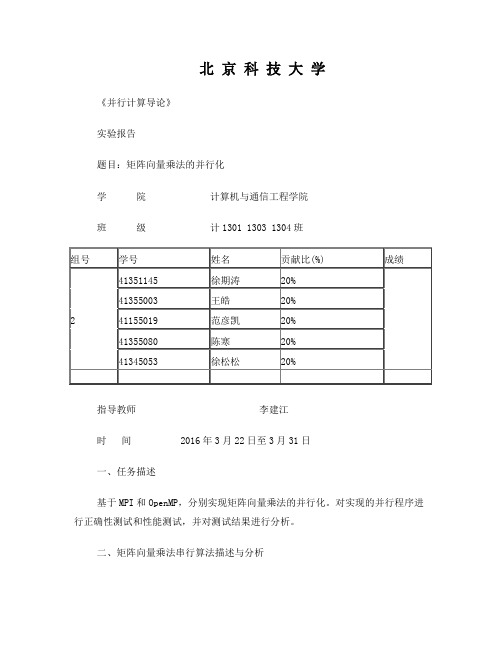
北京科技大学《并行计算导论》实验报告题目:矩阵向量乘法的并行化学院计算机与通信工程学院班级计1301 1303 1304班指导教师李建江时间 2016年3月22日至3月31日一、任务描述基于MPI和OpenMP,分别实现矩阵向量乘法的并行化。
对实现的并行程序进行正确性测试和性能测试,并对测试结果进行分析。
二、矩阵向量乘法串行算法描述与分析1. 串行算法描述在线性代数中,矩阵和向量的乘法是将每行矩阵的每个元素乘以向量中的每个元素,得到一个新的向量,要求矩阵是N*N阶,向量是N阶,这样相乘后,得到一个新的N阶向量。
利用串行算法,设置循环,让矩阵中的每一行的元素乘以完向量的每个元素后得到一个数值再进行下一行的乘法,一直到最后一行的乘法结束,得到新的向量。
2. 空间复杂度分析对于N阶的矩阵向量乘法,A*b=x,定义数据类型为long,则需要的存储空间为(N^2+2*N)*4 Byte 。
(矩阵数:N^2+向量数N+结果N)3. 时间复杂度分析对于N阶的矩阵向量乘法,A*b=x,需要串行算法执行的次数为:N^2*(N-1)三、矩阵向量乘法的并行化(一)基于MPI的矩阵向量的并行化1. 并行策略(含图示)因为矩阵乘以向量,每行的乘法是相互独立的,所以可以把N阶矩阵按行平均分配给各个进程,让每个进程分别处理分配给它的数据块。
2. 并行算法描述先为程序指定阶数,然后用随机数生成N阶方阵和向量,采用静态均匀负载,为每个处理器分配相同数量的数组元素,做到负载相对比较均衡(由于可能存在0元素,使得负载相对有些偏差)。
然后把N阶方阵和向量显示出来,做MPI静态并行计算,然后将得出的结果显示出来3. 空间复杂度分析设进程数为n,数据类型为long,则N阶矩阵向量乘法的所需的空间为:N^2+n*N+N,(矩阵空间N^2+n倍的b向量空间n*N+结果N)4. 时间复杂度分析假设负载均衡,假设最小的划分块大于等于矩阵的一行,由于将行分块划分给各个进程,所以整体的时间是1/n倍的串行算法的时间复杂度,即1/n*N^2*(N-1)(二)基于OpenMP的矩阵向量的并行化1. 并行策略(含图示)与MPI并行策略类似,把矩阵按行分块,与向量相乘,但是可以采用更为灵活的池技术动态调用,更加充分利用了计算资源。
并行计算课程设计

并行计算课程设计一、课程目标知识目标:1. 让学生理解并行计算的基本概念,掌握并行计算的发展历程及分类;2. 培养学生掌握并行编程的基本方法,了解并行算法的设计原则;3. 使学生了解并行计算在现实生活中的应用,并能结合实际问题进行分析。
技能目标:1. 培养学生运用并行计算技术解决实际问题的能力,提高计算思维;2. 培养学生掌握并行编程工具和软件的使用,能进行简单的并行程序设计;3. 培养学生通过团队合作,进行问题分析、方案设计和程序实现的能力。
情感态度价值观目标:1. 培养学生对并行计算的兴趣,激发其探索未知领域的热情;2. 培养学生具备良好的团队合作精神,学会尊重他人、沟通协作;3. 培养学生认识到科技发展对社会进步的重要性,树立正确的科技观。
课程性质:本课程为选修课,旨在拓展学生的计算思维和编程技能,提高解决实际问题的能力。
学生特点:学生具备一定的计算机基础,对编程有一定了解,对并行计算感兴趣,但可能对并行编程方法和技巧掌握不足。
教学要求:结合学生特点和课程性质,注重理论与实践相结合,充分调动学生的积极性,培养其创新能力和实践能力。
通过本课程的学习,使学生能够将并行计算技术应用于实际问题,达到学以致用的目的。
在教学过程中,将目标分解为具体的学习成果,便于教学设计和评估。
二、教学内容1. 并行计算基本概念:包括并行计算的定义、发展历程、分类及特点。
教材章节:第一章 并行计算概述2. 并行编程模型:介绍 Flynn 分类法,讲解共享内存和分布式内存编程模型。
教材章节:第二章 并行编程模型3. 并行编程语言与工具:学习 MPI、OpenMP、CUDA 等并行编程语言和工具。
教材章节:第三章 并行编程语言与工具4. 并行算法设计:讲解并行算法设计原则,分析常见并行算法。
教材章节:第四章 并行算法设计5. 并行计算应用:介绍并行计算在科学计算、大数据处理等领域的应用。
教材章节:第五章 并行计算应用6. 实践环节:安排学生进行并行程序设计和实现,针对实际问题进行团队协作。
并行计算的课程设计

并行计算的课程设计一、课程目标知识目标:1. 让学生理解并行计算的基本概念,掌握并行计算的核心原理。
2. 学会分析问题,识别适合并行计算的算法和场景。
3. 掌握并行编程的基本技巧,能运用所学知识对简单程序进行并行化改造。
技能目标:1. 培养学生运用并行计算技术解决问题的能力,提高计算效率。
2. 培养学生具备团队协作和沟通能力,能参与并行计算项目的开发和优化。
3. 培养学生具备自主学习能力,能够紧跟并行计算领域的发展趋势。
情感态度价值观目标:1. 激发学生对并行计算的兴趣,培养其探索精神和创新意识。
2. 培养学生具备良好的科学素养,认识到并行计算在科技发展中的重要作用。
3. 引导学生树立正确的价值观,明确并行计算为社会进步带来的积极影响。
分析课程性质、学生特点和教学要求,本课程将目标分解为以下具体学习成果:1. 学生能够解释并行计算的基本概念,阐述并行计算的核心原理。
2. 学生能够分析实际问题,提出并行计算解决方案,并评估其性能。
3. 学生能够掌握并行编程技巧,完成至少一个简单的并行程序设计。
4. 学生能够积极参与团队合作,共同完成并行计算项目。
5. 学生能够关注并行计算领域的发展动态,了解其应用前景。
本课程教学内容依据课程目标,结合教材章节,科学系统地组织如下:1. 并行计算基本概念:介绍并行计算的定义、分类及其发展历程,使学生了解并行计算的基本框架。
2. 并行计算原理:讲解并行计算的基本原理,如并发性、并行性、数据并行、任务并行等,并通过实例分析,使学生掌握并行计算的核心思想。
3. 并行计算模型:介绍 Flynn 分类法、SIMD、MIMD 等并行计算模型,让学生了解不同并行计算模型的特点及应用场景。
4. 并行编程技术:讲解并行编程的基本方法,如 OpenMP、MPI、CUDA 等,使学生掌握并行编程的技巧和注意事项。
5. 并行算法设计:分析常见并行算法设计方法,如分治法、迭代法、管道线法等,并通过实例让学生学会设计并行算法。
并行计算实验报告一

并行计算实验报告一江苏科技大学计算机科学与工程学院实验报告评定成绩指导教师实验课程:并行计算宋英磊实验名称:Java多线程编程学号: 姓名: 班级: 完成日期:2014年04月22日1.1 实验目的(1) 掌握多线程编程的特点;(2) 了解线程的调度和执行过程;(3) 掌握资源共享访问的实现方法。
1.2 知识要点1.2.1线程的概念(1) 线程是程序中的一个执行流,多线程则指多个执行流;(2) 线程是比进程更小的执行单位,一个进程包括多个线程;(3) Java语言中线程包括3部分:虚拟CPU、该CPU执行的代码及代码所操作的数据。
(4) Java代码可以为不同线程共享,数据也可以为不同线程共享; 1.2.2 线程的创建(1) 方式1:实现Runnable接口Thread类使用一个实现Runnable接口的实例对象作为其构造方法的参数,该对象提供了run方法,启动Thread将执行该run方法;(2) 方式2:继承Thread类重写Thread类的run方法;1.2.3 线程的调度(1) 线程的优先级, 取值范围1,10,在Thread类提供了3个常量,MIN_PRIORITY=1、MAX_ PRIORITY=10、NORM_PRIORITY=5;, 用setPriority()设置线程优先级,用getPriority()获取线程优先级; , 子线程继承父线程的优先级,主线程具有正常优先级。
(2) 线程的调度:采用抢占式调度策略,高优先级的线程优先执行,在Java 中,系统按照优先级的级别设置不同的等待队列。
1.2.4 线程的状态与生命周期说明:新创建的线程处于“新建状态”,必须通过执行start()方法,让其进入到“就绪状态”,处于就绪状态的线程才有机会得到调度执行。
线程在运行时也可能因资源等待或主动睡眠而放弃运行,进入“阻塞状态”,线程执行完毕,或主动执行stop方法将进入“终止状态”。
1.2.5 线程的同步--解决资源访问冲突问题(1) 对象的加锁所有被共享访问的数据及访问代码必须作为临界区,用synchronized加锁。
并行计算课程报告.docx

成绩:并行计算导论课程报告专业:软件工程班级:软件二班学号:************姓名:*** 2017 年6 月 1 日1、并行计算的实际意义并行计算或称平行计算是相对于串行计算来说的。
它是一种一次可执行多个指令的算法,目的是提高计算速度,及通过扩大问题求解规模,解决大型而复杂的计算问题。
所谓并行计算可分为时间上的并行和空间上的并行。
时间上的并行就是指流水线技术,而空间上的并行则是指用多个处理器并发的执行计算。
在应用需求方面,人类对计算机性能的需求总是永无止境的,在诸如预测模型的构造和模拟、工程设计和自动化、能源勘探、医学、军事以及基础理论研究等领域中都对计算提出了极高的具有挑战性的要求。
例如,在作数值气象预报时,要提高全球气象预报的准确性,据估计在经度、纬度和大气层方向上至少要取 200*100*20 =40 万各网格点。
并行计算机产生和发展的目的就是为了满足日益增长的大规模科学和工程计算、事务处理和商业计算的需求。
问题求解最大规模是并行计算机的最重要的指标之一,也是一个国家高新技术发展的重要标志。
2、拟优化的应用介绍应用 jacobi 迭代近似求解二维泊松方程。
二维泊松方程:u( x, y) f (x, y), ( x, y)u( x, y)g( x, y), ( x, y)其中2 2(0,W ) * (0, H ) ,u( x, y)x 2u ( x, y)y 2u( x, y)f (x, y) 和g (x, y) 已知函数,分 定 在的内部和 界上。
于任意正整数Mx和 N y,将网格剖分成 Mx* Ny个相同的方格。
在网格 点上,用二 中心差分来近似二 偏 数。
2ui 1, j2ui , jui 1, jx2u(ih x, jh y)h x 22 ui , j 12ui, jui , j 1u(ih x , jh y )h y 2y2将差分近似代入泊松方程, 便得到了五点差分离散格式,泊松方2(h 2h 2 )uh 2 (ui 1, jui 1, j ) h 2 (ui , j 1 ui , j 1) h 2h 2 fi , jxyi , jyxx y 程的求1 iM x 1,1 jN x之后用 典的 jacobi 算法来求解此方程 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
并行计算与多核多线程技术课程报告专业班级学号姓名成绩___________________年月日课程报告要求手写内容:设计目的、意义,设计分析,方案分析,功能模块实现,最终结果分析,设计体会等。
允许打印内容:设计原理图等图形、图片,电路图,源程序。
硬件类的设计,要有最终设计的照片图;软件类设计,要有各个功能模块实现的界面图、输入输出界面图等。
评价理论基础实践效果(正确度/加速比)难度工作量独立性目录1. 设计目的、意义(功能描述) (1)2. 方案分析(解决方案) (1)3. 设计分析 (1)3.1 串行算法设计 (1)3.2 并行算法设计 (1)3.3 理论加速比分析 (2)4. 功能模块实现与最终结果分析 (2)4.1 基于OpenMP的并行算法实现 (2)4.1.1 主要功能模块与实现方法 (2)4.1.2 实验加速比分析 (3)4.2 基于MPI的并行算法实现 (3)4.2.1 主要功能模块与实现方法 (3)4.2.2 实验加速比分析 (4)4.3 基于Java的并行算法实现 (4)4.3.1 主要功能模块与实现方法 (4)4.3.2 实验加速比分析 (5)4.4 基于Windows API的并行算法实现 (5)4.4.1 主要功能模块与实现方法 (5)4.4.2 实验加速比分析 (6)4.5 基于.net的并行算法实现 (6)4.5.1 主要功能模块与实现方法 (6)4.5.2 实验加速比分析 (6)4.6并行计算技术在实际系统中的应用 (6)4.6.1 主要功能模块与实现方法 (6)4.6.2 实验加速比分析 (7)5. 设计体会 (7)6. 附录 (9)6.1 基于OpenMP的并行程序设计 (9)6.1.1 代码及注释 (9)6.1.2 执行结果截图 (11)6.1.3 遇到的问题及解决方案 (12)6.2 基于MPI的并行程序设计 (12)6.1.1 代码及注释 (12)6.2.2 执行结果截图 (12)6.2.3 遇到的问题及解决方案 (16)6.3 基于Java的并行程序设计 (19)6.3.1 代码及注释 (19)6.3.2 执行结果截图 (22)6.3.3 遇到的问题及解决方案 (24)6.4 基于Windows API的并行程序设计 (25)6.4.1 代码及注释 (25)6.4.2 执行结果截图 (25)6.4.3 遇到的问题及解决方案 (30)6.5 基于.net的并行程序设计 (30)6.5.1 代码及注释 (30)6.5.2 执行结果截图 (34)6.5.3 遇到的问题及解决方案 (35)6.6并行计算技术在实际应用系统的应用 (37)6.6.1 代码及注释 (37)6.6.2 执行结果截图 (37)6.6.3 遇到的问题及解决方案 (42)1. 设计目的、意义(功能描述)设计一个计算向量夹角的WinForm窗体应用,用户只需要在窗体上输入向量的维度,系统随机产生两个向量并将计算结果显示在窗体上。
求两个n维向量的夹角,要用到求向量夹角的数学公式,当向量维度较小时计算量不大,而当维度过大时特别是百万级甚至千万级别的时候计算量就很大了,用并行计算求向量夹角,可以将任务分配给多个处理器,减小运算时间。
所以要设计一个并行计算夹角的方法,提高计算速度,把并行和串行计算时间做个比较显示在窗体上。
窗体应用比控制台程序更方便用户操作,简单直观,页面也更加友好。
2. 方案分析(解决方案)定义两个数组分别存放两个向量,用for循环将产生的随机数赋值给数组。
假设有两个向量X,Y X=(x1,x2,……,xn),Y=(y1,y2,……,yn)计算X,Y夹角的公式是:cos(X,Y)=XY/(|X|·|Y|)=(x1·y1+x2·y2+…+xn·yn)/[(x1²+x2²+…+xn²)1/2·(y1²+y2²+…+yn²)1/2]。
由3个for循环分别实现求向量积和两个向量的模,最后用公式计算即可。
3. 设计分析3.1 串行算法设计输入:向量的维度n输出:两个随机向量的夹角syy_angleBegin给存放向量的数组动态分配内存空间For i=0 to i=n-1 do产生随机数给数组x赋值endForFor i=0 to i=n-1 do产生随机数给数组y赋值endForFor i=0 to i=n-1 do计算向量积endForFor i=0 to i=n-1 do计算向量X模endForFor i=0 to i=n-1 do计算向量Y模endFor利用公式计算夹角End3.2 并行算法设计输入:向量的维度n输出:两个随机向量的夹角syy_angleBegin给存放向量的数组动态分配内存空间For i=0 to i=n-1 do产生随机数给数组x赋值endForFor i=0 to i=n-1 do产生随机数给数组y赋值endFor3个for循环串行执行,每个for循环由p个核并行执行:p个核同时执行第一个for循环For i=0 to i=n-1 do计算向量积endForp个核同时执行第二个for循环For i=0 to i=n-1 do计算向量X模endForp个核同时执行第三个for循环For i=0 to i=n-1 do计算向量Y模endFor利用公式计算夹角End3.3 理论加速比分析设加速比为S,串行运行时间为Ts,并行的运行时间为Tp。
假设一次运算作为一个时间单位,对于串行算法来说其时间复杂度为O(n) 即Ts=O(n) ,对于并行算法来说,由于有p个处理器同时运行,则其时间复杂度为O(n/p) 即Tp=O(n/p) ,所以理论加速比S=Ts/Tp=O(n)/O(n/p)=p。
4. 功能模块实现与最终结果分析4.1 基于OpenMP的并行算法实现4.1.1 主要功能模块与实现方法1:向量x,y赋值,用产生的随机数对存放向量的数组赋值,得到两个随机向量srand((int)time(0));//数组X赋值for(i=0;i<n;i++){j=(int)(100*rand()/(RAND_MAX+1.0)); //随机产生的数x[i]=j;}//数组Y赋值for(i=0;i<n;i++){j=(int)(100*rand()/(RAND_MAX+1.0)); //随机产生的数y[i]=j;}2:计算向量积,向量x,y的模用并行实现。
设置两个线程,用reduction实现并行计算,两个线程都会创建一个reduction变量的私有副本,在OPENMP区域结束后,将各个线程的计算结果相加赋值给原来的变量。
#pragma omp parallel for reduction(+:syy_outer_product)for(i=0;i<n;i++){syy_outer_product=syy_outer_product+x[i]*y[i];//计算向量积}计算向量X,Y的模方法与上面类似4.1.2 实验加速比分析线程数设置为2时,向量维数小时,由于精度问题,运行时间显示为0,加速比无法计算。
向量维数到达百万级以上,加速比介于1到2之间,根据向量维数的变化,加速比有一定的变化但不会超过范围。
4.2 基于MPI的并行算法实现4.2.1 主要功能模块与实现方法使用MPI群集通信,由0进程接收输入的数组长度n,给数组动态分配内存后,用产生的随机数给数组赋值。
用MPI_Bcast先将数组长度广播给其他进程,由其他进程给数组动态分配内存后,再将数组值广播给其他进程。
求向量积,向量模的for由多个进程同时执行,将0到n-1次循环分配给P个进程,每个进程从i=myid开始执行,循环一次i加进程数。
将每个进程的计算结果用MPI_Reduce函数规约。
1:由0进程进行随机数组动态分配内存和赋值操作if(myid==0){………//为数组x,y动态分配空间x = (int*)malloc(n * sizeof(int));y = (int*)malloc(n * sizeof(int));srand((int)time(0));//数组X赋值for(i=0;i<n;i++){j=(int)(10*rand()/(RAND_MAX+1.0)); //随即产生的数x[i]=j;}数组y赋值同上}starttime=MPI_Wtime();}2:用MPI_Bcast()函数将数组长度和值广播给其他进程MPI_Bcast(&n,1,MPI_LONG,0,MPI_COMM_WORLD);//将n值广播出去MPI_Bcast(x,n,MPI_INT,0,MPI_COMM_WORLD);//将x值广播出去MPI_Bcast(y,n,MPI_INT,0,MPI_COMM_WORLD);//将y值广播出去3:用MPI_Reduce()函数对各个进程的计算结果规约MPI_Reduce(&my_product,&syy_outer_product,1,MPI_LONG_DOUBLE,MPI_SUM,0,MPI_COMM_WORLD); MPI_Reduce(&my_mol_x,&syy_mol_x,1,MPI_LONG_DOUBLE,MPI_SUM,0,MPI_COMM_WORLD);MPI_Reduce(&my_mol_y,&syy_mol_y,1,MPI_LONG_DOUBLE,MPI_SUM,0,MPI_COMM_WORLD);4:多个进程同时执行for循环for(i=syy_myid;i<n;i+=syy_numprocs){product+=x[i]*y[i];//计算向量积}计算向量x,y模与上面类似5:串行部分由0进程完成,在执行完并行计算后,再由0进程单独完成串行操作. if(syy_myid==0 )里执行的串行操作4.2.2 实验加速比分析并行时间比串行时间要长,加速比低于1,MPI并行是进程间相互通信传递数据。
设置两个进程时,在0进程里输入向量维度,由0进程对向量数组赋值。
再将n值和x,y动态数组广播给其他进程。
串行计算只有0进程独立完成,可能是进程间通信过多使并行额外开销太大。
4.3 基于Java的并行算法实现4.3.1 主要功能模块与实现方法1:继承Thread类,创建两个线程thread1,thread2。
用start方法开始线程。
使用join()方法等待线程结束后再继续执行。
javaand thread1=new javaand(0,n,x,y);javaand thread2=new javaand(1,n,x,y);startTime=System.currentTimeMillis();thread1.start();thread2.start();thread1.join();thread2.join();2:两个线程同时执行run函数,thread1循环从0到n-1,每次循环i加2,thread2循环从1到n-1,每次循环i加2.最后两个线程的计算结果相加public void run(){for(long i=start;i<end;i+=2){syy_outer_product+=x[(int)i]*y[(int)i];//计算向量积}for(long i=start;i<end;i+=2){syy_mol_x+=x[(int)i]*x[(int)i];//计算向量X模}for(long i=start;i<end;i+=2){syy_mol_y+=y[(int)i]*y[(int)i];//计算向量Y模}}3:用count函数实现串行计算,循环从0到n-1,每次循环i加1.循环部分代码与run方法中类似。
