omp并行计算课程报告
多核多线程技术OpenMP_实验报告2
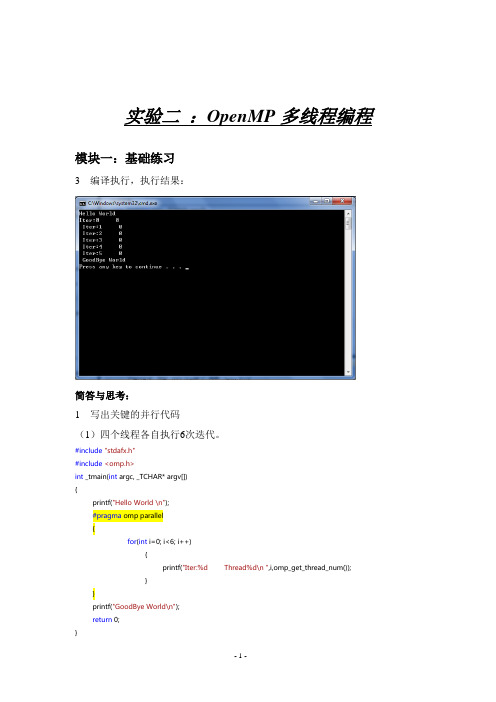
实验二:OpenMP多线程编程模块一:基础练习3 编译执行,执行结果:简答与思考:1 写出关键的并行代码(1)四个线程各自执行6次迭代。
#include"stdafx.h"#include<omp.h>int _tmain(int argc, _TCHAR* argv[]){printf("Hello World \n");#pragma omp parallel{for(int i=0; i<6; i++){printf("Iter:%d Thread%d\n ",i,omp_get_thread_num());}}printf("GoodBye World\n");return 0;}(2)四个线程协同完成6次迭代。
#include"stdafx.h"#include<omp.h>int _tmain(int argc, _TCHAR* argv[]){printf("Hello World \n");#pragma omp parallel{#pragma omp forfor(int i=0; i<6; i++){printf("Iter:%d Thread%d\n ",i,omp_get_thread_num());}}printf("GoodBye World\n");return 0;}2 附加练习:(1)编译执行下面的代码,写出两种可能的执行结果。
int i=0,j = 0;#pragma omp parallel forfor ( i= 2; i < 7; i++ )for ( j= 3; j< 5; j++ )printf(“i = %d, j = %d\n”, i, j);可能的结果:1种2种i=2,j=3 i=2,j=3i=2,j=4 i=2,j=4i=3,j=3 i=3,j=3i=3,j=4 i=3,j=4i=6,j=3 i=5,j=3i=6,j=4 i=5,j=4i=4,j=3 i=5,j=3i=4,j=4 i=5,j=4i=5,j=3 i=6,j=3i=5,j=4 i=6,j=4(2)编译执行下面的代码,写出两种可能的执行结果。
《并行算法》课程总结与复习

并行算法》课程总结与复习Ch1 并行算法基础1.1并行计算机体系结构并行计算机的分类SISD,SIMD,MISD,MIMD ; SIMD,PVP,SMP,MPP,COW,DSM 并行计算机的互连方式静态: LA(LC),MC,TC,MT,HC,BC,SE动态: Bus, Crossbar Switcher, MIN(Multistage InterconnectionNetworks)1.2并行计算模型PRAM 模型: SIMD-SM ,又分 CRCW(CPRAM,PPRAM,APRAM),CREW,EREWSIMD-IN 模型: SIMD-DM异步 APRAM 模型: MIMD-SMBSP模型:MIMD-DM,块内异步并行,块间显式同步LogP 模型: MIMD-DM ,点到点通讯1.3并行算法的一般概念并行算法的定义并行算法的表示并行算法的复杂度:运行时间、处理器数目、成本及成本最优、加速比、并行效率、工作量并行算法的 WT表示:Brent定理、WT最优加速比性能定律并行算法的同步和通讯Ch2 并行算法的基本设计技术基本设计技术平衡树方法:求最大值、计算前缀和倍增技术:表序问题、求森林的根分治策略: FFT 分治算法划分原理:均匀划分(PSRS排序)、对数划分(并行归并排序)、方根划分(Valiant归并排序)、功能划分((m,n)-选择)流水线技术:五点的 DFT 计算Ch3 比较器网络上的排序和选择算法3.1Batcher归并和排序0-1 原理的证明奇偶归并网络:计算流程和复杂性(比较器个数和延迟级数)双调归并网络:计算流程和复杂性(比较器个数和延迟级数)Batcher排序网络:原理、种类和复杂性3.2(m, n)-选择网络分组选择网络平衡分组选择网络及其改进Ch4 排序和选择的同步算法4.1一维线性阵列上的并行排序算法4.2二维Mesh上的并行排序算法ShearSort排序算法Thompson&Kung 双调排序算法及其计算示例4.3Sto ne双调排序算法4.4Akl并行k-选择算法:计算模型、算法实现细节和时间分析4.5Valia nt并行归并算法:计算模型、算法实现细节和时间分析4.7 Preparata并行枚举排序算法:计算模型和算法的复杂度Ch5 排序和选择的异步和分布式算法5.1MIMD-CREW 模型上的异步枚举排序算法5.2MIMD-TC 模型上的异步快排序算法5.3分布式k-选择算法Ch6 并行搜索6.1单处理器上的搜索6.2SIMD 共享存储模型上有序表的搜索:算法6.3SIMD 共享存储模型上随机序列的搜索:算法6.4树连接的 SIMD 模型上随机序列的搜索:算法6.5网孔连接的 SIMD 模型上随机序列的搜索:算法和计算示例Ch8 数据传输与选路8.1引言信包传输性能参数维序选路(X-Y选路、E-立方选路)选路模式及其传输时间公式8.2单一信包一到一传输SF和CT传输模式的传输时间(一维环、带环绕的Mesh、超立方)8.3一到多播送SF和CT传输模式的传输时间(一维环、带环绕的Mesh、超立方)及传输方法8.4多到多播送SF和CT传输模式的传输时间(一维环、带环绕的Mesh、超立方)及传输方法8.5贪心算法(书 8.2)二维阵列上的贪心算法蝶形网上的贪心算法8.6随机和确定的选路算法(书 8.3)Ch12 矩阵运算12.1矩阵的划分:带状划分和棋盘划分,有循环的带状划分和棋盘划分12.2矩阵转置:网孔和超立方连接的算法及其时间分析12.3矩阵向量乘法带状划分的算法及其时间分析棋盘划分的算法及其时间分析12.4矩阵乘法简单并行分块算法Cannon算法及其计算示例Fox 算法及其计算示例 DNS 算法及其计算示例 Systolic 算法Ch13 数值计算13.1稠密线性方程组求解 SIMD-CREW 的上三角方程组回代算法SIMD-CREW 上的 Gauss-Jordan算法MIMD-CREW 上的 Gauss-Seidel算法13.2稀疏线性方程组的求解三对角方程组的奇偶规约求解法Gauss-Seide迭代法的红黑着色并行算法13.3非线性方程的求根Ch14 快速傅立叶变换FFT14.1快速傅里叶变换 (FFT) 离散傅里叶变换 (DFT) 串行 FFT 递归算法及其计算原理串行 FFT 蝶式计算及其蝶式计算流图14.2DFT 直接并行算法SIMD-MT 上的并行 DFT 算法14.3并行 FFT 算法 SIMD-MC 上的 FFT 算法 SIMD-BF 上的 FFT 算法及其时间分析Ch15 图论算法15.1图的并行搜索P-深度优先搜索及其计算示例 p-宽深优先搜索及其计算示例 p-宽度优先搜索及其计算示例15.2图的传递闭包基于布尔矩阵乘积的算法原理计算示例SIMD-CC 上的传递闭包算法15.3图的连通分量基于传递闭包的算法基于顶点合并的算法15.4图的最短路径基于矩阵乘积的算法原理计算示例15.5图的最小生成树 SIMD-EREW 模型上的 Prim 算法算法的时间分析Ch17 组合搜索17.1基于分治法的与树搜索与树并行搜索过程处理器数目与搜索效率关系17.2基于分枝限界法的或树搜索串行分枝限界法示例: 0-1 背包问题,8- 谜问题及其搜索算法的并行化 TSP问题的分枝限界算法及其并行化Ch18 随机算法18.1引言基本知识:随机算法的定义、分类时间复杂性度量设计方法18.2低度顶点部分独立集串行算法随机并行算法及其正确性证明18.5多项式恒等的验证基本原理和方法矩阵乘积的验证原理。
华科并行实验报告

一、实验模块计算机科学与技术二、实验标题并行计算实验三、实验目的1. 了解并行计算的基本概念和原理;2. 掌握并行编程的基本方法;3. 通过实验加深对并行计算的理解。
四、实验环境1. 操作系统:Windows 102. 编程语言:C++3. 并行计算平台:OpenMP五、实验步骤1. 准备实验环境首先,在计算机上安装OpenMP库,并配置环境变量。
2. 编写并行计算程序编写一个简单的并行计算程序,实现以下功能:(1)计算斐波那契数列的第n项;(2)计算素数的个数;(3)计算矩阵乘法。
以下为斐波那契数列的并行计算程序示例:```cpp#include <omp.h>#include <iostream>using namespace std;int main() {int n = 30;int fib[31] = {0};fib[0] = 0;fib[1] = 1;#pragma omp parallel forfor (int i = 2; i <= n; i++) {fib[i] = fib[i - 1] + fib[i - 2];}cout << "斐波那契数列的第" << n << "项为:" << fib[n] << endl; return 0;}```3. 编译程序使用g++编译器编译程序,并添加OpenMP库支持。
```bashg++ -fopenmp -o fib fib.cpp```4. 运行程序在命令行中运行编译后的程序,观察结果。
5. 分析结果通过对比串行计算和并行计算的结果,分析并行计算的优势。
六、实验过程1. 准备实验环境,安装OpenMP库并配置环境变量;2. 编写并行计算程序,实现斐波那契数列的并行计算;3. 编译程序,并添加OpenMP库支持;4. 运行程序,观察结果;5. 分析结果,对比串行计算和并行计算的性能。
《并行计算导论》课程报告
北京科技大学《并行计算导论》实验报告题目:矩阵向量乘法的并行化学院计算机与通信工程学院班级计1301 1303 1304班指导教师李建江时间 2016年3月22日至3月31日一、任务描述基于MPI和OpenMP,分别实现矩阵向量乘法的并行化。
对实现的并行程序进行正确性测试和性能测试,并对测试结果进行分析。
二、矩阵向量乘法串行算法描述与分析1. 串行算法描述在线性代数中,矩阵和向量的乘法是将每行矩阵的每个元素乘以向量中的每个元素,得到一个新的向量,要求矩阵是N*N阶,向量是N阶,这样相乘后,得到一个新的N阶向量。
利用串行算法,设置循环,让矩阵中的每一行的元素乘以完向量的每个元素后得到一个数值再进行下一行的乘法,一直到最后一行的乘法结束,得到新的向量。
2. 空间复杂度分析对于N阶的矩阵向量乘法,A*b=x,定义数据类型为long,则需要的存储空间为(N^2+2*N)*4 Byte 。
(矩阵数:N^2+向量数N+结果N)3. 时间复杂度分析对于N阶的矩阵向量乘法,A*b=x,需要串行算法执行的次数为:N^2*(N-1)三、矩阵向量乘法的并行化(一)基于MPI的矩阵向量的并行化1. 并行策略(含图示)因为矩阵乘以向量,每行的乘法是相互独立的,所以可以把N阶矩阵按行平均分配给各个进程,让每个进程分别处理分配给它的数据块。
2. 并行算法描述先为程序指定阶数,然后用随机数生成N阶方阵和向量,采用静态均匀负载,为每个处理器分配相同数量的数组元素,做到负载相对比较均衡(由于可能存在0元素,使得负载相对有些偏差)。
然后把N阶方阵和向量显示出来,做MPI静态并行计算,然后将得出的结果显示出来3. 空间复杂度分析设进程数为n,数据类型为long,则N阶矩阵向量乘法的所需的空间为:N^2+n*N+N,(矩阵空间N^2+n倍的b向量空间n*N+结果N)4. 时间复杂度分析假设负载均衡,假设最小的划分块大于等于矩阵的一行,由于将行分块划分给各个进程,所以整体的时间是1/n倍的串行算法的时间复杂度,即1/n*N^2*(N-1)(二)基于OpenMP的矩阵向量的并行化1. 并行策略(含图示)与MPI并行策略类似,把矩阵按行分块,与向量相乘,但是可以采用更为灵活的池技术动态调用,更加充分利用了计算资源。
华科计算机并行实验报告

课程设计报告题目:并行实验报告课程名称:并行编程原理与实践专业班级:学号:姓名:指导教师:报告日期:计算机科学与技术学院目录1,实验一 (1)1 实验目的与要求 (1)1.1实验目的 (1)1.2实验要求 (1)2 实验内容 (1)2.1.1熟悉pthread编程 (1)2.1.2简单的thread编程 (2)2.2.1熟悉openMP编程 (3)2.3.1熟悉MPI编程 (4)2,实验2~5 (7)1 实验目的与要求 (7)2 算法描述 (7)3.实验方案 (8)4实验结果与分析 (8)3 心得体会 (10)附录: (10)3 蒙特.卡罗算法求π的并行优化 (19)1.蒙特.卡罗算法基本思想 (19)2.工作过程 (20)3.算法描述 (20)4 设计与实现 (21)5 结果比较与分析 (23)6 思考与总结 (24)1,实验一1 实验目的与要求1.1实验目的1)熟悉并行开发环境,能进行简单程序的并行开发,在Linux下熟练操作。
2)熟悉一些并行工具,如pthread,OpenMP,MPI等进行并行编程3)培养并行编程的意识1.2实验要求1)利用pthread、OpenMP、MPI等工具,在Linux下进行简单的并行编程,并且掌握其编译、运行的方法。
2)理解并行计算的基础,理解pthread、OpenMP、MPI等并行方法。
2 实验内容2.1.1熟悉pthread编程Linux系统下的多线程遵循POSIX线程接口,称为 pthread。
编写Linux下的多线程程序,需要使用头文件pthread.h,连接时需要使用库libpthread.a。
下面是pthread编程的几个常用函数:1,int pthread_create(pthread_t *restrict tidp,const pthread_attr_t *restrict attr, void *(*start_rtn)(void),void *restrict arg);返回值:若是成功建立线程返回0,否则返回错误的编号形式参数:pthread_t *restrict tidp 要创建的线程的线程id指针const pthread_attr_t *restrict attr 创建线程时的线程属性void* (start_rtn)(void) 返回值是void类型的指针函数void *restrict arg start_rtn的行参2 , int pthread_join( pthread_t thread, void **retval );thread表示线程ID,与线程中的pid概念类似;retval用于存储等待线程的返回值连接函数pthread_join()是一种在线程间完成同步的方法。
并行计算实验报告一

并行计算实验报告一江苏科技大学计算机科学与工程学院实验报告评定成绩指导教师实验课程:并行计算宋英磊实验名称:Java多线程编程学号: 姓名: 班级: 完成日期:2014年04月22日1.1 实验目的(1) 掌握多线程编程的特点;(2) 了解线程的调度和执行过程;(3) 掌握资源共享访问的实现方法。
1.2 知识要点1.2.1线程的概念(1) 线程是程序中的一个执行流,多线程则指多个执行流;(2) 线程是比进程更小的执行单位,一个进程包括多个线程;(3) Java语言中线程包括3部分:虚拟CPU、该CPU执行的代码及代码所操作的数据。
(4) Java代码可以为不同线程共享,数据也可以为不同线程共享; 1.2.2 线程的创建(1) 方式1:实现Runnable接口Thread类使用一个实现Runnable接口的实例对象作为其构造方法的参数,该对象提供了run方法,启动Thread将执行该run方法;(2) 方式2:继承Thread类重写Thread类的run方法;1.2.3 线程的调度(1) 线程的优先级, 取值范围1,10,在Thread类提供了3个常量,MIN_PRIORITY=1、MAX_ PRIORITY=10、NORM_PRIORITY=5;, 用setPriority()设置线程优先级,用getPriority()获取线程优先级; , 子线程继承父线程的优先级,主线程具有正常优先级。
(2) 线程的调度:采用抢占式调度策略,高优先级的线程优先执行,在Java 中,系统按照优先级的级别设置不同的等待队列。
1.2.4 线程的状态与生命周期说明:新创建的线程处于“新建状态”,必须通过执行start()方法,让其进入到“就绪状态”,处于就绪状态的线程才有机会得到调度执行。
线程在运行时也可能因资源等待或主动睡眠而放弃运行,进入“阻塞状态”,线程执行完毕,或主动执行stop方法将进入“终止状态”。
1.2.5 线程的同步--解决资源访问冲突问题(1) 对象的加锁所有被共享访问的数据及访问代码必须作为临界区,用synchronized加锁。
并行计算与分布式系统实验报告

并行计算与分布式系统实验报告1. 引言“彼岸花,开过就只剩残香。
”这是一句来自中国古代文学名篇《红楼梦》的名言。
它告诉我们,珍贵的事物往往难以长久保持,只有通过合理的分工与协作,才能实现最大的效益。
在计算机科学领域,这句话同样适用。
并行计算和分布式系统正是通过有效地利用计算资源,实现高效的数据处理与任务分工,从而提高计算效率和系统性能。
2. 并行计算介绍并行计算是一种利用多个处理器或计算节点同时执行计算任务的方法。
它通过将大型计算问题划分为多个小的子问题,并同时解决这些子问题,大幅提高计算速度。
并行计算有两种主要的形式:数据并行和任务并行。
数据并行将大型数据集分割成多个小块,分别交给不同的处理器进行处理;任务并行将不同的任务分配到不同的处理器上同时执行。
3. 分布式系统介绍分布式系统是一组互连的计算机节点,通过网络相互协作以实现共同的目标。
分布式系统可以分布在不同地理位置的计算机上,通过消息传递和远程过程调用等通信机制实现节点间的协作。
分布式系统具有高可靠性、可扩展性和容错性的特点,并广泛应用于云计算、大数据处理和分布式存储等领域。
4. 并行计算和分布式系统的关系并行计算和分布式系统之间存在密切的关系。
分布式系统提供了并行计算所需的底层基础设施和通信机制,而并行计算则借助分布式系统的支持,实现任务的并行处理和数据的高效交换。
通过充分利用分布式系统中的计算资源,可以实现更高效的并行计算,并加速大规模数据处理和科学计算。
5. 并行计算与分布式系统实验在完成本次实验中,我们使用了一台集群式分布式系统,包括8台计算节点和1台主控节点。
我们利用MPI(Message Passing Interface)实现了一个并行计算的案例,该案例通过并行处理大规模图像数据,实现图像的快速处理和分析。
实验中,我们首先将图像数据划分成多个小块,并分发给不同的计算节点进行处理。
每个计算节点利用并行算法对图像进行滤波和边缘检测,然后将处理结果返回给主控节点。
并行计算实验报告

分析 :这样的加速比 , 是符合预测 , 很好的 . 附 :(实验 源码 ) 1 pi.cpp #include <cstdio> #include <cstdlib> #include <cstring> #include <cctype> #include <cmath> #include <ctime> #include <cassert>
#include <climits> #include <iostream> #include <iomanip> #include <string> #include <vector> #include <set> #include <map> #include <queue> #include <deque> #include <bitset> #include <algorithm> #include <omp.h> #define MST(a, b) memset(a, b, sizeof(a)) #define REP(i, a) for (int i = 0; i < int(a); i++) #define REPP(i, a, b) for (int i = int(a); i <= int(b); i++) #define NUM_THREADS 4 using namespace std; const int N = 1e6; double sum[N]; int main() { ios :: sync_with_stdio(0); clock_t st, ed; double pi = 0, x; //串行 st = clock(); double step = 1.0 / N; REP(i, N) { x = (i + 0.5) * step; pi += 4.0 / (1.0 + x * x); } pi /= N; ed = clock(); cout << fixed << setprecision(10) << "Pi: " << pi << endl; cout << fixed << setprecision(10) << "串行用时: " << 1.0 * (ed - st) / CLOCKS_PER_SEC << endl; //并行域并行化 pi = 0; omp_set_num_threads(NUM_THREADS); st = clock(); int i; #pragma omp parallel private(i) { double x; int id; id = omp_get_thread_num();
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
并行计算与多核多线程技术课程报告专业班级学号姓名成绩2015 年9月21日4.1 基于OpenMP的并行算法实现4.1.1 主要功能模块与实现方法#pragma omp parallel num_threads(2){for (xxj_g = 0; xxj_g <xxj_M/2; xxj_g++){for (xxj_d = 0; xxj_d< xxj_P; xxj_d++){xxj_C[xxj_g][xxj_d] = 0;for (xxj_k = 0; xxj_k < xxj_N; ++xxj_k){xxj_C[xxj_g][xxj_d] += xxj_A[xxj_g][xxj_k] *xxj_B[xxj_k][xxj_d];}}}for (xxj_g = xxj_M/2; xxj_g <xxj_M; xxj_g++){for (xxj_d = 0; xxj_d < xxj_P; xxj_d++){xxj_C[xxj_g][xxj_d] = 0;for (xxj_k = 0; xxj_k < xxj_N; ++xxj_k){ // cout << "2num=" << omp_get_thread_num() << endl;xxj_C[xxj_g][xxj_d] += xxj_A[xxj_g][xxj_k] * xxj_B[xxj_k][xxj_d];}}}}(1)将两个矩阵的乘法进行并行运算打开2个进程#pragma omp parallel num_threads(4)注意输出和输入部分的for循环不能用并行,否则会出现输入输出的个数出错的问题。
(2)将得到最终结果的xxj_C[i][j]分成两个子矩阵进行运算第一个子矩阵为xxj_A[i][j]的M/2行乘以xxj_B[i][j]的P列的结果,第二个子矩阵为xxj_A[i][j]的M-M/2行乘以xxj_B[i][j]的P列的结果。
参照顺序型的程序for (xxj_i = 0; xxj_i < xxj_M; xxj_i++){for (xxj_j = 0; xxj_j < xxj_P; xxj_j++){xxj_C[xxj_i][xxj_j] = 0;for (xxj_k = 0; xxj_k < xxj_N; ++xxj_k){xxj_C[xxj_i][xxj_j] += xxj_A[xxj_i][xxj_k] * xxj_B[xxj_k][xxj_j];}}}4.1.2 实验加速比分析取三组数据进行比较第一次第二次第三次顺序时间124748 27512 31403串行时间72290 18597 18541加速比 1.7256 1.4793 1.69375. 设计体会通过这次实验,我了解了并行计算的运行与设计方式,更了解了它的方便和快捷,对于一个程序来说,节省了时间无疑是一个最大的优势,尤其是面对很多的数据的时候,特别的是在我测试数据的时候,要想办法找出成百上千的数据进行测试,虽然它的优点很多,也具有一定的挑战性,不过并行计算的地位始终是非常重要的。
6. 附录6.1 基于OMP的并行程序设计6.1.1 代码及注释并行代码:#include "stdafx.h"#include <windows.h>#include<stdio.h>#include<time.h>#include<omp.h>#include<iostream>//使用C++语句using namespace std;int _tmain(int argc, _TCHAR* argv[]){clock_t xxj_t1 = clock();//获取当前时间int xxj_M, xxj_N, xxj_P, xxj_i, xxj_j, xxj_k,xxj_a,xxj_b,xxj_g,xxj_d,xxj_e,xxj_f;cin >> xxj_M >>xxj_ N >> xxj_P;int xxj_A[100][100];int xxj_B[100][100];int xxj_C[100][100];for (xxj_i = 0; xxj_i < xxj_M;xxj_ i++){for (xxj_j = 0; xxj_j < xxj_N; xxj_j++){cin >> xxj_A[xxj_i][xxj_j];}}for (xxj_a = 0; xxj_a < N; xxj_a++){for (xxj_b = 0; xxj_b < xxj_P; xxj_b++){cin >> xxj_B[xxj_a][xxj_b];}}#pragma omp parallel num_threads(2){for (xxj_g = 0; xxj_g < xxj_M/2; xxj_g++){for (xxj_d = 0; xxj_d < xxj_P;xxj_ d++){xxj_C[xxj_g][xxj_d] = 0;for (xxj_k = 0; xxj_k < xxj_N; ++xxj_k){xxj_C[xxj_g][xxj_d] += xxj_A[xxj_g][xxj_k] * xxj_B[xxj_k][xxj_d];}}}for (xxj_g = xxj_M/2; xxj_g < xxj_M; xxj_g++){for (xxj_d = 0; xxj_d < xxj_P; xxj_d++){xxj_C[xxj_g][xxj_d] = 0;for (xxj_k = 0; xxj_k < xxj_N; ++xxj_k){// cout << "xxj_num=" << omp_get_thread_num() << endl;xxj_C[xxj_g][xxj_d] += xxj_A[xxj_g][xxj_k] * xxj_B[xxj_k][xxj_d];}}}}for (xxj_e = 0; xxj_e < xxj_M; xxj_e++){cout << endl;for (xxj_f = 0; xxj_f < xxj_P; xxj_f++){cout << xxj_C[xxj_e][xxj_f] << " ";}}clock_t xxj_t2 = clock();int xxj_t;xxj_t = xxj_t2 - xxj_t1;cout << endl;cout << "t=" << xxj_ct << "s" << endl;system("pause");return 0;}顺序代码:#include "stdafx.h"#include <windows.h>#include<stdio.h>#include<time.h>#include<omp.h>#include<iostream>//使用C++语句using namespace std;int _tmain(int argc, _TCHAR* argv[]){clock_t xxj_t1 = clock();//获取当前时间int xxj_M, xxj_N, xxj_P, xxj_i, xxj_j, xxj_k,xxj_a,xxj_b,xxj_g,xxj_d,xxj_e,xxj_f;cin >> xxj_M >>xxj_ N >> xxj_P;int xxj_A[100][100];int xxj_B[100][100];int xxj_C[100][100];for (xxj_i = 0; xxj_i < xxj_M;xxj_ i++){for (xxj_j = 0; xxj_j < xxj_N; xxj_j++){cin >> xxj_A[xxj_i][xxj_j];}}for (xxj_a = 0; xxj_a < N; xxj_a++){for (xxj_b = 0; xxj_b < xxj_P; xxj_b++){cin >> xxj_B[xxj_a][xxj_b];}}for (xxj_g = 0; xxj_g < xxj_M; xxj_g++){for (xxj_d = 0; xxj_d < xxj_P;xxj_ d++){xxj_C[xxj_g][xxj_d] = 0;for (xxj_k = 0; xxj_k < xxj_N; ++xxj_k){xxj_C[xxj_g][xxj_d] += xxj_A[xxj_g][xxj_k] * xxj_B[xxj_k][xxj_d];}}}for (xxj_e = 0; xxj_e < xxj_M; xxj_e++){cout << endl;for (xxj_f = 0; xxj_f < xxj_P; xxj_f++){cout << xxj_C[xxj_e][xxj_f] << " ";}}clock_t xxj_t2 = clock();int xxj_t;xxj_t = xxj_t2 - xxj_t1;cout << endl;cout << "xxj_st=" << xxj_t << "s" << endl;system("pause");return 0;}6.1.2 执行结果截图为了方便已经将顺序和并行部分合为一个代码,(1)小数据量验证正确性的执行结果首先利用小数据判断程序是否正确:截图为:(2)大数据量获得较好加速比的执行结果顺序的时间为xxj_st并行的时间为xxj_ct加速比为xxj_bi测试数据为50*50的两个矩阵,数据为随机生成的,生成随机数据的代码为:#include<iostream>#include<stdio.h>#include<time.h>#include<stdlib.h>#include <fstream>using namespace std;int main(){int xxj_nl=0;int xxj_nj=1000;int xxj_nCont=0;srand(time(NULL));ofstream xxj_ofs("xxj_d2.txt");while(1){xxj_nl=rand()%xxj_nj;xxj_ofs<<xxj_nl<<" ";xxj_nCont++;if(xxj_nCont==5000){break;}}xxj_ofs.close();}截图为:加速比为1.53896.1.3 遇到的问题及解决方案(1)问题一将输入输出的for循环放入了并行语句中错误代码及后果#pragma omp parallel num_threads(2){for (xxj_i = 0; xxj_i < xxj_M;xxj_ i++){for (xxj_j = 0; xxj_j < xxj_N; xxj_j++){cin >> xxj_A[xxj_i][xxj_j];}}for (xxj_a = 0; xxj_a < N; xxj_a++){for (xxj_b = 0; xxj_b < xxj_P; xxj_b++){cin >> xxj_B[xxj_a][xxj_b];}}for (xxj_g = 0; xxj_g < xxj_M/2; xxj_g++){for (xxj_d = 0; xxj_d < xxj_P;xxj_ d++){xxj_C[xxj_g][xxj_d] = 0;for (xxj_k = 0; xxj_k < xxj_N; ++xxj_k){xxj_C[xxj_g][xxj_d] += xxj_A[xxj_g][xxj_k] * xxj_B[xxj_k][xxj_d];}}}for (xxj_g = xxj_M/2; xxj_g < xxj_M; xxj_g++){for (xxj_d = 0; xxj_d < xxj_P; xxj_d++){xxj_C[xxj_g][xxj_d] = 0;for (xxj_k = 0; xxj_k < xxj_N; ++xxj_k){// cout << "xxj_num=" << omp_get_thread_num() << endl;xxj_C[xxj_g][xxj_d] += xxj_A[xxj_g][xxj_k] * xxj_B[xxj_k][xxj_d];}}}for (xxj_e = 0; xxj_e < xxj_M; xxj_e++){cout << endl;for (xxj_f = 0; xxj_f < xxj_P; xxj_f++){cout << xxj_C[xxj_e][xxj_f] << " ";}}}正确代码for (xxj_i = 0; xxj_i < xxj_M;xxj_ i++){for (xxj_j = 0; xxj_j < xxj_N; xxj_j++){cin >> xxj_A[xxj_i][xxj_j];}}for (xxj_a = 0; xxj_a < N; xxj_a++){for (xxj_b = 0; xxj_b < xxj_P; xxj_b++){cin >> xxj_B[xxj_a][xxj_b];}}#pragma omp parallel num_threads(2){for (xxj_g = 0; xxj_g < xxj_M/2; xxj_g++){for (xxj_d = 0; xxj_d < xxj_P;xxj_ d++){xxj_C[xxj_g][xxj_d] = 0;for (xxj_k = 0; xxj_k < xxj_N; ++xxj_k){xxj_C[xxj_g][xxj_d] += xxj_A[xxj_g][xxj_k] * xxj_B[xxj_k][xxj_d];}}}for (xxj_g = xxj_M/2; xxj_g < xxj_M; xxj_g++){for (xxj_d = 0; xxj_d < xxj_P; xxj_d++){xxj_C[xxj_g][xxj_d] = 0;for (xxj_k = 0; xxj_k < xxj_N; ++xxj_k){// cout << "xxj_num=" << omp_get_thread_num() << endl;xxj_C[xxj_g][xxj_d] += xxj_A[xxj_g][xxj_k] * xxj_B[xxj_k][xxj_d];}}}班级____________ 学号_________________ 姓名______________ 算法名称______________}for (xxj_e = 0; xxj_e < xxj_M; xxj_e++){cout << endl;for (xxj_f = 0; xxj_f < xxj_P; xxj_f++){cout << xxj_C[xxj_e][xxj_f] << " ";}}分析因为并行计算具有同时性,放到输入和输出上用的话会导致输入输出的矩阵含有的数字和个数发生混乱。
