1998年江苏省南京市中考数学试卷
七年级数学竞赛题：数形结合谈数轴
七年级数学竞赛题：数形结合谈数轴数学是研究数和形的学科，在数学里数和形是有密切联系的．我们常用代数的方法来处理几何问题；反过来，也借助于几何图形来处理代数问题，寻找解题思路，这种数与形之间的相互作用叫数形结合，是－种重要的数学思想．运用数形结合思想解题的关键是建立数与形之间的联系，现阶段数轴是数形结合的有力工具，主要体现在以下几个方面：1．利用数轴能形象地表示有理数；2．利用数轴能直观地解释相反数；3．利用数轴比较有理数的大小；4．利用数轴解决与绝对值相关的问题．例1 已知数轴上有A 、B 两点，A 、B 之间的距离为l ，点A 与原点0的距离为3，那么所有满足条件的点B 与原点0的距离之和等于 ． (北京市“迎春杯”竞赛题) 解题思路 确定A 、B 在数轴上的位置，求出A 、B 两点所表示的有理数．例2已知有理数a 、b 、c 在数轴上的对应位置如下图：则1-c +c a -+b a -化简后的结果是( )．(湖北省初中数学竞赛选拔赛试题)(A)b －l (B)2a －6—1(C)l+2a －b －2c (D)1—2c+b解题思路 从数轴上获取关于a 、b 、c 的相关信息，判断代数式c —l ，a －c ，a －b 的正负性．例3 a 、b 、c 在数轴上的位置如图所示：试判定b a b a +-，b a b a -+，cba cb a -+之间的大小关系． 解题思路 推断各分数分子、分母的正负性及大小关系。
……….例4(1)阅读下面材料：点A 、B 在数轴上分别表示实数a 、b ，A 、B两点之间的距离表示为|AB|．当A 、B 两点中有一点在原点时，不妨设点A 在原点，如图1，|AB|=|OB|=|b|=|a-b|；当A 、B 两点都不在原点时，①如图2，点A 、B 都在原点的右边|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|；②如图3，点A、B都在原点的左边，|AB|=|OB|—|OA|=|b|—|a|=-b-(-a)=|a-b|；③如图4，点A、B在原点的两边，|AB|=|OA|+|OB|=|a|+|b|=a+(-b)=|a-b|．综上，数轴上A、B两点之间的距离|AB|=|a-b|．(2)回答下列问题：．①数轴上表示2和5的两点之间的距离是______，数轴上表示一2和一5的两点之间的距离是_______，数轴上表示1和一3的两点之间的距离是_______；②数轴上表示x和－1的两点A和B之间的距离是_____，如果∣AB∣=2，那么x为______；③当代数式∣x+1∣+∣x-2∣取最小值时，相应的x的取值范围是______；④求∣x-1∣+∣x-2∣+∣x-3∣+…+∣x-1997∣的最小值．．(2002年南京市中考题)解题思路通过观察图形，阅读理解代数∣a-b∣所表示的意义，来回答所提出的具体问题．例5某城镇沿环形路有五所小学，依次为－小、二小、三小、四小、五小，它们分别有电脑15、7、1l、3、14台，现在为使各校电脑台数相等，各调几台给邻校：－小给二小，二小给三小，三小给四小，四小给五小，五小给－小，若甲小给乙小－3台，即为乙小给甲小3台，要使电脑移动的总台数最小，应作怎样安排?(湖北省荆州市竞赛题) 解题思路通过设未知数，把调动的电脑总台数用相关代数式表示，解题的关键是，如何将实际问题转化为类似“例4”的问题加以解决．．1．已知数轴上表示负有理数Ⅲ的点是点M，那么在数轴上与点M相距∣m∣个单位的点中，与原点距离较远的点对应的数是_______．(第十五届江苏省竞赛题)2．如果数轴上点A到原点的距离为3，点B到原点的距离为5，那么A、B两点的距离为______．3．在数轴上表示数a的点到原点的距离为3，则以a－3=______．4．已知a>0，b<O且以a+b<O，那么有理数a，b，-a，∣b∣的大小关系是_____________.(用“<”号连接)(北京市“迎春杯”竞赛题)5．已知有理数以在数轴上原点的右方，有理数b在原点的左方，那么( )．(A)ab<b (B)ab>b (C)a+b>0 (D)a－b>O6．如图，a、b为数轴上的两点表示的有理数，在a+b，b—2a，∣a-b∣,∣b∣-∣a∣中，负数的个数有( )．(“祖冲之杯”邀请赛试题)(A)1 (B)2 (C)3 (D))47．有理数a 、b 、c 在数轴上的位置如图所示，式子|a|+|b|+|a+b||b-c|化简结果为( )．(A)2a+3b －c (B)3b －c (C)b+c (D)c －b8．如图所示，在数轴上有六个点，且AB=BC=CD=DE=EF ，则与点C 所表示的数最接近的整数是( )．(A)－l (B)0 (C)1 (D)2(第十二届“希望杯”邀请赛试题)9．已知a 、b 、c 、d 为有理数，在数轴上的位置如图所示：且6∣a ∣=6∣b ∣=3∣c ∣=4∣d ∣=6，求∣3a －2d ∣—∣3b —2a ∣+∣2b －c ∣的值．10．电子跳蚤落在数轴上的某点K 0，第－步从K 。
江苏省南京市届中考考试试题数学(扫描版)
・9・南京市2010年初中毕业生学业考试数 学注車事項：1. 車试您共6页.全总M 分120分.考试时爾为120分仲.考生答II 全邛答在答II 卡上•答在本试卷上无效.2. 请认真播对监痔教師在答II 卡上所帖黙条融冈的姓名、考试证号是否与本人相村合.聲将自己的柱名、強才证号用o.5 色■水签字笔填乌衽答n 卡及本试e±.s .答选择n 必殖用2B1&笔将答•卡上对应的答*标号涂n .如霍改动，谓用warn 干净厨. 再选檢其16答務.答菲选捋•必殖用o.s«*J»fe ■水笺字在答■卡上的摇定位■•各 算他位i«a -w 无效.4.作图必须用2B 铅笔作答.并请加黑加粗，播耳清整・一、送择0（本大11共6小BL 毎小H 2分•共12分.庄毎小&所饴出的四个遶项中崔轩合廉目要求的，请将正■选项U 的字毋代号填涂在答•卡相&位■上）1. -3人一3B.3 G-寺2. it» J ・/的结果是 A. a«B. c rG a*3. 如阳・下列备散中•数紬匕点A 表示的可他是 A ・4的算术平方療 B.4的立方根 C ・8的算术平方根D.8的立方银4. 甲种笈菜保鲜适宜的刼度是1 9〜5・C ・乙种蔬菜保鲜适宜的沮度是3・C~8・C.将这两弹趙菜放在一起阿时保解•适宜的湿度是A. 1X-3TB. 3・C 〜5・C G 5U 〜8_CD.广C~895. 如!B ・在平面血角坐标疑中•芟形QABC 的IM 点C 的坐标ft<3.4）.««点A.B 的坐标分别殳 B.C4.0) J8.4) D.<5«0).(8.4>DiD.』(«38)A.(4.O)X7.4> C.<5.0),(7.4)(95S)效事试■ M2K (^6M>数儒试題« 1 «<共6页)6. toffl.夜晚•小廉从点A 经过踣灯C 的正*方沿A 线走到点B ・他的老长y 他与戊A 之何 的距离z的变化而变化•那么袁示，与工之何函效关麻的图◎大致为yo * oC.D ・二、填空K(水大11共】0小•■絳小題2分.共20分.不■乌出解答过程■请把答拓亶接填禹衽WSfffifittS 上)7. -2的龟对值的结果地 ▲・&殖敷，■士j 中•白变的取A ・9.懈京地铁2号线(介东窿戏八 号些晦恋絵开通乐・刈0憶帙总卵程约为85 000 m.^ 85 000用科鼻记数法表示为—A_・ /B10•如图・O 是恵拔f 上一点.ZAOB-100#・、s^ /g+Z2・▲•・° (MlOfl)订•计算辰*・v^(«>0)的结果是 ▲・12 •若反比例西效的图您绘过点《一2 • —1)・则这个函数的田猱位于第 A ftW. 13 •甲、乙两人S 次射击命中的环ttttT,甲 7 9 8 6 *10 乙7 8 9 8 8割这卿人5次射击命中的环数的平均效丘■■£.■8.方匹兴 ▲ 爲•(填">■、• V■或 ・□・如阳.以0为18心的两个同心Bi 中•大歸的號AB 腿小即的切披・C 为切点.若两08的半径 . 分别为3 em 和5 em •则AB 的长为 Acm.15•如图・点C在©O上•将BI心角ZAOB烧点O按連时什方向餐转利ZA0B，•離转角为a WVaV】80・〉・若ZAOB・30・.ZBCAJ40・.则Za・16. 如图・AB丄BC・AB・BC・2 cm-oX与 & 关于点O中心对称•则AB.BC&&序国成的BB形的面枳是▲cm—三大題共12小題.共88分.请衽答JH卡16定区域内作答，解答时应乌出文字说朗、证明过観成渣算步■）]2工+，・4・17. （6分）解方程姐《U+2y-5.UM6 分19. <6分）为了怙计西瓜•草果裙悽三种水眾一个月的・Sft>M水星店对这三种水果7天的钥售ft进行了统计・枕计结果如阳所示.（1>若西瓜■草果和弼蕉的鲁价分别为6元/千克.8元/千克和3元/千克•则这7天• • • 大的水果品斡地（▲>1A.两瓜B.草果 a（2〉估if 一个月（按30天计算）谏水果店可柄害草杲多少千克？数学试■第3页《共6貝〉(»16fl)• 11 •数学试题第4页（共6页）20. （7分》如用•小明欲利用测角仪AftH 的离度•巳知他鳥树的水平距戾BC 为10 m ■測角仪 的高度CD 为1・5 m ・j«得轲U A 的仰角为33••求轲的离度AB.54・cos33・*0. 84>un33e <*0. 65）(»20«)21.(7分)如田•四边形ABCD 的对角线AC.BD 相交于点€>•△ ABOfiABAD. 求 tf ：(l)OA-OBi(2)AB/7CD>(M2ia>22. （7 分〉巳知点 A （Ul ）ttZ 次斉数《1）用含4的代数式表示矢《2）如果谏二次甬数的囲您与x 紬只有一个交点•*这个二次函数的图您的頂点坐标.23. <9分〉栗厂为斷5!号电稅机上市券办促忻活动•窝客毎购买一台该曲号电視机•可获得一 次抽奖机令•谏厂应技10%设大奖•其余为小奖.厂家设计的抽奖方貳是，在一个不进期的盒子中•放入10个黄球和90个白球•这些球除・ 色外都相同•搅匀后从中任韋換出I 个球•揍列賛球的頤窑获得大奖•換狗白球的顾％获得 小奖.<1）厂家请枚了一位敷学老算・他设什的披奖方案趕'左一个不透期的盒子中•放入2个負 球和3个白球•这牲球除謨色外部相同•捷匀后从中任倉換出2个球•換到的2个球祁 是負M 的噸脅获得大奖•其余的JK 客茯得小奖•诛抽奖方案符合厂家的设奖！?*呀？请 说期理由8数学试M 第S 页(共6员)(2)下WM-个可以白由转动的转盘・请你将轻盘分为2个电形区域•分別涂上触■白沏种 畝色•并设计抽奖方棗•使加符合厂家的设奖更求.在转盘上用文R 注明 農色和廉形的踌心角的度数・2•结合转盘简述获奖方式•不需说明理由•)(B23S)24. (8分》甲车从A 地出发以60 km/h 的速度沿公路匀速行校・0.5 h 斥.乙车也从A 地出发.以80 km/h 的連度沿後公路与甲车剛向匀連行胶•求乙车出发后几小时迫上甲车・ 请建立一次除效关系解决上述何・•25. (8分》如用・AB 超©O 的玄牲•点D 在OO 上.^DAli^^.BC//AD.CD//AB.(DMVrA 线CD 与©O 的位flt 关廉.并说明理由I(2)若©O 的半径为1•求阳中阴形部分的面枳(结果保的x>.26. «8分〉滋习《阳形的相似》后•我幻可以倚助探承两个/!角三角形全务的条件所获得的经购■堆续探宋卿个直角三角形相似的条件•《】严对于两个立角三介滋•潰足一边一仗角对应相笹•成两克角边对应栢彎•两个H 角三角形全锣••类個地•你可以彻到•濃足 ▲ •戒▲ •两个伍如三角形相似J arm 足斜边和一条绘角边对应相第的却个“角三角形全好-•类似堆・你可以紂到-猜足△_ 一的耳个M 角三角形相似-•请结合下列所恰田形・尺出巳知•并丸成说理过R ・ 巳知z 如阳•—▲一. 试说明 R I AABC S R I AATTC ：27. （8分）某抵发裔以毎件50元的价粘科进800件T 怕•密一个月以单价80元的■•侮出了 200件;第二个月如果小价不变・預计仍可鲁出200件•批发商为堆加祈仰■・决定降价筍 傅•根张谢场调査•越价毎群低1元•可多售出】0件.但最低甌价应离于购进的价第(列26島)二个月结東后•就发命格对剧余的TH一次性清仓钥會•清仓时型价为40元•设第二个月m 价薛低XX.d）填表（不需化简八（228. （8分）如图•正方形ABCD的边斤超2.MMAD的中点•点E从点A岀发•沿AB运动到点B停止•连接EM并沧长求够嫂CQ 环尸比芦的乘效交射披BC于启G・连接EG、FG・（l>ift AE■工时•△EGF的面稅为y.^y关于工的議数矣杲式•并卑出自变債工的取值范Bh （2JPMMG的中点•请立接泾出点P运动路线的长•数事试■第6页《共6JO南京市2010年初中毕业生学业考试数学试题参考答案及评分标准说明：*评分标准褂題伶出了一种戒几种解隆供參考•如果号生的解法与本解裕不同•多轿本评分标椿的桶神纶分.一•遶择•（毎小IS2分•共】2分）解比二’由<D・阳y-4-lr. 4将③代入②•得xf2t4-Zlr)#F$: 篇这个方程•鮒二•填$fl(«小Bl 2分•共20分)7.2 &9.8.5X10・10.80 11.12•—•三13. > 14.8 15.110 16.2三、解答&($大■共12小19 .共88分)17・《*・6分》解法一QX2•得2x+4y-10. ®3y-6.篇这个方朝•得，・2・.........................................«y-2代人①•御x-1. ...............................................序以原方程组的解是x~lfy-2.将z ・1代入③•鮒 y ・2・ .................. =・1・y-2.18•《本題6分〉_6—a • (a4-&〉(《 — &〉 ■百丁—5—_&_a . ______ a b _____ ab (a+ 6)<a —A)—內• .............................19・《本題6分）Mt<l ）A ....................................................................（2）140+ 7 X 30 - 600（千丸人衿弭古计一个月诛水舉店可的倂罩来600千克.所以脈方桎粗的(卄 6)(d —6)数学符案第2页《共4页〉20•《本& 7分）■"如图•过点D 作DE 丄川3・乘足为E.在 RtAADE 中• DE-BC- 10.ZADE-33\umZADE ■箔・:・AE ・DE ・ unZADE*10X0.65-6.5.................................... 5 分A AB-AE4-BE-AE+CD-6.5+1.5・8«m).答‘側的豪度AB 约为8m. ................................... 7分21•《本題7分)证明：(1)7^ABCWABAD> AZCAB-ZDB^. ：.OA OB.(2) V AABCia^BAD..9. AC- HD.又VOA-OB./. OC-OD •:・ZOCD ・ZODC.••• ZAOB ・ZCOD ・ZCNBz 人CD ・:.ZCAB^ZACD. :.ABCD. .......................................................................................... 7 分22. 《本題7分）M>（DW 为点A 《l ・】）在二次帝敢y ・F-2"+6的图象上•所以l ・l-2a+6. 町得6-2«・ .... ...............................................................................................................<2方根J 4-2ax+6-0有却个郴第的实敷檢•所以2 —“■2-&1-0.MfU a-0,< a®2................................... . .......................................................... 5 分当a ・0时・y ・~ •这个二次 当a«-2时・yF-"X ・"一Q •.这个NWRM 图製的序点坐标为（2.0）. 所以•这个二次函数的图役的M 点坐标为（0.0>«（2,0）. .................. 7分23. «本& 9 分〉解，仃> 诛抽奖方杲符合厂察的设奖旻求.分别用黄1、黄2.白1、白2、白3淤示这5个球.从中任意用出2个球•可能岀现的 结案倉，（的l.M 2）UM 1.白負1.白2）.<M 1•白3>.（» 2.白1》,負2・ 白2）JW2.白3八《白I •白2八《白丨•白3>、《白2 •白3）・共冇10幷•它们出现的可 能性相同.所布的结果中•擠足損绅的2个球林趕黄球〈记为审件A 〉的结果材1科•即（黄1・ ■黄2〉.所以P （A>-占•即嶺霁获鮒大奖的談賂为10%•获側小奖的様序为90%...................................................................................................................................... 5分《2〉本題祥案不悟一 •下列解法供参勺.如田•榜转盘中8B 心角为36•的禺形区域涂上试 色・兀余的区放涂上白色.喷客每购买一台连型 号电襪机•可获鮒一次转动转盘的机会•任倉转 动这个转盘•当Kftff 止时•插什描向黄色区域 获得大奖•指向白色区城获得小奖.3分数学答案幣4页（共4页）24•《本勒8分》解，本題衿案不惟一・T 列解矗供參考.设乙车出发工h 肓•叩.乙烤车鹰A 地的路级分别趕力km 和必km.根据題怠•得刃■6O“+O.5)・6O 工+30°:・80几 .............................. 6分 当乙车追上甲车时・力■力・即60x+30-80z ・ 解这个方程•得x-1.5<h>・袴,乙车出发厉1.5 hifl 上叩车. ................................................. 8分25•《本& 8分〉W ：(i)AtftCD 与©O 相切.如阳•连ItOD.VOA-OD>ZDAB-45\AZODA-45e . •••ZAOD -901•:CD" AB..••ZODC -ZAOD-90MJP OD 丄CD. 又•••点D 在©O 上・・•・H 线C”与©O 相切.(2r ：BC//AD.CD^AU ・・•・四边形A BCD 是平行四边形.ACD-AB-2.• e _<OB+CD)XOD…(1 + 2)X>_ 3• •m-------------- g -丁・・・阳中阴形祁分的锂IFFS Of <»ro-S >imt »-«y —yXxX 1：~于・・26. «本& 8 分)Kt(l )-个枝角对应郴毎 ............彌M 角边对应成比例 .......(2)斜边和一条亞介边对应成比例在 RiAABC 和 RiAA'BU 中.ZC-ZU-90••耗館法一"设黑■第■*•则A ti A C住 RtAABC 和 RiAA'BV 中.■—、■ ■・・■・■・■・■—・・・■・一 ■上BC _ I• AB• •斗▼案第3页《共4页〉解袪二■如图•假设AB 上戏取 过点£T 作BU 丄AC.竄足为C.••• ZC ・ Z AC ； BC 〃肮二 ・・・R9ABaRt △八BV.・••箔■畚.口 •• AB = AC .AC. AC 又・柑疋…疋疋••• A IT u 仙• z u ■ z ACT ■ 90・• ••••••©△ABCsRtAATTC ： (8)............................................................................................................................... 分27•《本・8分)M ：(l)80-x 200+10* 800 - 200-<200 +lOx) ............................................................................... 3 .......................................................................................................................................................... 分《2)段据&盘•鮒80X200+(80-jr>(200+10x>+40[800-200-(200+10x)]-50X800-9 000.陵理•側 P-20M +100・0.解这个方程•側x a -x,-10. 当 x-10 时.80-x-70>50.-个月的小价应是70元. .................................................. 8分28•《本题8分〉当点E 与点A 敗合时.r ・0・y ・*X2X?・2； 当点E 与点A 不贾合时ev$W 仗正方形 ABCD 中•/*- ZA/X ■70二 •••ZMDF—90： •••乙/i ■厶MU 化 •••AM ・DM ・ZAME ・ZDMF.:心 AMWADMF. •••ME -MF.在 RtAAME 中ME-x.AM-1 .ME- yPTl.AEF-2ME-2 /T+T.过M 作MN 丄BC.a 足为N (如圈〉.WZMNG-90\Z^MN-90\MN-AB«AD-2AM.••• ZAME+ZEMNW.VZEMG-90\A ZCMN+Z EMN ■ 90\:•乙 AME ■乙 GMN.••• RSMEsRiANMG.• AM ME m ME 1-NM MG^MG^T：.^G-2ME-2>J7T\ ・Ay-yEFX MG-jX 2/r+T X 2/7TT ■ 2P +2・••“■21+2•其中 OW. ............................ .. .................................................................. 6 分«2）点P 运动路线的长为2. .............................................................................................. 8分\\4fr-A7r • AC AB …疋=丽— AUA。
中考数学试题及解析 江苏南京-解析版
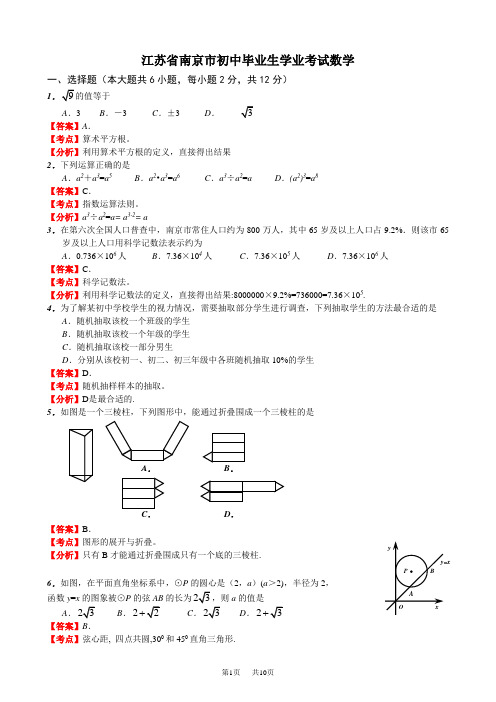
江苏省南京市初中毕业生学业考试数学一、选择题（本大题共6小题，每小题2分，共12分）1A ．3B ．－3C ．±3D ．【答案】A ．【考点】算术平方根。
【分析】利用算术平方根的定义，直接得出结果 2．下列运算正确的是A ．a 2＋a 3=a 5B ．a 2•a 3=a 6C ．a 3÷a 2=aD ．(a 2)3=a 8 【答案】C ．【考点】指数运算法则。
【分析】a 3÷a 2=a= a 3-2= a3．在第六次全国人口普查中，南京市常住人口约为800万人，其中65岁及以上人口占9.2%．则该市65岁及以上人口用科学记数法表示约为 A ．0.736×106人 B ．7.36×104人 C ．7.36×105人 D ．7.36×106 人 【答案】C ．【考点】科学记数法。
【分析】利用科学记数法的定义，直接得出结果:8000000×9.2%=736000=7.36×105.4．为了解某初中学校学生的视力情况，需要抽取部分学生进行调查，下列抽取学生的方法最合适的是A ．随机抽取该校一个班级的学生B ．随机抽取该校一个年级的学生C ．随机抽取该校一部分男生D ．分别从该校初一、初二、初三年级中各班随机抽取10%的学生 【答案】D ．【考点】随机抽样样本的抽取。
【分析】D 是最合适的.5．如图是一个三棱柱，下列图形中，能通过折叠围成一个三棱柱的是【答案】B ．【考点】图形的展开与折叠。
【分析】只有B 才能通过折叠围成只有一个底的三棱柱.6．如图，在平面直角坐标系中，⊙P 的圆心是（2，a ）(a ＞2)，半径为2， 函数y =x 的图象被⊙P 的弦AB的长为a 的值是 A． B．2 C．D．2+ 【答案】B ．【考点】弦心距, 四点共圆,300和450直角三角形.A ．B ．D ．【分析】连结PA,PB ,过点P 作PE ⊥AB 于E, 作PF ⊥X 轴于F,交AB 于G, 在 Rt PAE ∆中,2 1.AE PA PE ==⇒=,,,,,PE AB PF OF P O F E ⊥⊥∴ 四点共圆045EPG EPG GOF ∆∠=∠= 在中PG ⇒= 2.FGO FG OG a PG FG ∆== 在中｜因此=+二、填空题（本大题共10小题，每小题2分，共20分）7．－2的相反数是________． 【答案】2．【考点】相反数。
1999年江苏省南京市中考数学试卷
1999年江苏省南京市中考数学试卷一、选择题（共15小题，每小题2分，满分30分）1．（2分）12的相反数是（ ）A ．2B ．﹣2C ．12D ．﹣122．（2分）计算（a 3）2的结果是（ ） A ．a 5B ．a 6C ．a 8D ．a ﹣13．（2分）下列计算正确的是（ ） A ．（a +b ）（a 2+ab +b 2）=a 3+b 3 B ．（a +b ）2=a 2+b 2C ．（a ﹣b ）（a 2+2ab +b 2）=a 3﹣b 3D ．（a ﹣b ）2=a 2﹣2ab +b 24．（2分）若分式3x x−1有意义，则x 应满足（ ）A ．x=0B ．x ≠0C ．x=1D ．x ≠15．（2分）下列根式中，属于最简二次根式的是（ ） A ． 9B ． 3aC ． 3a 2D ． a36．（2分）△ABC 中，∠C=90°，∠A ，∠B ，∠C 所对的边分别是a ，b ，c ，则sinA 等于（ ）A ．a cB ．b cC ．a bD ．b a7．（2分）已知两个圆有且只有三条公切线，这两个圆的位置有关系是（ ）A ．外离B ．外切C ．相交D ．内切8．（2分）一个正多边形的内角和是720°，这个多边形是（ ） A ．正方形B ．正五边形C ．正六边形D ．正八边形9．（2分）甲，乙两人在相同条件下各射靶10次，他们命中的环数的平均数x 相等，但方差不同，S 甲2=4，S 乙2=2.5，则射击成绩较稳定的是（ ） A ．甲B ．乙C ．甲、乙一样稳定D ．无法确定10．（2分）观察下列平面图形：其中是轴对称图形的有（）A．1个B．2个C．3个D．4个11．（2分）如图所示，在△ABC中，AD=DF=FB，AE=EG=GC，FG=4，则（）A．DE=1，BC=7B．DE=2，BC=6C．DE=3，BC=5D．DE=2，BC=8 12．（2分）已知0＜x＜1，化简|x|+(x−1)2的结果是（）A．2x﹣1B．1﹣2x C．﹣1D．113．（2分）已知函数y=kx中，y随x的增大而增大，那么函数y=kx的图象大致是（）A．B．C．D．14．（2分）甲、乙两班参加植树造林，已知甲班每天比乙班每天多植5棵树，甲班植80棵树所用的天数与乙班植70棵树所用的天数相等，若设甲班每天植x棵，根据题意列出的方程是（）A．80x−5=70xB．80x=70x+5C．80x+5=70xD．80x=70x−515．（2分）如图，两个同心圆，大圆的弦AB与小圆相切于点P，大圆的弦CD 经过点P，且CD=13，PD=4，则两圆组成的圆环的面积是（）A．16πB．36πC．52πD．81π二、填空题（共10小题，每小题2分，满分20分）16．（2分）分解因式：xy2﹣x=．17．（2分）425的算术平方根是．18．（2分）∠α的补角是50度，∠α=度．19．（2分）如果两个相似三角形周长的比是2：3，那么它们面积的比是．20．（2分）点P（﹣3，2）与点Q关于原点对称，则点Q在第象限．21．（2分）关于x的一元二次方程mx2﹣2x+1=0有两个相等的实数根，则m=．22．（2分）在中考体育考试中，某校10名男生的考试成绩如表所示（满分是45分），则他们的平均成绩是分．23．（2分）在⊙O中，圆心角∠AOB=100°，则弦AB所对的圆周角=．24．（2分）矩形ABCD的边AB=4cm，AD=2cm，以直线AD为轴旋转一周，所得的圆柱的侧面积是cm2（结果保留π）．25．（2分）汽车由南京驶往相距300km的上海，它的平均速度为100km/h，则汽车距上海的路程s（km）关于行驶的时间t（h）的函数关系式为．三、解答题（共10小题，满分70分）26．（5分）计算：（2−3）0+2−1﹣(12)−127．（5分）解不等式组3(x+1)＞4x+2x2≥x−13，并写出不等式组的整数解．28．（6分）已知BD是▱ABCD的对角线，AE⊥BD，CF⊥BD，垂足分别为E、F．（1）根据题意补全图形；（2）求证：△ABE≌△CDF．29．（6分）解方程：（xx−2）2﹣5（xx−2）+6=0．30．（6分）如图，从20米高的甲楼顶A处望乙楼顶C处的仰角是30°，望乙楼底D处的俯角是45°．求乙楼的高度．（精确到0.1米，2≈1.1414，3≈1.732）31．（6分）某地长途汽车客运公司规定旅客可随身携带一定质量的行李，如果超过规定，则需要购买行李票，行李票费用y（元）是行李质量x（kg）的一次函数，其图象如图所示，求：（1）y与x之间的函数关系式；（2）旅客可免费携带的行李的质量是多少？32．（8分）已知：如图，在△ABC中，∠C=90°，BE是角平分线，DE⊥BE交AB 于D，⊙O是△BDE的外接圆．（1）求证：AC是⊙O的切线；（2）若AD=6，AE=62，求DE的长．33．（8分）某市场销售一批名牌衬衫，平均每天可销售20件，每件赢利40元．为了扩大销售，增加赢利，尽快减少库存，商场决定采取适当降价措施．经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件．求： （1）若商场平均每天要赢利1200元，每件衬衫应降价多少元？ （2）要使商场平均每天赢利最多，请你帮助设计方案．34．（10分）如图1，⊙O 1和⊙O 2内切于点P ，⊙O 2的弦BE 与⊙O 1相切于C ，PB 交⊙O 1于D ，PC 的延长线交⊙O 2于A ，连接AB ，CD ，PE ．（1）求证：①∠BPA=∠EPA ；②AB AC =BC BD；（2）若⊙O 1的切线BE 经过⊙O 2的圆心，⊙O 1、⊙O 2的半径分别是r 、R ，其中R ≥2r ，如图2，求证：PC•AC 是定值．35．（10分）如果抛物线y=﹣x 2+2（m ﹣1）x +m +1与x 轴都交于A ，B 两点，且A 点在x 轴的正半轴上，B 点在x 轴的负半轴上，OA 的长是a ，OB 的长是b ． （1）求m 的取值范围；（2）若a ：b=3：1，求m 的值，并写出此时抛物线的解析式；（3）设（2）中的抛物线与y 轴交于点C ，抛物线的顶点是M ，问：抛物线上是否存在点P ，使△PAB 的面积等于△BCM 面积的8倍？若存在，求出P 点的坐标；若不存在，请说明理由．1999年江苏省南京市中考数学试卷参考答案与试题解析一、选择题（共15小题，每小题2分，满分30分）1．（2分）12的相反数是（ ）A ．2B ．﹣2C ．12D ．﹣12【解答】解：12的相反数是﹣12．故选：D ．2．（2分）计算（a 3）2的结果是（ ） A ．a 5B ．a 6C ．a 8D ．a ﹣1【解答】解：原式=a 3×2=a 6． 故选：B ．3．（2分）下列计算正确的是（ ） A ．（a +b ）（a 2+ab +b 2）=a 3+b 3 B ．（a +b ）2=a 2+b 2C ．（a ﹣b ）（a 2+2ab +b 2）=a 3﹣b 3D ．（a ﹣b ）2=a 2﹣2ab +b 2【解答】解：A 、应为（a +b ）（a 2﹣ab +b 2）=a 3+b 3，故本选项错误； B 、应为（a +b ）2=a 2+2ab +b 2，故本选项错误；C 、应为（a ﹣b ）（a 2+ab +b 2）=a 3﹣b 3，故本选项错误；D 、（a ﹣b ）2=a 2﹣2ab +b 2，正确． 故选：D ．4．（2分）若分式3xx−1有意义，则x 应满足（ ）A ．x=0B ．x ≠0C ．x=1D ．x ≠1【解答】解：根据题意得：x ﹣1≠0，解得：x ≠1． 故选：D ．5．（2分）下列根式中，属于最简二次根式的是（ ）A ． 9B ． 3aC ．D ． a 3【解答】解：因为A 、 9=3，可化简； C 、 3a 2= 3|a |，可化简；D 、 a 3= 3a 3，可化简；所以，这三个选项都不是最简二次根式，故选B ．6．（2分）△ABC 中，∠C=90°，∠A ，∠B ，∠C 所对的边分别是a ，b ，c ，则sinA 等于（ ） A ．acB ．bcC ．abD ．ba【解答】解：由图可知，sinA=ac．故选：A ．7．（2分）已知两个圆有且只有三条公切线，这两个圆的位置有关系是（ ） A ．外离B ．外切C ．相交D ．内切【解答】解：根据两个圆有且只有三条公切线，则这两个圆的位置有关系是外切． 故选：B ．8．（2分）一个正多边形的内角和是720°，这个多边形是（ ） A ．正方形B ．正五边形C ．正六边形D ．正八边形【解答】解：设多边形的边数为n ， 依题意得（n ﹣2）•180°=720°， ∴n=6．所以是正六边形． 故选：C ．9．（2分）甲，乙两人在相同条件下各射靶10次，他们命中的环数的平均数x 相等，但方差不同，S 甲2=4，S 乙2=2.5，则射击成绩较稳定的是（ ） A ．甲B ．乙C ．甲、乙一样稳定D ．无法确定【解答】解：由于S 2甲＞S 2乙，故甲的方差大，波动大， ∴射击成绩较稳定的是乙． 故选：B ．10．（2分）观察下列平面图形：其中是轴对称图形的有（ ）A ．1个B ．2个C ．3个D ．4个【解答】解：第一个图形、第二个图形、第四个图形都是轴对称图形，而第三个图形不是轴对称图形． 故选：C ．11．（2分）如图所示，在△ABC 中，AD=DF=FB ，AE=EG=GC ，FG=4，则（ ）A ．DE=1，BC=7B ．DE=2，BC=6C ．DE=3，BC=5D ．DE=2，BC=8【解答】解：∵AD=DF=FB ，AE=EG=GC ∴DE ∥FG ∥BC∴△ADE ∽△AFG ∽△ABC∴DE FG =AD AF =AD AD +DF =12解得：DE=2 又∵DE BC=AD AB=AD AD +DF +FB=13∴BC=6 故选：B ．12．（2分）已知0＜x ＜1，化简|x |+ (x −1)2的结果是（ ）A ．2x ﹣1B ．1﹣2xC ．﹣1D ．1【解答】解：∵0＜x ＜1，∴|x |=x ， (x −1)2=﹣（x ﹣1）=1﹣x ． ∴|x |+ (x −1)2=x +1﹣x=1．故选D ．13．（2分）已知函数y=kx 中，y 随x 的增大而增大，那么函数y=kx的图象大致是（ ）A ．B ．C ．D ．【解答】解：∵函数y=kx 中，y 随x 的增大而增大，∴k ＞0，函数y=kx的图象在一、三象限．故选：A ．14．（2分）甲、乙两班参加植树造林，已知甲班每天比乙班每天多植5棵树，甲班植80棵树所用的天数与乙班植70棵树所用的天数相等，若设甲班每天植x 棵，根据题意列出的方程是（ ） A ．80x−5=70xB ．80x=70x +5C ．80x +5=70xD ．80x=70x−5【解答】解：若设甲班每天植x 棵， 那么甲班植80棵树所用的天数应该表示为：80x，乙班植70棵树所用的天数应该表示为：70x−5．所列方程为：80x =70x−5．故选：D ．15．（2分）如图，两个同心圆，大圆的弦AB 与小圆相切于点P ，大圆的弦CD 经过点P ，且CD=13，PD=4，则两圆组成的圆环的面积是（ ）A．16πB．36πC．52πD．81π【解答】解：连接OP、OB．∵大圆的弦AB与小圆相切于点P，∴OP⊥AB，∴PA=PB．∵CD=13，PD=4，∴PC=9．根据相交弦定理，得PA=PB=6，则两圆组成的圆环的面积是πOB2﹣πOP2=πPB2=π4AB2=36π．故选：B．二、填空题（共10小题，每小题2分，满分20分）16．（2分）分解因式：xy2﹣x=x（y﹣1）（y+1）．【解答】解：xy2﹣x，=x（y2﹣1），=x（y﹣1）（y+1）．故答案为：x（y﹣1）（y+1）．17．（2分）425的算术平方根是25．【解答】解：∵（25）2=425，∴425的算术平方根是25．18．（2分）∠α的补角是50度，∠α=130度．【解答】解：根据定义∠α的补角度数是180°﹣50°=130°．故答案为130°．19．（2分）如果两个相似三角形周长的比是2：3，那么它们面积的比是4：9．【解答】解：∵两个相似三角形周长的比是2：3，∴它们的相似比是2：3；∴它们的面积比为4：9．20．（2分）点P（﹣3，2）与点Q关于原点对称，则点Q在第四象限．【解答】解：∵点P（﹣3，2）与点Q关于原点对称，∴点Q（3，﹣2）．∴点Q在第四象限．21．（2分）关于x的一元二次方程mx2﹣2x+1=0有两个相等的实数根，则m=1．【解答】解：依题意，有：△=4﹣4m=0且m≠0，解得m=1．22．（2分）在中考体育考试中，某校10名男生的考试成绩如表所示（满分是45分），则他们的平均成绩是43分．【解答】解：由题意知10名男生考试的平均成绩==4310（分）．故答案为43．23．（2分）在⊙O中，圆心角∠AOB=100°，则弦AB所对的圆周角=50°或130°．【解答】解：根据圆周角定理，得弦AB所对的圆周角=100°÷2=50°或180°﹣50°=130°．24．（2分）矩形ABCD的边AB=4cm，AD=2cm，以直线AD为轴旋转一周，所得的圆柱的侧面积是16πcm2（结果保留π）．【解答】解：以直线AD为轴旋转一周，即圆柱的底面半径为4，高为2，∴圆柱的侧面积=2π×4×2=16πcm2．25．（2分）汽车由南京驶往相距300km的上海，它的平均速度为100km/h，则汽车距上海的路程s（km）关于行驶的时间t（h）的函数关系式为s=300﹣100t（0≤t≤3）．【解答】解：汽车距上海的路程s （km ）关于行驶的时间t （h ）函数关系式为s=300﹣100t （0≤t ≤3）．三、解答题（共10小题，满分70分）26．（5分）计算：（ 2−3）0+ 2−1﹣(12)−1 【解答】解：原式=1+ 2+1﹣(12)−1=1+ 2+1﹣2= 2．27．（5分）解不等式组 3(x +1)＞4x +2x 2≥x−13，并写出不等式组的整数解． 【解答】解：解不等式3（x +1）＞4x +2，去括号得，3x +3＞4x +2，移项、合并同类项得，﹣x ＞﹣1，化系数为1得，x ＜1；解不等式x 2≥x−13， 去分母得，3x ≥2x ﹣2，移项、合并同类项得x ≥﹣2，（3分）∴不等式组的解集是：﹣2≤x ＜1．（4分）∴不等式组的整数解是：﹣2，﹣1，0．（5分）28．（6分）已知BD 是▱ABCD 的对角线，AE ⊥BD ，CF ⊥BD ，垂足分别为E 、F ．（1）根据题意补全图形；（2）求证：△ABE ≌△CDF ．【解答】（1）解：如图．（2）证明：∵四边形ABCD 是平行四边形，∴AB=CD ，AB ∥CD ．∴∠ABE=∠CDF ．∵AE ⊥BD ，CF ⊥BD ，∴∠AEB=∠CFD=90°．∴△ABE ≌△CDF ．29．（6分）解方程：（x x−2）2﹣5（x x−2）+6=0． 【解答】解：设：y=xx−2（1分）则原方程变形为：y 2﹣5y +6=0．解得y 1=2，y 2=3．（3分）由x x−2=2，解得x 1=4（4分） 由x x−2=3，解得x 2=3（5分） 经检验：x 1=4，x 2=3都是原方程的根（6分）30．（6分）如图，从20米高的甲楼顶A 处望乙楼顶C 处的仰角是30°，望乙楼底D 处的俯角是45°．求乙楼的高度．（精确到0.1米， 2≈1.1414， 3≈1.732）【解答】解：过A 点作AE ⊥CD ，垂足是E ；（1分）∵AB ∥CD ，AE ∥BD ，∴DE=AB=20米；在Rt △ADE 中，∠DAE=45°，DE=20米，∴AE=20米；（2分）在Rt △ACE 中，∠CAE=30°，AE=20米，∴CE=AE•tan30°=2033米（4分）∴CD=CE +ED=203 3+20=20（ 33+1） ≈31.5（米）（5分）答：乙楼的高约是31.5米．（6分）31．（6分）某地长途汽车客运公司规定旅客可随身携带一定质量的行李，如果超过规定，则需要购买行李票，行李票费用y （元）是行李质量x （kg ）的一次函数，其图象如图所示，求：（1）y 与x 之间的函数关系式；（2）旅客可免费携带的行李的质量是多少？【解答】解：（1）设一次函数y=kx +b ，∵当x=60时，y=6，当x=80时，y=10，∴ 60k +b =680k +b =10解之，得 k =15b =−6， ∴所求函数关系式为y=15x ﹣6（x ≥30）； （2）当y=0时，15x ﹣6=0，所以x=30， 故旅客最多可免费携带30kg 行李．32．（8分）已知：如图，在△ABC 中，∠C=90°，BE 是角平分线，DE ⊥BE 交AB于D ，⊙O 是△BDE 的外接圆．（1）求证：AC 是⊙O 的切线；（2）若AD=6，AE=6 2，求DE 的长．【解答】（1）证明：连接OE ；（1分）∵⊙O 是△BDE 的外接圆，∠DEB=90°，∴BD 是⊙O 的直径，（不证直径，不扣分）∵BE 平分∠ABC ，∴∠CBE=∠OBE ，∵OB=OE ，∴∠OBE=∠OEB ，（2分）∴∠OEB=∠CBE ，∴OE ∥BC ，（3分）∵∠C=90°，∴∠AEO=90°，∴AC 是⊙O 的切线；（4分）（2）解：∵AE 是⊙O 的切线，AD=6，AE=6 2，∴AE 2=AD•AB ，（5分）∴AB=AE 2AD =(6 2)212=12， ∴BD=AB ﹣AD=12﹣6=6；∵∠AED=∠ABE ，∠A=∠A ，∴△AED ∽△ABE ，（6分）∴DE BE =AE AB； 设DE= 2x ，BE=2x ，∵DE 2+BE 2=BD 2，（7分）∴2x 2+4x 2=36，解得x=± 6（负的舍去），∴DE=2 3．（8分）33．（8分）某市场销售一批名牌衬衫，平均每天可销售20件，每件赢利40元．为了扩大销售，增加赢利，尽快减少库存，商场决定采取适当降价措施．经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件．求：（1）若商场平均每天要赢利1200元，每件衬衫应降价多少元？（2）要使商场平均每天赢利最多，请你帮助设计方案．【解答】解：设每天利润为w 元，每件衬衫降价x 元，根据题意得w=（40﹣x ）（20+2x ）=﹣2x 2+60x +800=﹣2（x ﹣15）2+1250（1）当w=1200时，﹣2x 2+60x +800=1200，解之得x 1=10，x 2=20．根据题意要尽快减少库存，所以应降价20元．答：每件衬衫应降价20元．（2）解：商场每天盈利（40﹣x ）（20+2x ）=﹣2（x ﹣15）2+1250．所以当每件衬衫应降价15元时，商场盈利最多，共1250元．答：每件衬衫降价15元时，商场平均每天盈利最多．34．（10分）如图1，⊙O 1和⊙O 2内切于点P ，⊙O 2的弦BE 与⊙O 1相切于C ，PB 交⊙O 1于D ，PC 的延长线交⊙O 2于A ，连接AB ，CD ，PE ．（1）求证：①∠BPA=∠EPA ；②AB AC =BC BD； （2）若⊙O 1的切线BE 经过⊙O 2的圆心，⊙O 1、⊙O 2的半径分别是r 、R ，其中R ≥2r ，如图2，求证：PC•AC 是定值．【解答】证明：（1）①过点P 作两圆公切线MN ．则∠MPB=∠PCD=∠A ．∴CD ∥AB ．∴∠ABC=∠BCD ．∵BC 是⊙O 1的切线，∴∠BCD=∠BPA ．∵∠ABC=∠EPA ，∴∠BPA=∠EPA ．②∵∠ABC=∠BPA ，∠A=∠A ，∴△ABC ∽△APB ．∴AB PA =BC PB， ∴AB BC =PA PB． ∵CD ∥AB ，∴PA PB =AC BD =AB BC． 即AB AC =BC BD． （2）连接O 1C ，PO 1．则PO 2经过点O 1，且O 1C=r ，O 1O 2=R ﹣r ．∵BE 与⊙O 1相切，∴O 1C ⊥BE ．在Rt △CO 1O 2中，CO 2= O 1O 22−O 1C 2= R 2−2Rr ，∴BC=BO 2+CO 2=R + R 2−2Rr ．EC=EO 2﹣CO 2=R ﹣ R 2−2Rr ．∵PC•AC=EC•BC=2Rr ．∴PC•AC 是定值．35．（10分）如果抛物线y=﹣x 2+2（m ﹣1）x +m +1与x 轴都交于A ，B 两点，且A 点在x 轴的正半轴上，B 点在x 轴的负半轴上，OA 的长是a ，OB 的长是b ．（1）求m 的取值范围；（2）若a ：b=3：1，求m 的值，并写出此时抛物线的解析式；（3）设（2）中的抛物线与y 轴交于点C ，抛物线的顶点是M ，问：抛物线上是否存在点P ，使△PAB 的面积等于△BCM 面积的8倍？若存在，求出P 点的坐标；若不存在，请说明理由．【解答】解：（1）设A ，B 两点的坐标分别是（x 1，0）、（x 2，0），∵A ，B 两点在原点的两侧，∴x 1x 2＜0，即﹣（m +1）＜0，解得m ＞﹣1．∵△=[2（m ﹣1）]2﹣4×（﹣1）×（m +1）=4m 2﹣4m +8=4×（m ﹣12）2+7 当m ＞﹣1时，△＞0，∴m 的取值范围是m ＞﹣1；（2）∵a ：b=3：1，设a=3k ，b=k （k ＞0），则x 1=3k ，x 2=﹣k ，∴ 3k −k =2(m −1)3k ⋅(−k )=−(m +1)， 解得m 1=2，m 2=13．∵m =13时，x 1+x 2=−43（不合题意，舍去）， ∴m=2，∴抛物线的解析式是y=﹣x 2+2x +3；（3）易求抛物线y=﹣x 2+2x +3与x 轴的两个交点坐标是A （3，0），B （﹣1，0） 与y 轴交点坐标是C （0，3），顶点坐标是M （1，4）．设直线BM 的解析式为y=px +q ，则 4=p ⋅1+q 0=p ⋅(−1)+q． 解得 p =2q =2． ∴直线BM 的解析式是y=2x +2．设直线BM 与y 轴交于N ，则N 点坐标是（0，2），∴S △BCM =S △BCN +S △MNC=12×1×1+12×1×1 =1设P 点坐标是（x ，y ），∵S △ABP =8S △BCM ，∴12×AB ×|y |=8×1．即12×4×|y |=8． ∴|y |=4．∴y=±4．当y=4时，P 点与M 点重合，即P （1，4）， 当y=﹣4时，﹣4=﹣x 2+2x +3，解得x =1±2 2．∴满足条件的P 点存在．P 点坐标是（1，4），（1+2 2，﹣4）（1﹣2 2，﹣4）．。
中考数学难题归纳
一．选择题（共3小题）1．（1998•南京）若双曲线的两个分支在第二、四象限内，则抛物线y=kx2﹣2x+k2的图象大致是图中的（ ）大致是图中的（A．B．C．D．2．如图，∠AOD=90°，OA=OB=BC=CD，那么下列结论成立的是（，那么下列结论成立的是（ ）OCA B B．△OAB∽△ODA A．△OAB∽△OCA C．△BAC∽△BDA D．以上结论都不成立．以上结论都不成立3．（2012•绵阳）已知△ABC中，∠C=90°，tanA=，D是AC上一点，∠CBD=∠A，则sin∠ABD=（）A．B． C．D．二．填空题（共11小题）4．（2012•黄石）“数学王子”高斯从小就善于观察和思考．在他读小学时就能在课堂上快速地计算出1+2+3+…+98+99+100=5050，今天我们可以将高斯的做法归纳如下：，今天我们可以将高斯的做法归纳如下：令S=1+2+3+…+98+99+100 ①S=100+99+98+…+3+2+1 ②①+②：有2S=（1+100）×100 解得：S=5050 请类比以上做法，回答下列问题：请类比以上做法，回答下列问题：若n为正整数，3+5+7+…+（2n+1）=168，则n=_________．5．如图，在平面直角坐标系中，点A的坐标是（10，0），点B的坐标为（8，0），点C，D在以OA为直的坐标为 _________．径的半圆M上，且四边形OCDB是平行四边形，则点C的坐标为6．如图，⊙O的半径是5cm，P是⊙O外一点，PO=8cm，∠P=30°，则AB=_________cm．7．（2000•甘肃）如图，AB 是半圆的直径，直线MN 切半圆于C ，CM ⊥MN ，BN ⊥MN ，如果AM=a ，BN=b ，那么半圆的半径是那么半圆的半径是 _________ ．8．已知双曲线y=与直线y=相交于A ，B 两点．第一象限上的点M （m ，n ）（在A 点左侧）是双曲线y=上的动点．过点B 作BD ∥y 轴交x 轴于点D ．过N （0，﹣n ）作NC ∥x 轴交双曲线y=于点E ，交BD于点C ．若B 是CD 的中点，四边形OBCE 的面积为4，则直线CM 的解析式为的解析式为 _________ ．9．如图，M 为双曲线y=上的一点，过点M 作x 轴、y 轴的垂线，分别交直线y=﹣x+m 于D 、C 两点，若直线y=﹣x+m 与y 轴、x 轴分别交于点A 、B ，则AD •BC 的值为的值为 _________ ．10．如图，正方形ABCD 的对角线AC 、BD 相交于点O ，E 是BC 的中点，DE 交AC 于F ，若DE=6，则EF 等于等于 _________ ．11．（2012•金山区二模）金山区二模）如图，如图，如图，已知已知AD 为△ABC 的角平分线，DE ∥AB 交AC 于E ，如果，那么=_________ ．12．如图，在△ABC中，D、E是BC的三等分点，M是AC的中点，BM交AD、AE于G、H，则BG：GH：HM=_________．13．（2013•上海）如图，在△ABC中，AB=AC，BC=8，tanC=，如果将△ABC沿直线l翻折后，点B落在边AC的中点处，直线l与边BC交于点D，那么BD的长为的长为 _________．14．（2013•芦淞区模拟）在Rt△ABC中，∠ACB=90°，CD⊥AB于点D．已知AC=，BC=2，那么sin∠ACD= _________．三．解答题（共9小题）15．已知：如图，△ABC内接于圆，AD⊥BC于D，弦BH⊥AC于E，交AD于F．求证：FE=EH．16．把抛物线y=x2+bx+c向右平移3个单位，再向下平移2个单位，所得图象的解析式是y=x2﹣3x+5，求b，c的值．的值．17．（2003•海南）已知抛物线y=ax2+bx+c开口向下，并且经过A（0，1）和M（2，﹣3）两点．）两点．，求此抛物线的解析式；（1）若抛物线的对称轴为直线x=﹣1，求此抛物线的解析式；的取值范围；（2）如果抛物线的对称轴在y轴的左侧，试求a的取值范围；的值．（3）如果抛物线与x轴交于B、C两点，且∠BAC=90°，求此时a的值．18．（2000•杭州）已知一个正三角形和一个正六边形的周长相等，求它们的面积的比值．杭州）已知一个正三角形和一个正六边形的周长相等，求它们的面积的比值． 19．（原创题）如图所示，扇形OAB从图①无滑动旋转到图②，再由图②到图③，∠O=60°，OA=1．点所运动的路径长；（1）求O点所运动的路径长；围成的面积．（2）O点走过路径与直线L围成的面积．20．（2013•重庆）重庆） 已知：如图，抛物线y=x 2+2x ﹣3与x 轴的交点为A 、B 两点，与y 轴交于点C ，直线AC 与抛物线交于A 、C 两点．两点．如图，的y=ax 2+bx+c （a ≠0）与x 轴相交于A 、B 两点，其中点A 的坐标为（﹣3，0）．（1）求点B 的坐标．的坐标．（2）在抛物线的对称轴x=﹣1上是否存在一点P ，使得△BCP 为等腰三角形，若存在，直接写出点P 的坐标；若不存在，说明理由．标；若不存在，说明理由．（3）若点Q 在直线AC 下方的抛物线上，且S △QOC =2S △BOC ，求点Q 的坐标．的坐标．21．（2014•徐州模拟）如图，已知抛物线y=﹣x 2+2x+1﹣m 与x 轴相交于A 、B 两点，与y 轴相交于点C ，其中点C 的坐标是（0，3），顶点为点D ，连接CD ，抛物线的对称轴与x 轴相交于点E ．（1）求m 的值；的值；（2）求∠CDE 的度数；的度数；（3）在抛物线对称轴的右侧部分上是否存在一点P ，使得△PDC 是等腰三角形？如果存在，求出符合条件的点P 的坐标；如果不存在，请说明理由．的坐标；如果不存在，请说明理由．22．（2006•锦州）如图，在平面直角坐标系中，在平面直角坐标系中，四边形四边形OABC 为菱形，为菱形，点点C 的坐标为（4，0），∠AOC=60°，垂直于x 轴的直线l 从y 轴出发，沿x 轴正方向以每秒1个单位长度的速度运动，设直线l 与菱形OABC的两边分别交于点M 、N （点M 在点N 的上方）．（1）求A 、B 两点的坐标；两点的坐标；（2）设△OMN 的面积为S ，直线l 运动时间为t 秒（0≤t ≤6），试求S 与t 的函数表达式；的函数表达式；（3）在题（2）的条件下，t 为何值时，S 的面积最大？最大面积是多少？的面积最大？最大面积是多少？23．（2007•济宁）如图，先把一矩形ABCD 纸片对折，设折痕为MN ，再把B 点叠在折痕线上，得到△ABE ，过B 点折纸片使D 点叠在直线AD 上，得折痕PQ ．（1）求证：△PBE ∽△QAB ；（2）你认为△PBE和△BAE相似吗？如果相似给出证明，如不相似请说明理由；相似吗？如果相似给出证明，如不相似请说明理由；上？为什么？（3）如果沿直线EB折叠纸片，点A是否能叠在直线EC上？为什么？2南京）若双曲线的两个分支在第二、四象限内，则抛物线A．B．C．D．考点：二次函数的图象；反比例函数的性质．分析：的符号判断抛物线的开口方向及对称轴． 根据双曲线的图象位置可知k＜0；再根据k的符号判断抛物线的开口方向及对称轴．解答：解：∵双曲线的两个分支在第二、四象限内，即k＜0，抛物线开口向下，∴抛物线开口向下，对称轴x=﹣=＜0，对称轴在y轴的左边．故选A．本题考查了反比例函数图象的性质和二次函数系数与抛物线形状的关系．点评：本题考查了反比例函数图象的性质和二次函数系数与抛物线形状的关系．A．△OAB∽△OCA B．△OAB∽△ODA C．△BAC∽△BDA D．以上结论都不成立上结论都不成立考点：相似三角形的判定．专题：常规题型．常规题型．根据已知及相似三角形的判定进行分析，从而得到答案．分析：根据已知及相似三角形的判定进行分析，从而得到答案．解答：解：∵∠AOD=90°，设OA=OB=BC=CD=x ∴AB=x，AC=x，AD=x，OC=2x，OD=3x，BD=2x ∴，，∴∴△BAC∽△BDA 故选C．点评：此题考查了相似三角形的判定：①如果两个三角形的三组对应边的比相等，那么这两个三角形相似；如果两个三角形的三组对应边的比相等，那么这两个三角形相似；如果两个三角形的两条对应边的比相等，且夹角相等，那么这两个三角形相似；②如果两个三角形的两条对应边的比相等，且夹角相等，那么这两个三角形相似；如果两个三角形的两个对应角相等，那么这两个三角形相似．③如果两个三角形的两个对应角相等，那么这两个三角形相似．3．（2012•绵阳）已知△ABC中，∠C=90°，tanA=，D是AC上一点，∠CBD=∠A，则sin∠ABD=（）A．B．C．D．考点：相似三角形的判定与性质；勾股定理；锐角三角函数的定义．压轴题．专题：压轴题．分析：作DE⊥AB于点E，根据相等的角的三角函数值相等即可得到===，设CD=1，则可以求得AD的长，然后利用勾股定理即可求得DE、AE的长，则BE可以求得，根据同角三角函数之间的关系即可求解．解答：解：作DE⊥AB于点E．∵∠CBD=∠A，∴tanA=tan∠CBD====，设CD=1，则BC=2，AC=4，∴AD=AC﹣CD=3，在直角△ABC中，AB===2，在直角△ADE中，设DE=x，则AE=2x，∵AE2+DE2=AD2，∴x2+（2x）2=9，解得：x=，则DE=，AE=．∴BE=AB﹣AE=2﹣=，∴tan∠DBA==，∴sin∠DBA=．故选：A．本题考查了三角函数的定义，以及勾股定理，正确理解三角函数就是直角三角形中边的比值是关键．点评：本题考查了三角函数的定义，以及勾股定理，正确理解三角函数就是直角三角形中边的比值是关键．n=12．考点：有理数的混合运算．压轴题；规律型．专题：压轴题；规律型．根据题目提供的信息，列出方程，然后求解即可．分析：根据题目提供的信息，列出方程，然后求解即可．解答：解：设S=3+5+7+…+（2n+1）=168①，则S=（2n+1）+…+7+5+3=168②，①+②得，2S=n（2n+1+3）=2×168，整理得，n2+2n﹣168=0，即（n﹣12）（n+14）=0，解得n1=12，n2=﹣14（舍去）．故答案为：12．点评：本题考查了有理数的混合运算，读懂题目提供的信息，表示出这列数据的和并列出方程是解题的关键．的坐标为 （1，3）．的坐标为考点：垂径定理；勾股定理；平行四边形的性质．计算题．专题：计算题．分析：过点M作MF⊥CD于点F，则CF=CD=4，过点C作CE⊥OA于点E，由勾股定理可求得MF的长，从而的坐标．得出OE的长，然后写出点C的坐标．解答：解：∵四边形OCDB是平行四边形，B（8，0），∴CD∥OA，CD=OB=8 过点M作MF⊥CD于点F，则CF=CD=4 过点C作CE⊥OA于点E，∵A（10，0），∴OE=OM﹣ME=OM﹣CF=5﹣4=1．连接MC，则MC=OA=5 ∴在Rt△CMF中，由勾股定理得∴点C的坐标为（1，3）本题考查了勾股定理、垂径定理以及平行四边形的性质，是基础知识要熟练掌握．点评：本题考查了勾股定理、垂径定理以及平行四边形的性质，是基础知识要熟练掌握．6．如图，⊙O的半径是5cm，P是⊙O外一点，PO=8cm，∠P=30°，则AB=6cm．考点：垂径定理；含30度角的直角三角形；勾股定理．的长，再解直角三角形并根据垂径定理即可求出．分析：首先作出辅助线，求出OD的长，再解直角三角形并根据垂径定理即可求出．解答：解：如图：作OD⊥AB于D，连接OB，因为∠P=30°所以OD=PO=×8=4cm 在直角三角形ODB中，BD===3cm 根据垂径定理，BD=AD，则AB=2BD=2×3=6cm．，根据垂径定理解答．点评：解答此题的关键是作出辅助线OD，根据垂径定理解答．7．（2000•甘肃）如图，AB是半圆的直径，直线MN切半圆于C，CM⊥MN，BN⊥MN，如果AM=a，BN=b，那么半圆的半径是 ．半圆的半径是考点：梯形中位线定理；切线的性质．分析：根据切线的性质，只需连接OC．根据切线的性质定理以及平行线等分线段定理得到梯形的中位线，再根据梯形的中位线定理进行计算即可．梯形的中位线定理进行计算即可．解答：解：连接OC，则OC⊥MN．∴OC∥AM∥BN，又OA=OB，则MC=NC．根据梯形的中位线定理，得该半圆的半径是．点评：此题主要是根据切线的性质定理和平行线等分线段定理，发现梯形的中位线，进而熟练运用梯形的中位线定理求解．定理求解．8．已知双曲线y=与直线y=相交于A，B两点．第一象限上的点M（m，n）（在A点左侧）是双曲线y=上的动点．过点B作BD∥y轴交x轴于点D．过N（0，﹣n）作NC∥x轴交双曲线y=于点E，交BD于点C．若B是CD的中点，四边形OBCE的面积为4，则直线CM的解析式为的解析式为 y=．考点：反比例函数与一次函数的交点问题．动点型．专题：动点型．根据一次函数和反比例函数的性质及点的坐标和解析式的关系解答．分析：根据一次函数和反比例函数的性质及点的坐标和解析式的关系解答．解答：解：设B点坐标为（x1，﹣），代入y=x得，﹣=x1，x1=﹣2n；∴B点坐标为（﹣2n，﹣）．因为BD∥y轴，所以C点坐标为（﹣2n，﹣n）．因为四边形ODCN的面积为2n•n=2n2，三角形ODB，三角形OEN的面积均为，四边形OBCE的面积为4．则有2n2﹣k=4﹣﹣﹣①；又因为2n•=k，即n2=k﹣﹣﹣②②代入①得，4=2k﹣k，解得k=4；则解析式为y=；又因为n2=4，故n=2或n=﹣2．M在第一象限，n＞0；将M（m，2）代入解析式y=，得m=2．故M点坐标为（2，2）；C（﹣4，﹣2）；设直线CM解析式为y=kx+b，则，解得∴一次函数解析式为：y=x+．点评：解答本题要明确两个关系：（1）双曲线中，xy=k；（2）S△DBO=|k|．9．如图，M为双曲线y=上的一点，过点M作x轴、y轴的垂线，分别交直线y=﹣x+m于D、C两点，若直线y=﹣x+m与y轴、x轴分别交于点A、B，则AD•BC的值为的值为 2．考点：反比例函数综合题．综合题．专题：综合题．分析：作CE⊥x轴于E，DF⊥y轴于F，如图所示，根据直线y=﹣x+m，表示出A与B坐标，可得出三角形OAB 为等腰直角三角形，进而确定出三角形ADF与三角形CEB都为等腰直角三角形，设M（a，b），代入反比的值．例解析式得到ab=，CE=b，DF=a，表示出AD与BC，即可求出AD•BC的值．解答：解：作CE⊥x轴于E，DF⊥y轴于F，如图，，如图，对于y=﹣x+m，令x=0，得到y=m；令y=0，得到x=m，∴A（0，m），B（m，0），为等腰直角三角形，∴△OAB为等腰直角三角形，都是等腰直角三角形，∴△ADF与△CEB都是等腰直角三角形，设M（a，b），则ab=，CE=b，DF=a，∴AD=DF=a，BC=CE=b，∴AD•BC=a•b=2ab=2．故答案为：2．点评：此题属于反比例函数综合题，涉及的知识有：等腰直角三角形的性质，坐标与图形性质，反比例函数的性质，以及矩形的性质，熟练掌握等腰直角三角形的性质是解本题的关键．质，以及矩形的性质，熟练掌握等腰直角三角形的性质是解本题的关键．10．如图，正方形ABCD的对角线AC、BD相交于点O，E是BC的中点，DE交AC于F，若DE=6，则EF等于等于 2．考点：相似三角形的判定与性质；正方形的性质．分析：因为四边形ABCD是正方形，E是BC中点，所以CE=AD，由相似三角形的判定定理得出△CEF∽△ADF，再根据相似三角形的对应边成比例可得出．再根据相似三角形的对应边成比例可得出．中点，解答：解：∵四边形ABCD是正方形，E是BC中点，∴CE=AD，∵AD∥BC，∴∠ADF=∠DEC，∠AFD=∠EFC，∴△CEF∽△ADF，∴=，∴，即，解得EF=2，故答案为2．点评：本题考查的是相似三角形的判定与性质及正方形的性质，先根据题意判断出△CEF∽△ADF，再根据相似三角形的对应边成比例进行解答是解答此题的关键．形的对应边成比例进行解答是解答此题的关键．11．（2012•金山区二模）如图，已知AD为△ABC的角平分线，DE∥AB交AC于E，如果，那么=．考点：相似三角形的判定与性质；等腰三角形的判定与性质．分析：的值． 根据角平分线的定义，平行线的性质易证EA=ED，△CED∽△CAB，从而求得的值．的角平分线，解答：解：∵AD为△ABC的角平分线，∴∠BAD=∠EAD，∵DE∥AB，∴△CED∽△CAB，∠BAD=∠EDA．∴∠EDA=∠EAD，∴EA=ED，∵=，∴ED：EC=2：3，∴=ED：EC=2：3．故答案为：．点评：本题主要考查了相似三角形的判定与性质，相似三角形的对应边对应成比例，同时考查了角平分线的定义．12．如图，在△ABC中，D、E是BC的三等分点，M是AC的中点，BM交AD、AE于G、H，则BG：GH：HM= 5：3：2．考点：平行线分线段成比例；三角形中位线定理．分析：首先过点M作MK∥BC，交AD，AE分别于K，N，由M是AC的中点与D、E是BC的三等分点，根据平行线分线段成比例定理，即可求得MN=NK=BD=DE=EC，然后根据比例的性质，即可求得BG：GH：HM的值．的值．解答：解：法一：过点M作MK∥BC，交AD，AE分别于K，N，∵M是AC的中点，的中点，∴=，的三等分点，∵D、E是BC的三等分点，∴BD=DE=EC，∴MN=NK，∵=，=1，∴MH=BH，MG=BG，设MH=a，BH=4a，BG=GM=，∴GH=GM﹣MH=，∴BG：GH：HM=：：a=5：3：2．故答案为：5：3：2．点评：此题考查了平行线分线段成比例定理与比例的性质．此题难度适中，解题的关键是注意辅助线的作法，注意数形结合思想的应用．意数形结合思想的应用．13．（2013•上海）如图，在△ABC中，AB=AC，BC=8，tanC=，如果将△ABC沿直线l翻折后，点B落在边AC的长为 ．的中点处，直线l与边BC交于点D，那么BD的长为考点：翻折变换（折叠问题）．压轴题．专题：压轴题．即可．分析：首先根据已知得出△ABC的高以及B′E的长，利用勾股定理求出BD即可．解答：解：过点A作AQ⊥BC于点Q，∵AB=AC，BC=8，tanC=，∴=，QC=BQ=4，∴AQ=6，的中点处，∵将△ABC沿直线l翻折后，点B落在边AC的中点处，过B′点作B′E⊥BC于点E，∴B′E=AQ=3，∴=，∴EC=2，设BD=x，则B′D=x，∴DE=8﹣x﹣2=6﹣x，∴x2=（6﹣x）2+32，解得：x=，直线l与边BC交于点D，那么BD的长为：．故答案为：．点评：此题主要考查了翻折变换的性质以及勾股定理和锐角三角函数关系，根据已知表示出DE的长是解题关键．AC=，ACD=．考点：解直角三角形．分析：在直角△ABC中，根据勾股定理即可求得AB，而∠B=∠ACD，即可把求sin∠ACD转化为求sinB．解答：解：在直角△ABC中，根据勾股定理可得：AB===3．∵∠B+∠BCD=90°，∠ACD+∠BCD=90°，∴∠B=∠ACD．∴sin∠ACD=sin∠B==．本题考查了解直角三角形中三角函数的应用，要熟练掌握好边角之间的关系．点评：本题考查了解直角三角形中三角函数的应用，要熟练掌握好边角之间的关系．考点：圆周角定理．证明题．专题：证明题．分析：首先连接AH，由AD⊥BC，BH⊥AC与∠AFE=∠BFD，即可得∠EAF=∠FBD，又由圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，即可得∠HAC=∠HBC，即可得∠HAE=∠F AE，则可用ASA证得△AEF≌△AEH，继而证得FE=EH．解答：证明：连接AH，∵AD⊥BC，BH⊥AC，∴∠FDB=∠AEF=90°，∵∠AFE=∠BFD，∴∠EAF=∠FBD，∵∠HAC=∠HBC，∴∠HAE=∠EAF，∵BH⊥AC，∴∠AEF=∠AEH=90°，中，在△AEF和△AEH中，∴△AEF≌△AEH（ASA），∴FE=EH．点评：此题考查了圆周角定理、直角三角形的性质、全等三角形的判定与性质．此题难度适中，解题的关键是准确作出辅助线，掌握在同圆或等圆中，同弧或等弧所对的圆周角相等定理的应用．确作出辅助线，掌握在同圆或等圆中，同弧或等弧所对的圆周角相等定理的应用．16．把抛物线y=x2+bx+c向右平移3个单位，再向下平移2个单位，所得图象的解析式是y=x2﹣3x+5，求b，c的值．值．考点：二次函数图象与几何变换．分析：先求出y=x2﹣3x+5的顶点坐标，再根据“左加右减”求出平移前的抛物线的顶点坐标，然后利用顶点式解析式写出，整理成二次函数的一般形式，再根据对应项系数相等解答．式写出，整理成二次函数的一般形式，再根据对应项系数相等解答．解答：解：∵y=x2﹣3x+5=（x﹣）2+，∴y=x2﹣3x+5的顶点坐标为（，），个单位，∵向右平移3个单位，向下平移2个单位，∴平移前的抛物线的顶点的横坐标为﹣3=﹣，纵坐标为+2=，∴平移前的抛物线的顶点坐标为（﹣，），∴平移前的抛物线为y=（x+）2+=x2+3x+7，∴b=3，c=7．点评：本题考查了二次函数的图象与几何变换，根据两个函数图象的顶点坐标确定平移方法更简便，要注意知道平移后的顶点坐标求平移前的顶点坐标的方法．平移后的顶点坐标求平移前的顶点坐标的方法．17．（2003•海南）已知抛物线y=ax2+bx+c开口向下，并且经过A（0，1）和M（2，﹣3）两点．）两点．，求此抛物线的解析式；（1）若抛物线的对称轴为直线x=﹣1，求此抛物线的解析式；的取值范围；（2）如果抛物线的对称轴在y轴的左侧，试求a的取值范围；的值．（3）如果抛物线与x轴交于B、C两点，且∠BAC=90°，求此时a的值．考点：二次函数综合题．压轴题．专题：压轴题．分析：（1）可将A、M的坐标代入抛物线的解析式中，用a替换掉b、c的值，再根据抛物线的对称轴为﹣1，即可求出a的值，也就确定了抛物线的解析式．的值，也就确定了抛物线的解析式．的取值范围． （2）抛物线的对称轴在y轴左侧，即抛物线对称轴方程小于0，由此可得出a的取值范围．（3）可设出B、C的坐标，如果∠BAC=90°，在直角三角形BAC中，可根据射影定理得出OA2=OC•OB，的值．据此可得出a的值．解答：解：将A、M的坐标代入抛物线的解析式中有：的坐标代入抛物线的解析式中有：，解得：∴抛物线的解析式为y=ax2﹣（2+2a）x+1．（1）∵x=﹣=﹣1，∴=﹣1，解得a=﹣．∴抛物线的解析式为y=﹣x2﹣x+1．（2）由题意知：x=﹣＜0，即﹣＜0；抛物线开口向下，∵抛物线开口向下，∴a＜0 ∴1+a＞0，且a＜0 ∴﹣1＜a＜0．（3）设B（x1，0），C（x2，0），x1＜x2；∵x1x2=，且a＜0．轴正半轴；∴x1x2＜0，即B在x轴负半轴，C在x轴正半轴；∴OB=﹣x1，OC=x2．∵∠BAC=90°，，根据射影定理可得：在直角三角形BAC中，AO⊥BC，根据射影定理可得：OA2=OB•OC=﹣x1•x2=1，即﹣=1，a=﹣1．本题主要考查了抛物线对称轴解析式、二次函数与一元二次方程的关系、韦达定理等知识．点评：本题主要考查了抛物线对称轴解析式、二次函数与一元二次方程的关系、韦达定理等知识．18．（2000•杭州）已知一个正三角形和一个正六边形的周长相等，求它们的面积的比值．杭州）已知一个正三角形和一个正六边形的周长相等，求它们的面积的比值．考点：正多边形和圆．分析：根据正多边形的面积等于周长与边心距的乘积的一半，所以只需根据它们的周长计算其边心距；在由正多边形的半径、边心距和边长组成的直角三角形中，根据锐角三角函数的概念可以分别求得它们的边心距，再进一步计算其面积，从而得到其比值．再进一步计算其面积，从而得到其比值．．根据题意，得解答：解：设它们的周长是1．根据题意，得正三角形的边长是，正六边形的边长是．则正三角形的边心距是，正六边形的边心距是．则正三角形的面积是，正六边形的面积是．则它们的面积比是2：3．点评：熟悉正多边形的面积公式：正多边形的面积等于周长与边心距的乘积的一半．能够根据由半径、边心距和半边组成的直角三角形，运用锐角三角函数进行计算．半边组成的直角三角形，运用锐角三角函数进行计算．19．（原创题）如图所示，扇形OAB从图①无滑动旋转到图②，再由图②到图③，∠O=60°，OA=1．点所运动的路径长；（1）求O点所运动的路径长；围成的面积．（2）O点走过路径与直线L围成的面积．考点：扇形面积的计算；弧长的计算．本题一共转动了三次，关键是分析每一次转动的圆心角和半径，然后利用弧长公式求．分析：本题一共转动了三次，关键是分析每一次转动的圆心角和半径，然后利用弧长公式求．解答：解：（1）运动路径第一段弧长=，第二段路径为线段长为，第三段路径为，即O在L上运动路径为．）围成面积，（2）围成面积，S1=．本题的难点是第二次，实际上就是扇形的弧长，其它二次则简单．点评：本题的难点是第二次，实际上就是扇形的弧长，其它二次则简单．20．（2013•重庆）重庆） 已知：如图，抛物线y=x2+2x﹣3与x轴的交点为A、B两点，与y轴交于点C，直线AC与抛两点．物线交于A、C两点．如图，的y=ax2+bx+c（a≠0）与x轴相交于A、B两点，其中点A的坐标为（﹣3，0）．的坐标．（1）求点B的坐标．（2）在抛物线的对称轴x=﹣1上是否存在一点P，使得△BCP为等腰三角形，若存在，直接写出点P的坐标；若不存在，说明理由．存在，说明理由．的坐标．（3）若点Q在直线AC下方的抛物线上，且S△QOC=2S△BOC，求点Q的坐标．考点：二次函数综合题．压轴题．专题：压轴题．分析：（1）由抛物线y=ax2+bx+c的对称轴为直线x=﹣1，交x轴于A、B两点，其中A点的坐标为（﹣3，0），点的坐标；根据二次函数的对称性，即可求得B点的坐标；（2）①a=1时，先由对称轴为直线x=﹣1，求出b的值，再将B（1，0）代入，求出二次函数的解析式为y=x2+2x ﹣3，得到C点坐标，然后设P点坐标为（x，x2+2x﹣3），根据S△POC=4S△BOC列出关于x的方程，解方程的坐标；求出x的值，进而得到点P的坐标；②先运用待定系数法求出直线AC的解析式为y=﹣x﹣3，再设Q点坐标为（x，﹣x﹣3），则D点坐标为（x，x2+2x﹣3），然后用含x的代数式表示QD，根据二次函数的性质即可求出线段QD长度的最大值．长度的最大值．解答：解：（1）∵对称轴为直线x=﹣1的抛物线y=ax2+bx+c（a≠0）与x轴相交于A、B两点，两点，对称，∴A、B两点关于直线x=﹣1对称，∵点A的坐标为（﹣3，0），∴点B的坐标为（1，0）；（2）①a=1时，∵抛物线y=x2+bx+c的对称轴为直线x=﹣1，∴=﹣1，解得b=2．将B（1，0）代入y=x2+2x+c，得1+2+c=0，解得c=﹣3．则二次函数的解析式为y=x2+2x﹣3，∴抛物线与y轴的交点C的坐标为（0，﹣3），OC=3．设P点坐标为（x，x2+2x﹣3），∵S△POC=4S△BOC，∴×3×|x|=4××3×1，∴|x|=4，x=±4．当x=4时，x2+2x﹣3=16+8﹣3=21；当x=﹣4时，x2+2x﹣3=16﹣8﹣3=5．∴点P的坐标为（4，21）或（﹣4，5）；）代入，②设直线AC的解析式为y=kx+t，将A（﹣3，0），C（0，﹣3）代入，得，解得，即直线AC的解析式为y=﹣x﹣3．设Q点坐标为（x，﹣x﹣3）（﹣3≤x≤0），则D点坐标为（x，x2+2x﹣3），QD=（﹣x﹣3）﹣（x2+2x﹣3）=﹣x2﹣3x=﹣（x+）2+，∴当x=﹣时，QD有最大值．点评：此题考查了待定系数法求二次函数、一次函数的解析式，二次函数的性质以及三角形面积、线段长度问题．此题难度适中，解题的关键是运用方程思想与数形结合思想．题难度适中，解题的关键是运用方程思想与数形结合思想．21．（2014•徐州模拟）如图，已知抛物线y=﹣x2+2x+1﹣m与x轴相交于A、B两点，与y轴相交于点C，其中点C的坐标是（0，3），顶点为点D，连接CD，抛物线的对称轴与x轴相交于点E．（1）求m的值；的值；的度数；（2）求∠CDE的度数；（3）在抛物线对称轴的右侧部分上是否存在一点P，使得△PDC是等腰三角形？如果存在，求出符合条件的点P的坐标；如果不存在，请说明理由．坐标；如果不存在，请说明理由．考点：二次函数综合题．综合题．专题：综合题．的值． 分析：（1）由于抛物线的解析式中只有一个未知数m，因此只需将C点的坐标代入抛物线中即可求出m的值．（2）此题可首先表示出抛物线的顶点式，就可以求出D点的坐标，然后过C点作DE的垂线CF，在△DCF的度数；中根据C、D、F三点的坐标求出DF和CF长度相等，得出∠CDE的度数；的坐标． （3）利用二次函数的对称性可求出，以及利用线段垂直平分线的性质求出P的坐标．解答：（1）∵抛物线过点C（0，3）∴1﹣m=3 ∴m=﹣2 （2）由（1）可知该抛物线的解析式为y=﹣x2+2x+3=﹣（x﹣1）2+4 ∴此抛物线的对称轴x=1 抛物线的顶点D（1，4）过点C作CF⊥DE，则CF∥OE ∴F（1，3）所以CF=1，DF=4﹣3=1 ∴CF=DF 又∵CF⊥DE ∴∠DFC=90°∴∠CDE=45°）存在．（3）存在．的对称点时，①延长CF交抛物线于点P1，则CP1∥X轴，所以P1正好是C点关于DE的对称点时，有DC=DP1，得出P1点坐标（2，3）；由y=﹣x2+2x+3得，D点坐标为（1，4），对称轴为x=1．②若以CD为底边，则PD=PC，，根据两点间距离公式，设P点坐标为（x，y），根据两点间距离公式，得x2+（3﹣y）2=（x﹣1）2+（4﹣y）2，即y=4﹣x．）在抛物线上，又∵P点（x，y）在抛物线上，∴4﹣x=﹣x2+2x+3，即x2﹣3x+1=0，，应舍去；解得：x=，＜1，应舍去；∴x=，∴y=4﹣x=则P2点坐标（，）．∴符合条件的点P坐标为（，）和（2，3）．点评：此题主要考查了二次函数的对称性，以及等腰三角形的判定方法和垂直平分线的性质等知识，题目综合性较强，是中考中热点题型．较强，是中考中热点题型．22．（2006•锦州）如图，在平面直角坐标系中，四边形OABC为菱形，点C的坐标为（4，0），∠AOC=60°，垂直于x轴的直线l从y轴出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线l与菱形OABC的两边分别交于点M、N（点M在点N的上方）．两点的坐标；（1）求A、B两点的坐标；的函数表达式；（2）设△OMN的面积为S，直线l运动时间为t秒（0≤t≤6），试求S与t的函数表达式；（3）在题（2）的条件下，t为何值时，S的面积最大？最大面积是多少？的面积最大？最大面积是多少？。
1998年江西省中考数学试卷
1998年江西省中考数学试卷一、单选题（每道小题3分共24分）1.（3分）下列运算正确的是（）A.x2+x2=x4B.x x4=x4C.x6-^-x2=x4D.（ab）2=ab12.（3分）如图，己知AB=AC,AE^AD,那么图中全等三角形共有（）A.0对B.1对C.2对D.3对3.（3分）如果两圆的半径分别是3cm和4cm,圆心距为5cm,那么两圆公切线的条数是（）A.1条B.2条C.3条D.4条4.（3分）下列四个式子：①—1—3=1；②2°=1；③3一2=：；④寸〒=2,其中正确的个数是（）A.1个B.2个C.3个D.4个5.（3分）用配方法解关于x的方程J+px+qM时，方程可变形为（）a.b.2 424C. D.（.4=^124 2 46.（3分）方程x2 -3x+2=0的两根之和与两根之积分别是（）A.3,-2B.3,2C.-3,-2D.-3,27.（3分）下列图形：其中既是轴对称图形又是中心对称图形的个数是（）M0O®A.4个B.3个C.2个D.1个8.（3分）甲、乙两队学生绿化校园.如果两队合作，6天可以完成；如果单独工作，甲队比乙队少用5天，两队单独工作各需多少天完成？若设甲队单独工作需x天完成，则依题意得到的方程是（）x x+5x x-5x x+56x x-56二、填空题（每道小题3分共36分）9.（3分）-3与-7的大小关系是.10.（3分）计算：|一2|=.11.（3分）函数、=后！中，自变量x的取值范围是.12.（3分）用科学记数法表示51098,应记作.13.（3分）一个面积为0.64平方米的正方形桌面，它的边长是.Y2-2x14.（3分）分式方程土仝=0的增根是____.x—215.（3分）已知一元二次方程x2+2x-1=0,它的根的判别式的值△=.16.（3分）抛物线>=2（x+3）2-5的顶点坐标是.17.（3分）一个角的补角是这个角的5倍，这个角的度数是度.18.（3分）在AABC■中，AB=AC,£8=25。
南京市中考数学复习题及答案 (83)
南京市中考数学复习题及答案27．（10分）问题提出旋转是图形的一种变换方式，利用旋转来解决几何问题往往可以使解题过程更简单，起到事半功倍的效果．初步思考（1）如图①，点P是等边△ABC内部一点，且∠APC＝150°，P A＝3，PC＝4．求PB 的长．小敏在解答此题时，利用了“旋转法”进行证明，她的方法如下：如图②，将△APC绕点A按顺时针方向旋转60°后得到△ADB，连接DP．（请你在下面的空白处完成小敏的证明过程．）推广运用（2）如图③，在△ABC中，∠BAC＝60°，AB＝2AC，点P是△ABC内部一点，且∠APC＝120°，P A＝，PB＝5．求PC的长．【分析】（1）只要证明△ADP是等边三角形，△PDB是直角三角形，两个勾股定理即可解决问题；（2）如图，作∠CAD＝∠BAP，使AD＝AP．连接CD、PD．只要证明△DPC是直角三角形，即可解决问题；【解答】解：（1）如图2中，∵将△APC绕点A按顺时针方向旋转60°后得到△ADB．∴AD＝AP＝3，DB＝PC＝4，∠P AD＝60°，∠ADB＝∠APC＝150°．∵AD＝AP，∠P AD＝60°，∴△ADP为等边三角形．∴PD＝P A＝3，∠ADP＝60°．又∠ADB＝150°，∴∠PDB＝90°．在Rt△PDB中，PD＝3，DB＝4，∴BP＝＝＝5，（2）如图，作∠CAD＝∠BAP，使AD＝AP．连接CD、PD．∵AB＝2AC，AD＝AP，∴＝＝．又∠CAD＝∠BAP，∴△ABP∽△ACD．∴CD＝BP＝2.5．在△P AD中，P A＝，∠P AD＝60°，AD＝，易证∠APD＝30°，∠PDA＝90°（取P A中点K，连接DK，利用等边三角形的性质即可证明）∴PD＝，∴∠DPC＝120°﹣30°＝90°在Rt△DPC中，PC＝＝＝2．【点评】本题考查几何变换综合题、等边三角形的性质、直角三角形30度角的性质、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识，解题的关键是学会利用旋转法添加辅助线，构造全等三角形或相似三角形解决问题，属于中考压轴题．。
1998年江苏省苏州市中考数学试卷
1998年江苏省苏州市中考数学试卷1998年江苏省苏州市中考数学试卷⼀、单选题（每道⼩题3分共42分）1．（3分）下列各对数中，互为相反数的⼀对是（）A．和B．和C．和D．和2．（3分）计算2x3（﹣3x2）的结果是（）A．﹣6x5B．6x5C．﹣12x5D．2x63．（3分）当a＜1时，化简得（）A．a﹣1B．a+1C．1﹣a D．﹣a﹣14．（3分）若关于x的⽅程x2﹣3x+t＝0有两个实数根，则t的取值范围是（）A．t B．t C．t＜D．t5．（3分）不等式组＜的解集是（）A．x≥2B．x＜4C．2≤x＜4D．x＞46．（3分）抛物线y＝x2﹣3x﹣6的对称轴是直线（）A．B．C．x＝3D．x＝﹣37．（3分）已知⼀组数据：2，5，2，8，3，2，6．这组数据的中位数和众数分别是（）A．中位数是3，众数是2B．中位数是2，众数是3C．中位数是4，众数是2D．中位数是3，众数是48．（3分）如图，AB∥CD，AF分别交AB、CD于点A、C，CE平分∠DCF，∠1＝100°，则∠2＝（）A．40°B．50°C．60°D．70°9．（3分）下列图形中，不是轴对称图形的是（）A．等腰三⾓形B．直⾓梯形C．矩形D．正⽅形10．（3分）已知四边形ABCD内接于圆，∠A＝2∠C，则∠C等于（）A．90°B．60°C．45°D．30°11．（3分）下列函数中，y随x的增⼤⽽减⼩的是（）A．y x B．y＝3x﹣4C．y＝﹣3x+4D．y12．（3分）下列命题中，假命题是（）A．对⾓线相等的梯形是等腰梯形B．三⾓形的⼀个外⾓⼤于任何⼀个内⾓C．如果两个圆只有两条公切线，那么这两个圆相交D．和线段两个端点距离相等的点轨迹是这条线段的垂直平分线13．（3分）若⽅程（x+1）（x+a）＝x2+bx﹣4，则（）A．a＝4，b＝3B．a＝﹣4，b＝3C．a＝4，b＝﹣3D．a＝﹣4，b＝﹣3 14．（3分）两圆的半径分别为R，r，且R＝3，r＝3，若它们的圆⼼距d是R和r 的⽐例中项，则这两个圆的位置关系是（）A．外离B．外切C．相交D．内含⼆、填空题（每道⼩题2分共24分）15．（2分）|﹣1|＝．16．（2分）分母有理化：．17．（2分）⽤代数式表⽰“a的与b的2倍的差”：．18．（2分）分解因式：x3﹣6x2+9x＝．19．（2分）当x＝时，分式的值为0．20．（2分）⽅程的根是．21．（2分）函数中⾃变量x的取值范围是．22．（2分）如图，⊙O的割线PB、PD分别交⊙O于A、B、C、D．已知P A＝4，PB＝10，PD＝8，则PC＝．23．（2分）甲、⼄两⼈加⼯某种零件．若单独⼯作，则⼄要⽐甲多⽤12天才能完成；若两⼈合作，则8天可以完成．设甲单独⼯作x天可以完成，则可以列出⽅程：．24．（2分）如图，菱形ABCD中，∠A＝60°，对⾓线DB长6cm，则它的周长是cm．25．（2分）如图，已知扇形的半径为3cm，圆⼼⾓为120°，则扇形的⾯积为cm2．（结果保留π）26．（2分）如图，在△ABC中，CE：EB＝1：2，DE∥AC，若△ABC的⾯积为S，则△ADE 的⾯积为．三、计算题（3分）27．（3分）计算：．四、解答题（1-2每题5分，3-4每题7分，第5⼩题11分，共35分）28．（5分）如图，平⾏四边形ABCD中，G是CD上⼀点，BG交AD延长线于E，AF＝CG，∠DGE＝100度．（1）试说明DF＝BG；（2）试求∠AFD的度数．29．（5分）如图，从⾼出海平⾯100⽶的灯塔的顶部A，测得它的正东⽅和正西⽅的两艘（最后结果精确到1⽶．下船C、D的俯⾓分别为30°和45°，求这两艘船之间的距离CD．列数据供选⽤： 1.414， 1.732）30．（7分）某电⼚规定，该⼚家属区的每户居民如果⼀个⽉的⽤电量不超过A度，那么这个⽉每户只需交10元的⽤电费，如果超过A度，则这个⽉除了仍要交10元的⽤电费外，超过部分还要按每度元交费．（1）该⼚某户居民王东2⽉份⽤电90度，超过了规定的A度，则超过部分应交电费元（⽤A表⽰）；（2）下表是这户居民3、4⽉份的⽤电情况和交费情况，根据表中的数据，求该电⼚规定的A度是多少．31．（7分）已知点A（m，2）和点B（2，n）都在反⽐例函数的图象上．（1）求m与n的值；（2）若直线y＝mx﹣n与x轴交于点C，求点C关于y轴的对称点C′的坐标．32．（11分）已知：a、b、c是△ABC中∠A、∠B、∠C的对边，抛物线y＝x2﹣2ax+b2交x 轴于两点M、N，交y轴于点P，其中点M的坐标是（a+c，0）．（1）求证：△ABC是直⾓三⾓形；（2）若△MNP的⾯积是△NOP的⾯积的3倍，①求cos C的值；②试判断，△ABC的三边长能否取⼀组适当的值，使以MN为直径的圆恰好过抛物线y＝x2﹣2ax+b2的顶点？如能，求出这组值；如不能，说明理由．五、证明题（9分）33．（9分）已知：如图，△ABC内接于⊙O，⊙B与⊙O相交于点A、D、AD交BC于点E，交⊙O的直径BF于点G．（1）求证：①△ABC∽△EBA；②AE?ED＝AB2﹣EB2．（2）AB，BF＝15，AE：ED＝1：3，求BC的长．六、画图题（第1⼩题3分，第2⼩题4分，共7分）34．（3分）已知：∠α和线段m、n．求作：△ABC，使∠A＝∠α，AB＝m，BC＝n．（⽤尺规作图，不写作法，保留作图痕迹．）35．（4分）如图，已知∠AOB，⽤直尺和圆规作出∠AOB的平分线OM（不要求写出作法，但必须保留作图痕迹）．1998年江苏省苏州市中考数学试卷参考答案与试题解析⼀、单选题（每道⼩题3分共42分）1．（3分）下列各对数中，互为相反数的⼀对是（）A．和B．和C．和D．和【解答】解：A、和不是互为相反数，故本选项错误；B、和是互为相反数，故本选项正确；C、和不是互为相反数，故本选项错误；D、和不是互为相反数，故本选项错误．故选：B．2．（3分）计算2x3（﹣3x2）的结果是（）A．﹣6x5B．6x5C．﹣12x5D．2x6【解答】解：2x3（﹣3x2）＝[2×（﹣3）]（x3?x2）＝﹣6x5．故选：A．3．（3分）当a＜1时，化简得（）A．a﹣1B．a+1C．1﹣a D．﹣a﹣1【解答】解：∵a＜1，∴a﹣1＜0，∴|a﹣1|＝1﹣a．故选：C．4．（3分）若关于x的⽅程x2﹣3x+t＝0有两个实数根，则t的取值范围是（）A．t B．t C．t＜D．t【解答】解：△＝b2﹣4ac＝（﹣3）2﹣4×1×t＝9﹣4t，∵⽅程x2﹣3x+t＝0有两个实数根，∴△≥0，∴9﹣4t≥0，解得：t，故选：D．5．（3分）不等式组＜的解集是（）A．x≥2B．x＜4C．2≤x＜4D．x＞4【解答】解：①＜②，由①得，x≥2；由②得，x＜4，故此不等式组的解集为：2≤x＜4．故选：C．6．（3分）抛物线y＝x2﹣3x﹣6的对称轴是直线（）A．B．C．x＝3D．x＝﹣3【解答】解：∵y＝x2﹣3x﹣6＝x2﹣3x6＝（x）2，∴抛物线y＝x2﹣3x﹣6的对称轴是直线x．故选：A．7．（3分）已知⼀组数据：2，5，2，8，3，2，6．这组数据的中位数和众数分别是（）A．中位数是3，众数是2B．中位数是2，众数是3C．中位数是4，众数是2D．中位数是3，众数是4【解答】解：将这组数据从⼩到⼤排列为：2，2，2，3，5，6，8，最中间的数是3，则这组数据的中位数是3；2出现了三次，出现的次数最多，则这组数据的众数是2；故选：A．8．（3分）如图，AB∥CD，AF分别交AB、CD于点A、C，CE平分∠DCF，∠1＝100°，则∠2＝（）A．40°B．50°C．60°D．70°【解答】解：∵AB∥CD，∴∠DCF＝∠1＝100°，∵CE平分∠DCF，∴∠2∠DCF100°＝50°．故选：B．9．（3分）下列图形中，不是轴对称图形的是（）A．等腰三⾓形B．直⾓梯形C．矩形D．正⽅形【解答】解：根据轴对称图形的意义可知，该图形沿⼀条直线对折后，直线两旁的部分不能完全重合，可得：A、等腰三⾓形是轴对称图形，B、直⾓梯形不是轴对称图形；C、矩形是轴对称图形；D、正⽅形是轴对称图形．故选：B．10．（3分）已知四边形ABCD内接于圆，∠A＝2∠C，则∠C等于（）A．90°B．60°C．45°D．30°【解答】解：∵四边形ABCD内接于圆，∴∠A+∠C＝180°，∵∠A＝2∠C，∴3∠C＝180°，∴∠C＝60°．故选：B．11．（3分）下列函数中，y随x的增⼤⽽减⼩的是（）A．y x B．y＝3x﹣4C．y＝﹣3x+4D．y【解答】解：A、∵⼀次函数y x中，k＞0，∴y随x的增⼤⽽增⼤，故本选项错误；B、∵⼀次函数y＝3x﹣4中，k＝3＞0，∴y随x的增⼤⽽增⼤，故本选项错误；C、∵⼀次函数y＝﹣3x+4中，k＝﹣3＜0，∴y随x的增⼤⽽减⼩，故本选项正确；D、∵反⽐例函数y中，k＝﹣3＜0，∴y随x的增⼤⽽增⼤，故本选项错误．故选：C．12．（3分）下列命题中，假命题是（）A．对⾓线相等的梯形是等腰梯形B．三⾓形的⼀个外⾓⼤于任何⼀个内⾓C．如果两个圆只有两条公切线，那么这两个圆相交D．和线段两个端点距离相等的点轨迹是这条线段的垂直平分线【解答】解：A、对⾓线相等的梯形是等腰梯形，是真命题；B、三⾓形的⼀个外⾓⼤于任何⼀个与它不相邻的内⾓，故原命题是假命题；C、如果两个圆只有两条公切线，那么这两个圆相交，是真命题；D、和线段两个端点距离相等的点轨迹是这条线段的垂直平分线，是真命题；故选：B．13．（3分）若⽅程（x+1）（x+a）＝x2+bx﹣4，则（）A．a＝4，b＝3B．a＝﹣4，b＝3C．a＝4，b＝﹣3D．a＝﹣4，b＝﹣3【解答】解：∵（x+1）（x+a）＝x2+x+ax+a＝x2+（a+1）x+a，∴由多项式相等的条件得：，解得a＝﹣4，b＝﹣3．故选：D．14．（3分）两圆的半径分别为R，r，且R＝3，r＝3，若它们的圆⼼距d是R和r 的⽐例中项，则这两个圆的位置关系是（）A．外离B．外切C．相交D．内含【解答】解：∵圆⼼距d是R和r的⽐例中项，R＝3，r＝3，∴d2＝R?r＝（3）（3）＝4∴d＝2，∴d＜R﹣r＝2∴两圆内含，故选：D．⼆、填空题（每道⼩题2分共24分）15．（2分）|﹣1|＝．【解答】解：|﹣1|＝||．故答案为：16．（2分）分母有理化：．【解答】解：与2的积为有理数的实数为2．故答案是：2．17．（2分）⽤代数式表⽰“a的与b的2倍的差”：a﹣2b．【解答】解：a的可表⽰为：a，b的2倍可表⽰为：2a，故可得代数式：a﹣2b．故答案为：a﹣2b．18．（2分）分解因式：x3﹣6x2+9x＝x（x﹣3）2．【解答】解：x3﹣6x2+9x，＝x（x2﹣6x+9），＝x（x﹣3）2．故答案为：x（x﹣3）2．19．（2分）当x＝﹣2时，分式的值为0．【解答】解：当分⼦2x+4＝0，且分母x2﹣1≠0，即x＝﹣2时，分式的值为0．故填：﹣2．20．（2分）⽅程的根是x＝2．【解答】解：移项得：两边平⽅得：4﹣x＝x，解得：x＝2，经检验x＝2是原⽅程的解，故答案为：x＝2．21．（2分）函数中⾃变量x的取值范围是x≤2．【解答】解：根据题意得：2﹣x≥0，解得：x≤2．故答案为x≤2．22．（2分）如图，⊙O的割线PB、PD分别交⊙O于A、B、C、D．已知P A＝4，PB＝10，PD＝8，则PC＝5．【解答】解：∵PB、PD分别是⊙O的割线，∴P A×PB＝PC×PD，即40＝8PC，解得：PC＝5．故答案为：5．23．（2分）甲、⼄两⼈加⼯某种零件．若单独⼯作，则⼄要⽐甲多⽤12天才能完成；若两⼈合作，则8天可以完成．设甲单独⼯作x天可以完成，则可以列出⽅程：1．【解答】解：设甲单独⼯作x天可以完成，则⼄单独⼯作（x+12）天才能完成，由题意，得1．故答案为1．24．（2分）如图，菱形ABCD中，∠A＝60°，对⾓线DB长6cm，则它的周长是24cm．【解答】解：∵四边形ABCD是菱形，∴AD＝DC＝BC＝AB，∵∠A＝60°，AD＝AB，∴△ABD是等边三⾓形，∴AD＝AB＝BD＝6cm，∴菱形ABCD的周长是AD+DC+AB+AD＝24cm．故答案为：24．25．（2分）如图，已知扇形的半径为3cm，圆⼼⾓为120°，则扇形的⾯积为3πcm2．（结果保留π）【解答】解：由S知Sπ×32＝3πcm2．26．（2分）如图，在△ABC中，CE：EB＝1：2，DE∥AC，若△ABC的⾯积为S，则△ADE 的⾯积为S．【解答】解：∵CE：EB＝1：2，设CE＝k，则EB＝2k，∵DE∥AC，⽽BE：BC＝2k：3k＝2：3，∴，S△BDE S∵DE∥AC∴，∴，则S△ADE S△BDE S．故答案为S．三、计算题（3分）27．（3分）计算：．【解答】解：原式＝4+3﹣1＝6．四、解答题（1-2每题5分，3-4每题7分，第5⼩题11分，共35分）28．（5分）如图，平⾏四边形ABCD中，G是CD上⼀点，BG交AD延长线于E，AF＝CG，∠DGE＝100度．（1）试说明DF＝BG；（2）试求∠AFD的度数．【解答】解：（1）证明：∵四边形ABCD是平⾏四边形，∵AB＝DC，⼜AF＝CG，∴AB﹣AF＝DC﹣CG，即GD＝BF．⼜DG∥BF，∴四边形DFBG是平⾏四边形，∴DF＝BG．（2）解：∵四边形DFBG是平⾏四边形，∴DF∥GB，∴∠GBF＝∠AFD．同理可得∠GBF＝∠DGE．∠AFD＝∠DGE＝100°．29．（5分）如图，从⾼出海平⾯100⽶的灯塔的顶部A，测得它的正东⽅和正西⽅的两艘（最后结果精确到1⽶．下船C、D的俯⾓分别为30°和45°，求这两艘船之间的距离CD．列数据供选⽤： 1.414， 1.732）【解答】解：由题意得，∠ADB＝45°，∠ACB＝30°，AB＝100⽶，在Rt△ABD中，BD＝AB＝100⽶，在Rt△ABC中，BC AB＝100⽶，故CD＝BD+BC＝（100+100）≈273⽶．答：这两艘船之间的距离CD为273⽶．30．（7分）某电⼚规定，该⼚家属区的每户居民如果⼀个⽉的⽤电量不超过A度，那么这个⽉每户只需交10元的⽤电费，如果超过A度，则这个⽉除了仍要交10元的⽤电费外，超过部分还要按每度元交费．（1）该⼚某户居民王东2⽉份⽤电90度，超过了规定的A度，则超过部分应交电费（90﹣A）元（⽤A表⽰）；（2）下表是这户居民3、4⽉份的⽤电情况和交费情况，根据表中的数据，求该电⼚规定的A度是多少．【解答】解：（1）超过部分应交电费元．（2）由三⽉份的⽤电量及所交电费可得：解这个⽅程的A1＝30，A2＝50∵4⽉份⽤电量45度，交费10元，可得A≥45，∴A＝30不符合题意，应舍去，答：该电⼚规定的A度是50度．31．（7分）已知点A（m，2）和点B（2，n）都在反⽐例函数的图象上．（1）求m与n的值；（2）若直线y＝mx﹣n与x轴交于点C，求点C关于y轴的对称点C′的坐标．【解答】解：（1）把A的坐标代⼊y得：2，解得：m＝3，∴y，把B的坐标代⼊y得：n3，即m＝3，n＝3．（2）把m＝3，n＝3代⼊直线y＝mx﹣n得：y＝3x﹣3，把y＝0代⼊y＝3x﹣3得：0＝3x﹣3，x＝1，即C的坐标是（1，0），∴点C关于y轴的对称点C′的坐标是（﹣1，0）．32．（11分）已知：a、b、c是△ABC中∠A、∠B、∠C的对边，抛物线y＝x2﹣2ax+b2交x 轴于两点M、N，交y轴于点P，其中点M的坐标是（a+c，0）．（1）求证：△ABC是直⾓三⾓形；（2）若△MNP的⾯积是△NOP的⾯积的3倍，①求cos C的值；②试判断，△ABC的三边长能否取⼀组适当的值，使以MN为直径的圆恰好过抛物线y＝x2﹣2ax+b2的顶点？如能，求出这组值；如不能，说明理由．【解答】解：（1）∵抛物线y＝x2﹣2ax+b2经过点M（a+c，0），∴（a+c）2﹣2a（a+c）+b2＝0，即a2＝b2+c2．由勾股定理的逆定理，得△ABC为直⾓三⾓形．（2）①如图1所⽰∵S△MNP＝3S△NOP，∴MN＝3ON，即MO＝4ON，⼜M（a+c，0），∴N（，0），∴x＝a+c和x是⽅程x2﹣2ax+b2＝0的两根，此时两个为x1，2a±，∴a+c2a，∴c a，由（1）知：在△ABC中，∠A＝90°，由勾股定理得b a，∴cos C．②能，由（1）知：y＝x2﹣2ax+b2＝x2﹣2ax+a2﹣c2＝（x﹣a）2﹣c2，∴顶点D（a，﹣c2）．过D作DE⊥x轴于点E，则NE＝EM，DN＝DM，要使以MN为直径的圆恰好过抛物线y＝x2﹣2ax+b2的顶点，则使△MND为等腰直⾓三⾓形，只须ED MN＝EM．∵M（a+c，0），D（a，﹣c2），∴DE＝c2，EM＝c，∴c2＝c，⼜c＞0，∴c＝1．∵c a，b a，∴a，b；∴当a，b，c＝1时，△MND为等腰直⾓三⾓形．此时，EM＝ED＝EN，以MN为直径的圆恰好过抛物线y＝x2﹣2ax+b2的顶点．五、证明题（9分）33．（9分）已知：如图，△ABC内接于⊙O，⊙B与⊙O相交于点A、D、AD交BC于点E，交⊙O的直径BF于点G．（1）求证：①△ABC∽△EBA；②AE?ED＝AB2﹣EB2．（2）AB，BF＝15，AE：ED＝1：3，求BC的长．【解答】（1）证明：①∵AD是⊙B与⊙O的公共弦，∴AD⊥OB，∴，∴∠C＝∠BAD，∵∠ABE＝∠CBA（公共⾓），∴△ABC∽△EBA；②∵AD⊥OB，∴AG＝DG，∵在Rt△ABG中，AB2＝BG2+AG2，在Rt△EBG中，EB2＝BG2+EG2，∴AB2﹣EB2＝AG2﹣EG2＝（AG+EG）（AG﹣EG）＝（DG+EG）（AG﹣EG）＝ED?AE，∴AE?ED＝AB2﹣EB2．（2）解：连接OA，CF，∵BF＝15，∴OB＝OA，设BG＝x，则OE x，在Rt△ABG中，AE2＝AB2﹣BG2，在Rt△OAG中，AE2＝OA2﹣OG2，∴AB2﹣BG2＝OA2﹣OG2，∵AB，∴（3）2﹣x2＝（）2﹣（x）2，解得：x＝3，∴BG＝3，∴AG6，∴AD＝2AG＝12，∵AE：ED＝1：，∴AE＝3，∴EG＝AG﹣AE＝3，∴△BEG是等腰直⾓三⾓形，∴∠EBG＝45°，∵BF是直径，∴∠BCF＝90°，∴BC＝BF?cos45°．六、画图题（第1⼩题3分，第2⼩题4分，共7分）34．（3分）已知：∠α和线段m、n．求作：△ABC，使∠A＝∠α，AB＝m，BC＝n．（⽤尺规作图，不写作法，保留作图痕迹．）【解答】解：如图所⽰的△ABC就是所要求作的图形．35．（4分）如图，已知∠AOB，⽤直尺和圆规作出∠AOB的平分线OM（不要求写出作法，但必须保留作图痕迹）．【解答】解：作法如下：（1）在OB上取C，以O为圆⼼，OC为半径画圆，交OA于点D，连接CD；（2）再分别以⼤于CD为半径，C，D，为圆⼼画圆，两圆相交于P，D，连接OP，则OP即为∠AOB的平分线．。
历年江苏省南京市中考数学试题(含答案)
南京市2016年初中毕业生学业考试数学一．选择题1．为了方便市民出行．提倡低碳交通，近几年南京市大力发展公共自行车系统．根据规划，全市公共自行车总量明年将达70 000辆．用科学计数法表示70 000是 A ．0.7⨯105 B. 7⨯104 C. 7⨯105 D. 70⨯103答案：B考点：本题考查科学记数法。
解析：科学记数的表示形式为10n a ⨯形式，其中1||10a ≤<，n 为整数，70000＝7×104。
故选B 。
2．数轴上点A 、B 表示的数分别是5、-3，它们之间的距离可以表示为 A ．－3＋5 B. －3－5 C. ｜－3＋5｜ D. ｜－3－5｜ 答案：D考点：数轴，数形结合思想。
解析：AB 之间的距离为：｜－3－5｜或｜5－（－3）｜，所以，选D 。
3．下列计算中，结果是6a 的是 A ． B.23a a C . 122a a ÷D.答案：D考点：单项式的运算。
解析：A 中，不是同类项不能相加减；B 中，23a a ＝5a ，故错误，C 中122a a ÷＝12210a a -=，错误。
D 是正确的。
4、下列长度的三条线段能组成钝角三角形的是A ．3，4，4 B. 3，4，5 C. 3，4，6 D. 3，4，7答案：C考点：构成三角形的条件，勾股定理的应用，钝角三角形的判断。
解析：由两边之和大于第三边，可排除D ；由勾股定理：222a b c +=，当最长边比斜边c 更长时，最大角为钝角， 即满足222a b c +<，所以，选C 。
5．己知正六边形的边长为2，则它的内切圆的半径为A． B. 3 C. 2 D. 23答案：B考点：正六边形、正三角形的性质，勾股定理。
解析：如下图，由正六边形的性质知，三角形AOB为等边形三角形，所以，OA＝OB＝AB＝2，AC＝1，由勾股定理，得内切圆半径：OC＝36、若一组数据2,3,4,5,x的方差与另一组数据5,6,7,8,9的方差相等，则x的值为A． B. C. 或6 D. 或答案：C考点：数据的方差，一元二次方程。
南京中考数学试题(word及答案)
南京市2011年初中毕业生学业考试数学数学注意事项：1. 本试卷共6页，全卷满分120分，考试时间为120分钟，考生答题全部答在答题卡上，答在本试卷上无效.2. 请认真核对监考教师在答题卡上所有粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、准考证号用0.5毫米的黑色墨水签字笔填写在答题卡及本试卷上.3. 答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑•如需要改动，请用橡皮擦干净后，再选涂其他答案，答非选择题必须0.5毫米黑色墨水签字笔写在答题卡上指定位置，在其他位置答题一律无效.4. 作图必须用2B铅笔作答，并请加黑加粗，描写清楚.一、选择题(本大题共6小题，每小题2分，共12分，在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确的选项的字母代号填涂在答题卡相应位置上)1. 、,9的值等于A. 3B. - 3C. ± 3D. -.32. 下列运算正确的是A. a2+ a3=a5B. a2?a3=a6C. a3* a2=a D . (a2)3=a83. 在第六次全国人口普查中，南京市常住人口约为800万人，其中65岁及以上人口占9.2% •则该市65岁及以上人口用科学记数法表示约为A. 0.736X 106人B. 7.36 X 104人C. 7.36X 105人 D . 7.36X 106人4. 为了解某初中学校学生的视力情况，需要抽取部分学生进行调查，下列抽取学生的方法最合适的是A. 随机抽取该校一个班级的学生B. 随机抽取该校一个年级的学生C .随机抽取该校一部分男生5.如图是一个三棱柱，下列图形中，能通过折叠围成一个三棱柱的是D .分别从该校初一、初二、初三年级中各班随机抽取10%的学生6.如图，在平面直角坐标系中，O 半径为2，函数y=x的图象被OA . 2、3B . 2 2、2 P的圆心是(2，a) (a>2)，P的弦AB的长为2.3，贝U a的值是C . 2 3 D . 2 3、填空题（本大题共10小题，每小题2分，共20分，不需要写出解答过程, 请把答案直接填写在答题卡相应位置上）9.计算（迈1）（213. __________ 如图，海边有两座灯塔 A 、B ，暗礁分布在经过 A 、B 两点的弓形（弓形的弧是O O的 一部分）区域内，/ AOB=80。
南京市中招数学试题及答案
（第6题）2008年南京市初中毕业生学业考试 数学全卷满分120分．考试时间为120分钟一、选择题（本大题共10小题，每小题2分，共计20分） 1．3-的绝对值是（ ） A ．3- B ．3 C ．13-D ．132．2008年5月27日，北京2008年奥运会火炬接力传递活动在南京境内举行，火炬传递路线全程约12 900m ，将12 900m 用科学记数法表示应为（ ）A ．50.12910⨯B ．41.2910⨯C ．312.910⨯ D ．212910⨯3．计算23()ab的结果是（ ）A ．5ab B ．6ab C ．35abD ．36ab4．2的平方根是（ ）A ．4BC． D．5．已知反比例函数的图象经过点(P ，则这个函数的图象位于（ ）A ．第一、三象限B ．第二、三象限C ．第二、四象限D ．第三、四象限 6．如图，将一张等腰梯形纸片沿中位线剪开，拼成一个新的图形，这个新的图形可以是下列图形中的（ ）A ．三角形B ．平行四边形C ．矩形D ．正方形 7．小刚身高1.7m ，测得他站立在阳光下的影子长为0.85m ，紧接着他把手臂竖直举起，测得影子长为1.1m ，那么小刚举起的手臂超出头顶（ ）A ．0.5mB ．0.55mC ．0.6mD ．2.2m 8．如图，O 是等边三角形ABC 的外接圆，O 的半径为2，则等边三角形ABC的边长为（ ）ABC．D．9．超市为了制定某个时间段收银台开放方案，统计了这个时间段本超市顾客在 收银台排队付款的等待时间，并绘制 成如下的频数分布直方图（图中等待 时间6分钟到7分钟表示大于或等于6分钟而小于7分钟，其它类同）．这 个时间段内顾客等待时间不少于6分 钟的人数为（ ） A ．5 B ．7 C ．16 D ．3310．如图，已知O 的半径为1，AB 与O 相切于点A ，OB 与O 交于点C ，OD OA ⊥，垂足为D ，则cos AOB ∠的值等于（ ） A ．OD B ．OA C ．CD D ．AB二、填空题（本大题共6小题，每小题3分，共计18分）11的结果是 ．12．函数1xy x-=中，自变量x 的取值范围是 ．13．已知1O 和2O 的半径分别为3cm 和5cm ，且它们内切，则圆心距12O O14．若等腰三角形的一个外角为70，则它的底角为 度．15的概率是0.2，摸出白球的概率是0.5，那么摸出黑球的概率是 ． 16．如图，有一圆形展厅，在其圆形边缘上的点A 是65．为了监控整个展厅，最少需在圆形边缘上共安装．．．这样的监视器台．三、解答题（本大题共12小题，共计82分） 17．（6分）先化简，再求值：2(21)2(21)3a a +-++，其中a =18．（6分）解方程22011xx x -=+-．（第8题）（第16题） 65（第19题）5-4-3-（第10题）（第9题）19．（6分）解不等式组205121123x x x ->⎧⎪+-⎨+⎪⎩，≥，并把解集在数轴上表示出来．20．（6分）我国从2008年6月1日起执行“限塑令”．“限塑令”执行前，某校为了了解本校学生所在家庭使用塑料袋的数量情况，随机调查了10名学生所在家庭月使用塑料袋的数量，结果如下（单位：只） 65，70，85，75，85，79，74，91，81，95．（1）计算这10名学生所在家庭平均月使用塑料袋多少只？（2）“限塑令”执行后，家庭月使用塑料袋数量预计将减少50％．根据上面的计算结果，估计该校1 000名学生所在家庭月使用塑料袋可减少多少只？ 21．（6分）如图，在ABCD 中，E F ，为BC 上两点，且BE CF =，AF DE =． 求证：（1）ABF DCE △≌△； （2）四边形ABCD 是矩形．22．（6分）如图，菱形ABCD （图1）与菱形EFGH （图2）的形状、大小完全相同．（1）请从下列序号中选择正确选项的序号填写； ①点E F G H ，，，；②点G F E H ，，，；③点E H G F ，，，；④点G H E F ，，，．如果图1经过一次平移后得到图2，那么点A B C D ，，，对应点分别是 ； 如果图1经过一次轴对称后得到图2，那么点A B C D ，，，对应点分别是 ； 如果图1经过一次旋转后得到图2，那么点A B C D ，，，对应点分别是 ； （2）①图1，图2关于点O 成中心对称，请画出对称中心（保留画图痕迹，不写画法）；②写出两个图形成中心对称的一条．．性质： ．（可以结合所画图形叙述）23．（6分）如图，山顶建有一座铁塔，塔高30m CD =，某人在点A 处测得塔底C 的仰角为20，塔顶D 的仰角为23，求此人距CD 的水平距离AB ．（参考数据：sin 200.342≈，cos 200.940≈， tan 200.364≈，sin 230.391≈， cos 230.921≈，tan 230.424≈）24．（7分）小明和小颖做掷骰子的游戏，规则如下：①游戏前，每人选一个数字； ②每次同时掷两枚均匀骰子；③如果同时掷得的两枚骰子点数之和，与谁所选数字相同，那么谁就获胜． （1）在下表中列出同时掷两枚均匀骰子所有可能出现的结果：（第21题） A BCDEF图1A（第22题）B CD 图2EF H（第23题） A BCD 2023 第2枚骰子掷得的点数 第1枚骰子 掷得的点数1 2 3 4 5 61 2 3 4 5 6（2）小明选的数字是5，小颖选的数字是6．如果你也加入游戏，你会选什么数字，使自己获胜的概率比他们大？请说明理由．25．（7分）某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为2:1．在温室内，沿前侧内墙保留3m 宽的空地，其它三侧内墙各保留1m 宽的通道．当矩形温室的长与宽各为多少时，蔬菜种植区域的面积是2288m ？26．（8分）已知二次函数2y x bx c =++中，函数y 与自变量x 的部分对应值如下表： x … 1- 0 1 2 3 4 … y… 10 5 2 1 25 … （1）求该二次函数的关系式；（2）当x 为何值时，y 有最小值，最小值是多少？ （3）若1()A m y ，，2(1)B m y +，两点都在该函数的图象上，试比较1y 与2y 的大小．27．（8分）如图，已知O 的半径为6cm ，射线PM 经过点O ，10cm OP =，射线PN 与O 相切于点Q ．A B ，两点同时从点P 出发，点A 以5cm/s 的速度沿射线PM 方向运动，点B 以4cm/s 的速度沿射线PN 方向运动．设运动时间为t s ． （1）求PQ 的长；（2）当t 为何值时，直线AB 与O 相切？（第25题）（第27题）28．（10分）一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为(h)x ，两车之间的距离．．．．．．．为(km)y ，图中的折线表示y 与x 之间的函数关系． 根据图象进行以下探究：信息读取（1）甲、乙两地之间的距离为 km ； （2）请解释图中点B 的实际意义；图象理解（3）求慢车和快车的速度； （4）求线段BC 所表示的y 与x 之间的函数关系式，并写出自变量x 的取值范围；问题解决（5）若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同．在第一列快车与慢车相遇30分钟后，第二列快车与慢车相遇．求第二列快车比第一列快车晚出发多少小时？南京市2008年初中毕业生学业考试数学试题参考答案及评分标准说明：本评分标准每题给出了一种或几种解法供参考，如果考生的解法与本解答不同，参照本评分标准的精神给分．一、选择题（每小题2分，共计20分）题号 1 2 3 4 5 6 7 8 9 10 答案BBDDCBACB A二、填空题（每小题3分，共计18分） 1112．0x ≠ 13．2 14．35 15．0.316．3三、解答题（本大题共12小题，共计82分） 17．（本题6分） 解：原式2441423aa a =++--+ ················································································ 3分（第28题）y242a =+． ··················································································································· 4分当a =22424210a +=⨯+=． ································································· 6分 18．（本题6分）解：方程两边同乘(1)(1)x x -+，得2(1)0x x --=． ·········································································································· 3分 解这个方程，得2x =． ························································································································· 5分 检验：当2x =时，(1)(1)0x x -+≠． 所以2x =是原方程的解． ································································································· 6分 19．（本题6分）解：解不等式①，得2x <． ······························································································ 2分 解不等式②，得1x -≥． ································································································· 4分 所以，不等式组的解集是12x -<≤． ··············································································· 5分 不等式组的解集在数轴上表示如下： ··········································································································· 6分 20．（本题6分） 解：（1）1(65708575857974918195)8010+++++++++=． 答：这10名学生所在家庭平均月使用塑料袋80只． ································································ 3分 （2）8010005040000⨯⨯=％．答：执行“限塑令”后，估计1 000名学生所在家庭月使用塑料袋可减少40 000只． ·························· 6分 21．（本题6分）解：（1）BE CF =，BF BE EF =+，CE CF EF =+，BF CE ∴=．················································································································ 1分 四边形ABCD 是平行四边形，AB DC ∴=． ··············································································································· 2分 在ABF △和DCE △中，AB DC =，BF CE =，AF DE =，ABF DCE ∴△≌△． ·································································································· 3分 （2）解法一：ABF DCE △≌△，B C ∴∠=∠．··············································································································· 4分 四边形ABCD 是平行四边形， AB CD ∴∥．180B C ∴∠+∠=． 90B C ∴∠=∠=． ······································································································ 5分 ∴四边形ABCD 是矩形． ································································································· 6分 解法二：连接AC DB ，． ABF DCE △≌△， AFB DEC ∴∠=∠．AFC DEB ∴∠=∠．····································································································· 4分 在AFC △和DEB △中，AF DE =，AFC DEB ∠=∠，CF BE =， AFC DEB ∴△≌△．AC DB ∴=． ··············································································································· 5分 四边形ABCD 是平行四边形， ∴四边形ABCD 是矩形． ································································································· 6分22．（本题6分） 解：（1）①；②；④；········································································································ 3分 （2）①画图正确； ············································································································ 5分 ②答案不惟一，例如：对应线段相等，OC OE =等． ··············································································································· 6分 23．（本题6分）解：在Rt ABC △中，20CAB∠=，tan tan 20BC AB CAB AB ∴=∠=．········································································· 2分 在Rt ABD △中，23DAB ∠=，tan tan 23BD AB DAB AB ∴=∠=． ········································································ 4分 tan 23tan 20(tan 23tan 20)CD BD BC AB AB AB ∴=-=-=-．30500(m)tan 23tan 200.4240.364CD AB ∴==--≈．答：此人距CD 的水平距离AB 约为500m ． ·········································································· 6分24．（本题7分） 解：（1）填表正确；··········································································································· 3分 （2）由上表可以看出，同时投掷两枚骰子，可能出现的结果有36种，它们出现的可能性相同． 所有的结果中，满足两枚骰子点数和为5（记为事件A ）的结果有4种，即（1，4），（2，3），（3，2）（4，1），所以小明获胜的概率为41()369P A ==； ······································································ 4分 满足两枚骰子点数和为6（记为事件B ）的结果有5种，即（1，5），（2，4），（3，3）（4，2），（5，1），所以小颖获胜的概率为5()36P B =；··················································································· 5分要想使自己获胜的概率比他们大，必须满足两枚骰子点数和出现的结果多于5种，由所列表格可知，只有两枚骰子点数和为7（记为事件C ）的结果多于5种，有6种，即（1，6），（2，5），（3，4）（4，3），（5，2），（6，1），所以61()366P C ==．因此，要想使自己获胜的概率比他们大，所选数字应为7． ····· 7分 25．（本题7分）解法一：设矩形温室的宽为m x ，则长为2m x ．根据题意，得(2)(24)288x x --=． ······························································································· 4分 解这个方程，得110x =-（不合题意，舍去），214x =． ··········································································· 6分 所以14x =，221428x =⨯=．答：当矩形温室的长为28m ，宽为14m 时，蔬菜种植区域的面积是2288m ． ······························· 7分解法二：设矩形温室的长为m x ，则宽为1m 2x ．根据题意，得12(4)2882x x ⎛⎫--= ⎪⎝⎭． ····························································································· 4分 解这个方程，得120x =-（不合题意，舍去），228x =． ··········································································· 6分所以28x =，11281422x =⨯=．答：当矩形温室的长为28m ，宽为14m 时，蔬菜种植区域的面积是2288m ． ······························· 7分26．（本题8分） 解：（1）根据题意，当0x =时，5y =；当1x =时，2y =．所以521.c b c =⎧⎨=++⎩，解得45.b c =-⎧⎨=⎩，所以，该二次函数关系式为245y x x =-+． ······································································ 2分（2）因为2245(2)1y x x x =-+=-+，所以当2x =时，y 有最小值，最小值是1． ········································································· 4分（3）因为1()A m y ，，2(1)B m y +，两点都在函数245y x x =-+的图象上， 所以，2145y m m =-+，222(1)4(1)522y m m m m =+-++=-+．2221(22)(45)23y y m m m m m -=-+--+=-． ······················································ 5分所以，当230m -<，即32m <时，12y y >； 当230m -=，即32m =时，12y y =； 当230m ->，即32m >时，12y y <． ············································································ 8分27．（本题8分） （1）连接OQ ．PN 与O 相切于点Q ， OQ PN ∴⊥，即90OQP ∠=． ··················································································· 2分10OP =，6OQ =，8(cm)PQ ∴==．························································································ 3分 （2）过点O 作OC AB ⊥，垂足为C ．点A 的运动速度为5cm/s ，点B 的运动速度为4cm/s ，运动时间为t s ， 5PA t ∴=，4PB t =． 10PO =，8PQ =， PA PB PO PQ ∴=． P P ∠=∠， PAB POQ ∴△∽△．90PBA PQO ∴∠=∠=．···························································································· 4分 90BQO CBQ OCB ∠=∠=∠=， ∴四边形OCBQ 为矩形． BQ OC ∴=．O 的半径为6，6BQ OC ∴==时，直线AB 与O 相切． ①当AB 运动到如图1所示的位置．84BQ PQ PB t =-=-． 由6BQ =，得846t -=．解得0.5(s)t =． ············································································································· 6分图1。
南京市中考数学复习题及答案 (866)
南京市中考数学复习题及答案
5．（2分）如图，在△ABC中，∠ACB＝90°，分别以点A和B 为圆心，以相同的长（大于AB）为半径作弧，两弧相交于点M和N，作直线MN交AB于点D，交BC于点E，连接CD，下列结论错误的是（）
A．AD＝BD B．BD＝CD C．∠A＝∠BED D．∠ECD＝∠EDC 【分析】由题意可知：MN为AB的垂直平分线，可以得出AD＝BD；CD为直角三角形ABC斜边上的中线，得出CD＝BD；利用三角形的内角和得出∠A＝∠BED；因为∠A≠60°，得不出AC＝AD，无法得出EC＝ED，则∠ECD＝∠EDC不成立；由此选择答案即可．
【解答】解：∵MN为AB的垂直平分线，
∴AD＝BD，∠BDE＝90°；
∵∠ACB＝90°，
∴CD＝BD；
∵∠A+∠B＝∠B+∠BED＝90°，
∴∠A＝∠BED；
∵∠A≠60°，AC≠AD，
∴EC≠ED，
∴∠ECD≠∠EDC．
故选：D．
【点评】此题考查了线段垂直平分线的性质以及直角三角形的性质．注意垂直平分线上任意一点，到线段两端点的距离相等．
第1 页共1 页。
1998年南京中考数学试题
98年南京市中考试题一、 单选题(每道小题 3分 共 60分 )1. 在数轴上表示不等式x ≥－2的解集，正确的是 [ ]2.在实数π，4,14.3,3,052--，中，无理数有[ ]A ．1个B ．2个C ．3个D ．4个 3. 3－2的算术平方根是[ ]A661331D C B4. 下列计算中，正确的是 [ ]5. 下列各组二次根式中，同类二次根式是 [ ]A.32,8.31,1221.15,53.23,631D C B 6. 某中学数学教研组有25名教师，将他们的年龄分成3组，在38～45(岁)组内有8名教师，那么这个小组的频率是 [ ]A ．0.12B ．0.38C ．0.32D ．3.127. 某市今年有6万名初中毕业生参加升学考试，为了了解6万名考生的数学成绩，从中抽取1500名考生的数学成绩进行统计分析，以下说法中正确的是[ ]A ．6万考生是总体B ．每名考生的数学成绩是个体C ．1500名考生是总体的一个样本D ．1500名是样本的容量8. 要测量河两岸相对的两点A 、B 的距离，先在AB 的垂线BF 上取两点C 、D ，使CD=BC ，再定出BF 的垂线DE ，使A 、C 、E 在一条直线上(如图所示)，可以证明△EDC ≌△ABC ，得ED=AB ，因此测得ED 的长就是AB 的长，判定△EDC ≌△ABC 的理由是 [ ]A ．边角边公理B ．角边角公理C ．边边边公理D ．斜边、直角边公理 9. 两根木棒的长分别是5cm 和7cm ，要选择第三根木棒，将它们钉成一个三角形，如果第三根木棒的长为偶数，那么第三根木棒长的取值情况有 [ ]A ．3种B ．4种C ．5种D ．6种 10. 计算sin30°+tan45°的结果等于 [ ]A221223223++DC B11.函数y=xx 1+中自变量x 的取值范围是[ ]A ．x ≥－1且x ≠0B ．x ＞－1且x ≠0C ．x ＞1D ．x ≥112.如图，桥拱是抛物线形，其函数的解析式为y=－241x ，当水位线在AB 位置时，水面的宽为12米，这时水面离桥顶的高度h 是[ ]米 A 3 B 62 C 43 D 913.点A （-5，y 1）, B(-2, y 2)都在直线x y 21-=上，则y 1与y 2的关系是[ ] A ．y 1≤y 2 B ．y 1=y 2 C ．y 1＜y 2 D ．y 1＞y 2 14. 在下列方程中，有实数根的方程是 [ ] A. 0132=+-x x Bx x -=+1 C 01=+x x D 0222=--xx x 15. 顺次连结圆内接梯形四边的中点所得的四边形是 [ ]A ．矩形B ．菱形C ．正方形D ．等腰梯形16. 如图，圆内接正五边形ABCDE 中，对角线AC 和BD 相交于点P ，则∠APB 的度数是 [ ]A ．36°B ．60°C ．72°D ．108° 17.双曲线)0(≠=k xky 的两分支各在第二、四象限内，则抛物线222k x kx y +-=的大致图形是_____18. 如图，⊙O 1和⊙O 2内切于点P ，⊙O 2的弦AB 经过⊙O 1的圆心O 1，交⊙O 1于点C 、D ，若AC ∶CD ∶BD=3∶4∶2，则⊙O 1与⊙O 2的直径之比为[ ] A ．2∶7 B ．2∶5 C ．1∶4 D ．1∶319. 如图，用铁皮做一个圆锥形的烟囱帽，它的底面直径是80cm ，高是30cm ，不计加工余料，则需用铁皮的面积最少是[ ] A ．4000π(cm 2) B ．2400π(cm 2)C ．2000π(cm 2)D ．1200π(cm 2)20. 设计一个商标图象(如图阴影部分)，矩形ABCD中，AB ＝2BC ，且AB ＝8cm ，以点A 为圆心，AD 的长为半径作半圆，则商标图案面积等于 [ ]A ．4π＋8B ．4π＋16C ．3π＋8D ．3π＋16二、 解答题(第1小题 4分, 2－8每题 6分, 第9小题 8分, 第10小题 12分, 共 66分)1. 已知：如图，菱形ABCD 的边长为3，延长AB 到点E ，使BE=2AB ，连结EC 并延长交AD 的延长线于点F ．求AF 的长．3. 把x 3+3x 2－4x －12分解因式．4. 先化简，再求值：)12(122+-÷++x x x x x ，其中x=2。
江苏省南京市中考数学真题及答案
江苏省南京市中考数学真题及答案一、选择题（本大题共6小题,每小题2分,共12分．在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上）1．（2分）计算3﹣（﹣2）的结果是（）A．﹣5 B．﹣1 C．1 D．52．（2分）3的平方根是（）A．9 B．√3C．−√3D．±√33．（2分）计算（a3）2÷a2的结果是（）A．a3B．a4C．a7D．a84．（2分）党的十八大以来,党中央把脱贫攻坚摆到更加突出的位置．根据国家统计局发布的数据,2012～2019年年末全国农村贫困人口的情况如图所示．根据图中提供的信息,下列说法错误的是（）A．2019年末,农村贫困人口比上年末减少551万人B．2012年末至2019年末,农村贫困人口累计减少超过9000万人C．2012年末至2019年末,连续7年每年农村贫困人口减少1000万人以上D．为在2020年末农村贫困人口全部脱贫,今年要确保完成减少551万农村贫困人口的任务5．（2分）关于x的方程（x﹣1）（x+2）＝p2（p为常数）的根的情况,下列结论中正确的是（）A．两个正根B．两个负根C ．一个正根,一个负根D ．无实数根6．（2分）如图,在平面直角坐标系中,点P 在第一象限,⊙P 与x 轴、y 轴都相切,且经过矩形AOBC 的顶点C ,与BC 相交于点D ．若⊙P 的半径为5,点A 的坐标是（0,8）．则点D 的坐标是（ ）A ．（9,2）B ．（9,3）C ．（10,2）D ．（10,3）二、填空题（本大题共10小题,每小题2分,共20分．请把答案填写在答题卡相应位置上） 7．（2分）写出一个负数,使这个数的绝对值小于3： ． 8．（2分）若式子1−1x−1在实数范围内有意义,则x 的取值范围是 ．9．（2分）纳秒（ns ）是非常小的时间单位,1ns ＝10﹣9s ．北斗全球导航系统的授时精度优于20ns ．用科学记数法表示20ns 是 s ． 10．（2分）计算√33+12的结果是 ．11．（2分）已知x 、y 满足方程组{x +3y =−1，2x +y =3，,则x +y 的值为 ．12．（2分）方程xx−1=x−1x+2的解是 ．13．（2分）将一次函数y ＝﹣2x +4的图象绕原点O 逆时针旋转90°,所得到的图象对应的函数表达式是 ．14．（2分）如图,在边长为2cm 的正六边形ABCDEF 中,点P 在BC 上,则△PEF 的面积为cm 2．15．（2分）如图,线段AB 、BC 的垂直平分线11、l 2相交于点O ,若∠1＝39°,则∠AOC ＝ ．16．（2分）下列关于二次函数y ＝﹣（x ﹣m ）2+m 2+1（m 为常数）的结论：①该函数的图象与函数y ＝﹣x 2的图象形状相同；②该函数的图象一定经过点（0,1）；③当x ＞0时,y 随x 的增大而减小；④该函数的图象的顶点在函数y ＝x 2+1的图象上．其中所有正确结论的序号是 ．三、解答题（本大题共11小题,共88分．请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤） 17．（7分）计算（a ﹣1+1a+1）÷a 2+2a a+1．18．（7分）解方程：x 2﹣2x ﹣3＝0．19．（8分）如图,点D 在AB 上,点E 在AC 上,AB ＝AC ,∠B ＝∠C ,求证：BD ＝CE ．20．（8分）已知反比例函数y =kx 的图象经过点（﹣2,﹣1）． （1）求k 的值． （2）完成下面的解答． 解不等式组{2−x ＞1，①k x＞1．②解：解不等式①,得 ．根据函数y =kx 的图象,得不等式②的解集 ． 把不等式①和②的解集在数轴上表示出来．从图中可以找出两个不等式解集的公共部分,得不等式组的解集．21．（8分）为了了解某地居民用电量的情况,随机抽取了该地200户居民六月份的用电量（单位：kW•h）进行调查,整理样本数据得到下面的频数分布表．组别用电量分组频数1 8≤x＜93 502 93≤x＜178 1003 178≤x＜263 344 263≤x＜348 115 348≤x＜433 16 433≤x＜518 17 518≤x＜603 28 603≤x＜688 1根据抽样调查的结果,回答下列问题：（1）该地这200户居民六月份的用电量的中位数落在第组内；（2）估计该地1万户居民六月份的用电量低于178kW•h的大约有多少户．22．（8分）甲、乙两人分别从A、B、C这3个景点中随机选择2个景点游览．（1）求甲选择的2个景点是A、B的概率；（2）甲、乙两人选择的2个景点恰好相同的概率是．23．（8分）如图,在港口A处的正东方向有两个相距6km的观测点B、C．一艘轮船从A处出发,沿北偏东26°方向航行至D处,在B、C处分别测得∠ABD＝45°、∠C＝37°．求轮船航行的距离AD．（参考数据：sin26°≈0.44,cos26°≈0.90,tan26°≈0.49,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75．）24．（8分）如图,在△ABC中,AC＝BC,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作DF∥BC,交⊙O于点F．求证：（1）四边形DBCF是平行四边形；（2）AF＝EF．25．（8分）小明和小丽先后从A地出发沿同一直道去B地．设小丽出发第xmin时,小丽、小明离B地的距离分别为y1m、y2m．y1与x之间的函数表达式是y1＝﹣180x+2250,y2与x 之间的函数表达式是y2＝﹣10x2﹣100x+2000．（1）小丽出发时,小明离A地的距离为m．（2）小丽出发至小明到达B地这段时间内,两人何时相距最近？最近距离是多少？26．（9分）如图,在△ABC和△A'B'C'中,D、D'分别是AB、A'B'上一点,ADAB =A′D′A′B′．（1）当CDC′D′=ACA′C′=ABA′B′时,求证△ABC∽△A'B'C．证明的途径可以用下面的框图表示,请填写其中的空格．（2）当CDC′D′=ACA′C′=BCB′C′时,判断△ABC与△A'B'C′是否相似,并说明理由．27．（9分）如图①,要在一条笔直的路边l上建一个燃气站,向l同侧的A、B两个城镇分别铺设管道输送燃气．试确定燃气站的位置,使铺设管道的路线最短．（1）如图②,作出点A关于l的对称点A',线段A'B与直线l的交点C的位置即为所求,即在点C处建燃气站,所得路线ACB是最短的．为了证明点C的位置即为所求,不妨在直线1上另外任取一点C',连接AC'、BC',证明AC+CB＜AC′+C'B．请完成这个证明．（2）如果在A、B两个城镇之间规划一个生态保护区,燃气管道不能穿过该区域．请分别给出下列两种情形的铺设管道的方案（不需说明理由）．①生态保护区是正方形区域,位置如图③所示；②生态保护区是圆形区域,位置如图④所示．2020年江苏省南京市中考数学试卷参考答案与试题解析一、选择题（本大题共6小题,每小题2分,共12分．在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上）1．（2分）计算3﹣（﹣2）的结果是（）A．﹣5 B．﹣1 C．1 D．5【解答】解：3﹣（﹣2）＝3+2＝5．故选：D．2．（2分）3的平方根是（）A．9 B．√3C．−√3D．±√3【解答】解：∵（±√3）2＝3,∴3的平方根±√3．故选：D．3．（2分）计算（a3）2÷a2的结果是（）A．a3B．a4C．a7D．a8【解答】解：（a3）2÷a2＝a3×2÷a2＝a6﹣2＝a4,故选：B．4．（2分）党的十八大以来,党中央把脱贫攻坚摆到更加突出的位置．根据国家统计局发布的数据,2012～2019年年末全国农村贫困人口的情况如图所示．根据图中提供的信息,下列说法错误的是（）A．2019年末,农村贫困人口比上年末减少551万人B．2012年末至2019年末,农村贫困人口累计减少超过9000万人C．2012年末至2019年末,连续7年每年农村贫困人口减少1000万人以上D．为在2020年末农村贫困人口全部脱贫,今年要确保完成减少551万农村贫困人口的任务【解答】解：A．2019年末,农村贫困人口比上年末减少1660﹣551＝1109（万人）,此选项错误；B．2012年末至2019年末,农村贫困人口累计减少超过9899﹣551＝9348（万人）,此选项正确；C．2012年末至2019年末,连续7年每年农村贫困人口减少1000万人以上,此选项正确；D．为在2020年末农村贫困人口全部脱贫,今年要确保完成减少551万农村贫困人口的任务,此选项正确；故选：A．5．（2分）关于x的方程（x﹣1）（x+2）＝p2（p为常数）的根的情况,下列结论中正确的是（）A．两个正根B．两个负根C．一个正根,一个负根D．无实数根【解答】解：∵关于x的方程（x﹣1）（x+2）＝p2（p为常数）,∴x2+x﹣2﹣p2＝0,∴△＝1+8+4p2＝9+4p2＞0,∴方程有两个不相等的实数根,∵两个的积为﹣2﹣p2,∴一个正根,一个负根,故选：C．6．（2分）如图,在平面直角坐标系中,点P在第一象限,⊙P与x轴、y轴都相切,且经过矩形AOBC的顶点C,与BC相交于点D．若⊙P的半径为5,点A的坐标是（0,8）．则点D的坐标是（）A．（9,2）B．（9,3）C．（10,2）D．（10,3）【解答】解：设⊙O与x、y轴相切的切点分别是F、E点,连接PE、PF、PD,延长EP与CD交于点G,则PE⊥y轴,PF⊥x轴,∵∠EOF＝90°,∴四边形PEOF是矩形,∵PE＝PF,PE∥OF,∴四边形PEOF为正方形,∴OE＝PF＝PE＝OF＝5,∵A（0,8）,∴OA＝8,∴AE＝8﹣5＝3,∵四边形OACB为矩形,∴BC＝OA＝8,BC∥OA,AC∥OB,∴EG∥AC,∴四边形AEGC为平行四边形,四边形OEGB为平行四边形,∴CG＝AE＝3,EG＝OB,∵PE⊥AO,AO∥CB,∴PG⊥CD,∴CD＝2CG＝6,∴DB＝BC﹣CD＝8﹣6＝2,∵PD＝5,DG＝CG＝3,∴PG＝4,∴OB ＝EG ＝5+4＝9, ∴D （9,2）．故选：A ．二、填空题（本大题共10小题,每小题2分,共20分．请把答案填写在答题卡相应位置上） 7．（2分）写出一个负数,使这个数的绝对值小于3： ﹣1（答案不唯一） ． 【解答】解：∵一个负数的绝对值小于3, ∴这个负数大于﹣3且小于0,∴这个负数可能是﹣2、﹣1.5、﹣1、…． 故答案为：﹣1（答案不唯一）． 8．（2分）若式子1−1x−1在实数范围内有意义,则x 的取值范围是 x ≠1 ．【解答】解：若式子1−1x−1在实数范围内有意义,则x ﹣1≠0, 解得：x ≠1． 故答案为：x ≠1．9．（2分）纳秒（ns ）是非常小的时间单位,1ns ＝10﹣9s ．北斗全球导航系统的授时精度优于20ns ．用科学记数法表示20ns 是 2×10﹣8s ． 【解答】解：20ns ＝20×10﹣9s ＝2×10﹣8s , 故答案为：2×10﹣8． 10．（2分）计算√3√3+√12的结果是 13 ． 【解答】解：原式=√3√3+2√3=√33√3=13．故答案为：13．11．（2分）已知x 、y 满足方程组{x +3y =−1，2x +y =3，,则x +y 的值为 1 ．【解答】解：{x +3y =−1①2x +y =3②,①×2﹣②得：5y ＝﹣5, 解得：y ＝﹣1,①﹣②×3得：﹣5x ＝﹣10, 解得：x ＝2, 则x +y ＝2﹣1＝1, 故答案为1．12．（2分）方程x x−1=x−1x+2的解是 x =14 ． 【解答】解：方程x x−1=x−1x+2, 去分母得：x 2+2x ＝x 2﹣2x +1, 解得：x =14,经检验x =14是分式方程的解．故答案为：x =14．13．（2分）将一次函数y ＝﹣2x +4的图象绕原点O 逆时针旋转90°,所得到的图象对应的函数表达式是 y =12x +2 ．【解答】解：在一次函数y ＝﹣2x +4中,令x ＝0,则y ＝4, ∴直线y ＝﹣2x +4经过点（0,4）,将一次函数y ＝﹣2x +4的图象绕原点O 逆时针旋转90°,则点（0,4）的对应点为（﹣4,0）, 旋转后得到的图象与原图象垂直,则对应的函数解析式为：y =12x +b , 将点（﹣4,0）代入得,12×(−4)+b ＝0,解得b ＝2,∴旋转后对应的函数解析式为：y =12x +2, 故答案为y =12x +2．14．（2分）如图,在边长为2cm 的正六边形ABCDEF 中,点P 在BC 上,则△PEF 的面积为 2√3cm 2．【解答】解：连接BF ,BE ,过点A 作AT ⊥BF 于T∵ABCDEF 是正六边形,∴CB ∥EF ,AB ＝AF ,∠BAF ＝120°, ∴S △PEF ＝S △BEF , ∵AT ⊥BE ,AB ＝AF ,∴BT ＝FT ,∠BAT ＝∠FAT ＝60°, ∴BT ＝FT ＝AB •sin60°=√3, ∴BF ＝2BT ＝2√3,∵∠AFE ＝120°,∠AFB ＝∠ABF ＝30°, ∴∠BFE ＝90°,∴S △PEF ＝S △BEF =12•EF •BF =12×2×2√3=2√3, 故答案为2√3．15．（2分）如图,线段AB 、BC 的垂直平分线11、l 2相交于点O ,若∠1＝39°,则∠AOC ＝ 78° ．【解答】解：过O作射线BP,∵线段AB、BC的垂直平分线11、l2相交于点O,∴AO＝OB＝OC,∠BDO＝∠BEO＝90°,∴∠DOE+∠ABC＝180°,∵∠DOE+∠1＝180°,∴∠ABC＝∠1＝39°,∵OA＝OB＝OC,∴∠A＝∠ABO,∠OBC＝∠C,∵∠AOP＝∠A+∠ABO,∠COP＝∠C+∠OBC,∴∠AOC＝∠AOP+∠COP＝∠A+∠ABC+∠C＝2×39°＝78°,故答案为：78°．16．（2分）下列关于二次函数y＝﹣（x﹣m）2+m2+1（m为常数）的结论：①该函数的图象与函数y＝﹣x2的图象形状相同；②该函数的图象一定经过点（0,1）；③当x＞0时,y 随x的增大而减小；④该函数的图象的顶点在函数y＝x2+1的图象上．其中所有正确结论的序号是①②④．【解答】解：①∵二次函数y＝﹣（x﹣m）2+m+1（m为常数）与函数y＝﹣x2的二次项系数相同,∴该函数的图象与函数y ＝﹣x 2的图象形状相同,故结论①正确； ②∵在函数y ＝﹣（x ﹣m ）2+m 2+1中,令x ＝0,则y ＝﹣m 2+m 2+1＝1, ∴该函数的图象一定经过点（0,1）,故结论②正确； ③∵y ＝﹣（x ﹣m ）2+m 2+1,∴抛物线开口向下,对称轴为直线x ＝m ,当x ＞m 时,y 随x 的增大而减小,故结论③错误； ④∵抛物线开口向下,当x ＝m 时,函数y 有最大值m 2+1,∴该函数的图象的顶点在函数y ＝x 2+1的图象上．故结论④正确, 故答案为①②④．三、解答题（本大题共11小题,共88分．请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤） 17．（7分）计算（a ﹣1+1a+1）÷a 2+2a a+1．【解答】解：原式＝（a 2−1a+1+1a+1）÷a(a+2)a+1=a 2a+1•a+1a(a+2) =a a+2．18．（7分）解方程：x 2﹣2x ﹣3＝0．【解答】解：原方程可以变形为（x ﹣3）（x +1）＝0x ﹣3＝0,x +1＝0∴x 1＝3,x 2＝﹣1．19．（8分）如图,点D 在AB 上,点E 在AC 上,AB ＝AC ,∠B ＝∠C ,求证：BD ＝CE ．【解答】证明：在△ABE 与△ACD 中{∠A =∠AAB =AC ∠B =∠C ,∴△ABE ≌△ACD ．∴AD＝AE．∴BD＝CE．20．（8分）已知反比例函数y=kx的图象经过点（﹣2,﹣1）．（1）求k的值．（2）完成下面的解答．解不等式组{2−x＞1，①kx＞1．②解：解不等式①,得x＜1 ．根据函数y=kx的图象,得不等式②的解集0＜x＜2 ．把不等式①和②的解集在数轴上表示出来．从图中可以找出两个不等式解集的公共部分,得不等式组的解集0＜x＜1 ．【解答】解：（1）∵反比例函数y=kx的图象经过点（﹣2,﹣1）,∴k＝（﹣2）×（﹣1）＝2；（2）解不等式组{2−x＞1，①kx＞1．②解：解不等式①,得x＜1．根据函数y=kx的图象,得不等式②的解集0＜x＜2．把不等式①和②的解集在数轴上表示为：∴不等式组的解集为0＜x＜1,故答案为：x＜1,0＜x＜2,0＜x＜1．21．（8分）为了了解某地居民用电量的情况,随机抽取了该地200户居民六月份的用电量（单位：kW•h）进行调查,整理样本数据得到下面的频数分布表．组别用电量分组频数1 8≤x＜93 502 93≤x＜178 1003 178≤x＜263 344 263≤x＜348 115 348≤x＜433 16 433≤x＜518 17 518≤x＜603 28 603≤x＜688 1根据抽样调查的结果,回答下列问题：（1）该地这200户居民六月份的用电量的中位数落在第 2 组内；（2）估计该地1万户居民六月份的用电量低于178kW•h的大约有多少户．【解答】解：（1）∵有200个数据,∴六月份的用电量的中位数应该是第100个和第101个数的平均数,∴该地这200户居民六月份的用电量的中位数落在第2组内；故答案为：2；（2）50+100200×10000＝7500（户）,答：估计该地1万户居民六月份的用电量低于178kW•h的大约有7500户．22．（8分）甲、乙两人分别从A、B、C这3个景点中随机选择2个景点游览．（1）求甲选择的2个景点是A、B的概率；（2）甲、乙两人选择的2个景点恰好相同的概率是13．【解答】解：甲选择的2个景点所有可能出现的结果如下：（1）共有6种可能出现的结果,其中选择A、B的有2种,∴P（A、B）=26=13；（2）用列表法表示所有可能出现的结果如下：共有9种可能出现的结果,其中选择景点相同的有3种,∴P（景点相同）=39=13．故答案为：13．23．（8分）如图,在港口A处的正东方向有两个相距6km的观测点B、C．一艘轮船从A处出发,沿北偏东26°方向航行至D处,在B、C处分别测得∠ABD＝45°、∠C＝37°．求轮船航行的距离AD．（参考数据：sin26°≈0.44,cos26°≈0.90,tan26°≈0.49,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75．）【解答】解：如图,过点D作DH⊥AC于点H,在Rt△DCH中,∠C＝37°,∴CH=DHtan37°,在Rt△DBH中,∠DBH＝45°,∴BH=DHtan45°,∵BC＝CH﹣BH,∴DHtan37°−DHtan45°=6,解得DH≈18,在Rt△DAH中,∠ADH＝26°,∴AD=DHcos26°≈20．答：轮船航行的距离AD约为20km．24．（8分）如图,在△ABC中,AC＝BC,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作DF∥BC,交⊙O于点F．求证：（1）四边形DBCF是平行四边形；（2）AF＝EF．【解答】证明：（1）∵AC＝BC,∴∠BAC＝∠B,∵DF∥BC,∴∠ADF＝∠B,∵∠BAC＝∠CFD,∴∠ADF＝∠CFD,∴BD∥CF,∵DF∥BC,∴四边形DBCF是平行四边形；（2）连接AE,∵∠ADF＝∠B,∠ADF＝∠AEF,∴∠AEF＝∠B,∵四边形AECF是⊙O的内接四边形,∴∠ECF+∠EAF＝180°,∵BD∥CF,∴∠ECF+∠B＝180°,∴∠EAF＝∠B,∴∠AEF＝∠EAF,∴AE＝EF．25．（8分）小明和小丽先后从A地出发沿同一直道去B地．设小丽出发第xmin时,小丽、小明离B地的距离分别为y1m、y2m．y1与x之间的函数表达式是y1＝﹣180x+2250,y2与x 之间的函数表达式是y2＝﹣10x2﹣100x+2000．（1）小丽出发时,小明离A地的距离为250 m．（2）小丽出发至小明到达B地这段时间内,两人何时相距最近？最近距离是多少？【解答】解：（1）∵y1＝﹣180x+2250,y2＝﹣10x2﹣100x+2000,∴当x＝0时,y1＝2250,y2＝2000,∴小丽出发时,小明离A地的距离为2250﹣2000＝250（m）,故答案为：250；（2）设小丽出发第xmin时,两人相距sm,则s＝（﹣180x+2250）﹣（﹣10x2﹣100x+2000）＝10x2﹣80x+250＝10（x﹣4）2+90, ∴当x＝4时,s取得最小值,此时s＝90,答：小丽出发第4min时,两人相距最近,最近距离是90m．26．（9分）如图,在△ABC和△A'B'C'中,D、D'分别是AB、A'B'上一点,ADAB =A′D′A′B′．（1）当CDC′D′=ACA′C′=ABA′B′时,求证△ABC∽△A'B'C．证明的途径可以用下面的框图表示,请填写其中的空格．（2）当CDC′D′=ACA′C′=BCB′C′时,判断△ABC与△A'B'C′是否相似,并说明理由．【解答】（1）证明：∵ADAB =A′D′A′B′,∴ADA′D′=ABA′B′,∵CDC′D′=ACA′C′=ABA′B′,∴CDC′D′=ACA′C′=ADA′D′,∴△ADC∽△A′D′C, ∴∠A＝∠A′,∵ACA′C′=ABA′B′,∴△ABC∽△A′B′C′．故答案为：CDC′D′=ACA′C′=ADA′D′,∠A＝∠A′．（2）如图,过点D,D′分别作DE∥BC,D′E′∥B′C′,DE交AC于E,D′E′交A′C′于E′．∵DE∥BC,∴△ADE∽△ABC,∴ADAB =DEBC=AEAC,同理,A′D′A′B′=D′E′B′C′=A′E′A′C′,∵ADAB =A′D′A′B′,∴DEBC =D′E′B′C′,∴DED′E′=BCB′C′,同理,AEAC =A′E′A′C′,∴AC−AEAC =A′C′−A′E′A′C′,即ECAC=E′C′A′C′,∴ECE′C′=ACA′C′,∵CDC′D′=ACA′C′=BCB′C′,∴CDC′D′=DED′E′=ECE′C′,∴△DCE∽△D′C′E′,∴∠CED＝∠C′E′D′,∵DE∥BC,∴∠CED+∠ACB＝90°,同理,∠C′E′D′+∠A′C′B′＝180°, ∴∠ACB＝∠A′B′C′,∵ACA′C′=CBC′B′,∴△ABC∽△A′B′C′．27．（9分）如图①,要在一条笔直的路边l上建一个燃气站,向l同侧的A、B两个城镇分别铺设管道输送燃气．试确定燃气站的位置,使铺设管道的路线最短．（1）如图②,作出点A关于l的对称点A',线段A'B与直线l的交点C的位置即为所求,即在点C处建燃气站,所得路线ACB是最短的．为了证明点C的位置即为所求,不妨在直线1上另外任取一点C',连接AC'、BC',证明AC+CB＜AC′+C'B．请完成这个证明．（2）如果在A、B两个城镇之间规划一个生态保护区,燃气管道不能穿过该区域．请分别给出下列两种情形的铺设管道的方案（不需说明理由）．①生态保护区是正方形区域,位置如图③所示；②生态保护区是圆形区域,位置如图④所示．【解答】证明：（1）如图②,连接A'C',∵点A,点A'关于l对称,点C在l上,∴CA＝CA',∴AC+BC＝A'C+BC＝A'B,同理可得AC'+C'B＝A'C'+BC',∵A'B＜A'C'+C'B,∴AC+BC＜AC'+C'B；（2）如图③,在点C出建燃气站,铺设管道的最短路线是ACDB,（其中点D是正方形的顶点）；如图④,̂+EB,（其中CD,BE都与圆相切）在点C出建燃气站,铺设管道的最短路线是ACD+DE。
中考数学解析题
中考数学解析题例1、（南京市1998年中考题）如图所示，⊙O1和⊙O2内切于点P，⊙O2的弦AB经过⊙O1的圆心O1，交⊙O1于C、D，若AC︰CD︰DB=3︰4︰2，则⊙O1与⊙O2的直径之比为（）A、2︰7B、2︰5C、1︰4D、1︰3解：作直线O1O2交⊙O2于E点，则直线O1O2必过两圆的切点P，设AC=3x，CD=4x，DB=2x，则⊙O1的半径为2x，由相交弦定理，得EO1·O1P=AO1·O1B．设⊙O2的半径为R，所以(2R－2x)·2x=(3x＋2x)·(2x＋2x)．整理后，得 4x︰2R=1︰3，故应选D．说明：解决本题的思路是通过作辅助线，在⊙O2中运用相交弦定理，得到一个含有两圆直径的等式，从而得两直径之比．例2、（哈尔滨市1998年中考试题）如图所示△ABC中，∠BAC的平分线与边BC和外接圆分别相交于点D 和E，延长AC交过D、E、C三点的圆于点F．（1）求证：EF2=ED·EA；（2）若AE=6，EF=3，求AF·AC的值．（1）证明：连结CE，DF．∵ AD平分∠BAC，∴ ∠1=∠2．∵∠3=∠4，∠1=∠3，∴ ∠2=∠4．∵∠AEF=∠FED，∴ △AEF∽△FED，∴ EF2=AE·ED．（2）解：由（1）知：EF2=AE·ED．∵ EF=3，AE=6，∴ ED=，∴ AD=．∵AD·AE=AC·AF，∴AC·AF=6×=27．说明：圆与相似三角形的综合应用是常见题型，关键在于利用圆中角的等量代换，转化成两个三角形中的对应角相等．例3、（2002年河南省中考试题）如图所示，已知△ABC内接于⊙O1，AB=AC，⊙O2与BC相切于点B，与AB相交于点E，与⊙O1相交于点D，直线AD交⊙O2于点F，交CB的延长线于点G．求证：（1）∠G=∠AFE；（2）AB·EB=DF·AG证明：（1）连结BD．∵∠FEB=∠FDB，∠FDB=∠C，∴∠FEB=∠C．又∵ AB=AC，∴ ∠ABC=∠C．∴∠FEB=∠ABC，∴ EF∥CG．∴∠G=∠A FE．（2）连接BF．∵∠ADE=∠ABF，∠DAE=∠BAF，∴△ADE∽△ABF，．∵∠BEF=∠ABC，∠ABC=∠BFE，∴∠BEF=∠BFE，∴ BE=BF．∴AB·EB=DE·AG。
南京市1998年初中毕业、升学统一考试数学试题及解答
南京市1998年初中毕业、升学统一考试数学试题及解答
佚名
【期刊名称】《中学数学月刊》
【年(卷),期】1998(000)009
【摘要】（第Ⅰ卷）第一部分（30分）一、选择题（每小题3分,共10题,计
30分） 1.在实数π,-（2/5）,0,3<sup>1/2</sup>,-3.14,4<sup>1/2</sup>中,无理数有…………………………………（）（A）1个（B）2个（C）3个（D）4个 2.在数轴上表示不等式x≥-2的解集,正确的是………………………………（） 3.计算sin30°+ctg45°的结果等于…（）
【总页数】5页(P46-50)
【正文语种】中文
【中图分类】G634.605
【相关文献】
1.2004年陕西省初中毕业生升学统一考试数学试题 [J], 考评
2.初中毕业、升学统一考试数学试题 [J], 李娜
3.1996年苏州市初中毕业暨升学考试数学试题及解答 [J],
4.1997年南通市初中毕业、升学考试数学试题及解答 [J],
5.北京市一九八五年初中毕业、升学统一考试数学试题 [J],
因版权原因，仅展示原文概要，查看原文内容请购买。
盐城1998年中考试卷
盐城1998年中考试卷语文试卷：第一部分积累与运用。
一、选择正确的答案。
1、下列词语中，每对加点字的读音都相同的一项是（）。
A、难堪/劫难蹒跚/姗姗来迟B、怂恿/踊跃挑逗/挑拨离间C、拘泥/淤泥烘托/哄堂大笑D、修葺/作揖累赘/伤痕累累2、下列词语中，没有错别字的一项是（）。
A、贸然春寒料峭雾霭雕梁画栋B、困厄神采奕奕推崇和颜悦色C、褴褛饥肠辘辘斡旋自圆其说D、告罄摧枯拉朽藻饰人情世故3、依次填入下列句子横线处的词语，最恰当的一项是（）。
开学在即，各种校外培训机构又在广州大大小小的中小学校及幼儿园门前上演“招生秀”，这些培训机构（），而培训机构的教学质量与广大学子的切身利益（），所以规范校外培训机构的发展已经（）了。
A、鱼龙混杂息息相关刻不容缓B、鱼目混珠息息相关众望所归C、鱼龙混杂休戚与共众望所归D、鱼目混珠休戚与共刻不容缓4、下列句子中，没有语病的一项是（）。
A、畅销读物能否成为经典作品，关键在于它具备能经受时间考验的思想性和艺术性。
B、为了提高大家阅读的兴趣，我校文学社开展了一系列的名著阅读和主题诗歌朗诵。
C、十三行博物馆举办非遗体验活动，旨在让人们领略传统文化魅力，增强文化自信。
D、广州市正在加快建立分类投放、分类处理、分类收集、分类运输的垃圾处理系统。
5、下列选项中，与上下文衔接最恰当的一项是（）。
打造粤港澳大湾区，要有追赶思维，更要有探索精神赶别人定下的目标，努力向前，但是，以往我们强调追赶思维，为了因为你会对前方的路一无所知。
而探索精神可以让我们看清前方的路，找到经济发展的突破口，实现突围。
A、如果没有追赶思维，就有可能落后B、如果只有追赶思维，就不可能领先C、只要拥有追赶思维，就不可能落后D、只要没有追赶思维，就有可能领先6、文学名著《水浒传》连环画中的一幅，请仔细观察，并按要求作答。
(1)《水浒传》中鲁达的绰号是________，与右图内容相关的情节是（）。
(2) 有人认为鲁达是个有担当的人，其他经典名著中也不乏担当的人物形象，请从《西游记》《海底两万里》《钢铁是怎样炼成的》三部作品中找出一个这样用不经法多，的人物，并作简要分析。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1998年江苏省南京市中考数学试卷一、单选题（每道小题3分共60分）1．（3分）在数轴上表示不等式x≥﹣2的解集，正确的是（）A．B． C．D．2．（3分）在实数π，中，无理数有（）A．1个 B．2个 C．3个 D．4个3．（3分）3﹣2的算术平方根是（）A．B．3 C．D．64．（3分）下列计算中，正确的是（）A．（﹣a2）2=a6B．a6÷a3=a2C．D．5．（3分）下列各组二次根式中，同类二次根式的是（）A．B．C． D．6．（3分）某中学数学教研组有25名教师，将他们的年龄分成3组，在38～45（岁）组内有8名教师，那么这个小组的频率是（）A．0.12 B．0.38 C．0.32 D．3.127．（3分）某市今年有6万名初中毕业生参加升学考试，为了了解6万名考生的数学成绩，从中抽取1500名考生的数学成绩进行统计分析，以下说法中正确的是（）A．6万考生是总体B．每名考生的数学成绩是个体C．1500名考生是总体的一个样本D．1500名是样本的容量8．（3分）要测量河两岸相对的两点A，B的距离，先在AB的垂线BF上取两点C，D，使CD=BC，再定出BF的垂线DE，使A，C，E在一条直线上（如图所示），可以说明△EDC≌△ABC，得ED=AB，因此测得ED的长就是AB的长，判定△EDC ≌△ABC最恰当的理由是（）A．边角边B．角边角C．边边边D．边边角9．（3分）两根木棒的长度分别是5cm和7cm，要选择第三根木棒，将它们钉成一个三角形，如果第三根木棒的长为偶数，那么第三根木棒长的取值情况有（）A．3种 B．4种 C．5种 D．6种10．（3分）计算sin30°+cot45°的结果等于（）A．B．C．2 D．11．（3分）函数y=中自变量x的取值范围是（）A．x≥﹣1且x≠0 B．x＞﹣1且x≠0 C．x＞1 D．x≥112．（3分）如图所示，桥拱是抛物线形，其函数的表达式为y=﹣x2，当水位线在AB位置时，水面宽12m，这时水面离桥顶的高度为（）A．3m B．m C．4m D．9m13．（3分）点A（﹣5，y1），B（﹣2，y2）都在直线y=﹣上，则y1与y2的关系是（）A．y1≤y2B．y1=y2C．y1＜y2D．y1＞y214．（3分）在下列方程中，有实数根的方程是（）A．3x2﹣x+1=0 B．C．D．15．（3分）顺次连接圆内接梯形四边的中点所得的四边形是（）A．矩形B．菱形C．正方形D．等腰梯形16．（3分）如图，圆内接正五边形ABCDE中，对角线AC和BD相交于点P，则∠APB的度数是（）A．36°B．60°C．72°D．108°17．（3分）若双曲线的两个分支在第二、四象限内，则抛物线y=kx2﹣2x+k2的图象大致是图中的（）A．B．C． D．18．（3分）如图，⊙O1和⊙O2内切于点P，⊙O2的弦AB经过⊙O1的圆心O1，交⊙O1于点C、D，若AC：CD：BD=3：4：2，则⊙O1与⊙O2的直径之比为（）A．B．C．D．19．（3分）如图，用铁皮做一个圆锥形的烟囱帽，它的底面直径是80cm，高是30cm，不计加工余料，则需用铁皮的面积最少是（）A．4000π（cm2）B．2400π（cm2）C．2000π（cm2）D．1200π（cm2）20．（3分）设计一个商标图象（如图阴影部分），矩形ABCD中，AB=2BC，且AB=8cm，以点A为圆心，AD的长为半径作半圆，则商标图案面积等于（）A．4π+8 B．4π+16 C．3π+8 D．3π+16二、解答题（第1小题4分，2-8每题6分，第9小题8分，第10小题12分，共66分）21．（4分）已知：如图，菱形ABCD的边长为3，延长AB到点E，使BE=2AB，连接EC并延长交AD的延长线于点F．求AF的长．22．（6分）设x1，x2是方程x2﹣（k+1）x﹣3=0的两根，且，求k的值．23．（6分）把x3+3x2﹣4x﹣12分解因式．24．（6分）先化简，再求值：，其中．25．（6分）阅读下面一题的解答过程，请判断是否正确？若不正确，请写出正确的解答．已知a为实数，化简．解：==（a﹣1）．26．（6分）解方程：x2﹣2x+．27．（6分）某区中学生足球联赛共赛8轮（即每队均需赛8场），胜一场得3分，平一场得1分，负一场得0分．在这次足球联赛中，小平安队踢平的场数是所负场数的2倍，共得17分，试问该队胜了几场？28．（6分）（1）已知反比例函数y=，当x=时，y=﹣6，求这个函数的解析式；（2）若一次函数y=mx﹣4的图象与（1）中的反比例函数y=的图象有交点，求m的取值范围．29．（8分）在⊙O的内接△ABC中，AB+AC=12，AD⊥BC，垂足为D，且AD=3，设⊙O的半径为y，AB的长为x．（1）求y关于x的函数关系式；（2）当AB的长等于多少时，⊙O的面积最大，并求出⊙O的最大面积．30．（12分）已知：抛物线y=x2﹣（m2+5）x+2m2+6．（1）求证：不论m取何值，抛物线与x轴必有两个交点，并且有一个交点是A （2，0）；（2）设抛物线与x轴的另一个交点为B，AB的长为d，求d与m之间的函数关系式；（3）设d=10，P（a，b）为抛物线上一点．①当△ABP是直角三角形时，求b的值；②当△ABP是锐角三角形、钝角三角形时，分别写出b的取值范围（第②题不要求写出解答过程）．三、证明题（第1小题4分，第2小题8分，第3小题12分，共24分）31．（4分）已知：如图，△ABC内接于⊙O，过圆心O作BC的垂线交⊙O于点P、Q，交AB于点D，QP、CA的延长线交于点E．求证：OA2=OD•OE．32．（8分）已知：如图，点P在∠AOB的边OA上．（1）作图（保留作图痕迹）①作∠AOB的平分线OM；②以P为顶点，作∠APQ=∠AOB，PQ交OM于点C；③过点C作CD⊥OB，垂足为点D．（2）当∠AOB=30°时，求证：PC=2CD．33．（12分）已知，如图，⊙O1与⊙O2相交，点P是其中一个交点，点A在⊙O2上，AP的延长线交⊙O1于点B，AO2的延长线交⊙O1于点C、D，交⊙O2于点E，连接PC、PE、PD，且，过A作⊙O1的切线AQ，切点为Q．求证：（1）∠CPE=∠DPE；（2）AQ2﹣AP2=PC•PD．1998年江苏省南京市中考数学试卷参考答案与试题解析一、单选题（每道小题3分共60分）1．（3分）在数轴上表示不等式x≥﹣2的解集，正确的是（）A．B． C．D．【分析】根据在数轴上表示不等式解集的方法利用排除法进行解答．【解答】解：∵不等式x≥﹣2中包含等于号，∴必须用实心圆点，∴可排除A、B，∵不等式x≥﹣2中是大于等于，∴折线应向右折，∴可排除D．故选：C．【点评】本题考查的是在数轴上表示不等式解集的方法，即“＞”空心圆点向右画折线，“≥”实心圆点向右画折线，“＜”空心圆点向左画折线，“≤”实心圆点向左画折线．2．（3分）在实数π，中，无理数有（）A．1个 B．2个 C．3个 D．4个【分析】根据无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数，结合所给数据进行判断即可．【解答】解：=2，所给数据中无理数有：π，，共两个．故选：B．【点评】本题考查了无理数的定义，属于基础题，解答本题的关键是熟练掌握无理数的三种形式．3．（3分）3﹣2的算术平方根是（）A．B．3 C．D．6【分析】先求出3的﹣2次方，再根据算术平方根的定义计算．【解答】解：3﹣2=，∵（）2=，∴的算术平方根是．故选：A．【点评】本题考查了算术平方根的定义、负整数指数次幂的运算，先计算负整数指数次幂是解题的关键．4．（3分）下列计算中，正确的是（）A．（﹣a2）2=a6B．a6÷a3=a2C．D．【分析】分别根据分式的加减法、同底数幂的除法法则及幂的乘方与积的乘方法则法则对各选项进行逐一判断即可．【解答】解：A、（﹣a2）2=a4，故本选项错误；B、a6÷a3=a6﹣3=a3，故本选项错误；C、原式==﹣1，故本选项正确；D、原式=+=，故本选项错误．故选：C．【点评】本题考查的是分式的加减法、同底数幂的除法法则及幂的乘方与积的乘方法则，熟知以上知识是解答此题的关键．5．（3分）下列各组二次根式中，同类二次根式的是（）A．B．C． D．【分析】将选项中的二次根式化为最简，然后根据同类二次根式的被开方数相同即可得出答案．【解答】解：A、与3的被开方数不同，不是同类二次根式，故本选项错误；B、3与的被开方数不同，不是同类二次根式，故本选项错误；C、=，=，被开方数相同，是同类二次根式，故本选项正确；D、=2，=，被开方数不同，不是同类二次根式，故本选项错误；故选：C．【点评】此题考查了同类二次根式的定义，解答本题的关键是掌握同类二次根式的特点，属于基础题，难度一般．6．（3分）某中学数学教研组有25名教师，将他们的年龄分成3组，在38～45（岁）组内有8名教师，那么这个小组的频率是（）A．0.12 B．0.38 C．0.32 D．3.12【分析】根据频率的求法：频率=频数÷数据总数即可求解．【解答】解：根据题意，38﹣45岁组内的教师有8名，即频数为8，而总数为25；故这个小组的频率是为8÷25=0.32．故选：C．【点评】本题考查频率、频数的关系，属于基础题，关键是掌握频率的求法：频率=频数÷数据总数．7．（3分）某市今年有6万名初中毕业生参加升学考试，为了了解6万名考生的数学成绩，从中抽取1500名考生的数学成绩进行统计分析，以下说法中正确的是（）A．6万考生是总体B．每名考生的数学成绩是个体C．1500名考生是总体的一个样本D．1500名是样本的容量【分析】总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，而样本容量则是指样本中个体的数目．我们在区分总体、个体、样本、样本容量，这四个概念时，首先找出考查的对象．从而找出总体、个体．再根据被收集数据的这一部分对象找出样本，最后再根据样本确定出样本容量．【解答】解：A、6万考生的数学成绩是总体，故选项错误；B、正确；C、1500名考生的数学成绩是样本，故选项错误；D、样本容量是1500，故选项错误．故选：B．【点评】解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象．总体、个体与样本的考查对象是相同的，所不同的是范围的大小．样本容量是样本中包含的个体的数目，不能带单位．8．（3分）要测量河两岸相对的两点A，B的距离，先在AB的垂线BF上取两点C，D，使CD=BC，再定出BF的垂线DE，使A，C，E在一条直线上（如图所示），可以说明△EDC≌△ABC，得ED=AB，因此测得ED的长就是AB的长，判定△EDC ≌△ABC最恰当的理由是（）A．边角边B．角边角C．边边边D．边边角【分析】由已知可以得到∠ABC=∠BDE，又CD=BC，∠ACB=∠DCE，由此根据角边角即可判定△EDC≌△ABC．【解答】解：∵BF⊥AB，DE⊥BD∴∠ABC=∠BDE又∵CD=BC，∠ACB=∠DCE∴△EDC≌△ABC（ASA）故选：B．【点评】本题考查了全等三角形的判定方法；需注意根据垂直定义得到的条件，以及隐含的对顶角相等，观察图形，找着隐含条件是十分重要的．9．（3分）两根木棒的长度分别是5cm和7cm，要选择第三根木棒，将它们钉成一个三角形，如果第三根木棒的长为偶数，那么第三根木棒长的取值情况有（）A．3种 B．4种 C．5种 D．6种【分析】首先根据三角形的三边关系确定第三边的取值范围，再根据第三边是偶数确定其值．【解答】解：根据三角形的三边关系，得第三根木棒的长大于2cm而小于12cm．又第三根木棒的长是偶数，则应为4cm，6cm，8cm，10cm．故选：B．【点评】三角形的三边关系：第三边大于两边之差而小于两边之和．注意：偶数这一条件．10．（3分）计算sin30°+cot45°的结果等于（）A．B．C．2 D．【分析】根据sin30°=，cot45°=1计算即可．【解答】解：∵sin30°=，cot45°=1，∴sin30°+cot45°=+1=，故选：A．【点评】此题很简单，解答此题的关键是熟知特殊角的三角函数值．11．（3分）函数y=中自变量x的取值范围是（）A．x≥﹣1且x≠0 B．x＞﹣1且x≠0 C．x＞1 D．x≥1【分析】根据被开方数大于等于0，分母不等于0列式计算即可得解．【解答】解：根据题意得，x+1≥0且x≠0，解得x≥﹣1且x≠0．故选：A．【点评】本题考查的知识点为：分式有意义，分母不为0；二次根式的被开方数是非负数．12．（3分）如图所示，桥拱是抛物线形，其函数的表达式为y=﹣x2，当水位线在AB位置时，水面宽12m，这时水面离桥顶的高度为（）A．3m B．m C．4m D．9m【分析】根据题意，把x=6直接代入解析式即可解答．【解答】解：由已知AB=12m知：点B的横坐标为6．把x=6代入y=﹣，得y=﹣9．即水面离桥顶的高度为9m．故选：D．【点评】本题考查点的坐标的求法及二次函数的实际应用．此题为数学建模题，借助二次函数解决实际问题．13．（3分）点A（﹣5，y1），B（﹣2，y2）都在直线y=﹣上，则y1与y2的关系是（）A．y1≤y2B．y1=y2C．y1＜y2D．y1＞y2【分析】先根据一次函数的解析式判断出其增减性，再根据A、B两点横坐标的大小即可得出结论．【解答】解：∵一次函数y=﹣x中，k=﹣＜0，∴y随x的增大而减小，∵﹣5＜﹣2，∴y1＞y2．故选：D．【点评】本题考查的是一次函数图象上点的坐标特点，熟知一次函数的增减性是解答此题的关键．14．（3分）在下列方程中，有实数根的方程是（）A．3x2﹣x+1=0 B．C．D．【分析】判断方程有无实数解，就是看方程的解是否有满足方程的左右两边相等的实数．【解答】解：A、△=b2﹣4ac=1﹣12=﹣11＜0，此方程无实数根，故此选项不合题意；B、，解得：﹣1≤x≤0，不等式组有解集，即原方程有实数解；故选项符合题意；C、去分母得：x2+1=0，△=b2﹣4ac=0﹣4=﹣4＜0此方程无实数根，故此选项不合题意；D、化简分式方程后，求得x=0或2，检验后，为增根，原分式方程无解，故此选项不合题意．故选：B．【点评】此题主要考查了方程是否有实数解，关键是掌握：1、一元二次方程根的情况与判别式△的关系：（1）△＞0⇔方程有两个不相等的实数根，（2）△=0⇔方程有两个相等的实数根，（3）△＜0⇔方程没有实数根；2、分式方程要验根．15．（3分）顺次连接圆内接梯形四边的中点所得的四边形是（）A．矩形B．菱形C．正方形D．等腰梯形【分析】由题意可知圆内接梯形是等腰梯形，所以根据等腰梯形的性质及中位线定理和菱形的判定，可推出四边形为菱形．【解答】解：如图，已知：等腰梯形ABCD中，AD∥BC，AB=CD，E、F、G、H 分别是各边的中点，求证：四边形EFGH是菱形．证明：连接AC、BD．∵E、F分别是AB、BC的中点，∴EF=AC，同理FG=BD，GH=AC，EH=BD，又∵四边形ABCD是等腰梯形，∴AC=BD，∴EF=FG=GH=HE，∴四边形EFGH是菱形．故选：B．【点评】此题主要考查了等腰梯形的性质，三角形的中位线定理和菱形的判定．用到的知识点：等腰梯形的两底角相等；三角形的中位线平行于第三边，并且等于第三边的一半；四边相等的四边形是菱形．16．（3分）如图，圆内接正五边形ABCDE中，对角线AC和BD相交于点P，则∠APB的度数是（）A．36°B．60°C．72°D．108°【分析】首先根据正五边形的性质得到AB=BC=CD，∠ABC=∠BCD=108度，然后利用三角形内角和定理得∠BAC=∠BCA=∠CBD=∠BDC==36°，最后利用三角形的外角的性质得到∠APB=∠DBC+∠ACB=72°．【解答】解：∵五边形ABCDE为正五边形，∴AB=BC=CD，∠ABC=∠BCD=108度，∴∠BAC=∠BCA=∠CBD=∠BDC==36°，∴∠APB=∠DBC+∠ACB=72°，故选：C．【点评】本题考查了正多边形和圆的知识，题目中还用到了三角形的外角的性质及正多边形的性质等，比较简单．17．（3分）若双曲线的两个分支在第二、四象限内，则抛物线y=kx2﹣2x+k2的图象大致是图中的（）A．B．C． D．【分析】根据双曲线的图象位置可知k＜0；再根据k的符号判断抛物线的开口方向及对称轴．【解答】解：∵双曲线的两个分支在第二、四象限内，即k＜0，∴抛物线开口向下，对称轴x=﹣=＜0，对称轴在y轴的左边．故选A．【点评】本题考查了反比例函数图象的性质和二次函数系数与抛物线形状的关系．18．（3分）如图，⊙O1和⊙O2内切于点P，⊙O2的弦AB经过⊙O1的圆心O1，交⊙O1于点C、D，若AC：CD：BD=3：4：2，则⊙O1与⊙O2的直径之比为（）A．B．C．D．【分析】根据相交线定理以及相且两圆的性质得出两圆直径，进而得出答案即可．【解答】解：圆O1与圆O2内切于点P，O1，O2，P在一直线上，此直线与圆O2的另一交点设为E．∴O1A•O1B=O1P•O1E，∵若AC：CD：BD=3：4：2，⊙O2的弦AB经过⊙O1的圆心O1，∴O1A：O1B=5：4，设O1A=5x，则O1B=4x，CO1=2x，∴O1E==10x，∴圆O1与圆O2的直径分别为：4x，12x，∴圆O1与圆O2的直径之比为：=．故选：D．【点评】此题主要考查了相切两圆的性质以及相交弦定理，根据已知得出O1A•O1B=O1P•O1E是解题关键．19．（3分）如图，用铁皮做一个圆锥形的烟囱帽，它的底面直径是80cm，高是30cm，不计加工余料，则需用铁皮的面积最少是（）A．4000π（cm2）B．2400π（cm2）C．2000π（cm2）D．1200π（cm2）【分析】利用勾股定理可求得圆锥的母线长，那么圆锥的侧面积=底面周长×母线长÷2．【解答】解：∵底面直径是80cm，高是30cm，∴根据勾股定理求得圆锥的母线长为50cm，∴圆锥的侧面积展开图是一个扇形，圆锥的母线长为50cm，底面直径为80cm，∴扇形的弧长为80π，∴圆锥形烟囱帽的侧面积=×50×80π=2000πcm2．故选：C．【点评】本题考查了圆锥的计算，利用了圆的周长公式和扇形面积公式求解．20．（3分）设计一个商标图象（如图阴影部分），矩形ABCD中，AB=2BC，且AB=8cm，以点A为圆心，AD的长为半径作半圆，则商标图案面积等于（）A．4π+8 B．4π+16 C．3π+8 D．3π+16【分析】根据矩形的性质得到AD=BC=4，∠FAD=90°，根据图形得到S阴=S矩ABCD+S扇ADF ﹣S△FBC．【解答】解：∵矩形ABCD中，AB=2BC，且AB=8cm，∴AD=BC=4，∴S阴=S矩ABCD+S扇ADF﹣S△FBC，∵S矩ABCD=AB•BC=8×4=32，S扇ADF==4π，S△FBC=BC•FB=×4×（8+4）=24，∴S阴=32+4π﹣24=（8+4π）cm2．所以商标图案的面积为（8+4π）cm2．故选：A．【点评】本题考查了扇形的面积公式：S=（其中n为扇形的圆心角的度数，r为半径）．也考查了矩形的性质．二、解答题（第1小题4分，2-8每题6分，第9小题8分，第10小题12分，共66分）21．（4分）已知：如图，菱形ABCD的边长为3，延长AB到点E，使BE=2AB，连接EC并延长交AD的延长线于点F．求AF的长．【分析】首先由菱形的性质：DC∥AE，进而证明：△DFC∽△AFE，再利用相似三角形的性质和已知条件即可求出DF的长，进而求出AF的长．【解答】解：∵四边形ABCD是菱形，∴DC∥AE，∴△DFC∽△AFE，∴，∵BE=2AB，AB=3，∴BE=6，AE=9，∴，∴DF=1.5，∴AF=AD+DF=3+1.5=4.5．【点评】本题考查了菱形的性质，相似三角形的判定和性质，题目的难度不大，属于基础性题目．22．（6分）设x1，x2是方程x2﹣（k+1）x﹣3=0的两根，且，求k的值．【分析】利用根与系数的关系表示出两根之和与两根之积，将已知等式左边通分并利用同分母分式的加法法则变形，把各自的值代入即可求出k的值．【解答】解：∵x1，x2是方程x2﹣（k+1）x﹣3=0的两根，∴x1+x2=k+1，x1x2=﹣3，∵+===2，解得：k=﹣7．【点评】此题考查了根与系数的关系，熟练掌握根与系数的关系是解本题的关键．23．（6分）把x3+3x2﹣4x﹣12分解因式．【分析】多项式前两项结合，后两项结合，分别提取公因式后，再提取公因式并利用平方差公式分解即可．【解答】解：原式=x2（x+3）﹣4（x+3）=（x+3）（x2﹣4）=（x+3）（x+2）（x﹣2）．【点评】此题考查了因式分解﹣分组分解法，难点是采用两两分组还是三一分组．比如本题利用的是两两分组．24．（6分）先化简，再求值：，其中．【分析】先把括号里式子通分，再把除法转化为乘法，约分化为最简，最后代值计算．【解答】解：原式=，当x=时，原式==2+．【点评】本题主要考查分式的化简求值这一知识点，把分式化到最简是解答的关键．25．（6分）阅读下面一题的解答过程，请判断是否正确？若不正确，请写出正确的解答．已知a为实数，化简．解：==（a﹣1）．【分析】根据二次根式的性质，成立，则a为负数，由此可先判断已知解答是错误的，再化简解答即可．【解答】解：不正确，根据题意，成立，所以a为负数，则=﹣a+=（1﹣a）．【点评】本题主要考查了二次根式的性质的灵活运用，关键是根据成立，则a为负数，注意：当a＜0时，=﹣a．26．（6分）解方程：x2﹣2x+．【分析】利用换元法求解本方程即可．【解答】解：令x2﹣2x=y，则原方程变为y+=7，移项得：=7﹣y两边平方得：y﹣1=（7﹣y）2．整理得：y2﹣15y+50=0，解得：y=5或y=10，经检验y=10是增根，∴x2﹣2x=5，解得：x1=1+，x2=1﹣．【点评】本题主要考查了无理方程的解法，在解无理方程是最常用的方法是两边平方法及换元法，本题用了换元法．27．（6分）某区中学生足球联赛共赛8轮（即每队均需赛8场），胜一场得3分，平一场得1分，负一场得0分．在这次足球联赛中，小平安队踢平的场数是所负场数的2倍，共得17分，试问该队胜了几场？【分析】表示出该队胜，负，平的场数，等量关系为：胜的场数的得分+平的场数的得分=17，把相关数值代入求解即可．【解答】解：设负的场数为x，则平的场数为2x，那么胜的场数为（8﹣x﹣2x），3（8﹣x﹣2x）+2x=17，解得x=1，∴8﹣x﹣2x=5．答：胜了5场．【点评】考查一元一次方程的应用，得到总分的等量关系是解决本题的关键；注意本题设间接未知数不易出差错．28．（6分）（1）已知反比例函数y=，当x=时，y=﹣6，求这个函数的解析式；（2）若一次函数y=mx﹣4的图象与（1）中的反比例函数y=的图象有交点，求m的取值范围．【分析】（1）把x=，y=﹣6代入y=求出k即可；（2）把y=mx﹣4代入y=﹣得出方程mx2﹣4x+2=0，根据根的判别式求出即可．【解答】解：（1）把x=，y=﹣6代入y=得：k=﹣6×=﹣2，即这个函数的解析式为y=﹣；（2）把y=mx﹣4代入y=﹣得：mx﹣4=﹣，mx2﹣4x+2=0，△=（﹣4）2﹣4m•2=16﹣8m，∵一次函数y=mx﹣4的图象与反比例函数y=﹣的图象有交点，∴16﹣8m≥0，m≠0，∴m≤2且m≠0，即m的取值范围是：m≤2且m≠0．【点评】本题考查了一次函数和反比例函数的交点问题，用待定系数法求反比例函数的解析式，根的判别式等知识点的应用，主要考查学生计算能力和理解能力．29．（8分）在⊙O的内接△ABC中，AB+AC=12，AD⊥BC，垂足为D，且AD=3，设⊙O的半径为y，AB的长为x．（1）求y关于x的函数关系式；（2）当AB的长等于多少时，⊙O的面积最大，并求出⊙O的最大面积．【分析】（1）由题意知，需作出圆的直径AE，利用直径所对的圆周角是直角，得出△ABD∽△AEC．根据相似三角形的性质得到边之间的对应比相等，建立函数关系式；（2）根据二次函数的最值的求法，结合（1）中的函数关系式进行求解．【解答】解：（1）作直径AE，连接CE，如图所示，则∠ACE=90°，∵AD⊥BC，∴∠ACE=∠ADB=90度．又∠B=∠E，∴△ABD∽△AEC．∴，即．整理得y=（x﹣6）2+6．（2）由（1）知y=（x﹣6）2+6，则当x=6时，y取得最大值，最大值为6．∴⊙O的最大面积为36π．【点评】此题主要考查三角形相似及二次函数最大值的求法．30．（12分）已知：抛物线y=x2﹣（m2+5）x+2m2+6．（1）求证：不论m取何值，抛物线与x轴必有两个交点，并且有一个交点是A（2，0）；（2）设抛物线与x轴的另一个交点为B，AB的长为d，求d与m之间的函数关系式；（3）设d=10，P（a，b）为抛物线上一点．①当△ABP是直角三角形时，求b的值；②当△ABP是锐角三角形、钝角三角形时，分别写出b的取值范围（第②题不要求写出解答过程）．【分析】（1）令抛物线中y=0，即可用十字相乘法求得两根的值，由此可得证．（2）在（1）中已经求得了两点的坐标，即可表示出AB的距离．（3）①根据d的长以及（2）中得出的d的表达式可确定出抛物线的解析式，也就能得出A、B的坐标．可以AB为直径作圆，圆与抛物线有交点，说明抛物线上存在符合条件的P点，可根据抛物线的解析式设出P点坐标（设横坐标，根据抛物线的解析式表示出纵坐标），在直角三角形ABP中，∠APB=90°，如果过P 作PQ⊥x轴于Q，那么根据射影定理可得出PQ2=AQ•QB，由此可求出P点坐标，确定出b的值；②根据图形与①求出的b值，即可分别确定出当△ABP是锐角三角形、钝角三角形时b的取值范围．【解答】解：（1）令y=0，得x2﹣（m2+5）x+2m2+6=0，即（x﹣2）（x﹣m2﹣3）=0，解得：x1=2，x2=m2+3，∴一定有交点A（2，0），B（m2+3，0）∴结论得证；（2）∵A（2，0），B（m2+3，0）∴d=AB=m2+1；（3）①d=AB=m2+1=10，∴y=x2﹣14x+24，∴A（2，0），B（12，0）以AB为直径画圆，由图可知与抛物线有两个交点，∴存在这样的点P，设点P坐标为（x，x2﹣14x+24），作P1Q⊥横轴于Q，则点Q（x，0），易得△AQP∽△PQB，∴=，∴PQ2=AQ•BQ=（x﹣2）（12﹣x）=（x2﹣14x+24）2，即（x﹣2）（12﹣x）=（x﹣2）2（x﹣12）2，（x﹣2）（x﹣12）≠0，∴解得x=7±2，∴点P为（7+2，﹣1），或（7﹣2，﹣1），则b=﹣1；②当△ABP是锐角三角形时，﹣25≤b＜﹣1；当△ABP为钝角三角形时，b＞﹣1且b≠0．【点评】本题考查了二次函数与一元二次方程的关系、直角三角形的判定等知识．综合性较强，难度适中．三、证明题（第1小题4分，第2小题8分，第3小题12分，共24分）31．（4分）已知：如图，△ABC内接于⊙O，过圆心O作BC的垂线交⊙O于点P、Q，交AB于点D，QP、CA的延长线交于点E．求证：OA2=OD•OE．【分析】作直径AM，连接BM，求出∠E=∠DAO，公共角∠DOA=∠DOA，推出△DOA∽△AOE，得出比例式，即可得出答案．【解答】证明：作直径AM，连接BM，∵∠C和∠M都对弧AB，∴∠C=∠M，∵OQ⊥BC，∴∠EQC=90°，∴∠C+∠E=90°，∵AM为⊙O直径，∴∠ABM=90°，∴∠M+∠OAD=90°，∴∠E=∠OAD，∵∠DOA=∠DOA，∴△DOA∽△AOE，∴=，即OA2=OD•OE．【点评】本题考查了圆周角定理和相似三角形的性质和判定的应用，注意：直径所对的圆周角是直角，相似三角形的对应边的比相等．32．（8分）已知：如图，点P在∠AOB的边OA上．（1）作图（保留作图痕迹）①作∠AOB的平分线OM；②以P为顶点，作∠APQ=∠AOB，PQ交OM于点C；③过点C作CD⊥OB，垂足为点D．（2）当∠AOB=30°时，求证：PC=2CD．【分析】（1）根据角平分线的作法以及作一角等于已知角进而得出图形即可；（2）利用在直角三角形中30度所对边等于斜边的一半得出即可．【解答】解：（1）如图所示：（2）过点P作PF⊥OB于点F，∵∠APC=∠AOB，∴PC∥OB，∴∠PCO=∠POC，∵OM平分∠AOB，∴∠AOC=∠MOB，∴∠POC=∠PCO，∴OP=PC，∵∠AOB=30°，∠PFO=90°，∴PF=OP，∵PC∥OB，PF⊥OB，CD⊥BO，∴PF=DC，∴DC=OP=PC，即PC=2CD．【点评】本题主要考查了角平分线的作法以及作一角等于已知角以及到角平分线的性质等知识，利用平行线的性质以及30度所对边等于斜边的一半得出是解题关键．33．（12分）已知，如图，⊙O1与⊙O2相交，点P是其中一个交点，点A在⊙O2上，AP的延长线交⊙O1于点B，AO2的延长线交⊙O1于点C、D，交⊙O2于点E，连接PC、PE、PD，且，过A作⊙O1的切线AQ，切点为Q．求证：（1）∠CPE=∠DPE；（2）AQ2﹣AP2=PC•PD．【分析】（1）过D作DM∥PE交CP的延长线于M，根据平行线分线段成比例定理求出PM=PD，推出∠M=∠PDM，根据平行线的性质得出∠M=∠CPE，∠DPE=∠PDM，即可得出答案；（2）根据切割线定理得出AQ2=AP×AB，证△APC∽△DPB，推出=，得出AP×BP=PC×PD，代入即可得出答案．【解答】（1）证明：过D作DM∥PE交CP的延长线于M，则=，∵=，∴PM=PD，∴∠M=∠PDM，∵PE∥MD，∴∠M=∠CPE，∠DPE=∠PDM，∴∠CPE=∠DPE；（2）证明：连接BD，∵O2在AE上，∴∠APE=∠BPE=90°，∵∠CPE=∠DPE，∴∠APC=∠BPD，∵P、B、D、C四点共圆，∴∠ACP=∠B，∴△APC∽△DPB，∴=，∴AP×BP=PC×PD，∵AQ切⊙O1于Q，APB是⊙O1的割线，∴AQ2=AP×AB，∴AQ2﹣AP2=AP×AB﹣AP2=AP（AB﹣AP）=AP×BP=PC•PD，即AQ2﹣AP2=PC•PD．【点评】本题考查了相似三角形的性质和判定，圆内接四边形的性质，等腰三角形的性质，平行线分线段成比例定理等知识点的应用，主要考查学生综合运用性质进行推理的能力．。