2412垂直于弦的直径(2)-课件【PPT】
合集下载
24.1.2_垂直于弦的直径(2)PPT课件
若油面宽AB = 600mm,求油的最大深度.
A
O
┌E
D
D
600
C
B
在直径为650mm的圆柱形油槽内装入一些油后,截面的油面宽 AB = 600mm,求油的最大深度.
④⑤ ①②③ 平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.
一、判断是非:
(1)平分弦的直径,平分这条弦所对的弧。
(2)平分弦的直线,必定过圆心。
(3)一条直线平分弦(这条弦不是直径),
那么这 条直线垂直这条弦。
A
C
C
C
OD
(1) B
•O
A
Байду номын сангаас
B
(2) D
•O
A
B
(3) D
(4)弦的垂直平分线一定是圆的直径。
B
M
OM⊥AB,ON⊥AC,垂足分别为M,
A
N,且OM=2,0N=3,则A6B= , AC=4 ,OA= 13
ON C
练习:5.在⊙O中,AB、AC为互相垂直且相等的两条弦, OD⊥AB于D,OE⊥AC于E.
求证:四边形ADOE是正方形.
C
E
O
D
A
B
1.在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.
(5)平分弧的直线,平分这条弧所对的 弦。 (6)弦垂直于直径,这条直径就被弦平分。 (7)平分弦的直径垂直于弦
•O ACB
(4)
B
•O D
C
A
(5)
C
•O A EB
D (6)
填空:
1、如图:已知AB是⊙O的直径,弦CD与AB相交于点E,若 _______A_B__⊥__C_D__(__或__A_C__=_A_D__,__或__B_C_=__B_D_)_________________, 则CE=DE(只需填写一个你认为适当的条件)
A
O
┌E
D
D
600
C
B
在直径为650mm的圆柱形油槽内装入一些油后,截面的油面宽 AB = 600mm,求油的最大深度.
④⑤ ①②③ 平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.
一、判断是非:
(1)平分弦的直径,平分这条弦所对的弧。
(2)平分弦的直线,必定过圆心。
(3)一条直线平分弦(这条弦不是直径),
那么这 条直线垂直这条弦。
A
C
C
C
OD
(1) B
•O
A
Байду номын сангаас
B
(2) D
•O
A
B
(3) D
(4)弦的垂直平分线一定是圆的直径。
B
M
OM⊥AB,ON⊥AC,垂足分别为M,
A
N,且OM=2,0N=3,则A6B= , AC=4 ,OA= 13
ON C
练习:5.在⊙O中,AB、AC为互相垂直且相等的两条弦, OD⊥AB于D,OE⊥AC于E.
求证:四边形ADOE是正方形.
C
E
O
D
A
B
1.在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.
(5)平分弧的直线,平分这条弧所对的 弦。 (6)弦垂直于直径,这条直径就被弦平分。 (7)平分弦的直径垂直于弦
•O ACB
(4)
B
•O D
C
A
(5)
C
•O A EB
D (6)
填空:
1、如图:已知AB是⊙O的直径,弦CD与AB相交于点E,若 _______A_B__⊥__C_D__(__或__A_C__=_A_D__,__或__B_C_=__B_D_)_________________, 则CE=DE(只需填写一个你认为适当的条件)
24.垂直于弦的直径PPT课件(人教版)

(√ ) (√ ) (×)
轴
经过圆心
中心
圆心
垂直于弦的 直径平分弦,并且平分弦所对的两条弧
垂直
弦所对的两条弧
问题:你知道赵州桥吗?它是1300多年前我国隋代建 造的石拱桥,是我国古代人民勤劳与智慧的结晶.它的主 桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵州桥主 桥拱的半径吗?
∵AB∥CD,∴ON⊥CD于N
在RtAOM中,AM 5cm,OM OA2 AM2 12cm. 在RtOCN中,CN 12cm,ON OC2 CN 2 5cm.
∵MN=OM-ON,∴MN=7cm. (2)当AB、CD在O点异侧时,如图②所示,
由(1)可知OM=12cm,ON=5cm,MN=OM+ON,
(并2且)平A分M=A(BBM及,AA(DCB=.BC,AD=BD,即直径CD平分弦AB,
这样,我们就得到下面的定理:垂直于弦的直径平分弦, 并且平分弦所对的两条弧。进一步,我们还可以得到结论:平 分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧 。
知识点一 垂径定理及其推论
C
知识点一 垂径定理及其推论
通过本节课的学习,我们就会很容易解决这一问题.
探究:1.圆是轴对称图形吗?如果是,它的对称轴是什 么?你能找到多少条对称轴?
分析讨论:圆是轴对称图形,它的对称轴是直径,我能找到 无数多条直径.
探究: 2.你是用什么方法解决上述问题的?与同伴进行 交流.
分析讨论我:是利用沿着圆的任意一条直径折叠的方法解决 圆的对称轴问题的.
.2垂直于弦的直径
判断:
(1)直径是弦.( √ )
(2)弦是直径. ( × )
垂直于弦的直径课件(共21张PPT)

C E A
O
D
B
三 垂径定理的有关计算 例2 如图,⊙ O的弦AB=8cm ,直径CE⊥AB于
D,DC=2cm,求半径OC的长.
解:连接OA,∵ CE⊥AB于D, ∴
1 1 AD AB 8 4 (cm) 2 2
E
方程思想
A
D C
Hale Waihona Puke O ·设OC=xcm,则OD=x-2,根据 勾股定理,得 x2=42+(x-2)2, 解得 x=5, 即半径OC的长为5cm.
试一试:根据刚刚所学,你能利用垂径定理求出引入 中赵州桥主桥拱半径的问题吗?
7.23米
37米
解:如图,用AB表示主桥拱,设 AB所在圆的圆心为O,半径为R. 经过圆心O作弦AB的垂线OC 垂足为D,与弧AB交于点C, 则D是AB的中点,C是弧AB的 中点,CD就是拱高. ∴ AB=37m,CD=7.23m.
C B O A
D
定理及推论,总结: 一条直线只需满足: (1)过圆心 (2)垂直于弦 (3)平分弦 (4)平分弦所对的优弧 (5)平分弦所对的劣弧 上述条件中的任意两个条件,就能推 出其它三个.
五 学以致用
例2 赵州桥(图24.1-7)是我国隋代建造白石拱桥,距今 约有1 400年的历史,是我国古代人民勤劳与智慧的结晶.它 的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37 m,拱高 (弧的中点到弦的距离)为7.23 m,求赵州桥主桥拱的半径(结果 保留小数点后一位).
一 三 垂径定理的有关计算 例1 如图,OE⊥AB于E,若⊙O的 半径 AB 为10cm, 16 61 cm. OE=6cm,则 半径为 AB=
A
E
B
解析:连接OA, ∵ OE⊥AB, ∴∠AEO=90°,AB=2AE
人教版数学九年级 24.1.2_垂直于弦的直径 (共20张PPT)
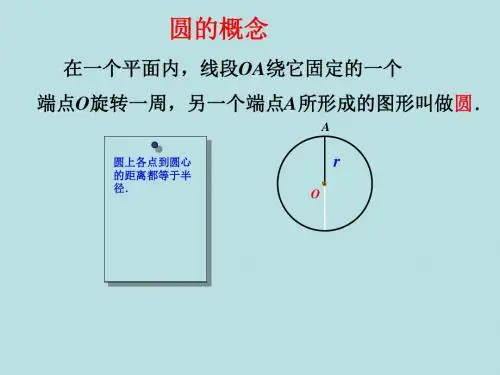
C
A r
D
B O
例2 如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是 弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD 垂足为F,EF=90m.求这段弯路的半径.
解:连接OC.
设弯路的半径为 Rm, 则OF ( R 90)m. OE CD, 1 1 CF CD 600 300 (m). 2 2 2 2 2 OC CF OF ,即 根据勾股定理 ,得
船能过拱桥吗
解:如图,用 AB 表示桥拱, AB所在圆的圆心为O,半径为Rm, 经过圆心O作弦AB的垂线OD,D为垂足,与 AB 相交于点C.根 据垂径定理,D是AB的中点,C是 AB 的中点,CD就是拱高. 由题设得 1
AB 7.2, CD 2.4, HN MN 1.5. 2 1 1 AD AB 7.2 3.6, 2 2 OD OC DC R 2.4.
2 2
1.过⊙o内一点M的最长的弦长为10㎝,最短弦长为8 ㎝,那么⊙o的半径是 5㎝ 2.已知⊙o的弦AB=6㎝,直径CD=10㎝,且AB⊥CD, 1㎝或9㎝ 那么C到AB的距离等于 3.已知⊙O的弦AB=4㎝,圆心O到AB的中点C的距离为1 ㎝,那么⊙O的半径为 5 Cm
4.如图,在⊙O中弦AB⊥AC,
E
B
A
M
B
(3).如图,有一圆弧形桥拱,拱形的半径为10米, 桥拱的跨度AB=16米,则拱高为 4 米。
C
A
·
O
D
B
船能过拱桥吗?
例3.如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水 面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的 货船要经过这里,此货船能顺利通过这座拱桥吗?
人教版数学九级上册 2412垂直于弦的直径(共21张PPT)

如图,P为⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径.
O
C.
(绍兴·中考)已知⊙O的半径为5,弦AB的弦心距为3,则AB的长是( )
C D C D 2、什么是垂径定理?它的推论是什么? A A 理解圆的轴对称性及垂径定理及其它的推证过程;
C
2.掌握垂径定理的推论,明确理解“知二推三”
AD=BC AC=BD
O O
【证明猜想】
垂径定理
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E.
求证:AE=BE,
AC=BC,AD=BD.
垂径定理 垂直于弦的直径平分 弦,并且平分弦所对的两条弧.
【定理辨析】
判断下列图形,能否使用垂径定理?
圆的两条平行弦所夹的弧相等.
B 延长AO交BC于点D,连接OB,
2、什么是垂径定理?它的推论是什么?
B
B
(绍兴·中考)已知⊙O的半径为5,弦AB的弦心距为3,则AB的长是( )
AO=BO=CO=DO,
1、结合81探究,同学们动手操作,你发现了什么?你得到什么结论?你会证明你的结论吗?
O O O 1、结合81探究,同学们动手操作,你发现了什么?你得到什么结论?你会证明你的结论吗?
• 学习难点:垂径定理及其推论。
自学指导
• 认真看书81-83页,独立完成以下问题,看 谁做得又对又快? 理解圆的轴对称性及垂径定理及其它的推证过程;
AE-CE=BE-DE. 1、结合81探究,同学们动手操作,你发现了什么?你得到什么结论?你会证明你的结论吗? 能初步应用垂径定理进行计算和证明. (安徽·中考)如图,⊙O过点B,C. 能初步应用垂径定理进行计算和证明.
结论吗? 如图,CD为⊙O的直径,AB⊥CD,EF⊥CD,你能得到什么结论?
O
C.
(绍兴·中考)已知⊙O的半径为5,弦AB的弦心距为3,则AB的长是( )
C D C D 2、什么是垂径定理?它的推论是什么? A A 理解圆的轴对称性及垂径定理及其它的推证过程;
C
2.掌握垂径定理的推论,明确理解“知二推三”
AD=BC AC=BD
O O
【证明猜想】
垂径定理
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E.
求证:AE=BE,
AC=BC,AD=BD.
垂径定理 垂直于弦的直径平分 弦,并且平分弦所对的两条弧.
【定理辨析】
判断下列图形,能否使用垂径定理?
圆的两条平行弦所夹的弧相等.
B 延长AO交BC于点D,连接OB,
2、什么是垂径定理?它的推论是什么?
B
B
(绍兴·中考)已知⊙O的半径为5,弦AB的弦心距为3,则AB的长是( )
AO=BO=CO=DO,
1、结合81探究,同学们动手操作,你发现了什么?你得到什么结论?你会证明你的结论吗?
O O O 1、结合81探究,同学们动手操作,你发现了什么?你得到什么结论?你会证明你的结论吗?
• 学习难点:垂径定理及其推论。
自学指导
• 认真看书81-83页,独立完成以下问题,看 谁做得又对又快? 理解圆的轴对称性及垂径定理及其它的推证过程;
AE-CE=BE-DE. 1、结合81探究,同学们动手操作,你发现了什么?你得到什么结论?你会证明你的结论吗? 能初步应用垂径定理进行计算和证明. (安徽·中考)如图,⊙O过点B,C. 能初步应用垂径定理进行计算和证明.
结论吗? 如图,CD为⊙O的直径,AB⊥CD,EF⊥CD,你能得到什么结论?
24.1.2垂直于弦的直径.PPT教学课件

(3)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
只要具备上述五个条件中任两个,就可以推出其余三个14.
练习 1.如图所示:
C
A M└
B
(1)若CD⊥AB, CD是直径,
●O
则 AM=BM 、A⌒D=B⌒D
⌒⌒ 、 AC=BC
.
(2)若AM=MB, CD是直径,
D
则 CD⊥AB 、 A⌒D=B⌒D 、A⌒C=B⌒C .
垂径定理的几个基本图形:
C
O
A
E
BA
D
CD过圆心 CD⊥AB于E
A
O
D
B
D
B
O
A
C
C
AE=BE
AC= BC AD= BD
O
C
B
17
1、如图,AB是⊙O的直径,CD为弦, CD⊥AB于E,则下列结论中不成C 立的是( )
A、∠COE=∠DOE B、CE=DE C、OE=AE
⌒⌒
D、BD=BC
A
C
D
C
·O
AE D
知二推三
∵ CD是直径, CD⊥AB ∴ AE=BE,A⌒C ⌒ A⌒D ⌒ =BC, =BD.
• 老师提示:
B • 垂径定理是圆中一个重要的定理
,三种语言要相互转化,形成整体,
才能运用自如.
9
问题 & 探究3 问题:把垂径定理中的题设垂直于弦的 直径换为平分弦的直径。你会得到什么结论?
• 学习难点:垂径定理及其推论。
3
自学指导
• 认真看书81-83页,独立完成以下问题,看 谁做得又对又快?
• 1、结合81探究,同学们动手操作,你发现 了什么?你得到什么结论?你会证明你的 结论吗?
