大学物理课后习题答案 稳恒磁场
大学物理稳恒磁场习题及答案 (1)

衡水学院 理工科专业 《大学物理B 》 稳恒磁场 习题解答一、填空题(每空1分)1、电流密度矢量的定义式为:dI j n dS ⊥=v v,单位是:安培每平方米(A/m 2) 。
2、真空中有一载有稳恒电流I 的细线圈,则通过包围该线圈的封闭曲面S 的磁通量? = 0 .若通过S 面上某面元d Sv的元磁通为d ?,而线圈中的电流增加为2I 时,通过同一面元的元磁通为d ?',则d ?∶d ?'= 1:2 。
3、一弯曲的载流导线在同一平面内,形状如图1(O 点是半径为R 1和R 2的两个半圆弧的共同圆心,电流自无穷远来到无穷远去),则O 点磁感强度的大小是2020100444R IR IR IB πμμμ-+=。
4、一磁场的磁感强度为k c j b i a B ϖϖϖϖ++= (SI),则通过一半径为R ,开口向z 轴正方向的半球壳表面的磁通量的大小为πR 2c Wb 。
5、如图2所示通有电流I 的两根长直导线旁绕有三种环路;在每种情况下,等于:对环路a :d B l ⋅⎰v v Ñ=____μ0I __;对环路b :d B l ⋅⎰vv Ñ=___0____; 对环路c :d B l ⋅⎰v v Ñ =__2μ0I __。
6、两个带电粒子,以相同的速度垂直磁感线飞入匀强磁场,它们的质量之比是1∶4,电荷之比是1∶2,它们所受的磁场力之比是___1∶2__,运动轨迹半径之比是_____1∶2_____。
二、单项选择题(每小题2分)( B )1、均匀磁场的磁感强度B v垂直于半径为r 的圆面.今以该圆周为边线,作一半球面S ,则通过S 面的磁通量的大小为A. 2?r 2BB.??r 2BC. 0D. 无法确定的量( C )2、有一个圆形回路1及一个正方形回路2,圆直径和正方形的边长相等,二者中通有大小相等的电流,它们在各自中心产生的磁感强度的大小之比B 1 / B 2为A. B. C. D.( D )3、如图3所示,电流从a 点分两路通过对称的圆环形分路,汇合于b 点.若ca 、bd 都沿环的径向,则在环形分路的环心处的磁感强度A. 方向垂直环形分路所在平面且指向纸内B. 方向垂直环形分路所在平面且指向纸外C .方向在环形分路所在平面内,且指向aD .为零( D )4、在真空中有一根半径为R 的半圆形细导线,流过的电流为I ,则圆心处的磁感强度为A.R 140πμ B. R120πμ C .0 D .R140μ ( C )5、如图4,边长为a 的正方形的四个角上固定有四个电荷均为q 的点电荷.此正方形以角速度??绕AC 轴旋转时,在中心O 点产生的磁感强度大小为B 1;此正方形同样以角速度??绕过O 点垂直于正方形平面的轴旋转时,在O 点产生的磁感强度的大小为B 2,则B 1与B 2间的关系为A. B 1 = B 2B. B 1 = 2B 2 C .B 1 =21B 2 D .B 1 = B 2 /4 ( B )6、有一半径为R 的单匝圆线圈,通以电流I ,若将该导线弯成匝数N = 2的平面圆线圈,导线长度不变,并通以同样的电流,则线圈中心的磁感强度和线圈的磁矩分别是原来的 (A) 4倍和1/8. (B) 4倍和1/2. (C) 2倍和1/4. (D) 2倍和1/2. 三、判断题(每小题1分,请在括号里打上√或×)( × )1、电源的电动势是将负电荷从电源的负极通过电源内部移到电源正极时,非静电力作的功。
大学物理第六章稳恒磁场习题参考答案

第六章稳恒磁场作业集第37讲毕奥-萨伐儿定律一、Ⅰ类作业:解:根据毕奥萨伐尔定律20sin d 4d r l I B θπμ=,方向由右手定则决定。
(1)202020d 490sin d 4sin d 4d L l I L l I r l I B πμπμθπμ=︒==方向垂直纸面向里(沿z 轴负向)。
(2)00sin d 4sin d 4d 2020=︒==L l I r l I B πμθπμ(3)202020d 490sin d 4sin d 4d L l I L l I r l I B πμπμθπμ=︒==,方向沿x 轴正向。
(4)因为2245sin sin ,2222=︒==+=θL L L r ,所以2020d 82sin d 4d Ll I r l I B πμθπμ==,方向垂直纸面向里(沿z 轴负向)。
37.2教材223页第6.2、6.4、6.6题解:(1)6.2:(2)6.4:(3)6.6:二、Ⅱ类作业:解:根据磁场叠加原理可知,中心点O 的磁感应强度是两根半无限长载流导线的B 和41载流圆弧的B 的矢量和。
即321B B B B ++=其中,半无限长载流导线在其延长线上的031==B B ,41载流圆弧的R I B 802μ=,方向垂直纸面向外。
所以RI B B 802μ==,方向垂直纸面向外第38讲磁场的性质一、Ⅰ类作业:38.1一块孤立的条形磁铁的磁感应线如图所示,其中的一条磁感线用L 标出,它的一部分在磁铁里面,你能根据安培环路定理判断磁铁里面是否有电流吗?如果有穿过L 的电流方向是怎样的?解:因为磁感应强度沿L 的线积分不为零,即环量不为零,根据安培环路定理,有电流穿过环路L 。
根据右手定则,电流是垂直纸面向里。
38.2教材229页6.7、6.9题二、Ⅱ类作业:38.3如图所示,有一根很长的同轴电缆,由两层厚度不计的共轴圆筒组成,内筒的半径为1r 1,外筒的半径为r 2,在这两导体中,载有大小相等而方向相反的电流I ,计算空间各点的磁感应强度.解:该电流产生的磁场具有轴对称性,可用安培环路定理计算磁感应强度。
河北科技大学大学物理答案稳恒磁场
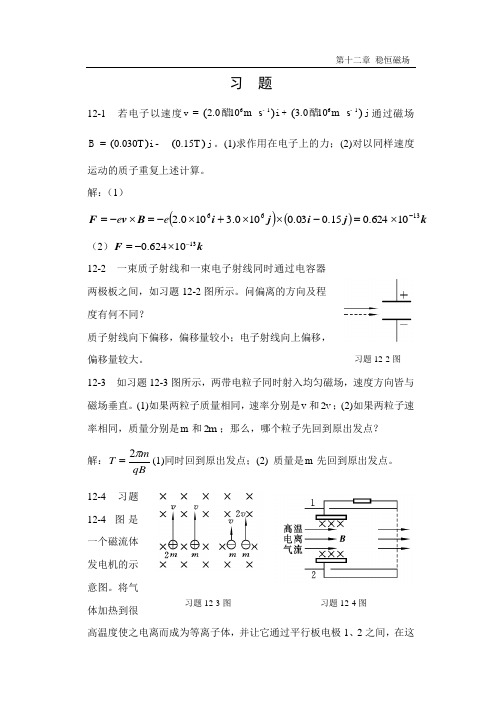
习 题12-1 若电子以速度()()616120103010.m s .m s --=醋+醋v i j 通过磁场()0030.T =-B i ()015.T j 。
(1)求作用在电子上的力;(2)对以同样速度运动的质子重复上述计算。
解:(1)()()kj i j i B v F 136610624.015.003.0100.3100.2-⨯=-⨯⨯+⨯-=⨯-=e e (2)k F 1310624.0-⨯-=12-2 一束质子射线和一束电子射线同时通过电容器两极板之间,如习题12-2图所示。
问偏离的方向及程度有何不同?质子射线向下偏移,偏移量较小;电子射线向上偏移,偏移量较大。
12-3 如习题12-3图所示,两带电粒子同时射入均匀磁场,速度方向皆与磁场垂直。
(1)如果两粒子质量相同,速率分别是v 和2v ;(2)如果两粒子速率相同,质量分别是m 和2m ;那么,哪个粒子先回到原出发点? 解:qBmT π2=(1)同时回到原出发点;(2) 质量是m 先回到原出发点。
12-4 习题12-4 图是一个磁流体发电机的示意图。
将气体加热到很高温度使之电离而成为等离子体,并让它通过平行板电极1、2之间,在这习题12-2图习题12-3图习题12-4图里有一垂直于纸面向里的磁场B 。
试说明这两极之间会产生一个大小为vBd 的电压(v 为气体流速,d 为电极间距)。
问哪个电极是正极? 解:qE qvB =,vB E =,vBd Ed U ==,电极1是正极。
12-5 一电子以713010.m s v -=醋的速率射入匀强磁场内,其速度方向与B 垂直,10T B =。
已知电子电荷191610.C e --=-?。
质量319110.kg m -=?,求这些电子所受到的洛仑兹力,并与其在地面上所受重力进行比较。
解:11719108.410100.3106.1--⨯=⨯⨯⨯⨯==evB F N ,3031109.88.9101.9--⨯=⨯⨯==g m G e N18104.5⨯=GF12-6 已知磁场B 的大小为04.T ,方向在xy 平面内,并与y 轴成3p 角。
大学物理(第四版)课后习题及答案磁场
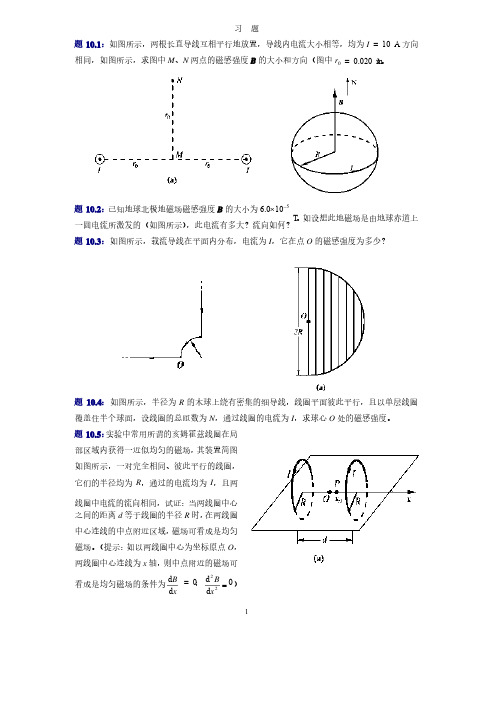
1 习题题10.1:如图所示,两根长直导线互相平行地放置,导线内电流大小相等,均为I = 10 A ,方向,方向相同,如图所示,求图中M 、N 两点的磁感强度B 的大小和方向(图中r 0 = 0.020 m )。
题10.2:已知地球北极地磁场磁感强度B 的大小为6.0´10-5 T 。
如设想此地磁场是由地球赤道上一圆电流所激发的(如图所示),此电流有多大?流向如何?题10.3:如图所示,载流导线在平面内分布,电流为I ,它在点O 的磁感强度为多少?题10.4:如图所示,半径为R 的木球上绕有密集的细导线,线圈平面彼此平行,且以单层线圈覆盖住半个球面,设线圈的总匝数为N ,通过线圈的电流为I ,求球心O 处的磁感强度。
题10.5:实验中常用所谓的亥姆霍兹线圈在局部区域内获得一近似均匀的磁场,其装置简图如图所示,一对完全相同、彼此平行的线圈,它们的半径均为R ,通过的电流均为I ,且两线圈中电流的流向相同,试证:当两线圈中心之间的距离d 等于线圈的半径R 时,在两线圈中心连线的中点附近区域,磁场可看成是均匀磁场。
(提示:如以两线圈中心为坐标原点O ,两线圈中心连线为x 轴,则中点附近的磁场可看成是均匀磁场的条件为x B d d = 0;0d d 22=x B )题10.6:如图所示,载流长直导线的电流为I ,试求通过矩形面积的磁通量。
,试求通过矩形面积的磁通量。
题10.7:如图所示,在磁感强度为B 的均匀磁场中,有一半径为R 的半球面,B 与半球面轴线的夹角为a ,求通过该半球面的磁通量。
,求通过该半球面的磁通量。
题10.8:已知10 10 mmmm 2裸铜线允许通过50 50 A A 电流而不会使导线过热。
电流在导线横截面上均匀分布。
求:(1)导线内、外磁感强度的分布;(2)导线表面的磁感强度。
)导线表面的磁感强度。
题10.9:有一同轴电缆,其尺寸如图所示,两导体中的电流均为I ,但电流的流向相反,导体的磁性可不考虑。
《大学物理》习题册题目及答案第12单元稳恒电流的磁场

第12单元 稳恒电流的磁场 第七章 静电场和恒定磁场的性质(三)磁感应强度序号序号 学号学号 姓名姓名 专业、班级专业、班级一 选择题[ C ]1.一磁场的磁感应强度为B ai bj ck =++(T ),则通过一半径为R ,开口向z 正方向的半球壳表面的磁通量的大小是:向的半球壳表面的磁通量的大小是: (A) Wb 2a R p(B) Wb 2b R p (C) Wb 2c R p (D) Wb 2abc R p[ B ]2. ]2. 若要使半径为若要使半径为4×103-m 的裸铜线表面的磁感应强度为7.07.0××105- T T,则铜线中需,则铜线中需要通过的电流为要通过的电流为((μ0=4π×107-T ·m ·A 1-)(A) 0.14A (B) 1.4A (C) 14A (D) 28A[ B ]3. [ B ]3. 一载有电流一载有电流I 的细导线分别均匀密绕在半径为R 和r 的长直圆筒上形成两个螺线管(R=2r)(R=2r),,两螺线管单位长度上的匝数相等,两螺线管中的磁感应强度大小R B 和r B 应满足: (A) R B =2r B(B) R B =rB (C) 2R B =r B (D) R B R=4r B[ D ]4.如图,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感应强度B 沿图中闭合路径L 的积分l B d ×ò等于等于(A)I 0m(B)I 031m (C) I041m(D)I032m[ D ]5. [ D ]5. 有一由有一由N 匝细导线绕成的平面正三角形线圈,边长为a ,通有电流I ,置于均匀外磁场外磁场 B 中,当线圈平面的法向与外磁场同向时,该线圈所受的磁力矩mM(A) 2/32IB Na (B) 4/32IB Na (C) 0260sin 3IB Na (D) 0abcdI L1201I 2I 1R 2R二 填空题1.1.一无限长载流直导线,通有电流一无限长载流直导线,通有电流I ,弯成如图形状,设各线段皆在纸面内,则P 点磁感应强度强度 B B 的大小为aIp m 830。
《大学物理学》习题解答(第13章 稳恒磁场)(1)

【13.1】如题图所示的几种载流导线,在 O 点的磁感强度各为多少?
(a)
(b) 习题 13-1 图
(c)
【13.1 解】 (a) B 0
I 1 0 I 0 0 ,方向朝里。 4 2R 8R 0 I 。 2R
(b) B
0 I
2R
(c) B
mv eB
2mE k eB
6.71 m 和 轨 迹 可 得 其 向 东 偏 转 距 离 为
x R R 2 y 2 2.98 10 3 m
【13.17 解】利用霍耳元件可以测量磁感强度,设一霍耳元件用金属材料制成,其厚度为 0.15 mm,载流 - 子数密度为 1024m 3,将霍耳元件放入待测磁场中,测得霍耳电压为 42μV,通过电流为 10 mA。求待测磁 场的磁感强度。 【13.17 解】由霍耳电压的公式可得 B
B 4
2 0 I 0 I 。 (cos 45 cos135) 4a a
习题 13-2 图
习题 13-3 图
【13.3】以同样的导线联接成如图所示的立方形,在相对的两顶点 A 及 C 上接一电源。试求立方形中心的 磁感强度 B 等于多少? 【13.3 解】由对称性可知,相对的两条棱在立方体中心产生的磁感强度相等而方向相反,故中心处的磁感 强度为零。 【13.4】如图所示,半径为 R 的半球上密绕有单层线圈,线圈平面彼此平行。设线圈的总匝数为 N,通过 线圈的电流为 I,求球心处 O 的磁感强度。 【13.4 解】在半球上距球心 y 处取一个宽度为 Rdθ 的园环,其对球心的张角为 θ,半径为 r=Rsinθ,包含 的电流为 dI
2rB 0, 2rB 0 NI , 2rB 0,
《大学物理》课后解答题 第七章稳恒磁场

第7章 稳恒磁场一、思考讨论题1、如图4.1所示的电流元Idl 是否在空间所有点的磁感应强度均不为零?请你指出Idl在a 、b 、c 、d 四点产生的磁感应强度的方向。
解:不是,电流元Idl在自身产生的磁感应强度为零。
a 、垂直纸面向外b 、垂直纸面向外c 、垂直纸面向内d 、垂直纸面向内2、分别求图4.2中的三种情况下,通有电流I 的直线电流在图中点产生磁感应强度B 的大小和方向。
解:a 图,()a I cos cos a I B πμπμ823145304--=-=方向垂直纸面向内 b 图,()aIcos cos a I B πμπμ82345604--=-= 方向垂直纸面向内 c 图() 30041cos cos a I B -=πμ () 1806030402cos cos tan c a I B -=πμ aIB B B πμ41312-=-= 方向垂直纸面向内3、电流分布如图4.3所示,分别求出各图中O 点的磁感应强度O B的大小和方向。
图4.1图4.2a图4.2ba图4.2c1 R 3解:a 图, 321B B B B ++=()30060431cos cos cos R IB B -==πμ23601202a I B μ=方向垂直纸面向内b 图, 01=B ,RIR I B 126122μμ==,()2322180150243-=-⋅=R I cos cos R I B πμπμ所以,⎪⎪⎭⎫⎝⎛-+=R R I B πμ432121 方向垂直纸面向内 c 图,RIR I B 834321μμ==,052==B B R I B B πμ16243==,所以,⎪⎪⎭⎫ ⎝⎛+=πμ238R I B 方向垂直纸面向外 4、若空间中存在两根无限长直载流导线,则磁场的分布就不存在简单的对称性,因此:(A )安培环路定理已不成立,故不能直接用此定理计算磁场分布。
(B )安培环路定理仍然成立,故仍可直接用此定理计算磁场分布。
大学物理学下册答案第11章-大学物理11章答案
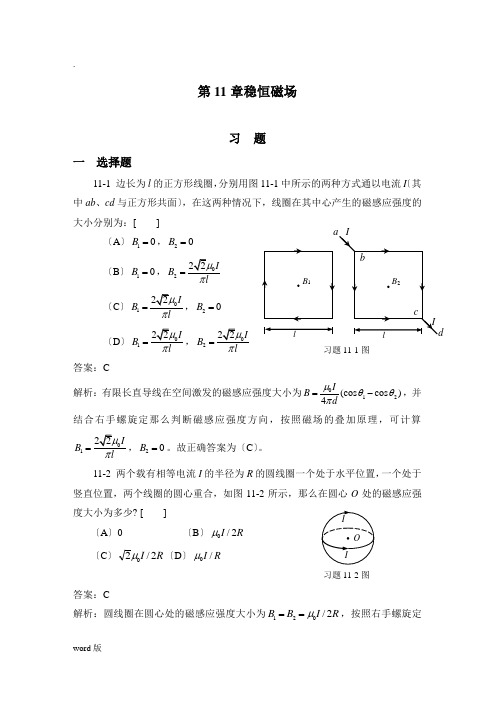
第11章稳恒磁场习 题一 选择题11-1 边长为l 的正方形线圈,分别用图11-1中所示的两种方式通以电流I 〔其中ab 、cd 与正方形共面〕,在这两种情况下,线圈在其中心产生的磁感应强度的大小分别为:[ ]〔A 〕10B =,20B = 〔B 〕10B =,02IB lπ= 〔C〕01IB lπ=,20B = 〔D〕01I B l π=,02IB lπ=答案:C解析:有限长直导线在空间激发的磁感应强度大小为012(cos cos )4IB dμθθπ=-,并结合右手螺旋定那么判断磁感应强度方向,按照磁场的叠加原理,可计算01IB lπ=,20B =。
故正确答案为〔C 〕。
11-2 两个载有相等电流I 的半径为R 的圆线圈一个处于水平位置,一个处于竖直位置,两个线圈的圆心重合,如图11-2所示,那么在圆心O 处的磁感应强度大小为多少? [ ]〔A 〕0 〔B 〕R I 2/0μ〔C 〕R I 2/20μ〔D 〕R I /0μ 答案:C解析:圆线圈在圆心处的磁感应强度大小为120/2B B I R μ==,按照右手螺旋定习题11-1图习题11-2图那么判断知1B 和2B 的方向相互垂直,依照磁场的矢量叠加原理,计算可得圆心O处的磁感应强度大小为0/2B I R =。
11-3 如图11-3所示,在均匀磁场B 中,有一个半径为R 的半球面S ,S 边线所在平面的单位法线矢量n 与磁感应强度B 的夹角为α,那么通过该半球面的磁通量的大小为[ ]〔A 〕B R 2π〔B 〕B R 22π〔C 〕2cos R B πα〔D 〕2sin R B πα 答案:C解析:通过半球面的磁感应线线必通过底面,因此2cos m B S R B παΦ=⋅=。
故正确答案为〔C 〕。
11-4 如图11-4所示,在无限长载流直导线附近作一球形闭合曲面S ,当曲面S 向长直导线靠近时,穿过曲面S 的磁通量ΦB 将如何变化?[]〔A 〕Φ增大,B 也增大〔B 〕Φ不变,B 也不变 〔C 〕Φ增大,B 不变〔D 〕Φ不变,B 增大 答案:D解析:根据磁场的高斯定理0SBdS Φ==⎰,通过闭合曲面S 的磁感应强度始终为0,保持不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一章 稳恒磁场 1、[E]依据()θπμθRIB 40=和载流导线在沿线上任一点的0=B 得出答案。
2、[E]依据rIB πμ40=和磁感强度的方向和电流的方向满足右手法则,得出答案。
3、[C]依据()210cos cos 4θθπμ-=RIB 和载流导线在沿线上任一点的0=B , 有:()[]445180cos 45cos 2401⨯--=lIB πμ; πμμπl I I l 00222222=⋅⨯,02=B 4、[D]依据()RIR I R I B 444000μππμθπμθ=⨯== 5、[C]rI B πμ40=、 2a r =、 4000108.0245sin 122-⨯==⨯⨯=a I aI B πμπμT 6、[D]依据()2100cos cos 4θθπμ-=r IB ,应用21I I I +=,分别求出各段直导线电流的磁感强度,可知03=B 、方向相反,∴0≠B7、[D]注意分流,和对L 回路是I 的正负分析得结论。
8、[B]洛伦兹力的方向向上,故从y 轴上方射出,qBm v R =,轨迹的中心在qB m v y =处故I I射出点:qBm vR y 22== 9、[B] 作出具体分析图是解决该题的关键。
从图上看出:D R =αsinqB DqB m v R ==peBDp qBD ==αsinpeBDsinarg =α 10、[D]载流线圈在磁场中向磁通量增加的方向移动。
当线圈在该状态时,磁通量已达最大,不可能通过转动来增加磁通量,因此不发生转动,而线圈靠近导线AB 磁通量增大。
应用安培力来进行分析:向左的磁力比向右的磁力大,因此想左靠近。
11、[B]载流线圈在磁场中向磁通量增加的方向转动或移动,该题中移动不能增加磁通量,则发生转动,从上向下看线圈作顺时针方向转动,结果线圈相当一个条形磁铁,右侧呈现S 级,因此靠近磁铁。
12、[D] B P M m ⨯=,αsin B P M m =, m P和B 平行,∴ 0=α,0sin =α,0=M13、[C]应用rIB πμ20=的公式分别计算出电流系统在各导线上代表点处的B ,然后用安培力的公式:B l I F⨯=d d 计算出1F ,2F用r 表示导线间的距离。
r Ir I r I B πμπμπμ4743220001=+=r I r I r I B πμπμπμ0002232=+-=111B I F =,222B I F =,2:47:21=F F ,2187F F = 14、[C]在均匀磁场中,线圈回路中的磁矩m P将向外磁场的愤怒感想旋转以增加其磁通量,通过直观分析,回路将逆时针转动。
15、r rIar Ba S B d 2d d d 0πμφ==⋅=2ln 2d 2d 020πμπμφφIar r Ia b b ⎰⎰===16、应用磁场的高斯定理0d =⋅⎰SS B0d d d )(=⋅+⋅=⋅⎰⎰⎰R S SSS B S B S B2)(2160cos d d d R B BS S B S B S B R S S π-=-=⋅-=⋅-=⋅⎰⎰ 17、应用()θπμθrIB 40=,和载流导线在其沿线上0=B ,对a 半圆弧,∴⎪⎭⎫⎝⎛+=b a I B 1140μ, 依据B 和I 的右旋法则,B方向⊗。
18、依据∑⎰=⋅i lI l B 0d μ,对电流i I 的取正、负的规定有:I l B a0d μ=⋅⎰ ,0d =⋅⎰bl B,I l B c02d μ=⋅⎰19、轨道电流:q R vnq I π2==,()=====200004224Rvq R v R I R I B πμμμθπμθ ()T ⨯=⨯⨯⨯⨯=⨯⨯⨯⨯⨯⨯⨯=-------6167142819571067.6103610100.80.3100.64100.8100.3104ππ 221198521020.710810610321212m A R q v R R q v S I p m ⋅⨯=⨯⨯⨯⨯⨯⨯=⋅⋅=⨯⋅=⋅=---ππ20、VBq m V 0VBq mV R mV VB q 0221==21、r rbI r Bb S B d 2d d d 0πμφ==⋅=2ln 2d 2d 0201πμπμφφIbr r Ib a a ⎰⎰=== 2ln 2d 2d 04202πμπμφφIbr r Ib a a ⎰⎰===∴1:1:21=φφ 22、应用回旋半径公式: 2l qB m v R ==作出粒子的运动轨迹,由运动轨迹讨论射出点与顶点的距离D ,从直角三角形可得:l D 23= 作辅助线后,从几何图形得:60=α23、()222m A 25.1115.05100⋅=⨯⨯===nIa nIS P24、在图上作适量ab l ,B l I F F⨯==ab ab ab 。
BIR B l I F 2ab ab ==方向由(B l ⨯ab )的方向决定,沿Y 轴正方向。
25、依据rIB πμ20=和B 和I 满足右旋法则,B = 0的区域在Ⅰ,Ⅲ象限,在第Ⅰ象限取一 代表点(x ,y ),y I x I πμπμ22300=∴x x y 3331== 26、将载流导线分成如图4个部分,应用载流导线在沿线上任一点B = 0,θπμθRIB 4)(0=和)cos (cos 42100θθπμ-=r IB 可知: 041==B B ,RIR I R I B 82440002μππμθπμ=⨯==,方向⊗。
R r 220=, 45cos cos 1=θ()45cos 45cos cos 2-=-=πθ RI R I r I B πμπμθθπμ221222)cos (cos 40021003=⨯=-=⎪⎭⎫⎝⎛+=+=πμ1412032R I B B B ,方向⊗。
27、解:其中四分之三圆环电流在D 处的aIa I B 832434001μππμ=⨯⨯=AB 段在D 处的磁感强度。
2244cos 2cos 4002⋅=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--=b I b I B πμππππμ BC 段在D 处的磁感强度32B B =另一边沿线通过D ,对D 处的磁感强度04=B ,因为方向相同,可知D 处总的B 为⎪⎪⎭⎫⎝⎛+=b a I B 22340ππμ 28、解:如图,将V 型导线的的两根长指导线分别标为1和2,导线1在P 点的磁感强度:aI a I B πμππμ42cos 0cos 4001=⎪⎭⎫ ⎝⎛-=, 方向垂直纸面向内。
⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛-=πθπθπμcos 2cos cos 402a IB ()1sin cos 40+=θθπμa I,方向垂直纸面向外。
P 的B 为()θθθπμcos 1sin cos 4012-+=-=a IB B B ,方向垂直纸面向外。
29、)(ln 20ππωλμ+=abB 21B B 、分别为带电的大半圆线圈和小半圆线圈转动产生的磁感强度,3B 为带电直线段转动时产生的磁感强度。
44,2010111λωμθπμλππω====R I B b nq I 44,2020222λωμθπμλππω====R I B a nq Ird rr dI r dI dB r d r d nq dI πωλμμθπμπωλλπω224,2203030333======abr dr dB B b a ln 220033πωλμπωλμ===⎰⎰yx)(ln 20321ππωλμ+=++=abB B B B 30、2ln 2400πμπμII + 圆柱体内、外的磁感强度的大小为:)(2)(202201R r r I B R r r RIB >=≤=πμπμr rd RIdS B S d B d 201112πμφ==⋅=πμπμφφ42002011Ir rd R I d R ===⎰⎰r d rIdS B S d B d πμφ20222==⋅=2ln 2202022πμπμφφIr r d I d R R ===⎰⎰ 2ln 240021πμπμφφφII +=+=31、解:洛伦兹力:B V F⨯=由于B V⊥∴RV m VB q F e 2==m VBq V m R e 721069.5-⨯==19108.22-⨯==s RVπν 33、分析:此题是通过正确作图来求解的题型,由图可知:45sin )(l R R +=l R )12()12(1+=-=mqBlm qBR V )12(+== 34、解:在导线2上取一线元l d,线元距o 点为l 。
该处的磁感应为:θπμsin 20⋅⋅=l IB方向垂直纸面向里,电流元l IdB l IdF d⨯= 方向如图其大小 dl lI dl B I dF ⋅=⋅⋅=θπμsin 220 该力对O 点的力矩为:dl I dF l dM θπμsin 220=⋅= 任一端单位长度导线所受磁力对O 点的力矩θπμθπμsin 2sin 220120I dl I dM M l l===⎰⎰+35、(1)圆弧AB ︵ 所受的磁力等于通有相同电流的AB →直线所受的磁力。
FAB ︵ N =⋅⋅⋅==283.02B R I F AB方向与AB 直线垂直,与OB 夹角45(2)磁力矩为n S I p m2102-⨯=⋅=π线圈平面与B 成 60角,则m p 与B 成30角,有力矩m B p B p M m m ⋅N ⨯=⋅⋅=⨯=-21057.130sin方向:力矩M 将驱使线圈法线转向与B平行。
36、解:考虑半圆形载流导线所受的安培力2R B I F m 2⋅⋅=列出力的平衡方程式:T R B I 22=⋅⋅故 R B I T ⋅⋅=。
