(新课标)二轮专题复习课件-导数及其应用
合集下载
2018学年高中数学新选修2-2课件：第一章 导数及其应用1.2.2基本初等函数的导数公式及导数的运
返回
1 2
)(1－2x2)′
＝(
1
u
3 2
)·(－4x)＝
1
(1
2
x2
)
3 2
(－4x)
2
2
＝2
x(1
2
x
2
)
3 2
.
解析答案
(4)y＝(2x2－3) 1＋x2.
解 令 y＝uv，u＝2x2－3，v＝ 1＋x2，
令 v＝ w，w＝1＋x2.
v′x＝v′w·w′x＝(
w)′(1＋x2)′＝
1
1
w2
2x
2
返回
题型探究
题型一 导数运算法则的应用
解 y′＝15x5＋23x3′＝15x5′＋23x3′ ＝x4＋2x2. (2)y＝lg x－ex； 解 y′＝(lg x－ex)′＝(lg x)′－(ex)′＝xln110－ex.
重点突破
解析答案
解析答案
(4)y＝x－sin
x 2·cos
x 2.
解
∵y＝x－sin
答案
(3)导数的和(差)运算法则对三个或三个以上的函数求导成立吗？ 答案 导数的和(差)运算法则对三个或三个以上的函数求导仍然成立. 两个函数和(差)的导数运算法则可以推广到有限个函数的情况， 即[f1(x)±f2(x)±f3(x)±…±fn(x)]′＝f′1(x)±f′2(x)±f′3(x)±…±f′n(x).
自主学习 重点突破 自查自纠
知识梳理
知识点一 导数运算法则
自主学习
法则
语言叙述
[f(x)±g(x)]′＝_f_′__(x_)_±__g_′__(_x)__
两个函数的和(或差)的导数，等于这 两个函数的导数的和(或差)
1 2
)(1－2x2)′
＝(
1
u
3 2
)·(－4x)＝
1
(1
2
x2
)
3 2
(－4x)
2
2
＝2
x(1
2
x
2
)
3 2
.
解析答案
(4)y＝(2x2－3) 1＋x2.
解 令 y＝uv，u＝2x2－3，v＝ 1＋x2，
令 v＝ w，w＝1＋x2.
v′x＝v′w·w′x＝(
w)′(1＋x2)′＝
1
1
w2
2x
2
返回
题型探究
题型一 导数运算法则的应用
解 y′＝15x5＋23x3′＝15x5′＋23x3′ ＝x4＋2x2. (2)y＝lg x－ex； 解 y′＝(lg x－ex)′＝(lg x)′－(ex)′＝xln110－ex.
重点突破
解析答案
解析答案
(4)y＝x－sin
x 2·cos
x 2.
解
∵y＝x－sin
答案
(3)导数的和(差)运算法则对三个或三个以上的函数求导成立吗？ 答案 导数的和(差)运算法则对三个或三个以上的函数求导仍然成立. 两个函数和(差)的导数运算法则可以推广到有限个函数的情况， 即[f1(x)±f2(x)±f3(x)±…±fn(x)]′＝f′1(x)±f′2(x)±f′3(x)±…±f′n(x).
自主学习 重点突破 自查自纠
知识梳理
知识点一 导数运算法则
自主学习
法则
语言叙述
[f(x)±g(x)]′＝_f_′__(x_)_±__g_′__(_x)__
两个函数的和(或差)的导数，等于这 两个函数的导数的和(或差)
《导数及其应用》课件(复习课
存在性：在闭区间[a，b]上连续函 数f(x)在[a，b]上必有最大值与最 小值．
求最大（小）值的方法：函数f(x)在闭区间[a，b]上最值求 法：
1. 求出f(x)在(a，b)内的极值； 2. 将函数f(x)的极值与f(a)，f(b)比较，其中较大的一个是最大值，
较小的一个是最小值.
例 6(05 北京 15)已知函数 f x x3 3x2 9x a . （Ⅰ）求 f x 的单调递减区间； （Ⅱ）若 f x 在区间2, 2 上的最大值为 20,求它在该
（II）由（I）知，
f
(x)
3mx2
6(m
1) x
3m
6
= 3m( x
1)
x
1
2 m
当 m 0 时,有1 1 2 ,当 x 变化时, f (x) 与 f (x) 的变化如下表： m
x
,1
2 m
1 2 m
1
2 m
,1
1
1,
f (x)
0
0
f (x)
极小值
极大值
故由上表知,当
m
0 时,
f
解： f/(x)=3x2－ 1，
∴k= f/(1)=2
∴所求的切 线方程为：
y－2=2(x －1),
即 y=2x
例1．已经曲线C：y=x3x+2和点(1,2)求在点A处 的切线方程？
变式1：求过点A的切线方程？
解：变1：设切点为P（x0，x03－x0+2）， k= f/(x0)= 3 x02－1，
∴切线方程为 y－ ( x03－x0+2)=(3 x02－1)(x－x0)
又∵切线过点A(1,2) ∴2－( x03－x0+2)=( 3 x02－1)(1－x0) 化简得(x0－1)2(2 x0+1)=0，
高考数学专题复习《导数的综合应用》PPT课件
3.函数不等式的类型与解法
(1)∀x∈D,f(x)≤k⇔f(x)max≤k;∃x∈D,f(x)≤k⇔f(x)min≤k;
(2)∀x∈D,f(x)≤g(x) ⇔f(x)max≤g(x)min;∃x∈D,f(x)≤g(x) ⇔ f(x)min≤g(x)max.
4.含两个未知数的不等式(函数)问题的常见题型及具体转化策略
(+1)ln
H(x)=
,则
-1
1
=
--2ln
(-1)
2
,
2 -2+1
K'(x)= 2 >0,于是
K(x)在(1,+∞)上单调递增,
所以 K(x)>K(1)=0,于是 H'(x)>0,从而 H(x)在(1,+∞)上单调递增.由洛必达法
(x+1)x
则,可得 lim+
x-1
→1
取值范围是(-∞,2].
第三章
高考大题专项(一) 导数的综合应用
内
容
索
引
01
突破1
利用导数研究与不等式有关的问题
必备知识预案自诊
关键能力学案突破
02
突破2
利用导数研究与函数零点有关的问题
必备知识预案自诊
关键能力学案突破
【考情分析】
从近五年的高考试题来看,对导数在函数中的应用的考查常常是一大一小
两个题目,其中解答题的命题特点是:以三次函数、对数函数、指数函数及
(1)∀x1∈[a,b],x2∈[c,d],f(x1)>g(x2)⇔f(x)在[a,b]上的最小值>g(x)在[c,d]上的
最大值.
(2)∃x1∈[a,b],x2∈[c,d],f(x1)>g(x2)⇔f(x)在[a,b]上的最大值>g(x)在[c,d]上的
(1)∀x∈D,f(x)≤k⇔f(x)max≤k;∃x∈D,f(x)≤k⇔f(x)min≤k;
(2)∀x∈D,f(x)≤g(x) ⇔f(x)max≤g(x)min;∃x∈D,f(x)≤g(x) ⇔ f(x)min≤g(x)max.
4.含两个未知数的不等式(函数)问题的常见题型及具体转化策略
(+1)ln
H(x)=
,则
-1
1
=
--2ln
(-1)
2
,
2 -2+1
K'(x)= 2 >0,于是
K(x)在(1,+∞)上单调递增,
所以 K(x)>K(1)=0,于是 H'(x)>0,从而 H(x)在(1,+∞)上单调递增.由洛必达法
(x+1)x
则,可得 lim+
x-1
→1
取值范围是(-∞,2].
第三章
高考大题专项(一) 导数的综合应用
内
容
索
引
01
突破1
利用导数研究与不等式有关的问题
必备知识预案自诊
关键能力学案突破
02
突破2
利用导数研究与函数零点有关的问题
必备知识预案自诊
关键能力学案突破
【考情分析】
从近五年的高考试题来看,对导数在函数中的应用的考查常常是一大一小
两个题目,其中解答题的命题特点是:以三次函数、对数函数、指数函数及
(1)∀x1∈[a,b],x2∈[c,d],f(x1)>g(x2)⇔f(x)在[a,b]上的最小值>g(x)在[c,d]上的
最大值.
(2)∃x1∈[a,b],x2∈[c,d],f(x1)>g(x2)⇔f(x)在[a,b]上的最大值>g(x)在[c,d]上的
人教A版高中数学选择性必修第二册精品课件 复习课 第2课时 一元函数的导数及其应用
故 f(x)在区间(0,+∞)内单调递增.
②当 Δ=0,即 a=2√2时,仅当 x=√2时,
有f'(x)=0,对其余的x>0都有f'(x)>0.
故函数f(x)在区间(0,+∞)内单调递增.
③当 Δ>0,即 a>2√2时,方程 g(x)=0 有两个不同的实根,
即
-√ 2 -8
+√ 2 -8
f'(x)=0 有两个不同的实根,x1= 2 ,x2= 2 ,0<x1<x2.
1 4
,
4 5
.
反思感悟 1.极值和最值是两个不同的概念,前者是函数的“局部”性质,而
后者是函数的“整体”性质.另函数有极值未必有最值,反之亦然.
2.判断函数“极值”是否存在时,务必把握以下原则:
(1)确定函数f(x)的定义域.
(2)求方程f'(x)=0的根.
(3)检验f'(x)=0的根的两侧f'(x)的符号.
的一个是最大值,最小的一个是最小值.
9.解决实际问题的基本思路
实际问题→用函数表示的数学问题
↓
实际问题的答案←用导数解决数学问题
【思考辨析】
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)函数在闭区间上的极大值就是最大值.( × )
(2)在闭区间[a,b]上连续的函数f(x)必存在最大值与最小值.( √ )
x2
0
极小值
(x2,+∞)
+
单调递增
【例3】
已知函数f(x)=x2+
求a的取值范围.
(x≠0,a∈R),若f(x)在区间[2,+∞)内单调递增,
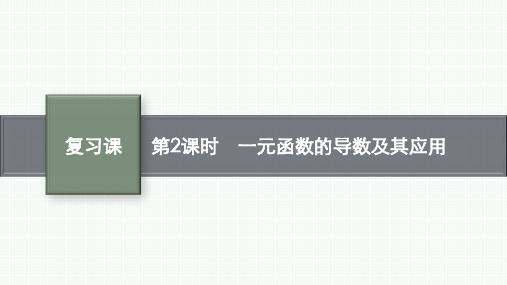
②当 Δ=0,即 a=2√2时,仅当 x=√2时,
有f'(x)=0,对其余的x>0都有f'(x)>0.
故函数f(x)在区间(0,+∞)内单调递增.
③当 Δ>0,即 a>2√2时,方程 g(x)=0 有两个不同的实根,
即
-√ 2 -8
+√ 2 -8
f'(x)=0 有两个不同的实根,x1= 2 ,x2= 2 ,0<x1<x2.
1 4
,
4 5
.
反思感悟 1.极值和最值是两个不同的概念,前者是函数的“局部”性质,而
后者是函数的“整体”性质.另函数有极值未必有最值,反之亦然.
2.判断函数“极值”是否存在时,务必把握以下原则:
(1)确定函数f(x)的定义域.
(2)求方程f'(x)=0的根.
(3)检验f'(x)=0的根的两侧f'(x)的符号.
的一个是最大值,最小的一个是最小值.
9.解决实际问题的基本思路
实际问题→用函数表示的数学问题
↓
实际问题的答案←用导数解决数学问题
【思考辨析】
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)函数在闭区间上的极大值就是最大值.( × )
(2)在闭区间[a,b]上连续的函数f(x)必存在最大值与最小值.( √ )
x2
0
极小值
(x2,+∞)
+
单调递增
【例3】
已知函数f(x)=x2+
求a的取值范围.
(x≠0,a∈R),若f(x)在区间[2,+∞)内单调递增,
高考数学总复习 第二章 函数、导数及其应用 第8讲 幂函数课件 理
【互动探究】
1．已知函数f(x)＝(m2＋2m)·xm2 m1，求当m为何值时， (1)f(x)是幂函数； (2)f(x)是正比例函数； (3)f(x)是反比例函数； (4)f(x)是二次函数．
解：(1)若f(x)为幂函数， 则m2＋2m＝1，∴m＝－1± 2.
(2)若f(x)为正比例函数，则mm22＋ ＋m2m－≠1＝ 0 1， ⇒m＝1. (3)若f(x)为反比例函数，则mm22＋ ＋m2m－≠1＝ 0 －1， ⇒m＝－1.
C.13，12
D.0，13
解析：设
f(x)＝
1 2
x
－
1
x3
，f(0)＝1>0，f13＝
1 2
1
3
－
1 3
1
3
，
1
1
1
由于幂函数
y＝
1
x3
单调递增，得
f13＝
1 2
3
－
1 3
3
>0；f12＝
图 2-8-4
1
1
A．①y＝ x3 ；②y＝x2；③y＝ x2 ；④y＝x－1
1
B．①y＝x3；②y＝x2；③y＝ x2 ；④y＝x－1
1
C．①y＝x2；②y＝x3；③y＝ x2 ；④y＝x－1
1
1
D．①y＝ x3 ；②y＝ x2 ；③y＝x2；④y＝x－1
1
解析：y＝x2 为偶函数，对应②；y＝x 2 定义域 x≥0，对应
即m>12或m<－2， 或－2<m<12，
0<m<2
m>2或m<0，
∴12<m<2或－2<m<0. ∵m∈N*，∴m＝1.此时 f(x)＝x3，x∈R. ∵f(－x)＝(－x)3＝－x3＝－f(x)， ∴函数 f(x)为奇函数． 【规律方法】(1)幂函数 y＝xα的特点： ①系数必须为 1；②指数必须为常数. (2)幂函数的单调性:①α>0 时，y＝xα在(0，＋∞)上为增函 数；②α<0 时，y＝xα在(0，＋∞)上为减函数.
知识讲解_《变化率与导数、导数的应用》全章复习与巩固_基础
《导数及其应用》全章复习与巩固【学习目标】1. 导数概念通过具体情境，感受在现实实际和实际生活中存在着大量的变化率问题，体会平均变化率、瞬时变化率和导数的实际意义，理解导数的几何意义2. 导数运算（1）会用导数定义计算一些简单函数的导数；（2）会利用导数公式表求出给定函数的导数；（3）掌握求导的四则运算法则，掌握求复合函数的导数，并会利用导数的运算法则求出函数的导函数3. 体会研究函数的意义（1 ）认识导数对于研究函数的变化规律的作用；（2）会用导数的符号来判断函数的单调性；（3）会利用导数研究函数的极值点和最值点.4•导数在实际问题中的应用（1）进一步体会函数是描述世界变化规律的基本数学模型；（2）联系实际生活和其他学科，进一步体会导数的意义；（3）从实际生活抽象出一些基本的用导数刻画的问题，并加以解决【知识网络】【要点梳理】要点一：导数的概念及几何意义导数的概念：函数y=f（x）在x0点的导数，通常用符号f ‘X。
）表示，定乂为:一山y 「 f (Xo +^X)—f (Xo )f(x0尸lim ——=lim ------- ----------- ----- ---瘵T0也X 2°氐X要点诠释：(1)丄[_^= _j—X L，它表示当自变量x从x°变X i，函数值从 f x°变到 f X1时，.X X—X°. X函数值关于X的平均变化率•当X趋于0时，如果平均变化率趋于一个固定的值，那么这个值就是函数y=f(x)在X°点的导数.(2)导数的本质就是函数的平均变化率在某点处的极限，即瞬时变化率•如瞬时速度即是位移在这一时刻的瞬间变化率.(3)对于不同的实际问题，平均变化率富于不同的实际意义.如位移运动中，位移S从时间1到t2的平均变化率即为t i到t2这段时间的平均速度.要点诠释：求曲线的切线方程时，抓住切点是解决问题的关键，有切点直接求，无切点则设切点，布列方程组.导数的物理意义：在物理学中，如果物体运动的规律是s=s t ,那么该物体在时刻t0的瞬时速度v就是s=s t在t=t0时的导数，即v=s' t。
2015届高考数学(文)二轮专题课件：1.4导数及其应用
Δx
栏 目 链 接
Δx
主干考 点梳理
2．导数的几何意义． 函数 y＝f(x)在 x0 处的导数 f′(x0)的几何意义是：曲 线 y＝f(x)在点___________处的切线的_____(瞬时速度就 是位移函数 s(t)对时间 t 的导数)．
(x0，f(x0)) 斜率
栏 目 链 接
主干考 点梳理
主干考 点梳理
1 3．函数 y＝4x2＋x的单调递增区间为( B ) A．(0，＋∞) C．(―∞，―1)
1 B.2，＋∞ 1 D.―∞，―2
1 解析：先求函数 y＝4x2＋ 的导数，再由 x 解析： 1 导数大于零解得 x∈2，＋∞.
栏 目 链 接
栏 目 链 接
′(x)＝0 ⇒函数f(x)在这个区间内是常数函数． (3)如果f ________
主干考 点梳理
2．函数的极值与导数的关系．
一般地，对于函数y＝f(x)，
(1)若在点x＝a处有f′(a)＝0，且在点x＝a附近的左侧 ________ ，右侧________ f′(x)＜0 f′(x)＞0，则称x＝a为f(x)的极小值点； f叫函数 (a) ______ f(x)的极小值．
栏 目 链 接
′·ux′ ． 之间的关系为yx′＝yu ________
主干考 点梳理
考点3
导数的应用
1．函数的单调性与导数的关系． 一般地，函数的单调性与其导数的正负有如下关系：
在某个区间(a，b)内，
′(x)＞0 ⇒函数f(x)在这个区间内单调递增． (1)如果f ________ (2)如果_________ f′(x)＜0 ⇒函数f(x)在这个区间内单调递减．
主干考 点梳理
高中总复习二轮数学精品课件 专题一 函数与导数 第2讲 基本初等函数、函数的应用 (2)
象,看其交点的横坐标有几个不同的值,就有几个不同的零点.
(4)形如f(g(x))的函数,可采用换元法,先令g(x)=t,求得当f(t)=0时t的值,然后
根据函数g(x)的图象及性质确定当g(x)=t时x的值的个数即为f(g(x))的零点
的个数,解答时注意数形结合,注意对函数f(x)与g(x)图象及性质的分析.
A.函数f(x)的定义域为R
B.函数f(x)在R上为增函数
C.函数f(x)的值域为(-3,+∞)
D.函数f(x)只有一个零点
)
答案 (1)B (2)AC
解析 (1)由于
1
4
c=log93= ,b=
2
9
1
5
=
2
3
2
5
<
2
3
1
3
=a,又 b=
4
9
1
5
>
1
32
1
5
=
1
,所
2
以 c<b<a.故选 B.
(2)对于选项A,由已知可得函数定义域为R,故A正确;
专题一
第2讲 基本初等函数、函数的应用
内
容
索
引
01
必备知识•精要梳理
02
关键能力•学案突破
必备知识•精要梳理
(1)log
b =logab(a>0,且 a≠1,b>0,m≠0).
n
(2)对数恒等式:lo g =N(a>0,且 a≠1,N>0).
log
(3)换底公式:logaN= log (a,b>0,且 a,b≠1,N>0).
25
(4)形如f(g(x))的函数,可采用换元法,先令g(x)=t,求得当f(t)=0时t的值,然后
根据函数g(x)的图象及性质确定当g(x)=t时x的值的个数即为f(g(x))的零点
的个数,解答时注意数形结合,注意对函数f(x)与g(x)图象及性质的分析.
A.函数f(x)的定义域为R
B.函数f(x)在R上为增函数
C.函数f(x)的值域为(-3,+∞)
D.函数f(x)只有一个零点
)
答案 (1)B (2)AC
解析 (1)由于
1
4
c=log93= ,b=
2
9
1
5
=
2
3
2
5
<
2
3
1
3
=a,又 b=
4
9
1
5
>
1
32
1
5
=
1
,所
2
以 c<b<a.故选 B.
(2)对于选项A,由已知可得函数定义域为R,故A正确;
专题一
第2讲 基本初等函数、函数的应用
内
容
索
引
01
必备知识•精要梳理
02
关键能力•学案突破
必备知识•精要梳理
(1)log
b =logab(a>0,且 a≠1,b>0,m≠0).
n
(2)对数恒等式:lo g =N(a>0,且 a≠1,N>0).
log
(3)换底公式:logaN= log (a,b>0,且 a,b≠1,N>0).
25
导数在函数中的应用课件-2023届高三数学二轮专题复习
只需证 ln x 2x xe2x 1 0
g ' ( x)
0
先证 ex x 1,令g(x) ex x 1, 则g '(x) ex 1,
当x ，0时，g'(x) 0,g(x)在，0上单调递减
当x 0， 时，g'(x) 0,g(x)在0， 上单调递增
g(x)
g(x) g(0) 0,即ex x 1， 当且仅当x=0时取等号. 0
导数中热点问题
二轮专题复习
导数大题是高考的压轴题，考 察内容主要体现在不等式的证 明问题，与函数零点有关的问 题，极值点偏移问题，端点效 应问题等，这些在导数考察中 既是难点，又是热点问题，
一：利用导数中的放缩公式证明不等式
先证 ex x 1,令g(x) ex x 1, 则g '(x) ex 1,
2e2 x
1 x2
0
(x 0)
h(x)在0， 单调递增，又 h(1) e 4 0, h(1) e 2 0
h(x)
4
2
0
x0
1 4
,
1 2
,
使得h(
x0
)
e2x0
1 x0
0 2 x0
ln
x0
x0
当x 0, x0 时，h(x) 0. 即g'(x) 0 g(x)在0, x0 上单调递减 当x x0, 时，h(x) 0,即g'(x) 0 g(x)在 x0， 上单调递增
xe2x eln x2x ln x 2x 1， 当且仅当lnx+2x=0时取等号
令h(x)=lnx+2x, h(1) 0, h(1) 0, e
x0
1 e
,1
,
使得lnx 0
高中数学第二章导数及其应用习题课用导数研究函数的单调性极值最值课件北师大版选择性必修第二册
若a≤0,则f'(x)=ln x-2ax+1>0在x>1时恒成立,从而f(x)在区间(1,+∞)上单调
递增,
所以f(x)>f(1)=0在区间(1,+∞)上恒成立,与已知矛盾,
故a≤0不符合题意.
若a>0,设φ(x)=f'(x)=ln x-2ax+1,x>1,
1
1
则 φ'(x)= -2a,且 ∈(0,1).
(3)注意区分“在区间上恒成立”与“在区间上存在x值使不等式成立”的区别.
分离参数后对应不同的最值类型.
【变式训练1】 已知函数f(x)=x2+aln x.
(1)当a=-2时,求函数f(x)的单调区间;
2
(2)若g(x)=f(x)+ 在[1,+∞)上是单调函数,求实数a的取值范围.
2 2(2 -1)
∴函数f(x)在区间(0,π)上单调递减.
答案:D
).
二、函数的极值、最值与导数
【问题思考】
1.(1)函数的极大值与极小值:
若函数y=f(x)在区间(a,x0)上单调递增,在区间(x0,b)上单调递减,则x0是极大
值点,f(x0)是极大值.
若函数y=f(x)在区间(a,x0)上单调递减,在区间(x0,b)上单调递增,则x0是极小
2 2
则 g'(x)≤0 在[1,+∞)上恒成立,即 a≤ -2x 在[1,+∞)上恒成立.
因为φ(x)没有最小值,不满足题意,
所以实数a的取值范围为[0,+∞).
探究二
用导数求函数的极值、最值
【例2】 已知函数f(x)= 1x2+aln x.
递增,
所以f(x)>f(1)=0在区间(1,+∞)上恒成立,与已知矛盾,
故a≤0不符合题意.
若a>0,设φ(x)=f'(x)=ln x-2ax+1,x>1,
1
1
则 φ'(x)= -2a,且 ∈(0,1).
(3)注意区分“在区间上恒成立”与“在区间上存在x值使不等式成立”的区别.
分离参数后对应不同的最值类型.
【变式训练1】 已知函数f(x)=x2+aln x.
(1)当a=-2时,求函数f(x)的单调区间;
2
(2)若g(x)=f(x)+ 在[1,+∞)上是单调函数,求实数a的取值范围.
2 2(2 -1)
∴函数f(x)在区间(0,π)上单调递减.
答案:D
).
二、函数的极值、最值与导数
【问题思考】
1.(1)函数的极大值与极小值:
若函数y=f(x)在区间(a,x0)上单调递增,在区间(x0,b)上单调递减,则x0是极大
值点,f(x0)是极大值.
若函数y=f(x)在区间(a,x0)上单调递减,在区间(x0,b)上单调递增,则x0是极小
2 2
则 g'(x)≤0 在[1,+∞)上恒成立,即 a≤ -2x 在[1,+∞)上恒成立.
因为φ(x)没有最小值,不满足题意,
所以实数a的取值范围为[0,+∞).
探究二
用导数求函数的极值、最值
【例2】 已知函数f(x)= 1x2+aln x.