机械振动基础作业(有答案-全版)
(完整版)机械振动习题答案

机械振动测验一、填空题1、 所谓振动,广义地讲,指一个物理量在它的①平均值附近不停地经过②极大值和③极小值而往复变化。
2、 一般来说,任何具有④弹性和⑤惯性的力学系统均可能产生机械振动。
3、 XXXX 在机械振动中,把外界对振动系统的激励或作用,①激励或输入;而系统对外界影响的反应,称为振动系统的⑦响应或输出。
4、 常见的振动问题可以分成下面几种基本课题:1、振动设计2、系统识别3、环境预测5、 按激励情况分类,振动分为:①自由振动和②强迫振动;按响应情况分类,振动分为:③简谐振动、④周期振动和⑤瞬态振动。
6、 ①惯性元件、②弹性元件和③阻尼元件是离散振动系统三个最基本的元件。
7、 在系统振动过程中惯性元件储存和释放①动能,弹性元件储存和释放②势能,阻尼元件③耗散振动能量。
8、 如果振动时系统的物理量随时间的变化为简谐函数,称此振动为①简谐振动。
9、 常用的度量振动幅值的参数有:1、峰值2、平均值3、均方值4、均方根值。
10、 系统的固有频率只与系统的①质量和②刚度有关,与系统受到的激励无关。
二、 试证明:对数衰减率也可以用下式表示,式中n x 是经过n 个循环后的振幅。
1ln nx xn δ=三、 求图示振动系统的固有频率和振型。
已知12m m m ==,123k k k k ===。
北京理工大学1996年研究生入学考试理论力学(含振动理论基础)试题自己去查双(二)自由度振动J,在平面上在弹簧k的限制下作纯滚动,如图所示,四、圆筒质量m。
质量惯性矩o求其固有频率。
五、物块M质量为m1。
滑轮A与滚子B的半径相等,可看作质量均为m2、半径均为r的匀质圆盘。
斜面和弹簧的轴线均与水平面夹角为β,弹簧的刚度系数为k。
又m1 g>m2 g sinβ , 滚子B作纯滚动。
试用能量法求:(1)系统的微分方程;(2)系统的振动周期。
六、在下图所示系统中,已知m和k。
计算系统的基频。
机械振动基础课后习题解答_第3章习题
m
0
0 m
u1 u2
3k k
k 3k
u1 u2
2ku0
sin 0
t
K
2M
3k
2m
k
k
3k 2m
H11 ( )
3k 2m ()
H 21 ( )
k ()
u1(t) u2 (t)
H11 ( ) H21()
2ku0
sin
t
3k 为反共振频率 m
P140,3-9: 图示系统初始静止,求左端基础产生阶跃位移u0后系统的响应。
ml2 1 0 M 3 0 7 /16
K
l2k 16
9 9
9
13
| K 2M | 0
1 0.65
k m
2 2.62
k m
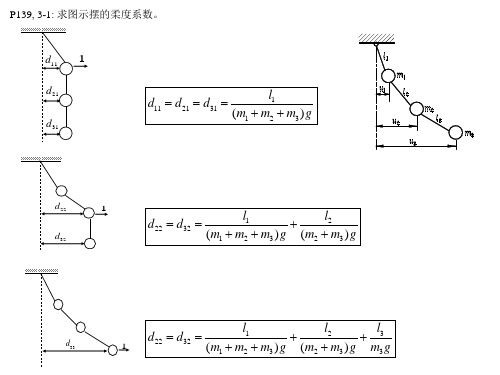
P139,3-3: 建立图示系统的运动微分方程,并求当ki k,i 1, 6, m1 m, m2 2m, m3 m时的固有 频率和固有振型。
m1
M
m2
u2
c
3c
2c
u2
k
3k
2k
u2
0
m u3 0 2c 2c u3 0 2k 2k u3 f0
1 0,2
k m
, 3
2k m
1 1 1
φ1
1 , φ2
0
, φ3
1
1
1/ 2
1
u1 1
u2
1
u3 1
1 0 1/ 2
1 q1
1
q2
1 q3
)d
u0 2
(1 cos1t)
q2
(t)
u0 2
(1
cos 2t )
机械振动答案

机械振动答案(1)选择题1解析:选D.如图所示,设质点在A 、B 之间振动,O 点是它的平衡位置,并设向右为正.在质点由O 向A 运动过程中其位移为负值;而质点向左运动,速度也为负值.质点在通过平衡位置时,位移为零,回复力为零,加速度为零,但速度最大.振子通过平衡位置时,速度方向可正可负,由F =-kx 知,x 相同时F 相同,再由F =ma 知,a 相同,但振子在该点的速度方向可能向左也可能向右.2.解析:选B.据简谐运动的特点可知,振动的物体在平衡位置时速度最大,振动物体的位移为零,此时对应题图中的t 2时刻,B 对.3.解析:选BD.质点做简谐运动时加速度方向与回复力方向相同,与位移方向相反,总是指向平衡位置;位移增加时速度与位移方向相同,位移减小时速度与位移方向相反.4解析:选C.因为弹簧振子固有周期和频率与振幅大小无关,只由系统本身决定,所以f 1∶f 2=1∶1,选C.5解析:选B.对于阻尼振动来说,机械能不断转化为内能,但总能量是守恒的.6.解析:选B.因质点通过A 、B 两点时速度相同,说明A 、B 两点关于平衡位置对称,由时间的对称性可知,质点由B 到最大位移,与由A 到最大位移时间相等;即t 1=0.5 s ,则T2=t AB +2t 1=2 s ,即T =4 s ,由过程的对称性可知:质点在这2 s 内通过的路程恰为2 A ,即2A =12 cm ,A =6 cm ,故B 正确.7.解析:选A.两球释放后到槽最低点前的运动为简谐运动且为单摆模型.其周期T =2πR g,两球周期相同,从释放到最低点O 的时间t =T4相同,所以相遇在O 点,选项A 正确.8.解析:选C.从t =0时经过t =3π2L g 时间,这段时间为34T ,经过34T 摆球具有最大速度,说明此时摆球在平衡位置,在给出的四个图象中,经过34T 具有负向最大速度的只有C 图,选项C 正确.9.解析:选CD.单摆做简谐运动的周期T =2πlg,与摆球的质量无关,因此两单摆周期相同.碰后经过12T 都将回到最低点再次发生碰撞,下一次碰撞一定发生在平衡位置,不可能在平衡位置左侧或右侧.故C 、D 正确.10.解析:选D.通过调整发生器发出的声波就能使酒杯碎掉,是利用共振的原理,因此操作人员一定是将声波发生器发出的声波频率调到500 Hz ,故D 选项正确. 二、填空题(本题共2小题,每小题8分,共16分.把答案填在题中横线上)11答案:(1)B (2)摆长的测量、漏斗重心的变化、液体痕迹偏粗、阻力变化……12答案:(1)ABC (2)①98.50 ②B ③4π2k计算题13.(10分)解析:由题意知弹簧振子的周期T =0.5 s ,振幅A =4×10-2m. (1)a max =kx max m =kA m=40 m/s 2. (2)3 s 为6个周期,所以总路程为s =6×4×4×10-2m =0.96 m.答案:(1)40 m/s 2(2)0.96 m14.(10分)解析:设单摆的摆长为L ,地球的质量为M ,则据万有引力定律可得地面的重力加速度和高山上的重力加速度分别为:g =G M R 2,g h =G M R +h2据单摆的周期公式可知T 0=2πLg ,T =2πL g h由以上各式可求得h =(T T 0-1)R . 答案:(T T 0-1)R15.(12分解析:球A 运动的周期T A =2πl g, 球B 运动的周期T B =2π l /4g =πl g. 则该振动系统的周期T =12T A +12T B =12(T A +T B )=3π2l g. 在每个周期T 内两球会发生两次碰撞,球A 从最大位移处由静止开始释放后,经6T =9πlg,发生12次碰 撞,且第12次碰撞后A 球又回到最大位置处所用时间为t ′=T A /4. 所以从释放A 到发生第12次碰撞所用时间为t =6T -t ′=9πl g -2T 2l g =17π2lg. 答案:17π2l g16.(12分解析:在力F 作用下,玻璃板向上加速,图示OC 间曲线所反映出的是振动的音叉振动位移随时间变化的规律,其中直线OC 代表音叉振动1.5个周期内玻璃板运动的位移,而OA 、AB 、BC 间对应的时间均为0.5个周期,即t =T 2=12f=0.1 s .故可利用匀加速直线运动的规律——连续相等时间内的位移差等于恒量来求加速度.设板竖直向上的加速度为a ,则有:s BA -s AO =aT 2①s CB -s BA =aT 2,其中T =152 s =0.1 s ②由牛顿第二定律得F -mg =ma ③ 解①②③可求得F =24 N. 答案:24 N机械振动(2)机械振动(3)1【解析】 如图所示,图线中a 、b 两处,物体处于同一位置,位移为负值,加速度一定相同,但速度方向分别为负、正,A 错误,C 正确.物体的位移增大时,动能减少,势能增加,D 错误.单摆摆球在最低点时,处于平衡位置,回复力为零,但合外力不为零,B 错误.【答案】 C2【解析】 质量是惯性大小的量度,脱水桶转动过程中质量近似不变,惯性不变,脱水桶的转动频率与转速成正比,随着转动变慢,脱水桶的转动频率减小,因此,t 时刻的转动频率不是最大的,在t 时刻脱水桶的转动频率与机身的固有频率相等发生共振,故C 项正确.【答案】 C3【解析】 摆球从A 运动到B 的过程中绳拉力不为零,时间也不为零,故冲量不为零,所以选项A 错;由动能定理知选项B 对;摆球运动到B 时重力的瞬时功率是mg v cos90°=0,所以选项C 错;摆球从A 运动到B 的过程中,用时T /4,所以重力的平均功率为P =m v 2/2T /4=2m v 2T ,所以选项D 错.【答案】 B4【解析】 由振动图象可看出,在(T 2-Δt )和(T2+Δt )两时刻,振子的速度相同,加速度大小相等方向相反,相对平衡位置的位移大小相等方向相反,振动的能量相同,正确选项是D.【答案】 D5【解析】 据受迫振动发生共振的条件可知甲的振幅较大,因为甲的固有频率接近驱动力的频率.做受迫振动物体的频率等于驱动力的频率,所以B 选项正确.【答案】 B6【解析】 由题意知,在细线未断之前两个弹簧所受到的弹力是相等的,所以当细线断开后,甲、乙两个物体做简谐运动时的振幅是相等的,A 、B 错;两物体在平衡位置时的速度最大,此时的动能等于弹簧刚释放时的弹性势能,所以甲、乙两个物体的最大动能是相等的,则质量大的速度小,所以C 正确,D 错误.【答案】 C题号 1 2 3 4 5 6 7 8 9 10答案 ACBADACBDACADD(T 2-T 1)R/T 17【答案】 C8【解析】 根据题意,由能量守恒可知12kx 2=mg (h +x ),其中k 为弹簧劲度系数,h 为物块下落处距O 点的高度,x 为弹簧压缩量.当x =x 0时,物块速度为0,则kx 0-mg =ma ,a =kx 0-mg m =kx 0m -g =2mg (h +x 0)mx 0-g =2g (h +x 0)x 0-g >g ,故正确答案为D.【答案】 D9【解析】 由题中条件可得单摆的周期为T =0.30.2s =1.5s ,由周期公式T =2πlg可得l=0.56m.【答案】 A10【解析】 当摆球释放后,动能增大,势能减小,当运动至B 点时动能最大,势能最小,然后继续摆动,动能减小,势能增大,到达C 点后动能为零,势能最大,整个过程中摆球只有重力做功,摆球的机械能守恒,综上可知只有D 项正确.【答案】 D机械振动(4)1解析:选A.周期与振幅无关,故A 正确.2解析:选C.由单摆周期公式T =2π lg知周期只与l 、g 有关,与m 和v 无关,周期不变频率不变.又因为没改变质量前,设单摆最低点与最高点高度差为h ,最低点速度为v ,mgh =12m v 2.质量改变后:4mgh ′=12·4m ·(v 2)2,可知h ′≠h ,振幅改变.故选C.3解析:选D.此摆为复合摆,周期等于摆长为L 的半个周期与摆长为L2的半个周期之和,故D 正确.4解析:选B.由简谐运动的对称性可知,t Ob =0.1 s ,t bc =0.1 s ,故T4=0.2 s ,解得T =0.8s ,f =1T=1.25 Hz ,选项B 正确.5解析:选D.当单摆A 振动起来后,单摆B 、C 做受迫振动,做受迫振动的物体的周期(或频率)等于驱动力的周期(或频率),选项A 错误而D 正确;当物体的固有频率等于驱动力的频率时,发生共振现象,选项C 正确而B 错误.6解析:选BD.速度越来越大,说明振子正在向平衡位置运动,位移变小,A 错B 对;速度与位移反向,C 错D 对.7解析:选AD.P 、N 两点表示摆球的位移大小相等,所以重力势能相等,A 对;P 点的速度大,所以动能大,故B 、C 错D 对.8解析:选BD.受迫振动的频率总等于驱动力的频率,D 正确;驱动力频率越接近固有频率,受迫振动的振幅越大,B 正确.9解析:选B.读图可知,该简谐运动的周期为4 s ,频率为0.25 Hz ,在10 s 内质点经过的路程是2.5×4A =20 cm.第4 s 末的速度最大.在t =1 s 和t =3 s 两时刻,质点位移大小相等、方向相反.。
机械振动习题及答案(20200723173312)

1•一简谐振动,振幅为,周期为,求最大速度和加速度。
解:2•—加速度计指示结构谐振在80HZ时具有最大加速度50g,求振动的振幅。
(g=10m/s2) 解: X max w2* X max (2* * f)2*X m a X3•—简谐振动,频率为10Hz,最大速度为s,求谐振动的振幅、周期、最大加速度。
解:4. 机械振动按激励输入类型分为哪几类?按自由度分为哪几类?答:按激励输入类型分为自由振动、强迫振动、自激振动按自由度分为单自由度系统、多自由度系统、连续系统振动5. 什么是线性振动?什么是非线性振动?其中哪种振动满足叠加原理?答:描述系统的方程为线性微分方程的为线性振动系统,如I。
巫mga 0描述系统的方程为非线性微分方程的为非线性振动系统I0&& mgasin 0线性系统满足线性叠加原理6•请画出同一方向的两个运动:x/t) 2sin(4 t),X2(t) 4sin(4 t)合成的的振动波形7.请画出互相垂直的两个运动:x,t) 2sin(4 t),X2(t) 2sin(4 t)合成的结果。
如果是x,(t) 2sin(4 t /2),x2(t) 2sin(4 t)第二章单自由度系统物体作简谐振动,当它通过距平衡位置为0.05m, 0.1m 处时的速度分别为0.2m/s 和0.08m/s2.一物体放在水平台面上, 当台面沿铅垂方向作频率为 5Hz 的简谐振动时,要使物体不跳离平台, 对台面的振幅有何限制?3.写出图示系统的等效刚度的表达式。
当m 2.5kg, k 1 k 2 2 1 05N/m, k 3 3 105N/m 时, 求系统的固有频率。
分析表明:&和k2并联,之后与k 3串联匕和k 2并联后的等效刚度:k eq k 1 k 2整个系统的等效刚度:k eq -k eq k 3(k 1 k 2)k 3k eq k 3k 1 k 2 k ?系统的固有频率:n 卜 261.86 rad/s\ m& (f) = a-i-p)Wi/rTlr, Skir i L>|L^ -M vJJ® =» v)1 >就a 田m 蜀琳卜厦1 J求其振动周期、振幅和最大速度。
机械振动习题及答案完整版.docx

1.1试举出振动设计'系统识别和环境预测的实例。
1.2如果把双轴汽车的质量分别离散到前、后轴上去,在考虑悬架质量和非悬架质量两个离散质量的情况下,画出前轴或后轴垂直振动的振动模型简图,并指出在这种化简情况下,汽车振动有几个自由度?1.3设有两个刚度分别为心,心的线性弹簧如图T-1.3所示,试证明:1)它们并联时的总刚度k eq为:k eq = k x+ k22)它们串联时的总刚度匕满足:丿-畔+ 土keq & k2解:1)对系统施加力P,则两个弹簧的变形相同为X,但受力不同,分别为: P x = k x x<由力的平衡有:P = ^ + P,=(k1+k2)xp故等效刚度为:k eq^- = k1+k2x2)对系统施加力P,则两个弹簧的变形为:P%i=r 111,弹簧的总变形为:x = x}+x2= P(——I ---- )故等效刚度为:k =—Xk x k2k,2+ k、1 1=—l-------k、k21.4求图所示扭转系统的总刚度。
两个串联的轴的扭转刚度分别为心, 解:对系统施加扭矩T,则两轴的转角为:VTrx系统的总转角为:0 = G + g = Hy- + T-)褊k,i故等效刚度为:犒=二+二1.5两只减振器的粘性阻尼系数分别为q, C2,试计算总粘性阻尼系数"在两只减振器并联时,2)在两只减振器串联时。
解:1)对系统施加力P,则两个减振器的速度同为厂受力分别为:P{ - c x x<P2=C2X由力的平衡有:P=£ + E =(q+C2)Xp故等效刚度为:c eq=- = c]+c2X2)对系统施加力P,则两个减振器的速度为:p 1 1故等效刚度为:c eq=- = - + -1.6 一简谐运动,振幅为0. 5cm,周期为0.15s,求最大速度和加速度。
解:简谐运动的a>n= — = /5),振幅为5x10 3m ;= 5x10-cos(^_ 2/r即:—5x10'丽fsin(丽血/s)*610=(話讥。
大学物理-机械振动习题-含答案

大学物理-机械振动习题-含答案一、选择题1. 质点作简谐振动,距平衡位置 2。
0cm 时, ,则该质点从一端运动到 C )C:2.2s --- 加速度 a=4.0cm /s 另一端的时间为( A:1.2s B: 2.4sD:4.4sX ,22.2s.2上 2 42 •—个弹簧振子振幅为2 10 2m 当t 0时振子在x 1.0 10 2m 处,且向 正方向运动,则振子的振动方 程是:[A ]A : 1.2题图22 10 cos( t )m ;3’6)m; 3)m;2 10 2 cos( t2 10 2 cos( tD :2x 2 10 cos( t —)m;解:由旋转矢量可 以得出振动的出现初相为:?3 •用余弦函数描述一简谐振动,若其速度与时间 -1v (m.s )1.3题图t (s )—►o 1 —v 2 m vm如图示,则振动的初相位为: (v —t )关系曲线[A ]A: e ; B : 3 ; C : 2 ;D : 2- ;E :「3丁6解:振动速度为:V V max Si n( t 0)t 0时,sin 01,所以。
-或。
2 6由知1.3图,t 0时,速度的大小是在增加,由旋转矢量图知,旋转矢量在 第一象限内,对应质点的运动是由正最大 位移向平衡位置运动,速度是逐渐增加的, 旋转矢量在第二象限内,对应质点的运动 是由平衡位置向负最大位移运动,速度是 逐渐减小的,所以只有。
-是符合条件的。
64 •某人欲测钟摆摆长,将钟摆摆锤上移 1毫 米,测得此钟每分快0。
1秒,则此钟摆的 ) B:30cm C:45cm丄理丁 160mm 30cm2 dT 2 ( 0.1):、填空题1 •有一放置在水平 面上的弹簧振子。
振幅A = 2.0 X 0_2m 周期摆长为( A:15cm D:60cm 解:单摆周期 有: 他2 . g,两侧分别对「和l 求导,j*T = 0.50s ,根据所给初始条件,作出简谐振动的矢量图,并写出振动方程式或初位相。
机械振动现象练习题(含答案)

机械振动现象练习题(含答案)1. 一个弹簧常数为3000 N/m, 质量为0.2 kg的物体,在弹簧下端受到一个向下的力2 sin(10t) N,其中t为时间(秒)。
求物体的振动方程。
根据牛顿第二定律,可以得到物体的振动方程为:m * x'' + k * x = F(t)其中,m是物体的质量,x是物体的位移,x''是位移对时间的二阶导数,k是弹簧的常数,F(t)是作用在物体上的外力。
根据题目中给出的数据,代入上述公式,我们可以得到:0.2 * x'' + 3000 * x = 2 sin(10t)这就是物体的振动方程。
2. 一个质点在受到一个力F(t) = 0.1 cos(3t) N的作用下进行振动,已知质点的质量为0.5 kg。
求质点的角频率和振动周期。
根据振动方程的形式,我们可以知道物体的振动频率和周期与力的形式有关。
在这个题目中,我们可以看出力的形式为cos(3t),它是一个正弦函数。
如果将cos(3t)函数展开,我们可以得到下面的表达式:F(t) = a cos(wt)其中,a是振幅,w是角频率。
根据题目中给出的数据,我们可以得到:a = 0.1 N,w = 3 rad/s由于振动的频率与角频率之间是有关联的,振动的周期T可以表示为:T = 2π/w代入上述数据,我们可以得到:T = 2π/3 s这就是质点的振动周期。
3. 一个质点质量为0.3 kg,在一竖直方向上的弹簧中振动,弹簧的劲度系数为2000 N/m。
当质点受到一个外力F(t) = 0.5 cos(5t) N时,求质点的振动方程。
根据题目中给出的数据,我们可以得到:m = 0.3 kg,k = 2000 N/m,F(t) = 0.5 cos(5t)代入振动方程的一般形式,我们可以得到:0.3 * x'' + 2000 * x = 0.5 cos(5t)这就是质点的振动方程。
231211 北交《机械振动基础》在线作业一 15秋答案

北交《机械振动基础》在线作业一一、单选题(共 15 道试题,共 30 分。
)1. 以下振动现象中表现为共振现象的是(). 钱塘江大桥上正通过一列火车时的振动. 挑水的人由于行走,使扁担和水桶上下振动,结果水桶中的水溢出. 工厂中机器开动引起厂房的振动. 快艇上的机关炮正连续向敌人射击时的振动正确答案:2. 下列各种振动,不属于受迫振动的是(). 敲击后的锣面的振动. 缝纫机针的振动. 人挑担时,担子上下振动. 蜻蜓、蝴蝶翅膀的振动正确答案:3. 下列说法错误的是(). 机械振动是指物体在平衡位置附近的往复运动。
. 钟摆的摆动,刀具的颤动,车辆车体的晃动,机器、桥梁、房屋和水坝的振动等,都是机械振动。
. 简谐运动图象能够反映简谐运动的运动规律,因此将简谐运动图象跟具体运动过程联系起来是讨论简谐运动的一种好方法。
. 如果实际振动系统可以简化为一个质量、一个弹簧和一个阻尼器组成,而质量在空间的位置可以用一个坐标完全地描述,则这个系统称为多自由度系统。
正确答案:4. 下列说法错误的有(). 系统在振动时的位移通常是比较小的,因为实际结构的变形一船是比较小的。
. 振动系统发生振动的原因是由于外界对系统运动状态的影响,即外界对系统的激励或作用。
. 在机械振动中,把外界对振动系统的激励或作用,如作用在结构上的外力,道路不平对行驶车辆的影响等等,称为振动系统的激励或输入。
. 系统对外界影响的反应,如振动系统某部位产生的位移、速度、加速度及应力等,称为振动系统的激励或输入。
正确答案:5. 一单摆的摆长为40m,摆球在t=0时刻正从平衡位置向右运动,若g取10m/s2,则在1s时摆球的运动情况是(). 正向左做减速运动,加速度正在增大. 正向左做加速运动,加速度正在减小. 正向右做减速运动,加速度正在增大. 正向右做加速运动,加速度正在减小正确答案:6. 一弹簧振子振动过程中的某段时间内其加速度数值越来越大,则在这段时间内(). 振子的速度越来越大. 振子正在向平衡位置运动. 振子的速度方向与加速度方向一致. 以上说法都不正确正确答案:7. 单摆的周期在下列何种情况时会增大(). 增大摆球质量. 减小摆长. 把单摆从赤道移到北极. 把单摆从海平面移到高山正确答案:8. 下列说法中不正确的是(). 实际的自由振动必然是阻尼振动. 在外力作用下的振动是受迫振动. 阻尼振动的振幅越来越小. 受迫振动稳定后的频率与自身物理条件无关正确答案:9. 一弹簧振子的周期为2s,当它从平衡位置向左运动经4.6s时,其运动情况是().. 向左减速. 向右加速. 向左减速. 向左加速正确答案:10. 振动着的单摆摆球,通过平衡位置时,它受到的回复力(). 指向地面. 指向悬点. 数值为零. 垂直摆线,指向运动方向正确答案:11. 两个弹簧振子,第一个弹簧振子自由振动时10秒内完成全振动20次,第二个弹簧振子自由振动时8秒内完成全振动4次,则两次振动周期之比T1∶T2为(). 1∶1. 1∶2. 2∶1. 1∶4正确答案:12. 下列说法错误的是(). 所谓过程,是指物理量随时间(或其他单调函数)变化的情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.2 如果把双轴汽车的质量分别离散到前、后轴上去,在考虑悬架质量和非悬架质量两个离散质量的情况下,画出前轴或后轴垂直振动的振动模型简图,并指出在这种化简情况下,汽车振动有几个自由度?解:前轴或后轴垂直振动的振动模型简图为图1.2所示,此时汽车振动简化为二自由度振动系统。
2m 为非悬架质量,1m 为悬架质量1. 3设有两个刚度分别为21,k k 的线性弹簧如图T-1.3所示, 试证明:1)它们并联时的总刚度eq k 为:21k k k eq +=2)它们串联时的总刚度eq k 为:21111k k k eq +=证明:1) 如图T-1.3(a)所示,21,k k 两个弹簧受到力的作用,变形相同, 即2211k F k F k F eq ==, 而F F F =+21,故有 F F k kF k k eq eq =+21, 从而 21k k k eq +=2)如图T-1.3(b)所示,21,k k 两个弹簧受到相同的力作用 即∆=∆=∆=eq k k k F 2211 (1)且21∆+∆=∆ (2)由(1)和(2)有:)(21k Fk F k F eq += (3) 由(3)得:21111k k k eq += 1.8证明:两个同频率但不同相角的简谐运动的合成仍是同频率的简谐运动,即)cos()cos(cos θωϕωω-=-+t C t B t A ,并讨论ϕ=0,ππ,2三种特例。
证明:因t B t B t B ωϕωϕϕωsin sin cos cos )cos(+=-从而有t B t B A t B t A ωϕωϕϕωωsin sin cos )cos ()cos(cos ++=-+令 ()ϕϕϕθ222sin cos sin sin B B A B ++=则()[]t t B B A t B t A ωθωθϕϕϕωωsin sin cos cos sin cos )cos(cos 222+++=-+=())cos(sin cos 222θωϕϕ-++t B B A令C=()ϕϕ222sin cos B B A ++,则有 )cos()cos(cos θωϕωω-=-+t C t B t A当ϕ=0时,C=A+B ;当ϕ=2π时,22B A C +=,22BA arcsin +=B θ ;当ϕ=π时,B A -=C ,0=θ1.13汽车悬架减振器机械式常规性能试验台,其结构形式之一如图T-1.13所示。
其激振器为曲柄滑块机构,在导轨下面垂向连接被试减振器。
试分析减振器试验力学的基本规律(位移,速度,加速度,阻尼力)。
解:tCA F t A xt A xtA x d ωωωωωωcos sin cos sin 2=-===ω2.1弹簧下悬挂一物体,弹簧静伸长为δ,设将物体向下拉,使弹簧有静伸长3δ,然后无初速度地释放,求此后的运动方程。
解:设静平衡位置为原点,向下坐标为正方向,则系统的微分方程为0=+x k xm由题意知,0,200==xx δ,且由mg k =δ,得δmgk =,从而δωgn=设方程的解为)cos(ϕω+=t A x n ,由初始条件有)cos(2t gx δδ=2.2弹簧不受力时长度为65cm,下端挂上1kg 物体后,弹簧长85cm 。
设用手拖住物体使弹簧回到原长后,无初速度地释放,试求物体的运动方程,振幅,周期及弹簧力的最大值。
解:由题意有,mg k =δ,得δmgk =,δωg m k n==,因δ=0.2 (m) , g=9.8 (m/2s ),故)/(7s rad n =ω 以平衡位置为原点,向下为正,可得运动微分方程和初始条件如下:⎪⎩⎪⎨⎧=-=-==+0,2.00002xx x x nδω故运动方程为t t x n 7sin 2.0)cos(2.0-=-=ω,振幅:0.2m, 周期:πωπ722=n 弹簧力的最大值:()(6.19)8.91492.0N =⨯+⨯2.3重物1m 悬挂在刚度为k 的弹簧上,并处于静平衡位置,另一重物2m 从高度为h 处自由落到1m 上无弹跳,如图T-2.3所示,求其后的运动。
解:根据题意,取M=1m +2m 所处的平衡位置为原点,向下为正,得系统运动的微分方程为:⎪⎩⎪⎨⎧+=-==+2120202,0m m gh m x k g m x kx x M , 解得t xt x x n nn ωωωsin cos 00 += =)sin(2)cos(212212t m m kk gh m t m m k k g m +++-2.6求如图T-2.6所示系统的周期,三个弹簧都成铅垂,且122k k =,13k k =。
解:等效刚度=132135)11(1k k k k =++,由n ω=mk mk 351=,故系统的周期为15322k m T n πωπ== 2.9求如图T-2.9所示系统微幅扭振的周期。
图中两个摩擦轮可分别绕水平轴1O ,2O 转动,它们相互啮合,不能相对滑动,在图示位置(半径1O A 与2O B 在同一水平线上),弹簧不受力。
摩擦轮可以看做等厚均质圆盘,质量分别为1m ,2m 。
解:坐标原点取为静平衡位置,故可不计重力势能,A 盘转动θ角,则B 盘转动θθBAB r r =。
A 盘的惯性矩424A A A r I πρ=, B 盘的惯性矩424BB B r I πρ= (A ρ,B ρ分别为A 盘和B 盘的单位面积的质量。
)因21AA r m πρ= ,22BB r m πρ=,故221A A r m I =, 222BB r m I = 系统的势能为22212221)(21)(21)(21θθθA B B A r k k r k r k U+=+=动能为222122)(412121θθθ A B B A A T r m m I I E +=+=故由0)(=+T E U d ,得0)()2(2121=+++θθk k m m, 21212121)(22,)(2m m k k T m m k k n ++=++=πω2.14一台电机重470N ,转速为1430 r/min,固定在两根5号槽钢组成的简支梁的中点,如图T-2.14所示。
每根槽钢长1.2m, 重65.28N, 弯曲刚度为EI=1.66×510N.m 2。
(a)不考虑槽钢质量,求系统的固有频率(b)设槽钢质量均布,考虑分布质量的影响,求系统的固有频率 (c)计算说明如何避开电机和系统的共振区解:a) 不考虑槽钢质量,每一根槽钢中点的静绕度为:45331051.01066.1482.1)2470(48-⨯≈⨯⨯⨯==∆EI pl从而每一根槽钢的刚度为:)2470(∆=∆=p k ,得)/(35.4388.9470224702s rad mkn ≈⨯∆==ω b) 考虑槽钢质量分布对系统动能的影响,不考虑它对静绕度的影响。
(分布载荷的静变形曲线为)43(4832x x L EIpy-=) 设梁的振动速度分布为33243)()(Lx x L t v t v x -=,v(t)为梁中点的速度,故整段梁的动能为⎰⎰-=2023262220)43()()(212L x L x d x x L Lt v x d t v ρρ =)3517)((212t v L ρ 故每一根槽钢的等效质量为钢等m m '='3517此时)/(5.4118.928.65351728.9470122470351722s rad m m kn≈⨯⨯+⨯∆='⨯+=)(ω钢c)电机的激励频率ω=1430602π⨯=149.926(rad/s )故激励频率远离系统的共振区。
2.15一质量m 固定于长L ,弯曲刚度为EI ,密度为ρ的弹性梁的一端,如图T-2.15所示,试以有效质量的概念计算其固有频率。
解:梁的自由端的绕度为 EI pl 33=∆,则等效刚度为 33lEI而其静变形曲线为EI x pl EI pl EI x l p y 26)(6233+--= (由 )(22x l p xd yd EI --=及0,000====x x dxdyy 求积分得到)从而可假设端v v y =∆,端v y v ∆=, 即梁系统的动能为20)(21v x d E L ρ⎰=梁x d v y L 2端22021∆=⎰ρ=09911.02121232端2L 022端2⨯⨯∆≈∆⎰L EIpl v x d y v )(ρρ=端2)892.0(21V L ρ 从而梁的等效质量为L ρ892.0;系统的固有频率可近似为)892.0(33L m l EIρ+ 2.19试证明:对数衰减率也可用下式表示nnx x l n1=δ (式中n x 是经过n 个循环后的振幅)。
并给出在阻尼比ξ为0.01,0.1,0.3时振幅减小到50%以下所需要的循环数。
证明:因10t n Xe x ωξ-=,)1(d nT t n n Xe x +-=ωξ故d T n n ne x xωξ=0,d n n T n x x ωξ=0ln, δn x x n =0ln ,故nx xn 0ln 1=δ ξ为0.01,0.1,0.3时振幅减小到50%以下所需要的循环数分别为12. , 2. ,1。
(这里设ωn d ω≈,从而π2≈d n T ω,由πξ22ln n =近似计算)2.24试指出在简谐激励下系统的复频率响应,放大因子和品质因子之间的关系,并计算当ξ=0.2,n ω=5rad/s 时系统的品质因子和带宽。
解:简谐激励下,系统复频率响应为:)()(n n i H ωωξωωω/2/-11)(2+=放大因子[]222)/2(/-11|)(|nn H ωξωωω+=)(ω ,品质因子ξωω21=∆n在小阻尼时,当频率比22-1/ξωω=n 时,放大因子达到最大值max |)(|ωH ,而m a x |)(|ωH 为Q ,即ξξξ212-121|)(|Q 2max ≈==ωH ,ξ=0.2,n ω=5rad/s 时,252.022,5.22.021=⨯⨯==∆=⨯=n Q ξωω2.29若振动物体受到的阻力与其运动速度平方成正比,即⎪⎩⎪⎨⎧-=≤=0022>xxa F x xa F d d 求其等效阻尼系数和共振时的振幅解:粘性阻尼力在一个周期内做的功为dt t c dx xc W c )(sin X 22/202ϕωωωπ-==⎰⎰ =2X c πω(这里设)cos(ϕω-=t X x ),而上述一周内所做的功为:⎰⎰==dt xF dx F W d d d =[]⎰⎰++-=ωϕωπωϕωϕωπωϕϕωω//2///2/)(in X -dt t s F dt xF d d令ωϕ-=*t t ,原式=[]**⎰dt t s F d )in(X -/20ωωωπ=[][]**++**⎰⎰dt t s a dt t s a 3/2/3/0)in(X -)()in(X -)(-ωωωωωπωπωπ=323232X 38X 34X 34ωωωa a a =+由c d W =W ,故有πωX38a C =等效其简谐强迫振动方程为:t i e F x k xa x m ω0)X38(=++πω设)(ϕω-=t i Xe x ,故有 0)(2)X 38(F e x k X i a X m i =⎥⎦⎤⎢⎣⎡++--ϕωπωω当在共振时,可设m k n=≈22ωω,则有0)(2≈-X m k ω,0)(2238F ie X a n =-ϕπω 故 X=aF a F nn23218302πωωπ=2.33如图T-2.33所示由悬架支承的车辆沿高低不平的道路行进。
