人教版数学七年级下册 第5章 相交线与平行线 单元测试题(附答案)
七年级数学下册第五章《相交线与平行线》单元检测卷-人教版(含答案)
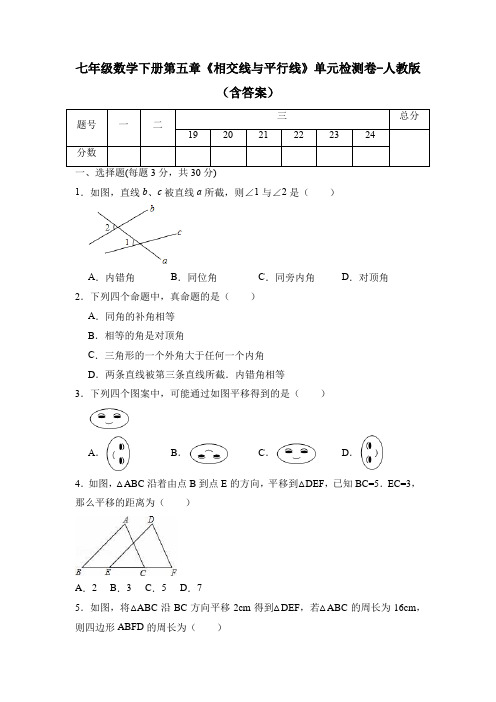
七年级数学下册第五章《相交线与平行线》单元检测卷-人教版(含答案)题号一二三总分192021222324分数1.如图,直线b、c被直线a所截,则∠1与∠2是()A.内错角B.同位角C.同旁内角D.对顶角2.下列四个命题中,真命题的是()A.同角的补角相等B.相等的角是对顶角C.三角形的一个外角大于任何一个内角D.两条直线被第三条直线所截.内错角相等3.下列四个图案中,可能通过如图平移得到的是()A.B.C.D.4.如图,△ABC沿着由点B到点E的方向,平移到△DEF,已知BC=5.EC=3,那么平移的距离为()A.2 B.3 C.5 D.75.如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为()A.16cm B.18cm C.20cm D.22cm6.如图,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A′点,连接A′B,则线段A′B与线段AC的关系是()A.垂直B.相等C.平分D.平分且垂直7.如图,下列说法错误的是()A.∠A与∠3是同位角B.∠4与∠B是同旁内角C.∠A与∠C是内错角D.∠1与∠2是同旁内角8.如图,下列条件中,能判断a∥b的条件有()①∠1=∠2;②∠1=∠4;③∠1+∠3=180°;④∠1+∠5=180°A.1个B.2个C.3个D.4个9.如图,直线a∥b,将三角尺的直角顶点放在直线b上,若∠1=35°,则∠2等于()A.45°B.55°C.35°D.65°10.如图,把矩形ABCD沿EF对折后使两部分重合,若∠1=50°,则∠AEF=()A.110°B.115°C.120°D.130°二、填空题(每题3分,共24分)11.如图,请填写一个条件,使结论成立:∵__________,∴//a b.12.. 如图,直线AB,CD,EF相交于点O,则∠BOE的对顶角是,∠COE的邻补角是,∠COG的邻补角是.13.如图,∠B的内错角是.14.如图,直线a∥b,∠1=75°,那么∠2的度数是.15.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠2=24°,则∠1的度数为.16.如图所示,点E在AC的延长线上,有下列条件:①∠1=∠2,②∠3=∠4,③∠A=∠DCE,④∠D=∠DCE,⑤∠A+∠ABD=180°,⑥∠A+∠ACD=180°,其中能判断AB∥CD的是.17.如图,将△ABC沿BC所在的直线平移得到△DEF.如果GC=2,DF=4.5,那么AG=.18.如图,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1=.三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)19.如图,已知AD⊥BC于点D,E是延长线BA上一点,且EC⊥BC于点C,若∠ACE=∠E.求证:AD平分∠BAC.20.给下面命题的说理过程填写依据.已知:如图,O是直线AB上的一点,OD是∠AOC的平分线,OE是∠COB的平分线.对OD⊥OE说明理由.理由:因为∠DOC=∠AOC().∠COE=∠COB().所以∠DOC+∠COE=∠AOC+∠COB=(∠AOC+∠COB)().所以∠DOE=∠AOB=×°=90°(两角和的定义)所以OD⊥OE().21.(8分)如图,已知AB∥CD,试再添加一个条件,使∠1=∠2成立.(1)写出两个不同的条件;(2)从(1)中选择一个来证明.22.(8分)如图,已知∠1+∠2=180°,∠3=∠B.(1)试判断DE与BC的位置关系,并说明理由.(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.23.如图,已知AB∥CD,EF∥MN,且∠1=110°.(1)求∠2和∠4的度数;(2)根据(1)的结果可知,如果两个角的两边分别平行,那么这两个角;(3)利用(2)中的结论解答:如果两个角的两边分别平行,其中一角是另一个角的两倍,求这两个角的大小.24. 如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F.(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为.请说明理由.(2)当△PMN所放位置如图②所示时,∠PFD与∠AEM的数量关系为.(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.参考答案一、选择题:题号12345678910答案B A C A C D A D B B二、填空题:11. 【答案】:∠1=∠4或∠2=∠4或∠3+∠4=180°【解析】本题考查了平行线的判定,∵∠1=∠4或∠2=∠4或∠3+∠4=180°,∴a∥b,因此本题填:∠1=∠4或∠2=∠4或∠3+∠4=180°.12. 【答案】∠AOF∠COF和∠DOE∠DOG13.解:∠B的内错角是∠BAD;故答案为:∠BAD.14.解:∵周长为12的三角形ABC沿BC方向平移2个单位长度得到三角形DEF,∴AD=CF=2,AC=DF,∴四边形ABFD的周长=AB+BC+CF+DF+AD=AB+BC+AC+AD+CF=△ABC 的周长+2AD=12+2×2=16.故答案为16.14.解:如图,∵a∥b,∴∠1=∠3=75°,而∠2+∠3=180°,∴∠2=180°﹣75°=105°.故答案为:105°.15.解:如图,延长AB交CF于E,∵∠ACB=90°,∠A=30°,∴∠ABC=60°,∵GH∥EF,∴∠AEC=∠2=24°,∴∠1=∠ABC﹣∠AEC=36°.故答案为:36°.16.解:①∵∠1=∠2,∴AB∥CD,正确;②∵∠3=∠4,∴BD∥AC,错误;③∵∠A=∠DCE,∴AB∥CD,正确;④∵∠D=∠DCE,∴BD∥AC,错误;⑤∵∠A+∠ABD=180°,∴BD∥AC,错误;⑥∵∠A+∠ACD=180°,∴AB∥CD,正确;故答案为:①③⑥17.解:∵△ABC沿BC所在的直线平移得到△DEF.∴AC=DF=4.5,∴AG=AC﹣GC=4.5﹣2=2.5.故答案为2.5.18.解:∵OP∥QR∥ST,∠2=100°,∠3=120°,∴∠2+∠PRQ=180°,∠3=∠SRQ=120°,∴∠PRQ=180°﹣100°=80°,∴∠1=∠SRQ﹣∠PRQ=40°,故答案是40°.三.解答题:19..证明:∵AD⊥BC于点D,EC⊥BC于点C,∴AD∥EC,∴∠BAD=∠E,∠DAC=∠ACE,∵∠ACE=∠E,∴∠BAD=∠DAC,即AD平分∠BAC.20.解:根据题意,可知前两个空分别为角平分线的定义,第三个空是利用上面等式右边的代入计算,故属于等量代换,第四个空属于垂直的定义.故答案为:角平分线的定义,角平分线的定义,等量代换,垂直的定义.21.解:此题答案不唯一,合理即可.(1)添加∠FCB=∠CBE或CF∥BE.(2)已知AB∥CD,CF∥BE.求证:∠1=∠2.证明:∵AB∥CD,∴∠DCB=∠ABC.∵CF∥BE,∴∠FCB=∠CBE,∴∠DCB-∠FCB=∠ABC-∠CBE,即∠1=∠2.22.解:(1)DE∥BC,理由如下:∵∠1+∠4=180°,∠1+∠2=180°,∴∠2=∠4,∴AB∥EF,∴∠3=∠5,∵∠3=∠B,∴∠5=∠B,∴DE∥BC,(2)∵DE平分∠ADC,∴∠5=∠6,∵DE∥BC,∴∠5=∠B,∵∠2=3∠B,∴∠2+∠5+∠6=3∠B+∠B+∠B=180°,∴∠B=36°,∴∠2=108°,∵∠1+∠2=180°,∴∠1=72°.23. 解:(1) 因为AB∥CD,所以∠1=∠2=110°,又因为EF∥MN,所以∠2+∠4=180°,∠4=70°(2)相等或互补(3)因为这两个角中,其中一角是另一个角的两倍,由(2)得,这两个角互补.设其中一个角的度数是x,则另一个角的度数为2x,根据题意,得x+2x=180°,解得x=60°.所以其中一个角是60°另一个角是120°24. 解:(1)作PG∥AB,如图①所示:则PG∥CD,∴∠PFD=∠1,∠2=∠AEM,∵∠1+∠2=∠P=90°,∴∠PFD+∠AEM=∠1+∠2=90°,故答案为:∠PFD+∠AEM=90°;(2)证明:如图②所示:∵AB∥CD,∴∠PFD+∠BHF=180°,∵∠P=90°,∴∠BHF+∠2=90°,∵∠2=∠AEM,∴∠BHF=∠PHE=90°﹣∠AEM,∴∠PFD+90°﹣∠AEM=180°,∴∠PFD﹣∠AEM=90°,故答案为∠PFD﹣∠AEM=90°;(3)如图③所示:∵∠P=90°,∴∠PHE=90°﹣∠FEB=90°﹣15°=75°,∵AB∥CD,∴∠PFC=∠PHE=75°,∵∠PFC=∠N+∠DON,∴∠N=75°﹣30°=45°.。
人教版初中数学七年级下册第五章《相交线与平行线》测试题(含答案)

第五章《相交线与平行线》检测题一、选择题(每小题只有一个正确答案)1.下列图形中,∠1与∠2是对顶角的是( )A. B. C. D.2.下列命题的逆命题不正确...的是()A. 同角的余角相等B. 等腰三角形的两个底角相等C. 两直线平行,内错角相等D. 线段中垂线上的点到线段两端的距离相等3.如图,AB∥CD,∠1=50°,∠2=110°,则∠3=()A. 60°B. 50°C. 70°D. 80°4.下列图形中线段PQ的长度表示点P到直线a的距离的是()A. B. C. D.5.如图,有下列说法:①若DE∥AB,则∠DEF+∠EFB=180º;②能与∠DEF构成内错角的角的个数有2个;③能与∠BFE构成同位角的角的个数有2个;④能与∠C构成同旁内角的角的个数有4个.其中结论正确的是()A. ①②B. ③④C. ①③④D. ①②④6.如图所示,已知∠1=∠2,那么下列结论正确的是( )A. AB∥BCB. AB∥CDC. ∠C=∠DD. ∠3=∠47.以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是().B. 如图2,展开后测得12∠=∠C. 如图3,测得12∠=∠D. 如图4,展开后再沿CD 折叠,两条折痕的交点为O ,测得OA OB =, OC OD = 8.如图,01,220,=B D ∠=∠∠=∠则( )A. 20B. 22C. 30D. 459.如图,从A 处出发沿北偏东60°方向行走至B 处,又沿北偏西20°方向行走至C 处,则∠ABC 的度数是( ) .A. 80°B. 90°C. 100°D. 95°10.如图,AB∥CD∥EF,则下列各式中正确的是( )A. ∠1+∠3=180°B. ∠1+∠2=∠3C. ∠2+∠3+∠1=180°D. ∠2+∠3﹣∠1=180°11.对于命题“若22a b >,则a b >”,下面四组关于a ,b 的值中,能说明这个命题是假命题的是( ).A. 3a =, 2b =-B. 2a =-, 3b =C. 2a =, 3b =-D. 3a =-, 2b = 12.下面的每组图形中,左面的平移后可以得到右面的是( )A. B. C. D.二、填空题13.如图,DF 平分∠CDE .∠CDF =50°.∠C =80°,则________∥________.a b c d,若a∥b. a⊥c. b⊥d,则直线,c d的位置14.同一平面内有四条直线,,,关系_________.15.如图.直线a.b.且∠1.28°..2.50°.则∠ABC._______.16.下列说法:①三角形的一个外角等于它的两个内角和;②三角形的内角和等于180°,外角和等于360°.③若一个三角形的三边长分别为3.5.x,则x的取值范围是2.x.8.④角是轴对称图形,角的对称轴是角的平分线;⑤圆既是轴对称图形,也是中心对称图形,圆有无数条对称轴.其中正确的有_ __.(填序号)17.如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D 在边OA上,将图中的△AOB绕点O按每秒20°的速度沿逆时针方向旋转一周,在旋转的过程中,在第t秒时,边CD恰好与边AB平行,则t的值为________.三、解答题18.将一副直角三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.19.如图,已知,AB∥CD,∠1=∠2,AE与EF平行吗?为什么?20.完成下面的证明:如图.AB和CD相交于点O.∠C.∠COA.∠D.∠BOD.求证:∠A.∠B.21.如图,在6×8 方格纸中,. ABC 的三个顶点和点P .Q都在小方格的顶点上.按要求画一个三角形,使它的顶点在方格的顶点上:. 1)在图1中画. DEF,使. DEF 与. ABC 全等,且使点P在. DEF 的内部.. 2. 在图2中画. MNH,使. MNH 与. ABC 的面积相等,但不全等,且使Q在. MNH的边上.22.如图,已知射线CB∥OA,∠C=∠OAB=100°,点E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.(1)求∠EOB的度数;(2)若向右平移AB,其他条件都不变,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值.参考答案1.C 2.A 3.A 4.C 5.A 6.B 7.C 8.A 9.C 10.D 11.D 12.D 13. DE BC14.c ∥d 15.78° 16.②③⑤17.5.5秒或14.5秒 18.CF ∥AB 19.AE∥DF, . 20.证明:∵∠C.∠COA.∠D.∠BOD(已知). 又∵∠COA.∠BOD(__对顶角相等__). ∴∠C.__∠D__(等量代换).∴AC ∥__BD__(__内错角相等.两直线平行__). ∴∠A.∠B(__两直线平行.内错角相等__).21. 1)利用三角形平移的规律进而得出对应点位置即可; . 2)利用三角形面积公式求出符合题意的图形即可. 试题解析:解:(1)如图所示:. DEF 即为所求;.2)如图所示:.MNH 即为所求.22. (1)∵CB ∥OA ,180.C COA ∴∠+∠=︒100C OAB ∠=∠=︒Q ,80.COA ∴∠=︒ ∵OE 平分COF ∠, .COE EOF ∴∠=∠2COA COE EOF FOB AOB EOB ∠=∠+∠+∠+∠=∠Q ,40.EOB ∴∠=︒(2)这个比值不变,比值为1∶2.理由: ∵CB ∥OA ,.OBC BOA OFC FOA ∴∠=∠∠=∠,FOB BOA ∠=∠Q , 12BOA FOA ∴∠=∠,OBC OFC ∴∠=∠,:1:2.OBC OFC ∴∠∠=。
人教版七年级下册数学第五章《相交线与平行线》单元练习题(含答案)

人教版七年级下册数学第五章《相交线与平行线》单元练习题(含答案)一、单选题1.如图,AB CD ∥ ,点E 在CA 的延长线上若50BAE ∠=︒,则ACD ∠的大小为( )A .100°B .120°C .130°D .110°2.如图,要修建一条公路,从A 村沿北偏东75°方向到B 村,从B 村沿北偏西25°方向到C 村.若要保持公路CE 与从A 村到B 村的方向一致,则应顺时针转动的度数为( )A .50°B .75°C .100°D .105°3.如图,直线AB ∥CD ,如果∠1=70°,那么∠BOF 的度数是( )A .70°B .100°C .110°D .120°4.具有下列关系的两角:①互为补角;②同位角;③对顶角;④内错角;⑤邻补角;⑥同旁内角.其中一定有公共顶点的两角的对数为( )A .1对B .2对C .3对D .4对5.如图,将三角板与直尺贴在一起,使三角板的直角顶点C (∠ACB =90°)在直尺的一边上,若∠2=65°,则∠1的度数是( )A .15°B .25°C .35°D .65°6.下列命题中,真命题是( )A .一条直线截另外两条直线所得到的同位角相等B .两个无理数的和仍是无理数C .有公共顶点且相等的两个角是对顶角D .等角的余角相等7.如图,AB ∥CD ,AE 平分∠CAB 交CD 于点E ,若∠C=70°,则∠AED=( )A .55°B .125°C .135°D .140°8.如图,12l l //,点O 在直线1l 上,若90AOB ︒∠=,135︒∠=,则2∠的度数为()A .65°B .55°C .45°D .35°9.下列命题是真命题的是( )A .如果一个数的相反数等于这个数本身,那么这个数一定是0B .如果一个数的倒数等于这个数本身,那么这个数一定是1C .如果一个数的平方等于这个数本身,那么这个数一定是0D .如果一个数的算术平方根等于这个数本身,那么这个数一定是010.如图,直线AB ∥ CD ,∠ B=50°,∠ C=40°,则∠E 等于( )A .70°B .80°C .90°D .100°二、填空题 11.如图,AD ∥BC ,EF ∥BC ,BD 平分∠ABC ,图中与∠ADO 相等的角有_______ 个,分别是___________.因为AB ∥CD ,EF ∥AB ,根据_____________________________,所以_____________.12.如图,在正方形网格中,三角形DEF 是由三角形ABC 平移得到的,则点C 移动了________格.13.如图,在ABC ∆中,4AB =,6BC =,60B ∠=︒,将ABC ∆沿射线BC 的方向平移2个单位后,得到A B C '''∆,连结A C ',则A B C ∆''的周长为______.14.下面三个命题: ①若是方程组的解,则或; ②函数通过配方可化为; ③最小角等于的三角形是锐角三角形. 其中正确命题的序号为 .15.设圆上有n 个不同的点,连接任两点所得线段,将圆分成若干个互不重合的区域,记()f n 为区域数的最大值,则(5)_________f =,(6)________f =.16.如图,已知AB ∥ED,∠ABC=300,∠EDC=400,则∠BCD 的度数是 .17.点M ,N 在线段AB 上,且MB =6cm ,NB =9cm ,且N 是AM 的中点,则AB =___cm ,AN =____cm .18.把命题“三个角都相等的三角形是等边三角形”改写成“如果……,那么……”的形式是_____;该命题的条件是_____,结论是_____.三、解答题19.如图,已知点A 是射线OP 上一点.(1)过点A 画OQ 的垂线,垂足为B ;过点B 画OP 的平行线BC ;(2)若50POQ ∠=,求ABC ∠的度数.20.(1)问题背景:已知:如图①-1,//AB CD ,点P 的位置如图所示,连结,PA PC ,试探究APC ∠与PAB ∠、PCD ∠之间有什么数量关系,并说明理由.(将下面的解答过程补充完整,括号内写上相应理由或数学式)解:(1)APC ∠与PAB ∠、PCD ∠之间的数量关系是:360APC PAB PCD ∠+∠+∠=︒(或360()APC PAB PCD ∠=︒∠+∠只要关系式形式正确即可)理由:如图①-2,过点P 作//PE AB .∵//PE AB (作图),∴180PAB APE ∠+∠=︒( ),∴//AB CD (已知)//PE AB (作图),∴//PE _______( ),∴CPE PCD ∠+∠=_______( ),∴180180360PAB APE CPE PCD ∠+∠+∠+∠=+︒=︒(等量代换)又∵APE CPE APC ∠+∠=∠(角的和差),∴360APC PAB PCD ∠+∠+∠=︒(等量代换)总结反思:本题通过添加适当的辅助线,从而利用平行线的性质,使问题得以解决.(2)类比探究:如图②,//AB CD ,点P 的位置如图所示,连结PA 、PC ,请同学们类比(1)的解答过程,试探究APC ∠与PAB ∠、PCD ∠之间有什么数量关系,并说明理由.(3)拓展延伸:如图③,//AB CD ,ABP ∠与CDP ∠的平分线相交于点1P ,若128P ∠=︒,求P ∠的度数,请直接写出结果,不说明理由.21.如图,抛物线y =ax 2+bx ﹣3与x 轴交于A (﹣1,0),B (3,0),与y 轴交于点C ,顶点为D .(1)求抛物线的解析式及点D的坐标.(2)在线段BC下方的抛物线上,是否存在异于点D的点E,使S△BCE=S△BCD?若存在,求出点E的坐标;若不存在,请说明理由.(3)点M3,2m⎛⎫- ⎪⎝⎭在抛物线上,点P为y轴上一动点,求2MP+2PC的最小值.22.如图,在96⨯网格中,已知△ABC,请按下列要求画格点三角形A' B' C'(三角形的三个顶点都是小正方形的顶点).(1)在图①中,将△ABC平移,使点O落在△ABC的边AB(不包括点A和点B)上;(2)在图②中,将△ABC平移,使点O落在△ABC的内部.23.如图.一次函数y=12x+1的图象L1交y轴于点A,一次函数y=﹣x+3的图象L2交x轴于点B,L1与L2交于点C.(1)求点A与点B的坐标;(2)求△ABC的面积.24.在如图所示的方格纸中,每个小正方形的边长为1,每个小正方形的顶点都叫做格点.△ABC的顶点A、B、C都在格点上.(1)过B作AC的平行线BD.(2)作出表示B到AC的距离的线段BE.(3)线段BE与BC的大小关系是:BE BC(填“>”、“<”、“=”).(4)△ABC的面积为.25.如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由.解:∵∠1=∠2(已知)∠2=∠DGF∴∠1=∠DGF(____________)∴BD∥CE∴∠3+∠C=180°( )又∵∠3=∠4(已知)∴∠4+∠C=180°∴∥(同旁内角互补,两直线平行)∴∠A=∠F( ).26.如图,所有小正方形的边长都为1,A、B、C都在格点上.(1)过点C画直线AB的平行线(不写画法,下同);(2)过点A画直线BC的垂线,并注明垂足为G;过点A画直线AB的垂线,交BC于点H.(3)线段_____的长度是点A到直线BC的距离;(4)线段AG、AH的大小关系为AG_____AH.(填“>”或“<”或“=”),理由________.27.如图,AB∥CD,∠1=∠2,求证:AM∥CN参考答案1.C2.C3.C4.B5.B6.D7.B8.B9.A10.C11.4 ∠DOF、∠EOB、∠ABD、∠DBC平行于同一直线的两条直线平行CD∥EF 12.513.1214.②③15.16;3116.70°17. 12 318.如果一个三角形的三个角都相等,那么这个三角形是等边三角形一个三角形的三个角都相等这个三角形是等边三角形19.(2)40°20.(1)∠APC+∠PAB+∠PCD=360°,理由见解析;两直线平行,同旁内角互补;CD,如果两条直线都和第三条直线平行,那么这两条直线也互相平行;180°,两直线平行,同旁内角互补;(2)∠APC=∠PAB+∠PCD,(3)∠P=56°.21.(1)y=x2﹣2x﹣3,D的坐标为(1,﹣4);(2)存在异于点D的点E,使S△BCE=S△BCD,点E的坐标为(2,﹣3);(3)最小值为23.(1)A(0,1),B(3,0);(2)5 324. (3) <;(4) 9 26.(3)AG;(4)<.。
人教版七年级数学下册第5章《相交线与平行线》单元测试卷(解析版)

人教版七年级数学下册第5章《相交线与平行线》单元测试卷一.选择题1.下列说法,正确的是( )A. 若ac=bc,则a=bB. 两点之间的所有连线中,线段最短C. 相等的角是对顶角D. 若AC=BC,则C是线段AB的中点【答案】B【解析】【分析】根据等式的性质可判断A的正误;根据线段的性质判断B的正误;根据对顶角的性质判断C的正误;根据中点的性质判断D的正误.【详解】解:A、若ac=bc(c≠0),则a=b,故此选项错误,B、两点之间的所有连线中,线段最短,说法正确,故此选项正确,C、相等的角是对顶角,说法错误,应是对顶角相等,故此选项错误,D、若AC=BC,则点C是线段AB的中点,说法错误,应是若AC=BC=AB,则点C是线段AB的中点,故此选项错误,故选:B.【点睛】此题主要考查了等式的性质、对顶角的性质、线段的性质、中点,关键是熟练掌握课本基础知识,牢固掌握定理.2.如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是( )A. 50°B. 55°C. 60°D. 70°【答案】D【解析】【分析】先根据平行线的性质求出∠C的度数,再由三角形外角的性质即可得出结论.【详解】∵AB∥CD,∠1=40°,∠2=30°,∴∠C=40°.∵∠3是△CDE的外角,∴∠3=∠C+∠2=40°+30°=70°.故答案选D.【点睛】本题考查的知识点是平行线的性质,解题的关键是熟练的掌握平行线的性质.3.如图,将含30°角的直角三角板ABC的直角顶点C放在直尺的一边上,已知∠A=30°,∠1=40°,则∠2的度数为( )A. 55°B. 60°C. 65°D. 70°【答案】D【解析】【分析】根据平行线的性质求出∠3=∠1=40°,根据三角形的外角性质求出∠2=∠3+∠A,代入求出即可.【详解】∵EF∥MN,∠1=40°,∴∠1=∠3=40°.∵∠A=30°,∴∠2=∠A+∠3=70°.故选D.【点睛】本题考查了平行线的性质,三角形外角性质的应用,能求出∠3的度数是解答此题的关键,注意:两直线平行,内错角相等.4.图中的∠1、∠2可以是对顶角的是( )A. B.C. D.【答案】C【解析】【分析】根据对顶角的定义,具有公共顶点且角的两边互为反向延长线对各图形分析判断后进行解答.【详解】解:A、∠1与∠2不是对顶角,B、∠1与∠2不是对顶角,C、∠1与∠2是对顶角,D、∠1与∠2不是对顶角,故选:C.【点睛】本题主要考查了对顶角的定义,熟练掌握定义是解题关键.5.如图,若AB,CD相交于点O,∠AOE=90°,则下列结论不正确的是( )A. ∠EOC与∠BOC互为余角B. ∠EOC与∠AOD互为余角C. ∠AOE与∠EOC互为补角D. ∠AOE与∠EOB互为补角【答案】C【解析】【分析】直接利用垂直的定义结合互余以及互补的定义分析得出答案.【详解】解:∵∠AOE=90°,∴∠BOE=90°,∵∠AOD=∠BOC,∴∠EOC+∠BOC=90°,∠EOC+∠AOD=90°,∠AOE+∠EOB=180°,故A、B、D选项正确,C错误.故选:C.【点睛】此题主要考查了垂直的定义、互余以及互补的定义,正确把握相关定义是解题关键.6.已知:如图,直线BO⊥AO于点O,OB平分∠COD,∠BOD=22°.则∠AOC的度数是( )A. 22°B. 46°C. 68°D. 78°【答案】C【解析】【分析】由垂直的定义可知∠AOB=90°,由角平分线的定义可知∠BOC=∠BOD=22°,从而求得∠AOC的度数. 【详解】解:∵BO⊥AO,∴∠AOB=90°,∵OB平分∠COD,∴∠BOC=∠BOD=22°,∴∠AOC=90°-22°=68°.故选C.【点睛】本题考查了垂直的定义,角平分线的定义.7.如图,∠1=68°,直线a平移后得到直线b,则∠2﹣∠3的度数为( )A. 78°B. 132°C. 118°D. 112°【答案】D【解析】【分析】根据补角的性质、对角的性质,再进行代换可以求出∠2-∠3的度数.【详解】延长直线c与b相交,令∠2的补角是∠4,则∠4=180º-∠2,令∠3的对顶角是∠5,则∠3=∠5,∵a∥b,∴∠6=∠1=68°.又∠4+∠5=∠6.∴(180º-∠2)+∠3=68°即:∠2-∠3= 112°【点睛】本题考查了补角的性质、对角的性质等知识点,熟练掌握是本题的解题关键.8.如图,下列条件中,能判断AB∥CD的是( )A. ∠FEC=∠EFBB. ∠BFC+∠C=180°C. ∠BEF=∠EFCD. ∠C=∠BFD【答案】C【解析】【分析】根据平行线的判定定理对各选项进行逐一判断即可.【详解】A.由∠FEC=∠EFB,可得CE∥BF,故本选项错误;B.由∠BFC+∠C=180°,可得CE∥BF,故本选项错误;C.由∠BEF=∠EFC,可得AB∥CD,故本选项正确;D.由∠C=∠BFD,可得CE∥BF,故本选项错误.故选C.【点睛】本题考查了平行线的判定,解题时注意:内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行.9.如图,P是直线l外一点,A,B,C三点在直线l上,且PB⊥l于点B,∠APC=90°,则下列结论:①线段AP是点A到直线PC的距离;②线段BP的长是点P到直线l的距离;③PA,PB,PC三条线段中,PB 最短;④线段PC的长是点P到直线l的距离,其中,正确的是( )A. ②③B. ①②③C. ③④D. ①②③④【答案】A【解析】【分析】根据“从直线外一点到这条直线上各点所连的线段中,垂线段最短”;“从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离”进行判断,即可解答.【详解】①线段AP是点A到直线PC的距离,错误;②线段BP的长是点P到直线l的距离,正确;③P A,PB,PC三条线段中,PB最短,正确;④线段PC的长是点P到直线l的距离,错误.故选A.【点睛】本题考查了垂线的两条性质:①从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.②从直线外一点到这条直线上各点所连的线段中,垂线段最短.10.将长方形ABCD纸片沿AE折叠,得到如图所示的图形,已知∠CED′=70°,则∠AED的大小是( )A. 60°B. 50°C. 75°D. 55°【答案】D【解析】【分析】根据折叠的性质得到∠AED=∠AED′,由平角的定义得到∠AED+∠AED′+∠CED′=180°,而∠CED′=60°,则2∠DEA=180°-70°=110°,即可得到∠AED的度数.【详解】解:∵长方形ABCD沿AE折叠得到△AED′,∴∠AED=∠AED′,而∠AED+∠AED′+∠CED′=180°,∠CED′=70°,∴2∠DEA=180°-70°=110°,∴∠AED=55°.故选:D.【点睛】本题考查了折叠的性质:折叠前后两图形全等,即对应角相等,对应边相等.二.填空题11.如图,已知∠1=75°,将直线m平行移动到直线n的位置,则∠2﹣∠3=_____°.【答案】105【解析】【分析】直接利用平移的性质结合三角形外角的性质得出答案.【详解】由题意可得:m∥n,则∠CAD+∠1=180°.∵∠3=∠4,∴∠4+∠CAD=∠2,∴∠2﹣∠3=∠CAD+∠3﹣∠3=∠CAD=180°﹣∠1=180°﹣75°=105°.故答案为:105.【点睛】本题考查了平移的性质、三角形外角的性质以及平行线的性质,正确转化角的关系是解题的关键.12.如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,CD⊥BE,垂足为D.给出下列结论:①∠1是∠ACD的余角;②图中互余的角共有3对;③∠1的补角只有∠DCF;④与∠ADC互补的角共有3个.其中正确结论有_____.【答案】①④【解析】【分析】根据垂直定义可得∠BCA=90°,∠ADC=∠BDC=∠ACF=90°,然后再根据余角定义和补角定义进行分析即可.【详解】∵AC⊥BF,∴∠BCA=90°,∴∠ACD+∠1=90°,∴∠1是∠ACD的余角,故①正确;∵CD⊥BE,∴∠ADC=∠CDB=90°,∴∠B+∠BCD=90°,∠ACD+∠DAC=90°.∵∠BCA=90°,∴∠B+∠BAC=90°,∠1+∠ACD=90°,∴图中互余的角共有4对,故②错误;∵∠1+∠DCF=180°,∴∠1的补角是∠DCF.∵∠1+∠DCA=90°,∠DAC+∠DCA=90°,∴∠1=∠DAC.∵∠DAC+∠CAE=180°,∴∠1+∠CAE=180°,∴∠1的补角有∠CAE,故③说法错误;∵∠ACB=90°,∠ACF=90°,∠ADC=∠BDC=90°,∴∠BDC,∠ACB,∠ACF和∠ADC互补,故④说法正确.正确的是①④.故答案为:①④.【点睛】本题考查了余角和补角,关键是掌握两角之和为90°时,这两个角互余,两角之和为180°时,这两个角互补.13.如图,射线OA⊥OC,射线OB⊥OD,若∠AOB=40°,则∠COD=____°.【答案】40【解析】【分析】根据OA⊥OC,OB⊥OD,可得∠AOC=90°,∠BOD=90°,然后得到∠AOB与∠BOC互余,∠COD与∠BOC互余,根据同角的余角相等,继而可求解即可.【详解】解:∵OA⊥OC,OB⊥OD,∴∠AOC=90°,∠BOD=90°,∴∠AOB与∠BOC互余,∠COD与∠BOC互余,∴∠AOB=∠COD =40°,故答案为:40°.【点睛】本题考查了余角的知识,关键发现∠AOB、∠COD都是∠BOC余角,根据同角的余角相等解答.14.点P是直线l外一点,点A,B,C,D是直线l上的点,连接PA,PB,PC,PD.其中只有PA与l垂直,若PA=7,PB=8,PC=10,PD=14,则点P到直线l的距离是_____.【答案】7【解析】【分析】根据“直线外一点到直线上各点的所有线中,垂线段最短”进行解答.【详解】解:∵直线外一点与直线上各点连接的所有线段中,垂线段最短.∵P A与l垂直, P A=7,∴点P到直线l的距离=PA,即点P到直线l的距离=7故答案为:7.【点睛】本题主要考查了垂线段最短的性质,熟记性质是解题的关键.15.如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°,∠BCD=40°,则∠BED的度数为______.【答案】55°【解析】【分析】过点E作EF∥AB,则EF∥CD,可得∠ABE=∠BEF, ∠DEF=∠CDE.先根据角平分线的定义,得出∠ABE =∠CBE=20°,∠ADE=∠CDE=35°,进而求得∠E的度数.【详解】过点E作EF∥AB,则EF∥CD,∴∠ABE=∠BEF, ∠DEF=∠CDE.∵AB∥CD,∴∠BCD=∠ABC=40°,∠BAD=∠ADC=70°,∵BE平分∠ABC,DE平分∠ADC,∴∠ABE=∠CBE=∠ABC=20°,∠ADE=∠CDE=∠ADC=35°,∴∠BED=∠BEF+∠DEF=20°+35°=55°.故答案为:55°.【点睛】此题考查了平行线的性质,角平分线的定义,正确做出辅助线是解题的关键.本题也考查了数形结合的数学思想.16.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是_____.【答案】40°【解析】【分析】由EF⊥BD,∠1=50°,结合三角形内角和为180°,即可求出∠D的度数,再由“两直线平行,同位角相等”即可得出结论.【详解】解:在△DEF中,∠1=50°,∠DEF=90°,∴∠D=180°-∠DEF-∠1=40°.∵AB∥CD,∴∠2=∠D=40°.故答案为:40°.【点睛】本题考查平行线的性质以及三角形内角和为180°,解题关键是求出∠D=40°.解决该题型题目时,根据平行线的性质,找出相等或互补的角是解题技巧.三.解答题17.如图,点D、E在AB上,点F、G分别在BC、CA上,且DG∥BC,∠1=∠2.(1)求证:DC∥EF;(2)若EF⊥AB,∠1=55°,求∠ADG的度数.【答案】(1)见解析(2)35°【解析】【分析】(1)由知∠1=∠DCF,则∠2=∠DCF,即可证明;(2)由得∠B=90°-∠2=35°,再根据(1)可知的度数.【详解】∵∴∠1=∠DCF,∵∴∠2=∠DCF,∴;(2)∵,∴∠BEF=90°,∴∠B=90°-∠2=35°,又∵∴=∠B=35°.【点睛】此题主要考察平行线的性质与判定.18.如图,直线AB,CD相交于点O.OF平分∠AOE,OF⊥CD于点O.(1)请直接写出图中所有与∠AOC相等的角:______.(2)若∠AOD=150°,求∠AOE的度数.【答案】(1)∠BOD,∠DOE;(2)∠AOE=120°.【解析】【分析】(1)根据邻补角的定义确定出∠AOC和∠BOD,再根据角平分线的定义可得∠AOF=∠EOF,根据垂直的定义可得∠COF=∠DOF=90°,然后根据等角的余角相等求出∠DOE=∠AOC,从而最后得解;(2)根据垂直的定义得到∠DOF,根据角平分线的定义求出即可得到结论.【详解】解:(1)∵直线AB,CD相交于点O,∴∠AOC=∠BOD,∵OF平分∠AOE,∴∠AOF=∠EOF,∵OF⊥CD,∴∠COF=∠DOF=90°,∴∠DOE=∠AOC,∴与∠AOD相等的角有∠BOD,∠DOE,故答案为:∠BOD,∠DOE.(2)∵OF⊥CD,∴∠DOF=90°,∵∠AOD=150°,∴∠AOF=60°,∵OF平分∠AOE,∴∠AOE=2∠AOF=120°.【点睛】本题考查了垂线,余角和补角,对顶角相等的性质,角平分线的定义.19.如图,已知EF⊥BC,∠1=∠C,∠2+∠3=180°.试说明直线AD与BC垂直.(请在下面的解答过程的空格内填空或在括号内填写理由).理由:∵∠1=∠C,(已知)∴_______∥______,(_______)∴∠2=______.(______)又∵∠2+∠3=180°,(已知)∴∠3+_____=180°.(等量代换)∴______∥______,(______)∴∠ADC=∠EFC.(______)∵EF⊥BC,(已知)∴∠EFC=90°,∴∠ADC=90°,∴______⊥_____.【答案】略【解析】【分析】结合图形,根据平行线的判定和性质逐一进行填空即可.【详解】∵∠1=∠C,(已知)∴GD∥AC,(同位角相等,两直线平行)∴∠2=∠DAC.(两直线平行,内错角相等)又∵∠2+∠3=180°,(已知)∴∠3+∠DAC=180°.(等量代换)∴AD∥EF,(同旁内角互补,两直线平行)∴∠ADC=∠EFC.(两直线平行,同位角相等)∵EF⊥BC,(已知)∴∠EFC=90°,∴∠ADC=90°,∴AD⊥BC.故答案为:GD,AC,同位角相等,两直线平行;∠DAC,两直线平行,内错角相等;∠DAC;AD,EF,同旁内角互补,两直线平行;两直线平行,同位角相等;AD,BC.【点睛】本题考查平行线的判定和性质,已经垂线的定义,解题关键是注意平行线的性质和判定定理的综合运用.20.如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF.(1)求证:∠DAF=∠F;(2)在不添加任何辅助线的情况下,请直接写出所有与∠CED互余的角.【答案】(1)证明见解析;(2)与∠CED互余的角有∠ADE,∠CDE,∠F,∠FAD.【解析】【分析】(1)依据AB⊥BC于点B,DC⊥BC于点C,即可得到AB∥CF,进而得出∠BAF+∠F=180°,再根据∠BAF =∠EDF,即可得出ED∥AF,依据三角形外角性质以及角平分线的定义,即可得到∠DAF=∠F;(2)结合图形,根据余角的概念,即可得到所有与∠CED互余的角.【详解】解:(1)∵AB⊥BC于点B,DC⊥BC于点C,∴∠B+∠C=180°,∴AB∥CF,∴∠BAF+∠F=180°,又∵∠BAF=∠EDF,∴∠EDF+∠F=180°,∴ED∥AF,∴∠ADE=∠DAF,∠EDC=∠F,∵DE平分∠ADC,∴∠ADE=∠CDE,∴∠DAF=∠F;(2)∵∠C=90°,∴∠CED+∠CDE=90°,∴∠CED与∠CDE互余,又∵∠ADE=∠DAF=∠EDC=∠F,∴与∠CED互余的角有∠ADE,∠CDE,∠F,∠FAD.【点睛】本题主要考查了平行线的判定与性质、余角的概念,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.21.【探究】如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.(2)若∠AFH+∠CHF=100°,求∠FOH的度数.【拓展】如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)【答案】【探究】(1)30,125;(2)∠FOH=130°;【拓展】∠FOH=90°﹣α.【解析】【分析】(1)先根据角平分线的定义求出∠OFH,∠FHO的度数,再根据三角形的内角和定理求出∠FOH的度数;(2)先根据角平分线的定义求出∠OFH+∠FHO的度数,再根据三角形的内角和定理求出∠FOH的度数;(拓展)先根据角平分线的定义求出∠OFH=∠AFH,∠OHI=∠CHI=(180°-∠CHF),再根据两直线平行内错角相等得∠FOH=∠OHI﹣∠OFH即可。
新人教版七年级下册第五章《相交线与平行线》单元检测试卷(含答案解析)

人教版七年级下册数学第五章相交线与平行线单元练习卷一、填空题1.如图,直线AB,CD相交于点O, EO⊥AB于点O,∠EOD=50°,则∠BOC的度数为______.【答案】140°2.一条公路两次转弯后又回到原来的方向(即AB∥CD,如图),如果第一次转弯时的∠B=140°,那么,∠C应是____________。
【答案】140°3.如图边长为4cm的正方形ABCD先向上平移2cm,再向右平移1cm,得到正方形A′B′C′D′,此时阴影部分的面积为___________..【答案】6cm24.下列语句∶①对顶角相等;②OA是∠BOC的平分线;③相等的角都是直角;④线段AB.其中不是命题的是.【答案】④5.过直线外一点与已知直线平行【答案】有且只有一条直线6.如图,已知直线l1与l2交于点O,且∠1:∠2 =1:2,则∠3= ,∠4 = .【答案】60° 120°二、选择题7.下列说法正确的是( C )A.一个角的补角一定比这个角大B.一个角的余角一定比这个角小C.一对对顶角的两条角平分线必在同一条直线上D.有公共顶点并且相等的两个角是对顶角8.如图,能判定EC∥AB的条件是( D )A.∠B=∠ACE B.∠A=∠ECD C.∠B=∠ACB D.∠A=∠ACE9.如图所示,下列说法不正确的是(A)A. ∠与∠是同位角B. ∠与∠是同位角C. ∠与∠是同位角D. ∠与∠是同位角10.下列各图中,过直线l外的点P画l的垂线CD,三角尺操作正确的是( D )11.下列说法正确的有( B )①不相交的两条直线是平行线;②在同一平面内,两条直线的位置关系有两种;③若线段AB与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交.A.1个 B.2个 C.3个 D.4个12.如图,将△ABC沿AB方向平移至△DEF,且AB=5,DB=2,则CF的长度为( B )A.5B.3C.2D.113.下列语句中,是命题的是(A)①若∠1=60°,∠2=60°,则∠1=∠2;②同位角相等吗?③画线段AB=CD;④如果a>b,b>c,那么a>c;⑤直角都相等.A.①④⑤B.①②④C.①②⑤D.②③④⑤14.如图,直线AB,CD相较于点O,OE⊥AB于点O,若∠BOD=40°,则下列结论不正确的是( C )A.∠AOC=40°B.∠COE=130°C.∠EOD=40°D.∠BOE=90°15.如图,若∠A+∠B=180°,则有( D )A.∠B=∠C B.∠A=∠ADC C.∠1=∠B D.∠1=∠C16.如下图,在下列条件中,能判定AB//CD的是( C )A. ∠1=∠3B. ∠2=∠3C. ∠1=∠4D. ∠3=∠4三、解答题17.已知,如图,AB∥CD,∠EAB+∠FDC=180°。
人教版七年级数学下册第五章相交线与平行线单元测试卷(含答案)
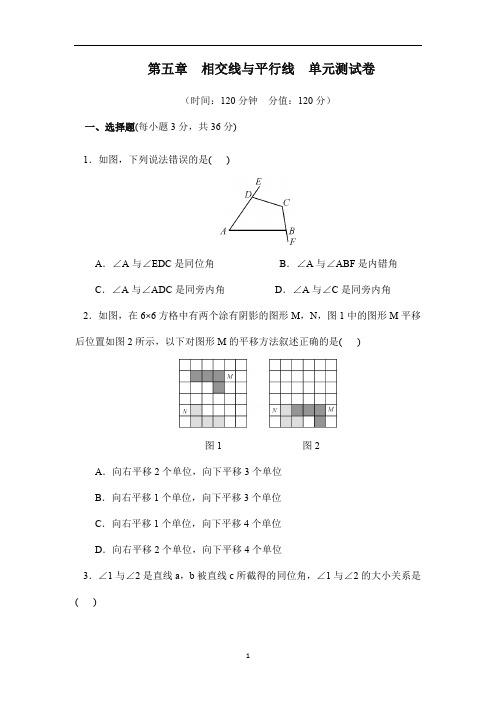
第五章相交线与平行线单元测试卷(时间:120分钟分值:120分)一、选择题(每小题3分,共36分)1.如图,下列说法错误的是( )A.∠A与∠EDC是同位角B.∠A与∠ABF是内错角C.∠A与∠ADC是同旁内角D.∠A与∠C是同旁内角2.如图,在6×6方格中有两个涂有阴影的图形M,N,图1中的图形M平移后位置如图2所示,以下对图形M的平移方法叙述正确的是( )图1 图2A.向右平移2个单位,向下平移3个单位B.向右平移1个单位,向下平移3个单位C.向右平移1个单位,向下平移4个单位D.向右平移2个单位,向下平移4个单位3.∠1与∠2是直线a,b被直线c所截得的同位角,∠1与∠2的大小关系是( )A.∠1=∠2 B.∠1>∠2C.∠1<∠2 D.无法确定4.如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是( )A.∠2=70° B.∠2=100°C.∠2=110° D.∠3=110°5.对于图中标记的各角,下列条件能够推理得到a∥b的是( )A.∠1=∠2 B.∠2=∠4C.∠3=∠4 D.∠1+∠4=180°6.如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,那么∠ACD的度数为( )A.40° B.35° C.50° D.45°7.如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )A.∠EMB=∠END B.∠BMN=∠MNCC.∠CNH=∠BPG D.∠DNG=∠AME8.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=( )A.60° B.120° C.150° D.180°9.如图,AB∥CD,EF∥AB,AE∥MN,BF∥MN,由图中字母标出的互相平行的直线共有( )A.4组B.5组C.6组D.7组10.下列说法正确的有( )①在平面内,过直线上一点有且只有一条直线垂直于已知直线;②在平面内,过直线外一点有且只有一条直线垂直于已知直线;③在平面内,可以过任意一点画一条直线垂直于已知直线;④在平面内,有且只有一条直线垂直于已知直线.A.1个B.2个C.3个D.4个11.点P为直线l外一点,点A,B,C为直线上三点,PA=2 cm,PB=3 cm,PC=4 cm,则点P到直线l的距离为( )A.等于2 cm B.小于2 cmC.大于2 cm D.不大于2 cm12.下列说法正确的是( )A.“作线段CD=AB”是一个命题B.过一点作已知直线的平行线有一条且只有一条C.命题“若x=1,则x2=1”是真命题D.所含字母相同的项是同类项二、填空题(每小题4分,共24分)13.如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东.14.一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD=.15.在同一平面内,一条直线和两条平行线中的一条直线相交,那么这条直线与平行线中的另一条直线必.16.如图,直线AB,CD相交于点O,若∠AOC=90°,则AB与CD的位置关系是;若已知AB⊥CD,则∠AOC=∠COB=∠BOD=∠AOD=.17.如图,田径运动会上,七年级二班的小亮同学从C点起跳,假若落地点是D.当AB与CD 时,他跳得最远.18.如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=.三、解答题(共60分)19.(8分)如图,用几何语言表示下列句子.(1)因为∠1和∠B相等,根据“同位角相等,两直线平行”,所以DE和BC 平行;(2)因为∠1和∠2相等,根据“内错角相等,两直线平行”,所以AB和EF平行;(3)因为∠BDE和∠B互补,根据“同旁内角互补,两直线平行”,所以DE 和BC平行.20.(8分)如图,张三打算在院落里种上蔬菜,已知院落为东西长32 m,南北宽20 m的长方形,为了行走方便,要修筑同样宽的三条道路:东西两条,南北一条,南北道路垂直于东西道路,余下的部分要分别种上西红柿、青椒、菜豆、黄瓜等蔬菜,若每条道路的宽均为1 m,求蔬菜的总种植面积是多少?21.(8分)如图,直线EF分别与直线AB,CD相交于点P和点Q,PG平分∠APQ,QH平分∠DQP,并且∠1=∠2,说出图中哪些直线平行,并说明理由.22.(8分)某次考古发掘出的一个梯形残缺玉片,工作人员从玉片上量得∠A =115°,∠D=100°,已知梯形的两底AD∥BC,请你帮助工作人员求出另外两个角的度数,并说明理由.23.(8分)如图,两直线AB,CD相交于点O,OE平分∠BOD,如果∠AOC∶∠AOD=7∶11.(1)求∠COE;(2)若OF⊥OE,求∠COF.24.(8分)如图,直线AB和直线CD,直线BE和直线CF都被直线BC所截.在下面三个条件中,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并证明.①AB⊥BC,CD⊥BC,②BE∥CF,③∠1=∠2.25.(12分)阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.参考答案第五章相交线与平行线单元测试卷(时间:120分钟分值:120分)一、选择题(每小题3分,共36分)1.如图,下列说法错误的是(D)A.∠A与∠EDC是同位角B.∠A与∠ABF是内错角C.∠A与∠ADC是同旁内角D.∠A与∠C是同旁内角2.如图,在6×6方格中有两个涂有阴影的图形M,N,图1中的图形M平移后位置如图2所示,以下对图形M的平移方法叙述正确的是(B)图1 图2A.向右平移2个单位,向下平移3个单位B.向右平移1个单位,向下平移3个单位C.向右平移1个单位,向下平移4个单位D.向右平移2个单位,向下平移4个单位3.∠1与∠2是直线a,b被直线c所截得的同位角,∠1与∠2的大小关系是(D)A.∠1=∠2 B.∠1>∠2C.∠1<∠2 D.无法确定4.如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是(C)A.∠2=70° B.∠2=100°C.∠2=110° D.∠3=110°5.对于图中标记的各角,下列条件能够推理得到a∥b的是(D)A.∠1=∠2 B.∠2=∠4C.∠3=∠4 D.∠1+∠4=180°6.如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,那么∠ACD的度数为(A)A.40° B.35° C.50° D.45°7.如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是(D)A.∠EMB=∠END B.∠BMN=∠MNCC.∠CNH=∠BPG D.∠DNG=∠AME8.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=(A)A.60° B.120° C.150° D.180°9.如图,AB∥CD,EF∥AB,AE∥MN,BF∥MN,由图中字母标出的互相平行的直线共有(C)A.4组B.5组C.6组D.7组10.下列说法正确的有(C)①在平面内,过直线上一点有且只有一条直线垂直于已知直线;②在平面内,过直线外一点有且只有一条直线垂直于已知直线;③在平面内,可以过任意一点画一条直线垂直于已知直线;④在平面内,有且只有一条直线垂直于已知直线.A.1个B.2个C.3个D.4个11.点P为直线l外一点,点A,B,C为直线上三点,PA=2 cm,PB=3 cm,PC=4 cm,则点P到直线l的距离为(D)A.等于2 cm B.小于2 cmC.大于2 cm D.不大于2 cm12.下列说法正确的是(C)A.“作线段CD=AB”是一个命题B.过一点作已知直线的平行线有一条且只有一条C.命题“若x=1,则x2=1”是真命题D.所含字母相同的项是同类项二、填空题(每小题4分,共24分)13.如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东42°.14.一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD=270°.15.在同一平面内,一条直线和两条平行线中的一条直线相交,那么这条直线与平行线中的另一条直线必相交.16.如图,直线AB,CD相交于点O,若∠AOC=90°,则AB与CD的位置关系是垂直;若已知AB⊥CD,则∠AOC=∠COB=∠BOD=∠AOD=90°.17.如图,田径运动会上,七年级二班的小亮同学从C点起跳,假若落地点是D.当AB与CD垂直时,他跳得最远.18.如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=110°.三、解答题(共60分)19.(8分)如图,用几何语言表示下列句子.(1)因为∠1和∠B相等,根据“同位角相等,两直线平行”,所以DE和BC 平行;(2)因为∠1和∠2相等,根据“内错角相等,两直线平行”,所以AB和EF 平行;(3)因为∠BDE和∠B互补,根据“同旁内角互补,两直线平行”,所以DE 和BC平行.解:(1)∵∠1=∠B(已知),∴DE∥BC(同位角相等,两直线平行).(2)∵∠1=∠2(已知),∴EF∥AB(内错角相等,两直线平行).(3)∵∠BDE+∠B=180°(已知),∴DE∥BC(同旁内角互补,两直线平行).20.(8分)如图,张三打算在院落里种上蔬菜,已知院落为东西长32 m,南北宽20 m的长方形,为了行走方便,要修筑同样宽的三条道路:东西两条,南北一条,南北道路垂直于东西道路,余下的部分要分别种上西红柿、青椒、菜豆、黄瓜等蔬菜,若每条道路的宽均为1 m,求蔬菜的总种植面积是多少?解:如图,将三条道路都平移到边上去,则空白部分的面积(即蔬菜的总种植面积)不变,因此,蔬菜的总种植面积为(20-2×1)(32-1)=558(m2).21.(8分)如图,直线EF分别与直线AB,CD相交于点P和点Q,PG平分∠APQ,QH平分∠DQP,并且∠1=∠2,说出图中哪些直线平行,并说明理由.解:PG∥QH,AB∥CD.∵PG平分∠APQ,QH平分∠DQP,∴∠1=∠GPQ=12∠APQ,∠PQH=∠2=12∠PQD.又∵∠1=∠2,∴∠GPQ=∠PQH,∠APQ=∠PQD.∴PG∥QH,AB∥CD.22.(8分)某次考古发掘出的一个梯形残缺玉片,工作人员从玉片上量得∠A =115°,∠D=100°,已知梯形的两底AD∥BC,请你帮助工作人员求出另外两个角的度数,并说明理由.解:∵AD∥BC,∠A=115°,∠D=100°,∴∠B=180°-∠A=180°-115°=65°,∠C=180°-∠D=180°-100°=80°.23.(8分)如图,两直线AB,CD相交于点O,OE平分∠BOD,如果∠AOC∶∠AOD=7∶11.(1)求∠COE;(2)若OF⊥OE,求∠COF.解:(1)因为∠AOC∶∠AOD=7∶11,∠AOC+∠AOD=180°,所以∠AOC=70°,∠AOD=110°.所以∠BOD=∠AOC=70°,∠BOC=∠AOD=110°.又因为OE平分∠BOD,所以∠BOE=∠DOE=12∠BOD=35°.所以∠COE=∠BOC+∠BOE=110°+35°=145°.(2)因为OF⊥OE,所以∠FOE=90°.所以∠FOD=∠FOE-∠DOE=90°-35°=55°.24.(8分)如图,直线AB和直线CD,直线BE和直线CF都被直线BC所截.在下面三个条件中,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并证明.①AB⊥BC,CD⊥BC,②BE∥CF,③∠1=∠2.解:答案不唯一,如:已知:如图,AB⊥BC,CD⊥BC,BE∥CF.求证:∠1=∠2.证明:∵AB⊥BC,CD⊥BC,∴AB∥CD,∠ABC=∠DCB=90°.又∵BE∥CF,∴∠EBC=∠FCB.∴∠ABC-∠EBC=∠DCB-∠FCB,即∠1=∠2.25.(12分)阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.解:过点P作PE∥AB.∵AB∥CD,∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).∴∠1+∠A=180°(两直线平行,同旁内角互补),∠2+∠C=180°(两直线平行,同旁内角互补).∴∠1+∠A+∠2+∠C=360°.又∵∠APC=∠1+∠2,∴∠APC+∠A+∠C=360°.如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C 之间的关系.解:如图乙,过点P作PE∥AB.∵AB∥CD(已知),∴PE∥AB∥CD(平行于同一直线的两条直线平行).∴∠A=∠EPA,∠EPC=∠C(两直线平行,内错角相等).∵∠APC=∠EPA+∠EPC,∴∠APC=∠A+∠C(等量代换).如图丙,过点P作PF∥AB.∴∠FPA=∠A(两直线平行,内错角相等).∵AB∥CD(已知),∴PF∥CD(平行于同一直线的两条直线平行).∴∠FPC=∠C(两直线平行,内错角相等).∵∠FPC-∠FPA=∠APC,∴∠C-∠A=∠APC(等量代换).。
最新人教版七年级下册第五章《相交线与平行线》单元测试及答案

人教版七年级下册第 5 章订交线与平行线能力水平测试卷一.选择题(共10 小题)1.如图,直线AB,CD 订交于点O,OE,OF,OG分别是∠ AOC,∠ BOD,∠ BOC 的均分线,以下说法不正确的选项是()A.∠ DOF与∠ COG 互为余角B.∠ COG与∠ AOG 互为补角C.射线 OE,OF不必定在同一条直线上D.射线 OE,OG 相互垂直2.如图,直线AB、CD订交于点O,EO⊥ AB,垂足为 O,∠ EOC=35° 15′.则∠ AOD 的度数为()A.55° 15′B. 65°15′C.125° 15′D. 165°15′3.如图 ,∠ ACB=90° ,CD⊥ AB,垂足为 D,则点 B 到直线 CD的距离是指()A.线段 BC的长度B.线段 CD的长度C.线段 AD 的长度D.线段 BD 的长度4.在以下图形中,由∠1=∠ 2 必定能获得AB∥ CD 的是()A.B.C.D.5.如图,以下条件:①∠1=∠2,②∠ 3+∠4=180 °,③∠ 5+∠ 6=180 °,④∠ 2=∠ 3,⑤∠ 7=∠ 2+∠3,⑥∠ 7+∠4-∠ 1=180°中能判断直线a∥ b 的有()A.3 个B.4 个C.5 个D.6 个6.以下命题中是假命题的是()A.过一点有且只有一条直线与已知直线平行B.同角(或等角)的余角相等C.两点确立一条直线D.两点之间的全部连线中,线段最短7.如图,直线EF分别交 AB、CD 于点 E、F,EG均分∠ BEF,AB∥ CD.若∠ 1=72 °,则∠ 2 的度数为()A.54°B. 59°C.72°D. 108 °A、B 两8.已知直线m∥ n,将一块含30°角的直角三角板ABC,按如下图方式搁置,此中点分别落在直线m、 n 上,若∠ 1=25°,则∠ 2 的度数是()A.25°B. 30°C. 35°D.55°9.如图,将三角板与直尺贴在一同,使三角板的直角极点C(∠ ACB=90°)在直尺的一边上,若∠ 2=56°,则∠ 1的度数等于()A.54°B. 44°C. 24°D.34°10.如图在一块长为12m, 宽为 6m 的长方形草地上,有一条曲折的柏油小道(小道任何地方的水平宽度都是2m)则空白部分表示的草地面积是()A.70B. 60C. 48D.18二.填空题(共 6 小题)11.如图,∠ 1=15° ,∠ AOC=90°,点 B、 O、 D 在同向来线上,则∠2的度数为.12.命题“同位角相等”的抗命题是13.如图,直线 a,b 与直线 c 订交,给出以下条件:①∠ 1=∠ 2;②∠ 3=∠ 6;③∠ 4+∠7=180 °;④∠ 5+∠ 3=180°;⑤∠ 6=∠ 8,此中能判断a∥ b 的是(填序号)14.如图,∠ A=70°,O 是 AB 上一点,直线OD 与 AB 所夹的∠ AOD=100°,要使 OD∥ AC,直线OD 绕点 O 按逆时针方向起码旋转.15.将一块 60°的直角三角板DEF搁置在 45°的直角三角板ABC上,挪动三角板DEF使两条直角边DE、 DF恰分别经过B、 C 两点,若EF∥ BC,则∠ ABD=°.16.在长为 a(m), 宽为 b(m)一块长方形的草坪上修了一条宽2(m)的笔挺小道,则余下草坪的面积可表示为m2;先为了增添美感,把这条小道改为宽恒为2(m) 的曲折小道(如图),则此时余下草坪的面积为m2.三.解答题(共7 小题)17.如图,直线AB 和直线 CD 订交于点 O,已知∠ AOC=30°,作 OE均分∠ BOD.(1)求∠ AOE 的度数;(2)作 OF⊥ OE,请说明 OF 均分∠ AOD 的原因.18.如图, AB、 CD 交于点 O,∠ AOE=4∠ DOE,∠ AOE 的余角比∠ DOE小 10°(题中所说的角均是小于平角的角).(1)求∠ AOE 的度数;(2)请写出∠ AOC在图中的全部补角;(3)从点 O 向直线 AB 的右边引出一条射线 OP,当∠ COP=∠ AOE+∠ DOP 时,求∠ BOP 的度数.19.如图, OD 是∠ AOB 的均分线 ,∠ AOC=2∠BOC.(1)若 AO⊥ CO,求∠ BOD 的度数;(2)若∠ COD=21°,求∠ AOB 的度数.20.填空或标注原因:如图,已知∠ 1=∠ 2,∠A=∠ D,试说明: AE∥ BD证明:∵∠ 1=∠ 2(已知)∴AB∥ CD()∴∠ A=()()∵∠ A=∠ D(已知)∴=∠D()∴AE∥ BD()21.如图,已知点D、E、B、C 分别是直线m、 n 上的点,且m∥ n,延伸 BD、CE交于点 A,DF 均分∠ ADE,若∠ A=40° ,∠ ACB=80°.求:∠ DFE的度数.22.如图,直线A B∥ CD,而且被直线 MN 所截, MN 分别交 AB 和 CD于点 E、 F,点 Q 在 PM 上,且∠ AEP=∠ CFQ.求证:∠ EPM=∠ FQM.23.如图,在 6× 6 的正方形网格中,每个小正方形的边长为1,点 A、B、C、D、E、F、M 、N、 P 均为格点(格点是指每个小正方形的极点).(1)利用图①中的网格,过P 点画直线MN 的平行线和垂线.(2)把图②网格中的三条线段AB、CD、EF经过平移使之首尾按序相接构成一个三角形(在图②中画出三角形).(3)第( 2)小题中线段AB、 CD、EF首尾按序相接构成一个三角形的面积是.答案:1-5CCDAC6-10 AACDB11. 10512.相等的角是同位角13.①③④⑤14.10 °15.1516.( ab-2a) , ( ab-2a)17.解:( 1)∵∠ AOC=30°,∴∠ BOD=∠AOC=30°,∵OE均分∠ BOD,∴∠ EOB=15°,∴∠ AOE=180° -15 °=165°,(2)∵∠ AOC=30°,∴∠ AOD180° -30 ° =150°,∵∠ DOE=∠EOB=15°,∵OF⊥ OE,∴∠ EOF=90°,∴∠ DOF=90° -15 ° =75°,∴∠ DOF=∠AOF=150° -75 ° =75°,∴OF均分∠ AOD18.解:( 1)设∠ DOE=x,则∠ AOE=4x,∵∠ AOE的余角比∠ DOE小 10°,∴90° -4x=x-10°,∴x=20°,∴∠ AOE=80°;(2)∠ AOC 在图中的全部补角是∠ AOD 和∠ BOC;(3)∵∠ AOE=80°,∠ DOE=20°,∴∠ AOD=100°,∴∠ AOC=80°,如图,当OP 在 CD 的上方时,设∠ AOP=x,∴∠ DOP=100° -x,∵∠ COP=∠ AOE+∠ DOP,∴80° +x=80°+100° -x,∴x=50°,∴∠ AOP=∠ DOP=50°,∵∠ BOD=∠AOC=80°,∴∠ BOP=80° +50°=130°;当OP 在CD 的下方时,设∠ DOP=x,∴∠ BOP=80° -x,∵∠COP=∠AOE+∠DOP,∴100° +x=80° +80° -x,∴x=30°,∴∠BOP=30°,综上所述,∠ BOP的度数为 130°或 30°.19.解:( 1)∵ AO⊥ CO,∴∠ AOC=90°,∵∠ AOC=2∠ BOC,∴∠ BOC=45°,∴∠ AOB=∠AOC+∠ BOC=135°,∵OD是∠ AOB的均分线,∴∠ BOD=∠ AOB=67.5°;(2)∵∠ AOC=2∠ BOC,∴∠ AOB=3∠ BOC,∵OD是∠ AOB的均分线,∴∠ BOD=∠ AOB=∠ BOC,∵∠ COD=21°,∴21° +∠ BOC=∠ BOC,∴∠ BOC=42°,∴∠ AOB=3∠ BOC=126°.20. 故答案为:内错角相等,两直线平行;∠AEC;两直线平行,内错角相等;∠AEC;等量代换;同位角相等,两直线平行.21.解:∵ m∥n,∠ ACB=80°∴∠ AED=∠ACB=80°,∵∠ A=40°,∴△ ADE中,∠ ADE=180° - (∠ A+∠ AED) =180°- ( 40°+80°) =60°,七年级人教版数学下册第 5 章订交线与平行线单元测试题人教版七年级数学下册第 5 章订交线与平行线单元检测题一、选择题:1.下边四个语句:(1)只有铅垂线和水平线才是垂直的;(2)经过一点起码有一条直线与已知直线垂直;(3)垂直于同一条直线的垂线只有两条;(4)两条直线订交所成的四个角中,假如此中有一个角是直角,那么其他三个角也必定相等.此中错误的选项是()A. ( 1)( 2)( 4)B. ( 1)( 3)( 4)C.( 2)( 3)( 4)D.(1)( 2)( 3)2.点 P为直线 MN外一点 , 点 A、B、C为直线 MN上三点 ,PA=4 厘米 ,PB=5 厘米 ,PC=2 厘米 , 则 P到直线MN的距离为()A.4 厘米B.2厘米C.小于2厘米D.不大于2厘米3.如图 , 以下结论错误的选项是()A. ∠1与∠ B是同位角B.∠ 1与∠ 3 是同旁内角C. ∠2与∠ C是内错角D.∠ 4与∠ A是同位角4.如图, AB∥CD, CD⊥EF,若∠ 1=125°,则∠ 2=()A.25 °B.35°C.55°D.65°5.如图, a∥ b,将三角尺的直角极点放在直线 a 上,若∠ 1=40°,则∠ 2=()A.30 °B.40°C.50°D.60 °6. 将如下图的图案经过平移后能够获得的图案是()A. B. C. D.7.如图,AB ∥ CD,AE 均分∠CAB交 CD于点 E, 若∠C=50°, 则∠AED=()A.65 °B.115 °C.125 °D.130 °8.如图, AE∥BD,∠ 1=120°,∠ 2=40°,则∠ C的度数是()A.10 °B.20°C.30°D.40°9.如下图,已知AB∥CD, EF均分∠ CEG,∠ 1=80°,则∠ 2 的度数为 ()A.20°B.40°C.50°D.60°10.如图,若两条平行线EF, MN与直线 AB, CD订交,则图中共有同旁内角的对数为()A.4B.8C.12D.1611. 以下条件中能获得平行线的是()①邻补角的角均分线;②平行线内错角的角均分线;③平行线同旁内角的角均分线.A. ①②B.②③人教版七年级数学下册第 5 章订交线与平行线单元测试题(分析版)一.选择题(共10 小题)1.如图各图中,∠ 1 与∠ 2 是对顶角的是()A.B.C.D.2.以下表达中正确的选项是()A.相等的两个角是对顶角B.若∠ 1+∠2+ ∠ 3= 180°,则∠ 1,∠ 2,∠ 3 互为补角C.和等于 90°的两个角互为余角D.一个角的补角必定大于这个角3.在如图图形中,线段PQ 能表示点P 到直线 L 的距离的是()A.B.C.D.4.在以下图形中,由条件∠1+∠ 2= 180°不可以获得AB∥ CD 的是()A.B.C.D.5.如图,已知∠1=68°,要使AB∥ CD ,则须具备另一个条件()A .∠ 2= 112°B .∠ 2= 122°C.∠ 2=68°D.∠ 3= 112°6.如下图,点 E 在AC 的延伸线上,以下条件中能判断AB∥ CD ()A.∠1=∠2B.∠3=∠ 4C.∠ D =∠ DCE D.∠D +∠ ACD= 180°7.如图,直线a∥ b, AC⊥ AB, AC 交直线 b 于点C,∠1=55°,则∠ 2 的度数是()A .35°B .25°C. 65°D. 50°8.如图,已知AB∥ DE,∠ ABC = 75°,∠ CDE = 145°,则∠BCD的值为()A .20°B .30°C. 40°D. 70°9.如下图是一条街道的路线图,若 AB∥ CD ,且∠ ABC = 130°,那么当∠CDE等于()时, BC∥ DE.A .40°B .50°C. 70°D. 130°10.如图,在直角三角形ABC 中,∠ BAC= 90°, AB= 3,AC= 4,将△ ABC 沿直线 BC 平移 2.5 个单位获得三角形DEF ,连结 AE.有以下结论:① AC∥ DF;② AD∥BE,AD=BE ABE DEF ED ACA.4 个B.3 个C.2 个D.1 个二.填空题(共8 小题)11.在体育课上某同学立定跳远的状况如下图,l 表示起跳线,在丈量该同学的实质立定跳远成绩时,应丈量图中线段PC 的长,原因是.12.如图,直线 AD 与 BE 订交于点O,∠ COD = 90°,∠COE = 70°,则∠ AOB=.13.如图,直线a, b 与直线 c 订交,给出以下条件:① ∠ 1=∠ 2;② ∠ 3=∠ 6;③ ∠ 4+∠ 7= 180°;④ ∠ 5+∠ 3= 180°;⑤ ∠ 6=∠ 8,此中能判断a∥b 的是(填序号)14.如图:请你增添一个条件能够获得DE∥AB15.如图, AB∥ EF ,设∠ C= 90°,那么x, y,z 的关系是.16.如图,将一张矩形纸片按图中方式折叠,若∠1= 63°,则∠ 2 为度.17.如图,已知长方形纸片的一条边经过直角三角形纸片的直角极点,则图中∠1与∠2之间的数目关系为.18.如下图,一块正方形地板,边长60cm,上边横竖各有两道宽为5cm 的花纹(图中阴影部分),空白部分的面积是.三.解答题(共7 小题)19.如图,点O 在直线 AB 上, CO⊥ AB,∠ BOD﹣∠ COD = 34°,求∠ AOD 的度数.20.如图, AO⊥ CO, DO⊥ BO.(1)∠ AOD 与∠ BOC 相等吗?为何?(2)已知∠ AOB= 140°,求∠ COD 的度数.21.已知:如图,直线AB 与 CD 被 EF 所截,∠ 1=∠ 2,求证: AB∥ CD .22.如图,∠ DAC +∠ACB= 180°, CE 均分∠ BCF ,∠ FEC =∠ FCE ,∠ DAC = 3∠ BCF ,∠ACF =20°.(1)求证: AD ∥ EF;(2)求∠ DAC、∠ FEC 的度数.23.如图,在△ ABC 中,GD ⊥ AC 于点 D,∠AFE =∠ ABC,∠1+∠ 2= 180°,∠ AEF =65°,求∠ 1 的度数.解:∠ AFE =∠ ABC(已知)∴(同位角相等,两直线平行)∴∠ 1=∠(两直线平行,内错角相等)∠ 1+∠2= 180°(已知)∴(等量代换)∴EB∥ DG∴∠ GDE=∠ BEAGD⊥ AC(已知)∴(垂直的定义)∴∠ BEA=90°(等量代换)∠ AEF = 65°(已知)∴∠ 1=∠﹣∠= 90°﹣ 65°= 25°(等式的性质)24.如图,已知∠1=∠ 2= 50°, EF∥ DB .(1)DG 与 AB 平行吗?请说明原因.(2)若 EC 均分∠ FED ,求∠ C 的度数.25.直线AB、 CD 被直线EF 所截, AB∥ CD ,点 P 是平面内一动点.设∠PFD =∠ 1,∠PEB=∠ 2,∠ FPE =∠α.( 1)若点 P 在直线 CD 上,如图①,∠α= 50°,则∠ 1+∠ 2=°;(2)若点 P 在直线 AB、CD 之间,如图②,试猜想∠α、∠ 1、∠ 2 之间的等量关系并给出证明;(3)若点 P 在直线 CD 的下方,如图③,( 2)中∠α、∠ 1、∠2 之间的关系还建立吗?请作出判断并说明原因.人教版七年级数学下册第 5 章订交线与平行线单元测试题参照答案与试题分析一.选择题(共10 小题)1.【剖析】依据对顶角的定义判断即可.【解答】解:依据两条直线订交,才能构成对顶角进行判断,A、C、 B 都不是由两条直线订交构成的图形,错误,D是由两条直线订交构成的图形,正确,应选: D.【评论】本题主要考察了对顶角的定义,有一个公共极点,而且一个角的两边分别是另一个角的两边的反向延伸线,拥有这类地点关系的两个角,互为对顶角.2.【剖析】依据余角、补角、对顶角的定义进行判断即可.【解答】解: A、两个对顶角相等,但相等的两个角不必定是对顶角;故 A 错误;B、余、补角是两个角的关系,故 B 错误;C、假如两个角的和是一个直角,那么这两个角互为余角;故 C 正确;D 、锐角的补角都大于这个角,而直角和钝角不切合这样的条件,故 D 错误.应选: C.【评论】本题考察对顶角的定义,余角和补角.若两个角的和为90°,则这两个角互余;若两个角的和等于180°,则这两个角互补.3.【剖析】依据直线外一点到这条直线的垂线段的长度,叫做点到直线的距离的观点判断.P 到直【解答】解:图A、B、C中,线段PQ不与直线L 垂直,故线段PQ 不可以表示点线 L 的距离;图 D 中,线段 PQ 与直线 L 垂直,垂足为点 Q,故线段 PQ 能表示点 P 到直线 L 的距离;应选:D.【评论】本题考察了点到直线的距离的观点,重点是依据直线外一点到这条直线的垂线段的长度,叫做点到直线的距离的观点解答.4.【剖析】在三线八角的前提下,同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.据此判断即可.【解答】解: A、∠ 1 的对顶角与∠ 2 的对顶角是同旁内角,它们互补,因此能判断AB∥CD;B、∠ 1 的对顶角与∠ 2 是同旁内角,它们互补,因此能判断AB∥ CD;C、∠ 1 的邻补角∠BAD =∠ 2,因此能判断AB∥CD ;D 、由条件∠ 1+ ∠ 2=180°能获得AD ∥ BC,不可以判断AB∥ CD;应选: D.【评论】本题考察了平行线的判断,解题的重点是注意平行判断的前提条件一定是三线八角.5.【剖析】欲证 AB∥ CD,在图中发现AB、CD 被向来线所截,且已知∠ 1= 68°,故可按同旁内角互补,两直线平行增补条件.【解答】解:∵∠ 1= 68°,∴只需∠ 2= 180°﹣ 68°= 112°,即可得出∠ 1+∠2= 180°.应选: A.【评论】本题主要考察了判断两直线平行的问题,可环绕截线找同位角、内错角和同旁内角.本题是一道探究性条件开放性题目,能有效地培育学生“执果索因”的思想方式与能力.6.【剖析】依据平行线的判断分别进行剖析可得答案.【解答】解: A、依据内错角相等,两直线平行可得AB∥ CD,故此选项正确;B、依据内错角相等,两直线平行可得C、依据内错角相等,两直线平行可得 D 、依据同旁内角互补,两直线平行可得应选: A.BD ∥AC,故此选项错误;BD ∥AC,故此选项错误;BD ∥ AC,故此选项错误;【评论】本题主要考察了平行线的判断,解答此类要判断两直线平行的题,可环绕截线找同位角、内错角和同旁内角.7.【剖析】依据平行线的性质求出∠3,再求出∠ BAC= 90°,即可求出答案.【解答】解:∵直线a∥b,∴∠ 1=∠ 3= 55°,∵AC⊥ AB,∴∠ BAC= 90°,∴∠ 2= 180°﹣∠ BAC﹣∠ 3= 35°,应选: A.【评论】本题考察了平行线的性质的应用,注意:平行线的性质有① 两直线平行,同位角相等,② 两直线平行,内错角相等,③ 两直线平行,同旁内角互补.8.【剖析】延伸 ED 交 BC 于 F,依据平行线的性质求出∠MFC =∠ B= 75°,求出∠ FDC = 35°,依据三角形外角性质得出∠C=∠ MFC ﹣∠ MDC ,代入求出即可.【解答】解:延伸ED 交 BC 于 F,如下图:∵AB∥DE ,∠ABC=75°,∴∠ MFC =∠ B= 75°,∵∠ CDE= 145°,∴∠ FDC = 180°﹣ 145°= 35°,∴∠ C=∠ MFC ﹣∠ MDC = 75°﹣ 35°= 40°,应选: C.【评论】本题考察了三角形外角性质,平行线的性质的应用,解本题的重点是求出∠ MFC 的度数,注意:两直线平行,同位角相等.9.【剖析】第一利用平行线的性质定理获得∠BCD = 130°,而后利用同旁内角互补两直线平行获得∠ CDE 的度数即可.【解答】解:∵ AB∥CD ,且∠ ABC = 130°,∴∠ BCD=∠ ABC= 130°,∵当∠ BCD +∠ CDE = 180°时 BC∥ DE,∴∠ CDE= 180°﹣∠ BCD= 180°﹣ 130°= 50°,应选: B.【评论】本题考察了平行线的判断与性质,注意平行线的性质与判断方法的差别与联系.10.【剖析】依据平移的性质获得AC∥ DF ,AB∥ DE ,AD ∥ CF,AD = CF= 2.5,∠ EDF =∠BAC=90°,则利用平行线的性质得∠ ABE=∠ DEF ,利用垂直的定义得 DE ⊥ DF ,于是依据平行线的性质可判断 DE⊥ AC.【解答】解:∵将△ ABC 沿直线向右平移 2.5 个单位获得△ DEF ,∴ AC∥ DF ,AB ∥ DE,AD ∥ CF , AD= CF = 2.5,∠ EDF =∠ BAC=90°,∴∠ ABE=∠ DEF ,DE⊥ DF ,∴ DE⊥ AC,∴ ①②③④ 都正确.应选: A.【评论】本题考察了平移的性质:把一个图形整体沿某向来线方向挪动,会获得一个新的图形,新图形与原图形的形状和大小完整同样;新图形中的每一点,都是由原图形中的某一点挪动后获得的,这两个点是对应点.连结各组对应点的线段平行(或共线)且相等.二.填空题(共8 小题)11.【剖析】依据垂线段的性质:垂线段最短进行解答即可.【解答】解:这样做的原因是依据垂线段最短.故答案为:垂线段最短.【评论】本题主要考察了垂线段的性质,重点是掌握性质定理.12.【剖析】由题意可知∠DOE= 90°﹣∠ COE,∠ AOB 与∠ DOE 是对顶角相等,由此得解.【解答】解:∵已知∠COD = 90°,∠ COE= 70°,∴∠ DOE= 90°﹣ 70°= 20°,又∵∠ AOB 与∠ DOE 是对顶角,∴∠ AOB=∠ DOE= 20°,故答案为: 20°.【评论】本题考察了对顶角与邻补角,利用余角的定义、对顶角的性质是解题重点.13.【剖析】直接利用平行线的判断方法分别剖析得出答案.【解答】解:① ∵∠ 1=∠ 2,∴ a∥ b,故此选项正确;② ∠ 3=∠ 6 没法得出a∥b,故此选项错误;③ ∵∠ 4+∠ 7= 180°,∴ a∥ b,故此选项正确;④ ∵∠ 5+∠ 3= 180°,∴∠ 2+∠ 5= 180°,∴ a∥ b,故此选项正确;⑤ ∵∠ 7=∠ 8,∠ 6=∠ 8,∴∠ 6=∠ 7,∴a∥ b,故此选项正确;综上所述,正确的有①③④⑤ .故答案为:①③④⑤ .【评论】本题主要考察了平行线的判断,正确掌握平行线的几种判断方法是解题重点.14.【剖析】依照平行线的判断条件进行增添,即内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行.【解答】解:若∠ EDC =∠ C 或∠ E=∠ EBC 或∠ E+∠ EBA=180°,则 DE∥ AB,故答案为:∠ EDC=∠ C 或∠ E=∠ EBC 或∠ E+∠ EBA= 180°等.【评论】本题主要考察了平行线的判断,正确辨别“三线八角”中的同位角、内错角、同旁内角是正确答题的重点,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.15.【剖析】过 C 作 CM ∥AB ,延伸 CD 交 EF 于 N,依据三角形外角性质求出∠CNE= y ﹣z,依据平行线性质得出∠ 1= x,∠ 2=∠ CNE ,代入求出即可.【解答】解:过 C 作 CM∥ AB,延伸 CD 交 EF 于 N,则∠ CDE=∠ E+∠ CNE,即∠ CNE= y﹣ z∵CM∥ AB,AB∥ EF,∴CM∥ AB∥EF,∴∠ ABC= x=∠ 1,∠ 2=∠ CNE,∵∠ BCD= 90°,∴∠ 1+∠ 2= 90°,∴x+y﹣ z=90°,∴z+90 °= y+x,即 x+y﹣ z= 90°.【评论】本题考察了平行线的性质和三角形外角性质的应用,注意:平行线的性质有:① 两直线平行,同位角相等,② 两直线平行,内错角相等,③ 两直线平行,同旁内角互补,题目比较好,难度适中.16.【剖析】依据平行线的性质和平角的定义即可获得结论.【解答】解:∵ a∥ b,∴∠ 5=∠ 1= 63°,∠ 2=∠ 3,又由折叠的性质可知∠4=∠ 5,且∠ 3+∠ 4+∠ 5= 180°,∴∠ 3= 180°﹣∠ 5﹣∠ 4= 54°,∴∠ 2= 54°,故答案为: 54.【评论】本题主要考察平行线的性质和判断,掌握平行线的判断和性质是解题的重点,即①两直线平行 ? 同位角相等,②两直线平行 ? 内错角相等,③两直线平行 ? 同旁内角互补,④ a∥ b, b∥ c? a∥c.17.【剖析】先依据平角的定义得出∠3= 180°﹣∠ 2,再由平行线的性质得出∠4=∠ 3,依据∠ 4+∠ 1= 90°即可得出结论.【解答】解:∵∠ 2+∠ 3=180°,∴∠ 3= 180°﹣∠ 2.∵直尺的两边相互平行,∴∠ 4=∠ 3,∴∠ 4= 180°﹣∠ 2.∵∠ 4+∠ 1= 90°,∴ 180°﹣∠ 2+∠1= 90°,即∠ 2﹣∠ 1= 90°.∴∠ 1 与∠ 2 之间的数目关系为:∠2﹣∠ 1=90°,故答案为:∠2﹣∠ 1= 90°.【评论】本题考察的是平行线的性质,用到的知识点为:两直线平行,同位角相等.18.【剖析】由题意可知:利用“挤压法”,将图形中的花纹挤去,求出节余的正方形的边长,即可求出白色部分的面积.【解答】解:( 60﹣ 2× 5)2,=50×50,=2500(平方厘米);∴空白部分的面积是 2500 平方厘米.故答案为: 2500平方厘米【评论】本题考察了生活中的平移现象,解答本题的重点是:利用“挤压法”,求出节余的长方形的边长,从而求其面积.三.解答题(共7 小题)19.【剖析】依据垂直的定义获得∠AOC=∠ BOC= 90°,获得∠ BOD +∠ COD =90°,根据已知条件即可获得结论.【解答】解:∵ CO⊥ AB,∴∠ AOC=∠ BOC= 90°,∴∠ BOD+∠ COD = 90°,∵∠ BOD﹣∠ COD = 34°,∴∠ COD = 28°,∴∠ AOD=∠ AOC+∠ COD = 118°.【评论】本题主要考察了垂线以及角的计算,正确掌握垂线的定义是解题重点.20.【剖析】( 1)依据垂线的定义获得∠AOC=∠ BOD= 90°,依据余角的性质即可获得结论;(2)依据角的和差即可获得结论.【解答】解:( 1)∠ AOD=∠ BOC,原因:∵ AO⊥ CO,DO⊥ BO,∴∠ AOC=∠ BOD= 90°,∵∠ COD =∠ COD ,∴∠ AOC﹣∠ COD =∠ BOD ﹣∠ COD ,∴∠ AOD=∠ BOC;(2)∵∠ AOB=140°,∠ BOD = 90°,∴∠ AOD=∠ AOB﹣∠ BOD = 50°,∴∠ COD =∠ AOC﹣∠ AOD =40°.【评论】本题考察了垂线,余角的定义,娴熟掌握垂线的定理是解题的重点.21.【剖析】依据对顶角相等,等量代换和平行线的判断定理进行证明即可.【解答】证明:∵∠ 2=∠ 3(对顶角相等),又∵∠ 1=∠ 2(已知),∴∠ 1=∠ 3,∴ AB∥ CD (同位角相等,两直线平行).【评论】本题考察的是平行线的判断,掌握平行线的判断定理是解题的重点.22.【剖析】( 1)依据同旁内角互补,两直线平行,可证BC∥ AD,依据角均分线的性质和已知条件可知∠FEC =∠ BCE ,依据内错角相等,两直线平行可证BC∥ EF,依据两条直线都和第三条直线平行,那么这两条直线平行,可证AD∥ EF;( 2)先依据CE 均分∠ BCF,设∠ BCE=∠ ECF =∠ BCF=x.由∠ DAC=3∠ BCF可得出∠ DAC = 6x,由平行线的性质即可得出x 的值,从而得出结论.【解答】( 1)证明:∵∠ DAC +∠ACB= 180°,∴ BC∥ AD,∵ CE 均分∠ BCF ,∴∠ ECB=∠ FCE ,∵∠ FEC=∠ FCE ,∴∠ FEC=∠ BCE,∴BC∥ EF,∴AD∥ EF;(2)设∠ BCE=∠ ECF =∠ BCF = x.由∠ DAC =3∠ BCF 可得出∠ DAC= 6x,则6x+x+x+20°= 180°,解得 x=20°,则∠ DAC 的度数为120°,∠ FEC 的度数为20°.【评论】本题考察的是平行线的判断,平行线的性质,用到的知识点为:同旁内角互补,两直线平行;内错角相等,两直线平行;两条直线都和第三条直线平行,那么这两条直线平行;两直线平行,同旁内角互补.23.【剖析】依据平行线的性质和判断可填空.【解答】解:∠ AFE =∠ ABC(已知)∴EF∥ BC(同位角相等,两直线平行)∴∠ 1=∠ EBC(两直线平行,内错角相等)∠ 1+∠2= 180°(已知)∴∠ EBC+∠ 2= 180°(等量代换)∴EB∥ DG (同旁内角互补,两直线平行)∴∠ GDE=∠ BEA (两直线平行,同位角相等)GD⊥ AC(已知)∴∠ GDE= 90°(垂直的定义)∴∠ BEA=90°(等量代换)∠ AEF = 65°(已知)∴∠ 1=∠ BEA﹣∠ AEF = 90°﹣ 65°= 25°(等式的性质)故答案为: EF∥ BC ,∠ EBC,∠ EBC +∠ 2= 180°,同旁内角互补,两直线平行,两直线平行,同位角相等,∠GDE ,∠ BEA,∠ AEF .【评论】本题考察了平行线的判断和性质,灵巧运用平行线的性质和判断解决问题是本题的重点.24.【剖析】(1)依照 EF ∥ DB 可得∠ 1=∠ D,依据∠ 1=∠ 2,即可得出∠ 2=∠ D,从而判断 DG∥ AC;( 2)依照 EC 均分∠ FED ,∠ 1=50°,即可获得∠DEC =∠ DEF=65°,依照DG∥AC,即可获得∠C=∠ DEC= 65°.【解答】解:( 1) DG 与 AB 平行.∵EF∥ DB∴∠ 1=∠ D,又∵∠ 1=∠ 2,∴∠ 2=∠ D,∴DG ∥AC;( 2)∵ EC均分∠FED ,∠ 1=50°,∴∠ DEC=∠DEF =×( 180°﹣ 50°)= 65°,∵DG ∥AC,∴∠ C=∠ DEC= 65°.【评论】本题考察了平行线的性质和判断的应用,能正确运用定理进行推理是解本题的重点.25.【剖析】( 1)依据平行线的性质即可获得结论;(2)过点 P 作 PG∥ AB,依据平行线的性质即可获得结论;(3)过点 P 作 PG∥ CD ,依据平行线的性质即可获得结论.【解答】解:( 1)∵ AB∥ CD ,∴∠ α= 50°,故答案为: 50;(2)∠α=∠ 1+∠2,证明:过点P 作 PG∥∵ AB∥ CD,∴PG∥ CD,∴∠ 2=∠ 3,∠ 1=∠ 4,∴∠ α=∠ 3+∠ 4=∠ 1+ ∠2;( 3)∠α=∠ 2﹣∠ 1,证明:过点P 作 PG∥ CD ,∵AB∥ CD ,∴ PG∥ AB,∴∠ 2=∠ EPG,∠ 1=∠ 3,∴∠ α=∠ EPG﹣∠ 3=∠ 2﹣∠ 1.【评论】本题考察了平行线的性质,娴熟掌握平行线的性质是解题的重点.。
人教版七年级数学下册《第五章-相交线与平行线》单元测试卷-附参考答案

人教版七年级数学下册《第五章 相交线与平行线》单元测试卷-附参考答案(测试时间:90分钟 卷面满分:100分)班级 姓名 学号 分数一 选择题(本大题共10个小题 每小题3分 共30分 在每小题给出的四个选项中 只有一项是符合题目要求的)1.(2022春·全国·七年级单元测试)下图中 1∠和2∠是对顶角的是( )A .B .C .D . 【答案】B 【分析】根据对顶角的定义解答即可.【详解】解:A 1∠和2∠的某一边不是互为反向延长线 则不是对顶角 此项不符合题意B 1∠和2∠是对顶角 则此项符合题意C 1∠和2∠没有公共顶点 则不是对顶角 此项不符合题意D 1∠和2∠的某一边不是互为反向延长线 则不是对顶角 此项不符合题意故选:B .【点睛】本题考查了对顶角 解题的关键是熟记对顶角的定义:有一个公共顶点 并且一个角的两边分别是另一个角的两边的反向延长线 具有这种位置关系的两个角 互为对顶角. 2.(2022·全国·七年级单元测试)如图 直线AD BE 、 被直线BF 和AC 所截 则2∠的同位角有( )个.A .2B .3C .4D .1【答案】B【分析】根据同位角的定义求解即可:同位角:两条直线被第三条直线所截形成的角中 若两个角都在两直线的同侧 并且在第三条直线(截线)的同旁 则这样一对角叫做同位角.【详解】解:∠2的同位角有:∠1 ∠F AC ∠4 共三个.故选:B .【点睛】本题考查了同位角熟记同位角定义是解题的关键.3.(2022春·七年级单元测试)如图所示的图案可以看作由“基本图案”经过平移得到的是()A.B.C.D.【答案】B【分析】根据平移的概念:在平面内把一个图形整体沿某一的方向移动这种图形的平行移动叫做平移变换简称平移即可选出答案.【详解】解:A 不是由“基本图案”经过平移得到故此选项不符合题意B 是由“基本图案”经过平移得到故此选项符合题意C 不是由“基本图案”经过平移得到故此选项不符合题意D 不是由“基本图案”经过平移得到故此选项不符合题意故选B.【点睛】本题考查生活中的平移现象仔细观察各选项图形是解题的关键.4.(2022秋·江苏连云港·七年级校考单元测试)下列语句中属于命题的是()A.等角的余角相等B.两点之间线段最短吗C.连接P Q两点D.花儿会不会在春天开放【答案】A【分析】根据命题的定义对选项一一进行分析即可.【详解】解:选项A:是用语言可以判断真假的陈述句是命题故符合题意选项B C D:都不是可以判断真假的陈述句都不是命题故不符合题意.故选:A【点睛】本题考查了命题的定义解本题的关键在判断给出的语句是否用语言符号或式子表达是否为可以判断真假的陈述句.一般地对某件事情作出正确或不正确的判断的句子叫做命题命题可看做由题设和结论两部分组成.5.(2022·全国·七年级单元测试)如图若图形A经过平移与下方图形(阴影部分)拼成一个长方形则平移方式可以是()A .向右平移4个格 再向下平移4个格B .向右平移6个格 再向下平移5个格C .向右平移4个格 再向下平移3个格D .向右平移5个格 再向下平移4个格 【答案】A【分析】根据平移的性质 结合图形解答即可.【详解】解:图形A 向右平移4个格 再向下平移4个格可以与下方图形(阴影部分)拼成一个长方形 故选:A .【点睛】本题考查的是平移的性质 把一个图形整体沿某一直线方向移动 会得到一个新的图形 新图形与原图形的形状和大小完全相同.6.(2022春·黑龙江哈尔滨·七年级校考单元测试)如图 已知直线AB CD ∥ 130GEF ∠=︒ 135EFH ∠=︒ 则12∠+∠的度数为( )A .35︒B .45︒C .65︒D .85︒ 【答案】D【分析】由130GEF ∠=︒ 135EFH ∠=︒可得1324265︒∠+∠+∠+∠= 由ABCD 得34180∠+∠=︒ 进而可求出12∠+∠的度数.【详解】解:如下图所示∠130GEF ∠=︒∠13130︒∠+∠=∠135EFH ∠=︒∠24135︒∠+∠=∠1324265︒∠+∠+∠+∠=∠AB CD∠34180∠+∠=︒∠121324(34)26518085︒∠∠︒+∠=∠+∠+∠+∠-+∠=︒=-故选:D .【点睛】本题考查了平行线的性质 解题的关键是根据平行线的性质找出图中角度之间的关系.7.(2022春·江苏·七年级单元测试)下列说法中 错误的有( )①若a b ∥ b c ∥ 则a c ∥②若a 与c 相交 b 与c 相交 则a 与b 相交③相等的角是对顶角④过一点有且只有一条直线与已知直线平行.A .3个B .2个C .1个D .0个【答案】A【分析】根据平行公理及推论可判断① 若a 与c 相交 b 与c 相交 则a 与b 可能相交或平行 可判断② 对顶角相等 但相等的角不一定是对顶角 可判断③ 根据平行公理及推论可判断④.【详解】解:根据平行线公理及推论可知 ①正确若a 与c 相交 b 与c 相交 则a 与b 可能相交或平行 ②错误对顶角相等 但相等的角不一定是对顶角 ③错误过直线外一点有且只有一条直线与已知直线平行④错误.故错误的有3个故选:A.【点睛】本题考查平行公理及推论平行线的判定与性质熟练掌握平行线的判定与性质是解答本题的关键.8.(2022·全国·七年级单元测试)如图P为直线l外一点A B C在l上且PB∠l下列说法中正确的个数是()①P A PB PC三条线段中PB最短②线段PB叫做点P到直线l的距离③线段AB的长是点A到PB 的距离④线段AC的长是点A到PC的距离.A.1个B.2个C.3个D.4个【答案】B【分析】根据直线外一点到这条直线的垂线段的长度叫做点到直线的距离从直线外一点到这条直线上各点所连的线段中垂线段最短.逐一判断.【详解】解:①线段BP是点P到直线l的垂线段根据垂线段最短可知P A PB PC三条线段中PB 最短故原说法正确②线段BP是点P到直线l的垂线段故线段BP的长度叫做点P到直线l的距离故原说法错误③线段AB是点A到直线PB的垂线段故线段AB的长度叫做点P到直线l的距离故故原说法正确④由题意及图形无法判断线段AC的长是点A到PC的距离故原说法错误综上所述正确的说法有①③故选:B.【点睛】本题主要考查了垂线段最短的性质和点到直线的距离的概念.垂线的两条性质:①从直线外一点到这条直线的垂线段的长度叫做点到直线的距离.②从直线外一点到这条直线上各点所连的线段中垂线段最短.∥的是()9.(2022春·天津·七年级校考单元测试)如图下列条件中能判断AB CDA .12∠=∠B .34∠∠=C .180DAB ABC ∠+∠=︒D .B D ∠=∠ 【答案】A 【分析】结合图形分析两角的位置关系 根据平行线的判定方法逐项进行判断即可得到结论.【详解】解:∠12∠=∠∠AB CD ∥故①选项符合题意∠34∠∠=∠AD BC ∥故②选项不符合题意∠180DAB ABC ∠+∠=︒∠AD BC ∥故③选项不符合题意∠B D ∠=∠ 不能判定AB CD ∥故④选项不符合题意故选:A .【点睛】本题主要考查了平行线的判定 能根据图形准确找出同位角 内错角和同旁内角是解决问题的关键.10.(2022秋·江苏盐城·七年级校联考单元测试)如图 在宽为20m 长为30m 的矩形地面上修建两条同样宽的道路 余下部分作为耕地.根据图中数据 计算耕地的面积为( )A .600m 2B .551m 2C .550m 2D .500m 2【答案】B【详解】由图可以看出两条路的宽度为:1m 长度分别为:20m 30m所以 可以得出路的总面积为:20×1+30×1-1×1=49m 2又知该矩形的面积为:20×30=600m 2所以 耕地的面积为:600-49=551m 2.故选B.二 填空题(本大题共8个小题 每题2分 共16分)11.(2022春·黑龙江哈尔滨·七年级哈尔滨工业大学附属中学校校考单元测试)如图 要把池水引到C 处 可作CD AB ⊥于点D 然后沿CD 开渠 可使所开渠道最短 依据是______.【答案】垂线段最短【分析】根据直线外一点到直线的距离解答.【详解】解:因为直线外一点到直线上各点的连线中 垂线段最短所以沿CD 开渠故答案为:垂线段最短.【点睛】本题考查垂线段的性质 熟练掌握垂线段最短是解决本题的关键.12.(2022秋·重庆铜梁·七年级校考单元测试)如图 O 是直线AB 上一点 32COB ∠=︒ 则1∠=___.【答案】148︒##148度 【分析】依据邻补角进行计算 即可得到∠1的度数.【详解】解:∠O 是直线AB 上一点 32COB ∠=︒∠118032148∠=︒-︒=︒故答案为:148︒.【点睛】本题主要考查了邻补角的概念 只有一条公共边 它们的另一边互为反向延长线 具有这种关系的两个角 互为邻补角.邻补角互补 即和为180︒.13.(2022秋·河南安阳·七年级统考单元测试)如图 给出下列条件:①∠1=∠2 ②∠3=∠4 ③∠A =∠CDE ④∠A +∠ADC =180°.其中 能推出AB //DC 的条件为_______.【答案】①③④【分析】根据平行线的判定定理逐个分析判断即可求解.【详解】解:①∠∠1=∠2∥符合题意∠AB DC②∠∠3=∠4∥不符合题意∠BC AD③∠∠A=∠CDE∥符合题意∠AB DC④∠∠A+∠ADC=180°∥符合题意∠AB DC故答案为:①③④.【点睛】本题考查了平行线的判定定理掌握平行线的判定定理是解题的关键.14.(2022秋·云南昭通·七年级校考单元测试)如图把三角尺的直角顶点放在直线b上.若∠1= 50° 则当∠2=____时a∥b.【答案】40°##40度【分析】根据三角尺的直角顶点在直线b上∠1=50° 即可得到∠3=180°−90°−∠1=40° 再根据a//b即可得到∠2=∠3=40°.【详解】解:如图∠三角尺的直角顶点在直线b上∠1=20°∠∠3=180°−90°−∠1=40°又∠要使得a b∠只需要∠2=∠3=40°故答案为:40.【点睛】本题主要考查了平行线的性质熟记两直线平行线同位角相等是解题的关键.15.(2022秋·河北石家庄·七年级统考单元测试)在同一平面内直线a b相交于P 若a∠c 则b与c的位置关系是______.【答案】相交【详解】解:因为a∠c 直线b相交所以直线b与c也有交点故答案为:相交.【点睛】本题考查了平行线和相交线.同一平面内一条直线与两条平行线中的一条相交则必与另一条直线也相交.16.(2022秋·北京·七年级校考单元测试)如图快艇从P处向正北航行到A处时向右转60︒航行到B处再向左转90︒继续航行此时的航行方向为北偏西______°.【答案】30【分析】根据平行线的性质与方位角的定义即可求解.【详解】解:如图∠//PC BE 60CAB ∠=︒∠60EBF ∠=︒∠906030DBE此时的航行方向为:北偏西30︒故答案为:30.【点睛】此题主要考查方位角 解题的关键是熟知方位角的定义及平行线的性质.17.(2022·全国·七年级单元测试)如图 在三角形ABC 中 90BAC ∠=︒ 4cm AB = 5cm =BC 3cm AC = 将三角形ABC 沿BC 方向平移cm(5)a a <得到三角形DEF 且AC 与DE 相交于点G 连接AD .(1)阴影部分的周长为______cm(2)若三角形ADG 的面积比三角形EGC 的面积大24.8cm 则a 的值为______.【答案】 12 4.5##92##142 【分析】(1)由平移的性质可得出cm AD BE a == 5cm DE AB ==.再根据()5cm CE BC BE a =-=- 即ADG S ABC CEG ABEG S S S =+四边形 即可得出1342ADG CEG S S =⨯⨯- 再根据24.8cm ADG CEG S S -= 列出关于a 的等式 解出a 即可.【详解】(1)∠三角形ABC 沿BC cm(5)a <得到三角形DEFCE BC =∴阴影部分的周长为故答案为:(2)过AABC S =3AH =ADG ABED S四边形 ADG S . ABC CEG ABEG S S S =+四边形1342CEG ABEG S S =⨯⨯-四边形121342ADG CEG BE S S ⨯-=⨯⨯- 即125ADG CEG S S -=ADG 的面积比三角形EGC 的面积大24.8cm 4.8cm ADG CEG SS -=4 4.8⨯= 18.(2022春·黑龙江哈尔滨·七年级单元测试)如图 直线AB CD ∥ 点E F 分别为直线AB 和CD 上的点 点P 为两条平行线间的一点 连接PE 和PF 过点P 作EPF ∠的平分线交直线CD 于点G 过点F 作FH PG ⊥ 垂足为H 若120DGP PFH ∠-∠=︒ 则AEP ∠=________︒.【答案】30︒【分析】设FPG x GPM y ∠∠=︒=︒, 过P 作PM CD ∥ 则AB CD PM ∥∥ 用x y ︒︒,表示PGD ∠ PFH ∠ 代入求出x y ︒-︒ 即AEP ∠的值可以解出.【详解】解:设FPG x GPM y ∠∠=︒=︒,PG 平分EPF ∠EPG FPG x ∠∠∴==︒过P 作PM CD ∥∥AB CDAB CD PM ∴∥∥AEP EPM EPG MPG x y ∠∠∠∠∴==-=︒-︒ 180180PGD MPG y ∠∠=︒-=︒-︒FH PG ⊥90PHF ∠∴=︒909090PFH FPG FPG x ∠∠∠∴=︒-=︒-=︒-︒120DGP PFH ∠-∠=︒()()18090120y x ∴︒-︒-︒-︒=︒ 即30x y ︒-︒=︒30AEP x y ∠∴=︒-︒=︒.故答案为:30︒.【点睛】本题考查平行线的性质 角平分线的性质 垂线的性质 熟练运用性质计算是解题的关键.三 解答题(本大题共8个小题 共54分 第19-22每小题6分 23-24每小题7分 25-26每小题8分)19.(2022·全国·七年级单元测试)如图 在边长为1个单位的正方形网格中 ABC 经过平移后得到A B C ''' 点B 的对应点为B ' 根据下列条件 利用网格点和无刻度的直尺画图并解答 保留痕迹:(1)画出A B C ''' 线段AC 扫过的图形的面积为______(2)在A B ''的右侧确定格点Q 使A B Q ''△的面积和ABC 的面积相等 请问这样的Q 点有______个? 根据平移的性质得出'''ABC线段)根据平行线之间的距离处处相等可得答案.A B C '''即为所求111022612411022A B ∥ 则点1234,,,Q Q Q Q 即为所求本题主要考查了作图——平移变换20.(2022秋·北京海淀·七年级校考单元测试)如图 点C 在MON ∠的一边OM 上 过点C 的直线AB ON ∥CD 平分ACM ∠.当60DCM ∠=︒时 求O ∠的度数.解:∠CD 平分ACM ∠∠ACM ∠= .∠60DCM ∠=︒∠ACM ∠= °.∠直线AB 与OM 交于点C∠OCB ∠=ACM ∠= °( )∠AB ON ∥∠+=180O OCB ∠∠︒( )∠O ∠= °.【答案】2DCM ∠ 120 120 对顶角相等 两直线平行 同旁内角互补 60【分析】根据角平分线的定义 即可得到∠ACM 的度数 进而得出∠OCB 的度数 再依据平行线的性质 即可得到∠O 的度数.【详解】解:∠CD 平分ACM ∠∠=2ACM DCM ∠∠.∠∠60DCM ∠=︒∠=120ACM ∠︒.∠直线AB 与OM 交于点C∠==120OCB ACM ∠∠︒(对顶角相等)∠AB ON ∥∠+=180O OCB ∠∠︒(两直线平行 同旁内角互补)∠=60O ∠︒.故答案为:2DCM ∠ 120 120 对顶角相等 两直线平行 同旁内角互补 60.【点晴】本题主要考查了角的计算 平行线的性质以及角平分线的定义 解题的关键是熟练掌握平行线的性质:两直线平行 同旁内角互补.21.(2022秋·重庆铜梁·七年级校考单元测试)如图 在四边形ABCD 中 130A ∠=︒ 50ADC ∠=︒ 试说明12∠=∠.【答案】AB CD 同旁内角互补 两直线平行 两直线平行 内错角相等【分析】由180A ADC ∠+∠=︒ 利用同旁内角互补 两直线平行可得AB CD ∥ 再利用平行线的性质可得答案.【详解】证明:∠130A ∠=︒ 50ADC ∠=︒(已知)∠180A ADC ∠+∠=︒(等式的性质)∠AB CD ∥ (同旁内角互补 两直线平行)∠12∠=∠(两直线平行 内错角相等).【点睛】本题考查的是平行线的判定与性质 熟记平行线的性质与判定方法是解本题的关键.22.(2022·全国·七年级单元测试)如图 己知点P Q 分别在AOB ∠的边OA OB 、上 按下列要求画图:(1)画射线PQ(2)过点P 画垂直于射线OB 的线段PC 垂足为点C(3)过点Q画直线QM平行于射线OA.【答案】(1)见解析(2)见解析(3)见解析【分析】根据题意过用直尺作图分别P画垂直于射线OB的射线PC垂足为点C过点Q画直线QM平行于射线OA.【详解】(1)如图射线PQ为所求(2)如图线段PC为所求(3)如图直线QM为所求【点睛】此题主要考查了基本作图正确把握相关定义是解题关键.23.(2022春·七年级单元测试)如图汽车站码头分别位于A B,两点直线b和波浪线分别表示公路与河流.(1)从汽车站A到码头B怎样走最近?画出最近路线并说明理由(2)从码头B到公路b怎样走最近?画出最近路线BC并说明理由.【答案】(1)作图见解析 理由见解析(2)作图见解析 理由见解析【分析】(1)根据两点之间线段最短解决问题.(2)根据垂线段最短解决问题.【详解】(1)解:如图 连接,A B 线段AB 即为所求作.(2)如图 过点B 作BC b ⊥于点C 线段BC 即为所求作.【点睛】本题考查作图﹣应用与设计作图 垂线段最短 两点之间线段最短等知识 解题的关键是理解题意 灵活运用所学知识解决问题.24.(2022春·七年级单元测试)如图 AB CD ⊥ 垂足为O .(1)比较AOD EOB AOE ∠∠∠,,的大小 并用“<”号连接.(2)若28EOC ∠=︒ 求EOB ∠和EOD ∠的度数.【答案】(1)AOE AOD EOB ∠<∠<∠(2)118152EOB EOD ∠=︒∠=︒,【分析】(1)根据图形可判断各角的大小.(2)根据图形可得90118EOB EOC ∠=∠+︒=︒,根据平角的定义求得EOD ∠. 【详解】(1)解:∠AB CD ⊥∠909090AOD EOB EOC AOE EOC ∠=︒∠=︒+∠∠=︒-∠,,∠AOE AOD EOB ∠<∠<∠(2)∠AB CD ⊥∠90118EOB EOC ∠=∠+︒=︒∠180********EOD EOC ∠=︒-∠=︒-︒=︒.【点睛】本题考查了角的关系 垂直的定义 通过已知角求得未知角 数形结合是解题的关键. 25.(2022春·广东·七年级单元测试)如图 直线CD EF 交于点O OA OB 分别平分COE ∠和DOE ∠ 已知1290∠+∠=︒ 且2:32:5∠∠=.(1)求BOF ∠的度数(2)试说明AB CD 的理由.∠+∠)解:12AOCAB CD.【点睛】本题主要考查了平行线的判定与性质是解题的关键.26.(2022秋·上海宝山·七年级校考单元测试)已知AB∠CD点M为平面内的一点∠AMD=90°.(1)当点M在如图1的位置时求∠MAB与∠D的数量关系(写出说理过程)(2)当点M在如图2的位置时则∠MAB与∠D的数量关系是(直接写出答案)(3)在(2)条件下如图3 过点M作ME∠AB垂足为E∠EMA与∠EMD的角平分线分别交射线EB于点F G回答下列问题(直接写出答案):图中与∠MAB相等的角是∠FMG=度.【答案】(1)∠MAB+∠D=90°见解析(2)∠MAB﹣∠D=90°(3)∠MAB=∠EMD45【分析】(1)在题干的基础上通过平行线的性质可得结论(2)仿照(1)的解题思路过点M作MN∠AB由平行线的性质可得结论(3)利用(2)中的结论结合角平分线的性质可得结论.【详解】(1)解:如图①过点M作MN∥AB∵AB∥CD∴MN∥AB∥CD(如果一条直线和两条平行线中的一条平行那么它和另一条也平行).∴∠D=∠NMD.∵MN∥AB∴∠MAB+∠NMA=180°.∴∠MAB+∠AMD+∠DMN=180°.∵∠AMD=90°∴∠MAB+∠DMN=90°.∴∠MAB+∠D=90°(2)解:如图②过点M作MN∥AB∵MN∥AB∴∠MAB+∠AMN=180°.∵AB∥CD∴MN∥AB∥CD.∴∠D=∠NMD.∵∠AMD=90°∴∠AMN=90°﹣∠NMD.∴∠AMN=90°﹣∠D.第21页共22页第22页共22页。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版数学七年级下册第5章相交线与平行线单元测试题一.选择题(共10小题)1.三条直线相交,交点最多有()A.1个B.2个C.3个D.4个2.如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,∠EOD=30°,则∠BOC=()A.150°B.140°C.130°D.120°3.下列语句正确的有()个①任意两条直线的位置关系不是相交就是平行②过一点有且只有一条直线和已知直线平行③过两条直线a,b外一点P,画直线c,使c∥a,且c∥b④若直线a∥b,b∥c,则c∥a.A.4B.3C.2D.14.如图,已知CD∥BE,如果∠1=60°,那么∠B的度数为()A.70°B.100°C.110°D.120°5.能说明命题“如果两个角互补,那么这两个角一个是锐角,另一个是钝角”为假命题的两个角是()A.120°,60°B.95°,105°C.30°,60°D.90°,90°6.如图,直线L1是由直线L2平移得到的,若∠1=56°,则∠2的度数为()A.∠2=56°B.∠2=124°C.∠2=134°D.∠2=114°7.如图,直线AB、CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,则∠EOB的度数为()A.60°B.90°C.120°D.150°8.如图,下列说法正确的是()A.∠A与∠B是同旁内角B.∠1与∠2是对顶角C.∠2与∠A是内错角D.∠2与∠3是同位角9.如图,若∠1=∠2,则下列选项中可以判定AB∥CD的是()A.B.C.D.10.下列现象中是平移的是()A.将一张长方形纸片对折B.电梯的升降C.飞碟快速转动D.电风扇的叶片高速转动二.填空题(共8小题)11.“同位角相等”的逆命题是.12.若a∥b,l∥a,则l与b的位置关系是.13.如图,AH⊥BC,若AB=3cm、AC=4.5cm、AH=2cm,则点A到直线BC的距离为.14.如图,直线AB、CD相交于点O,∠1=∠2,若∠AOD=68°,则∠1的度数为.15.如图,一块长为a(cm),宽为b(cm)的长方形地板中间有一条裂痕(如图甲),若把裂痕右边的一块向右平移1cm(如图乙),则产生的裂缝的面积是cm2.16.已知:如图,∠1=∠2=∠3=55°,则∠4的度数是.17.如图是利用直尺和三角板过直线l外一点P作直线l的平行线的方法,这样做的依据是.18.如图,∠1与∠2是同位角的是.三.解答题(共8小题)19.如图,直线CD与∠AOB的边OB相交.(1)写出图中的同位角、内错角和同旁内角;(2)如果∠1=∠2,那么∠1与∠4相等吗?∠1与∠5互补吗?为什么?20.如图,直线AB,CD相交于点O,且∠DOE=3∠COE,∠EOB=90°,求∠AOD的度数.21.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.如果∠AOD =40°,求∠POF的度数.22.(1)△ABC经过平移后,点A移到了点A',请在表格中作出平移后的△A′B′C'(2)如图,过P点画出OA、OB的垂线.23.如图,AB、CD、NE相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°(1)线段的长度表示点M到NE的距离;(2)比较MN与MO的大小(用“<”号连接):,并说明理由:;(3)求∠AON的度数.24.按要求完成下列证明:已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点,且∠1+∠2=90°.求证:DE∥BC.证明:∵CD⊥AB(已知),∴∠1+=90°().∵∠1+∠2=90°(已知),∴=∠2().∴DE∥BC().25.已知如图,已知∠1=∠2,∠C=∠D.(1)判断BD与CE是否平行,并说明理由;(2)说明∠A=∠F的理由.26.如图,AD平分∠BDC,∠1=∠2,∠B+∠F=180°.(1)写出3个∠B的同旁内角;(2)若∠B=105°,求∠ADC的度数.(3)求证:CD∥EF.参考答案与试题解析一.选择题(共10小题)1.解:如图:,交点最多3个,故选:C.2.解:∵EO⊥AB,∴∠BOE=90°,∵∠EOD=30°,∴∠BOD=90°﹣∠EOD=90°﹣30°=60°,∴∠BOC=180°﹣∠BOD=180°﹣60°=120°,故选:D.3.解:①根据同一平面内,任意两条直线的位置关系不是相交就是平行,说法错误;②过一点有且只有一条直线和已知直线平行,说法错误,应为过直线外一点有且只有一条直线和已知直线平行;③过两条直线a,b外一点P,画直线c,使c∥a,且c∥b,说法错误;④若直线a∥b,b∥c,则c∥a,说法正确;故选:D.4.解:∵∠1=60°,∴∠2=180°﹣60°=120°.∵CD∥BE,∴∠2=∠B=120°.故选:D.5.解:当两个角都是90°时,满足两个角互补,不满足这两个角一个是锐角,另一个是钝角.故选:D.6.解:∵直线L1是由直线L2平移得到的,∴L1∥L2,∴∠3=∠1=56°,∵∠3+∠2=180°,∴∠2=180°﹣56°=124°.故选:B.7.解:设EOA=x,∵OE平分∠AOC,∴∠AOC=2x,∵∠EOA:∠AOD=1:4,∴∠AOD=4x,∵∠COA+∠AOD=180°,∴2x+4x=180°,解得x=30°,∴∠EOB=180°﹣30=150°.故∠EOB的度数是150°.故选:D.8.解:A、∠A与∠B是同旁内角,故说法正确;B、∠2与∠1是邻补角,故说法错误;C、∠A与∠2是同位角,故说法错误;D、∠2与∠3是内错角,故说法错误;故选:A.9.解:若∠1=∠2,则下列四个选项中,能够判定AB∥CD的是D,故选:D.10.解:A、将一张长方形纸片对折是翻折变换,不是平移,故本选项错误;B、电梯的升降,符合平移定义,故本选项正确;C、飞碟快速转动是旋转变换,不是平移,故本选项错误;D、电风扇的叶片高速转动是旋转变换,不是平移,故本选项错误.故选:B.二.填空题(共8小题)11.解:“同位角相等”的逆命题为:相等的两个角为同位角.故答案为:相等的角是同位角.12.解:∵a∥b,l∥a,∴l∥b,故答案为:l∥b.13.解:点A到直线BC的距离是线段AH的长度,AH=2,∴点A到直线BC的距离为2cm.故答案为:2cm14.解:∵∠BOC=∠AOD=68°,∠1=∠2,∴∠1=.故答案为:34°15.解:如图乙,﹣ab=(a+1)b﹣ab=b(cm2).产生的裂缝的面积=S矩形ABCD故答案为b.16.解:给各角标上序号,如图所示.∵∠1=∠2,∠2=∠5,∴∠1=∠5,∴l1∥l2,∴∠3+∠6=180°.∵∠3=55°,∴∠6=180°﹣55°=125°,∴∠4=∠6=125°.故答案为:125°.17.解:由图形得,有两个相等的同位角存在,这样做的依据是:同位角相等,两直线平行.故答案为:同位角相等,两直线平行.18.解:这四个图中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,符合的有图①②.故答案为:①②.三.解答题(共8小题)19.解:(1)∠1与∠4是同位角;∠1与∠2是内错角;∠1与∠5是同旁内角;(2)如果∠1=∠2,那么∠1与∠4相等,∠1与∠5互补;理由如下:∵∠1=∠2,∠2=∠4,∠2+∠5=180°,∴∠1=∠4,∠1+∠5=180°.20.解:∵∠DOE=3∠COE,∠DOE+∠COE=180°,∴∠DOE=135°,∵OE⊥AB,∴∠BOD=45°,∵∠AOB=180°,∴∠AOD=∠AOB﹣∠BOD=135°.21.解:由对顶角相等,得∠BOC=∠AOD=40°,由OP是∠BOC的平分线,得∠COP=∠BOC=20°.由余角的定义,得∠POD=∠COD﹣∠COP=90°﹣20°=70°.22.解:(1)如图•,△A′B′C′为所作;(2)如图,直线l和l′为所作.23.解:(1)线段MO的长度表示点M到NE的距离;(2)比较MN与MO的大小为:MO<MN,是因为垂线段最短;(3)∵∠BOD=∠AOC=50°,OM平分∠BOD,∴∠BOM=25°,∴∠AON=180°﹣∠BOM﹣∠MON=180°﹣25°﹣90°=65°.故答案为:MO;MO<MN;垂线段最短.24.证明:∵CD⊥AB(已知),∴∠1+∠EDC=90°(垂直定义).∵∠1+∠2=90°(已知),∴∠EDC=∠2(同角的余角相等).∴DE∥BC(内错角相等,两直线平行).故答案为:∠EDC;垂直定义;∠EDC;同角的余角相等;内错角相等,两直线平行.25.解:(1)BD∥CE,理由如下:∵∠1=∠2,∠2=∠3,∴∠1=∠3,∴BD∥CE;(2)理由如下:∵BD∥CE,∴∠C=∠4.∵∠C=∠D,∴∠D=∠4,∴AC∥DF,∴∠A=∠F.26.解:(1)∠B的同旁内角有:∠2、∠BDC、∠F;(2)∵AD平分∠BDC,∴∠ADC=∠2=∠BDC,∵∠1=∠2,∴∠1=∠ADC,∴AB∥CD,∴∠BDC=180°﹣∠B=180°﹣105°=75°,∴∠ADC=∠BDC=×75°=37.5°;(3)证明:由(2)得AB∥CD,∵∠B+∠F=180°,∴AB∥EF,∴EF∥CD.。
