长方体和正方体知识点汇总
(完整版)长方体和正方体知识点汇总(最新整理)
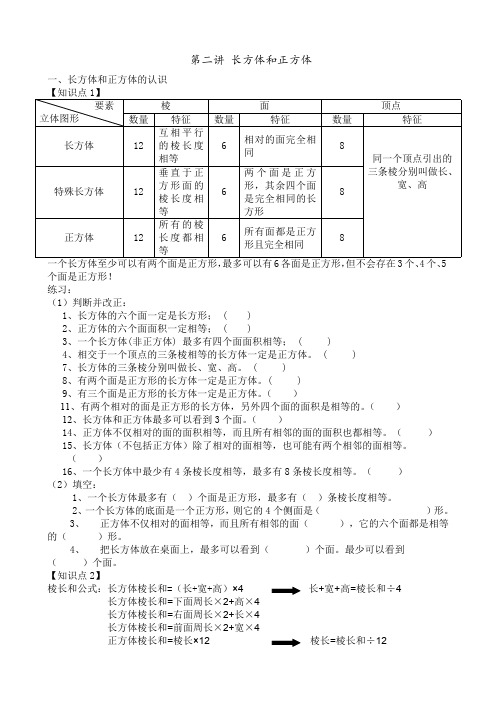
第二讲 长方体和正方体一、长方体和正方体的认识【知识点1】棱面顶点要素立体图形数量特征数量特征数量特征长方体12互相平行的棱长度相等6相对的面完全相同8特殊长方体12垂直于正方形面的棱长度相等6两个面是正方形,其余四个面是完全相同的长方形8正方体12所有的棱长度都相等6所有面都是正方形且完全相同8同一个顶点引出的三条棱分别叫做长、宽、高一个长方体至少可以有两个面是正方形,最多可以有6各面是正方形,但不会存在3个、4个、5个面是正方形!练习:(1)判断并改正:1、长方体的六个面一定是长方形; ( )2、正方体的六个面面积一定相等; ( )3、一个长方体(非正方体) 最多有四个面面积相等; ( )4、相交于一个顶点的三条棱相等的长方体一定是正方体。
( )7、长方体的三条棱分别叫做长、宽、高。
( )8、有两个面是正方形的长方体一定是正方体。
( )9、有三个面是正方形的长方体一定是正方体。
( )11、有两个相对的面是正方形的长方体,另外四个面的面积是相等的。
( )12、长方体和正方体最多可以看到3个面。
( ) 14、正方体不仅相对的面的面积相等,而且所有相邻的面的面积也都相等。
( ) 15、长方体(不包括正方体)除了相对的面相等,也可能有两个相邻的面相等。
( )16、一个长方体中最少有4条棱长度相等,最多有8条棱长度相等。
( )(2)填空:1、一个长方体最多有( )个面是正方形,最多有( )条棱长度相等。
2、一个长方体的底面是一个正方形,则它的4个侧面是( )形。
3、正方体不仅相对的面相等,而且所有相邻的面( ),它的六个面都是相等的( )形。
4、把长方体放在桌面上,最多可以看到( )个面。
最少可以看到( )个面。
【知识点2】棱长和公式:长方体棱长和=(长+宽+高)长+宽+高=棱长和÷4长方体棱长和=下面周长×2+高×4长方体棱长和=右面周长×2+长×4长方体棱长和=前面周长×2+宽×4正方体棱长和=棱长×12 棱长=棱长和÷12棱长和的变形:例如:有一个礼盒需要用彩带捆扎,捆扎效果如图,打结部分需要10厘米彩带,一共需要多长的彩带?分析:本题虽然并未直接提出求棱长和,但由于彩带的捆扎是和棱相互平行的, 因此,在解决问题时首先确定每部分彩带与那条棱平行,从而间接去求棱长和。
长正方体知识点

第一单元长、正方体知识点概括1.长方体有6个面,每个面一般都是长方形(也可能有2个相对的面是正方形);有3组相对的面,相对的面形状相同,面积相等;有12条棱,有3组相对的棱,每组棱的长度相等;有8个顶点。
2.长方体有4个长、4个宽、4个高。
3.在同一长方体中,至少有4条棱是相等的,最多有8条棱是相等的。
4.长、宽、高都相等的长方体叫做正方体(也叫做立方体)。
5.正方体是特殊的长方体。
6.长方体:(长+宽+高)×4=棱长之和棱长之和÷4-长-宽=高正方体:棱长×12=棱长之和棱长之和÷12=棱长7.长方体或正方体六个面面积的和,分别叫做长方体或正方体的表面积。
8.物体所占空间的大小,叫做物体的体积。
9.棱长1厘米的正方体,它的体积是1立方厘米,记作1cm3。
棱长1分米的正方体,它的体积是1立方分米,记作1dm3。
棱长1米的正方体,它的体积是1立方米,记作1m3. 10.长方体的体积=长×宽×高11.正方体的体积=棱长×棱长×棱长12.长方体的体积=底面积×高13.1立方米=1000立方分米1立方分米=1000立方厘米14.物体所能容纳物体的体积,叫做它们的容积。
15.计量容器内液体的多少,通常用升、毫升作单位。
16.从里面量,棱长1分米的正方体盒子的容积是1立方分米,可以容纳1升的液体。
17.容积的计算方法和体积的计算方法相同。
但是,一般要从容器的里面测量容器的长、宽、高。
18.一个正方体的棱长扩大3倍,表面积就扩大9倍,体积就扩大27倍。
第五单元因数倍数概念1.一个数的因数的个数是有限的,其中最小的因数是一,最大的因数是它本身。
2.一个数的倍数的个数是无限的,最小的倍数是它本身,没有最大的倍数。
3.个位上是0、2、4、6、8的数,都是2的倍数。
4.个位上是0或5的数,都是5的倍数。
5.在自然数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
(完整版)长方体和正方体知识点

一、知识点一:长方体和正方体的认识
6个面,每个面都是长方形(特殊的有一组对面是正方形),相对的面完全相同;有12条棱,相对的棱平行且相等;有8个顶点。
正方形有6个面,每个面都是正方形,所有的面都完全相同;有12条棱,所有的棱都相等;有8个顶点。
长方体的长、宽、高。
=(长+宽+高)×4
用字母表示:(a+b+h)×4
正方体的棱长总和= 棱长×12
用字母表示:12a
二、知识点二:长方体和正方体的表面积的计算
6个面的总面积叫做它的表面积。
=(长×宽+长×高+宽×高)×2用字母表示:S=(ab+ah+bh)×2
正方体的表面积= 棱长×棱长×6
用字母表示:S=6a2
6
7、1m2 =100dm2 1dm2 =100cm2
三、知识点三:长方体和正方体的体积的计算
= 长×宽×高
用字母表示:V=abh
正方体的体积= 棱长×棱长×棱长
用字母表示:V=a3
1m3=1000dm3 1dm3=1000cm3 1m3=100 0000cm3
长方体或正方体的体积=底面积×高
用字母表示:V=Sh
把高级单位化成低级单位,用高级单位数乘以进率;------大乘小
把低级单位聚成高级单位,用低级单位数除以进率。
-----------小除大
四、知识点三:长方体和正方体的容积的计算
L和ml)
1L=1000ml 1L= 1dm3 1ml= 1cm3
跟体积的计算方法相同,但要从里面量长、宽、高。
长方体正方体.知识点总结

长方体的再认识一、 概念1、 长方体的元素:六个面、八个顶点、十二条棱2、 长方体的三元素的特点:(主要是外观特征和数量关系)①长方体的每个面都是长方形;②长方体的十二条棱可以分为三组,每组中的四条棱的长度相等。
③长方体的六个面可以分为三组,每组中的两个面形状大小都相同。
3、 正方体是特殊的长方体。
4、 平面是平的,无边无沿,没有厚度和大小,一般用平行四边形来表示。
记作:平面ABCD 或平面α。
5、 将水平放置的平面画成一边是水平位置,另一边与水平线成45度角的平行四边形。
6、 斜二侧画法画长方体时要注意:宽画成标注尺寸的一半;看不到的线画成虚线;要标字母和尺寸,要写结论。
长方体ABCD-EFGH 、平面ABCD 、棱AB 、顶点A 。
7、 空间中两直线的位置关系有三种:相交、平行、异面① 如果两条直线在同一平面内,有唯一公共点,称这两条直线的位置关系是相交; ② 如果两条直线在同一平面内,没有唯一公共点,称这两条直线的位置关系是平行; ③ 如果两条直线既不平行也不相交,称这两条直线的位置关系是异面。
8、直线垂直于平面记作:直线P Q ⊥平面ABCD ;直线平行于平面记作:直线P Q ∥平面ABCD 。
9、 计算公式之一:(三条棱长分别是a 、b 、c 的长方体)① 棱长和 = 4()a b c ++ ; ② 体积 = abc ;③ 表面积 = 2()ab bc ac ++ ; ④ 无盖表面积 = S ab -、S bc -、S bc - 10、计算公式之二:(边长是a 正方体)① 棱长和= 12a ;②体积= 3a ;③表面积= 26a ;④无盖表面积 =25a 。
11、长方体不一定是正方体;正方体一定是长方体。
12、长方体中棱与棱的位置关系有3种,分别是平行、相交、异面。
13、长方体中棱与面的位置关系有2种,分别是:平行、垂直。
14、长方体中面与面的位置关系有2种,分别是:平行、垂直。
正方体长方体知识点 、易错题、小升初难题

第三单元正方体和长方体知识点长方体. 正方体概念. 特征:长方体和正方体都是立体图形。
正方体是特殊的长方体。
相交于一个顶点的三条棱的长度分别叫做长方体的长. 宽. 高。
正方体都叫做棱。
(长. 宽. 高都各有4条,分别平行并且相等,正方体的棱都相等。
)各部分特征:长方体:面:有6个面,都是长方形(特殊情况下最多有两个相对的面是正方形)。
相对的面完全相同。
棱:有12条棱。
相对的棱长度相等。
顶点:有8个顶点。
正方体:面:有6个面都是正方形,6个面完全相同。
棱:有12条棱。
12条棱的长度相等。
顶点:有8个顶点。
棱长总和公式:长方体的棱长总和=(长+宽+高)×4 L=4(a+b+h)长=12a正方体的棱长总和=棱长×12 L正表面积:长方体或正方体6个面和总面积叫做它的表面积。
基本公式:长方体的表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)表长=a×a×6正方体的表面积=棱长×棱长×6 S表正公式延伸:①无底(或无盖):(少一个长×宽)长方体表面积=长×宽+(长×高+宽×高)×2S=2(ab+ah+bh)-ab S=2(ah+bh)+ab②无底又无盖:(一般烟囱)长方体表面积=(长×高+宽×高)×2 S=2(ah+bh)体积:物体所占空间的大小叫做物体的体积。
符号:V单位:常用:立方米m3立方分米dm3立方厘米cm3不常用:立方千米 km3(描述天体星球)立方毫米mm3(微星科技)基本公式:长方体的体积=长×宽×高 V=abh正方体的体积=棱长×棱长×棱长 V=a3公式延伸:长方体或正方体底面的面积叫做底面积。
底面积=长×宽 V=sh (长. 正方体的体积都=底面积×高)容积:箱子. 油桶. 仓库等容器所能容纳物体的体积,通常叫做他们的容积。
第三单元 长方体与正方体知识归纳及练习

本题求体积用的公式是“底面积×高”,也可以说用的是“横截面积×长”。
另外对于把一个长方体截成两段,截了一次,增加了两个面,如果是截成三段,就是截了两次,增加了四个面。
也就是说每截一次,增加两个面。
10、综合运用体积单位、长度单位的知识。
将一个大的形体分成一个小的形体。
将小正方体紧紧地排成一排,能排多少米,实际上就是将这些小正方体的棱长加起来,看有多长。
棱长是1米的正方体,它的体积是1立方米,棱长是1分米的正方体,它的体积是1立方分米,1立方米= 1000立方分米,所以能分成1000个。
顺次紧紧地排成一排,那么就能排成1000分米,1000分米= 100米。
长方体和正方体练习题一、填空题。
1、一个正方体的棱长之得84厘米,它的棱长是(),一个面的面积是(),表面积是(),体积是()。
2、一个长方体的长、宽、高都扩大2倍,它的表面积就()。
3、两个棱长2厘米的正方体木块,拼成一个长方体,这个长方体的表面积是()。
体积是()。
4、把一个长12厘米,宽和高都是3厘米的长方体分割成4个大小一样的正方体,表面积增加了(),每个正方体的表面积是()。
5、用棱长1厘米的小正方体木块拼成一个较大的的正方体,至少要()块这样的小木块,拼成的正方体的棱长是(),表面积是()。
6、估计下列物体的体积有多大,并填空。
教室讲台()家里冰箱()一本数学书()一支粉笔()一个苹果()课室的空间()一瓶大可乐()电脑主机()一块橡皮()7、把一个正方体切成两个完全相等的长方体,每个长方体有()顶点。
8、把一个容积是500ml的量杯里先注入200ml的水,然后放入一个土豆,这时测量杯里的容量为350ml,这个土豆的体积是()cm29、一个底面周长是1。
6分米的正方体鱼缸的容积是()升。
10、一个长方体中,最多有()个面面积相等,最多有()条棱长度相等。
11、把一个棱长2分米的正方体切成两个体积相等的长方体,其中一个长方体的表面积是()平方分米。
长方体与正方体总复习

【知识点讲解】长方体的棱长总和=(长+宽+高)×4=长×4+宽×4+高×4 L=(a+b+h)×4 长=棱长总和÷4-宽-高a=L÷4-b-h宽=棱长总和÷4-长-高b=L÷4-a-h高=棱长总和÷4-长-宽h=L÷4-a-b正方体的棱长总和=棱长×12 L=a×12正方体的棱长=棱长总和÷12 a=L÷123、长方体或正方体6个面和总面积叫做它的表面积。
长方体的表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)无底(或无盖)长方体表面积= 长×宽+(长×高+宽×高)×2无底又无盖长方体表面积=(长×高+宽×高)×2 S=2(ah+bh)贴墙纸正方体的表面积=棱长×棱长×6 S=a×a×6 用字母表示:S= 6a2生活实际:油箱、罐头盒等都是6个面游泳池、鱼缸等都只有5个面水管、烟囱等都只有4个面。
注意1:用刀分开物体时,每分一次增加两个面。
(表面积相应增加)注意2:长方体或正方体的长、宽、高同时扩大几倍,表面积会扩大倍数的平方倍。
(如长、宽、高各扩大2倍,表面积就会扩大到原来的4倍)。
4、物体所占空间的大小叫做物体的体积。
长方体的体积=长×宽×高V=abh长=体积÷宽÷高a=V÷b÷h宽=体积÷长÷高b=V÷a÷h高=体积÷长÷宽h= V÷a÷b正方体的体积=棱长×棱长×棱长长方体或正方体底面的面积叫做底面积。
长方体(或正方体)的体积=底面积×高用字母表示:V=S h (横截面积相当于底面积,长相当于高)。
正方体和长方体的知识归纳

正方体和长方体的知识归纳正方体和长方体是几何学中最基本的立体几何体之一。
它们在我们生活中随处可见,具有很多共同点和不同点。
下面我将对正方体和长方体进行知识归纳,详细介绍它们的定义、性质、特点以及在我们生活中的应用。
1. 正方体正方体是指六个面都是正方形的立体图形。
它具有以下特点:形状:正方体的六个面都是相等的正方形,它们的边长相等,相邻面之间的夹角为直角。
边长:正方体的六条边长度相等。
角度:正方体的所有内角均为直角(90度)。
顶点:正方体有8个顶点,每个顶点有3个相邻面。
对角线:通过正方体的任意两个顶点都可以得到一条对角线,正方体共有4根空间对角线。
2. 长方体长方体是指六个面都是矩形的立体图形。
它具有以下特点:形状:长方体的六个面都是矩形,它们的边长不全相等,相邻面之间的夹角为直角。
边长:长方体的六条边长度不全相等。
角度:长方体的所有内角均为直角(90度)。
顶点:长方体有8个顶点,每个顶点有3个相邻面。
对角线:通过长方体的任意两个顶点都可以得到一条对角线,长方体共有4根空间对角线。
3. 正方体和长方体的共同点正方体和长方体都属于多面体,是立体几何中的基本形状。
它们都由直角矩形面组成,内角都为直角。
正方体和长方体都具有8个顶点和12条边。
它们都具有对称性,对称轴是顶点到顶点的连线。
正方体和长方体都是稳定的立方体,它们可以在不倒塌的情况下保持平衡。
4. 正方体和长方体的不同点形状:正方体的六个面都是正方形,而长方体的六个面都是矩形,边长不全相等。
边长:正方体的六条边长度相等,而长方体的六条边长度不全相等。
顶点:正方体有8个顶点,每个顶点有3个相邻面,而长方体的顶点数量和相邻面数量与正方体相同。
对角线:正方体和长方体都有4根空间对角线,但它们的长度不同。
在正方体中,对角线长度等于边长的根号2倍。
在长方体中,对角线长度等于边长的根号3倍。
5. 正方体和长方体的应用建筑:正方体和长方体是建筑设计中常用的形状,例如房屋、大厦、桥梁等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长方体和正方体知识点汇总
一、长方体
长方体是一种具有六个面,每个面均为长方形的立体图形。
它的特点是长宽高不相等,分别对应着长方体的三条棱。
下面总结一些长方体的基本知识:
1. 长方体的表面积公式为:S=2×(ab+bc+ac),其中a、 b、 c 分别为长方体的三个面的长宽高。
2. 长方体的体积公式为:V=abc,其中a、b、c分别为长方体的三个面的长宽高。
3. 长方体的对角线长度公式为:d=√(a²+b²+c²),其中a、b、c 分别为长方体的三个面的长宽高。
4. 长方体的中心对称轴是一条连接长方体两面中心点的直线,它与长方体的三条棱垂直。
5. 长方体的垂直截面是长方形,水平截面是正方形或长方形。
6. 长方体的立体对称轴有3条:一条是连接对角面中心的对称轴,另外两条是互相垂直的,分别连接相对边中心的对称轴。
7. 长方体的顶点个数为8个。
顶点是立方体的八个角。
二、正方体
正方体是一种有六个面,每个面均为正方形的立体图形。
它具有的特点是长宽高相等,都是边长,下面总结一些正方体的基本知识:
1. 正方体的表面积公式为:S=6a²,其中a为正方体的边长。
2. 正方体的体积公式为:V=a³,其中a为正方体的边长。
3. 正方体的对角线长度公式为:d=√3a,其中a为正方体的边长。
4. 正方体的中心对称轴是一条连接正方体两面中心点的直线,它与正方体的任何一边垂直。
5. 正方体的垂直截面和水平截面都是正方形。
6. 正方体的立体对称轴有4条:一条是连接对角面中心的对称轴,另外三条是互相垂直的,分别连接相对边中心的对称轴。
7. 正方体的顶点个数为8个。
顶点是正方体的八个角。
总结:长方体和正方体相比,长方体的三条棱长度不相等,而正方体的三条棱长度相等。
在实际生活中,我们可以用长方体来描述一些长宽高不相同的物品,例如房屋、柜子等;而正方体通常用来描述一些长宽高相同的物品,例如小盒子等。
长方体和正方体都是常见的几何图形,它们在数学、物理、工程等领域都有着广泛的应用。
下面进一步阐述长方体和正方体的相
关内容。
1. 长方体和正方体的应用
(1)工程中的应用:长方体和正方体在工程领域中有着广泛的应用。
例如,长方体的物品如柜子、电视、电脑等是人们日常生活中常用的物品,制造这些物品需要考虑物品的尺寸、外观、稳定性等因素;而正方体在工程中经常用来表示物体的体积,例如建筑物的体积、物品的大小等。
(2)数学、物理学中的应用:长方体和正方体在数学、物理学中也有着广泛的应用。
例如,长方体和正方体的表面积、体积公式可以帮助人们做几何运算,寻求最优解。
此外,物理学中的碰撞、反弹等过程中,长方体和正方体的形状也会影响物体的速度、方向等变量。
(3)艺术设计中的应用:长方体和正方体同时也是一种常见的图像表现形式。
例如,在平面设计中,长方体和正方体的几何图形可以用来表示空间层次、美感等元素。
此外,长方体和正方体还被应用在雕塑、建筑等领域,表现出不同的美感和立体感。
2. 长方体和正方体的性质比较
(1)表面积和体积:长方体和正方体的表面积和体积可以通过不同的公式求得。
由于长方体的三条棱不相等,因此长方体的表面积和体积都比正方体大。
而正方体的六个面是相等的正
方形,所有正方体的表面积和体积都相等。
(2)对角线长度:长方体和正方体的对角线长度也有所不同。
由于长方体的棱不相等,因此长方体的对角线长度比正方体长。
而正方体的八个角度量相等,因此正方体的对角线长度为√3
倍边长。
(3)立体对称轴:长方体和正方体的立体对称轴也有所不同。
正方体有四个立体对称轴,其中一条是连接对角面中心的对称轴,另外三条是互相垂直的对称轴。
长方体只有三条立体对称轴,其中一条是连接对角面中心的对称轴,另外两条是互相垂直的对称轴。
综上所述,长方体和正方体都是常见的三维几何形体,它们在不同领域有着广泛的应用,如工程、数学、物理学、艺术设计等。
长方体和正方体的性质和特点不同,需要根据具体情况分别分析。
掌握长方体和正方体的相关知识,能够提高我们在工程、数学、物理学等方面的应用能力。
除了上面提到的,长方体和正方体还有一些其他的性质需要了解。
首先,长方体和正方体的空间角度量不同。
长方体的顶点角和边角度量都不相等,而正方体的顶点角和边角度量相等。
其次,长方体和正方体的对称性也不同。
长方体只有三个对称面,而正方体有六个对称面。
此外,长方体和正方体还有一些特殊的类型需要特殊关注。
一种特殊的正方体是立方体,它有六个相等的面,八个相等的顶
点和十二条相等的边,是最简单的三维几何体之一。
另一种特殊的长方体是正交六面体,它有六个相等的面,并且每个面都是一个矩形。
它的八个顶点和边角都相等,是标准的长方体。
总之,长方体和正方体是我们日常生活中常见的几何体。
了解它们的性质和特点,能够帮助我们更好地理解和应用它们。
对于学习和研究几何学、物理学、工程学等学科的人来说,掌握长方体和正方体的相关知识是非常重要的。
长方体和正方体是我们生活、学习和工作中经常遇到的几何体。
长方体和正方体有许多相似之处,例如它们都是有六个面的,都有八个顶点和十二条边。
长方体和正方体的区别主要在于它们的面积和体积计算公式、顶点角和边角度量、对称性等方面。
长方体和正方体的面积和体积计算公式是我们最常用的计算方法。
长方体的面积计算公式是2ab+2bc+2ac,体积计算公式是abc。
而正方体则是6a^2和a^3。
在我们生活的各个领域,这些计算公式都发挥了非常重要的作用。
除了计算公式,长方体和正方体还有很多其他性质。
长方体和正方体的空间角度量、对称性等方面也有所不同。
我们需要通过学习和理解这些性质和特点,才能更好地应用长方体和正方体。
长方体和正方体还有一些特殊的类型,例如立方体和正交六面体。
了解这些特殊类型的性质和特点,也能够帮助我们更好地应用它们。
总之,掌握长方体和正方体的相关知识,对于学习和研究几何学、物理学、工程学等学科的人来说非常重要。
通过学习长方体和正方体的性质和特点,我们可以更好地理解和应用它们,提高我们的学习和工作效率。
