2013年数学建模A题概念解释--通行能力
2013年数学建模瓶颈路段通行能力分析

数据分析。依据道路瓶颈路段交通设计的基本原理,对实际调查数据及交通状况进行分析,得出制约交叉口通行能力的影响因数。
4、瓶颈路段交通组织设计探讨。
5、瓶颈路段交通组织设计策略研究。
1).设计准备
(1)收集基础资料
(2)现场勘察及分析问题
(3)交通政策的研究
2).概略设计
主要包括的设计内容有:
2.国内研究现状
目前国内外学者对城市交通优化控制方面的研究工作已进行的较为深入,出现了如神经网络控制、模糊控制、多Agent控制等多种控制算法。但总的来说,以上的研究工作多针对与路口相关路段交通流处于正常状态(包括饱和状态与非饱和状态)的情况,而在实际过程中,当某路口的相关路段因发生事故或占道施工而出现路段交通瓶颈的现象时,为避免发生交通混乱(如路口发生车辆拥阻或发生二次事故等) ,如何对路口的信号控制策略进行相应的改变,也是一个值得研究的问题。
仅仅依靠单一的交通控制或者交通管理已解决不了车流量的增加对道路的影响,应从系统优化的角度进行综合整治。对主干道瓶颈区段问题进行通行能力分析并提出相关的对策,分别从路段资源整合、主辅路结合以及禁左与单行线设置等交通组织优化设计方法来缓解主干道瓶颈区段的交通压力,并进行具体实例对交通组织优化设计方法进行多方案论证。
稳定流状态是指车辆行驶速度受到前车的制约,但车辆行驶状态比较稳定,车流本身具有一定的抗干扰能力,在该状态下交通流量可以达到最大流量值,但是当交通需求继续增加,就会使车流产生较大的波动,车流运行速度出现显著下降,流量呈现出很大的波动性。
强制流状态下,交通密度较大,速度受前车制约性强,车辆行驶自由度小,车速稳定性较差,显示出较大的波动性,当流量继续增加,车流会出现走走停停现象。
2013全国数模竞赛A题优秀论文祥解

2013高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):车道被占用对城市道路通行能力的影响摘要本文主要研究车道被占用对城市道路通行能力的影响并建立了相应的数学模型。
针对问题一,考虑到交通信号灯的周期,我们选择1分钟为周期,结合不同车辆的标准车当量的折算系数,求出每个采样点的交通量,通过MATLAB作图,从定性方面对道路通行能力进行分析,然后通过基本通行能力和4个修正系数建立动态通行能力的模型。
图像显示,事故发生后(采样点5附近),实际通行能力下降至一个较低水平,并且横断面处的实际能力变化过程呈先下后上的波形变化,在事故解决(第20个采样点)以后,由图像看出实际通行能力持续上升。
针对问题二,利用问题一建立的模型,结合视频二,比较交通事故所占不同车道时横断面的实际通行能力,可以发现二者实际通行能力变化趋势大致相同,但视频二实际通行能力大于视频一实际通行能力。
可见占用车流量大的车道使道路通行能力降低更多。
针对问题三,首先我们建立单车道排队车辆数目的积分模型,单个车道的滞留车辆为上游车流量和实际通行能力的差值。
我们以30s为一个时间段,对视频一中的车流量进行统计,得到横截面处每个监测段的实际通行能力。
本题要求考虑三车道,总体排队长度不容易通过积分模型确定,所以我们将队列长度问题转化为车辆数目问题,通过视频资料统计120米对应24辆车,据此关系转换,从而得到车辆排队长度与事故横断面实际通行能力、事故持续时间和上游车流量的关系。
针对问题四,在对问题3研究的基础上,根据问题3建立的数学模型,建立起某一段时间间隔车辆排队的长度,然后,通过求得的关系得到当排队长度为140m的时候所对应的时间段,由于每段时间间隔设为30s,因此,可以求得排队长度到达上游时用的时间为347.7273s。
关键词:交通事故车道占用通行能力排队论一、问题的重述车道被占用是指因交通事故、路边停车、占道施工等因素,导致车道或道路横断面通行能力在单位时间内降低的现象。
2013全国数学建模竞赛题目A-B

2013高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A题车道被占用对城市道路通行能力的影响车道被占用是指因交通事故、路边停车、占道施工等因素,导致车道或道路横断面通行能力在单位时间内降低的现象。
由于城市道路具有交通流密度大、连续性强等特点,一条车道被占用,也可能降低路段所有车道的通行能力,即使时间短,也可能引起车辆排队,出现交通阻塞。
如处理不当,甚至出现区域性拥堵。
车道被占用的情况种类繁多、复杂,正确估算车道被占用对城市道路通行能力的影响程度,将为交通管理部门正确引导车辆行驶、审批占道施工、设计道路渠化方案、设置路边停车位和设置非港湾式公交车站等提供理论依据。
视频1(附件1)和视频2(附件2)中的两个交通事故处于同一路段的同一横断面,且完全占用两条车道。
请研究以下问题:1.根据视频1(附件1),描述视频中交通事故发生至撤离期间,事故所处横断面实际通行能力的变化过程。
2.根据问题1所得结论,结合视频2(附件2),分析说明同一横断面交通事故所占车道不同对该横断面实际通行能力影响的差异。
3.构建数学模型,分析视频1(附件1)中交通事故所影响的路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间的关系。
4.假如视频1(附件1)中的交通事故所处横断面距离上游路口变为140米,路段下游方向需求不变,路段上游车流量为1500pcu/h,事故发生时车辆初始排队长度为零,且事故持续不撤离。
请估算,从事故发生开始,经过多长时间,车辆排队长度将到达上游路口。
附件1:视频1附件2:视频2附件3:视频1中交通事故位置示意图附件4:上游路口交通组织方案图附件5:上游路口信号配时方案图注:只考虑四轮及以上机动车、电瓶车的交通流量,且换算成标准车当量数。
附件3视频1中交通事故位置示意图附件4附件5上游路口信号配时方案本题附件1、2的数据量较大,请竞赛开始后从竞赛合作网站“中国大学生在线”网站下载:试题专题页面:/service/jianmo/index.shtml试题下载地址:/service/jianmo/sxjmtmhb/2013/0525/969401.shtml2013高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)B题碎纸片的拼接复原破碎文件的拼接在司法物证复原、历史文献修复以及军事情报获取等领域都有着重要的应用。
2013数学建模A题公路通行能力的计算方法

车道被占用对城市道路通行能力的影响影响道路通行能力的主要因素有道路状况、车辆性能、交通条件、交通管理、环境、驾驶技术和气候等条件。
道路条件是指道路的几何线形组成,如车道宽度、侧向净空、路面性质和状况、平纵线形组成、实际能保证的视距长度、纵坡的大小和坡长等。
车辆性能是指车辆行驶的动力性能,如减速、加速、制动、爬坡能力等。
交通条件是指交通流中车辆组成、车道分布、交通量的变化、超车及转移车道等运行情况的改变。
环境是指街道与道路所处的环境、景观、地貌、自然状况、沿途的街道状况、公共汽车停站布置和数量、单位长度的交叉数量及行人过街道等情况。
气候因素是指气温的高低、风力大小、雨雪状况!公路通行能力的计算方法公路通行能力的计算方法(一)、无平交路段通行能力(1)基本通行能力一般路段是指不受信号、暂停标志、铁公路口等外界因素的中断,保证大体连续的交通流的公路部分。
多车道公路的基本通行能力是以高速公路上观测到的最大交通量为基准确定的。
根据观测结果,城市快速路比城际间高速公路的值来得大一些,在大体接近城市快速路最大交通量处确定了多车道公路的基本通行能力为每车道2200pcu/h。
往返2车道公路的基本通行能力用往返合计值表示。
其理由为往返2车道公路通常不进行往返车道的分离,以供对面车辆超车用,这种方法是比较现实的。
实际上,在往返2车道公路上发生超车时的最大交通量的观测数据非常少,在美国《公路通行能力手册》中写明往返2车道公路的基本通行能力大约为多车道公路中2车道基本通行能力的二分之一,并确定为2500pcu/h。
另外,与多车道公路相同,对单向通行公路,把其基本通行能力定为每车道2200pcu/h。
(2)可能通行能力可能通行能力是用基本通行能力乘以公路的几何结构、交通条件对应的各种补偿系数求出的。
亦即C= CB*γL*γC*γI*……(2.1)式中,C:可能通行能力;CB:基本通行能力;γLγCγI:各种补偿系数。
就多车道公路而言,先用(2.1)式求出每车道的可能通行能力,然后乘以车道数求出公路截面的可能通行能力。
2013年国赛A题

2. 3. 指导教师或指导教师组负责人 (打印并签名): (论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。以上内容 请仔细核对,提交后将不再允许做任何修改。如填写错误,论文可能被取消评奖资格。)
日期: 2013 年 9 月 15 日
赛区评阅编号(由赛区组委会评阅前进行编号):
2013 高教社杯全国大学生数学建模竞赛
车道被占用的情况种类繁多、复杂,正确估算车道被占用对城市道路通行能力的影 响程度,将为交通管理部门正确引导车辆行驶、审批占道施工、设计道路渠化方案、设 置路边停车位和设置非港湾式公交车站等提供理论依据。
我们根据视频 1 和视频 2 中的交通事故情形,提出以下问题: 1、根据视频 1,描述视频中交通事故发生至撤离时间,事故所处横断面实际通行能力的 变化过程。 2、根据问题 1 所得结论,结合视频 2,分析说明同一横断面交通事故所占车道不同对该 横断面实际通行能力影响的差异。 3、构建数学模型,分析视频 1 中交通事故所影响的路段车辆排队长度与事故横断面实 际通行能力、事故持续时间、路段上游车流量间的关系。 4、假如视频 1 中的交通事故所处横断面距离上游路口变为 140 米,路段下游方向需求 不变,路段上游车流量为 1500pcu/h,事故发生时车辆初始排队长度为零,且事故持续不 撤离。请估算,从事故发生开始,经过多长时间,车辆排队长度将到达上游路口。
2013年数学建模A题思路解析

2013年数学建模A题思路解析2013国赛思路解析A题(仅供参考,内部使用,请勿外传)此题为交通运输类问题,可以视作优化类问题,而且本题重点在于目标的选取和目标函数的建立,而最优值的求解反而不是问题的重点(因为哪里会发生交通事故、持续时间、车流量等等都是不可控制的参数,本题几乎没有可决策变量)。
可以用到的知识有排队论,元胞自动机,模拟仿真等等,用这些手段来建立函数关系;关键概念:通行能力,指单位时间内通过断面的最大车辆数TC (traffic capacity)=n/t=vd (n为通过车辆数,t是时间,v为车辆平均速度,d是道路宽度);问题一:求出函数表达式TC=f(t),可以根据视频中的信息,隔一段时间求一次对应的TC值,再通过插值方法求出解f,或者深入研究事故发生时对车辆行进情况的变化机理来求解f,最后用图像或者解析式来表达出结果;问题二:求出泛函数表达式TC=g(LN),LN表示车道编号或其组合,此处TC代表问题一中的f函数,这个处理和问题一是一样的,可以用的方法也可以是直接从视频中读取,可以得到LN=(1,2)或(2,3)时的TC关于t的函数,如果采用机理分析方法,如排队论,元胞自动机来仿真这个过程,则可以求出LN=1,2,3时的情况;比较有两种形式:直观比较:将几个函数图像画在一起相互比较,就可以比较LN不同时,对通行能力的影响;数量化比较:可以将LN不同时的TC关于t的函数作差后积分,求得不同堵车形式对总的通行车辆数的影响;问题三: ················问题四:用问题三求出的函数表达式计算结果即可。
相关有用的资料我会及时上传群共享,大家加油!。
2013数学建模A题分析

1 交通事故影响时间分析由于从交通事故发生到检测到事故、接警、事故现场勘测、处理、清理事故现场恢复交通,以及恢复交通后车辆排队不再增加都需要一定的时间。
这部分时间主要由三部分构成: 第一部分是事故发生到警察到达现场的时间1T ; 第二部分是交通事故现场处理时间2T ,由现场测、处理到事故族除、恢复交通;第三部分是交通事故持续影响时间T3,部分时间从恢复事故场交通开始,到事故上游车辆排队不再增加,即排队开始减弱。
在T1内,事故现场保持原状,没有进行处理,这里分两种情况考虑: ( 1) 当交通事故占部分车道时,这时事故点的剩余通行能力Qs ≠0,交通事故越严重,则相应Qs 越小。
若事故点上游的交通需求Q < Qs ,则车辆以较低的速度通过事故点,上游不会形成车辆拥挤排队; 若Q > Qs ,则交通流可按事故点的剩余断面通行能力通过事故点,超过该通行能力的车流在事故点上游排队。
( 2) 当交通事故十分严重时,事故点的剩余通行能力Qs = 0,造成事发路段断流,事故点上游车辆排队,发生交通拥挤堵塞,进而排队一直向上游延伸。
在T2内,确认交通事故发生后,相关部门到现场处理异常事件,在此过程中,事故点交通可能会受到进一步影响,事故断面通行能力也随之发生变化[5],一般会变小,甚至变为0( 全封闭处理) ,视事件处理具体情况而定,事发点上游交通处于严重拥挤状态,车辆排队增加。
由于在交通事故接警时间T1和处理时间T2阶段事故点上游交通车辆产生排队,若没有车辆排队,则T3 = 0; 若有车辆排队,则当事故处理完毕、道路恢复交通时,排队车辆开始消散。
交通事故持续影响时间T3是事故处理完毕、道路恢复交通至车辆排队不再增加这段时间,即交通流消散波从车辆排队队列的头部传到尾部这段时间。
2、事故路段车辆排队长度分析如下图图发生交通事故的路段该事故路段长度为L( m) ,单方向车道数为n,单方向车道宽度为D( m) ,在道路上t = 0 时刻发生了一起交通事故,事故车辆占用道路宽度为b( m) ,长度为a( m) ,事故点上游路段长度为L'。
2013数学建模A题问题一解析--车道被占用对城市道路通行能力的影响
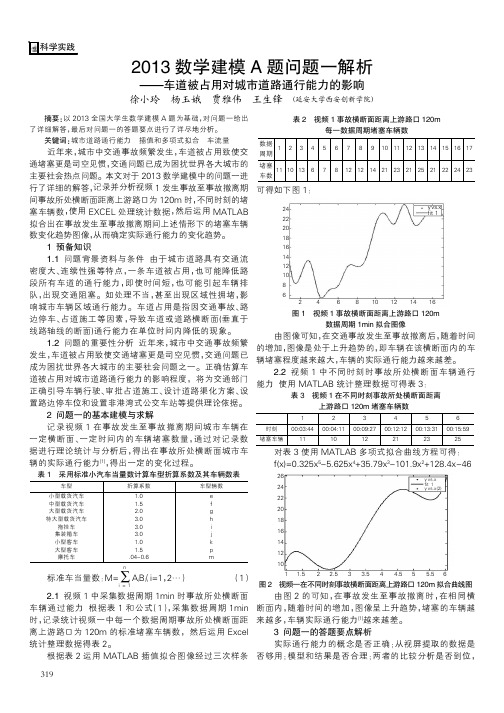
车型
小型载货汽车 中型载货汽车 大型载货汽车 特大型载货汽车
拖挂车 集装箱车 小型客车 大型客车 摩托车
折算系数
1.0 1.5 2.0 3.0 3.0 3.0 1.0 1.5 .04-0.6
车型辆数
e f g h i j k p m
n
移 标准车当量数:M= AiB(i i=1,2…) i=1
(1)
26
车辆通过能力 根据表 1 和公式(1),采集数据周期 1min 断面内,随着时间的增加,图像呈上升趋势,堵塞的车辆越
时,记录统计视频一中每一个数据周期事故所处横断面距 来越多,车辆实际通行能力[1]越来越差。
离上游路口为 120m 的标准堵塞车辆数,然后运用 Excel
3 问题一的答题要点解析
统计整理数据得表 2。
降,好的结果应该明确指出这一点。事故横断面下游交通
问题一数据的合理收集也是答题的必备条件。根据视
流方向需求不同,会导致上游每条车道分配到的车辆数不 频收集数据的类型:车流量(堵车点的车流量、上游路口的车
同,使两种情况事故所处道路横断面形成多车道排队的机 流量、小区出入的车流量、大车、小车、摩托车),排队长度。时
高外,具有重量轻,携带性好等特点。因此,上述产品价格均 想,电气控制系统包括充、供电
电气控制系统
较高。本文研究一种低价位多功能助站轮椅,更有助于患关 系统和速度控制等功能转换系 图 1 系统结构框图
(上接第 319 页)
以上四点为问题一的关键所在。道路被占用后,实际的通 整程度、行车视野、驾驶员对交通规则的遵守情况、车辆的
由的陈述或分析;在被占用道路没有车辆排队时,通行能 基本通行能力为基础,考虑到实际的地形、道路和交通状
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实际通行能力
由于道路、交通和管制条件以及服务水平不同,通行能力分为:基本(理论)通行能力,可能(实际)通行能力和设计(规划)通行能力。
理论通行能力是理想的道路与交通条件下的通行能力。
以理论通行能力为基础,考虑到实际的地形、道路和交通状况,确定其修正系数,再以此修正系数乘以前述的理论通行能力,即得实际道路、交通在一定环境条件下的可能通行能力。
公式(参《路网环境下高速公路交通事故影响传播分析与控制》):
单向车行道的可能通行能力Qx=CB*N*fw*fHV*fp
Qx是单向车行道可能通行能力,即在具体条件下,采用四级服务水平时所能通过的最大交通量veh/h。
CB是基本(理论)通行能力。
N是单向车行道的车道数。
fw是车道宽度和侧向净宽对通行能力的修正系数。
fHV是大型车对通行能力的修正系数,计算公式是:fHV=1/[1+ PHV(EHV-1)],EHV 是大型车换算成小客车的车辆换算系数;PHV是大型车交通量占总交通量的百分比。
fp驾驶员条件对通行能力的修正系数,一般在0.9~1之间
基本通行能力
基本通行能力【basic traffic capacity】指的是在理想的道路和交通条件下,单位时间一个车道或一条道路某一路段通过小客车最大数,是计算各种通行能力的基础。
通行能力
通行能力【traffic capacity】指的是在一定的道路和交通条件下,道路上某一路段单位时间内通过某一断面的最大车辆数。
可分为基本通行能力、可能通行能力和设计通行能力三种。
计算公式为:CAP=s1*λ1+s2*λ2+....+sn*λn(s为饱和流量,λ为绿信比)
全红时间越长,通行能力越小
周期时长一定的情况下,相位数越多,通行能力越大
它是指道路上某一地点、某一车道或某断面处,单位时间内可能通过的最大的交通实体(车辆或行人)数,亦称道路容量、交通容量或简称容量。
一般以辆/h、人/h表示。
车辆多指小汽车,当有其它车辆混入时,均采用等效通行能力的当量小客车单位
道路通行能力与交通量不尽相同,交通量是指道路在某一定时段内实际通过的车辆数。
一般道路的交通量均小于道路的通行能力,当道路上的交通量比其通行能力小得多时,则司机驾车行进时操作的自由度就越大,既可以随意变更车速,转移车道,还可以方便地实现超车。
当交通量等于或接近于道路通行能力时,车辆行驶的自由度就逐渐降低,一般只能以同一速度循序行进,如稍有意外,就会发生降速、拥挤,甚至阻滞。
当交通量超过通行能力时,车辆就会出现拥挤,甚至堵塞。
因此,道路通行能力同河流的过水能力一样,是道路在一定条件下所能通过的车辆的极限数值,条件不同,要求不同,其通行能力也就不同。
故通行能力是一个变数。
