用Excel手把手实现交通规划4阶段法教程
用excel的线性规划解决运输最优解问题

用excel的规划求解解决运输最优解问题
题目:
操作步骤:
1.启动excel(本人用的是金山的)。
2.在表格上按题目填写运费表。
如图:
3.另绘制一个可变量表,也就是待求解的运量表。
如图:
其中实际销量单元格填上公式,如:此单元格为它的纵向前三个单元格相加。
实际产量就为它的横向前四个单元格相加。
因为现在还没进行求解,所以都为0.
4.设立目标函数:=sumproduct(运价区域,运量区域)
5.选择规划求解功能,如图:
如果在“工具”中没有“规划求解”的,就选择“加载宏”,添加“规划求解”。
6.在“设置目标”选中写了目标函数的单元格。
选择“最小值”。
在“通过可更改可变单元格”选中运量区域。
遵守约束条件:每个实际销量=对应的题设销量。
每个实际产量=相应的题设产量。
运量区域≥0。
点击“求解”。
7.结果:。
excel交通规划“四阶段法”教程
Low
Middle
High Low
Middle
0
0
0
0
0
2000
8000 10000
0 4000
8000
22000 30000
0 16000
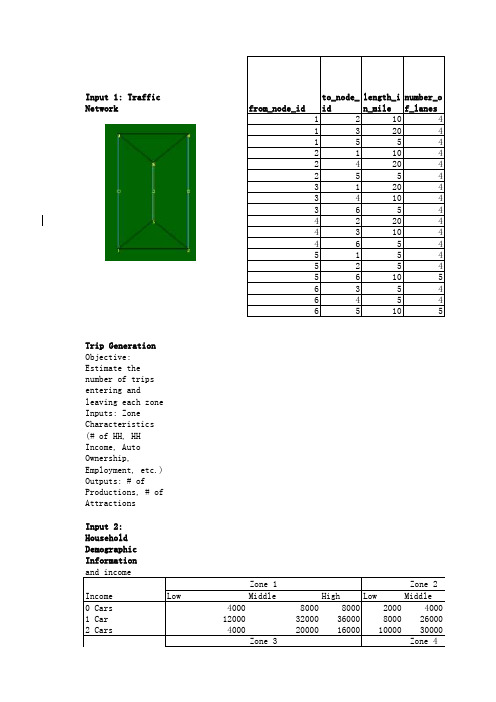
Input 4: Trip Production Table: Cars/HH
0
1
2
HH Income
HBW
Low
Middle
High
Low
Middle
High
5
5
Origin
Input 7: Friction Factor Coefficients:
Trip Purpose
a
HBW HBO
NHB
b
28507 139173
c
-0.02 -0.123 -1.285 -0.094
219113
-1.332 -0.1
Friction Factor Model: (Gamma Model)
Low
Middle
High
Source: based on
Martin and
McGuckin (1998),
Table 7, pg. 27.
Martin,W.A. and
N.A.McGuckin
(1998). Travel
Estimation
Techniques for
Urban Planning,
1.7 10 2
Other 1.7 0.5 2.5
Trip Distribution Objective: Estimate the number of trips made between each zone Inputs: Productions, Attractions, Travel time between zones Outputs: # of Person Trips from Zone i to Zone j
如何使用Excel的“规划求解”功能进行优化

如何使用Excel的“规划求解”功能进行优化在日常工作和生活中,我们经常会遇到需要优化的问题,比如如何在有限的资源条件下实现最大的效益,或者如何找到满足多个条件的最优方案。
这时候,Excel 的“规划求解”功能就可以派上用场了。
“规划求解”是 Excel 中一个强大的工具,它可以帮助我们通过建立数学模型来找到最优解。
接下来,让我们详细了解一下如何使用这个功能。
首先,确保您的 Excel 中已经加载了“规划求解”功能。
如果没有,可以通过以下步骤进行加载:点击“文件”选项卡,选择“选项”,在弹出的“Excel 选项”对话框中,选择“加载项”,然后在“管理”下拉菜单中选择“Excel 加载项”,点击“转到”按钮,在弹出的“加载宏”对话框中勾选“规划求解加载项”,点击“确定”即可。
在使用“规划求解”之前,我们需要明确问题的目标和约束条件,并将其转化为数学模型。
例如,假设我们有一个生产问题,需要决定生产两种产品 A 和 B 的数量,已知产品 A 的单位利润为 10 元,产品 B 的单位利润为 15 元,我们拥有的原材料限制为 100 单位,生产产品 A 每单位需要消耗 2 单位原材料,生产产品 B 每单位需要消耗 3 单位原材料。
我们的目标是最大化总利润。
接下来,我们在 Excel 中建立表格来表示这个问题。
在第一列中输入产品名称(A 和 B),第二列输入生产数量(假设初始值为 10),第三列输入单位利润(分别为 10 和 15),第四列计算每种产品的利润(数量乘以单位利润),第五列输入每种产品消耗的原材料数量(分别为 2 和 3),第六列计算总的原材料消耗(数量乘以消耗的原材料数量)。
然后,我们设置目标单元格。
在这个例子中,目标是最大化总利润,所以我们选择计算总利润的单元格作为目标单元格。
接下来,设置变量单元格,即生产数量所在的单元格。
再然后,添加约束条件。
在这个例子中,约束条件是总的原材料消耗不能超过 100 单位,所以我们添加这个约束条件。
Excel表格法求解路径规划问题

实验四: Excel 表格法求解路径规划问题
根据题意及决策变量与目标函数得出本问题的 线性规划模型。
minY=6×X11+3×X12+2×X13+5×X14+7×X21+5×X2 2+8×X23+4×X24+3×X31+2×X32 +9×X33+7×X34
s.t. X11+ X12+ X13+ X14=5(满足A1矿的产量) X21+ X22+ X23+ X24=2(满足A2矿的产量) X31+ X32+ X33+ X34=3(满足A3矿的产量) X11+ X21+ X31 =2(满足B1厂的需求量) X12+ X22 +X32 =3(满足B2矿的需求量) X13+ X23 +X33 =1(满足B3矿的需求量) X14+ X24 +X34 =4(满足B4矿的需求量) Xij >=0(i=1,2,3,j=1,2,3,4)(决策变量非负约束)
实验四: Excel 表格法求解路径规划问题
根据题意,设置本问题的决策变量和目标 函数。 设:Xij为每天从Ai矿运往Bj厂的矿石数量 (百吨),Y为总运费 Y=6×X11+3×X12+2×X13+5×X14+7 ×X21+5×X22+8×X23+4×X24+3×X3 1+2×X32 +9×X33+7×X34 ,则本问题 的目标函数为求minY 。
B1
铁矿
B2
B3
B4
产量(百吨)
A1
excel规划求解的使用教程详细图文步骤

excel规划求解的使用教程详细图文步骤
规划求解使用步骤2:创建表格,如下。
单击“数据“工具栏,选择”规划求解“,随即弹出【规划求解参数】对话框,在【设置目标单元格】中输入“$B$12”;在【可变单元格】中输入“$C$3:$C$5”,单击“添加”按钮,弹出【添加约束】对话框,在【单元格引用位置】输入“$B$10”,在其右侧的下拉列表中选择【<=】,在【约束值】中输入“$B$7”。
规划求解使用步骤3:单击“添加”按钮,继续添加约束条件。
使用相同方式,再添加4个约束条件。
规划求解使用步骤4:约束条件添加完毕,单击“确定”按钮,返回【规划求解参数】对话框,此时可发现在【约束】列表中显示出了添加的所有约束条件,然后单击“选项”按钮。
随即弹出【规划求解选项】对话框,选中“采用线性模型”和“假定非负”,其余保持默认设定,单击“确定”。
返回【规划求解参数】对话框,单击“求解”按钮。
excel2007进行规划求解的操作

excel2007进行规划求解的操作
Excel的基础统计分析功能主要体现在众多的统计函数中,这些函数的熟练应用有助于方便我们直接求得数据的统计量,如数学期望和方差等。
当然Excel还包涵了更复杂的数据分析功能都在Excel的【规划求解】模块当中,今天,店铺就教大家如何进行规划求解的方法!
Excel2007规划求解的步骤如下:
打开Excel2007工作文件——>【鼠标左键】单击【Microsoft office】按钮——>【鼠标左键】单击【Excel 选项】按钮;
然后在弹出的【Excel选项】下——>【鼠标左键】单击【加载项】——>在【管理:】右方选择【Excel 加载项】选项卡——>【鼠标左键】单击【转到】按钮;
再在弹出的【加载宏】方框下——>【鼠标左键】勾选【规划求解加载项】——>【鼠标左键】单击【确定】按钮;
4最后在Excel工作文档中【鼠标左键】单击【数据】选项卡即可看到位于该选项卡下右方的【数据分析】模块,【鼠标左键】单击【规划求解】即可看到【规划求解】模块。
注意事项:
第2步必须是在【Excel 加载项】选项卡下【鼠标左键】单击【转到】按钮!。
Excel规划求解功能的使用教程
本文整理于网络,仅供阅读参考
Excel规划求解功能的使用教程
excel规划求解功能的使用教程:
规划求解使用步骤1:安装规划求解:规划求解是excel的一个插件,需要安装。
打开新建文档左上角office按钮——excel 选项——自定义——从下列位置选择命令(所有命令)——加载宏——添加——确定。
点击“加载宏”工具,弹出【加载宏】对话框,勾选“分析工具库“和”规划求解加载项“,点击”确定“。
随即弹出microsoft office excel对话框,点击”是“。
开始安装。
规划求解使用步骤2:创建表格,如下。
单击“数据“工具栏,选择”规划求解“,随即弹出【规划求解参数】对话框,在【设置目标单元格】中输入“$b$12”;在【可变单元格】中输入“$c$3:$c$5”,单击“添加”按钮,弹出【添加约束】对话框,在【单元格引用位置】输入“$b$10”,在其右侧的下拉列表中选择【看了excel规划求解功能的使用教程。
利用EXCEL进行线性规划
解:依题意,设置四种家具的日产量分别为决策变量
x1, x2 , x3, x4 ,目标要求是日利润最大化,
约束条件为三种资源的供应量限制和产品销售量限制。 据此,列出下面的线性规划模型:
MaxZ 60x1 20x2 40x3 30x4
4x1 2x2 x3 2x4 600
x1, x2 , x3 , x4 0 (非负约束)
其中 x1, x2 , x3, x4 分别为四种家具的日产量。
下面介绍用Excel中的“规划求解”功能求此题。 第一步 在Excel中描述问题、建立模型,如下图所示。
=SUMPRODUCT(B6:E6,$B$15:$E$15)
第二步 在“工具”菜单中选择“规划求解”。
第三步 在“规划求解参数”对话框进行选择如下图。
第四步 点击“选项”按钮,弹出“规划求解选项”对话框
第五步 选择“采用线性模型”和“假定非负”, 单击“确定”,返回下图。单击“求解”,即可解 决此题。
最后结果如下页图所示。
应如何安排这四种家具的日产量,使得该厂的日利 润最大?
表1 雅致家具厂基本数据
12
3
4
家具类型
劳动时间
21 3
2
(小时/件)
木材
42 1
2
(单位/件)
玻璃(单位/ 6 2
1
2
件)
单位利润
60 20 40
30
(元/件)
最大销量 100 200 50
100
(件)
可提供两 400小时 600单位 1000单位
• 单击“添加”,显示添加约束对话框
• 选项:显示”规划求解选项”对话框.在其中可 以加载或保存规划求解模型,并对规划求解过 程的高级属性进行控制
Excel规划求解使用说明
规划模型的线性规划标准型式为:
2-21
规划求解使用说明
5.规划求解小结..............................................................................................................................19 6.Excel补注 ....................................................................................................................................19
Max z = C T X
⎧ AX = bΒιβλιοθήκη s .t .⎨ ⎩X
≥0
X 为决策变量向量 其中: C 为价值向量
b 为资源向量 A 为技术矩阵
这些都是经济生产中所具有的现实意义。
1.3.利用规划求解解决现实问题的步骤
z 建立对应的规划模型 z 在 Excel 表中输入已知数据(如线性规划模型的 A、b、C),以及指定规划模型三
4.人员安排模型..............................................................................................................................16 4.1.Excel关于规划求解自带的系统示例文件......................................................................16 4.2.问题描述...........................................................................................................................17 4.3.模型分析、建立...............................................................................................................17 4.4.规划求解...........................................................................................................................18
Excel求解线性规划问题实验教程要点
数学与信息科学学院Excel求解线性规划问题实验教程二零一三零八月目录1.关于“规划求解” (1)2.如何加载“规划求解” (2)3.“规划求解”各参数解释和设置 (3)4.“规划求解”的步骤 (6)5.Excel求解线性规划问题 (8)6.Excel求解运输问题 (14)7.Excel求解目标规划问题 (18)8.Excel求解整数规划问题 (22)1.关于“规划求解”“规划求解”是Excel中的一个加载宏,借助“规划求解”,可求得工作表上某个单元格(被称为目标单元格)中公式(公式:单元格中的一系列值、单元格引用、名称或运算符的组合,可生成新的值。
公式总是以等号(=)开始)的最优值。
“规划求解”将对直接或间接目标单元格中公式相关联的一组单元格中的数值进行调整,最终在目标单元格公式中求得期望的结果。
“规划求解”通过调整所指定的可更改的单元格(可变单元格)中的值,从目标单元格公式中求得所需的结果。
在创建模型过程中,可以对“规划求解”中的可变单元格数值应用约束条件(约束条件:“规划求解”中设置的限制条件。
可以将约束条件应用于可变单元格、目标单元格或其它与目标单元格直接或间接相关的单元格。
而且约束条件可以引用其它影响目标单元格公式的单元格。
使用“规划求解”可通过更改其它单元格来确定某个单元格的最大值或最小值。
)Microsoft Excel的“规划求解”工具取自德克萨斯大学奥斯汀分校的Leon Lasdon 和克里夫兰州立大学的Allan Waren共同开发的Generalized Reduced Gradient(GRG2)非线性最优化代码。
线性和整数规划问题取自Frontline Systems公司的John Watson 和Dan F ylstra提供的有界变量单纯形法和分支边界法。
2.如何加载“规划求解”安装office的时候,系统默认的安装方式不会安装宏程序,需要用户根据自己的需求选择安装。
