反比例函数与几何综合(讲义及答案)
反比例函数与几何综合(讲义及答案)

y
y
B Al
DA
B E
DO C
x
O
Cx
第 1 题图
第 2 题图
2. 如图,在平面直角坐标系中,一条直线与反比例函数 y 8(x x
>0)的图象交于两点 A,B,与 x 轴交于点 C,且点 B 是 AC
的中点,分别过两点 A,B 作 x 轴的平行线,与反比例函数 y 2 x
(x>0)的图象交于两点 D,E,连接 DE,则四边形 ABED
10. 如图,点 A 在双曲线 y k 的第二象限的分支上,AB⊥y 轴于 x
点 B,点 C 在 x 轴负半轴上,且 OC=2AB,点 E 在线段 AC 上,且 AE=3EC,点 D 为 OB 的中点.若△ADE 的面积为 3,
则 k 的值为________.
11. 如图,一次函数 y ax b 的图象与 x 轴,y 轴分别交于 A,B
两点,与反比例函数 y k 的图象交于 C,D 两点,过 C,D x
两点分别作 y 轴,x 轴的垂线,垂足为 E,F,连接 CF,DE. 有下列四个结论:①△DEF 与△CEF 的面积相等;
②△AOB∽△FOE;③△DCE≌△CDF;④AC=BD.
其中正确的结论序号是___________.
y D
B
AO
F
x
C
E
5
【参考答案】
课前预习
1
知识点睛
反比例函数与几何综合的处理思路: 1. 从关键点入手.“关键点”是信息汇聚点,通常是_________
和________的______.通过___________和_______________ 的互相转化可将_________与________综合在一起进行研究. 2. 梳理题干中的函数和几何信息,依次转化. 3. 借助___________或__________列方程求解.
中考反比例函数与几何综合
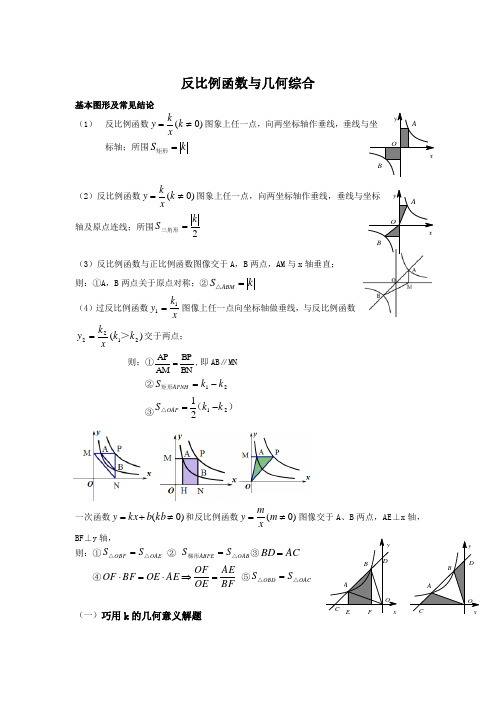
Oy xBAABxy O反比例函数与几何综合基本图形及常见结论 (1) 反比例函数)0(≠=k xky 图象上任一点,向两坐标轴作垂线,垂线与坐标轴;所围k S =矩形(2)反比例函数)0(≠=k xky 图象上任一点,向两坐标轴作垂线,垂线与坐标轴及原点连线;所围2k S =三角形(3)反比例函数与正比例函数图像交于A ,B 两点,AM 与x 轴垂直; 则:①A ,B 两点关于原点对称;②k S ABM =△(4)过反比例函数xk y 11=图像上任一点向坐标轴做垂线,与反比例函数)(2122k k xk y >=交于两点; 则:①BNBP AM AP =,即AB ∥MN②21k k S APNH -=矩形③)(△2121k k S OAP -=一次函数)0(≠+=kb b kx y 和反比例函数)0(≠=m xmy 图像交于A 、B 两点,AE ⊥x 轴,BF ⊥y 轴,则:①OAE OBF S S △△= ② OAB ABFE S S △梯形=③AC BD =④BFAEOE OF AE OE BF OF =⇒⋅=⋅ ⑤OACOBD S S △△=(一)巧用k 的几何意义解题y x ABO CDy xDC F EO B A例1.函数y=和y=在第一象限内的图象如图,点P 是y=的图象上一动点,PC ⊥x 轴于点C ,交y=的图象于点B .给出如下结论:①△ODB 与△OCA 的面积相等;②PA 与PB 始终相等;③四边形PAOB 的面积大小不会发生变化;④CA=AP .其中所有正确结论的序号是________。
迁移练习1(1).如图,双曲线)0x (k>=xy 经过Rt △OAB 斜边OB 的中点D ,与AB 交于点C .若△OBC 面积为3,则k =_______迁移练习1(2)..双曲线)0x (k>=xy 经过矩形OABC 边AB 的中点F ,交BC 于点E ; 若梯形OEBA 的面积为9,则k=________。
专题九-反比例函数与几何的综合应用

在物理学中,一些物理量之间可能存在反比例关系,如电阻与电流、压力与面积等。通过运用反 比例函数的性质,可以更好地理解和解决这些物理问题。
反比例函数在经济学中的应用
在经济学中,一些经济指标之间可能存在反比例关系,如价格与需求量、成本与产量等。通过运 用反比例函数的性质,可以对这些经济指标进行更准确的预测和分析。
如长度、面积等。
利用反比例函数性质建立关系
02
根据反比例函数的性质,结合几何图形的特点,建立所求最值
与相关量之间的关系。
求解最值
03
通过求解反比例函数的最值,得到所求几何量的最值。
判定存在性问题
根据题意列出方程或不等式
01
根据题目条件,列出与几何图形相关的方程或不等式
。
利用反比例函数性质分析解的情况
反比例关系在圆中的应用
在圆中,当一个圆的半径增加时,其 面积会按平方比例增加,但其周长只 会按线性比例增加。这种关系虽然不 是严格的反比例关系,但也可以用于 解决一些与圆相关的问题。
解题技巧与实例分析
通过利用圆的性质和上述关系, 可以求解一些与圆相关的问题。 例如,已知一个圆的半径和另一 个圆的面积或周长,可以求解未 知圆的半径或面积等。
仔细阅读题目要求,明确题意 ,避免答非所问。
合理安排答题顺序
先做易做的题目,确保会做的 题目不丢分,再攻克难题。
控制答题时间
每道题目分配合理的时间,避 免时间不够用或浪费过多时间
。
检查答案
做完题目后要认真检查答案, 确保没有遗漏或错误。
THANKS FOR WATCHING
感谢您的观看
解题技巧与实例分析
对于其他几何图形中的反比例关系问题,可以通过设定未知数、利用几何图形的性质和反比例关系来求解。 需要注意的是,在解题过程中要仔细分析题目条件和数据特点,选择合适的解题方法和思路。
反比例函数的综合(含答案)
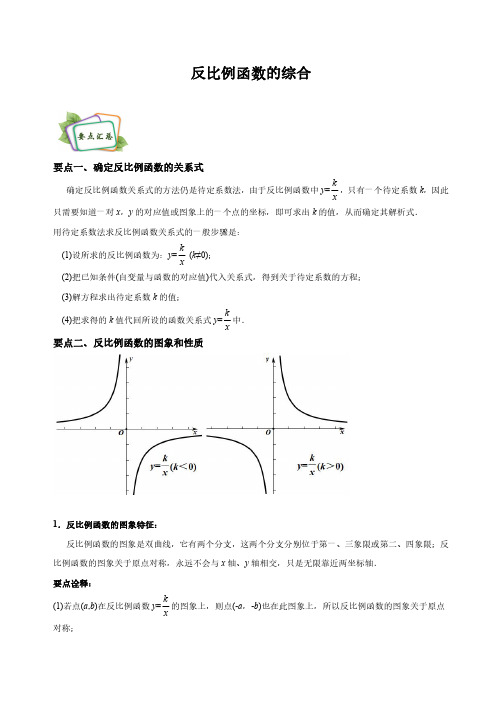
反比例函数的综合要点一、确定反比例函数的关系式确定反比例函数关系式的方法仍是待定系数法,由于反比例函数中y=kx,只有一个待定系数k,因此只需要知道一对x,y的对应值或图象上的一个点的坐标,即可求出k的值,从而确定其解析式.用待定系数法求反比例函数关系式的一般步骤是:(1)设所求的反比例函数为:y=kx(k≠0);(2)把已知条件(自变量与函数的对应值)代入关系式,得到关于待定系数的方程;(3)解方程求出待定系数k的值;(4)把求得的k值代回所设的函数关系式y=kx中.要点二、反比例函数的图象和性质1.反比例函数的图象特征:反比例函数的图象是双曲线,它有两个分支,这两个分支分别位于第一、三象限或第二、四象限;反比例函数的图象关于原点对称,永远不会与x轴、y轴相交,只是无限靠近两坐标轴.要点诠释:(1)若点(a,b)在反比例函数y=kx的图象上,则点(-a,-b)也在此图象上,所以反比例函数的图象关于原点对称;(2)在反比例函数y =k x(k 为常数,k ≠0)中,由于x ≠0且y ≠0,所以两个分支都无限接近但永远不能达到x 轴和y 轴.2.反比例函数的性质(1)如图1,当k >0时,双曲线的两个分支分别位于第一、三象限,在每个象限内,y 值随x 值的增大而减小.(2)如图2,当k <0时,双曲线的两个分支分别位于第二、四象限,在每个象限内,y 值随x 值的增大而增大.要点诠释:反比例函数的增减性不是连续的,它的增减性都是在各自的象限内的增减情况,反比例函数的增减性都是由反比例系数k 的符号决定的;反过来,由双曲线所在的位置和函数的增减性,也可以推断出k 的符号.要点三、反比例函数y =k x(k ≠0)中的比例系数k 的几何意义过双曲线y =k x (k ≠0)上任意一点作x 轴、y 轴的垂线,所得矩形的面积为|k|.过双曲线y =k x (k ≠0)上任意一点作一坐标轴的垂线,连接该点和原点,所得三角形的面积为||2k .要点诠释:只要函数式已经确定,不论图象上点的位置如何变化,这一点与两坐标轴的垂线和两坐标轴围成的面积始终是不变的.例1.两个反比例函数y =3x ,y =6x在第一象限内的图象如图所示,点P 1,P 2,P 3……P 2020在反比例函数y =6x 图象上,它们的横坐标分别是x 1,x 2,x 3……x 2020,纵坐标分别是1,3,5,…,共2020个连续奇数,过点P 1,P 2,P 3……P 2020分别作y 轴的平行线,与反比例函数y =3x的图象交点依次是Q 1(x 1,y 1),Q 2(x 2,y 2),Q 3(x 3,y 3)……Q 2020(x 2020,y 2020),则y 2020等于()A .2019.5B .2020.5C .2019D .4039例2.如图,直线y =k 1x +b 与双曲线y =2k x A ,B 两点,其横坐标分别为1和5,则不等式k 1x <2k x +b 的解集是.1.一次函数y 1=k 1x +b 和y 2=2k x (k 2>0)相交于A (1,m ),B (3,n )两点,则不等式k 1x +b >2k x的解集为()A.1<x<3B.x<1或x>3C.x<0或x>3D.1<x<3或x<02.反比例函数y=kx和正比例函数y=mx的图象如图.由此可以得到方程kx=mx的实数根为()A.x=﹣2B.x=1C.x1=2,x2=﹣2D.x1=1,x2=﹣2例3.如图,点A在双曲线y=kx的第一象限的那一支上,AB垂直y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为.1.如图,在反比例函数y=4x的图象上有一点A向x轴作垂线交x轴于点C,B为线段AC的中点,又D点在x轴上,且OD=3OC,则△OBD的面积为.例4.在平面直角坐标系xOy中,反比例函数y=kx(k≠0,x>0)的图象经过点A(1,-4),直线y=-2x+m与x轴交于点B(1,0).(1)求k,m的值;(2)已知点P(n,-2n)(n>0),过点P作平行于x轴的直线,交直线y=-2x+m于点C,过点P作平行于y轴的直线交反比例函数y=kx(k≠0,x>0)的图象于点D,当PD=2PC时,结合函数的图象,求出n的值.1.如图,正比例函数y1=mx,一次函数y2=ax+b和反比例函数y3=kx的图象在同一直角坐标系中,若y3>y2>y1,则自变量x的取值范围是()A.x<﹣1B.﹣1<x<0或x>1.6C.﹣1<x<0D.x<﹣1或0<x<12.设函数y1=kx,y2=kx (k>0),当2≤x≤3时,函数的y1最大值是a,函数y2的最小值是a﹣4,则ak=()A.4B.6C.8D.103.已知反比例函数y=8x和y=3x在第一象限内的图象如图所示,则△AMN的面积为.4.如图,P1是反比例函数y=kx(k>0)图象在第一象限上的一点,点A1的坐标为(2,0).(1)当点P1的横坐标逐渐增大时,△P1OA1的面积将如何变化?逐渐减少.(2)若点P2在反比例函数图象上,点A2在x轴上,△P1OA1与△P2A1A2均为等边三角形,①求次反比例函数的解析式;②求点A2的坐标.5.如图,反比例函数y=kx图象和一次函数y=ax+b经过M(1,6)和N(2,a).(1)求一次函数解析式;(2)一次函数y=ax+b与x轴交于点B,与y轴交于点A,求证:AM=BN.6.已知:A (a ,y 1).B (2a ,y 2)是反比例函数y =k x (k >0)图象上的两点.(1)比较y 1与y 2的大小关系;(2)若A 、B 两点在一次函数y =43x+b 第一象限的图象上(如图所示),分别过A 、B 两点作x 轴的垂线,垂足分别为C 、D ,连接OA 、OB ,且S △OAB =8,求a 的值;(3)在(2)的条件下,如果3m =-4x +24,3n =32x ,求使得m >n 的x 的取值范围.7.如图,在平面直角坐标系xOy 中,函数y =k x(x <0)的图象经过点A (﹣1,6),直线y =mx ﹣2与x 轴交于点B (﹣1,0).(1)求k ,m 的值;(2)过第二象限的点P (n ,﹣2n )作平行于x 轴的直线,交直线y =mx ﹣2于点C ,交函数y =k x(x <0)的图象于点D .①当n =﹣1时,判断线段PD 与PC 的数量关系,并说明理由;②若PD ≥2PC ,结合函数的图象,直接写出n 的取值范围.8.在平面直角坐标系xOy中,函数y=mx(x>0)的图象G与直线l:y=kx-4k+1交于点A(4,1),点B(1,n)(n≥4,n为整数)在直线l上.(1)求m的值;(2)横、纵坐标都是整数的点叫做整点.记图象G与直线l围成的区域(不含边界)为W.①当n=5时,求k的值,并写出区域W内的整点个数;②若区域W内恰有5个整点,结合函数图象,求k的取值范围.【经典例题1】A【解析】解:∵P n 的纵坐标为:2n -1,∴P 2020的纵坐标为2×2020-1=4039.∵y =与y =在横坐标相同时,y =的纵坐标是y =的纵坐标的2倍,∴y 2020=×4039=2019.5.∴A 答案正确.【经典例题2】-5<x <-1或x >0【解析】解:根据一次函数平移和反比例函数的对称性可得,直线y =k 1x -b 与双曲线y =2k x 交于第三象限点的坐标为(-5,-1)和(-1,-5),如下图所示,∴不等式k 1x <2k x +b ,即k 1x -b <2k x 的解集,即当直线y =k 1x -b 的图象在反比例函数y =2k x 图象的下方对应的自变量x 的取值范围为:-5<x <-1或x >0.【举一反三1】D【解析】解:如图,由图象可得:不等式k 1x +b >2k x 的解集是1<x <3或x <0.故选:D .【举一反三2】C【解析】解:如图,反比例函数y =和正比例函数y =mx 相交于点A (﹣2,1),∴另一个交点为:(2,﹣1),∴方程=mx 的实数根为:x 1=2,x 2=﹣2.故选:C .【经典例题3】163【解析】解:连DC ,∵AE =3EC ,S △ADE =3,∴S △CDE =1.∴S △ADC =4.设A (a ,b ),则AB =a ,OC =2AB =2a .∵D 为OB 的中点,∴BD =OD =12b .∵S 梯形OBAC =S △ABD +S △ADC +S △ODC ,12(a +2a )·b =12a ·12b +4+12·2a ·b ,∴ab =163.把A (a ,b )代入y =,得k =ab =163.【举一反三1】3【解析】解:设A (x 、y ),由反比例函数y =4x可知xy =4,BC =AC =y ,OD =3OC =3x ,∴S △OBD =BC ×OD =×y ×3x =xy =×4=3.故答案为:3.【经典例题4】【解析】解:(1)把A(1,-4)代入y=k x,得k=1×(-4)=-4;把B(1,0)代入y=-2x+m,得-2+m=0,解得m=2;(2)反比例函数解析式为y=-(x>0),一次函数解析式为y=-2x+2,如图,当y=-2n时,-2x+2=-2n,解得x=n+1,则C(n+1,-2n),∴PC=n+1-n=1,当y=-2n时,y=-=,∴D(n,-),∴PD=|-2n+|,∵PD=2PC,∴|-2n+|=2,当-2n+=2时,解得n1=-2(舍去),n2=1,当-2n+=-2时,解得n1=-1(舍去),n2=2,综上所述,当PD=2PC时,n=1或n=2.【自我检测1】B【解析】解:由图象可知,当﹣1<x<0或x>1.6时,双曲线y3落在直线y2上方,且直线y2落在直线y1上方,即y3>y2>y1,所以若y3>y2>y1,则自变量x的取值范围是﹣1<x<0或x>1.6.故选:B.【自我检测2】C【解析】解:∵k>0,2≤x≤3,∴y1随x的增大而减小,y2随x的增大而增大,∴当x=2时,y1取最大值,最大值为=a①;当x=2时,y2取最小值,最小值为﹣=a﹣4②;由①②得a=2,k=4,∴ak=8,故选:C.【自我检测3】25 16【解析】解:设A(a,),则M(a,),N(,),∴AN=a﹣=,AM=﹣=,∴△AMN的面积=AN×AM=××=25 16,故答案为:25 16.【自我检测4】【解析】解:(1)△P1OA1的面积逐渐减少;(2)作P1C⊥OA1于C,∵△P1OA1为等边三角形,A1(2,0),∴OC=1,P1C3P1(1,3).∴反比例函数的解析式为y=3 x.(3)作P2D⊥A1A2于D,如上图,设A1D=x,则OD=2+x,P2D3x,∴P2(2+x3x).将点P2代入y=3x,得y332x=+.x2+2x-1=0,解得x1=-2,x2=-12<0(舍).∴x=-2,OA2=2+x+x=2+2x=2+2(-2)=22.∴A2(22,0).【自我检测5】【解析】解:(1)∵点M(1,6)在反比例函数y=图象上,∴k=1×6=6,∴反比例函数的关系式为y=,把N(2,a)代入得,a==3,∴N(2,3).∵点M(1,6)和N(2,3)在一次函数y=ax+b的图象上,∴a+b=6,2a+b=3,解得a=﹣3,b=9,∴一次函数的关系式为y=﹣3x+9;(2)过点M、N分别作MC⊥OA,ND⊥OB,垂足分别为C、D,当x=0时,y=9,当y=0时,x=3,∴一次函数y=﹣3x+9与x轴的交点B(3,0),与y轴的交点A(0,9),由于A(0,9),B(3,0),M(1,6),N(2,3),∴MC=1,AC=9﹣6=3,ND=3,BD=3﹣2=1,∴MC=BD=1,AC=ND=3,又∵∠ACM=∠NDB=90°,∴△ACM≌△NDB(SAS),∴AM=BN.【自我检测6】【解析】解:(1)∵A、B是y=kx(k>0)图象上的两点,∴a≠0.当a>0时,A、B在第一象限,a<2a,∴此时y1>y2,同理,a<0时,y1<y2.(2)∵A(a,y1)、B(2a,y2)在y=kx(k>0)图象上,∴AC=y1=,BD=y2=.∴y1=2y2.又A (a ,y 1)、B (2a ,y 2)在y =a +b 图象上,∴y 1=a +b ,y 2=a +b .∴a +b =2(a +b ),得b =4a .∵S △AOC +S 梯形ACDB =S △AOB +S △BOD ,又S △AOC =S △BOD ,∴S 梯形ACDB =S △AOB ,即[(a +b )+(a +b )]•a =8.∴a 2=4,由a >0,得a =2.(3)由(2)知,一次函数y =x +8,反比例函数y =.∵A 、B 两点的横坐标分别为2,4,且m =x +8,n =,∴使得m >n 的x 的范围,是反比例函数的图象在一次函数图象下方的点的横坐标取值范围.∴由图可知,2<x <4或x <0.【自我检测7】【解析】解:(1)∵函数y =k x (x <0)的图象经过点A (﹣1,6),∴k =﹣6.∵直线y =mx ﹣2与x 轴交于点B (﹣1,0),∴m =﹣2.(2)①判断:PD =2PC .理由如下:当n =﹣1时,点P 的坐标为(﹣1,2),∵y =﹣2x ﹣2交于于点C ,且点P (﹣1,2)作平行于x 轴的直线,∴点C 的坐标为(﹣2,2),∵函数y =k x(x <0)的图象于点D ,且点P (﹣1,2)作平行于x 轴的直线,点D 的坐标为(﹣3,2).∴PC =1,PD =2.∴PD =2PC .②当PD=2PC时,有两种情况,分别为:y=2,或者y=6.若PD≥2PC,0<y≤2,或y≥6即0<﹣2n≤2,或﹣2n≤6解得﹣1≤n<0.或n≤﹣3【自我检测8】【解析】(1)解:把A(4,1)代入y=mx(x>0),得m=4×1=4;(2)①当n=5时,把B(1,5)代入直线l:y=kx-4k+1得,5=k-4k+1,解得k=4 3-,如图所示,区域W内的整点有(2,3),(3,2),有2个;(3)直线l:y=kx-4k+1过(1,6)时,k=53-,区域W内恰有4个整点,直线l:y=kx-4k+1过(1,7)时,k=-2,区域W内恰有5个整点,∴区域W内恰有5个整点时,k的取值范围是-2≤k<5 3-.。
反比例函数与几何综合讲义及答案

反比例函数与几何综合讲义及答案一、反比例函数的定义及性质1.反比例函数的定义:如果两个变量的乘积为常数,那么它们之间存在反比例关系,可以表示为y=k/x。
2.反比例函数的性质:函数图像关于坐标轴对称;随着x的增大,y 的值逐渐减小;随着x的减小,y的值逐渐增大。
二、反比例函数的图像与性质1.绘制反比例函数y=k/x的图像。
2.如果k为正数,当x趋近于无穷大时,y趋近于0;当x趋近于0时,y趋近于正无穷大。
3.如果k为负数,当x趋近于无穷大时,y趋近于负无穷大;当x趋近于0时,y趋近于0。
三、反比例函数的解析表达式和图像的关系1.根据解析表达式y=k/x,结合k的正负性质,分析函数图像的大致形状。
2.当k为正数时,函数图像在第一象限逐渐接近于x轴,且没有定义域为x=0的点。
3.当k为负数时,函数图像在第三象限逐渐接近于x轴,且没有定义域为x=0的点。
四、反比例函数的应用1. 反比例函数的例题:如果旅行的时间与旅行的速度成反比例关系,当速度增大时,时间会减少。
求出速度为60 km/h时需要的时间。
答案:假设旅行的时间为t小时,则速度为60 km/h,根据反比例函数的定义可得60 = k/t,解得k = 60t。
根据题意可得t = k/60 = 1小时。
2.反比例函数出题:已知两个变量x和y成反比例关系,在一组数据中,当x=2时,y=5;当x=4时,y=10。
求出该反比例函数的解析表达式。
答案:根据反比例函数的定义可得k = xy,由已知数据可得2k = 5;4k = 10。
解方程可得k = 5/2、将k带入反比例函数中得到y = (5/2)x。
请注意,以上是一些常见的反比例函数综合讲义及试题及答案,实际上反比例函数的应用非常广泛,可以结合实际问题进行更多的应用练习。
反比例函数与几何综合
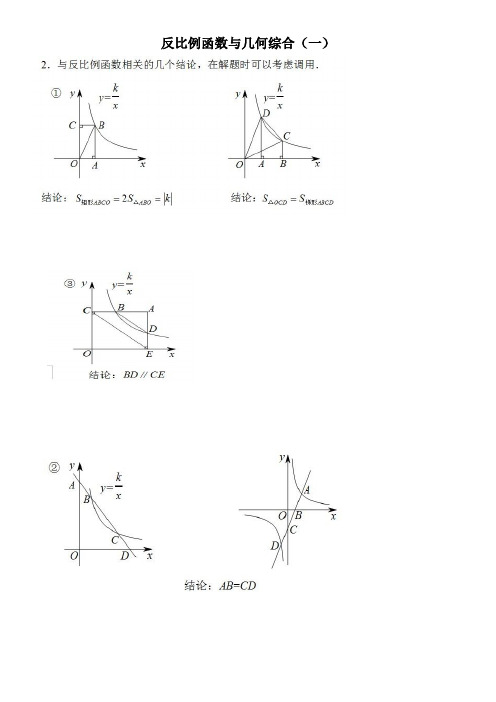
反比例函数与几何综合(一)反比例函数与一次函数、几何图形综合题类型一 反比例函数与一次函数综合 1. 已知反比例函数y =kx的图象过点A (3,1).(1)求反比例函数的解析式;(2) 若一次函数y =ax +6(a ≠0)的图象与反比例函数的图象只有一个交点,求一次函数的解析式.2. 如图,直线y =2x +4与反比例函数y =kx 的图象相交于A (-3,a )和B 两点.(1)求k 的值;(2)直线y =m (m >0)与直线AB 相交于点M ,与反比例函数y =kx的图象相交于点N .若MN =4,求m 的值.第2题图3. 如图,已知A (-4,n ),B (2,-4)是一次函数y =kx +b 和反比例函数y =mx 的图象的两个交点.(1)求一次函数和反比例函数的解析式; (2)求△AOB 的面积;(3)观察图象,直接写出方程kx +b -mx=0的解.第3题图4. 如图,已知直线y =kx 与双曲线y =4x (x >0)相交于点A (2,m ),将直线y =kx 向下平移2个单位长度后与y 轴相交于点B ,与双曲线交于点C ,连接AB 、AC .第4题图(1)求直线BC 的函数表达式; (2)求△ABC 的面积.类型二 反比例函数与几何图形综合5. 如图,已知,A (0,4),B (-3,0),C (2,0),D 为B 点关于AC 的对称点,反比例函数y =kx 的图象经过D 点.(1)证明四边形ABCD 为菱形; (2)求此反比例函数的解析式;(3)已知在y =kx的图象(x >0)上有一点N ,y 轴正半轴上有一点M ,且四边形ABMN 是平行四边形,求M 点的坐标.第5题图6. 如图,在平面直角坐标系中,Rt △AOB 的斜边OA 在x 轴的正半轴上,∠OBA =90°,且tan ∠AOB =12,OB =25,反比例函数y =kx的图象经过点B .(1)求反比例函数的表达式;(2)若△AMB 与△AOB 关于直线AB 对称,一次函数y =mx +n 的图象过点M 、A ,求一次函数的表达式.第6题图类型三 反比例函数与一次函数、几何图形综合7. 如图,双曲线y =kx (x >0)经过△OAB 的顶点A 和OB 的中点C ,AB ∥x 轴,点A 的坐标为(4,6),连接AC 交x 轴于D ,连接BD . (1)确定k 的值;(2)求直线AC 的解析式;(3)判断四边形OABD 的形状,并说明理由; (4)求△OAC 的面积.第7题图8. 如图,直线y =-x +b 与反比例函数y =kx 的图象相交于A (1,4),B 两点,延长AO 交反比例函数图象于点C ,连接OB .(1)求k 和b 的值;(2)直接写出一次函数值小于反比例函数值的自变量x 的取值范围;(3)在y 轴上是否存在一点P ,使S △PAC =25S △AOB ?若存在,请求出点P 坐标;若不存在,请说明理由.第8题图。
反比例函数与几何综合(一)(含答案)

学生做题前请先回答以下问题问题1:思考反比例函数与几何综合的处理思路是什么?问题2:什么是关键点?问题3:将函数特征与几何特征联系起来的桥梁是什么?问题4:围绕关键点以及横平竖直线段长将几何特征与函数特征结合分析时有几种方式?分别是什么?以下是问题及答案,请对比参考:问题1:思考反比例函数与几何综合的处理思路是什么?答:反比例函数与几何综合的处理思路:①从关键点入手.通过关键点坐标和横平竖直线段长的互相转化可将函数特征和几何特征综合在一起进行研究.②对函数特征和几何特征进行转化、组合,列方程求解.若借助反比例函数模型,能快速将函数特征转化为几何特征.问题2:什么是关键点?答:关键点是几何图形与函数图象的交点,在处理反比例函数与几何综合的问题时从关键点入手分析.问题3:将函数特征与几何特征联系起来的桥梁是什么?答:通过关键点坐标与横平竖直线段长的相互转化,可将函数特征与几何特征综合起来一起进行研究.问题4:围绕关键点以及横平竖直线段长将几何特征与函数特征结合分析时有几种方式?分别是什么?答:可以采用两种方式:①根据函数特征设出坐标,表达线段长,利用几何特征建等式;②根据几何特征设出线段长,表达坐标,代入函数建立等式.反比例函数与几何综合(一)一、单选题(共8道,每道12分)1.如图,直线与双曲线在第一象限内的交点为R,与x轴的交点为P,与y轴的交点为Q;作RM⊥x轴于点M,若△OPQ与△PRM的面积之比为4:1,则k的值为( )A. B.C.2D.3答案:B解题思路:试题难度:三颗星知识点:反比例函数与几何综合2.如图,均是等腰直角三角形,点在反比例函数的图象上,斜边都在x轴上,则点的坐标是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:反比例函数与几何综合3.如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x 轴,y轴上,反比例函数(x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为( )A.(1,14)B.(2,8)C.(2,7)D.(1,16)答案:C解题思路:试题难度:三颗星知识点:反比例函数与几何综合4.如图,矩形ABCD的顶点D在反比例函数(x<0)的图象上,顶点B,C在x轴上,对角线AC的延长线交y轴于点E,连接BE,若△BCE的面积是6,则k的值为( )A.-6B.-8C.-9D.-12答案:D解题思路:试题难度:三颗星知识点:反比例函数与几何综合5.如图,在反比例函数的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数的图象上运动.若tan∠CAB=2,则k的值为( )A.2B.4C.6D.8答案:D解题思路:试题难度:三颗星知识点:反比例函数与几何综合6.如图,直线与双曲线交于点A,将直线向上平移4个单位长度后,与y轴交于点C,与双曲线交于点B,若OA=3BC,则k的值为( )A.3B.6C. D.答案:D解题思路:试题难度:三颗星知识点:反比例函数与几何综合7.如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=,反比例函数在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )A.60B.80C.30D.40答案:D解题思路:试题难度:三颗星知识点:反比例函数与几何综合8.直线y=-2x-2与反比例函数的图象交于点A,与x轴交于点B,过点B作x 轴垂线交双曲线于点C,若AB=AC,则k的值为( )A.-1B.-2C.-4D.-8答案:C解题思路:试题难度:三颗星知识点:反比例函数与几何综合。
反比例函数与几何的综合应用讲义+2023-2024学年人教版数学九年级下册

反比例函数与几何的综合应用点石成金解反比例函数与几何图形的综合题,一般先设出几何图形中的未知量,然后结合函数的图象用代数式表示出几何图形与图象的交点坐标,再由函数解析式及几何图形的性质写出含未知数及待定字母的方程(组) ,解方程(组) 即可得所求几何图形中的未知量或函数解析式中待定字母的值.经典实例剖析如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,其边长为2,点A,点C分别在x轴,y轴的正半轴上,函数y=2x的图象与CB交于点D,函数y=k(k为常数,k≠0)的图象经x过点D,与AB交于点E,与函数y=2x的图象在第三象限内交于点F,连接AF、EF.(1)求函数y=k的表达式,并直接写出E、F两点的坐标;x(2)求△AEF的面积.分析:(1)根据正方形的性质,以及函数上点的坐标特征可求点D的坐标为(1,2),根据待定系数法可求反比例函数表达式,进一步得到E、F两点的坐标;(2)过点F作FG⊥AB,与AB的延长线交于点G,根据两点间的距离公式可求AE=1,FG=3,再根据三角形面积公式可求△AEF的面积.解:(1)∵正方形OABC的边长为2,∴点D的纵坐标为2,即y=2,将y=2代入y=2x,得x=1,∴点D的坐标为(1,2),的图象经过点D,∵函数y=kx,∴2=k1解得k =2,∴函数y =k x 的表达式为y =2x ,∴E (2,1),F (﹣1,﹣2);(2)过点F 作FG ⊥AB ,与BA 的延长线交于点G ,∵E (2,1),F (﹣1,﹣2),∴AE =1, FG =2﹣(﹣1)=3,∴△AEF 的面积为:12AE •FG =12×1×3=32.分类训练应用1 反比例函数与三角形的综合1.如图,一次函数y =kx +94(k 为常数,k ≠0)的图象与反比例函数y =m x (m 为常数,m ≠0)的图象在第一象限交于点A (1,n ),与x 轴交于点B (﹣3,0).(1)求一次函数和反比例函数的解析式.(2)点P 在x 轴上,△ABP 是以AB 为腰的等腰三角形,请直接写出点P 的坐标.应用2 反比例函数你与四边形的综合类型1 反比例函数与平行四边形的综合2.如图,一次函数y =kx +b 的图象与反比例函数y =m x 的图象相交于A (﹣1,4),B (a ,﹣1)两点.(1)求反比例函数和一次函数的表达式;的图象于点Q,连接PQ.当(2)点P(n,0)在x轴负半轴上,连接AP,过点B作BQ∥AP,交y=mxBQ=AP时,求n的值.类型2反比例函数与矩形的综合(k<0)的图象与矩形ABCO的边相交于E、F两点,且BE=2AE,E(﹣1,3.如图,反比例函数y=kx2).(1)求直线EF的解析式;(2)连接EF,求△BEF的面积.类型3反比例函数与菱形的综合4.如图,在直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反(k>0,x>0)的图象上,点D的坐标为(4,3).比例函数y=kx(1)求k的值.(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在该函数的图象上时,求菱形ABCD沿x轴正方向平移的距离.类型4反比例函数与正方形的综合5.如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,(x>0,k≠0)的图象经过线段BC的中点D.点B的坐标为(2,2),反比例函数y=kx(1)求k的值;(2)若点P(x,y)在该反比例函数的图象上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围.应用3反比例函数与菱形、正方形的综合6.如图1,四边形ABCD为正方形,点A在y轴上,点B在x轴上,且OA=2OB,反比例函数y=27x 在第一象限的图象经过正方形的顶点C.(1)求点C的坐标;(2)如图2,将正方形ABCD沿x轴向右平移得到正方形A'B'CD',点A'恰好落在反比例函数的图象上,求此时点D'的坐标;(3)在(2)的条件下,点P为y轴上一动点,平面内是否存在点Q,使以点O、A'、P、Q为顶点的四边形为菱形,若存在,请直接写出点Q的坐标,若不存在,请说明理由.应用4 反比例函数与正六边形的综合(k>0,x>0)7.如图,在平面直角坐标系中,正六边形ABCDEF的对称中心P在反比例函数y=kx的图象上,边CD在x轴上,点B在y轴上,已知CD=2.(1)点A是否在该反比例函数的图象上?请说明理由;(2)若该反比例函数图象与DE交于点Q,求点Q的横坐标;(3)平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数与几何综合(讲义)
➢课前预习
前期学习一次函数与几何综合问题时,解决思路是将坐标、几何图形和一次函数综合起来分析、转化.如:坐标与线段长互转,由坐标求解表达式,根据函数表达式计算坐标等,请尝试解决下列问题,并体会整个解决问题的过程:
如图,已知直线l1:y =2
x +
8
与直线l2:y=-2x+16 相交于点
3 3
C,直线l1,l2 分别交x 轴于A,B 两点,矩形DEFG 的顶点D,E 分别在l1,l2 上,顶点F,G 都在x 轴上,且点G 与点B 重合,那么S 矩形DEFG:S△ABC = .
解决一次函数与几何综合问题的核心在于:找坐标,转线段长,借助几何或函数特征建等式求解.
1
➢知识点睛
反比例函数与几何综合的处理思路:
1
.从关键点入手.“关键点”是信息汇聚点,通常是和的.通过和
的互相转化可将与综合在一起进行研究.
2.梳理题干中的函数和几何信息,依次转化.
3.借助或列方程求解.
与反比例函数相关的几个结论,在解题时可以考虑调用.
结论:S
矩形ABCO = 2S
△ABO
=| k | 结论:S
△OCD
=S
梯形ABCD 结论:AB=CD
结论:BD∥CE 函数几何特征常见转化作法:
1.函数→坐标→几何
①借助表达式设出点坐标;
②将点坐标转化为横平竖直线段长;
③结合几何特征利用线段长列方程.
2.几何→坐标→函数
①研究几何特征,考虑线段间关系;
②通过设线段长进而表达点坐标;
③将点坐标代入函数表达式列方程.若(x1,y1),(x2,y2)是同一反比例函
数上的点,则:
①当x1,y1,x2,y2 都用同一字母表达出来时,往往利用x1y1=x2y2=k 列方程求解.
②当两点的横坐标有比例关系时,对应的纵坐标也有比例关系.这样的比例关系常通过横平竖直的线段放在相似三角形中使用.
如:
x
1 =
y
2
x
2
y
1
3 ➢ 精讲精练
1.
如图,A ,B 是双曲线 y = k
(k <0)上的点,且 A ,B 两点的
x
横坐标分别为 a ,2a ,线段 AB 的延长线交 x 轴于点 C .若S △AOC =6,则 k =
.
第 1 题图
第 2 题图
2.
如图,已知第一象限内的图象是反比例函数 y = 1
图象的一个
x 分支,第二象限内的图象是反比例函数 y = - 2
图象的一个分
x
支,在 x 轴上方有一条平行于 x 轴的直线 l 与它们分别交于点A ,B ,过点 A ,B 作 x 轴的垂线,垂足分别为点 C ,D .若四边形 ACDB 的周长为 8,且 AB <AC ,则点 A 的坐标是 .
3.
如图,已知第一象限内的点 A 在反比例函数 y = 2
的图象上,
x
第二象限内的点B 在反比例函数 y = k
的图象上,且OA ⊥OB ,
x
OB
= ,则 k 的值为 . OA
第 3 题图
第 4 题图
4.
如图,反比例函数 y = k
(x > 0)的图象经过矩形 OABC 对角
x
线的交点 M ,分别与 AB ,BC 相交于点 D ,E .若四边形 ODBE 的面积为 6,则
k
的值为
.
5.如图,正方形
OAPB 的顶点
B 以及等腰直角三角形AFD 的顶
点A,D 在坐标轴上,点P,F 在函数y =
9
(x > 0 )的图象
x
上,则点F 的坐标为.
第5 题图第6 题图
6.如图,若正方形OABC 的顶点B 和正方形ADEF 的顶点E 都
在函数y =
1
(x > 0 )的图象上,则点E 的坐标是.
x
7.如图,直线y =kx - 2 (k > 0 )与双曲线y =
k
在第一象限内
x
的交点为R,与x 轴的交点为P,与y 轴的交点为Q.作RM ⊥x 轴于点M,若△OPQ 与△PRM 的面积之比为4:1,则k= .
第7 题图第8 题图
8.如图,直线y =
4
x 与双曲线y =
k
(x>0)交于点A .将直线y =
4
x
3
3
向右平移
9
2
x
个单位后,与双曲线y =
k
(x>0)交于点
x
B ,与x 轴交于点
C ,若
AO
= 2 ,则k= .
BC
9.如图,在平面直角坐标系中有Rt△ABC ,∠CAB=90°,
AB=AC,A(-1,0),B(1,1),将△ABC 沿x 轴的正方向平移,在第一象限内B,C 两点的对应点B1,C1 正好落在反比例函
数y =k
的图象上,则k= .x
10.如图,双曲线y =k
经过点A(2,2)与点B(4,m),则△AOB x
的面积为.
11.如图,平行四边形OABC 的顶点O 在坐标原点,顶点A,C
在反比例函数y =k
(x>0)的图象上,点 A 的横坐标为4,x
点 B 的横坐标为6,且平行四边形OABC 的面积为9,则k 的值为.
12.反比例函数y
1=
1
,y
x 2
=
3
在第一象限内的图象如图所示,过
x
y2 上的任意一点A 作x 轴的平行线,交y1 于点B,交y 轴于点C,过点A 作x 轴的垂线,交y1 于点D,交x 轴于点E,
连接BD,CE,则BD
= .CE
13.如图,一次函数y =ax +b 的图象与x 轴,y轴交于A,B 两点,
与反比例函数y =k
的图象交于C,D 两点,过C,D 两点分x
别作y 轴,x 轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:①△DEF 与△CEF 的面积相等;
②△AOB∽△FOE;③△DCE≌△CDF;
④AC=BD.其中正确的结论序号是.
6
【参考答案】 ➢ 课前预习
8:9
➢ 知识点睛
1. 函数图象;几何图形;交点;关键点坐标;
横平竖直的线段长;函数特征;几何特征 3. 函数特征;几何特征
➢ 精讲精练
1. -4
2. ( 1 ,3)
3 3. -6 4. 2
5. ( 3 + 3 5 , -3 + 3 5 )
6. ( 1+
2 2 5 , -1+ 5 )
2 2 7. 3
8. 12 9. 6 10. 3 11. -6 12.
2 3
13. ①②④。
