自动控制原理的仿真实验
《自动控制原理》控制系统的simulink仿真实验一
《自动控制原理》控制系统的simulink仿真实验一、实验目的1.初步了解Matlab中Simulink的使用方法，熟悉simulink模块的操作和信号线的连接。
2.通过观察典型环节在单位阶跃信号作用下的动态特性，熟悉各种典型环节的响应曲线。
3.定性了解各参数变化对典型环节动态特性的影响。
二、实验仪器Matlab7.0 , 计算机三、实验原理Simulink是MATLAB中的一种可视化仿真工具。
Simulink是一个模块图环境，用于多域仿真以及基于模型的设计。
它支持系统设计、仿真、自动代码生成以及嵌入式系统的连续测试和验证。
四、实验内容及步骤1、建立仿真模型系统1.1 运行Matlab，在命令窗口“Command Window”下键入“Simulink”后回车，则打开相应的系统模型库；或者点击工具栏上的“Simulink”图标，进入系统仿真模型库，然后点击左上角“新文件”图标，打开模型编辑窗口。
1.2 调出模块在系统仿真模型库中，把要求的模块都放置在模型编辑窗口里面。
从信号源模块包(Sources)中拖出1个阶跃信号(step)和1个白噪声信号发生器(band-limited white noise)；从数学运算模块包(Math Operations)中拖出1个比例环节(gain)和1个加法器(sum)；从连续系统典型环节模块包(Continuous) 中拖出1个微分环(Derivative)和3个传函环节(transfer Fcn)；从信号与系统模块包(Signals Routing) 拖出1个汇流排(mux)；从输出模块包(Sinks)中拖出1个示波器(scope)；所有模块都放置在模型编辑窗口里面。
1.3 模块参数设置（鼠标左键双击各典型环节，则可进行参数设置）双击打开白噪声信号发生器，设定功率(Noise power)为0.0001，采样时间(Sample time)为0.05。
打开比例环节，设定比例增益为2；打开3个传函环节(transfer Fcn)，通过参数设定，分别构成积分、惯性和二阶环节。
自控仿真实验报告
一、实验目的1. 熟悉MATLAB/Simulink仿真软件的基本操作。
2. 学习控制系统模型的建立与仿真方法。
3. 通过仿真分析，验证理论知识，加深对自动控制原理的理解。
4. 掌握控制系统性能指标的计算方法。
二、实验内容本次实验主要分为两个部分：线性连续控制系统仿真和非线性环节控制系统仿真。
1. 线性连续控制系统仿真（1）系统模型建立根据题目要求，我们建立了两个线性连续控制系统的模型。
第一个系统为典型的二阶系统，其开环传递函数为：\[ G(s) = \frac{1}{(s+1)(s+2)} \]第二个系统为具有迟滞环节的系统，其开环传递函数为：\[ G(s) = \frac{1}{(s+1)(s+2)(s+3)} \]（2）仿真与分析（a）阶跃响应仿真我们对两个系统分别进行了阶跃响应仿真，并记录了仿真结果。
（b）频率响应仿真我们对两个系统分别进行了频率响应仿真，并记录了仿真结果。
（3）性能指标计算根据仿真结果，我们计算了两个系统的性能指标，包括上升时间、超调量、调节时间等。
2. 非线性环节控制系统仿真（1）系统模型建立根据题目要求，我们建立了一个具有饱和死区特性的非线性环节控制系统模型。
其传递函数为：\[ W_k(s) = \begin{cases}1 & |s| < 1 \\0 & |s| \geq 1\end{cases} \]（2）仿真与分析（a）阶跃响应仿真我们对非线性环节控制系统进行了阶跃响应仿真，并记录了仿真结果。
（b）相轨迹曲线绘制根据仿真结果，我们绘制了四条相轨迹曲线，以分析非线性环节对系统性能的影响。
三、实验结果与分析1. 线性连续控制系统仿真（a）阶跃响应仿真结果表明，两个系统的性能指标均满足设计要求。
（b）频率响应仿真结果表明，两个系统的幅频特性和相频特性均符合预期。
2. 非线性环节控制系统仿真（a）阶跃响应仿真结果表明，非线性环节对系统的性能产生了一定的影响，导致系统响应时间延长。
(最新版)自动控制原理MATLAB仿真实验报告
实验一 MATLAB及仿真实验（控制系统的时域分析）一、实验目的学习利用MATLAB进行控制系统时域分析，包括典型响应、判断系统稳定性和分析系统的动态特性；二、预习要点1、系统的典型响应有哪些？2、如何判断系统稳定性？3、系统的动态性能指标有哪些？三、实验方法（一）四种典型响应1、阶跃响应：阶跃响应常用格式：1、；其中可以为连续系统，也可为离散系统。
2、；表示时间范围0---Tn。
3、；表示时间范围向量T指定。
4、；可详细了解某段时间的输入、输出情况。
2、脉冲响应：脉冲函数在数学上的精确定义：其拉氏变换为：所以脉冲响应即为传函的反拉氏变换。
脉冲响应函数常用格式：①；②③（二）分析系统稳定性有以下三种方法：1、利用pzmap绘制连续系统的零极点图；2、 利用tf2zp 求出系统零极点；3、 利用roots 求分母多项式的根来确定系统的极点 （三） 系统的动态特性分析Matlab 提供了求取连续系统的单位阶跃响应函数step 、单位脉冲响应函数impulse 、零输入响应函数initial 以及任意输入下的仿真函数lsim.四、实验内容 (一) 稳定性1． 系统传函为()27243645232345234+++++++++=s s s s s s s s s s G ，试判断其稳定性2． 用Matlab 求出的极点。
%Matlab 计算程序num=[3 2 5 4 6];den=[1 3 4 2 7 2];G=tf(num,den);pzmap(G);p=roots(den) 运行结果： p =-1.7680 + 1.2673i -1.7680 - 1.2673i 0.4176 + 1.1130i 0.4176 - 1.1130i -0.2991P ole-Zero MapReal AxisI m a g i n a r y A x i s-2-1.5-1-0.500.5-1.5-1-0.50.511.5图1-1 零极点分布图由计算结果可知，该系统的2个极点具有正实部，故系统不稳定。
自动控制原理MATLAB仿真实验报告
实验一 MATLAB 及仿真实验（控制系统的时域分析）一、实验目的学习利用MATLAB 进行控制系统时域分析，包括典型响应、判断系统稳定性和分析系统的动态特性； 二、预习要点1、 系统的典型响应有哪些2、 如何判断系统稳定性3、 系统的动态性能指标有哪些 三、实验方法（一） 四种典型响应1、 阶跃响应：阶跃响应常用格式：1、)(sys step ；其中sys 可以为连续系统，也可为离散系统。
2、),(Tn sys step ；表示时间范围0---Tn 。
3、),(T sys step ；表示时间范围向量T 指定。
4、),(T sys step Y =；可详细了解某段时间的输入、输出情况。
2、 脉冲响应：脉冲函数在数学上的精确定义：0,0)(1)(0〉==⎰∞t x f dx x f其拉氏变换为：)()()()(1)(s G s f s G s Y s f ===所以脉冲响应即为传函的反拉氏变换。
脉冲响应函数常用格式： ① )(sys impulse ； ②);,();,(T sys impulse Tn sys impulse③ ),(T sys impulse Y =（二） 分析系统稳定性 有以下三种方法：1、 利用pzmap 绘制连续系统的零极点图；2、 利用tf2zp 求出系统零极点；3、 利用roots 求分母多项式的根来确定系统的极点 （三） 系统的动态特性分析Matlab 提供了求取连续系统的单位阶跃响应函数step 、单位脉冲响应函数impulse 、零输入响应函数initial 以及任意输入下的仿真函数lsim.四、实验内容 (一) 稳定性1． 系统传函为()27243645232345234+++++++++=s s s s s s s s s s G ，试判断其稳定性2． 用Matlab 求出253722)(2342++++++=s s s s s s s G 的极点。
%Matlab 计算程序num=[3 2 5 4 6];den=[1 3 4 2 7 2];G=tf(num,den);pzmap(G);p=roots(den)运行结果： p =+ - + -P ole-Zero MapReal AxisI m a g i n a r y A x i s-2-1.5-1-0.500.5-1.5-1-0.50.511.5图1-1 零极点分布图由计算结果可知，该系统的2个极点具有正实部，故系统不稳定。
自动控制原理MATLAB仿真实验(于海春)
自动控制原理MATLAB仿真实验（于海春）实验一典型环节的MATLAB仿真一、实验目的1．熟悉MATLAB桌面和命令窗口，初步了解SIMULINK功能模块的使用方法。
2．通过观察典型环节在单位阶跃信号作用下的动态特性，加深对各典型环节响应曲线的理解。
3．定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK 的使用MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK功能模块可以快速的建立控制系统的模型，进行仿真和调试。
1．运行MATLAB软件，在命令窗口栏“>>”提示符下键入imulink命令，按Enter键或在工具栏单击按钮，即可进入如图1-1所示的SIMULINK仿真环境下。
2．选择File菜单下New下的Model命令，新建一个imulink仿真环境常规模板。
图1-1SIMULINK仿真界面图1-2系统方框图3．在imulink仿真环境下，创建所需要的系统。
以图1-2所示的系统为例，说明基本设计步骤如下：1）进入线性系统模块库，构建传递函数。
点击imulink下的“Continuou”，再将右边窗口中“TranferFen”的图标用左键拖至新建的“untitled”窗口。
2）改变模块参数。
在imulink仿真环境“untitled”窗口中双击该图标，即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数，数字之间用空格隔开；设置完成后，选择OK，即完成该模块的设置。
3）建立其它传递函数模块。
按照上述方法，在不同的imulink的模块库中，建立系统所需的传递函数模块。
例：比例环节用“Math”右边窗口“Gain”的图标。
4）选取阶跃信号输入函数。
用鼠标点击imulink下的“Source”，将右边窗口中“Step”图标用左键拖至新建的“untitled”窗口，形成一个阶跃函数输入模块。
5）选择输出方式。
自动控制原理实验报告
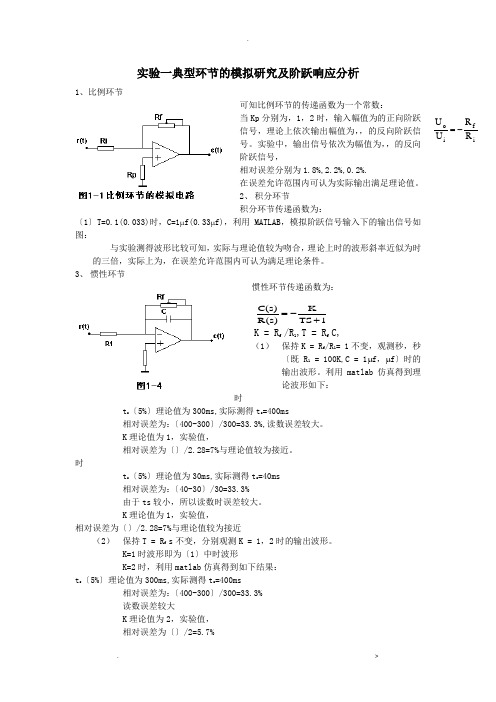
实验一典型环节的模拟研究及阶跃响应分析1、比例环节可知比例环节的传递函数为一个常数：当Kp 分别为，1，2时，输入幅值为的正向阶跃信号，理论上依次输出幅值为，，的反向阶跃信号。
实验中，输出信号依次为幅值为，，的反向阶跃信号，相对误差分别为1.8%,2.2%,0.2%.在误差允许范围内可认为实际输出满足理论值。
2、 积分环节积分环节传递函数为：〔1〕T=0.1(0.033)时，C=1μf(0.33μf)，利用MATLAB ，模拟阶跃信号输入下的输出信号如图：与实验测得波形比较可知，实际与理论值较为吻合，理论上时的波形斜率近似为时的三倍，实际上为，在误差允许范围内可认为满足理论条件。
3、 惯性环节惯性环节传递函数为：K = R f /R 1,T = R f C,（1） 保持K = R f /R 1= 1不变，观测秒，秒〔既R 1 = 100K,C = 1μf ，μf 〕时的输出波形。
利用matlab 仿真得到理论波形如下：时t s 〔5%〕理论值为300ms,实际测得t s =400ms 相对误差为：〔400-300〕/300=33.3%,读数误差较大。
K 理论值为1，实验值，相对误差为〔〕/2.28=7%与理论值较为接近。
时t s 〔5%〕理论值为30ms,实际测得t s =40ms 相对误差为：〔40-30〕/30=33.3% 由于ts 较小，所以读数时误差较大。
K 理论值为1，实验值，相对误差为〔〕/2.28=7%与理论值较为接近（2） 保持T = R f s 不变，分别观测K = 1，2时的输出波形。
K=1时波形即为〔1〕中时波形K=2时，利用matlab 仿真得到如下结果：t s 〔5%〕理论值为300ms,实际测得t s =400ms相对误差为：〔400-300〕/300=33.3% 读数误差较大K 理论值为2，实验值， 相对误差为〔〕/2=5.7%if i o R RU U -=1TS K)s (R )s (C +-=与理论值较为接近。
自动控制原理实验一 典型环节的电路模拟与软件仿真
实验一 典型环节的电路模拟与软件仿真一、实验目的1.熟悉THSSC-4型信号与系统·控制理论·计算机控制技术实验箱及上位机软件的使用；2.熟悉各典型环节的阶跃响应特性及其电路模拟；3.测量各典型环节的阶跃响应曲线，并了解参数变化对其动态特性的影响。
二、实验设备1.THSSC-4型信号与系统·控制理论·计算机控制技术实验箱；2.PC 机一台(含上位机软件)、USB 数据采集卡、37针通信线1根、16芯数据排线、USB 接口线；3.双踪慢扫描示波器一台(可选)； 三、实验内容1.设计并组建各典型环节的模拟电路；2.测量各典型环节的阶跃响应，并研究参数变化对其输出响应的影响；3.在上位机仿真界面上，填入各典型环节数学模型的实际参数，据此完成它们对阶跃响应的软件仿真，并与模拟电路测试的结果相比较。
四、实验原理自控系统是由比例、积分、微分、惯性等环节按一定的关系组建而成。
熟悉这些典型环节的结构及其对阶跃输入的响应，将对系统的设计和分析是十分有益的。
本实验中的典型环节都是以运放为核心元件构成，其原理框图 如图1-1所示。
图中Z 1和Z 2表示由R 、C 构成的复数阻抗。
1.比例（P ）环节 图1-1比例环节的特点是输出不失真、不延迟、成比例地复现输出信号的变化。
它的传递函数与方框图分别为：K S U S U S G i O ==)()()(当U i (S)输入端输入一个单位阶跃信号，且比例系数为K 时的响应曲线如图1-2所示。
图1-22.积分（I ）环节积分环节的输出量与其输入量对时间的积分成正比。
它的传递函数与方框图分别为：TsS U S U s G i O 1)()()(==设U i (S)为一单位阶跃信号，当积分系数为T 时的响应曲线如图1-3所示。
图1-33.比例积分(PI)环节比例积分环节的传递函数与方框图分别为：)11(11)()()(21211212CSR R R CS R R R CS R CS R S U S U s G i O +=+=+==其中T=R 2C ，K=R 2/R 1设U i (S)为一单位阶跃信号，图1-4示出了比例系数(K)为1、积分系数为T 时的PI 输出响应曲线。
自动控制原理实验
自动控制原理实验实验一 控制系统的数学模型一、 实验目的1. 熟悉Matlab 的实验环境，掌握Matlab 建立系统数学模型的方法。
2. 学习构成典型环节的模拟电路并掌握典型环节的软件仿真方法。
3. 学习由阶跃响应计算典型环节的传递函数。
二、 实验内容1. 已知图1.1中()G s 和()H s 两方框相对应的微分方程分别是：()610()20()()205()10()dc t c t e t dtdb t b t c t dt+=+=且满足零初始条件，用Matlab 求传递函数()()C s R s 和()()E s R s 。
图1.1 系统结构图2. 构成比例环节、惯性环节、积分环节、比例-积分环节、比例-微分环节和比例-积分-微分环节的模拟电路并用Matlab 仿真；3. 求以上各个环节的单位阶跃响应。
三、 实验原理1. 构成比例环节的模拟电路如图1.2所示，该电路的传递函数为：21().R G s R =-图1.2 比例环节的模拟电路原理图2. 构成惯性环节的模拟电路如图1.3所示，该电路的传递函数为：221(),,.1R KG s K T R C Ts R =-==+图1.2 惯性环节的模拟电路原理图3. 构成积分环节的模拟电路如图1.3所示，该电路的传递函数为：1(),.G s T RC Ts==图1.3 积分环节的模拟电路原理图4. 构成比例-积分环节的模拟电路如图1.4所示，该电路的传递函数为：2211()1,,.R G s K K T R C Ts R ⎛⎫=-+== ⎪⎝⎭图1.4 比例-积分环节的模拟电路原理图5. 构成比例-微分环节的模拟电路如图1.5所示，该电路的传递函数为：221()(1),,.R G s K Ts K T R C R =-+==图1.5 比例-微分环节的模拟电路原理图6. 构成比例-积分-微分环节的模拟电路如图1.6所示，该电路的传递函数为：121211212121121()1(1)()()()()()p d i f p i i ff i f f f f f d f f G s K T s T s R R R R C K R R C T R CT R R C R R C R R R R R R CC T R R C R R C⎛⎫=++ ⎪⎝⎭++=+==+++++=+++图1.6 比例-积分-微分环节的模拟电路原理图四、实验要求1.画出各环节的模拟电路图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
hold
当前图形是否具备被刷新功能的双向切换开关。
2. 使用多窗口绘制图形
figure ( N ) 命令功能是创建编号为N的新窗口，等待绘制图形。
3. 图形窗口的分割
subplot ( )，在一个图形窗口显示多幅图形，把图形窗口分割成m行与
n列的子窗口，并选定第i个窗口为当前窗口。
命令调用格式 subplot（m，n，i）
黄
.
小黑点（标数据用）
洋红
。
小圈号（标数据用）
青
×
叉号（标数据用）
红
+
十字号（标数据用）
绿
*
星号（标数据用）
蓝
—
实连线
白
：
虚点连线
黑
--
双划连线
2020/8/15
自动控制原理实验教程
1. 多次重叠绘制图形
hold on 使当前轴与图形保持不变，再重叠绘制一条或多条新的曲
线。
hold off 使当前轴与图形不再具备被刷新功能。
普通高等教育“十一五”国家级规划教材配套教材
自动控制原理实验教程 (硬件模拟与MATLAB仿真)
熊晓君主编 机械工业出版社
2020/8/15
自动控制原理实验教程
第1章 MATLAB7.1与Simulink6.1入门基础
1.1 自动控制系统仿真介绍
一、优点
（1）仿真对象是物理系统的数学模型，而不是实物系统 本身，因此研究成本低。 （2）仿真方法灵活多样，易于实现。 （3）通过仿真研究可以得到大量的、充分的数据和曲线， 便于分析。 （4）虚拟现实技术可以缩短开发周期。
2020/8/15
自动控制原理实验教程
1.2.4 MATLAB常用图形编辑
基本二维曲线绘图命令是plot ( )。 调用格式：plot (x1, y1, ’option1’, x2, y2, ’option
常用选项控制字符option说明
指定色彩 绘图字符 指定绘图形式
光标移到行尾
Ctrl＋F →
光标右移一个字符
Ctrl＋U Esc
删除一行
Ctrl＋R Ctrl＋→
光标右移一个单词
Ctrl＋A Home
光标移到行首
Ctrl＋L Ctrl＋←
光标左移一个单词
Ctrl＋K
从光标处删除到行尾
2020/8/15
自动控制原理实验教程
MATLAB的帮助系统 （1）使用联机帮助窗口 （2）使用帮助命令help，查找已知命令的使用方法 。 （3）使用lookfor命令，通过一般关键词找到命令和帮助标 题。
1
a ln(1 x a) 2a
【范例1-2】（1）建立矩阵
A 7 8 9
逗号或空格：分隔列
7 B 8
9
分号：分隔行
1 1 2
C
3
5
8
10 12 15
2020/8/15
自动控制原理实验教程
常用的多项式运算函数及功能说明
函数
功能
Conv
多项式乘法（卷积）
Poly
由根求多项式
Deconv 多项式除法（解卷）
自动控制原理实验教程
1.2 控制系统MATLAB7.1环境简述
MATLAB命令窗口的快捷键及其功能
快捷键 对应按键
功能
Ctrl＋P ↑
光标上移一行
Ctrl＋H Backspace 删除光标前一个字符
Ctrl＋N ↓
光标下移一行
Ctrl＋D Del
删除光标后一个字符
Ctrl＋B ←
光标左移一个字符
Ctrl＋E End
【范例1-8】绘制红色的正弦曲线（实线）和蓝色的余弦 曲线（虚线），X轴是时间轴，用“time”标注，范围是 （0，2）；Y轴是幅值轴，用“amp”标注，范围是（-1， 1）；图形标题用“正弦和余弦曲线”说明，并显示网格。
%This is a graph program. graph1.m t = 0 : pi /12 : 2*pi ; y1 = sin (t) ; y2 = cos(t) ; plot ( t , y1 , 'r-', t , y2 , 'b--' ) ; axis ([0 , 2*pi , -1 ,+1]) ; xlabel ('time') ; ylabel ('amp') ; title (‘正弦和余弦曲线') grid %This is the end.
4. 图形控制函数
axis ( [xmin, xmax, ymin, ymax] )
设定坐标轴的范围。
title (‘字符串’)
在所画图形的最上端标注图形标题。
xlabel (‘字符串’)、ylabel (‘字符串’) 设置x，y 坐标轴的名称。
grid 增加网格。
2020/8/15
自动控制原理实验教程
（4）演示帮助 在命令窗口执行demos命令
2020/8/15
自动控制原理实验教程
1.2.3 MATLAB基本运算 MATLAB基本运算中符号特殊含义说明
符号 名称
含义
： 冒号
表示间隔
( ) 圆括号 在算术表达式中先后次序
； 分号
用于分隔行
[ ] 方括号 用于构成向量和矩阵
， 逗号
用于分隔列
{ } 大括号 用于构成单元数组
高校的关于MATLAB方面的BBS网站。http://
，http:// ，http://
，http:// 。
2020/8/15
自动控制原理实验教程
2020/8/15
数运算书写为exp( )。
（6）MATLAB的符号运算中，求e为底的自然对数，其函数书
写形式为log（）。
（7）MATLAB中特殊变量的含义：“pi”表示圆周率π；“i”或
“j”表示虚数单位；“inf”或“INF”表示无穷大；NaN表示0/0
不定式。 2020/8/15
自动控制原理实验教程
【范例1-1】 y
Roots
多项式求根
Polyval 多项式求值
Polyfit 多项式曲线拟合
【范例1-3】求多项式的展开式。
D(s) (5s 2 3)(s 1)(s 2)
【范例1-4】（1）求多项式的根。
P(x) 2x4 5x3 6x2 x 9
Conv()函数只能用于 两个多项式相乘；多 于两个必须嵌套使用
2020/8/15
自动控制原理实验教程
MATLAB的数学表达式输入格式注意以下几方面：
（1）表达式必须在同一行内书写。
（2）数值与变量或变量与变量相乘都不能连写，中间必须用
乘号“*”。
（3）分式的书写要求分子、分母最好分别用小括号限定。
（4）当MATLAB函数嵌套调用时，使用多重小括号限定。
（5）求幂运算的指数两侧最好用小括号限定，自然常数e的指
2020/8/15
自动控制原理实验教程
二、内容
控制系统仿真实验主要从各个角度对控制系统进行全面分析， 并对系统进行校正及设计控制器，改善闭环系统的性能。内 容包括：
控制系统的建模与模型间的相互转换 控制系统稳定性分析 线性系统时域分析 根轨迹分析 频域分析及非线性系统分析等
三、工具
研究MATLAB语言，请参考其他相关的书籍或浏览国内各大