2019届高三文科数学测试题(三)附答案
2019年高考文科数学全国Ⅲ卷试题及详细解析(Word版,精校版)

2019年普通高等学校招生全国统一考试文科数学一、选择题:本题共12小题,每小题5分,共60分。
在每小题给的四个选项中,只有一项是符合题目要求的。
1.已知集合2{1,0,1,2}{1}A B x x =-=≤,,则A B =A .{}1,0,1-B .{}0,1C .{}1,1-D .{}0,1,22.若(1i)2i z +=,则z = A .1i --B .1+i -C .1i -D .1+i3.两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是 A .16B .14C .13D .124.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为 A .0.5B .0.6C .0.7D .0.85.函数()2sin sin2f x x x =-在0,2π]的零点个数为 A .2B .3C .4D .56.已知各项均为正数的等比数列{a n }的前4项和为15,且a 5=3a 3+4a 1,则a 3= A . 16B . 8C .4D . 27.已知曲线e ln xy a x x =+在点(1,a e )处的切线方程为y =2x +b ,则 A .a=e ,b =-1B .a=e ,b =1C .a=e -1,b =1D .a=e -1,1b =-8.如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则A .BM =EN ,且直线BM 、EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM 、EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线9.执行下边的程序框图,如果输入的为0.01,则输出的值等于A.4122-B. 5122-C. 6122-D. 7122-10.已知F 是双曲线C :22145x y -=的一个焦点,点P 在C 上,O 为坐标原点,若=OP OF ,则OPF △的面积为A .32B .52 C .72 D .9211.记不等式组6,20x y x y +⎧⎨-≥⎩…表示的平面区域为D .命题:(,),2p x y D x y ∃∈+…;命题:(,),212q x y D x y ∀∈+….下面给出了四个命题①p q ∨②p q ⌝∨③p q ∧⌝④p q ⌝∧⌝这四个命题中,所有真命题的编号是 A .①③B .①②C .②③D .③④12.设()f x 是定义域为R 的偶函数,且在()0,+∞单调递减,则A .f (log 314)>f (322-)>f (232-) B .f (log 314)>f (232-)>f (322-)C .f (322-)>f (232-)>f (log 314) D .f (232-)>f (322-)>f (log 314)二、填空题:本题共4小题,每小题5分,共20分。
2019年高考全国卷3文科数学及答案

11.记不等式组表示的平面区域为D.命题p: (x, y) D,2x
2x y 0
q
①
这四个命题中,所有真命题的编号是()
A.
①③
B.①②
C.②③
D.③④
12.设
f x是定义域为
R的偶函数,且在°
单调递减,则(
)
A.
B.
C.
D.
1
(log3丄)
>
f
(
3
22
)
>
4
2
(log31)
>
f
(
23
)
>
4
3
2
(22
擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3•考试结束后,将本试卷和答题卡一并交回。
(选择题,共
、选择题:本题共12小题,每小题5分,共60分。在每小题给的四个选项中,只有一项是符合题目要 求的。
1.已知集合A {
A.1,0,1
1,0,1,2},B {x
2
x 1},则AI B()
36 20
贝U M的坐标为.
16•学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCDABQjD挖去四棱
锥OEFGH后所得的几何体,其
AB
原料的质量为g.Leabharlann )>f(
2
3)
>
f
2
3
(23
)>
f
(
2
2)
>
f
2
f
3
f
(log3-)
4
1
【解析版】2019年高考全国Ⅲ卷文数试题

2019年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、选择题:本题共12小题,每小题5分,共60分,在每小题给的四个选项中,只有一项是符合题目要求的.1.已知集合,则( ){}{}21,0,1,21A B x x ,=-=≤A B ⋂=A.B.C. D.{}1,0,1-{}0,1{}1,1-{}0,1,2【答案】A 【解析】【分析】先求出集合B 再求出交集.【详解】由题意得,,则.故选A .{}11B x x =-≤≤{}1,0,1A B ⋂=-【点睛】本题考查了集合交集的求法,是基础题.2.若,则( )(1i)2i z +=z =A. B. C. D. 1i --1+i-1i-1+i【答案】D 【解析】【分析】根据复数运算法则求解即可.【详解】.故选D .()(2i 2i 1i 1i 1i 1i 1i )()z -===+++-【点睛】本题考查复数的商的运算,渗透了数学运算素养.采取运算法则法,利用方程思想解题.3.两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是( )A. B. C. D. 16141312【答案】D 【解析】【分析】男女生人数相同可利用整体发分析出两位女生相邻的概率,进而得解.【详解】两位男同学和两位女同学排成一列,因为男生和女生人数相等,两位女生相邻与不相邻的排法种数相同,所以两位女生相邻与不相邻的概率均是.故选D .12【点睛】本题考查常见背景中的古典概型,渗透了数学建模和数学运算素养.采取等同法,利用等价转化的思想解题.4.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为( )A. B. C. D. 0.50.60.70.8【答案】C 【解析】【分析】根据题先求出阅读过西游记的人数,进而得解.【详解】由题意得,阅读过《西游记》的学生人数为90-80+60=70,则其与该校学生人数之比为70÷100=0.7.故选C .【点睛】本题考查抽样数据的统计,渗透了数据处理和数学运算素养.采取去重法,利用转化与化归思想解题.5.函数在的零点个数为( )()2sin sin2f x x x =-[]0,2πA. 2B. 3C. 4D. 5【答案】B 【解析】【分析】令,得或,再根据x 的取值范围可求得零点.()0f x =sin 0x =cos 1x =【详解】由,得()2sin sin 22sin 2sin cos 2sin (1cos )0f x x x x x x x x =-=-=-=或,,.在的零点个数sin 0x =cos 1x =[]0,2x π∈ 02x ππ∴=、或()f x ∴[]0,2π是3..故选B .【点睛】本题考查在一定范围内的函数的零点个数,渗透了直观想象和数学运算素养.采取特殊值法,利用数形结合和方程思想解题.6.已知各项均为正数的等比数列的前4项和为15,且,则( ){}n a 53134a a a =+3a =A. 16 B. 8C. 4D. 2【答案】C 【解析】【分析】利用方程思想列出关于的方程组,求出,再利用通项公式即可求得的值.1,a q1,a q3a 【详解】设正数的等比数列{a n }的公比为,则,q 2311114211115,34a a q a q a q a q a q a ⎧+++=⎨=+⎩解得,,故选C .11,2a q =⎧⎨=⎩2314a a q ∴==【点睛】应用等比数列前项和公式解题时,要注意公比是否等于1,防止出错.n 7.已知曲线在点处的切线方程为,则( )e ln x y a x x =+()1,ae 2y x b =+A. B. C.D.,1a e b ==-,1a eb ==1,1a e b -==1,1a eb -==-【答案】D【解析】【分析】通过求导数,确定得到切线斜率的表达式,求得,将点的坐标代入直线方程,求得.b 【详解】详解:/ln 1,x y ae x =++/11|12x k y ae a e =-==+=∴=将代入得,故选D .(1,1)2y x b =+21,1b b +==-【点睛】准确求导数是进一步计算的基础,本题易因为导数的运算法则掌握不熟,二导致计算错误.求导要“慢”,计算要准,是解答此类问题的基本要求.8.如图,点为正方形的中心,为正三角形,平面平面N ABCD ECD ∆ECD ⊥是线段的中点,则( ),ABCD M EDA. ,且直线是相交直线BM EN =,BM ENB. ,且直线是相交直线BM EN ≠,BM ENC. ,且直线是异面直线BM EN =,BM END. ,且直线是异面直线BM EN ≠,BM EN 【答案】B 【解析】【分析】利用垂直关系,再结合勾股定理进而解决问题.【详解】,为中点为中点,,共面相交,选项C ,DBDE ∆∵N BD M DE ∴BM EN为错.作于,连接,过作于.EO CD ⊥O ON M MF OD ⊥F 连,平面平面.BF CDE ⊥ABCD 平面,平面,平面,,EO CD EO ⊥⊂CDE EO ∴⊥ABCD MF ⊥ABCE 与均为直角三角形.MFB ∴∆EON ∆设正方形边长为2,易知,012EO N EN ===.52MF BF BM ===∴==,故选B .BM EN ∴≠【点睛】本题为立体几何中等问题,考查垂直关系,线面、线线位置关系.9.执行如图所示的程序框图,如果输入的为,则输出的值等于( )ε0.01sA.B.C.D.4122-5122-6122-7122-【答案】D 【解析】【分析】根据程序框图,结合循环关系进行运算,可得结果.【详解】不成立11.0,01,0.01?2x S S x ===+=<不成立1101,0.01?24S x =++=<成立611101,0.00781250.01?22128S x =++++==< 输出,故选D .767111112121122212S -⎛⎫=++⋯+==- ⎪⎝⎭-【点睛】循环运算,何时满足精确度成为关键,加大了运算量,输出前项数需准确,此为易错点.10.已知是双曲线的一个焦点,点在上,为坐标原点,若F 22:145x y C -=P C O ,则的面积为( )=OP OFOPF A. B. C. D. 32527292【答案】B 【解析】【分析】设,因为再结合双曲线方程可解出,再利用三角形面积公式可()00,P x y =OP OFy 求出结果.【详解】设点,则①.又,()00,P x y 2200145x y -=3OP OF ===②.由①②得,即,22009x y ∴+=20259y =053y =.故选B .0115532232OPF S OF y ∆∴==⨯⨯= 【点睛】本题考查以双曲线为载体的三角形面积的求法,渗透了直观想象、逻辑推理和数学运算素养.采取公式法,利用数形结合、转化与化归和方程思想解题.11.记不等式组表示的平面区域为,命题;命题620x y x y +⎧⎨-≥⎩…D :(,),29p x y D x y ∃∈+….给出了四个命题:①;②;③;④:(,),212q x y D x y ∀∈+…p q ∨p q ⌝∨p q ∧⌝,这四个命题中,所有真命题的编号是( )p q ⌝∧⌝A. ①③ B. ①②C. ②③D. ③④【答案】A 【解析】【分析】根据题意可画出平面区域再结合命题可判断出真命题.【详解】如图,平面区域D 为阴影部分,由得即A (2,4),直线2,6y x x y =⎧⎨+=⎩2,4x y =⎧⎨=⎩与直线均过区域D ,则p 真q 假,有假真,所以①③真②④29x y +=212x y +=p ⌝q ⌝假.故选A.【点睛】本题考点为线性规划和命题的真假,侧重不等式的判断,有一定难度.不能准确画出平面区域导致不等式误判,根据直线的斜率和截距判断直线的位置,通过直线方程的联立求出它们的交点,可采用特殊值判断命题的真假.12.设是定义域为的偶函数,且在单调递减,则( )()f x R ()0,∞+A. 233251log 224f f f --⎛⎫⎛⎫⎛⎫>> ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭B. 233281log 224f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭C. 23325122log 4f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭D. 23325122log 4f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭【答案】C 【解析】【分析】由已知函数为偶函数,把,转化为同一个单调区间上,再233231log ,2,24f f f --⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭比较大小.【详解】是R 的偶函数,.()f x ()331log log 44f f ⎛⎫∴= ⎪⎝⎭,又在(0,+∞)单调递减,323log 4122-∴>=>()f x ,()23323log 422f f f --⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭,故选C .23323122log 4f f f --⎛⎫⎛⎫⎛⎫∴>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭【点睛】本题主要考查函数的奇偶性、单调性,考查学生转化与化归及分析问题解决问题的能力.二、填空题:本题共4小题,每小题5分,共20分.13.已知向量,则___________.(2,2),(8,6)a b ==- cos ,a b <>=【答案】【解析】【分析】根据向量夹角公式可求出结果.【详解】详解:.cos ,a b a b a b <>===【点睛】本题考点为平面向量的夹角,为基础题目,难度偏易.不能正确使用平面向量坐标的运算致误,平面向量的夹角公式是破解问题的关键.14.记为等差数列的前项和,若,则___________.nS {}n a n 375,13a a ==10S =【答案】100【解析】【分析】根据题意可求出首项和公差,进而求得结果.【详解】详解: 得317125,613a a d a a d =+=⎧⎨=+=⎩11,2a d =⎧⎨=⎩101109109101012100.22S a d ⨯⨯∴=+=⨯+⨯=【点睛】本题考点为等差数列的求和,为基础题目,难度不大.不能构造等数列首项和公差的方程组致使求解不通,应设出等差数列的公差,为列方程组创造条件,从而求解数列的和.15.设为椭圆的两个焦点,为上一点且在第一象限.若12F F ,22:+13620x y C =M C 为等腰三角形,则的坐标为___________.12MF F △M 【答案】(【解析】【分析】根据椭圆的定义分别求出,设出的坐标,结合三角形面积可求出的坐标.12MF MF 、M M 【详解】由已知可得,2222236,36,16,4a b c a b c ==∴=-=∴=.11228MF F F c ∴===.122212,4MF MF a MF +=== 设点的坐标为,则,M ()()0000,0,0x y x y >>121200142MF F S F F y y =⋅⋅=△又,解得,12014,42MF F S y =⨯=∴=△0y =,解得(舍去),2136x∴=03x =03x =-的坐标为.M \(【点睛】本题考查椭圆标准方程及其简单性质,考查数形结合思想、转化与化归的能力,很好的落实了直观想象、逻辑推理等数学素养.16.学生到工厂劳动实践,利用打印技术制作模型.如图,该模型为长方体3D 挖去四棱锥后所得的几何体,其中为长方体的中心,1111ABCD A B C D -O EFGH -O 分别为所在棱的中点,,打印所用原料密,,,E F G H 16cm 4cm AB =BC =, AA =3D 度为,不考虑打印损耗,制作该模型所需原料的质量为___________.30.9/g cm g 【答案】118.8【解析】【分析】根据题意可知模型的体积为四棱锥体积与四棱锥体积之差进而求得模型的体积,再求出模型的质量.【详解】由题意得,四棱锥O-EFGH 的底面积为,其高为点2146423122cm ⨯-⨯⨯⨯=O 到底面的距离为3cm ,则此四棱锥的体积为.又长方体11BB C C 211123123V cm =⨯⨯=的体积为,所以该模型体积为1111ABCD A B C D -22466144V cm =⨯⨯=,其质量为.22114412132V V V cm =-=-=0.9132118.8g ⨯=【点睛】此题牵涉到的是3D 打印新时代背景下的几何体质量,忽略问题易致误,理解题中信息联系几何体的体积和质量关系,从而利用公式求解.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:17.为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成两组,每组100只,其中组小鼠给服甲离子溶液,组小鼠给服乙离子溶液.每只,A B A B 小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:记为事件:“乙离子残留在体内的百分比不低于”,根据直方图得到的估计C 5.5()P C 值为.0.70(1)求乙离子残留百分比直方图中的值;,a b (2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).【答案】(1) ,;(2) ,.0.35a =0.10b = 4.056【解析】【分析】(1)由可解得和的值;(2)根据公式求平均数.()0.70P C =b 【详解】(1)由题得,解得,由0.200.150.70a ++=0.35a =,解得.0.050.151()10.70b P C ++=-=-0.10b =(2)由甲离子的直方图可得,甲离子残留百分比的平均值为,0.1520.2030.3040.2050.1060.057 4.05⨯+⨯+⨯+⨯+⨯+⨯=乙离子残留百分比的平均值为0.0530.1040.1550.3560.2070.1586⨯+⨯+⨯+⨯+⨯+⨯=【点睛】本题考查频率分布直方图和平均数,属于基础题.18.的内角的对边分别为,已知.ABC ∆,,A B C ,,a b c sinsin 2A Ca b A +=(1)求;B (2)若为锐角三角形,且,求面积的取值范围.ABC ∆1c =ABC ∆【答案】(1);(2).3B π=【解析】【分析】(1)利用正弦定理化简题中等式,得到关于B 的三角方程,最后根据A,B,C 均为三角形内角解得.(2)根据三角形面积公式,又根据正弦定理和得到3B π=1sin 2ABC S ac B =⋅ 1225关于的函数,由于是锐角三角形,所以利用三个内角都小于来计算ABCS C V ABC 2π的定义域,最后求解的值域.C ()ABC S C 【详解】(1)根据题意由正弦定理得,sinsin 2A C a b A +=sin sin sin sin 2A CA B A +=因为,故,消去得。
2019年6月高考全国3卷文科数学及答案

绝密★启用前2019年普通高等学校招生全国统一考试文科数学本试卷共23题,共150分,共4页。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合2{1,0,1,2}{1}A B x x =-=≤,,则A B = A .{}1,0,1-B .{}0,1C .{}1,1-D .{}0,1,22.若(1i)2i z +=,则z =A .1i --B .1+i -C .1i -D .1+i 3.两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是A .16B .14C .13D .124.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为A .0.5B .0.6C .0.7D .0.85.函数()2sin sin2f x x x =-在[0,2π]的零点个数为A .2B .3C .4D .56.已知各项均为正数的等比数列{a n }的前4项和为15,且a 5=3a 3+4a 1,则a 3=A .16B .8C .4D .27.已知曲线e ln x y a x x =+在点(1,a e )处的切线方程为y =2x +b ,则A .a=e ,b =-1B .a=e ,b =1C .a=e -1,b =1D .a=e -1,1b =-8.如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M是线段ED 的中点,则A .BM =EN ,且直线BM 、EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM 、EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线9.执行下边的程序框图,如果输入的ε为0.01,则输出s 的值等于A .4122-B .5122-C .6122-D .7122-10.已知F 是双曲线C :22145x y -=的一个焦点,点P 在C 上,O 为坐标原点,若=OP OF ,则OPF △的面积为A .32B .52C .72D .9211.记不等式组6,20x y x y +⎧⎨-≥⎩表示的平面区域为D .命题:(,),29p x y D x y ∃∈+;命题:(,),212q x y D x y ∀∈+.下面给出了四个命题①p q∨②p q⌝∨③p q ∧⌝④p q ⌝∧⌝这四个命题中,所有真命题的编号是A .①③B .①②C .②③D .③④12.设()f x 是定义域为R 的偶函数,且在()0,+∞单调递减,则A .f (log 314)>f (322-)>f (232-)B .f (log 314)>f (232-)>f (322-)C .f (322-)>f (232-)>f (log 314)D .f (232-)>f (322-)>f (log 314)二、填空题:本题共4小题,每小题5分,共20分。
2019年全国III卷文科数学高考试卷(原卷 答案)

绝密★启用前2019年普通高等学校招生全国统一考试(全国III 卷)(适用地区:云南、广西、贵州、四川、西藏)文科数学本试卷共23题,共150分。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给的四个选项中,只有一项是符合题目要求的。
1.已知集合2{1,0,1,2}{1}A B x x =−=≤,,则A B =A .{}1,0,1−B .{}0,1C .{}1,1−D .{}0,1,22.若(1i)2i z +=,则z = A .1i −− B .1+i − C .1i − D .1+i 3.两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是A .16 B .14 C .13 D .124.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为 A .0.5 B .0.6 C .0.7 D .0.8 5.函数()2sin sin2f x x x =−在[0,2π]的零点个数为A .2B .3C .4D .5 6.已知各项均为正数的等比数列{a n }的前4项和为15,且a 5=3a 3+4a 1,则a 3= A .16 B .8 C .4 D .2 7.已知曲线e ln x y a x x =+在点(1,ae )处的切线方程为y =2x +b ,则A .a =e ,b =–1B .a =e ,b =1C .a =e –1,b =1D .a =e –1,1b =−8.如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则A .BM =EN ,且直线BM ,EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM ,EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线9.执行下边的程序框图,如果输入的ε为0.01,则输出s 的值等于A.4122−B. 5122−C. 6122−D. 7122−10.已知F 是双曲线C :22145x y −=的一个焦点,点P 在C 上,O 为坐标原点,若=OP OF ,则OPF △的面积为 A .32B .52C .72D .9211.记不等式组6,20x y x y +≥⎧⎨−≥⎩表示的平面区域为D .命题:(,),29p x y D x y ∃∈+≥;命题:(,),212q x y D x y ∀∈+≤.下面给出了四个命题①p q ∨②p q ⌝∨③p q ∧⌝ ④p q ⌝∧⌝ 这四个命题中,所有真命题的编号是A .①③B .①②C .②③D .③④12.设()f x 是定义域为R 的偶函数,且在()0,+∞单调递减,则A .f (log 314)>f (322−)>f (232−)B .f (log 314)>f (232−)>f (322−)C .f (322−)>f (232−)>f (log 314) D .f (232−)>f (322−)>f (log 314)二、填空题:本题共4小题,每小题5分,共20分。
2019年山西省高考数学三模试卷(文科)(解析版)
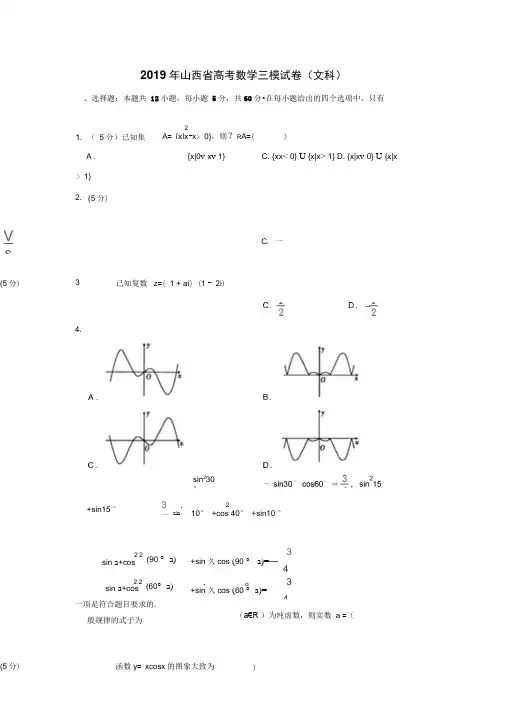
2019年山西省高考数学三模试卷(文科)、选择题:本题共 12小题,每小题 5分,共60分•在每小题给出的四个选项中,只有一项是符合题目要求的.般规律的式子为1. ( 5分)已知集合 2A = {x|x -x > 0},则?R A =()A . {x|0W {x|0v x v 1}C . {xx < 0} U {x|x > 1}D . {x|x v 0} U {x|x> 1} 2. (5分)C . 一Vs3.(5分)已知复数 z =( 1 + ai ) (1 - 2i )4.sin 230 °+sin15 ° cos453 .一 sin210° +cos 40° +sin10 °2 2sin a +cos(90 °- a)2 2sin a +cos (60°- a) 3 +sin 久cos (90 ° - a)=—4. o3 +sin 久cos (60 °- a)=4函数y = xcosx 的图象大致为(5分) )(a€R )为纯虚数,则实数 a =()+cos2( a- 15°) +sin ( a+15°) cos ( a- 15°) sin2( a+152 2sin ( a- 15 ° ) +cos ( a+15 ° ) +sin ( a- 15 ° ) cos ( a+15 ° )6. (5分)已知一个几何体的三视图如图所示,则其体积为((1 , 3),其两条渐近线方程为 y =± 2x ,则C 的离心率为()T(5 分)设 m = log o.30.6, n =丄log 20.6,则(10. (5 分)在厶 ABC 中,|BC|cosA = |AC|cosB ,则△ ABC 是(7.B . 16nC .(5分)中国是发现和研究勾股定理最古老的国家之一,古代数学家称直角三角形较短的 直角边3股4弦5的三角形放入 平面直角坐标系xOy 中,在坐标平面中任取一点M (x , y ),其中x€{0, 1 , 2, 3, 4},y€{0, 1,2,3},则点M 落在该三角形内(含边界)的概率为(C. 1(5分)已知双9.A . m+n > mnB . m+n v mnC . n — m >mnm — n v mnC .等腰直角三角形D .等腰或直角三角形A .等腰三角形AB - ::' ■-IC -D .11.17]二、 填空题:本题共 4小题,每小题5分,共20分.13. ___________________________________________________________________ ( 5分)已知向量 吕,b 满足|b |= 2|引=1,也丄(目—b ),则|2扫+b |= ______________________ •r2i-3j^2<014. ___________________________________________________________________ (5分)若x , y 满足约束条件-3x-2y+3>0,则z = 2x+y 的最小值为 _____________________________ .L K +J TAO2 2 2 、15. (5 分)已知直线 I : xcos a +ysin a= 1 ( a^R )与圆 C : x +y = r (r >0)相交,则 r 的取 值范围是 ________ .16. (5分)函数f (x )为偶函数,当x > 0时,f (x )= e x ,则线y = f (x )在x =— 1处的切 线方程为 ________ .三、 解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第 17-21题为必考题, 每个试题考生都必须作答.第 22、23题为选考题,考生根据要求作答. (一)必考题:共60分.17. (12分)已知数列{a n }的前n 项和S n = n ,数列{b n }为等比数列,且 b 1 = a 1, b 2= a 2.(1) 求数列{a n } , { b n }的通项公式;(2) 数列{C n }满足c n = —,求{C n }的前项和T n .b n18. (12 分)在三棱柱 ABC — ABC'中,AB = BC = CA = AA' = 2,侧面 AA'C'C 丄底面 ABC , D 是棱BB'的中点.B .直角三角形 11. ( 5分)已知正方形ABCD 的边长为2, CD 边的中点为E ,现将△ADE , △ BCE 分另U 沿 AE , BE 折起,使得 C , D 两点重合为一点记为 P ,则四面体P — ABE 外接球的表面积是厂19兀 C .IE .312. (5 分)已知函数.:I. I , i 1 ■■ ¥ :■■- i :的一个零点是.,且在,.内flA. I有且只有两个极值点,则()(1)求证:平面DA'C丄平面ACC'A';(2)若/ A'AC = 60。
2019届高三第三次阶段考试题(文科数学)参考答案
2019届高三第三次阶段考试题(文科数学) 参考答案1-12 CACBD BDDBC DB13. 25− 14. 15. 310 16.3π17.解:(1)由正弦定理及2sin cos b B b A =+可得2cos A A =+,............2分 即有sin 16A π⎛⎫+= ⎪⎝⎭,.....4分 因0A π<<,∴7666A πππ<+<,∴62A ππ+=,∴3A π=....6分 (2)设BD CD x ==,则2BC x =,由()221621cos 82b x A b +−==,可得224416x b b =−+ ①,...8分因为0180ADB ADC ∠=−∠,所以cos cos 0ADB ADC ∠+∠=, 222=可推出2222x b =+ ②,............10分 联立①②得24120b b +−=,故2b =,............11分因此11sin 2422ABC S bc A ∆==⨯⨯=............12分 18. 【解析】(1)取BC 中点为N ,连结1,MN C N ,………1分∵,M N 分别为,AB CB 中点, ∴MN ∥AC ∥11AC ,∴11,,,A M N C 四点共面, ………3分 且平面11BCC B 平面11A MNC 1C N ,又DE 平面11BCC B ,且DE ∥平面11A MC∴DE ∥1C N ∵D 为1CC 的中点,∴E 是CN 的中点, ………5分 ∴13CE EB =. ………6分(2)因为三棱柱111ABC A B C −为直三棱柱,∴1AA 平面ABC , 又AC AB ⊥,则AC ⊥平面11ABB A设122AB AA ==,又三角形11A MC 是等腰三角形,所以1112A M AC .如图,将几何体11AA M CC N −补成三棱柱11AA M CC F −∴几何体11AA M CC N −的体积为:1111111111111232232V AM AA AC CF CC NF =⋅⋅⋅−⋅⋅⋅⋅=⨯⨯⨯⨯⨯= ……9分 又直三棱柱111ABC A B C −体积为:1212V =⨯= ………11分 故剩余的几何体棱台111BMN B AC −的体积为:21V V V =−=∴较小部分的体积与较大部分体积之比为:1257V V =. ………12分 19解:(Ⅰ)在区间[30,60)的频率为73364156=--------1分[来源:学|科|网Z|X|X|K]31==73070⨯频率组距,--------2分 设在区间[0,30)上,a =频率组距,则130)21011051701(=⨯+++a , 解得2101=a , -----------3分补充频率分布直方图如右;----5分(Ⅱ)当日泄流量X≥30(万立方米)时,小型发电机可以运行,则一年中一台小型发电机可运 行的天数为:136430364312210−⨯⨯=(天);-----------------------------------------------------7分 当日泄流量X≥60(万立方米)时,中型发电机可以运行,则一年中一台中型发电机可运行 的天数为:11()30364156105210+⨯⨯=(天);---------------------------9分 ①若运行一台小型发电机,则一年的日均利润值为:11(312400052500)33573647⨯⨯−⨯=(或723500)(元)----------------10分 ②若运行一台中型发电机,则一年的日均利润值为:14(15610000208800)38283647⨯⨯−⨯=(或726800)(元)----------11分 因为413828335777>,故为使水电站一年的日均利润值最大,应安装中型发电机.--12分 20.解析(1)由题可知(,0)2p F ,则该直线方程为:2p y x =−,………1分 代入22(0)y px p =>得:22304p x px −+=,设1122(,),(,)M x y N x y ,则有123x x p +=…3分∵8MN =,∴128x x p ++=,即38p p +=,解得p =2∴抛物线的方程为:24y x =.………5分(2)设l 方程为y x b =+,代入24y x =,得22(24)0x b x b +−+=,因为l 为抛物线C 的切线,∴0∆=,解得1b =,∴:l 1y x =+ …7分由(1)可知:126x x +=,121x x =设(,1)P m m +,则1122(,(1)),(,(1))PM x m y m PN x m y m =−−+=−−+所以1212()()[(1)][(1)]PM PN x m x m y m y m ⋅=−−+−+−+ 2212121212()(1)()(1)x x m x x m y y m y y m =−+++−++++126x x +=,121x x =,21212()1616y y x x ==,124y y =−,2212124()y y x x −=−,∴12121244x x y y y y −+==− 221644(1)(1)PM PN m m m m ⋅=−+−−+++………10分222[43]2[(2)7]14m m m =−−=−−≥−当且仅当2m =时,即点P 的坐标为(2,3)时,PM PN ⋅的最小值为14−.………12分21. 解:(1)函数的定义域为),0(+∞,xa x x x f +−='22)(2,且0)(='x f 有两个不同的根21,x x ,0222=+−∴a x x 的判别式084>−=∆a 即21<a ,且).21,0(∈∴a ……4分 .因此.…………6分(2)由(1)可知,因此 . ……9分 ∴.即. 12分)(x f .00.22112211121>>−+=−−=a x a x a x ,故又,()()0;002121<'<<>'><<x f x x x x f x x x x 时,当时,或当()()()上单调递减,上单调递增,在,和,在21210)(x x x x x f ∞+()22212121122,2,1x x x x a a x x x x −====+所以()()()121ln 121ln 1)(2222222222<<−+−=+−=x x x x x x a x x f ,其中()()()则设),121(ln 1212<<−+−=t t t t t t h ()()()()(),0ln 21211ln 21212>−=⎥⎦⎤⎢⎣⎡−+−+−='t t t t t t t t t h 42ln 21)21()(121)(−=>⎪⎭⎫ ⎝⎛h t h t h 单调递增,所以,在42ln 21)(2−>xf22.解:(Ⅰ)因为cos x ρθ=,sin y ρθ=,由2cos ρθ=,得22cos ρρθ=,……2分 所以曲线1C 的直角坐标方程为()2211x y −+=;……3分 由()cos 4cos ρρθθ=⋅+⋅,得22sin 4cos ρθρθ=,……4分所以曲线2C 的直角坐标方程为24y x =.……5分(Ⅱ)四点在l 上的排列顺序从下到上依次为H ,I ,J ,K ,它们对应的参数分别为1t ,2t ,3t ,4t . 连接1C J ,则1C IJ ∆为正三角形,所以1IJ =.……6分 HI JK HI IK IJ −=−+=()141411t t t t −+=−++,……8分将12232x t y t ⎧=−⎪⎪⎨⎪=⎪⎩代入24y x =,得:23824t t =−,……9分 即238320t t +−=,故1283t t +=−,所以113HI JK −=.……10分 23解析(1)22()69816f x x x x x =−++++[来源22(3)(4)|3||4|x x x x =−++=−++∴()(4)f x f ≥即|3||4|x x −++9≥……1分∴4349x x x ≤−⎧⎨−−−≥⎩① 或43349x x x −<<⎧⎨−++≥⎩② 或3349x x x ≥⎧⎨−++≥⎩③……2分 解得不等式①:5x ≤−;②:无解 ③:4x ≥所以()(4)f x f ≥的解集为{|5x x ≤−或4}x ≥.………5分(2)()()f x g x >即()|3||4|f x x x =−++的图象恒在()(3)g x k x =−图象的上方……6分21,4()|3||4|7,4321,3x x f x x x x x x −−≤−⎧⎪=−++=−<<⎨⎪+≥⎩()(3)g x k x =−图象为恒过定点P (3,0),且斜率k 变化的一条直线作函数(),()y f x y g x ==图象如图,其中2PB k =,(4,7)A −,∴1PA k =−……9分由图可知,要使得()f x 的图象恒在()g x 图象的上方∴实数k 的取值范围为12k −<≤. ………10分。
2019年全国III卷文科数学高考真题
2019年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给的四个选项中,只有一项是符合题目要求的。
1.已知集合2{1,0,1,2}{1}A B x x =-=≤,,则A B =A .{}1,0,1-B .{}0,1C .{}1,1-D .{}0,1,22.若(1i)2i z +=,则z = A .1i --B .1+i -C .1i -D .1+i3.两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是 A .16B .14C .13D .124.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为 A .0.5B .0.6C .0.7D .0.85.函数()2sin sin2f x x x =-在[0,2π]的零点个数为 A .2B .3C .4D .56.已知各项均为正数的等比数列{a n }的前4项和为15,且a 5=3a 3+4a 1,则a 3= A .16B .8C .4D .27.已知曲线e ln x y a x x =+在点(1,ae )处的切线方程为y =2x +b ,则 A .a =e ,b =–1B .a =e ,b =1C .a =e –1,b =1D .a =e –1,1b =-8.如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则A .BM =EN ,且直线BM ,EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM ,EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线9.执行下边的程序框图,如果输入的ε为0.01,则输出s 的值等于A.4122-B. 5122-C. 6122-D. 7122-10.已知F 是双曲线C :22145x y -=的一个焦点,点P 在C 上,O 为坐标原点,若=OP OF ,则OP F △的面积为 A .32B .52C .72D .9211.记不等式组6,20x y x y +≥⎧⎨-≥⎩表示的平面区域为D .命题:(,),2p x y D x y ∃∈+≥;命题:(,),212q x y D x y ∀∈+≤.下面给出了四个命题①p q ∨②p q ⌝∨③p q ∧⌝④p q ⌝∧⌝这四个命题中,所有真命题的编号是 A .①③B .①②C .②③D .③④12.设()f x 是定义域为R 的偶函数,且在()0,+∞单调递减,则A .f (log 314)>f (322-)>f (232-)B .f (log 314)>f (232-)>f (322-)C .f (322-)>f (232-)>f (log 314) D .f (232-)>f (322-)>f (log 314) 二、填空题:本题共4小题,每小题5分,共20分。
2019年高考真题答案及解析:文科数学(全国Ⅲ卷)『一流精品』
2019年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给的四个选项中,只有一项是符合题目要求的。
1.已知集合2{1,0,1,2}{1}A B x x =-=≤,,则A B =A .{}1,0,1-B .{}0,1C .{}1,1-D .{}0,1,22.若(1i)2i z +=,则z =A .1i --B .1+i -C .1i -D .1+i 【3.两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是 A .16B .14C .13D .124.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为 A .0.5 B .0.6 C .0.7 D .0.8 5.函数()2sin sin2f x x x =-在[0,2π]的零点个数为A .2B .3C .4D .5 6.已知各项均为正数的等比数列{a n }的前4项和为15,且a 5=3a 3+4a 1,则a 3= A .16 B .8 C .4 D .2 7.已知曲线e ln xy a x x =+在点(1,ae )处的切线方程为y =2x +b ,则A .a =e ,b =–1B .a =e ,b =1C .a =e –1,b =1 D .a =e –1,1b =- 8.如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则A .BM =EN ,且直线BM ,EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM ,EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线9.执行下边的程序框图,如果输入的ε为0.01,则输出s 的值等于A.4122-B. 5122-C. 6122-D. 7122-10.已知F 是双曲线C :22145x y -=的一个焦点,点P 在C 上,O 为坐标原点,若=OP OF ,则OPF △的面积为 A .32B .52C .72D .9211.记不等式组6,20x y x y +≥⎧⎨-≥⎩表示的平面区域为D .命题:(,),29p x y D x y ∃∈+≥;命题:(,),212q x y D x y ∀∈+≤.下面给出了四个命题①p q ∨②p q ⌝∨③p q ∧⌝ ④p q ⌝∧⌝ 这四个命题中,所有真命题的编号是 A .①③ B .①②C .②③D .③④12.设()f x 是定义域为R 的偶函数,且在()0,+∞单调递减,则A .f (log 314)>f (322-)>f (232-)B .f (log 314)>f (232-)>f (322-)C .f (322-)>f (232-)>f (log 314) D .f (232-)>f (322-)>f (log 314) 二、填空题:本题共4小题,每小题5分,共20分。
【全国Ⅲ卷】(精校版)2019年高等学校招生全国统一考试文数试题(含答案).docx
2019年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号填写在答题卡上,并认真核准条形码上的准考证号、姓名、考场号、座位号及科目,在规定的位置贴好条形码。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合{|1012}A x =-,,,,2{|1}B x x =≤,则A ∩B =A .{-1,0,1}B .{0,1}C .{-1,1}D .{0,1,2}2. 若(1i)2i z +=,则z =A .-1-iB .-1+iC .1-iD .1+i3. 两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是A .16B .14C .13D .124. 《西游记》《三国演义》《水浒传》和《红楼梦》是中国古代文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》和《红楼梦》的学生共有90位,阅读过《红楼梦》的学生有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为 A .0.5B .0.6C .0.7D .0.85. 函数()2sin sin2f x x x =-在[0,2]π的零点个数A .2B .3C .4D .56. 已知各项为正数的等比数列{}n a 的前4项和为15,且53134a a a =+,则3a =A .16B .8C .4D .27.已知曲线e ln x y a x x =+在点(1e)a ,处的切线方程为2y x b =+,则A .e 1a b ==-,B .e 1a b ==,C .-1e 1a b ==,D .-1e 1a b ==-,8. 如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD⊥平面ABCD ,M 是线段ED 的中点,则 A .BM =EN ,且直线BM ,EN 是相交直线 B .BM ≠EN ,且直线BM ,EN 是相交直线 C .BM =EN ,且直线BM ,EN 是异面直线 D .BM ≠EN ,且直线BM ,EN 是异面直线9.执行右边的程序框图,如果输入的ε为0.01,则输出s 的值为A .4122-B .5122-C .6122-D .7122-10.已知F 是双曲线C :22145x y -=的一个焦点,点P 在C 上,O 为坐标原点.若||||OP OF =,则△OPF 的面积为 A .32 B .52C .72D .9211.记不等式组62x y x y +⎧⎨-⎩,≥≥0表示的平面区域为D .命题p :(,)29x y D x y ∃∈+,≥;命题q :(,)212x y D x y ∀∈+,≤.下面给出了四个命题①p q ∨ ②p q ⌝∨ ③p q ∧⌝④p q ⌝∧⌝ 这四个命题中,所有真命题的编号是 A .①③B .①②C .②③D .③④12.设()f x 是定义域为R 的偶函数,且在(0+)∞,单调递减,则A .233231(log )(2)(2)4f f f -->>B .233231(log )(2)(2)4f f f -->>C .233231(2)(2)(log )4f f f -->>D .233231(2)(2)(log )4f f f -->>二、填空题:本题共4小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019届高三文科数学测试题(三)注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}|1A x x =<,{}|e 1x B x =<,则( ) A .{}|1AB x x =< B .R AB=R C .{}|e AB x x =< D .{}R |01AB x x =<<2.为了反映国民经济各行业对仓储物流业务的需求变化情况,以及重要商品库存变化的动向,中国物流与采购联合会和中储发展股份有限公司通过联合调查,制定了中国仓储指数.如图所示的折线图是2016年1月至2017年12月的中国仓储指数走势情况.根据该折线图,下列结论正确的是( ) A .2016年各月的仓储指数最大值是在3月份 B .2017年1月至12月的仓储指数的中位数为54% C .2017年1月至4月的仓储指数比2016年同期波动性更大D .2017年11月份的仓储指数较上月有所回落,显示出仓储业务活动仍然较为活跃,经济运行稳中向好3.下列各式的运算结果为实数的是( ) A .2(1i)+B .2i (1i)-C .2i(1i)+D .i(1i)+4.三世纪中期,魏晋时期的数学家刘徽首创割圆术,为计算圆周率建立了严密的理论和完善的算法.所谓割圆术,就是不断倍增圆内接正多边形的边数求出圆周率的方法.如图是刘徽利用正六边形计算圆周率时所画的示意图,现向圆中随机投掷一个点,则该点落在正六边形的概率为( )A .33B .33πC .32D .3π 5.双曲线()2222:10,0x y E a b a b-=>>的离心率是5,过右焦点F 作渐近线l 的垂线,垂足为M ,若OFM △的面积是1,则双曲线E 的实轴长是( ) A .1B .2C .2D .226.如图,各棱长均为1的直三棱柱111C B A ABC -,M ,N 分别为线段1A B ,1B C 上的动点,且MN ∥平面11A ACC ,则这样的MN 有( )A .1条B .2条C .3条D .无数条7.已知实数x ,y 满足⎪⎩⎪⎨⎧≤≤+≥-04242y y x y x ,则y x z 23-=的最小值是( )A .4B .5C .6D .78.函数()()22cos x x f x x -=-在区间[]5,5-上的图象大致为( )9.已知函数()lg4xf x x=-,则( ) A .()f x 在()0,4单调递减B .()f x 在()0,2单调递减,在()2,4单调递增C .()y f x =的图象关于点()2,0对称D .()y f x =的图象关于直线2=x 对称10.如图是为了求出满足201822221>+++n的最小整数n , 和两个空白框中,可以分别填入( )A .?2018>S ,输出1-nB .?2018>S ,输出nC .?2018≤S ,输出1-nD .?2018≤S ,输出n11.ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,已知3cos b a C C ⎛⎫= ⎪ ⎪⎝⎭,2=a ,362=c ,则角=C ( ) A .34πB .3π C .6π D .4π 12.设A ,B 是椭圆14:22=+ky x C 长轴的两个端点,若C 上存在点P 满足120APB ∠=︒,则k 的取值范围是( )A .[)40,12,3⎛⎤+∞ ⎥⎝⎦B .[)20,6,3⎛⎤+∞ ⎥⎝⎦C .[)20,12,3⎛⎤+∞ ⎥⎝⎦D .[)40,6,3⎛⎤+∞ ⎥⎝⎦第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.已知向量()2,3=-a ,(),2x =-b ,若()2⊥+a a b ,则实数x 的值为 .14.曲线e sin x y x =+在点()0,1处的切线方程是 . 15.若tan 3α=,0,2απ⎛⎫∈ ⎪⎝⎭,则cos 4απ⎛⎫-= ⎪⎝⎭ .16.已知球的直径4=SC ,A ,B 是该球球面上的两点,3=AB ,30ASC BSC ∠=∠=︒,则棱锥ABC S -的体积为 .三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(12分)设n S 为数列{}n a 的前n 项和,已知37a =,()12222n n a a a n -=+-≥. (1)证明:{}1n a +为等比数列;(2)求{}n a 的通项公式,并判断n ,n a ,n S 是否成等差数列?18.(12分)如图,在三棱柱111C B A ABC -中,⊥BC 平面B B AA 11,21==AA AB ,160A AB ∠=︒. (1)证明:平面⊥C AB 1平面BC A 1;(2)若四棱锥C C BB A 11-的体积为332,求该三棱柱的侧面积.19.(12分)噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了了解声音强度D (单位:分贝)与声音能量I (单位:2/cm W )之间的关系,将测量得到的声音强度i D 和声音能量i I ,()1,2,,10i =数据作了初步处理,得到如图散点图及一些统计量的值.表中i i I W lg =,∑==101101i i W W .(1)根据散点图判断,I b a D 11+=与I b a D lg 22+=哪一个适宜作为声音强度D 关于声音能量I 的回归方程类型?(给出判断即可,不必说明理由)(2)根据表中数据,求声音强度D 关于声音能量I 的回归方程;(3)当声音强度大于60分贝时属于噪音,会产生噪音污染,城市中某点P 共受到两个声源的影响,这两个声源的声音能量分别是1I 和2I ,且10211041=+I I .已知点P 的声音能量等于声音能量1I 与2I 之和.请根据(1)中的回归方程,判断P 点是否受到噪音污染的干扰,并说明理由. 附:对于一组数据()11,u v ,()22,u v ,,(),n n u v 其回归直线αβ+=u v 的斜率和截距的最小二乘估计分别为121()()ˆ()nii i nii uu v v uu β==--=-∑∑,ˆˆav u β=-.20.(12分)过抛物线()2:20C x py p =>的焦点F 作直线l 与抛物线C 交于A ,B 两点,当点A 的纵坐标为1时,2AF =. (1)求抛物线C 的方程;(2)若直线l 的斜率为2,问抛物线C 上是否存在一点M ,使得MB MA ⊥,并说明理由.21.(12分)已知a ∈R ,函数()()2e 2x f x x a ax =--.(1)若()f x有极小值且极小值为0,求a的值;(2)当x∈R时,()()0f x f x+-≥,求a的取值范围.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.(10分)【选修4-4:坐标系与参数方程】在平面直角坐标系xOy中,曲线1C的参数方程为:⎩⎨⎧==θθsincosyx(θ为参数,[]0,θ∈π),将曲线1C经过伸缩变换:⎩⎨⎧==yyxx3''得到曲线2C.(1)以原点O为极点,x轴的正半轴为极轴建立极坐标系,求2C的极坐标方程;(2)若直线l:⎩⎨⎧==ααsincostytx(t为参数)与1C,2C相交于A,B两点,且1AB=,求α的值.23.(10分)选【修4-5:不等式选讲】已知函数()12f x x x=+--,2()g x x x a=--.(1)当5=a时,求不等式()()f xg x≥的解集;(2)若不等式()()f xg x≥的解集包含[]2,3,求a的取值范围.高三文科数学(三)答 案一、选择题. 1.【答案】B 2.【答案】D 3.【答案】C 4.【答案】A 5.【答案】B 6.【答案】D 7.【答案】C 8.【答案】B 9.【答案】C 10.【答案】A 11.【答案】D 12.【答案】A 二、填空题. 13.【答案】1014.【答案】012=+-y x15.【答案】552 16.【答案】3 三、解答题.17.【答案】(1)见解析;(2)12-=n n a ,是.【解析】∵37a =,3232a a =-,∴32=a , ∴121+=-n n a a ,∴11=a ,()11221-n n a n a +=≥+,∴{}1n a +是首项为2公比为2的等比数列.(2)由(1)知,n n a 21=+,∴12-=nn a ,∴22212211--=---=++n n S n n n ,∴()12222210n n n n n S a n n ++-=+----=, ∴n n a S n 2=+,即n ,n a ,n S 成等差数列. 18.【答案】(1)见解析;(2)623S =+.【解析】(1)证明:三棱柱111C B A ABC -的侧面B B AA 11中,1AA AB =, ∴四边形B B AA 11为菱形,∴B A AB 11⊥,又⊥BC 平面B B AA 11,⊂1AB 平面B B AA 11,∴BC AB ⊥1, ∵1A BBC B =,∴⊥1AB 平面BC A 1,⊂1AB 平面C AB 1,∴平面⊥C AB 1平面BC A 1(2)过1A 在平面B B AA 11内作⊥D A 11BB 于D , ∵⊥BC 平面B B AA 11,⊂BC 平面C C BB 11,∴平面⊥C C BB 11平面B B AA 11于1BB ,⊂D A 1平面B B AA 11, ∴⊥D A 1平面C C BB 11.在11Rt A B D △中,211==AB B A ,11160A B B A AB ∠=∠=︒, ∴31=D A ,∵11AA BB ∥,∴A 点到平面C C BB 11的距离为3. 又四棱锥-A C C BB 11的体积332233131111=⨯⨯⨯==BC D A S V C C BB ,∴1=BC 在平面C C BB 11内过点D 作DE BC ∥交1CC 于E ,连接E A 1,则1==BC DE ,22211=+=DE D A E A ,∴())1113122623S A D DE A E AA =++⋅=+⨯=+19.【答案】(1)I b a D lg 22+=更适合;(2)7.160ln 10ˆ+=I D ;(3)是,见解析.【解析】(1)I b a D lg 22+=更适合.(2)令i i I W lg =,先建立D 关于W 的线性回归方程,由于10121()()5.1ˆ0.51()iii nii W W D D WW β==--==-∑∑,∴7.160ˆˆ=-=W D aβ, ∴D 关于W 的线性回归方程是7.16010ˆ+=W D,即D 关于I 的回归方程是7.160ln 10ˆ+=I D . (3)点P 的声音能量21I I I +=,∵10211041=+I I ,∴21I I I +=()1010102112121241410105910I I I I I I I I ---⎛⎫⎛⎫=++=++≥⨯ ⎪ ⎪⎝⎭⎝⎭,根据(2)中的回归方程,点P 的声音强度D 的预报值()10min ˆ10lg 910160.710lg960.760D -=⨯+=+>, ∴点P 会受到噪声污染的干扰.20.【答案】(1)C :y x 42=;(2)存在M 点,见解析.【解析】(1)由抛物线的定义可得2212=⇒=+p p ,故抛物线方程为y x 42=.(2)假设存在满足条件的点()00,M x y ,则设直线1:+=kx y AB ,代入y x 42=可得0442=--kx x ,设()11,A x y ,()22,B x y ,则124x x k +=,124x x =-,因为()1010,MA x x y y =--,()2020,MB x x y y =--,则由MB MA ⊥可得()()()()102010200x x x x y y y y --+--=,即()()()()1020102011016x x x x x x x x ⎡⎤--+++=⎢⎥⎣⎦,也即()()1020160x x x x --+=,所以0124020=++kx x ,由于判别式()2164816430k ∆=-=->,此时12x =-,26x =-,则存在点()2,1M -,()6,9M -,即存在点()00,M x y 满足题设. 21.【答案】(1)21=a ;(2)(],1-∞. 【解析】(1)()()()()'e 2e 21e 2x x x f x a x ax x a =-+-=+-,x ∈R , ①若0≤a ,则由()'0f x =解得1-=x ,当(),1x ∈-∞-时,()'0f x <,()f x 递减;当()1,x ∈-+∞时,()'0f x >,()f x 递增;故当1-=x 时,()f x 取极小值()11e f a --=-,令1e 0a --=,得1e a =(舍去),若0>a ,则由e 20x a -=,解得()ln 2x a =. (i )若()ln 21a <-,即102ea <<时,当()(),ln 2x a ∈-∞,()'0f x >,()f x 递增; 当()()ln 2,1x a ∈-,()'0f x >,()f x 递增;故当1-=x 时,()f x 取极小值()11e f a --=-,令1e 0a --=,得1e a =(舍去).(ii )若()ln 21a =-,即12ea =时,()'0f x ≥,()f x 递增不存在极值; (iii )若()ln 21a >-,即12ea >时,当(),1x ∈-∞-时,()'0f x >,()f x 递增; 当()()1,ln 2x a ∈-时,()'0f x <,()f x 递减;当()()ln 2,x a ∈+∞时,()'0f x >,()f x 递增; 故当()ln 2x a =时,()f x 取极小值()()()2ln 2ln 20f a a a =-=,得21=a 满足条件, 故当()f x 有极小值且极小值为0时,21=a . (2)()()0f x f x +-≥等价于()2e e 20x x x ax ---≥,即()2e e 2x x x ax --≥,当0=x 时,①式恒成立;当0≠x 时,()e e 0x x x -->,故当0≤a 时,①式恒成立;以下求当0>x 时,不等式()2e e 20x x x ax ---≥恒成立,且当0<x 时不等式()2e e 20x x x ax ---≤恒成立时正数a 的取值范围,令e x t =,()12ln g t t a t t =--以下求当1>t ,()12ln 0g t t a t t=--≥恒成立,且当10<<t ,()12ln 0g t t a t t=--≤恒成立时正数a 的取值范围,对()g t 求导,得()22212211a t at g t t t t-+'=+-=,记()221h t t at =-+,244a ∆=-, (i )当10≤<a 时,0442≤-=∆a ,()2210h t t at =-+≥,()'0g t >,故()g t 在()0,+∞上递增,又()10g =,故1>t ,()()10g t g >=,01t <<,()()10g t g <=, 即当10≤<a 时,()2e e 2x x x ax --≥式恒成立;(ii )当1>a 时,()010h =>,()1220h a =-<,故()h t 的两个零点即()'g t 的两个零点()10,1t ∈和()21,t ∈+∞,在区间()12,t t 上,()0h t <,()'0g t <,()g t 是减函数,又11<t ,所以()()110g t g >=,当1>a 时①式不能恒成立. 综上所述,所求a 的取值范围是(],1-∞. 22.【答案】(1)[]()2222230,3cos sin 2cos 1ρθθθθ==∈π++;(2)3απ=或23απ=. 【解析】(1)1C 的普通方程为()2210x y y +=≥,把⎩⎨⎧==yy x x 3''代入上述方程得,()22''1'03y x y +=≥,∴2C 的方程为()22103y x y +=≥,令cos x ρθ=,sin y ρθ=,所以2C 的极坐标方程为[]()2222230,3cos sin 2cos 1ρθθθθ==∈π++. (2)在(1)中建立的极坐标系中,直线l 的极坐标方程为()θαρ=∈R ,由⎩⎨⎧==αθρ1,得1=A ρ,由⎪⎩⎪⎨⎧=+=αθθρ1cos 2322,得1cos 232+=αρB , 而1211cos 232-=-+α,∴21cos ±=α,而[]0,α∈π,∴3απ=或23απ=. 23.【答案】(1)⎡-⎢⎣⎦;(2)[)3,+∞. 【解析】(1)当5=a 时,不等式()()f x g x ≥等价于2125x x x x +--≥--,① 当1-<x 时,①式化为022≤--x x ,无解;当21≤≤-x 时,①式化为0432≤--x x ,得21≤≤-x ;当2>x 时,①式化为082≤--x x ,得23312+≤<x , 所以()()f x g x ≥的解集为⎡-⎢⎣⎦.(2)当[]2,3x ∈时,()3f x =,所以()()f x g x ≥的解集包含[]2,3,等价于[]2,3x ∈时,()3g x ≤, 又()2g x x x a =--在[]2,3上的最大值为()36g a =-, 所以()33g ≤,即36≤-a ,得3≥a , 所以a 的取值范围为[)3,+∞.。
