特殊四边形的性质与判定练习题
特殊四边形的计算与证明问题(真题10道+模拟30道)-中考数学重难题型押题培优导练案【原卷版】

专题14特殊四边形的计算与证明问题(北京真题10道+模拟30道)【方法归纳】题型概述,方法小结,有的放矢考点考查年份考查频率十年8考特殊四边形的计算与证明(大题)2013.2014.2015.2016.2017.2020.2021.2022以四边形为载体的计算与证明是北京市中考数学常考的一类解答题,要求学生理解和掌握平行四边形、矩形、菱形、正方形的性质定理和判定定理,会画出四边形全等变换后的图形,并会结合其他知识解答一些有探索性、开放性的问题,提高解决问题的能力.解决此类问题的关键是要牢牢把握四边形的性质与特征,挖掘相关图形之间的联系,利用所给图形及图形之间形状、大小、位置关系,进行观察、实验、比较、联想、类比、分析、综合等.常用到的矩形、菱形、正方形的解题策略有:(1)对于矩形:①判定四边形是矩形,一般先判定是平行四边形,然后再判定是矩形;②矩形的内角是直角和对角线相等,相对于平行四边形来说是矩形特殊的性质;③利用矩形的性质计算或证明时,常常运用勾股定理,锐角三角函数或相似三角形求解.(2)对于菱形:①判定四边形是菱形,一般先判定是平行四边形,然后再判定是菱形;②菱形的邻边相等和对角线垂直,相对于平行四边形来说是菱形特殊的性质;③利用菱形的性质计算或证明时,常常运用勾股定理,锐角三角函数或相似三角形求解;④求线段和的最小值时,往往运用菱形的轴对称的性质转化为求线段的长度.(3)对于正方形:①判定四边形是正方形,一般先判定是平行四边形,然后再判定是矩形或菱形,最后判定这个四边形是正方形;②正方形是最特殊的四边形,在正方形的计算或证明时,要特别注意线段或角的等量转化.【典例剖析】典例精讲,方法提炼,精准提分【例1】(2021·北京·中考真题)如图,在四边形ABCD中,∠ACB=∠CAD=90°,点E在BC上,AE//DC,EF⊥AB,垂足为F.(1)求证:四边形AECD是平行四边形;,求BF和AD的长.(2)若AE平分∠BAC,BE=5,cosB=45【例2】(2022·北京·中考真题)如图,在▱ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.(1)求证:四边形EBFD是平行四边形;(2)若∠BAC=∠DAC,求证:四边形EBFD是菱形.【真题再现】必刷真题,关注素养,把握核心1.(2014·北京·中考真题)如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.(1)求证:四边形ABEF是菱形;(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.2.(2016·北京·中考真题)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.(1)求证:BM=MN;(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.3.(2017·北京·中考真题)如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.(1)求证:四边形BCDE为菱形;(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.4.(2017·北京·中考真题)数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.,(以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)请根据上图完成这个推论的证明过程.证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),S矩形EBMF=S△ABC-(____________+____________).易知,S△ADC=S△ABC,_____________=______________,______________=_____________.可得S矩形NFGD= S矩形EBMF.5.(2013·北京·中考真题)如图,在▱ABCD中,F是AD的中点,延长BC到点E,使CE=1BC,连结DE,2CF.(1)求证:四边形CEDF是平行四边形;(2)若AB=4,AD=6,∠B=60°,求DE的长.6.(2015·北京·中考真题)在▱ABCD,过点D作DE∠AB于点E,点F在边CD上,DF=BE,连接AF,BF.(1)求证:四边形BFDE是矩形;(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.7.(2020·北京·中考真题)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF∠AB,OG∠EF.(1)求证:四边形OEFG是矩形;(2)若AD=10,EF=4,求OE和BG的长.8.(2016·北京·中考真题)如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE.【模拟精练】押题必刷,巅峰冲刺,提分培优一、解答题1.(2022·北京房山·二模)已知:如图,在四边形ABCD中,AB∥DC,AC⊥BD,垂足为M,过点A作AE⊥AC,交CD的延长线于点E.(1)求证:四边形ABDE是平行四边形;(2)若AC=8,sin∠ABD=4,求BD的长.52.(2022·北京西城·二模)如图,菱形ABCD的对角线AC,BD交于点O,点E,F分别在DA,BC的延长线上,且BE∠ED,CF=AE.(1)求证:四边形EBFD是矩形;(2)若AB=5,cos∠OBC=4,求BF的长.53.(2022·北京朝阳·二模)如图,在菱形ABCD中,O为AC,BD的交点,P,M,N分别为CD,OD,OC 的中点.(1)求证:四边形OMPN是矩形;(2)连接AP,若AB=4,∠BAD=60∘,求AP的长.4.(2022·北京东城·二模)如图,在平行四边形ABCD中,DB=DA,点F是AB的中点,连接DF并延长,交CB的延长线于点E,连接AE.(1)求证:四边形AEBD是菱形;(2)若DC=√10,tan∠DCB=3,求菱形AEBD的边长.5.(2022·北京平谷·二模)如图,在□ABCD中,连接AC,点E是AB中点,点F是AC的中点,连接EF,过E作EG∥AF,交DA的延长线于点G.(1)求证:四边形AGEF是平行四边形;(2)若sin∠G=3,AC=10,BC=12,连接GF,求GF的长.56.(2022·北京北京·二模)如图,在等边△ABC中,D是BC的中点,过点A作AE∥BC,且AE=DC,连接CE.(1)求证:四边形ADCE是矩形;(2)连接BE交AD于点F,连接CF.若AB=4,求CF的长.7.(2022·北京丰台·二模)如图,在∠ABC中,∠BAC=90∘,AD∠BC,垂足为D,AE∠BC,CE∠DA.(1)求证:四边形AECD是矩形;(2)若AB=5,cosB=3,求AE的长.58.(2022·北京密云·二模)如图,在平行四边形ABCD中,AC平分∠BAD,点E为AD边中点,过点E作AC的垂线交AB于点M,交CB延长线于点F.(1)求证:平行四边形ABCD是菱形;(2)若FB=2,sinF=3,求AC的长.59.(2022·北京市十一学校模拟预测)如图,在四边形ABCD中,AD=CD,BD⊥AC于点O,点E是DB延长线上一点,OE=OD,BF⊥AE于点F.(1)求证:四边形AECD是菱形;(2)若AB平分∠EAC,OB=3,tan∠CED=3,求EF和AD的长.410.(2022·北京昌平·二模)如图,在矩形ABCD中,对角线AC,BD交于点O,分别过点C,D作BD,AC的平行线交于点E,连接OE交AD于点F.(1)求证:四边形OCED是菱形;(2)若AC=8,∠DOC=60°,求菱形OCED的面积.11.(2022·北京海淀·二模)如图,在Rt∠ABC中,∠A =90°,点D,E,F分别为AB,AC,BC的中点,连接DF,EF.(1)求证:四边形AEFD是矩形;(2)连接BE,若AB = 2,tan C =1,求BE的长.212.(2022·北京东城·一模)如图,在正方形ABCD中,E为对角线AC上一点(AE>CE),连接BE,DE.(1)求证:BE=DE;(2)过点E作EF⊥AC交BC于点F,延长BC至点G,使得CG=BF,连接DG.∠依题意补全图形;∠用等式表示BE与DG的数量关系,并证明.13.(2022·北京东城·一模)如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,∠EAO=∠DCO.(1)求证:四边形AECD是平行四边形;(2)若AB=BC,CD=5,AC=8,tan∠ABD=2,求BE的长.314.(2022·北京市十一学校二模)如图,在平行四边形ABCD中,CE⊥AD于点E,延长DA至点F,使得AF=DE,连接BF,CF.(1)求证:四边形BCEF是矩形;(2)若AB=6,CF=8,DF=10,求EF的长.15.(2022·北京石景山·一模)如图所示,△ABC中,∠ACB=90°,D,E分别为AB,BC的中点,连接DE 并延长到点F,使得EF=DE,连接CD,CF,BF.(1)求证:四边形BFCD是菱形;(2)若cos A=5,DE=5,求菱形BFCD的面积.1316.(2022·北京大兴·一模)如图,在平面四边形ABCD中,点E,F分别是AB,CD上的点,CF=BE.(1)求证:四边形AEFD是平行四边形;(2)若∠A=60°,AD=2,AB=4,求BD的长.17.(2022·北京丰台·一模)如图,在四边形ABCD中,∠DCB=90°,AD∥BC,点E在BC上,AB∥DE,AE 平分∠BAD.(1)求证:四边形ABED为菱形;(2)连接BD,交AE于点O.若AE=6,sin∠DBE=3,求CD的长.518.(2022·北京市师达中学模拟预测)如图,四边形ABCD是平行四边形,AE∠BC,AF∠CD,垂足分别为E,F,且BE=DF.(1)求证:四边形ABCD是菱形;(2)连接EF并延长,交AD的延长线于点G,若∠CEG=30°,AE =2,求EG的长.19.(2022·北京四中模拟预测)如图,在四边形ABCD中,AD=CD,BD∠AC于点O,点E是DB延长线上一点,OE=OD,BF∠AE于点F.(1)求证:四边形AECD是菱形;(2)若AB平分∠EAC,OB=3,BE=5,求EF和AD的长.20.(2021·北京丰台·一模)如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AE∠BC于E,延长BC到点F,使CF=BE,连接DF.(1)求证:四边形AEFD是矩形;(2)连接OE,若AD=10,EC=4,求OE的长度.21.(2022·北京市燕山教研中心一模)如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作DE⊥BD 交BC的延长线于点E.(1)求证:四边形ACED是平行四边形;(2)若BD=4,AC=3,求sin∠CDE的值.22.(2022·北京平谷·一模)如图,∠ABC中,∠ACB=90°,点D为AB边中点,过D点作AB的垂线交BC 于点E,在直线DE上截取DF,使DF=ED,连接AE、AF、BF.(1)求证:四边形AEBF是菱形;(2)若cos∠EBF=3,BF=5,连接CD,求CD的长.523.(2022·北京市第一六一中学分校一模)在矩形ABCD中,AC,BD相交于点O,过点C作CE∠BD交AD的延长线于点E.(1)求证:∠ACD=∠ECD;(2)连接OE,若AB=2,tan∠ACD=2,求OE的长.24.(2022·北京房山·一模)如图,在平行四边形ABCD中,过点B作BE∠CD交CD的延长线于点E,过点C作CF∥EB交AB的延长线于点F.(1)求证:四边形BFCE是矩形;(2)连接AC,若AB=BE=2,tan∠FBC=1,求AC的长225.(2022·北京朝阳·一模)如图,在矩形ABCD中,AC,BD相交于点O,AE//BD,BE//AC.(1)求证:四边形AEBO是菱形;(2)若AB=OB=2,求四边形AEBO的面积.26.(2022·北京·中国人民大学附属中学分校一模)如图,正方形ABCD中,P为BD上一动点,过点P作PQ⊥AP 交CD边于点Q.(1)求证:PA=PQ;(2)用等式表示PB、PD、AQ之间的数量关系,并证明;(3)点P从点B出发,沿BD方向移动,若移动的路径长为4,则AQ的中点M移动的路径长为(直接写出答案).BC,27.(2022·北京市三帆中学模拟预测)已知:△ABC中,AB=AC,AD⊥BC于点D,过点A作AE,且AE=12连结DE.(1)求证:四边形ABDE是平行四边形;(2)作FG⊥AB于点G,AG=4,cos∠GAF=4,求FG和FD的长.528.(2022·北京西城·一模)如图,在∠ABC中,BA=BC,BD平分∠ABC交AC于点D,点E在线段BD上,点F在BD的延长线上,且DE=DF,连接AE,CE,AF,CF.(1)求证:四边形AECF是菱形;(2)若BA∠AF,AD=4,BC=4√5,求BD和AE的长.29.(2022·北京顺义·一模)如图,在四边形ABCD中,AD∥BC,AC⊥BD,垂足为O,过点D作BD的垂线交BC的延长线于点E.(1)求证:四边形ACED是平行四边形;(2)若AC=4,AD=2,cos∠ACB=4,求BC的长.530.(2022·北京通州·一模)如图.在∠ABC中,AB=BC,BD平分∠ABC交AC于点D.点E为AB的中点,连接DE,过点E作EF∥BD交CB的延长线于点F.(1)求证:四边形DEFB是平行四边形;(2)当AD=4,BD=3时,求CF的长.。
初二正方形性质及判定练习题

初二正方形性质及判定练习题
形状与性质
正方形是一种特殊的四边形,具有以下性质:
1. 四条边相等:正方形的四条边的长度相等。
2. 四个角相等:正方形的四个角的大小都是90度。
3. 对角线相等:正方形的对角线长度相等。
4. 正方形是菱形:正方形的对角线相互垂直,且长度相等,因此也是菱形的一种特殊情况。
判定练题
以下是一些判定练题,帮助你巩固对正方形性质的理解:
1. 判断下列图形是否为正方形:
A. 
B. 
C. 
D. 
答案:A是正方形,B是正方形,C不是正方形,D不是正方形。
2. 若两个正方形的边长分别为4cm和6cm,哪个正方形的面积更大?
答案:边长为6cm的正方形面积更大,因为面积与边长的平方成正比。
3. 若一个正方形的对角线长度为10cm,求其边长。
答案:根据正方形的性质,对角线长度等于边长乘以√2,所以边长等于10cm除以√2,约为7.07cm。
4. 若一个四边形的边长均为5cm,四个角的大小均为90度,是否一定是正方形?
答案:不一定,虽然满足了长宽相等和角度为90度的条件,但没有保证对角线相等,因此不一定是正方形。
5. 若一个四边形的对角线相等,四个角的大小均为90度,是否一定是正方形?
答案:是的,根据这些条件可以确定该四边形是正方形,因为这些是正方形的定义性质。
以上是关于初二正方形性质及判定练习题的内容。
希望能够帮助你更好地理解和应用正方形的性质。
菱形的性质与判定练习题

菱形的性质与判定练习题
菱形是一种特殊的四边形,具有一些独特的性质。
本文将通过练题的形式来帮助读者更好地理解菱形的性质和判定方法。
练题一
已知四边形ABCD,如果AD=BC,且∠ADC=90°,请回答下列问题:
1. 该四边形是否为菱形?
2. 四边形ABCD的对角线相互垂直吗?
3. 如果∠BAC=60°,该四边形的其他三个内角分别是多少?
练题二
给定四边形EFGH的坐标:E(2, 4), F(6, 2), G(4, -2), H(0, 0),请回答下列问题:
1. 该四边形是否为菱形?
2. 该四边形的对角线是否相等?
3. 如果用勾股定理来判定,该四边形是否为直角菱形?
练题三
已知四边形IJKL的边长:IJ=KL=5cm,JK=IL=8cm,请回答下列问题:
1. 该四边形是否为菱形?
2. 如果∠IJK=90°,该四边形是否为直角菱形?
3. 该四边形的其他两个内角分别是多少?
练题四
给定四边形MNOP的内角度量:∠M=90°,∠N=45°,
∠O=135°,请回答下列问题:
1. 该四边形是否为菱形?
2. 如果该四边形是菱形,对角线是否相等?
3. 该四边形的内角和是多少度?
以上是关于菱形性质与判定的练习题。
通过解答这些问题,读者能够更加深入地了解菱形的性质和判定方法。
四边形经典中考题

四边形经典考点1 特殊的平行四边形的性质与判定1.矩形的定义、性质与判定(1)矩形的定义:有一个角是直角的平行四边形是矩形。
(2)矩形的性质:矩形的对角线_________;矩形的四个角都是________角。
矩形具有________的一切性质。
矩形是轴对称图形,对称轴有_____________条,矩形也是中心对称图形,对称中心为_____________的交点。
矩形被对角线分成了____________个等腰三角形。
(3)矩形的判定有一个是直角的平行四边形是矩形;有三个角是_____________的四边形是矩形;对角线__ ___的平行四边形是矩形。
温馨提示:矩形的对角线是矩形比较常用的性质,当对角线的夹角中,有一个角为60度时,则构成一个等边三角形;在判定矩形时,要注意利用定义或对角线来判定时,必须先证明此四边形为平行四边形,然后再一个角为直角或对角线相等。
很多同学容易忽视这个问题。
2.菱形的定义、性质与判定(1)菱形的定义:有一组邻边相等的平行四边形是菱形。
(2)菱形的性质菱形的_______都相等;菱形的对角线互相____ ___,并且每一条对角线______一组对角;菱形也具有平行四边形的一切性质。
菱形即是轴对称图形也是中心对称图形,对称轴有__ __条。
(3)菱形的面积菱形的面积=底×高,菱形的面积=21ab ,其中a ,b 分别为菱形两条对角线的长。
菱形被对角线分成了4个全等的直角三角形。
(4)菱形的判定:_______都相等的四边形是菱形;对角线______的平行四边形是菱形;有一组邻边相等的平行四边形是菱形。
温馨提示:在利用菱形的判定时,也要注意所要证明的四边形是不是平行四边形,而你用的判定定理需不需要证明它是平行四边形,有对角线时,通常考虑利用对角线互相垂直的平行四边形是菱形来证明,否则一般不利用此定理。
3.正方形的性质及判定方法(1)正方形的性质:正方形的四个角都是_____________,四条边都_____________;正方形的两条对角线____________,并且互相垂直平分,每条对角线平分一组对角;正方形即是轴对称图形也是中心对称图形。
特殊平行四边形的性质和判定(一)(人教版)(含答案)
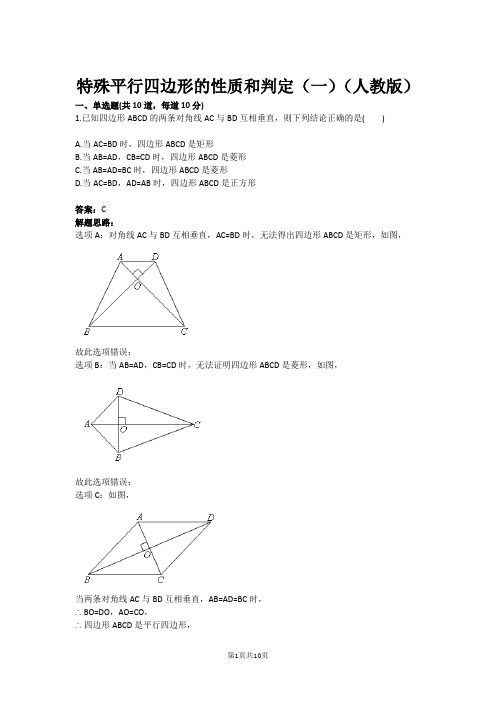
特殊平行四边形的性质和判定(一)(人教版)一、单选题(共10道,每道10分)1.已知四边形ABCD的两条对角线AC与BD互相垂直,则下列结论正确的是( )A.当AC=BD时,四边形ABCD是矩形B.当AB=AD,CB=CD时,四边形ABCD是菱形C.当AB=AD=BC时,四边形ABCD是菱形D.当AC=BD,AD=AB时,四边形ABCD是正方形答案:C解题思路:选项A:对角线AC与BD互相垂直,AC=BD时,无法得出四边形ABCD是矩形,如图,故此选项错误;选项B:当AB=AD,CB=CD时,无法证明四边形ABCD是菱形,如图,故此选项错误;选项C:如图,当两条对角线AC与BD互相垂直,AB=AD=BC时,∴BO=DO,AO=CO,∴四边形ABCD是平行四边形,又∵AC⊥BD∴平行四边形ABCD是菱形,故此选项正确;选项D:当AC=BD,AD=AB时,无法得到四边形ABCD是正方形,如图,故此选项错误;故选C.试题难度:三颗星知识点:正方形的判定2.如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点处,折痕与边BC交于点E,则CE的长为( )A.6cmB.4cmC.2cmD.1cm答案:C解题思路:∵沿AE对折,点B落在边AD上的点处,∴,,又∵∠BAD=90°,∴四边形是正方形,∴BE=AB=6,∴CE=BC-BE=8-6=2(cm).故选C.试题难度:三颗星知识点:折叠问题3.如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为( )A. B.C. D.答案:D解题思路:在正方形ABCD中,M为边AD的中点,∴,∴,∴,∵,∵四边形EDGF是正方形,∴.故选D.试题难度:三颗星知识点:正方形的性质4.如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.乙:分别作∠BAD,∠ABC的平分线AE,BF,交BC,AD于E,F,连接EF,则四边形ABEF 是菱形.根据两人的作法可判断( )A.甲正确,乙错误B.乙正确,甲错误C.甲、乙均正确D.甲、乙均错误答案:C解题思路:解:甲的作法正确;在平行四边形ABCD中,AD∥BC,∴∠DAC=∠ACN,∵MN是AC的垂直平分线,∴AO=CO,又∵∠AOM=∠CON∴△AOM≌△CON(ASA),∴MO=NO,∴四边形ANCM是平行四边形,∵AC⊥MN,∴四边形ANCM是菱形;乙的作法正确;如图,在平行四边形ABCD中,AD∥BC,∴∠1=∠2,∠6=∠7,∵BF平分∠ABC,AE平分∠BAD,∴∠2=∠3,∠5=∠6,∴∠1=∠3,∠5=∠7,∴AB=AF,AB=BE,∴AF=BE∵AF∥BE,且AF=BE,∴四边形ABEF是平行四边形,∵AB=AF,∴平行四边形ABEF是菱形;故选C.试题难度:三颗星知识点:菱形的判定5.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )A.1B.C. D.答案:C解题思路:在正方形ABCD中,∠ABD=∠ADB=45°,∵∠BAE=22.5°,∴∠DAE=67.5°,在△ADE中,∠AED=180°-45°-67.5°=67.5°,∴∠DAE=∠DEA,∴AD=DE=4,∵正方形的边长为4,∴,∴,∵EF⊥AB,∠ABD=45°,∴△BEF是等腰直角三角形,∴.故选C.试题难度:三颗星知识点:正方形的性质6.如图,在△ABC中,AC的垂直平分线分别交AC,AB于点D,F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )A. B.C.4D.答案:A解题思路:∵DE是AC的垂直平分线,F是AB的中点,∴DF是△ABC的中位线,∴DF∥BC,∴∠C=90°,∴四边形BCDE是矩形.∵∠A=30°,∠C=90°,BC=2,∴AB=4,∴.∴.∴.故选A.试题难度:三颗星知识点:矩形的判定与性质7.如图,矩形ABCD的对角线相交于点O,AE平分∠BAD交BC于E,连接OE,若∠CAE=15°,则∠AEO=( )A.30°B.25°C.22.5°D.20°答案:A解题思路:在矩形ABCD中,∵AE平分∠BAD交BC于E,∴∠AEB=45°,AB=BE,∵∠CAE=15°,∴∠ACB=30°,∴∠BAO=60°,又∵OA=OB,∴△BOA是等边三角形,∴OA=OB=AB,即OB=AB=BE,∴△BOE是等腰三角形,且∠OBE=∠OCB=30°,∴∠BOE=∠BEO=75°,∴∠AEO=∠BEO-∠BEA=75°-45°=30°,故选A.试题难度:三颗星知识点:矩形的性质8.如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( )A.4B.8C.6D.9答案:C解题思路:∵AB∥CD,∴∠EAF=∠AED.又AE是∠DAB的平分线,∴∠DAE=∠AED,∴AD=ED.∵AB∥CD,EF∥AD∥BC,∴四边形ADEF和四边形BCEF是平行四边形.∴四边形ADEF是菱形.∴AD=DE=DC-EC=5,,AE⊥DF.∴∴DF=2DO=6.故选C.试题难度:三颗星知识点:菱形的判定9.如图,在菱形ABCD中,延长AD到点E,连接BE交CD于点H,交AC于点F,且BF=DE,若DH=2,则FH的长为( )A.1B.C.2D.答案:C解题思路:如图,连接DF,在菱形ABCD中,AB=AD,∠BAF=∠DAF,又∵AF=AF,∴△ABF≌△ADF(SAS),∴∠ABF=∠ADF,BF=DF,∵∠ABC=∠ADC,∴∠CBH=∠CDF,∵BF=DE,∴DE=DF,∴∠DFE=∠E,∵BC∥AE,∴∠CBE=∠E,∴∠DFE=∠CDF,∴FH=DH=2.故选C试题难度:三颗星知识点:菱形的性质10.如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,点G,F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为( )A.cmB.4cmC.cmD.cm答案:D解题思路:∵点D,E分别是边AB,AC的中点,∴DE是△ABC的中位线,∴,∵DE=2,∴BC=4,∵AB=AC,∴DB=EC,在正方形DEFG中,DG=EF,∠DGF=∠EFG=90°,∴∠DGB=∠EFC=90°,∴△BDG≌△CEF(HL),∴BG=CF=1,∴,∴.故选D.试题难度:三颗星知识点:正方形的性质。
专题30 四边形的判定与性质综合大题专项训练(30道)

专题5.4 四边形的判定与性质综合大题专项训练(30道)【浙教版】1.(2021秋•九江期末)如图,在四边形ABCD中,∠B=∠C.点E、F、G分别在边AB、BC、CD上,AE=GF =GC.(1)求证:四边形AEFG是平行四边形;(2)当∠FGC与∠EFB满足怎样的关系时,四边形AEFG是矩形.请说明理由.2.(2021秋•崂山区期末)如图,在▱ABCD中,AC⊥CD.(1)延长DC到E,使CE=CD,连接BE,求证:四边形ABEC是矩形;(2)若点F,G分别是BC,AD的中点,连接AFCG,试判断四边形AFCG是什么特殊的四边形?并证明你的结论.3.(2021秋•渝中区校级期末)如图,平行四边形ABCD的对角线AC,BD相交于O点,DE⊥AC于E点,BF⊥AC于F.(1)求证:四边形DEBF为平行四边形;(2)若AB=20,AD=13,AC=21,求△DOE的面积.4.(2021秋•沙坪坝区校级期末)如图,在▱ABCD中,E、F分别为AB、CD边上两点,FB平分∠EFC.(1)如图1,若AE=2,EF=5,求CD的长;(2)如图2,∠BCD=45°,BC⊥BD,若G为EF上一点,且∠GBF=∠EFD,求证:FG+2FD=AB.5.(2021秋•莱芜区期末)点E是▱ABCD的边CD上的一点,连接EA并延长,使EA=AM,连接EB并延长,使EB=BN,连接MN,F为MN的中点,连接CF,DM.(1)求证:四边形DMFC是平行四边形;(2)连接EF,交AB于点O,若OF=2,求EF的长.6.(2021秋•市南区期末)已知:在平行四边形ABCD中,分别延长BA,DC到点E,H,使得BE=2AB,DH=2CD.连接EH,分别交AD,BC于点F,G.(1)求证:AF=CG;(2)连接BD交EH于点O,若EH⊥BD,则当线段AB与线段AD满足什么数量关系时,四边形BEDH是正方形?7.(2021秋•砚山县期末)如图,四边形ABCD是菱形,点H为对角线AC的中点,点E在AB的延长线上,CE ⊥AB,垂足为E,点F在AD的延长线上,CF⊥AD,垂足为F,∠ECA=60°.(1)求证:四边形CEHF是菱形;(2)已知四边形CEHF的周长为16cm,求菱形ABCD的面积.8.(2021秋•寿光市期末)如图,点E是平行四边形ABCD对角线AC上一点,点F在BE延长线上,且EF=BE,EF与CD交于点G.(I)求证:DF∥AC;(2)连接DE、CF,若2AB=BF,G恰好是CD的中点,求证:四边形CFDE是矩形.9.(2021秋•成都期末)如图,在四边形ABCD中AD∥CB,O为对角线AC的中点,过点O作直线分别与四边形ABCD的边AD,BC交于M,N两点,连接CM,AN.(1)求证;四边形ANCM为平行四边形;(2)当MN平分∠AMC时,①求证;四边形ANCM为菱形;②当四边形ABCD是矩形时,若AD=8,AC=4√5,求DM的长.10.(2021秋•南岗区期末)已知:在▱ABCD中,对角线AC与BD交于点O,过点O作EF⊥BD,分别交AB,DC于点E,F,连接BF,DE.(1)如图1,求证:四边形DEBF是菱形;(2)如图2,AD∥EF,且AD=AE,在不添加任何辅助线的条件下,请直接写出图2中四个度数为30°的角.11.(2021秋•和平县期末)如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.(1)求证:CF=AE;(2)当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.12.(2021秋•太平区期末)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为F,交直线MN于E,连接CD,BE.(1)求证:CE=AD;(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)在满足(2)的条件下,当△ABC满足什么条件时,四边形BECD是正方形?(不必说明理由)13.(2021秋•法库县期末)如图,在四边形ABCD中,AC、BD相交于点O,AD∥BC,∠ADC=∠ABC,OA=OB.(1)如图1,求证:四边形ABCD为矩形;(2)如图2,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,若AD=12,AB=5,求PE+PF 的值.14.(2021秋•兰州期末)如图,在正方形ABCD中,点E、F分别为边BC、CD上两点,∠EAF=45°,过点A 作∠GAB=∠F AD,且点G为边CB延长线上一点.①△GAB≌△F AD吗?说明理由.②若线段DF=4,BE=8,求线段EF的长度.③若DF=4,CF=8.求线段EF的长度.15.(2020秋•安丘市期末)如图,在平行四边形ABCD中,对角线AC与BD交于点O,点M,N分别为OA、OC 的中点,延长BM至点E,使EM=BM,连接DE.(1)求证:△AMB≌△CND;(2)若BD=2AB,且AM=3,DN=4,求四边形DEMN的面积.16.(2020秋•市南区期末)已知:如图,在平行四边形ABCD中,E、F分别为AB、CD的中点,G、H分别为DE、BF的中点.(1)试判断四边形EHFG的形状,并证明;(2)若∠ABC=90°,试判断四边形EHFG的形状并加以证明.17.(2020秋•沈北新区校级期末)如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=12AC,连接AE、CE.(1)求证:四边形OCED为矩形;(2)若菱形ABCD的边长为8,∠BCD=60°,则AE=.18.(2021春•冠县期末)如图,在△ABC中,O是AC边上一点,过点O作BC的平行线,交∠BCA的平分线于点E,交外角∠ACD的平分线于点F.(1)求证:EO=OF;(2)连接AE,AF,当点O沿AC移动时,四边形AECF是否能成为一个矩形?此时,点O在什么位置?说明理由19.(2021•长兴县模拟)如图,在▱ABCD中,对角线AC,BD相交于点O,BD=2AD,点E在线段OC上,且OE=CE.(1)求证:∠OBE=12∠ADO;(2)若F,G分别是OD,AB的中点,且BC=10,①求证:△EFG是等腰三角形;②当EF⊥EG时,求▱ABCD 的面积.20.(2021春•富平县期末)在▱ABCD中,点O是对角线BD的中点,点E在边BC上,EO的延长线与边AD交于点F,连接BF、DE如图1.(1)求证:四边形BEDF是平行四边形;(2)若DE=DC,∠CBD=45°,过点C作DE的垂线,与DE、BD、BF分别交于点G、H、P如图2.①当CD=6.CE=4时,求BE的长;②求证:CD=CH.21.(2021春•临沧期末)如图,菱形ABCD的对角线AC、BD相交于点O,过点B作BE∥AC,且BE=12AC,连接EC.(1)求证:四边形BECO是矩形;(2)连接ED交AC于点F,连接BF,若AC=6,AB=5,求BF的长.22.(2021春•淮阳区校级期末)如图,在平行四边形ABCD中,M,N是对角线BD上的点,且BM=DN,DE平分∠ADB交AB于点E,BF平分∠DBC交CD于点F.(1)求证:四边形EMFN是平行四边形;(2)当四边形EMFN是菱形时,求证:四边形BEDF是菱形.23.(2021春•肥东县期末)如图1,在平行四边形ABCD中,AB=8,AD=14,∠BAD的平分线交BC于点E交DC的延长线于F,以EC,CF为邻边作▱ECFG.(1)求EC的长;24.(2021春•大连期末)如图,四边形ABCD和CEFG都是正方形,点E在BC的延长线上,且CE<BC,连接BG并延长交DE于H.(1)写出BH与DE的位置关系,并证明;(2)求证:∠BHC=45°.25.(2021春•法库县期末)如图,平行四边形ABCD中,CG⊥AB于点G,∠ABF=45°,点F在CD上,BF交CG于点E,连接AE,AE⊥AD.(1)若BG=1,BC=√5,求EF的长度;(2)求证:△BCG≌△EAG;(3)直接写出三条线段CD,CE,BE之间的数量关系.26.(2021春•迁安市期末)已知:如图,在▱ABCD中,对角线AC、BD相交于点O,点G、H分别是AD、BC 的中点,点E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.(1)求证:四边形GEHF是平行四边形;(2)若四边形GEHF是菱形.①线段AB和BD有何位置关系?请说明理由.②若AB=2,BD=2AB时,求四边形GEHF的面积.27.(2021春•上城区校级期末)如图,在△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交△ABC的外角∠ACD的平分线于点F.(1)探究线段OE与OF的数量关系并说明理由.(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?请说明理由.(3)当点O在边AC上运动时,四边形BCFE是菱形(填“可能”或“不可能”).请说明理由.28.(2021春•酒泉期末)(1)如图1,正方形ABCD中,E、F分别是BC、CD边上的点,且满足BE=CF,连接AE、BF交于点H.请直接写出线段AE与BF的数量关系和位置关系.(2)如图2,在正方形ABCD中,E、F分别是BC、CD边上的点,连接BF,过点E作EG⊥BF于点H,交AD 于点G,试判断线段BF与GE的数量关系,并证明你的结论.29.(2021春•鞍山期末)如图,在正方形ABCD中,边长为3.点M,N是边AB,BC上两点,且BM=CN=1,连接CM,DN;(1)则DN与CM的数量关系是,位置关系是.(2)若点E,F分别是DN与CM的中点,计算EF的长;(3)延长CM至P,连接BP,若∠BPC=45°,试求PM的长.30.(2021春•修水县期末)如图,在▱ABCD中,对角线AC,BD相交于点O,OA=5cm,E,F为直线BD上的两个动点(点E,F始终在▱ABCD的外面),连接AE,CE,CF,AF.(1)若DE=12OD,BF=12OB,①求证:四边形AFCE为平行四边形;②若CA平分∠BCD,∠AEC=60°,求四边形AFCE的周长.(2)若DE=13OD,BF=13OB,四边形AFCE还是平行四边形吗?请写出结论并说明理由.若DE=1n OD,BF=1n OB呢?请直接写出结论.。
特殊平行四边形的性质与判定-专题练习

特殊平行四边形的性质与判定专题练习1. 如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点(且点P不与点B,C 重合),PE⊥AB于点E,PF⊥AC于点F,则EF的最小值为______.2.如图,在矩形ABCD中,AB=8,BC=4,点E在AB上,点F在CD上,点G,H在对角线AC上,若四边形EGFH是菱形,则AE的长是()A.2 5 B.3 5 C.5 D.63.如图,在矩形ABCD中,点E,F分别在边CD,BC上,且DC=3DE=3a.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP=________.4. 如图,在▱ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.(1)求证:四边形BFDE是矩形;(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.45 如图,平行四边形ABCD的两条对角线相交于点O,E是BO的中点,过点B作AC的平行线,交CE的延长线于点F,连接AF.(1)求证:FB=AO;(2)当平行四边形ABCD满足什么条件时,四边形AFBO是菱形?证明你的结论.6. 把一个长方形的纸片按如图所示折两次,然后剪下一部分,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为()A.15°或30° B.30°或45° C.45°或60° D.30°或60°7.如图,两张等宽的纸带交叉重叠地放在一起,重合部分的四边形ABCD是______,若AD=6,∠ABC=60°,则四边形ABCD的面积为_______.8.如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE ⊥AB于点E,OF⊥AD于点F.(1)对角线AC的长是____,菱形ABCD的面积是____;(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否会发生变化?请说明理由;(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否会发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系,并说明理由.9. 如图,P是矩形ABCD内一点,AP⊥BP于点P,CE⊥BP于点E,BP=EC.(1)请判断四边形ABCD是否是正方形?若是,写出证明过程;若不是,说明理由;(2)延长EC到点F,使CF=BE,连接PF交BC的延长线于点G,求∠BGP的度数.10.如图,在正方形ABCD中,E,F分别是边CD,AD上的点,且CE=DF.AE与BF相交于点O,则下列结论错误的是()A.AE=BF B.AE⊥BF C.AO=OE D.S△AOB=S四边形DEOF11.如图①,在正方形ABCD中,P是BD上的一点,点E在AD延长线上,且PA=PE,PE交CD于点F.(1)求证:PC=PE;(2)求∠CPE的度数;(3)如图②,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.。
初中数学特殊平行四边形的性质与判定基础题(含答案)

初中数学特殊平行四边形的性质与判定基础题一、单选题(共12道,每道8分)1.菱形具有而一般平行四边形不具有的性质是()A.两组对边分别平行B.两组对边分别相等C.一组邻边相等D.对角线相互平分答案:C试题难度:三颗星知识点:菱形的性质2.菱形的两对角线的长分别为12、16,那么菱形的面积是()A.192B.96C.48D.24答案:B试题难度:三颗星知识点:菱形的面积3.已知菱形周长是24,一个内角为60°,则菱形的面积为()A.6B.18C. D.答案:C试题难度:三颗星知识点:菱形的性质4.下列命题正确的是(__)A.邻角相等的四边形是菱形B.有一组邻边相等的四边形是菱形C.对角线互相垂直的四边形是菱形D.对角线互相垂直平分的四边形是菱形答案:D试题难度:三颗星知识点:菱形的判定5.平行四边形ABCD的对角线AC,BD相交于点O,且AB=5,AO=4,BO=3,则四边形ABCD 是()A.菱形B.矩形C.正方形D.梯形答案:A试题难度:三颗星知识点:菱形的判定6.矩形具有而平行四边形不具有的性质()A.两组对角分别相等B.对角线相等C.对角线互相平分D.两组对边分别相等答案:B试题难度:三颗星知识点:矩形的性质7.下列说法中不能判定四边形是矩形的是(__)A.四个角都相等的四边形B.有一个角为90°的平行四边形C.对角线相等的平行四边形D.对角线互相平分的四边形答案:D试题难度:三颗星知识点:矩形的判定8.如图,四边形ABCD是矩形,且∠AOB=60°,AB=4,则BD的长为()A.4B.6C.8D.10答案:C试题难度:三颗星知识点:矩形的计算9.正方形ABCD的两条对角线AC,BD相交于点O,则图中共有()个等腰直角三角形A.6B.8C.10D.4答案:B试题难度:三颗星知识点:正方形性质10.能判定四边形是正方形的是()A.对角线互相垂直且相等的四边形B.对角线互相垂直的平行四边形C.对角线相等的菱形D.对角线互相垂直平分的四边形答案:C试题难度:三颗星知识点:正方形判定11.将4个边长都为1cm的正方形按如图所示摆放,点A1,A2,…,A4分别是正方形的中心,则这4个正方形重叠形成的重叠部分的面积和为(__)cm2.A.2B.1C.4D.答案:B试题难度:三颗星知识点:正方形的性质与计算112.已知如图,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F,求证:四边形AEDF是菱形.证明:如图,∵DE∥AC交AB于E,DF∥AB交AC于F∴_______________________________∵AD是△ABC的角平分线∴∠1=∠2∵______________________________∴∠1=∠3∴___________________________∴AF=DF∴__________________________下列选项填入以上空格,正确的是()①四边形AEDF是菱形;②∠2=∠3;③四边形AEDF为平行四边形;④DF∥AB.A.③④①②B.③①②④C.③①④②D.③④②①答案:D试题难度:三颗星知识点:特殊平行四边形的证明题规范书写。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P
M
N
A
B
C
D
R
特殊四边形的性质与判定练习题
1. 若矩形的一条角平分线分一边为3cm 和5cm 两部分,则矩形的周长为 ( ) A .22 B .26
C .22或26
D .28
2.已知一矩形的周长是24cm ,相邻两边之比是1:2,那么这个矩形的面积是 ( ) A .24cm 2
B .32cm 2
C .48cm 2
D .128cm 2
3.由矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为1:3两部分,则该垂线与另一条对
角线的夹角为( )
A 、22.5°
B 、45°
C 、30°
D 、60°
4.如图,在矩形ABCD 中,DE ⊥AC,∠ADE= ∠CDE,那么∠BDC 等于( )
A .60°
B .45°
C .30°
D .22.5°
5.如图,过矩形ABCD 的对角线BD 上一点R 分别作矩形两边的平行线MN 与PQ ,那么图中矩形AMRP
的面积S 1,与矩形QCNR 的面积S 2的大小关系是 ( ) A. S 1> S 2 B. S 1= S 2 C. S 1< S 2 D. 不能确定
6.平行四边形的一边长是10cm ,那么这个平行四边形的两条对角线的长可以是() A.4cm 和6cm B.6cm 和8cm C.8cm 和10cm D.10cm 和12cm
7.在四边形ABCD 中,O 是对角线的交点,能判定这个四边形是正方形的条件是( ) A.AC =BD ,AB =CD ,AB ∥CD B.AD //BC ,∠A =∠C
C.AO =BO =CO =DO ,AC ⊥BD
D.AO =CO ,BO =DO ,AB =BC
8.下列命题中,真命题是( )
A 、有两边相等的平行四边形是菱形
B 、对角线垂直的四边形是菱形
C 、四个角相等的菱形是正方形
D 、两条对角线相等的四边形是矩形 9.平行四边形各角平分线若围成一个四边形,则这个四边形一定是( ) A 、矩形 B 、平行四边形 C 、菱形 D 、正方形
10.任意四边形四边中点所得的四边形一定是()
A、平行四边形
B、矩形
C、菱形
D、正方形
11.已知菱形两条对角线的长分别为5cm和8cm,则这个菱形的面积是______cm.
12.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是( )
A.AC=BD,AB=CD,AB∥CD
B.AD//BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
13、矩形ABCD的两条对角线相交于O,∠AOB=60o,AB=8,则矩形对角线的长___
14、矩形的两条对角线的夹角为60°,若一条对角线与短边的和为15,则短边的长是,对角线的长是。
15.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,
设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F。
①EO与FO有何等量关系
②当O点运动到何处时,四边形AECF是什么四边形
16.下面性质中菱形有而矩形没有的是()
(A)邻角互补(B)角和为360°(C)对角线相等(D)对角线互相垂直
17.菱形ABCD中,∠BAD=60°,BD=4,则菱形ABCD的周长是_______.
18.知菱形两条对角线的长分别为5cm和8cm,则这个菱形的面积是______cm.
19.知四边形ABCD是平行四边形,下列结论不正确的是()
A. 当AB=BC时,它是菱形;
B. 当AC⊥BD时,它是菱形;
C. 当∠ABC=90°时,它是矩形;
D. 当AC=BD时,它是菱形
20.圆规作一个菱形,如图,能得到四边形ABCD是菱形的依据是()
A、一组临边相等的四边形是菱形
B、每条对角线平分一组对角的平行四边形是菱形
C、对角线互相垂直的平行四边形是菱形
D、四边相等的四边形是菱形
21.顺次连结一个四边形的四边中点所组成的四边形是矩形,则原四边形一定是()A.一般平行四边形 B.对角线互相垂直的四边形 C.对角线相等的四边形 D.矩形
22、如图,矩形ABCD 的对角线相交于点O ,DE ∥CA ,AE ∥BD . (1)则四边形AODE 是什么四边形?__________________
(2)若将题设中“矩形ABCD ”这一条件改为“菱形ABCD ”,其余条件不变, 则四边形AODE 又是什么四边形?__________________ 23.列条件中,能判断一个四边形是矩形的有( )个
A. 一组对边平行且相等,有一个角是直角 B 对角线互相平分且相等
C. 对角线互相垂直且相等 D对边平行,另一组对边相等.且两条对角线相等 24.下列条件中,不能判定四边形ABCD 为矩形的是( ). A .AB ∥CD ,AB=CD ,AC=BD B .∠A=∠B=∠D=90° C .AB=BC ,AD=CD ,且∠C=90° D .AB=CD ,AD=BC ,∠A=90° 25.如图,四边形ABCD 是由两个全等的正三角形ABD 和BCD 组成的, M 、N•分别为BC 、AD 的中点.则边形BMDN 是什么四边形 26.如图,在梯形ABCD 中,AD BC AB DE AF DC E F ∥,∥,∥,、 两点在边BC 上,且四边形AEFD 是平行四边形.则 (1)AD 与BC 有何等量关系
(2)当AB DC 时,□AEFD 是什么四边形 27.在矩形ABCD 中,E 是BC 的中点,且EA ⊥ED .•若矩形ABCD•的 周长为48cm ,•则矩形ABCD 的面积为_______cm 2
.
28、矩形一个角的平分线分矩形一边成2cm 和3cm ,则这个矩形的面积为 。
29.在矩形ABCD 中,AE 平分∠BAD ,∠1=15°. (1)求∠2的度数.(2)求证:BO =BE
A D
C
E B
N
M D C
B
A
30.已知:AB=AC,AE=AF,且∠EAB=∠FAC,EF=BC.求证:四边形EBCF是矩形.
31.在平行四边形ABCD中,AE平分∠BAD,与BC相交于点E,EF//AB,与AD相交于点F.
求证:四边形ABEF是菱形.
32.平行四边形ABCD中,∠DAB=60°,AB=2AD,点 E、F分别是CD的中点,过点A作AG∥BD,交CB的延长线于点G.
(1)求证:四边形DEBF是菱形;(2)请判断四边形AGBD是什么特殊四边形?并加以证明.F
E
B
A
33、在△ABC 中,∠ACB=90°,BC 的垂直平分线DE 交BC 于D ,交AB 于E ,F 在DE 上,且AF=CE=AE . (1)说明四边形ACEF 是平行四边形;
(2)当∠B 满足什么条件时,四边形ACEF 是菱形,并说明理由.
34.已知:在▱ABCD 中,O 为对角线BD 的中点,过点O 的直线EF 分别交AD ,BC 于E ,F 两点,连结BE ,
DF .
(1)求证:△DOE ≌△BOF .
(2)当∠DOE 等于多少度时,四边形BFED 为菱形?请说明理由.
35.在△ABC 和△DCB 中,AB = DC ,AC = DB ,AC 与DB 交于点M . (1)求证:△ABC ≌△DCB ;
(2)过点C 作CN ∥BD ,过点B 作BN ∥AC ,CN 与BN 交于点N ,试判断线段
BN 与CN 的数量关系,并证明你的结论.
B C
A D
M
N。
