特殊平行四边形的性质和判定总结
平行四边形性质总结

平行四边形性质总结平行四边形是高中数学中一个重要的几何概念,它具有一系列特殊的性质。
本文将对平行四边形的性质进行总结,并展示其在几何证明和问题求解中的应用。
一、平行四边形的定义和特征平行四边形是指有四个边两两平行的四边形。
其特征包括:1. 两对对边分别相等(对边)。
2. 两对对角线互相平分(对角线)。
3. 对角线互相等长(对角线)。
4. 具有相对的顶点角和内角互补(角)。
二、平行四边形的性质和定理1. 对边性质:平行四边形的两对对边相等。
证明方法:利用平行线之间的性质,应用等腰三角形的性质进行证明。
2. 对角线性质:平行四边形的两对对角线互相平分且等长。
证明方法:利用平行线之间的性质,应用垂直线的性质进行证明。
3. 顶点角性质:平行四边形的相对的顶点角互补。
证明方法:利用平行线之间的性质,应用同位角的性质进行证明。
4. 内角性质:平行四边形的内角以及相对的补角相等。
证明方法:利用平行线之间的性质,应用同位角和内错角的性质进行证明。
5. 边性质:平行四边形的对边平行且相等。
证明方法:利用平行线之间的性质进行证明。
三、平行四边形的证明方法和例题1. 判断平行四边形:通过观察边的性质,判断是否为平行四边形。
如果边平行并且长度相等,则可判断为平行四边形。
2. 证明平行四边形:根据给定条件,利用平行线的性质和等腰三角形的性质进行推导和证明。
例题1:已知ABCD为平行四边形,证明对角线AC和BD相等。
证明:首先,根据平行四边形的性质,可以得出AB∥CD且AB=CD,以及AD∥BC且AD=BC。
然后,根据平行四边形的对角线性质,可以得出对角线AC和BD 互相平分且相等。
因此,根据等分线的性质,AC=BD。
例题2:已知ABCD为平行四边形,证明∠A=∠C。
证明:首先,根据平行四边形的性质,可以得出AB∥CD且AD∥BC。
然后,根据平行线的性质,∠A和∠C是同位角,同位角相等。
因此,∠A=∠C。
四、平行四边形的应用1. 几何证明:平行四边形常用于几何定理的证明过程中,通过利用平行四边形的特性和性质,简化证明过程,提高证明的效率。
平行四边形的性质与判定

平行四边形的性质与判定平行四边形是几何学中常见的一个概念,具有一些特殊的性质和判定条件。
本文将介绍平行四边形的性质,并通过实例展示如何判定一组线段或角度是否构成平行四边形。
一、平行四边形的定义平行四边形是指具有两对对边分别平行的四边形。
根据定义,我们可以得出平行四边形的性质和判定条件。
二、平行四边形的性质1. 相对边相等:平行四边形的对边长度相等。
即AB=CD,AD=BC。
2. 相对角相等:平行四边形的对角角度相等。
即∠A=∠C,∠B=∠D。
3. 对角线互相平分:平行四边形的对角线互相平分。
即AC平分BD,BD平分AC。
4. 对角线相等:平行四边形的对角线相等。
即AC=BD。
5. 内角和为360度:平行四边形的内角和等于360度。
三、判定平行四边形的条件要判定一组线段或角度构成平行四边形,需要满足以下条件之一。
1. 对边相等:如果四边形的对边长度相等,即AB=CD,AD=BC,则这个四边形是平行四边形。
2. 对角线互相平分:如果四边形的对角线互相平分,即AC平分BD,BD平分AC,则这个四边形是平行四边形。
3. 相对角相等:如果四边形的相对角度相等,即∠A=∠C,∠B=∠D,则这个四边形是平行四边形。
在实际问题中,我们可以通过测量边长、角度或线段平分关系来判定是否为平行四边形。
下面举例说明。
例题一:已知线段AB与线段CD互相平分,且∠A=∠C,∠B=∠D,判断ABCD是否为平行四边形。
解析:根据给定条件得知,线段AB与线段CD互相平分,且相对角度相等。
根据判定平行四边形的条件,我们可以得出这个四边形是平行四边形。
例题二:在平面直角坐标系中,顶点坐标分别为A(2, 3),B(7, 3),C(9, -2),D(4, -2)的四边形ABCD,判断是否为平行四边形。
解析:根据给定坐标可以计算出AB的斜率为0,CD的斜率也为0。
根据斜率的性质,我们可以得出AB与CD是平行的。
另外,根据对边长度可以计算出AB=CD,AD=BC。
平行四边形的特征与性质

平行四边形的特征与性质平行四边形是一种特殊的四边形,具有一些独特的特征和性质。
了解这些特征和性质有助于我们更好地理解和应用平行四边形的知识。
本文将介绍平行四边形的定义、特征以及与其他几何形状的关系。
一、平行四边形的定义平行四边形是指具有两对对边分别平行的四边形。
这意味着平行四边形的相邻边线是平行的,而且对角线之间也是平行的。
二、平行四边形的特征与性质1. 对边性质:平行四边形的对边长度相等。
这意味着它的两对对边分别相等。
2. 对角线性质:平行四边形的对角线互相平分。
也就是说,平行四边形的对角线相交于一点,并且把对角线分成相等的两段。
3. 内角性质:平行四边形的内角之和是180度。
由于相邻边是平行的,所以对应的内角互补,即相加等于180度。
4. 外角性质:平行四边形的外角等于其不相邻的内角。
也就是说,平行四边形的外角是其相邻内角的补角。
5. 高度性质:平行四边形的任意一条边都可以看做是它的底边,并且这条底边上的高度是固定的。
三、平行四边形与其他几何形状的关系1. 矩形:矩形是一种特殊的平行四边形,它的所有内角都是直角(90度)。
也就是说,矩形具备平行四边形的所有性质,并且还具有所有角度相等的特征。
2. 菱形:菱形是一种特殊的平行四边形,它的所有边长都相等。
虽然菱形的对边平行,但不一定是直角。
因此,菱形在某些性质上与矩形和普通平行四边形有所不同。
3. 正方形:正方形是一种特殊的矩形和菱形,它既具有所有内角都是直角的特点,也具有所有边长相等的特点。
因此,正方形不仅是一个平行四边形,同时也是一个矩形和菱形。
总结:平行四边形具有对边相等、对角线互相平分、内角之和为180度等特征与性质。
通过了解这些特征和性质,我们可以更好地理解和应用平行四边形的知识。
此外,平行四边形还与矩形、菱形和正方形等几何形状存在一定的关联。
通过比较和分析这些形状之间的关系,我们可以更全面地认识几何学中不同形状的特征和性质。
让我们深入学习平行四边形的特征与性质,为我们的几何学知识打下坚实的基础。
平行四边形的定义及特殊四边形的性质及判定

平行四边形之马矢奏春创作二、平行四边形1.平行四边形界说:两组对边分别平行的四边形是平行四边形.2.平行四边形的判定定理:(1)判定界说:两组对边分别平行的四边形是平行四边形.(2)判定定理1:一组对边平行且相等的四边形是平行四边形.(3)判定定理2:两组对边分别相等的四边形是平行四边形.(4)判定定理3:两组对角分别相等的四边形是平行四边形.(5)判定定理4:对角线互相平分的四边形是平行四边形.3.平行四边形的性质:(6)平行四边形的邻角互补, 对角相等.(7)平行四边形的对边平行且相等.(8)夹在两条平行线间的平行线段相等.(9)平行四边形的对角线互相平分.(10)平行四边形是中心对称图形.4.平行四边形的面积:面积=底边长×高= ah(a是平行四边形任何一边长, h必需是a边与其对边的距离.)三、矩形1.矩形的界说:有一个角是直角的平行四边形是是矩形.2.矩形的判定定理:(1)判定界说:有一个角是直角的平行四边形是是矩形.(2)判定定理1:有三个角是直角的四边形是矩形.(3)判定定理2:对角线相等的平行四边形是矩形.3.矩形的性质:(1)具有平行四边形的一切性质.(2)矩形的四个角都是直角.(3)矩形的对角线相等.(4)矩形既是轴对称图形又是中心对称图形.4.矩形的面积:矩形的面积=长×宽四、菱形1.菱形的界说:有一组邻边相等的平行四边形是菱形.2.菱形的判定定理:(1)判定界说:有一组邻边相等的平行四边形是菱形.(2)判定定理(1):四边都相等的四边形是菱形.(3)判定定理(2):对角线互相垂直的平行四边形是菱形. 3.菱形的性质:(1)具有平行四边形的一切性质.(2)菱形的四条边都相等.(3)菱形的对角线互相垂直, 而且每一条对角线平分一组对角.(4)菱形既是轴对称图形又是中心对称图形.4.菱形的面积:菱形的面积=底×高=对角线乘积的一半五、正方形1.正方形的界说:四边都相等且有一个角是直角的四边形是正方形.2.正方形的判定定理:(1)判定界说:四边都相等且有一个角是直角的四边形是正方形.(2)有一组邻边相等而且由一个角是直角的平行四边形是正方形.(3)有一组邻边相等的矩形是正方形.(4)有一个角是直角的菱形是正方形.(5)既是矩形又是菱形的四边形是正方形.3.正方形的性质:(1)正方形具有平行四边形、矩形、菱形的一切性质.(2)边——四边相等, 邻边垂直, 对边平行且相等.(3)角——四个角都是直角.(4)对角线——相等, 互相垂直平分, 每一条对角线平分一组对角.(5)正方形既是轴对称图形又是中心对称图形.(6)正方形一条对角线上一点到另一条对角线上的两端距离相等.(7)正方形既是轴对称图形又是中心对称图形.4.正方形的面积:正方形的面积=边长的平方=两条对角线乘积的一半六、平行四边形、矩形、菱形和正方形的边、角、对角线之间的关系:。
平行四边形及特殊的平行四边形的性质和判定

平行四边形及特殊的平行四边形一、性质:1.平行四边形的对角;邻角;对边;对角线;是中心对称图形。
2.矩形的四个角为;对边;对角线;是中心对称图形,也是轴对称图形,对称轴有条。
3.菱形的对角;邻角;四条边都;对角线;是中心对称图形,也是轴对称图形,对称轴有条。
4.正方形的四个角为;四条边都;对角线;是中心对称图形,也是轴对称图形,对称轴有条。
二、判定:1.平行四边形的判定:(1)叫做平行四边形。
(定义)(2)的四边形是平行四边形。
(3)的四边形是平行四边形。
(4)的四边形是平行四边形。
2.矩形的判定:(1)的平行四边形叫做矩形。
(定义)(2)的四边形是矩形。
(3)的平行四边形是矩形。
3.菱形的判定:(1)的平行四边形叫做菱形。
(定义)(2)的四边形是菱形。
(3)的平行四边形是菱形。
4.正方形的判定:(1)的平行四边形叫做正方形。
(定义)(2)的矩形是正方形。
(3)的菱形是正方形。
三、其它:1.n边形的内角和为(n≥3),外角和为。
2.平行线的性质定理:夹在两条平行线间的相等。
推论:夹在两条平行线间的相等。
3.对称中心平分连结两个的线段。
4.连结三角形两边中点的线段叫做。
5.中位线定理:三角形的中位线平行于,并且等于第三边的。
6.平行线的传递性:在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也互相。
7.在证明一个命题时,人们有时先假设命题,从这样的假设出发,经过推理得出和已知条件矛盾,或者与、基本事实、等矛盾,从而得出假设命题不成立是错误的,即所求证的命题正确。
这种证明方法叫做。
1。
平行四边形的定义及特殊四边形的性质及判定

平行四边形的定义及特殊四边形的性质及判定在我们的数学世界中,四边形家族有着各种各样的成员,其中平行四边形是非常重要的一类。
接下来,让我们一起深入了解平行四边形的定义,以及几种特殊四边形的性质和判定方法。
首先,平行四边形的定义很简单:两组对边分别平行的四边形叫做平行四边形。
这就像是给平行四边形打上了一个独特的标签,让我们能够轻易地识别它。
那平行四边形都有哪些性质呢?其一,平行四边形的两组对边分别相等。
想象一下,平行四边形的左右两条边和上下两条边就像是双胞胎,长度是一样的。
其二,平行四边形的两组对角分别相等。
也就是说,相对的两个角大小是相同的。
其三,平行四边形的对角线互相平分。
这就好像两条对角线在平行四边形的内部进行了一场平分的游戏。
其四,平行四边形是中心对称图形,对称中心是两条对角线的交点。
把平行四边形绕着这个交点旋转180 度,它能和原来的图形完全重合。
了解了平行四边形的性质,那怎么判定一个四边形是不是平行四边形呢?方法一,如果两组对边分别相等,那么这个四边形就是平行四边形。
就好像我们通过比较四边形的四条边,发现两两相等,那就可以确定它是平行四边形啦。
方法二,如果两组对边分别平行,那也能判定是平行四边形。
这是从定义出发的判定方法,边的平行关系直接决定了四边形的类型。
方法三,一组对边平行且相等的四边形是平行四边形。
想象一下,有一组边既平行又长度相等,那这个四边形自然就具备了平行四边形的特征。
方法四,两组对角分别相等的四边形是平行四边形。
从角的角度来判断,只要相对的角大小一样,那它就是平行四边形。
方法五,对角线互相平分的四边形是平行四边形。
当两条对角线友好地把对方平分时,这个四边形也就成了平行四边形。
在平行四边形这个大家庭中,还有一些特殊的成员,比如矩形、菱形和正方形。
矩形,也叫长方形,它不仅具有平行四边形的所有性质,还有自己独特的地方。
矩形的四个角都是直角。
那怎么判定一个平行四边形是矩形呢?首先,如果一个平行四边形有一个角是直角,那么它就是矩形。
特殊平行四边形性质与判定归纳
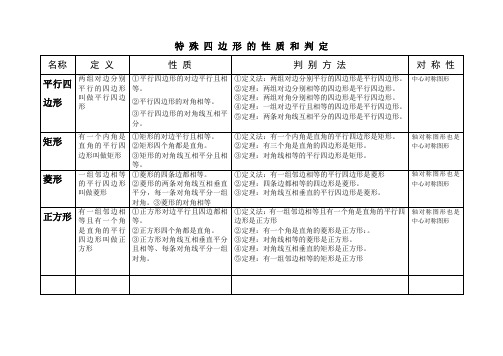
特殊四边形的性质和判定
名称定义性质判别方法对称性
直角三角形有一个角是直角
的三角形是直角
三角形
①两个锐角互余
②勾股定理:如果直角三角形的两
直角边为a、b,斜边为c。
那么
2
2
2c
b
a=
+
③直角三角形中,30°的角所对的
直角边是斜边的一半,反之也成立
④直角三角形斜边的中线等于斜边
的一半
①有一个角是直角的三角形是直角三角形
②两个内角互余的三角形是直角三角形
③勾股定理逆定理:如果三角形的三边长a、b、c满足
2
2
2c
b
a=
+,那么这个三角形是直角三角形
④一边中线是这边一半的三角形是直角三角形
特殊四边形的关系。
小学五年级数学重要知识总结平行四边形的性质与判断

小学五年级数学重要知识总结平行四边形的性质与判断小学五年级数学重要知识总结:平行四边形的性质与判断在小学五年级的数学学习中,平行四边形是一个非常重要的概念。
本文将以此为重点,总结平行四边形的性质与判断方法。
一、平行四边形的定义平行四边形是一个特殊的四边形,它的对边是平行的。
我们知道,平行的线段具有相同的斜率,因此平行四边形的对边斜率相等。
二、平行四边形的性质1. 对边性质:平行四边形的对边相等。
即如果ABCD是一个平行四边形,那么AB与CD的长度相等,AD与BC的长度也相等。
2. 同位角性质:平行四边形的同位角相等。
同位角是指位于平行四边形相邻的两边之间且在同一侧的角。
3. 内角性质:平行四边形的内角和为180度。
即平行四边形的任意两个内角之和等于180度。
4. 对角性质:平行四边形的对角线相等且平分。
即平行四边形的对角线AC和BD相等且平分,即点O为AC和BD的交点,AO=OC=BO=OD。
三、根据性质判断平行四边形1. 判断对边是否相等:如果已知一个四边形的对边相等,那么可以判断它是平行四边形。
2. 判断同位角是否相等:如果已知一个四边形的同位角相等,那么可以判断它是平行四边形。
3. 判断内角之和是否为180度:如果已知一个四边形的内角之和为180度,那么可以判断它是平行四边形。
4. 判断对角线是否相等且平分:如果已知一个四边形的对角线相等且平分,那么可以判断它是平行四边形。
通过以上的性质和判断方法,我们可以判断一个四边形是否是平行四边形。
在实际问题中,平行四边形的特性也常常被用到,例如在绘制图形、计算面积等方面。
总结:平行四边形是小学五年级数学学习中的重要知识点。
了解平行四边形的定义、性质以及判断方法,有助于我们更好地理解和运用它们。
通过积极的练习和实践,我们能够在数学学习中轻松应对相关问题,并提高自己的数学素养。
以上就是小学五年级数学重要知识总结的文章内容。
希望对你有所帮助!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行四边形有一组领边相等_菱形
性质:
判定
周长
面积
菱形具有平行四边形的所有性质
边
四条边相等的四边形是菱形
边长×4
对角线积的一半或底×高
菱形的四条边都相等
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角
对角线
对角线互相垂直的平行四边形是菱形
对角线互相垂直且平分的四边形是菱形
3.正方形:
对角线互相垂直的矩形是正方形
对角线相等的菱形是正方形
对角线互相垂直且相等的平行四边形是正方形
对角线互相垂直平分且相等的四边形是正方形
一.平行四边形的性质及判定:
特殊的平行四边形:1.矩形:
平行四边形_有一个角是直角_矩形
性质:
判定
周长
面积
矩形具有平行四边形的所有性质
角
有一个角是直角的平行四边形是矩形
邻边之和的二倍
底×高
矩形的四个角都是直角
有三个角是直角的四边形是矩形
矩形的对角线相等
对角线
对角线相等的平行四边形是矩形
对角线互相平分且相等的四边形是矩形
性质:
判定:
周长
面积
平行四边形的对边平行且相等
边
两组对边分别平行的四边形是平行四边形
邻边之和的二倍
底×高
平行四边形的对角相等
两组对边分别相等
一组对边平行且相等的四边形是平行四边形
平行四边形的邻角互补
角
两组对角分别相等的四边形是平行四边形
对角线
对角线互相平分的四边形是平行四边形
平行四边形有一组邻边相等且有一个角是直角___正方形
性质:
判定:
周长
面积
正方形具有平行四边形、矩形、菱形的所有性质
边
一组邻边相等的矩形是正方形
边长×4
边长的平方或对角线积的一半
四个角都是直角,四条边都相等
角
有一角是直角的菱形是正方形
正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角
对角线
