第十二讲 频谱的线性搬移电路3
合集下载
5[1].1频谱搬移及调幅的基本原理
![5[1].1频谱搬移及调幅的基本原理](https://img.taocdn.com/s3/m/173d7935eefdc8d376ee321d.png)
上,下边频分量的振幅 不超过载波振幅的一半
BW = 2F
13
例5.1
已知调制信号u (t) = Um cos t (V),AM波的振幅峰值
U AM (t ) max=1.9V,振幅谷值 U AM (t ) min =0.6V,比例常数 K a =0.9 (1/V),求已调波载频分量的振幅 U cm,原调制信号的振幅 U m以 及调幅系数 ma .
二,AM调幅电路组成模型 调幅电路组成模型 uc(t) uc(t) u(t) + UQ X AMXY Y uAM(t) 或 u(t) X AMXY Y uAM(t)
+ + – – UQ
uAM ( t ) = AM [U Q + u ( t )]U cm cos ω c t = [ AMU QU cm + AMU cm u ( t )] cos ω c t
15
2.抑制载波的双边带调幅 DSB) 2.抑制载波的双边带调幅(DSB)
1)表达式
uDSB (t ) = kau (t ) × cos ωct
"相乘"实现! 相乘"实现! 单频调制时 ka由调制电路和B (t ) = maU c cos t cos ωc t maU c = [cos(ωc + )t + cos(ωc )t ] 2
20
5.调幅波的功率 5.调幅波的功率 调幅波的
故载波分量功率 边频分量功率: 边频分量功率:
PSSB
1 Pc = T
1 = T
∫
∫
T 0
(U c m c o s ω c t ) 2 d t RL
1 U 2 cm = 2 RL
T
0
[
BW = 2F
13
例5.1
已知调制信号u (t) = Um cos t (V),AM波的振幅峰值
U AM (t ) max=1.9V,振幅谷值 U AM (t ) min =0.6V,比例常数 K a =0.9 (1/V),求已调波载频分量的振幅 U cm,原调制信号的振幅 U m以 及调幅系数 ma .
二,AM调幅电路组成模型 调幅电路组成模型 uc(t) uc(t) u(t) + UQ X AMXY Y uAM(t) 或 u(t) X AMXY Y uAM(t)
+ + – – UQ
uAM ( t ) = AM [U Q + u ( t )]U cm cos ω c t = [ AMU QU cm + AMU cm u ( t )] cos ω c t
15
2.抑制载波的双边带调幅 DSB) 2.抑制载波的双边带调幅(DSB)
1)表达式
uDSB (t ) = kau (t ) × cos ωct
"相乘"实现! 相乘"实现! 单频调制时 ka由调制电路和B (t ) = maU c cos t cos ωc t maU c = [cos(ωc + )t + cos(ωc )t ] 2
20
5.调幅波的功率 5.调幅波的功率 调幅波的
故载波分量功率 边频分量功率: 边频分量功率:
PSSB
1 Pc = T
1 = T
∫
∫
T 0
(U c m c o s ω c t ) 2 d t RL
1 U 2 cm = 2 RL
T
0
[
频谱的线搬移电路
50 200 150 2 1 350 200 150 2 1
电流中所含的频率分量
1,2,31,32,21 2,22 1
不能出现50 kHz和 350 kHz的频率成分
《高频电路原理与分析》第5源自 频谱的线性搬移电路5.1.2 线性时变电路分析法
i f u f EQ u1 u2
1,2 ,3,21,22 ,23,31,32 ,33, 1 2 ,2 3,3 1 21 2 ,21 3,22 3 22 1,23 1,23 2 1 2 3
《高频电路原理与分析》
第5章 频谱的线性搬移电路
例： 若非线性器件的伏安特性幂级数表示i=a0+a1u+a3u3 ,式中 a0、a1、a3是不为零的常数，信号u是频率为150 kHz和 200 kHz的两个正弦波，问电流中能否出现 50 kHz和 350 kHz的频率成分？为什么？
2.滤波器具有选频的功能，即从前级频率产生电路输出的 众多频谱中选出所需的频率，并且滤掉多余的频率成分
3.不同的功能电路对输入输出的频谱要求不同。
《高频电路原理与分析》
第5章 频谱的线性搬移电路
频谱搬移的数学模型 幂级数展开法和线性时变分析法
非线性器件 二极管、三极管、场效应管、集成模拟乘法器
《高频电路原理与分析》
第5章 频谱的线性搬移电路
5.1
5.1.1 非线性函数的级数展开分析法
非线性器件的伏安特性
i f (u) u EQ u1 u2
i
an
用泰勒级a数n 展n开1!
d
n f (u dun
)
a0 a1(u1 u2 ) a2(u1 u2 )2 n
(u u )
n
1n0d n!
电流中所含的频率分量
1,2,31,32,21 2,22 1
不能出现50 kHz和 350 kHz的频率成分
《高频电路原理与分析》第5源自 频谱的线性搬移电路5.1.2 线性时变电路分析法
i f u f EQ u1 u2
1,2 ,3,21,22 ,23,31,32 ,33, 1 2 ,2 3,3 1 21 2 ,21 3,22 3 22 1,23 1,23 2 1 2 3
《高频电路原理与分析》
第5章 频谱的线性搬移电路
例： 若非线性器件的伏安特性幂级数表示i=a0+a1u+a3u3 ,式中 a0、a1、a3是不为零的常数，信号u是频率为150 kHz和 200 kHz的两个正弦波，问电流中能否出现 50 kHz和 350 kHz的频率成分？为什么？
2.滤波器具有选频的功能，即从前级频率产生电路输出的 众多频谱中选出所需的频率，并且滤掉多余的频率成分
3.不同的功能电路对输入输出的频谱要求不同。
《高频电路原理与分析》
第5章 频谱的线性搬移电路
频谱搬移的数学模型 幂级数展开法和线性时变分析法
非线性器件 二极管、三极管、场效应管、集成模拟乘法器
《高频电路原理与分析》
第5章 频谱的线性搬移电路
5.1
5.1.1 非线性函数的级数展开分析法
非线性器件的伏安特性
i f (u) u EQ u1 u2
i
an
用泰勒级a数n 展n开1!
d
n f (u dun
)
a0 a1(u1 u2 ) a2(u1 u2 )2 n
(u u )
n
1n0d n!
调幅、检波与混频—频谱搬移电路
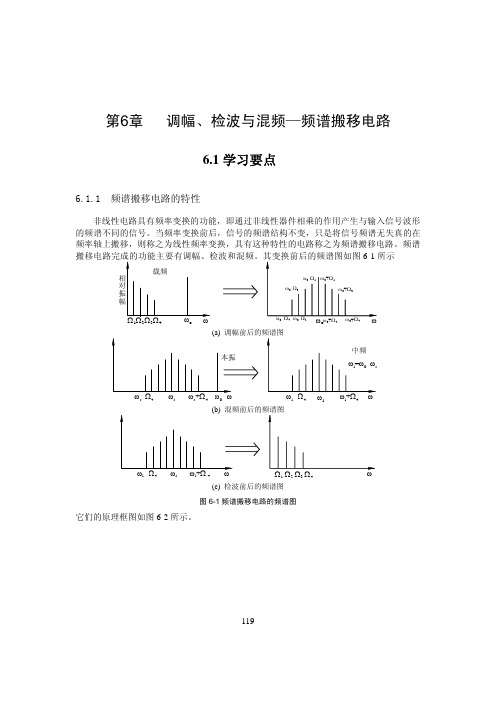
第6章 调幅、检波与混频—频谱搬移电路6.1学习要点6.1.1 频谱搬移电路的特性非线性电路具有频率变换的功能，即通过非线性器件相乘的作用产生与输入信号波形的频谱不同的信号。
当频率变换前后，信号的频谱结构不变，只是将信号频谱无失真的在频率轴上搬移，则称之为线性频率变换，具有这种特性的电路称之为频谱搬移电路。
频谱o 1 23404o 0 4 0202i 4ii 4s4s s 40i 4i i 41234(c) 检波前后的频谱图 图6-1频谱搬移电路的频谱图它们的原理框图如图6-2所示。
119max 00f1m11mfiifS(c) 混频原理图6-2 调幅、检波与混频的原理框图由以上几种频率变换电路的原理框图和频谱图可知，尽管各个电路所要完成的功能完全不同，但是这些频率变换电路之间有很多相似之处：1) 它们的实现框图几乎是相同的，都是利用非线性器件对输入信号频谱实行变换以产生新的有用频率成分后，再用适当中心频率（或截止频率）和适当带宽的滤波器获得所需频率分量并滤除无用频率分量。
2) 从频谱结构看，上述频率变换电路都只是对输入信号频谱实行横向搬移而不改变原来的谱结构，因而都属于所谓的线性频率变换。
3) 频谱的横向平移，从时域角度看相当于输入信号与一个参考正弦信号相乘，而平移的距离由此参考信号的频率决定，因此都可以用乘法电路实现。
6.1.2 振幅调制原理调制是将要传送的信息装载到某一高频振荡（载频）信号上去的过程。
按照所采用的载波波形区分，调制可分为连续波（正弦波）调制和脉冲调制。
连续波调制以单频正弦波为载波，可用数学式)t (cos A )t (ϕ+ω=a 表示，受控参数可以是载波的幅度A ，频率ω或相位ϕ。
因而有调幅（AM ）、调频（FM ）和调相（PM ）三种方式。
脉冲调制以矩形脉冲为载波，受控参数可以是脉冲高度、脉冲重复频率、脉冲宽度或脉冲位置。
相应地，就有脉冲调幅（PAM ，包括脉冲编码调制PCM ），脉冲调频（PFM ），脉冲调宽（PWM ）和脉冲调位120（PPM ）。
《高频电路原理与分析》教案05 频谱的线性搬移电路
第5章 频谱的线性搬移电路分为频谱的线性搬移电路和非线性搬移电路。
线性搬移电路：频谱结构不发生变化，如振幅调制与解调、混频。
非线性搬移电路：频谱结构也发生了变化。
频率调制与解调、相位调制与解调等电路5.1 非线性电路的分析方法有两种分析方法：1、级数展开分析2、线性时变分析5.1.1 非线性函数的级数展开分析法//////////////////////////////////////////////////////////////////////////////////////////补充：泰勒级数1、定理 （泰勒定理） 正次幂设函数在区域D 内解析，为D 内的一点，)(z f 0z R 为到D 的边界上各点的最短距离，则当时，可展开为幂级数0z R z z <−||0)(z f n n n R z z z f n C z z C z f n n )()(00||)(!100)(−========∑∞=<−=其中 n=0，1,2,… )(z f 在处的泰勒展开式是唯一的。
0z //////////////////////////////////////////////////////////////////////////////////////////非线性器件的伏安特性，可用下面的非线性函数来表示: i =f (u ) (5-1)式中, u 为加在非线性器件上的电压。
一般情况下, u ＝E Q +u 1+u 2,其中E Q 为静态工作点，u 1和u 2为两个输入电压。
展开成E Q 处的泰勒级数，可得∑∞=+=++++++++=02212122122110)( )()()(n n n n u u a u u a u u a u u a a i LL式中，a n(n =0，1，2，…)为各次方项的系数，由下式确定: )(!1)(!1Q )(QE f n du u f d n a n E u n n n === (5-3) 由于∑=−=+nm m m n m n nu u C u u 02121)( (5-4)式中，为二项式系数，故)!(!/!m n m n C m n −=∑∑=−∞==n m m m n m n n n u u C a i 0210 (5-5)以下分析， u 2=0情况，见p144作用在非线性器件上的两个电压均为余弦信号，即u 1＝U 1cos ω1t ，u 2＝U 2cos ω2t ，利若用式(5-7)和三角函数的积化和差公式)cos(21)cos(1cos cos x y x y x ++−=2y (5-9) 由式(5-5)不难看出，i 中将包含由下列通式表示的无限多个频率组合分量5.1.2 线性时变电路分析法对式(5-1)在 E Q +u 2上对i 用泰勒级数展开，有ωp,q =|±p ω1±q ω2|++=u u E f i 1Q )(L L +++++′′++′++=n n u u E f n u u E f u u E f u E f 12Q )(212Q 12Q 2Q 2)(!1 )(!21)()( 5-11 ―――――――――――――――――――――――――――由于5-5和5-11是等价的。
第四章 调幅、检波、混频—频谱的线性搬移电路
iC 根据模电的知识可以知道，在放大区， iB也就是ic由iB 来控制，这样就没有办法让Ucc u (t )来控制ic了。所以集 电极调制不能工作在放大状态（欠压区）。
放大器工作在过压区时，集电极电压的变化才会引起集 电极电流的明显变化。
而在饱和状态（过压状态）下，由模电的知识我们可以知 道，Uce受U‘cc的控制，而Uce控制ic，因此，U’cc控制ic。
B、避免措施
从图中可以看出引起失真的原因除了从以上分析的原因上 来看外，还可以从另一个角度上来考虑：就是Ma如果过大的 话，会使得凹陷越深，这样也容易引起惰性失真。 要消除这个失真，最关键在于合理选择RLC。
所谓合理：保证电容电压变化的速度高于包络变化的速度 （使高频振幅慢慢的变）
分析： 设包络表达式为： u 'i U cm (1 M a cos t )
20 Ω 20 Ω 0 Ω 0 Ω 20 2Ω 0 2 Ω 0 0
a3 3 V0 4
0
Ω 2Ω3Ω
30ω
最后通过谐振回路（带通滤波器）选频，以Wc为中心频 率，以 2 Ω 为通频带宽。选出载波和上下边带即可。
6、双边带调幅电路
二极管平衡调幅电路
4.4 检波原理及检波电路
对调幅信号的解调
二、调制方式 调幅、调频、调相 三、为什么要调制 (1)为了提高信号的频率,以便更有效地将信号从天线辐射出去. (2)为实现信道复用.
4.2 调幅信号分析
调幅方式：普通调幅AM（产生AM信号） 抑制载波的双边带调幅DSB（DSB信号）
单边带调幅SSB（SSB信号）。
一、调幅信号的波形以及表达式
U c U cm (1 cos t ) cosc t U cm
线性移不变系统课件
05
线性移不变系统的设计方 法
状态反馈控制
状态反馈控制是线性移不变系统设计中常用的一种方法，通过将系统的 状态变量反馈到输入端，实现对系统的精确控制。
状态反馈控制器的设计通常采用状态空间法，通过构造状态反馈矩阵， 使得闭环系统满足特定的性能指标，如稳定性、跟踪性能等。
状态反馈控制适用于各种类型的线性移不变系统，具有较好的鲁棒性和 适应性。
GPU（图形处理器） GPU具有并行处理能力，可用于加速线性移不变 系统的计算和数据处理。
系统实现中的关键技术
数字信号处理
数字信号处理技术是实现线性移 不变系统的关键，包括信号的采
样、量化、滤波、频谱分析等。
算法优化
针对线性移不变系统的算法进行优 化，以提高系统的实时性和能效。
硬件描述语言
使用硬件描述语言（如VHDL或 Verilog）进行系统设计和实现，能 够提高系统的可重用性和可维护性。
能观性判定
对于线性移不变系统，可以通过判断系统的可观性矩阵是否满秩来确定系统是否 具有能观性。可观性矩阵是系统状态矩阵A的转置与输出矩阵C的乘积。如果可 观性性移不变系统，如果该系统既是能控的又是能 观的，则称该系统是能对偶的。
对偶性的意义
对偶性是线性移不变系统的一个重要性质，它表明系统的控 制性能和观测性能之间存在一定的关系。在实际应用中，了 解系统的对偶性有助于更好地设计控制系统和观测系统，以 达到更好的控制效果和观测效果。
06
线性移不变系统的实现与 应用
系统实现的硬件平台
1 2 3
FPGA（现场可编程门阵列） FPGA是一种高度灵活的硬件平台，适用于实现 线性移不变系统的硬件描述语言（如VHDL或 Verilog）编程。
通信电子线路-频谱搬移电路(new)
变为负值，出现过调幅失真。
(a)
(b)
图 4-1-3 过调幅失真
图 4-1-2
在实际调幅电路中，由于管子截止，
过调幅的波形变为图 4-1-3(b) 。
调幅信号的波形
(3)频谱 将式(4-1-2)
vO(t) = Vm0 (1 + Ma cos t) cos ct
用三角函数展开
vO(t) V m0cosct MaV m0cos Ωt cosct
4.4 振幅调制与解调电路
第 4 章 振幅调制、解调 与混频电路
4.1 频谱搬移电路的组成模型
4.1.1 振幅调制电路的组成模型 4.1.2 振幅解调和混频电路的组成模型
4.1.1 振幅调制电路的组成模型
一、调幅波的数学表式
设：调制信号
v(t) = V cos t
(1)
载波信号
vc(t) = Vcmcos ct
i a1Vcm cosct a2VcmV [cos(c Ω)t cos(c Ω)t]
a1Vcm cosct 2a2VcmV cosct cos Ωt
a1Vcm (1
2a2V a1
cos Ωt )cosct
(7)
i
a1Vcm(1
2a 2V a1
cos Ωt)cosct
(7)
所以，输出调幅波电流的数学表达式为
在广播电视系统中，由于图像信号频带较宽，为 了节约频带，同时又便于接收机进行检波，所以对 图像信号采用了残留边带调幅方式，而对于伴音信 号则采用了调频方式。现以电视图像信号为例，说 明残留边带调幅方式的调制与解调原理。
例如：电视图像信号带宽为6MHz。
在发射端先产生普通调幅信号，然后利用具有 图4.1.12(a)所示特性的滤波器取出一个完整的上边 带、一部分下边带以及载频分量。
(a)
(b)
图 4-1-3 过调幅失真
图 4-1-2
在实际调幅电路中，由于管子截止，
过调幅的波形变为图 4-1-3(b) 。
调幅信号的波形
(3)频谱 将式(4-1-2)
vO(t) = Vm0 (1 + Ma cos t) cos ct
用三角函数展开
vO(t) V m0cosct MaV m0cos Ωt cosct
4.4 振幅调制与解调电路
第 4 章 振幅调制、解调 与混频电路
4.1 频谱搬移电路的组成模型
4.1.1 振幅调制电路的组成模型 4.1.2 振幅解调和混频电路的组成模型
4.1.1 振幅调制电路的组成模型
一、调幅波的数学表式
设：调制信号
v(t) = V cos t
(1)
载波信号
vc(t) = Vcmcos ct
i a1Vcm cosct a2VcmV [cos(c Ω)t cos(c Ω)t]
a1Vcm cosct 2a2VcmV cosct cos Ωt
a1Vcm (1
2a2V a1
cos Ωt )cosct
(7)
i
a1Vcm(1
2a 2V a1
cos Ωt)cosct
(7)
所以，输出调幅波电流的数学表达式为
在广播电视系统中，由于图像信号频带较宽，为 了节约频带，同时又便于接收机进行检波，所以对 图像信号采用了残留边带调幅方式，而对于伴音信 号则采用了调频方式。现以电视图像信号为例，说 明残留边带调幅方式的调制与解调原理。
例如：电视图像信号带宽为6MHz。
在发射端先产生普通调幅信号，然后利用具有 图4.1.12(a)所示特性的滤波器取出一个完整的上边 带、一部分下边带以及载频分量。
第十二讲 频谱的线性搬移电路3
端口 z ，因而它是一个三端口的非线性网络，其电
路符号如图5-20所示。
ux(t)
uz(t)
ux(t)
uz(t)
uy(t)
uy(t)
图5-20 模拟相乘器电路符号
如果理想模拟相乘器两输入电压分别为
ux t Ux cos1t , uy t U y cos2t
那么输出电压为
uz t kUxU y cos1t cos2t
uB
UT
ln
ie5 ie6
1 2
(ie5
ie6 )Re2
1 2
(ie5
ie6 )Re2
UT
ln
ie5 ie6
uB
1 2
(ie5
ie6 )Re2
1 2
(i5
i6 )Re2
(5-80) (5-81) (5-82)
考虑到ie5＋ie6=I0,则由式（5-82）可知,为了保证ie5 和ie6大于零 , uB 的最大动态范围为
VCC(+12 V) 3.9 kΩ Rc Rc 3.9 kΩ
V1 V2
V3 V4
9
+ -
uo
6
8
ux -
+7
+4
V5
uy
-
1
5
6.8 kΩ V9
V7
10
500
500
VEE(-8V)
V6 V8
+
ux
-
+
2
uy
Ry -
3
500
MC1596
Ry
Rc
2
3
7
9
8
MC1596
4
4.1 频谱搬移电路的组成模型
第4章
振幅调制、 振幅调制、解调 与混频电路
4.1 频谱搬移电路的组成模型
4.1.1 振幅调制电路的组成模型 4.1.2 振幅解调和混频电路的组成模型
4.1.1 振幅调制电路的组成模型
一、普通调幅信号及其电路组成模型
1．电路组成模型 ． vO(t ) = [vc (t ) + A vΩ (t )vc (t )]⋅ A M = [ AVcm + AMAVcmvΩ (t )]⋅ cosωct = [Vm0 + kavΩ (t )]⋅ cosωct 式中， 乘器乘积系数； 式中，AM ：相乘器乘积系数； A：相加器的加权系数，且 A = k，AM AVcm = ka。 ：相加器的加权系数， ， 2．单音调制 ． (1)表达式：vO(t) = Vm0 (1 + Ma cos Ω t) cos ωct )表达式： 式中： 的振幅， 式中： Vm0 (1 + Ma cos Ω t) ：vO(t) 的振幅，反映调制信号的 变化，称为调幅信号的包络 调幅信号的包络。 变化，称为调幅信号的包络。
(2)表达式 ) 普通调幅： 普通调幅： vO(t) = [Vm0 + kavΩ(t) ]cos ωct 双边带调幅： 双边带调幅： vO(t) = kavΩ(t) cos ωct 特点： 特点： ① 普通调幅：调制波叠加在载波振幅 Vm0 上； 普通调幅： 双边带调幅： ② 双边带调幅：调制波不再依托 Vm0 。当 vΩ(t) 进入负 半周时， 也变为负值， 半周时，vO(t) 也变为负值，载波电压产生 180° 相移。调制 ° 相移。 信号波形在过零处出现 180° 的相位突变。 ° 的相位突变。
(3)波形 )
图 4-1-6 - (a) 波形 )
频谱的线性搬移电路
T1 ＋ u1 － ＋ u1 －
＋
VD1 i1
i4
VD 4
VD 2
VD 3 i3
i2
u2
－
(a)
T2 iL RL
T1 ＋ u1 － ＋ u1 －
＋
VD1 i1
VD2 i2
u2
－
(b)
T2 iL1 RL
T1 ＋ u1 － ＋ u1 －
＋
VD 4
i4
T2 iL2
RL
VD 3
i3
u2
－
(c)
图5―9 二极管环形电路
2
g DU 1 cos( 2
1)t
2 5
g DU 1 cos(5 2
1)t
2 5
g DU 1 cos(5 2
1)t
(5―38)
由上式可以看出,流过二极管的电流iD中的频率分量有: （1）输入信号u1和控制信号u2的频率分量ω1和ω2; （2）控制信号u2的频率ω2的偶次谐波分量; （3）由输入信号u1的频率ω1与控制信号u2的奇次谐波分
频谱的线性搬移电路
5.1
f
f
0
0
fc
(a)
f
f
0
0
fc
(b)
图5―1 频谱搬移电路 （a）频谱的线性搬移;（b）频谱的非线性搬移
5.1.1 非线性函数的级数展开分析法
非线性器件的伏安特性,可用下面的非线性函数来
表示:
i f (u)
(5―1)
式中,u为加在非线性器件上的电压。一般情况下,
u＝EQ+u1+u2,其中EQ为静态工作点,u1和u2为两个输入电 压。用泰勒级数将式（5―1）展开,可得
频谱搬移
AM (t) 为负值，如图4.1.2（a）所示，包络 Vm (t)
已不能反映 原调制信号的变化规律而产生了失真， 通常称这种失真为过调制失真（Over Modulation）。
但在实际调幅电路中，由于管子截止，过调制失真 的波形如图4.1.2（b）所示。
图4.1.2 过调制失真波形
4.1.1
（3）频谱图： 将调幅信号表达式改写成
（1）包络不同。AM信号的包络正比于调制信号 (t) 而DSB信号的包络g(t)正比于 (t) Vm cos t ，当调制 信号 (t) 0 时，即 cos t 0 ，DSB信号的幅度也为零。 DSB信号的包络已不再反映调制信号 (t) 的变化。
4.1.1
（2）DSB信号的高频载波在调制信号自正值或负值 通过零点时，出现180°的相位突变。因此，严格地讲， DSB信号已非单纯的振幅调制信号，而是既调幅又调 相的信号。
图4.1.12(a)所示特性的滤波器取出一个完整的上边 带、一部分下边带以及载频分量。
在接收端，采用具有图4.1.12(b)所示特性的滤波 器从残留边带调幅信号中取出所需频率分量。
由图4.1.12可见，若采用普通调幅，每一频道 电视图像信号的带宽需12MHz，而采用残留边带 调幅只需8MHz，另外，对于滤波器过渡带的要求 远不如单边带调幅那样严格，故容易实现。
则混频器的输出信号频率为pfqf若设两个输入信号的频率分别为413一混频器的功能图4116混频器的功能a混频前后的波形图b混频前后的频谱图413混频原理动画3从频域角度看混频前后各频率分量的相对大小和相互间隔并不发生变化即混频是一种频谱的线性搬移输出中频信号与输入高频信号的频谱结构相同惟一不同的也是载频如图4116b所示
4.1.3
fI大于 fc 的混频称为上混频，fI 小于fc 的混频称为下 混频。调幅广播收音机普遍采用下混频，它的中频规定为 465kHz。
已不能反映 原调制信号的变化规律而产生了失真， 通常称这种失真为过调制失真（Over Modulation）。
但在实际调幅电路中，由于管子截止，过调制失真 的波形如图4.1.2（b）所示。
图4.1.2 过调制失真波形
4.1.1
（3）频谱图： 将调幅信号表达式改写成
（1）包络不同。AM信号的包络正比于调制信号 (t) 而DSB信号的包络g(t)正比于 (t) Vm cos t ，当调制 信号 (t) 0 时，即 cos t 0 ，DSB信号的幅度也为零。 DSB信号的包络已不再反映调制信号 (t) 的变化。
4.1.1
（2）DSB信号的高频载波在调制信号自正值或负值 通过零点时，出现180°的相位突变。因此，严格地讲， DSB信号已非单纯的振幅调制信号，而是既调幅又调 相的信号。
图4.1.12(a)所示特性的滤波器取出一个完整的上边 带、一部分下边带以及载频分量。
在接收端，采用具有图4.1.12(b)所示特性的滤波 器从残留边带调幅信号中取出所需频率分量。
由图4.1.12可见，若采用普通调幅，每一频道 电视图像信号的带宽需12MHz，而采用残留边带 调幅只需8MHz，另外，对于滤波器过渡带的要求 远不如单边带调幅那样严格，故容易实现。
则混频器的输出信号频率为pfqf若设两个输入信号的频率分别为413一混频器的功能图4116混频器的功能a混频前后的波形图b混频前后的频谱图413混频原理动画3从频域角度看混频前后各频率分量的相对大小和相互间隔并不发生变化即混频是一种频谱的线性搬移输出中频信号与输入高频信号的频谱结构相同惟一不同的也是载频如图4116b所示
4.1.3
fI大于 fc 的混频称为上混频，fI 小于fc 的混频称为下 混频。调幅广播收音机普遍采用下混频，它的中频规定为 465kHz。
频谱的线性搬移电路
随着绿色环保理念的深入人心，低功耗、环保型的频谱的线性搬值
研究意义
频谱的线性搬移电路在通信、雷达、电子对抗等领域 具有广泛的应用价值。对频谱的线性搬移电路的研究 有助于深入理解信号处理和传输的基本原理，推动相 关领域的技术进步和创新。同时，频谱的线性搬移电 路的研究也有助于培养高水平的专业人才，为国家的 科技发展和社会进步做出贡献。
在音频处理中的应用
均衡器
音频处理中的均衡器利用频谱的线性搬移电路，对音频信号的特定频段进行提升或衰减， 以调整音频的音色和音量。
滤波器
音频滤波器用于滤除信号中的噪声或干扰，频谱的线性搬移电路可以将特定频段的信号进 行搬移或抑制。
效果器
在音乐制作和演出中，效果器用于给音频信号添加各种效果，如延时、混响等，频谱的线 性搬移电路用于实现各种音效处理。
02
频谱的线性搬移可以通过调频 （FM）和调相（PM）等方式实现。
频谱的线性搬移电路的重要性
在通信系统中，频谱的线性搬移电路 是实现信号传输的关键环节之一。
频谱的线性搬移电路的设计和实现对 于通信系统的性能和稳定性具有重要 意义。
通过频谱的线性搬移，可以将信号从低频段 搬移到高频段，或者将信号从高频段搬移到 低频段，从而实现信号在不同频段的传输和 接收。
软件实现方式
算法实现
通过编写算法在通用计算机上实现频谱的线性搬移，具有灵活性，但处理速度相 对较慢，且对计算机性能要求较高。
云计算平台
利用云计算平台的强大计算能力实现频谱搬移，可实现大规模并行处理，但需要 网络连接和数据传输。
频谱的线性搬移电路
04
的性能优化
提高频率响应
采用高性能的电子元件
选用具有低失真、低噪声、高稳定性的电子元件，如高品质 的电阻、电容、电感等，以减小电路中的非线性失真，提高 频率响应的准确性。
研究意义
频谱的线性搬移电路在通信、雷达、电子对抗等领域 具有广泛的应用价值。对频谱的线性搬移电路的研究 有助于深入理解信号处理和传输的基本原理，推动相 关领域的技术进步和创新。同时，频谱的线性搬移电 路的研究也有助于培养高水平的专业人才，为国家的 科技发展和社会进步做出贡献。
在音频处理中的应用
均衡器
音频处理中的均衡器利用频谱的线性搬移电路，对音频信号的特定频段进行提升或衰减， 以调整音频的音色和音量。
滤波器
音频滤波器用于滤除信号中的噪声或干扰，频谱的线性搬移电路可以将特定频段的信号进 行搬移或抑制。
效果器
在音乐制作和演出中，效果器用于给音频信号添加各种效果，如延时、混响等，频谱的线 性搬移电路用于实现各种音效处理。
02
频谱的线性搬移可以通过调频 （FM）和调相（PM）等方式实现。
频谱的线性搬移电路的重要性
在通信系统中，频谱的线性搬移电路 是实现信号传输的关键环节之一。
频谱的线性搬移电路的设计和实现对 于通信系统的性能和稳定性具有重要 意义。
通过频谱的线性搬移，可以将信号从低频段 搬移到高频段，或者将信号从高频段搬移到 低频段，从而实现信号在不同频段的传输和 接收。
软件实现方式
算法实现
通过编写算法在通用计算机上实现频谱的线性搬移，具有灵活性，但处理速度相 对较慢，且对计算机性能要求较高。
云计算平台
利用云计算平台的强大计算能力实现频谱搬移，可实现大规模并行处理，但需要 网络连接和数据传输。
频谱的线性搬移电路
04
的性能优化
提高频率响应
采用高性能的电子元件
选用具有低失真、低噪声、高稳定性的电子元件，如高品质 的电阻、电容、电感等，以减小电路中的非线性失真，提高 频率响应的准确性。
频谱的线性搬移电路PPT课件
THANKS
感谢观看
未来研究方向与挑战
针对频谱线性搬移电路中的关键 技术问题，如线性度、动态范围 和稳定性等，需要深入研究并寻
求突破。
探索新型的频谱线性搬移电路结 构和设计方法，以满足不断增长 的性能需求和多样化的应用场景。
解决频谱线性搬移电路在高温、 高湿、高震等恶劣环境下的稳定 性和可靠性问题，提高其环境适
应性。
02
频谱线性搬移电路的实现方式
模拟实现方式
01
02
03
模拟信号处理
通过模拟电子器件（如运 算放大器、滤波器等）对 信号进行线性变换，实现 频谱的搬移。
优点
实时性好、处理速度快、 精度高。
缺点
对器件参数敏感，容易受 到环境温度和电源电压的 影响，稳定性较差。
数字实现方式
数字信号处理
通过数字信号处理器（DSP）或 现场可编程门阵列（FPGA）等数
BIG DATA EMPOWERS TO CREATE A NEW
ERA
定义与工作原理
定义
频谱线性搬移电路是一种能够将 输入信号的频谱进行线性搬移的 电路，即将信号的频率按照一定 的比例进行上变频或下变频。
工作原理
频谱线性搬移电路通过改变信号 的频率，使其与系统的固有频率 相匹配，从而实现信号的传输、 处理或控制。
BIG DATA EMPOWERS TO CREATE A NEW ERA
频谱的线性搬移电路ppt课
件
• 频谱线性搬移电路概述 • 频谱线性搬移电路的实现方式 • 频谱线性搬移电路的性能指标 • 频谱线性搬移电路的设计与优化 • 频谱线性搬移电路的发展趋势与展望
目录
CONTENTS
01
频谱搬移电路的基本工作原理
普通AM波的三种情况
假设:
v AM V0 (1 M a cost ) cos0t 2(1 M a cost ) cos0t
Vm-----假设-uAM(t)= Vm cosω ct= 2(1+ Mα cosΩ t)cosω ct 00 1 900 0 1800 —1 2700 0 3600 1
对一般的调幅波,通常满足ωc>>Ω。根据振幅调制信号的定义,已调 信号的振幅随调制信号uΩ线性变化。
由于调 幅信号的振幅与调制信号成线性关系，即有：
Vm (t ) V0 kaV cost ，式中
k a 为比例常数,与两信号在电路接入端有关，见下页图示
即：
2019/1/19
kaV Vm (t ) V0 (1 cost ) V0 (1 ma cost ) V0
二极管检波器 三极管检波器
小信号检波器 大信号检波器 包络检波器 同步检波器
25
器件
检波
信号大小
工作原理
2019/1/19
3 检波器的输入输出波形
2019/1/19
检波器的输入输出波形
26
4 检波前后的频谱
检波器检波前后的频谱
2019/1/19 27
5 典型的AM振幅解调框图-----包络检波
信号带宽 B 2Ωmax
调制信号 载波
Ωmax
调幅波 下边带
2019/1/19
ω0
上边带
o11
4.2.3 调幅波中的功率关系---引出双边带与单边带
调幅波一般表达式：
v (t ) Vo (1 ma cosΩt) cos ot
V0，
V0
ma V0 2 ma V0 2
频谱搬移
i
a0
a1vD
a
2v
2 D
a3v
3 D
vD v0 v V0 cos0t V cosct
当vD很小时，级数可只取前四项
28
第6章 振幅调制、解调与混频 利用三角公式展开，并分类整理，可得
i a0 a1{V0 cos 0 t V cos t}
a2
1 2
V02
1
cos
20 t
V0 V cos0
是使高频振荡的振幅与调制信号成线性关系， 其它参数(频率和相位)不变。 振幅调制的三种方式：
(AM)：普通的调幅； (DSB)：抑制载波的双边带调制； (SSB)：抑制载波的单边带调制。
5
第6章 振幅调制、解调与混频
（一） 调幅波的分析
1、表示式及波形
设载波电压为: uC = UCcosωct 调制电压: uΩ = UΩcosΩt
载波被抑制双边带调幅波
maV0 cost cos0t
波形图
频谱图
信号 带宽
0-
0+
2( ) 2
vo
t
1 2 ma V0m
0-
0+
2( ) 2
单边带信号
ma 2
V0
cos(0
)t
(或
ma 2
V0
cos(0
)t)
1 2 ma V0m
0-
0+
() 2
25
第6章 振幅调制、解调与混频
6.3 振幅调制方法与电路
1 Vo 2 2R
1 22 2
2(W)
PDSB
1 2
ma2
PoT
1 0.32 2
2
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
式(5-71)中有两个输入信号uA和uB的乘积项，故可构成频 谱线性搬移电路。
二、双差分对电路
双差分对频谱搬移电路如图5-18所示。它由三
个基本的差分电路组成 , 也可看成由两个单差分对
电路组成。V1、V2、V5组成差分对电路Ⅰ；V3、V4、 V6组成差分对电路Ⅱ。两个差分对电路的输出端交
叉耦合。
（5-68） (5-69) (5-70) (5-71)
uA uB uA i0 (t ) I 0 (t ) tanh( ) I 0 (1 ) tanh( ) 2U T U ee 2U T uB u A i0 (t ) I 0 (1 ) U ee 2U T
(当|uA|< 26mV时)
(5-93)
p.q p2 q1
p, q 0,1,2,
（5-94）
一般情况下 , 由于U1<<U2 , 通常可以不考虑高次项 ,式(5-
93)化简为
ic= Ic0(t) + gm(t) u1 (5-95)
等效为一线性时变电路 , 其组合频率也大大减少 , 只有 ω2 的 各 次 谐 波 分 量 及 其 与 ω1 的 组 合 频 率 分 量 n=0,1,2,…。 特点：有增益; 动态范围小; 内部噪声大、组合干扰大。 nω2±ω1,
限乘法器。
图5-22所示的是单片集成模拟乘法器MC1596的内部电
路及外围电路。与图5-18所示的电路结构基本相同，仅是 电流源I0被V7、V8和二极管V9所构成的镜像恒流源取代。其 中，二极管与500欧姆的电阻构成V7、V8的偏置电路；射极 负反馈电阻 Ry 接在第 2、3脚，可扩展输入信号 uy 的动态 范围，并可调整相乘系数 k；接于模拟乘法器5脚的电阻R5 为负载电阻(图中取6.8kΩ采用了外接方式)。
ube U BB ( t )
, n 1, 2,3, (5-91)
也随u2周期性变化，可以用傅里叶级数展开为
f (n) [UBB (t )] Cn0 Cn1 cos 2t Cn2 cos22t , n 1,2,3,
(5-92)
将式(5-88)、(5-90)、(5-92)代入式(5-87)，可得
Ic0 t 的表达式为
Ic0 (t ) Ic00 Ic01 cos 2t Ic02 cos22t
f [U BB (t )] dic dube
ube U BB ( t )
(5-88) (5-89)
df (ube ) dube
ube U BB ( t )
gm(t)是u2的函数，故是随u2周期性变化的,可以用 傅里叶级数展开,
即，输出频率组合分量是ω1和ω2奇次谐的组合。
② 当U1< 26mV ( U1<UT) 时，
可求得输出频率组合为
2n 1 2 1
③ U1、U2< 26mV时，输出差动电流为
I0 u1 u2 i0 I 0 u1 u2 2 2UT 2UT 4UT
为理想乘法器--模拟乘法器
gm (t ) gm0 gm1 cos 2t gm2 cos 22t
（5-90）
式中，gm0 是 gm(t) 的平均分量（直流分量）, 它不一 定是直流工作点UBB处的跨导。gm1是gm(t)中角频率为ω2
分量的振幅---时变跨导的基波分量振幅。
d nic 1 (n) f [U BB (t )] n n! dube
3. 差分对频谱搬移电路
差分对电路的可控通道有两个 : 一个为输入差模电压 , 另一个为电流源 I0 这两个通道。
H(jω)
； 故可让输入信号和控制信号分别控制
Ucc
H(jω)
+ u o
VT1
VT2 VT3
uA uB Re -Ucc
图5-17 差分对频谱搬移电路
uB ube3 ie3 Re U ee U ee uB uB i0 (t ) ie3 I 0 (1 ) Re Re U ee U ee I0 Re
在MC1596的应用图中，如果首先调节平衡电位器
56kΩ使得流过接在“2”、“3”脚电阻Ry的静态电流为零，
那么，当同时加入ux和uy，且 uxmax< 26mV时，输出差动电 压为 u0 = Rc/2 RyUT·ux(t)uy(t) 如果调节平衡电位器56kΩ，使得流过接在“2”、“3” 脚电阻Ry的静态电流不为零，则流经Ry的电流为 iy = Iy0 + uy / Ry u0≈ RcIy0 / 2 UT(1 + uy / RyIy0)·ux(t) 该应用常用来实现普通AM调幅。
(5-72) (5-73) (5-74) (5-75)
（5-76）
分析：
① 当u1=U1cosω1t，u2=U2cosω2t 时，代入式(5-76)有
i0 I 0
m0 n 0
2 m1
( x1 )2n1 ( x2 )cos(2m 1)1t cos(2n 1)2t
(5-77)
(5-87) 图 5-24(a) 给出了 ic ～ ube 曲线 , 同时画出了时变工作 点处的电流 Ic0(t) 的波形。
ic
Q1
Ic0(t)
Q2 0 0
ube ube
U2
0
t
t
图5-24(a)
三极管电路中的时变电流
gm
gm(t)
0 0
UBB
ube ube
0
t
t
图5-24 (b) 三极管电路中的时变跨导
1 1 (n) 2 ic I c 0 (t ) g m (t )u1 f [U BB (t )]u1 f [U BB (t )]u12 2 n! I c 00 I c 01 cos 2t I c02 cos 22t ( g m 0 g m1 cos 2t g m 2 cos 22t )U1 cos 1t 1 (Cn 0 Cn1 cos 2t Cn 2 cos 22t )U1n cos n 1t n!
u0
-
MC1596
-Uee
R5
VEE (-8V)
图5-22 MC1596的内部电路
MC1596外围电路
0.01μF 1 kΩ
1kΩ
3k9
3k9
+12V 51
0.01μF
1kΩ
ux uy
10kΩ
3 7 2 9 8 4 MC1596 6 1 10 5
u0
51
6k8 56 kΩ
- 8V
MC1596的基本应用电路图
VCC(+12 V)
3.9 kΩ
Rc Rc
3.9 kΩ
9 6
V1 V2 V3 V4
+ uo -
Ry Rc 2 3 9 + 7 8 Rc
Ucc
ux
+
8 7 4 1 5 6.8 kΩ
10 V9 500 V7 500 V8 500
ux
+
uy
+
-
V5
V6
2 Ry 3
+ -
uy
4 1
MC1596
6 10 5
(5-80) (5-81) (5-82)
考虑到ie5＋ie6=I0,则由式（5-82）可知,为了保证ie5 和ie6大于零 , uB 的最大动态范围为
I 0 uB I 0 2 Re 2 2
可近似为
(5-83)
将式 (5-82) 代入式 (5-76), 双差分对的差动输出电流
2u B uA i0 tanh( ) Re 2 2U T 2 i0 K ( At )u B Re 2
二、场效应管频谱线性搬移电路
结型场效应管是利用栅漏极间的非线性转移特 性实现频谱线性搬移功能的。场效应管转移特性 iD～uGS 近似为平方律关系，其表示式为
uGS 2 iD I
uGS diD gm gm0 (1 ) duGS Up
ux t U x cos 1t , u y t U y cos 2t
那么输出电压为
uz t kU xU y cos 1t cos 2t k U xU y cos 1 2 t cos 1 2 t 2
显然，经过模拟乘法器相乘，将ω1的信号频率线性 搬移到ω2的信号频率点处了。如果ux(t) 是一个实用的限 带信号，那么可实现限带信号的频谱搬移。
i0 i i i1 i3 i2 i4 i1 i2 i4 i3
(5-72)
Ucc
RL RL
iI
uA
+ +
uo
iII
VT3 VT4 i3 VT6 i6 I0 i4
VT1 VT2 i1 VT5 i5 i2
uB
图5-18
双差分对电路
2. 模拟相乘器的工作象限
根据模拟乘法器两输入电压的极性，乘法器有四
个工作区域(又称工作象限)。如图5-21所示，输入电 压可能有四种极性组合：
ux(t) × uy(t) = u z( t )
Ⅱ Ⅲ
0
uy(t) Ⅰ Ⅳ ux(t)
(+)
(-) (-) (+)
(+)
(+) (-) (-)
(+) 第Ⅰ象限
上述应用常用来实现双边带调幅。
§5.4 其它频谱线性搬移电路
一、 晶体三极管频谱线性搬移电路
晶体三极管频谱搬移电路如图5-23所示。
ic
+ +
u1
VT
C Ucc