matlab经典习题及解答(可编辑修改word版)
(完整word版)含答案《MATLAB实用教程》

第二章 MATLAB 语言及应用实验项目实验一 MATLAB 数值计算三、实验内容与步骤1.创建矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a(1(2)用(3)用(42.矩阵的运算(1)利用矩阵除法解线性方程组。
⎪⎪⎩⎪⎪⎨⎧=+++=-+-=+++=+-12224732258232432143214321421x x x x x x x x x x x x x x x 将方程表示为AX=B ,计算X=A\B 。
(2)利用矩阵的基本运算求解矩阵方程。
已知矩阵A 和B 满足关系式A -1BA=6A+BA ,计算矩阵B 。
其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=7/10004/10003/1A ,Ps: format rata=[1/3 0 0;0 1/4 0;0 0 1/7];b=inv(a)*inv(inv(a)-eye(3))*6*a(3)计算矩阵的特征值和特征向量。
已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=1104152021X ,计算其特征值和特征向量。
(4)Page:322利用数学函数进行矩阵运算。
已知传递函数G(s)=1/(2s+1),计算幅频特性Lw=-20lg(1)2(2w )和相频特性Fw=-arctan(2w),w 的范围为[0.01,10],按对数均匀分布。
3.多项式的运算(1)多项式的运算。
已知表达式G(x)=(x-4)(x+5)(x 2-6x+9),展开多项式形式,并计算当x 在[0,20]内变化时G(x)的值,计算出G(x)=0的根。
Page 324(2)多项式的拟合与插值。
将多项式G(x)=x 4-5x 3-17x 2+129x-180,当x 在[0,20]多项式的值上下加上随机数的偏差构成y1,对y1进行拟合。
对G(x)和y1分别进行插值,计算在5.5处的值。
Page 325 四、思考练习题1.使用logspace 函数创建0~4π的行向量,有20个元素,查看其元素分布情况。
Ps: logspace(log10(0),log10(4*pi),20) (2) sort(c,2) %顺序排列 3.1多项式1)f(x)=2x 2+3x+5x+8用向量表示该多项式,并计算f(10)值. 2)根据多项式的根[-0.5 -3+4i -3-4i]创建多项式。
(完整word版)matlab经典习题及解答

第1章 MATLAB概论1.1与其他计算机语言相比较,MATLAB语言突出的特点是什么?MATLAB具有功能强大、使用方便、输入简捷、库函数丰富、开放性强等特点.1.2 MATLAB系统由那些部分组成?MATLAB系统主要由开发环境、MATLAB数学函数库、MATLAB语言、图形功能和应用程序接口五个部分组成。
1.4 MATLAB操作桌面有几个窗口?如何使某个窗口脱离桌面成为独立窗口?又如何将脱离出去的窗口重新放置到桌面上?在MATLAB操作桌面上有五个窗口,在每个窗口的右上角有两个小按钮,一个是关闭窗口的Close按钮,一个是可以使窗口成为独立窗口的Undock按钮,点击Undock按钮就可以使该窗口脱离桌面成为独立窗口,在独立窗口的view菜单中选择Dock ……菜单项就可以将独立的窗口重新防止的桌面上。
1.5 如何启动M文件编辑/调试器?在操作桌面上选择“建立新文件”或“打开文件"操作时,M文件编辑/调试器将被启动.在命令窗口中键入edit命令时也可以启动M文件编辑/调试器.1.6 存储在工作空间中的数组能编辑吗?如何操作?存储在工作空间的数组可以通过数组编辑器进行编辑:在工作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输入修改内容即可。
1。
7 命令历史窗口除了可以观察前面键入的命令外,还有什么用途?命令历史窗口除了用于查询以前键入的命令外,还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中。
1。
8 如何设置当前目录和搜索路径,在当前目录上的文件和在搜索路径上的文件有什么区别?当前目录可以在当前目录浏览器窗口左上方的输入栏中设置,搜索路径可以通过选择操作桌面的file菜单中的Set Path 菜单项来完成。
在没有特别说明的情况下,只有当前目录和搜索路径上的函数和文件能够被MATLAB运行和调用,如果在当前目录上有与搜索路径上相同文件名的文件时则优先执行当前目录上的文件,如果没有特别说明,数据文件将存储在当前目录上。
MATLAB40道题与答案修正版

操作方法:首先点击File —New —M-File ,输入相应代码,然后点击运行按钮即可。
P1.已知两序列[]0.8{[][5]}nx n u n u n =--,[]{1,1,1,1,1}h n =计算两序列的卷积并绘制其波形。
%function a1 for i=1:5x(i)=0.8^(i-1); endh=[1 1 1 1 1]; y=conv(x,h) m=0:8;stem(m,y,'filled')P2。
已知复指数序列(1.52)[] 1.2j nx n e +=,绘制20点该序列的实部和虚部。
n=0:19;x=1.2*exp((1.5+j*2)*n); subplot(211); stem(n,real(x)); ylabel('real part'); xlabel('n'); legend('x[n]'); subplot(212); stem(n,imag(x)); ylabel('imag part'); xlabel('n'); legend('x[n]');P3.编写长度为5的中值滤波器程序。
原始未受干扰的序列为:s[n]=3[n(0.5) ]n ,加性噪声信号d[n]为随机序列,幅度0.4,分别绘制长度为40的受干扰序列,以及中值滤波器的输出。
% Program 2_5% Illustration of Median Filtering N = 5; R = 40;a = 0.8*rand(1,R)-0.4;b = round(a); % Generate impulse noise m = 0:R-1;s =3*m.*(0.5.^m); % Generate signalx = s + b; % Impulse noise corrupted signal y = medfilt1(x,N); % Median filtering subplot(2,1,1) stem(m,x);xlabel('n');ylabel('Amplitude');title('Impulse Noise Corrupted Signal'); subplot(2,1,2) stem(m,y);xlabel('n');ylabel('Amplitude'); title('Output of Median Filter'); P4. 已知序列x1[n]={2.2,3,1.5,4.2,1.8}, x2[n]= {0.8,1,1.6,0.8},x[n]=x1[n]∗x2[n] (卷积),分别绘制序列x1[n] ,x2[n]和x [n]的波形。
matlab20道试题及解答

试题1.“数学黑洞”:任意一个4位自然数,将组成该数的各位数字重新排列,形成一个最大数和一个最小数,之后两数相减,其差仍为一个自然数。
重复进行上述运算,最终会出现一个神秘的数,请编程输出这个神秘的数。
clear;a=input('请输入一个四位正整数:');str_a=num2str(a); %将a转化为一个字符串b_min=str2double(sort(str_a)); %形成最小数b_max=str2double(sort(str_a,'descend')); %形成最大数b=b_max-b_min; %求最大数与最小数之差while (b~=a)a=b;str_a=num2str(a); %将a转化为一个字符串b_min=str2double(sort(str_a)); %形成最小数b_max=str2double(sort(str_a,'descend')); %形成最大数b=b_max-b_min; %求最大数与最小数之差endb试题2.将数字1、2、3、4、5、6填入一个2行3列的表格中,要使得每一列右边的数字比左边的数字大,每一行下面的数字比上面的数字大。
请编写程序求出按此要求可有几种填写方法。
a(1)=1;a(6)=6;count=0; %用来计数b=perms('2345'); %产生2345的全排列[m,n]=size(b);for i=1:mtemp=b(i,:);a(2)=str2double(temp(1));a(3)=str2double(temp(2));a(4)=str2double(temp(3));a(5)=str2double(temp(4));if ((a(4)>a(2))&&(a(4)>a(3))&&(a(5)>a(3)))count=count+1;c=reshape(a,2,3); %将a向量转化为2*3矩阵输出disp(c);endenddisp(['共有',num2str(count),'种填写方法']); %输出填写方法的种数试题3.编写成绩排序程序。
完整word版,Matlab课后习题

习题 11. 执行下列指令,观察其运算结果, 理解其意义: (1) [1 2;3 4]+10-2i(2) [1 2; 3 4].*[0.1 0.2; 0.3 0.4] (3) [1 2; 3 4].\[20 10;9 2] (4) [1 2; 3 4].^2 (5) exp([1 2; 3 4]) (6)log([1 10 100]) (7)prod([1 2;3 4])(8)[a,b]=min([10 20;30 40]) (9)abs([1 2;3 4]-pi)(10) [1 2;3 4]>=[4,3;2 1](11)find([10 20;30 40]>=[40,30;20 10])(12) [a,b]=find([10 20;30 40]>=[40,30;20 10]) (提示:a 为行号,b 为列号) (13) all([1 2;3 4]>1) (14) any([1 2;3 4]>1) (15) linspace(3,4,5) (16) A=[1 2;3 4];A(:,2)2. 执行下列指令,观察其运算结果、变量类型和字节数,理解其意义: (1) clear; a=1,b=num2str(a),c=a>0, a= =b, a= =c, b= =c (2) clear; fun='abs(x)',x=-2,eval(fun),double(fun)3. 本金K 以每年n 次,每次p %的增值率(n 与p 的乘积为每年增值额的百分比)增加,当增加到rK 时所花费的时间为)01.01ln(ln p n rT +=(单位:年)用MA TLAB 表达式写出该公式并用下列数据计算:r =2, p =0.5, n =12.4.已知函数f (x )=x 4-2x 在(-2, 2)内有两个根。
取步长h =0.05, 通过计算函数值求得函数的最小值点和两个根的近似解。
matlab上机练习题答案(可编辑修改word版)

a ⎣ ⎦ 1. 计算 a = 5⎦ >> a=[6 9 3;2 7 5]; >> b=[2 4 1;4 6 8]; >> a.*b ans =⎣4 8⎦>> d=deconv([3 13 6 8],[1 4]) d =312⎡2 4 7 4⎤⎡8⎤1236 36 求欠定方程组⎢9 3 5 6⎥ x = ⎢5⎥ 的最小范数解84240⎡4 9 2⎤⎡37⎤⎣ >> a=[2 4 7 4;9 3 5 6]; >> b=[8 5]'; ⎦ ⎣ ⎦2. 对于 AX = B ,如果 A = ⎢7 6 4⎥ , B = ⎢26⎥ ,求解 X 。
>> x=pinv(a)*b⎢ ⎥ ⎢ ⎥x =>> A=[4 9 2;7 6 4;3 5 7]; >> B=[37 26 28]’; >> X=A\B X =⎢⎣3 5 7⎥⎦ ⎢⎣28⎥⎦-0.2151 0.4459 0.7949 0.27077 用符号函数法求解方程 a t 2+b*t +c=0-0.5118 >> r=solve('a*t^2+b*t+c=0','t') 4.0427 r =1.3318[ 1/2/a*(-b+(b^2-4*a*c)^(1/2))] ⎡1 2 5 ⎤ ⎡8 - 7 4⎤ [ 1/2/a*(-b-(b^2-4*a*c)^(1/2))]3. a = ⎢3 6 - 4⎥ , b = ⎢3 6 2⎥ ,观察 a 与 b 之间的⎣ ⎦ ⎣ ⎦⎡a 11 a 12 ⎤六种关系运算的结果 >> a=[1 2 3;4 5 6];8 求矩阵 A = ⎢ ⎣ 21 ⎥ 的行列式值、逆和特征根a 22 ⎦>> b=[8 –7 4;3 6 2];>> syms a11 a12 a21 a22;>> a>b >> A=[a11,a12;a21,a22] ans =>> AD=det(A) % 行列式 0 1 0 >> AI=inv(A) % 逆 11>> AE=eig(A) % 特征值 >> a>=b ans =0 1 0 1 01>> a<b ans =1 0 1 0 1>> a<=b ans =1 0 1 010 A = [ a11, a12][ a21, a22] AD =a11*a22-a12*a21 AI =[ -a22/(-a11*a22+a12*a21), a12/(-a11*a22+a12*a21)] [ a21/(-a11*a22+a12*a21), -a11/(-a11*a22+a12*a21)] AE = [1/2*a11+1/2*a22+1/2*(a11^2- 2*a11*a22+a22^2+4*a12*a21)^(1/2)] [1/2*a11+1/2*a22-1/2*(a11^2->> a==b2*a11*a22+a22^2+4*a12*a21)^(1/2)] ans =9 因式分解: x 4 - 5x 3 + 5x 2 + 5x - 60 0 0 >> syms x;0 00 >> f=x^4-5*x^3+5*x^2+5*x-6; >> a~=b ans =>> factor(f) ans =(x-1)*(x-2)*(x-3)*(x+1)4 计算多项式乘法(x 2+2x +2)(x 2+5x +4) ⎡10 f = ⎢ x 21 x ⎤⎥ ,用符号微分求 df/dx 。
matlab习题及答案

matlab习题及答案Matlab习题及答案Matlab是一种强大的数学计算软件,被广泛应用于科学计算、数据分析和工程设计等领域。
在学习和使用Matlab的过程中,习题是一种非常有效的学习方式。
本文将给出一些常见的Matlab习题及其答案,帮助读者更好地掌握Matlab的使用技巧。
一、基础习题1. 计算1到100之间所有奇数的和。
解答:```matlabsum = 0;for i = 1:2:100sum = sum + i;enddisp(sum);```2. 编写一个函数,计算任意两个数的最大公约数。
解答:```matlabfunction gcd = computeGCD(a, b)while b ~= 0temp = b;a = temp;endgcd = a;end```3. 编写一个程序,生成一个5×5的随机矩阵,并计算矩阵的行和列的平均值。
解答:```matlabmatrix = rand(5);row_average = mean(matrix, 2);col_average = mean(matrix);disp(row_average);disp(col_average);```二、进阶习题1. 编写一个程序,实现插入排序算法。
解答:```matlabfunction sorted_array = insertionSort(array)n = length(array);for i = 2:nj = i - 1;while j > 0 && array(j) > keyarray(j+1) = array(j);j = j - 1;endarray(j+1) = key;endsorted_array = array;end```2. 编写一个程序,实现矩阵的转置。
解答:```matlabfunction transposed_matrix = transposeMatrix(matrix) [m, n] = size(matrix);transposed_matrix = zeros(n, m);for i = 1:mfor j = 1:ntransposed_matrix(j, i) = matrix(i, j);endendend```3. 编写一个程序,实现二分查找算法。
matLAB经典例题及答案
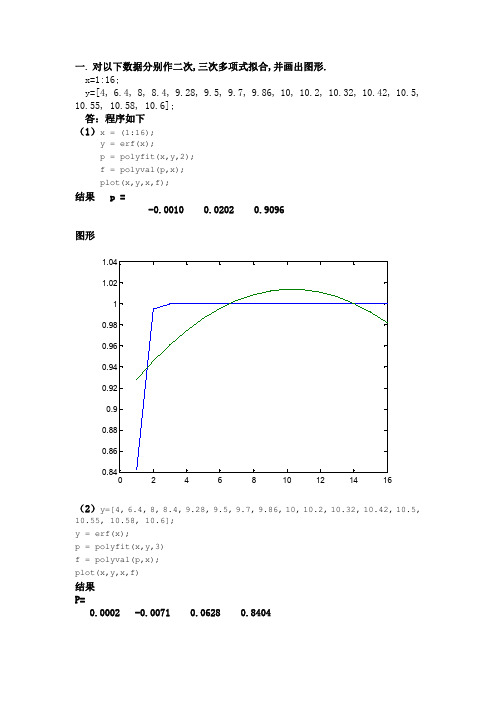
一.对以下数据分别作二次,三次多项式拟合,并画出图形.x=1:16;y=[4,6.4,8,8.4,9.28,9.5,9.7,9.86,10,10.2,10.32,10.42,10.5, 10.55,10.58,10.6];答:程序如下(1)x=(1:16);y=erf(x);p=polyfit(x,y,2);f=polyval(p,x);plot(x,y,x,f);结果p=-0.00100.02020.9096(2)y=[4,6.4,8,8.4,9.28,9.5,9.7,9.86,10,10.2,10.32,10.42,10.5, 10.55,10.58,10.6];y=erf(x);p=polyfit(x,y,3)f=polyval(p,x);plot(x,y,x,f)结果P=0.0002-0.00710.06280.8404二.在[0,4pi]画sin(x),cos(x)(在同一个图象中);其中cos(x)图象用红色小圆圈画.并在函数图上标注“y=sin(x)”,“y=cos(x)”,x轴,y轴,标题为“正弦余弦函数图象”.答:程序如下x=[0:720]*pi/180;plot(x,sin(x),x,cos(x),'ro');x=[2.5;7];y=[0;0];s=['y=sin(x)';'y=cos(x)'];text(x,y,s);xlabel('正弦余弦函数图象'),ylabel('正弦余弦函数图象')图形如下三.选择一个单自由度线性振动系统模型,自定质量、弹簧刚度、阻尼、激振力等一组参数,分别编程(m 文件)计算自由和强迫振动时的响应,并画出振动曲线图。
(要求画出该单自由度线性振动系统模型图)其中质量为m=1000kg,弹性刚度k=48020N/m,阻尼c=1960N.s/m,激振力f(t)=0.阻尼比ζ的程序p=1960/(2*sqrt(48020*1000))求得p=0.1414而p为阻尼比ζ强迫振动时的响应程序g =tf([-101],[48020048020*1.9848020]);bode(g)图形g =tf([001],[0001]);bode(g)振动曲线图程序:函数文件function dx =rigid(t,x)dx =zeros(2,1);dx(1)=x(2);dx(2)=(-48020*x(1)-1960*x(2))/1000;命令文件options =odeset('RelTol',1e-4,'AbsTol',[1e-41e-4]);[T,X]=ode45(@rigid,[012],[11],options);plot(T,X(:,1),'-')其图形如下024681012-6-5-4-3-2-11234单自由度线性强迫振动系统模型图其中质量为m=1000kg,弹性刚度k=48020N/m,阻尼c=1960N.s/m,f(t)=cos(3*pi*t)振动曲线图程序:函数文件function dx=rigid(t,x)dx=zeros(2,1);dx(1)=x(2);dx(2)=(-48020*x(1)-1960*x(2))/1000+cos(3*pi*t);命令文件options=odeset('RelTol',1e-4,'AbsTol',[1e-41e-4]);[T,X]=ode45(@rigid,[020],[11],options);plot(T,X(:,1),'-')力等一组参数,建立Simulink仿真模型框图进行仿真分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 第 1 章 MATLAB 概论1.1与其他计算机语言相比较,MATLAB 语言突出的特点是什么?MATLAB 具有功能强大、使用方便、输入简捷、库函数丰富、开放性强等特点。
1.2MATLAB 系统由那些部分组成?MATLAB 系统主要由开发环境、MATLAB 数学函数库、MATLAB 语言、图形功能和应用程序接口五个部分组成。
1.4MATLAB 操作桌面有几个窗口?如何使某个窗口脱离桌面成为独立窗口?又如何将脱离出去的窗口重新放置到桌面上?在MATLAB 操作桌面上有五个窗口,在每个窗口的右上角有两个小按钮,一个是关闭窗口的 Close 按钮,一个是可以使窗口成为独立窗口的 Undock 按钮,点击 Undock 按钮就可以使该窗口脱离桌面成为独立窗口,在独立窗口的 view 菜单中选择Dock ……菜单项就可以将独立的窗口重新防止的桌面上。
1.5如何启动 M 文件编辑/调试器?在操作桌面上选择“建立新文件”或“打开文件”操作时,M 文件编辑/调试器将被启动。
在命令窗口中键入 edit 命令时也可以启动 M 文件编辑/调试器。
1.6存储在工作空间中的数组能编辑吗?如何操作?存储在工作空间的数组可以通过数组编辑器进行编辑:在工作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输入修改内容即可。
1.7命令历史窗口除了可以观察前面键入的命令外,还有什么用途?命令历史窗口除了用于查询以前键入的命令外,还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到 M 文件中。
1.8如何设置当前目录和搜索路径,在当前目录上的文件和在搜索路径上的文件有什么区别?当前目录可以在当前目录浏览器窗口左上方的输入栏中设置,搜索路径可以通过选择操作桌面的 file 菜单中的 Set Path 菜单项来完成。
在没有特别说明的情况下,只有当前目录和搜索路径上的函数和文件能够被 MATLAB 运行和调用,如果在当前目录上有与搜索路径上相同文件名的文件时则优先执行当前目录上的文件,如果没有特别说明,数据文件将存储在当前目录上。
1.9在 MATLAB 中有几种获得帮助的途径?在MATLAB 中有多种获得帮助的途径:(1)帮助浏览器:选择 view 菜单中的 Help 菜单项或选择 Help 菜单中的 MATLAB Help 菜单项可以打开帮助浏览器;(2)help 命令:在命令窗口键入“help” 命令可以列出帮助主题,键入“help函数名”可以得到指定函数的在线帮助信息;(3)lookfor 命令:在命令窗口键入“lookfor 关键词”可以搜索出一系列与给定关键词相关的命令和函数(4)模糊查询:输入命令的前几个字母,然后按 Tab 键,就可以列出所有以这几个字母开始的命令和函数。
注意:lookfor 和模糊查询查到的不是详细信息,通常还需要在确定了具体函数名称后用 help 命令显示详细信息。
第 2 章 MATLAB 矩阵运算基础⎡5 2.1在MATLAB 中如何建立矩阵⎢⎣ 7 3⎤⎥,并将其赋予变量 a?9 ⎦>> a=[5 7 3;4 9 1]2.2有几种建立矩阵的方法?各有什么优点?可以用四种方法建立矩阵:①直接输入法,如 a=[2 5 7 3],优点是输入方法方便简捷;②通过 M 文件建立矩阵,该方法适用于建立尺寸较大的矩阵,并且易于修改;③由函数建立,如 y=sin(x),可以由 MATLAB 的内部函数建立一些特殊矩阵;④通过数据文件建立,该方法可以调用由其他软件产生数据。
2.3在进行算术运算时,数组运算和矩阵运算各有什么要求?进行数组运算的两个数组必须有相同的尺寸。
进行矩阵运算的两个矩阵必须满足矩阵运算规则,如矩阵 a 与b 相乘(a*b)4⎣⎦ 2.4 数组运算和矩阵运算的运算符有什么区别?在加、减运算时数组运算与矩阵运算的运算符相同,乘、除和乘方运算时,在矩阵运算的运算符前加一个点即为数组运算, 如 a*b 为矩阵乘,a.*b 为数组乘。
⎡5 3 5⎤ ⎡2 4 2⎤ 2.5 计算矩阵⎢3 7 4⎥ 与⎢6 7 9⎥ 之和。
⎢ ⎢⎣7 9 ⎥ 8⎥⎦ ⎢ ⎢⎣8 ⎥3 6⎥⎦>> a=[5 3 5;3 7 4;7 9 8];>> b=[2 4 2;6 7 9;8 3 6];>> a+bans =77 7 914 13 15 12 14⎡4 + 8i 2.6 求 x = ⎢3 + 2i 3 + 5i 7 - 6i 2 - 7i 9 + 4i 1+ 4i 3 - 9i 7 - 5i ⎤4 + 4i ⎥ 的共轭转置。
>> x=[4+8i 3+5i 2-7i 1+4i 7-5i;3+2i 7-6i 9+4i 3-9i 4+4i];>> x ’ans =4.0000 - 8.0000i3.0000 - 2.0000i 3.0000 - 5.0000i7.0000 + 6.0000i 2.0000 + 7.0000i9.0000 - 4.0000i 1.0000 - 4.0000i3.0000 + 9.0000i 7.0000 + 5.0000i4.0000 - 4.0000i⎡6 9 3⎤ ⎡2 4 1⎤ 2.7 计算 a = ⎢2 7 5⎥ 与b = ⎢4 6 8⎥ 的数组乘积。
⎣ ⎦ ⎣ ⎦>> a=[6 9 3;2 7 5];>> b=[2 4 1;4 6 8];>> a.*bans =1236 3 8 42 402.8 “左除”与“右除”有什么区别?在通常情况下,左除 x=a\b 是 a*x=b 的解,右除 x=b/a 是 x*a=b 的解,一般情况下,a\b ≠b/a 。
⎡4 9 2⎤ ⎡37⎤ 2.9 对于 AX = B ,如果 A = ⎢7 6 4⎥ , B = ⎢26⎥ ,求解 X 。
⎢ ⎥ ⎢ ⎥⎢⎣3 5 7⎥⎦ ⎢⎣28⎥⎦>> A=[4 9 2;7 6 4;3 5 7];>> B=[37 26 28]’;>> X=A\B⎢ ⎥ -0.51184.04271.3318⎡1 2.10 已知: a = ⎢4 ⎢⎣72 3⎤ 5 6⎥ ,分别计算 a 的数组平方和矩阵平方,并观察其结果。
8 9⎥⎦>> a=[1 2 3;4 5 6;7 8 9];>> a.^2ans =14 9 1625 36 4964 81>> a^2 ans =3036 42 66 81 96 102 126 150⎡1 2 5 ⎤ ⎡8 - 7 4⎤ 2.11 a = ⎢3 6 - 4⎥ , b = ⎢3 6 2⎥ ,观察 a 与 b 之间的六种关系运算的结果。
⎣ ⎦ ⎣ ⎦>> a=[1 2 3;4 5 6];>> b=[8 –7 4;3 6 2];>> a>bans =1 0 10 1 >> a>=bans =0 1 0 10 1 >> a<bans =1 0 1 01 0 >> a<=bans =1 0 1 01 0 >> a==bans =0 0 0 00 0>> a~=b⎢ ⎥ 11 1 11 12.12 a = [5 0.2 0 -8 -0.7],在进行逻辑运算时,a 相当于什么样的逻辑量。
相当于 a=[1 1 0 1 1]。
2.13 在 sin(x )运算中,x 是角度还是弧度?在 sin(x)运算中,x 是弧度,MATLAB 规定所有的三角函数运算都是按弧度进行运算。
2.14 角度 x = [30 45>> x=[30 45 60];>> x1=x/180*pi;>> sin(x1)ans =60],求 x 的正弦、余弦、正切和余切。
0.50000.7071 0.8660 >> cos(x1)ans =0.86600.7071 0.5000 >> tan(x1)ans =0.57741.0000 1.7321 >> cot(x1)ans =1.73211.0000 0.57742.15 用四舍五入的方法将数组[2.4568 6.39823.9375 8.5042]取整。
>> b=[2.4568 6.3982 3.9375 8.5042];>> round(b)ans =2 6 4 9⎡9 1 2.16 矩阵 a = ⎢5 6 ⎢⎣8 22⎤ 3⎥ ,分别对 a 进行特征值分解、奇异值分解、LU 分解、QR 分解及 Chollesky 分解。
7⎥⎦>> [v,d]=eig(a,b)v =-0.4330 -0.2543 -0.1744-0.56570.9660 -0.6091 -0.70180.0472 0.7736d =13.54820 00 4.8303 0 0 03.6216 >> a=[9 1 2;5 6 3;8 2 7];5 762 83u =-0.5601 0.5320 -0.6350-0.4762 -0.8340 -0.2788-0.6779 0.1462 0.7204s =15.5234 0 00 4.5648 00 0 3.3446v =-0.8275 0.3917 -0.4023-0.3075 -0.9156 -0.2592-0.4699 -0.0907 0.8781>> [l,u]=lu(a)l =1.0000 0 00.5556 1.0000 00.8889 0.2041 1.0000u =9.0000 1.0000 2.00000 5.4444 1.88890 0 4.8367>> [q,r]=qr(a)q =-0.6903 0.3969 -0.6050-0.3835 -0.9097 -0.1592-0.6136 0.1221 0.7801r =-13.0384 -4.2183 -6.82600 -4.8172 -1.08070 0 3.7733>> c=chol(a)c =3.0000 0.3333 0.66670 2.4267 1.14470 0 2.2903⎡4 2⎤ ⎡7 1⎤ ⎡5 9⎤2.17 将矩阵a =⎢5 7⎥、b =⎢8 3⎥和c =⎢6 2⎥组合成两个新矩阵:⎣⎦⎣⎦⎣⎦(1)组合成一个 4 3 的矩阵,第一列为按列顺序排列的 a 矩阵元素,第二列为按列顺序排列的 b 矩阵元素,第三列为按列顺序排列的 c 矩阵元素,即⎡4 7 5⎤⎢⎥⎢⎥⎢2 1 9⎥⎢⎥⎣⎦[4 5 2 7 7 8 1 3 5 6 9 2]>> a=[4 2;5 7];>> b=[7 1;8 3];>> c=[5 9;6 2];% (1)>> d=[a(:) b(:) c(:)]d =4 7 55 8 62 1 97 3 2% (2)>> e=[a(:);b(:);c(:)]'e =4 5 2 7 7 8 1 3 5 6 9 2或利用(1)中产生的 d>> e=reshape(d,1,12)ans =4 5 2 7 7 8 1 3 5 6 9 2第 3 章数值计算基础3.2 求解多项式x3-7x2+2x+40=0 的根。
