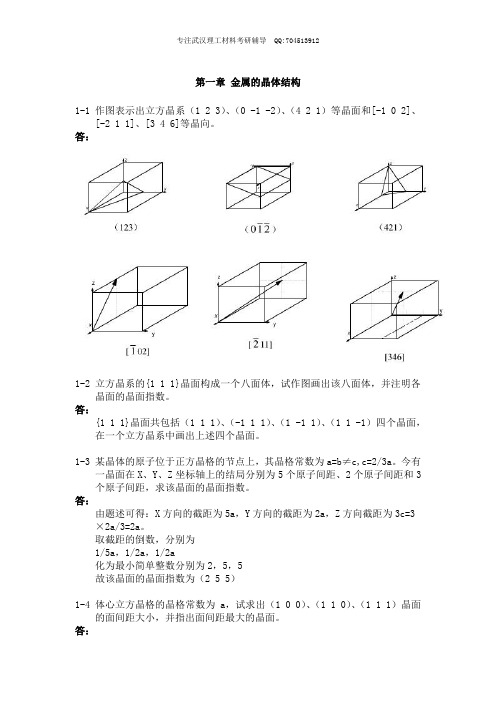
体心立方晶格与面心立方晶格
《固体物理学》房晓勇主编教材-习题解答参考01第一章 晶体的结构

(h
2 1
2 + k + l12 ) i( h22 + k22 + l2 ) 2 1 12
h1h2 + k1k2 + l1l2
12
பைடு நூலகம்
解:三个晶轴相互垂直且等于晶格常数 a,则晶胞基矢为
a1 = ai, a2 = a j, a3 = ak ,
其倒格子基矢为
b1 =
2π 2π 2π i, b2 = i, b3 = i a a a 2π ( hi + k j + lk ) a
a 2 +j a 0 − 2
a 2
a 2 +k a 0 2
0 a 2
=−
b 1=
a2 a2 a2 i+ j+ k 4 4 4
2π 2π a 2 ⎛ a 2 a2 a2 a 2 × a3 = 3 − i + j + ⎜ a Ω 2 ⎝ 4 4 4 4 2π 2π b 2= i − j + k ,b 3= i+ j−k a a
i = −( h + k )
得证 (2)由上可知,h,k,i 不是独立的, ( 001) , 133 , 110 , 323 , (100 ) , ( 010 ) , 213 . 中各 i 等于
( )( )( )
( )
i1 = −(h1 + k1 ) = −(0 + 0) = 0, i2 = 2 , i3 = 0 , i4 = 1 , i5 = 1 i6 = 1 , i7 = 3 即得
a1 ⋅ n = h1d , a2 ⋅ nh2 d , a3 ⋅ n = h3d ,
假定 h1 , h2 , h3 不是互质的数,则有公约数 p,且 p>1;设 k1 , k2 , k3 为互质的三个数,满足
《金属学与热处理》崔忠圻(第二版)课后答案完整版
第一章金属的晶体结构1-1 作图表示出立方晶系(1 2 3)、(0 -1 -2)、(4 2 1)等晶面和[-1 0 2]、[-2 1 1]、[3 4 6]等晶向。
答:1-2 立方晶系的{1 1 1}晶面构成一个八面体,试作图画出该八面体,并注明各晶面的晶面指数。
答:{1 1 1}晶面共包括(1 1 1)、(-1 1 1)、(1 -1 1)、(1 1 -1)四个晶面,在一个立方晶系中画出上述四个晶面。
1-3 某晶体的原子位于正方晶格的节点上,其晶格常数为a=b≠c,c=2/3a。
今有一晶面在X、Y、Z坐标轴上的结局分别为5个原子间距、2个原子间距和3个原子间距,求该晶面的晶面指数。
答:由题述可得:X方向的截距为5a,Y方向的截距为2a,Z方向截距为3c=3×2a/3=2a。
取截距的倒数,分别为1/5a,1/2a,1/2a化为最小简单整数分别为2,5,5故该晶面的晶面指数为(2 5 5)1-4 体心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:H==a/2(1 0 0)==√2a/2H(1 1 0)==√3a/6H(1 1 1)面间距最大的晶面为(1 1 0)1-5 面心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:==a/2H(1 0 0)H==√2a/4(1 1 0)==√3a/3H(1 1 1)面间距最大的晶面为(1 1 1)注意:体心立方晶格和面心立方晶格晶面间距的计算方法是:1、体心立方晶格晶面间距:当指数和为奇数是H=,当指数和为偶数时H=2、面心立方晶格晶面间距:当指数不全为奇数是H=,当指数全为奇数是H=。
1-6 试从面心立方晶格中绘出体心正方晶胞,并求出它的晶格常数。
答:1-7 证明理想密排六方晶胞中的轴比c/a=1.633。
七种晶系

正方形晶格:
、
六角形晶格:
、
矩形晶格:
、
有心矩形晶格
三维晶格类型
、
,但在矩形晶格正中间上有一晶格点,固有两种绘法。
布拉维晶格在三维平面上有七大晶系,14 种晶格分别为三斜晶系、单斜晶系、正交晶系、 四方晶系、立方晶系、三方晶系、六方晶系。依照简单、体心、面心及底心,总共有 14 种 晶格。
晶系与布拉维格子及空间点群的关系[编辑]
晶系 crystal system
根据晶体的特征对称元素所进行的分类。晶体根据其在晶体理想外形或综合 宏观物理性质中呈现的特征对称元素可划分为立方、六方、三方、四方、正交、 单斜、三斜等 7 类,是为 7 个晶系,分属于 3 个不同的晶族。高级晶族中只有一 个立方晶系;中级晶族中有六方、四方和三方三个晶系;低级晶族中有正交、单 斜和三斜三个晶系。特征对称元素亦能确认与每种晶系对应晶胞的形状或晶胞参 数相关性的特征。各晶系的晶胞类型一般用晶胞参数 a、b、c 和 α、β、γ 表示。 其中 a、b 和 c 是晶胞三个边的长度,习惯上叫轴长,α、β 和 γ 叫轴角,它们分 别是 b 和 c、a 和 c、a 和 b 的夹角。如唯一高次轴方向四重轴或反轴的存在决定 晶体属四方晶系并具有四方柱形状的晶胞,晶胞参数必有 a=b≠c 和 α=β=γ=90° 的相关性。
面心立方晶 立 方 晶
格
系
氯化铯结构
CsCl structure B2 型
简单立方晶 立 方 晶
格
系
立方硫化锌结构[10]
zinc
blende B3 型
ቤተ መጻሕፍቲ ባይዱ
[11]
structure
立方晶 系
六方硫化锌结构
wurtzite structure B4 型
固体物理课后习题答案

(
)
⎞ 2π k⎟= −i + j + k 同理 ⎠ a
(
)
(
)
(
)
2π ⎧ ⎪b1 = a −i + j + k ⎪ 2π ⎪ i− j+k ⎨b 2 = a ⎪ 2π ⎪ ⎪b3 = a i + j − k ⎩
(
)
(
)
(
)
由此可得出面心立方格子的倒格子为一体心立方格子; 所以体心立方格子和面心立方格子互为正倒格子。 2.2 在六角晶系中,晶面常用四个指数(hkil)来表示,如图 所示,前三个指数表示晶面族中最靠近原点的晶面在互成 1200的 共面轴 a1 , a2 , a3 上的截距为
设两法线之间的夹角满足
K 1 i K 2 = K1 i K 2 cos γ
K 1iK 2 cos γ = = K1 i K 2 2π 2π (h1 i + k1 j + l1 k )i (h2 i + k2 j + l2 k ) a a 2π 2π 2π 2π (h1 i + k1 j + l1 k )i (h1 i + k1 j + l1 k ) i (h2 i + k2 j + l2 k )i (h2 i + k2 j + l2 k ) a a a a
a1 a2 a3 , , ,第四个指数表示该晶面 h k i
在六重轴c上的截距为
c 。证明: l
i = −(h + k )
并将下列用(hkl)表示的晶面改用(hkil)表示:
2
第一章 晶体的结构
( 001) , (133) , (110 ) , ( 323) , (100 ) , ( 010 ) , ( 213) .
固体物理 讲习题参考答案

解:(1)由平衡条件
∂U ∂r
r0
=
mα r m+1
−
nβ r n+1
=
0 ,得
1
平衡间距
r0
=
nβ mα
n−m
(2)将 U(r)理解为晶体中所有其他原子对某一个原子的相互作用
则系统总的内能为对所有原子求和
U
total
2
r0 ∝ q1−n
,
U0
∝
q2 r0
当 q → 2q ,
r0′
=
4−
1 n−1
r0
因为晶格常数 a ∝ r0 ,故晶格常数满足相同的变化规律
n
结合能 W ′ = −U0′ = 4n−1W0
2.3.若一晶体的相互作用能可以表示为
U (r) = − α + β rm rn
试求(1)平衡间距 r0 (2)结合能 W(单个原子的) (3)体弹性模量 (4)若 m=2,n=10,r0=3A,W=4eV,求α,β值。
1.11
证明六角晶体的介电常数张量为
0
ε2
0
0 0 ε2
证
1:六角晶体,设介电常数为
ε ε
xx yx
ε xy ε yy
ε ε
xz yz
,取坐标架如图示
ε zx ε zy ε zz
选电场方向在 x 轴方向,有
Dx ε xx
Dy
0
− sin 60
,可得
ε yy
= ε zz
cos 60
第六讲
2.2.讨论使离子电荷加倍所引起的对 NaCl 晶格常数及结合能得影响。(排斥势看作不变) 解:NaCl 为离子晶体,系统内能可写为
《固体物理学》部分习题解答

《固体物理学》部分习题解答1.3 证明:体心立方晶格的倒格子是面心立方;面心立方晶格的倒格子是体心立方。
解由倒格子定义体心立方格子原胞基矢倒格子基矢同理可见由为基矢构成的格子为面心立方格子面心立方格子原胞基矢倒格子基矢同理可见由为基矢构成的格子为体心立方格子1.4 证明倒格子原胞的体积为,其中为正格子原胞体积证倒格子基矢倒格子体积1.5证明:倒格子矢量垂直于密勒指数为的晶面系。
证:容易证明与晶面系正交。
1.6如果基矢构成简单正交系证明晶面族的面间距为说明面指数简单的晶面,其面密度较大,容易解理证简单正交系倒格子基矢倒格子矢量晶面族的面间距面指数越简单的晶面,其晶面的间距越大晶面上格点的密度越大,这样的晶面越容易解理1.9 指出立方晶格(111)面与(100)面,(111)面与(110)面的交线的晶向解(111)面与(100)面的交线的AB-AB平移,A与O重合。
B点位矢(111)与(100)面的交线的晶向——晶向指数(111)面与(110)面的交线的AB——将AB平移,A与原点O重合,B点位矢(111)面与(110)面的交线的晶向――晶向指数2.1.证明两种一价离子组成的一维晶格的马德隆常数为.证设想一个由正负两种离子相间排列的无限长的离子键,取任一负离子作参考离子(这样马德隆常数中的正负号可以这样取,即遇正离子取正号,遇负离子取负号),用r表示相邻离子间的距离,于是有前边的因子2是因为存在着两个相等距离的离子,一个在参考离子左面,一个在其右面,故对一边求和后要乘2,马德隆常数为当X=1时,有2.3 若一晶体的相互作用能可以表示为求1)平衡间距2)结合能W(单个原子的)3)体弹性模量4)若取,计算值。
解1)晶体内能平衡条件2) 单个原子的结合能3) 体弹性模量晶体的体积——A为常数,N为原胞数目晶体内能体弹性模量由平衡条件体弹性模量()4)2.6.用林纳德—琼斯(Lennard—Jones)势计算Ne在bcc(球心立方)和fcc(面心立方)结构中的结合能之比值.解2.7.对于,从气体的测量得到Lennard—Jones势参数为计算结合成面心立方固体分子氢时的结合能(以KJ/mol单位),每个氢分子可当做球形来处理.结合能的实验值为0.751kJ/mo1,试与计算值比较.解以为基团,组成fcc结构的晶体,如略去动能,分子间按Lennard—Jones势相互作用,则晶体的总相互作用能为:因此,计算得到的晶体的结合能为2.55KJ/mol,远大于实验观察值0.75lKJ/mo1.对于的晶体,量子修正是很重要的,我们计算中没有考虑零点能的量子修正,这正是造成理论和实验值之间巨大差别的原因.3.1.已知一维单原子链,其中第个格波,在第个格点引起的位移为,,为任意个相位因子,并已知在较高温度下每个格波的平均能量为,具体计算每个原子的平方平均位移。
固体物理第一章总结

固体物理(黄昆)第一章总结(总5页)页内文档均可自由编辑,此页仅为封面第一章晶体结构1.晶格实例1.1面心立方(fcc)配位数12 格点等价格点数4 致密度0.74原胞基矢:()()()123222aa j kaa k iaa i j=+=+=+原胞体积3123()/4Ωa a a a=⋅⨯=NaCl: 两组面心立方格子平行穿套而成的复式格子基元= Na+ + Cl-具有面心立方:简单格子(Al、Cu、Ag; Ar Kr Xe Ne)、复式格子(Cao MgS 碱卤族等)1.2简单立方(SC)配位数6 格点等价格点数1 致密度0.52CsCl两组简单立方格子穿套而成的复式结构基元= Cs+ + Cl-钙钛矿结构:CaTiO3五个简单立方穿套而成基元:Ca、Ti、OI、OII、OIII (OI、OII、OIII 的化学环境各不相同,氧八面体) 典型晶体:BaTiO3、PbZrO3、LiNbO3、LiTaO3氯化铯型结构: CsCl, CsBr, CsI, TlCl, TlBr, TlI 等1.3体心立方(bcc)配位数8 格点等价格点数2 致密度0.68原胞基矢:123()2()2()2aa i j kaa i j kaa i j k=-++=-+=+-原胞体积:3123()/2Ωa a a a=⋅⨯=体心立方晶体: 碱金属、W、Mo、Nb、V、Fe等1.4六角密堆(hcp)配位数12 两种格点原子数6 基元数3 致密度0.74典型晶体举例:He, Be, Mg, Ti, Zn, Cd, Co, Y, Lu 等1.5金刚石结构最近邻原子数4 次近邻原子数12 致密度0.34晶体结构=布拉维格子(面心立方)+ 基元(A+B)*将金刚石结构中的基元置换成一对硫离子和锌离子,则为两个面心立方复合而成的复式结构,典型晶体:SiC, ZnSe, AlAs, GaP, GaAs 等2.晶体的周期性结构2.1基本概念晶体:1. 化学性质相同 2. 几何环境相同 基元:晶体结构中最小的重复单元布拉维点阵(布拉维格子): 112233R n a n a n a =++ 晶体结构 = 布拉维格子+基元原胞:由基矢1a 、2a 、3a 确定的平行六面体,是体积最小的周期性结构单元,原胞只包含一个格点晶胞:同时计及周期性及对称性的尽可能小的重复单元,原胞实际上是体积最小的晶胞2.2维格纳-赛茨原胞(WS 原胞)1. 作某个格点与其它格点的连接矢量2. 作所有这些连接矢量的垂直平分面3. 这些垂直平分面围起的凸多面体就是维格纳-赛茨原胞3. 晶向、晶面及其标志 晶列(向)指数:[l m n]晶面指数(米勒指数):( h k l )米勒指数是以晶胞基矢为基准,而面指数则以原胞基矢为基准标定4. 布里渊区倒格子空间中的维格纳-赛茨(WS )原胞,即所谓的第一布里渊区,布里渊区包含了所有能在晶体上发生布拉格反射的波的波矢22h h k G G ⋅=4.1简单立方的倒格矢(简单立方——简单立方)基矢123a aia aj a ak ⎧=⎪=⎨⎪=⎩ 倒格矢123(2π/a)(2π/a)(2π/a)b i b j b k ⎧=⎪=⎨⎪=⎩4.2体心立方晶格的倒格子(体心立方——面心立方)基矢1231()21()21()2a a i j k a a i j k a a i j k ⎧=-++⎪⎪⎪=-+⎨⎪⎪=+-⎪⎩ 倒格矢1232π()2π()2π()b j k a b k i a b i j a ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩倒格矢可以表示为:1122332331122π[()()()]h G h b h b h b h h i h h j h h k a=++=+++++ 其中(h1 h2 h3)是米勒指数,h G 垂直于米勒指数,其第一布里渊区是一个正十二面体4.3面心立方晶格的倒格子(面心立方——体心立方)基矢1231()21()21()2a a j k a a k i a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩ 倒格矢1232π()2π()2π()b i j k a b i j k a b i j k a ⎧=-++⎪⎪⎪=-+⎨⎪⎪=+-⎪⎩第一布里渊区为截角八面体即5. 晶体的宏观对称性xx xy xz x x y yx yy yz y z zx zy zz z D E D E D E εεεεεεεεε⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭5.1对于所有立方对称的晶体中,介电常数是一个对角张量:0 (,,,)x y z αβαβεεδαβ==该结论适用于一切具有二阶张量形式的宏观性质 (如电导率、热导率)5.2六角对称的晶体中,若坐标轴选取在六角轴的方向和与它垂直的平面内,则介电常数有如下形式// 0 00 00 0 εεε⊥⊥⎛⎫ ⎪ ⎪ ⎪⎝⎭ ,//////D E ε=, D E ε⊥⊥⊥=,六角对称的晶体有双折射现象5.3对称操作(正交变换:旋转、中心反演、镜面反映) 1. 旋转绕 z 轴旋转 q 角的正交矩阵cos sin 0sin cos 0 0 0 1θθθθ-⎛⎫ ⎪⎪ ⎪⎝⎭,中心反演的正交矩阵1 0 0 0 1 0 0 0 1-⎛⎫⎪- ⎪ ⎪-⎝⎭由于cost = (1 - m)/2 所以 m = -1 0 1 2 3,所以t = 0 2π/6 2π/4 2π/3 2π/2,没有所谓的5度轴和7度轴。
机械工程材料-思考与练习题答案

能
10. 金属再结晶后的晶粒大小与( )和( )有关。预先变形度;再结晶温度
11. 工业金属不能在( )变形度进行变形,否则再结晶后的晶粒( ),使机械性能( )。
2-10%临界;粗大;降低
12. 铸钢锭经过热轧后,粗大的晶粒会( ),缩松、气孔等缺陷会( ),并且还会出现
(
)组织。细化;焊合;流线或纤维
晶粒细化
16. 金属热加工纤维组织是( )呈纤维状,此种组织的机械性能呈现( )。夹杂物及枝晶
偏析;方向性
17. 钢的锻造温度高于(
)温度,故属于( )加工。再结晶;热
18. 材料的弹性模量愈高,其刚度愈( )。刚度( )通过热处理改变;材料一定时,可通
过( )和(
)的方法来提高零件的刚度。高;不能;增加零件的横截面积;
版权归河北工业大学 材料学院 材料科学系所有--禁止在网上传播-----022-26582288
A,去应力退火 B,再结晶退火 C,完全退火 D,重结晶退火
3. 实测的晶体滑移需要的临界分切应力值比理论计算的小,这说明晶体滑移机制是( )。B
A,滑移面的刚性移动 B,位错在滑移面上运动 C,空位、间隙原子迁移 D,晶界迁移
A,属于热加工 B,属于冷加工 C,不是热加工或冷加工 D,无法确定
7. 晶体滑移总是沿着( )晶面和晶向进行。A
A,原子密度最大的 B,与外力成 45 度的 C,任意的 D,原子密度最小的
8. 为了提高零件的机械性能,通常将热轧圆钢中的流线(纤维组织)通过(
)。C
A,热处理消除 B,切削来切断 C,锻造使其分布合理 D,锻造来消除
相作用。∨ 5. 金属化合物以细小颗粒或片状均匀分布在固溶体中会使强度提高,化合物愈细小、分布愈均
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
体心立方、面心立方晶格主要晶面的原子排列和密度
体心立方晶格面心立方晶格
晶面指数晶面原子
排列示意图
晶面原子密度
(原子数/面积)
晶面原子
排列示意图
晶面原子密度
(原子数/面积)
{100} {110} {111}
体心立方、面心立方晶格主要晶向的原子排列和密度
体心立方晶格面心立方晶格
晶向指数晶向原子
排列示意图
晶向原子密度
(原子数/长度)
晶向原子
排列示意图
晶向原子密度
(原子数/长度)
<100>
<110>
<111>
第1章小结
1.三种常见金属的晶体结构
体心立方晶格(胞):晶格常数a、90°,晶胞原子数为2个,原子半径:,
致密度为68%,最大空隙半径r四=0.29r原子,配位数为8面心立方晶格(胞):晶格常数a、90°,晶胞原子数为4个,
原子半径:
,
致密度为74%,最大空隙半径r八=0.414r原子,配位数为12。
密排六方晶格(胞):晶格常数a、c、90°、120°,晶胞原子数为6个,
原子半径:,
致密度为74%,最大空隙半径r八=0.414r原子,配位数为12。
2.晶面与晶向可用晶面指数与晶向指数来表达。
不同晶面、不同晶向上的原子排列情况不同。
体心立方晶格的最密面为{110},最密方向为<111>。
面心立方晶格的最密面为{111},最密方向为<110>。
密排六方晶格的最密面为{0001},最密方向为。
3.实际金属中含有点缺陷(空位、间隙原子、异类原子)、线缺陷(位错)、面缺陷(晶界、亚晶界)三类晶体缺陷,位错密度增加,材料强度增加。
晶界越多,晶粒越细,金属的强度越高,同时塑性越好(即细晶强化)。
4.合金中有两类基本相:固溶体和金属化合物。
固溶强化是金属强化的一种重要形式。
细小弥散分布的金属化合物可产生弥散强化或第二相强化。
材料的微观组成和微观形貌称组织,材料的组织取决于化学成分和工艺过程。
5.金属材料的性能特点是:强度高,韧性好,塑性变形能力强,综合机械性能好,通过热处理可以大幅度改变机械性能。
金属材料导电、导热性好。
不同的金属材料耐蚀性相差很大,钛、不锈钢耐蚀性好,碳钢、铸铁耐蚀性差。
6.高分子材料结构由大分子链组成,大分子链之间的相互作用力为分子键,分子链的原子之间、链节之间的相互作用力为共价键。
高分子材料的大分子链结构与聚集态及其性能密切相关。
高分子的聚集态结构分无定形和晶态两种。
线型非晶态高聚物在不同温度下表现三种物理状态:玻璃态、高弹态、粘流态。
高分子材料的性能特点:高聚物轻,其特有的机械性能是高弹性和粘弹性。
由于可以处于不同的力学状态,高分子材料可以是硬脆、强硬、强韧、柔韧或软弱的,机械性能不高,刚度小,强度不高,韧性较低。
高分子材料耐磨、减摩性能好,绝缘、绝热、绝声,耐蚀性能好,但耐热性不高,存在老化问题。
7. 陶瓷材料的生产过程包括原料的制备、坯料的成形和制品的烧结三大步骤。
典型陶瓷的组织由晶体相、玻璃相和气相组成。
晶体相是陶瓷的主要组成,决定材料的基本性能。
普通陶瓷的晶体相主要是硅酸盐,特种陶瓷的晶体相为氧化物、碳化物、氮化物、硼化物和硅化物,金属陶瓷则还有金属。
玻璃相为非均质的酸性和碱性氧化物的非晶态固体,起粘结剂作用。
气相是陶瓷组织中残留的孔洞,极大地破坏材料的机械性能。
陶瓷的性能特点是:具有不可燃烧性、高耐热性、高化学稳定性、不老化性、高的硬度和良好的抗压能力,但脆性很高,温度急变抗力很低,抗拉、抗弯性能差,不易加工。
