求晶格常数为a的面心立方和体心立方晶体晶面族hhh的面间距

合集下载

材料科学基础习题库第一章-晶体结构

（一）．填空题1．同非金属相比，金属的主要特性是__________2．晶体与非晶体的最根本区别是__________3．金属晶体中常见的点缺陷是__________ ，最主要的面缺陷是__________ 。

4．位错密度是指__________ ，其数学表达式为__________ 。

5．表示晶体中原子排列形式的空间格子叫做__________ ，而晶胞是指__________ 。

6．在常见金属晶格中，原子排列最密的晶向，体心立方晶格是__________ ，而面心立方晶格是__________ 。

7．晶体在不同晶向上的性能是__________，这就是单晶体的__________现象。

一般结构用金属为__________ 晶体，在各个方向上性能__________ ，这就是实际金属的__________现象。

8．实际金属存在有__________ 、__________ 和__________ 三种缺陷。

位错是__________ 缺陷。

实际晶体的强度比理想晶体的强度__________ 得多。

9．常温下使用的金属材料以__________ 晶粒为好。

而高温下使用的金属材料在一定范围内以__________ 晶粒为好。

‘10．金属常见的晶格类型是__________、__________ 、__________ 。

11．在立方晶格中，各点坐标为：A (1，0，1)，B (0，1，1)，C (1，1，1/2)，D(1/2，1，1/2)，那么AB晶向指数为__________ ，OC晶向指数为__________ ，OD晶向指数为__________ 。

12．铜是__________ 结构的金属，它的最密排面是__________ ，若铜的晶格常数a=0.36nm,那么最密排面上原子间距为__________ 。

13 α-Fe、γ-Fe、Al、Cu、Ni、Pb、Cr、V、Mg、Zn中属于体心立方晶格的有__________ ，属于面心立方晶格的有__________ ，属于密排六方晶格的有__________ 。

面心立方晶面间距公式

面心立方晶面间距公式
面心立方晶格是一种常见的晶体结构，其原子排列方式为每个原子周围有12个等距离的原子。

在这种结构中，原子之间的键角为109.5度，因此每个面心立方晶胞包含8个原子。

面心立方晶格的晶面间距公式可以通过以下步骤推导得出：
1. 首先，我们需要找到晶胞中的两个相邻原子之间的距离。

由于每个原子周围有12个等距离的原子，因此这两个原子之间的距离等于一个晶胞边长的一半。

设晶胞边长为a,则相邻原子之间的距离为a/2。

2. 然后，我们需要找到晶胞中的三个相邻原子之间的夹角。

由于每个原子周围有12个等距离的原子，因此这三个原子之间的夹角等于一个面心立方晶胞的一个顶角。

设顶角为θ，则三个相邻原子之间的夹角为θ。

3. 最后，我们可以利用勾股定理计算出晶胞中的一个边长和一个高。

设晶胞中的一个边长为b,一个高为c,则有：
b^2 = a^2/4 + c^2 - 2accos(π/3)
c^2 = a^2/4 + b^2 - 2abcos(π/3)
将上述两个式子联立求解，得到：
b = (√6-√2)/4a
c = (√6+√2)/4a
因此，面心立方晶格的晶面间距公式为：d = a/√3。

固体物理题库-zzk-第一至第五章

第一章晶体结构和X 射线1、试证体心立方和面心立方各自互为正、倒格子2、如果基矢a,b,c 构成正交关系，证明晶面族（h k l ）的面间距满足：222)()()(1c l b k a hd hkl ++=3、证明以下结构晶面族的面间距：（1）立方晶系：d hkl =a [h 2+k 2+l 2]-1/2（2）六角晶系：2/12222])()(34[-+++=c l ahk k h d hkl 4、等体积的硬球堆积成体心立方结构和面心立方结构，试求他们在这两种结构中的致密度分别为0.68和0.74。

5、试证密积六方结构中，c/a=1.633。

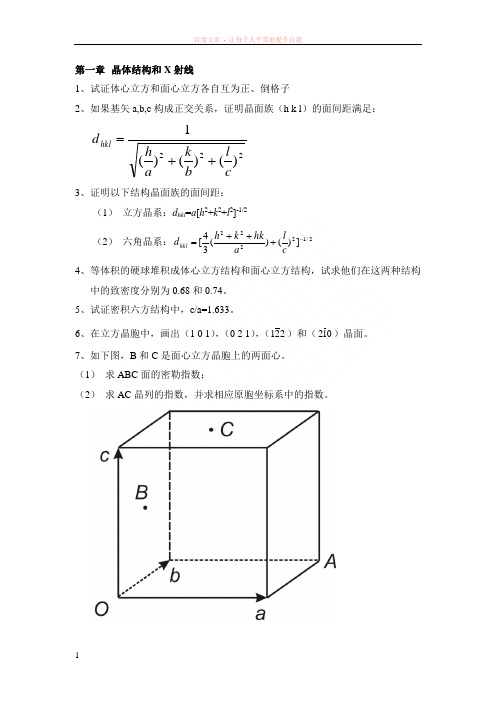
6、在立方晶胞中，画出（1 0 1），（0 2 1），（221）和（012）晶面。

7、如下图，B 和C 是面心立方晶胞上的两面心。

（1）求ABC 面的密勒指数；（2）求AC 晶列的指数，并求相应原胞坐标系中的指数。

8、六角晶胞的基矢为.,223,223k c c j a i a b j a i a a =+-=+=求其倒格子基矢。

9、求晶格常数为a 的面心立方和体心立方晶体晶面族（h 1 h 2 h 3）之间的面间距（指导p30,10）。

10、讨论六角密积结构，X 光衍射的消光条件。

11、求出体心立方、面心立方的几何因子和消光条件。

12、原胞和晶胞的区别？13、倒空间的物理意义？14、布拉格衍射方程，原子和几何结构因子在确定晶格结构上分别起何作用？15、什么是布拉格简单格子，什么是复式格子？第二章自由电子气1、设有一个长度为L 的一维金属线，它有N 个导电电子，若把这些导电电子看成自由电子气，试求：（1）电子的状态密度（2）绝对零度下的电子费米能级，以及费米能级随温度的变化关系。

（3）电子的平均能量。

（4）电子的比热。

2、二维电子气的能态密度2)( πm E N =，证明费米能 ]1ln[/2-=T mk n B F b eT k E π 3、求出一维金属中自由电子的能态密度、费米能级、电子的平均动能以及一个电子对于比热的贡献。

固体物理13年复习题考试重点1

固体复习题型：一．简答题（共30分，每小题6分）5道小题二．证明题(共25分）两道小题三．计算题（共45分）分布在第四章2道,第二章、第三章各一道。

一．简答题1简述晶体的定义，说明晶体的5条宏观性质。

晶体：原子按一定的周期排列规则的固体，在微米量级的范围是有序排列的①一定的熔点；②晶体的规则外形;③在不同的带轴方向上，晶体的物理性质不同——晶体的各向异性；④晶面角守恒——同一品种的晶体，两个相应的晶面间夹角恒定不变；⑤晶体的解理性-—晶体常具有沿某些确定方位的晶面劈裂的性质.2列举晶体结合的基本类型.离子性结合、共价结合、金属性结合、范德瓦尔斯结合和氢键结合。

3.说出简立方晶体、面心立方晶体和体心立方晶体的原胞和晶胞中所包含的原子数。

4。

说出氯化钠、氯化铯和金刚石结构晶体它们的原胞的晶格类型，每个原胞中包含的原子数.5.下面几种种典型的晶体由哪种布拉菲格子套构而成？6。

下面几种典型的晶体结构的配位数（最近邻原子数）是多少？体心立方8 金刚石型结构 4简立方 6 立方硫化锌结构 47。

画出体心立方结构的金属在)111(,)(面上原子排列．100(,)110体心立方8画出面心立方晶格结构的金属在)111(，)(面上原子排列．100(，)110面心立方9试述晶态、非晶态、准晶、多晶和单晶的特征性质。

解：晶态固体材料中的原子有规律的周期性排列，或称为长程有序.非晶态固体材料中的原子不是长程有序地排列,但在几个原子的范围内保持着有序性,或称为短程有序。

准晶态是介于晶态和非晶态之间的固体材料，其特点是原子有序排列，但不具有平移周期性.另外,晶体又分为单晶体和多晶体：整块晶体内原子排列的规律完全一致的晶体称为单晶体;而多晶体则是由许多取向不同的单晶体颗粒无规则堆积而成的。

10晶格点阵与实际晶体有何区别和联系？解:晶体点阵是一种数学抽象,其中的格点代表基元中某个原子的位置或基元质心的位置，也可以是基元中任意一个等价的点.当晶格点阵中的格点被具体的基元代替后才形成实际的晶体结构。

第二章晶体的结构习题和答案

第二章晶体的结构习题及答案1．晶面指数为（123）的晶面ABC 是离原点O 最近的晶面，0A ，0B 和0C 分别与基矢1a ，2a 和3a 重合，除0点外，0A ，0B ，和0C 上是否有格点？若ABC 面的指数为（234），情况又如何？[解答] 晶面家族（123）截1a ，2a ，和3a 分别为1，2，3等份，ABC 面是离原点0最近的晶面，0A 的长度等于1a 长度，0B 的长度等于2a 的长度的1/2 ，0C 的长度等于3a 的长度的1/3 ，所以只有A 点是格点。

若ABC 面的指数为（234）的晶面族，则A 、B 、和C 都不是格点。

2．在结晶学中，晶胞是按晶体的什么特性选取的？[解答] 在结晶学中，晶胞选取的原则是既要考虑晶体结构的周期性又要考虑晶体的宏观对称性。

3. 在晶体衍射中，为什么不能用可见光？[解答] 晶体中原子间距的数量级为1010-米，要使原子晶格成为光波的衍射光栅，光波的波长应小于1010-米。

但可见光的波长为7.6 — 7100.4-⨯米,是晶体中原子间距的1000倍。

因此，在晶体衍射中，不能用可见光。

4．温度升高时，衍射角如何变化？X 光波长变化时，衍射角如何变化？[解答] 温度升高时，由于热膨胀，面间距h k l d 逐渐变大，由布拉格反射公式λθn d hkl =sin 2可知，对应同一级衍射，当X 光波长不变时，面间距hkl d 逐渐变大，衍射角θ逐渐变小。

所以温度升高，衍射角变小。

当温度不变，X 光波长变大时，对于同一晶面族，衍射角θ随之变大。

5．以刚性原子球堆积模型，计算以下各结构的致密度（一个晶胞中刚性原子球占据的体积与晶胞体积的比值称为结构的致密度）分别为：（1）简立方，6π ；（2）体心立方，π83 ；（3）面心立方，π62 ；（4）金刚石结构，π163。

[解答] 该想晶体是由刚性原子球堆积而成。

一个晶胞中刚性原子球占据的体积与晶胞体积的比值称为结构的致密度。

立方晶系晶面间距公式

立方晶系晶面间距公式立方晶系是一种晶体结构，它的晶格常数a、b、c相等，轴角α、β、γ都等于90°。

立方晶系有三种类型：简单立方（SC）、面心立方（FCC）和体心立方（BCC）。

不同类型的立方晶系的晶面间距公式也不同。

简单立方晶面间距公式简单立方是最简单的晶体结构，它的每个顶点上都有一个原子。

简单立方的晶面间距公式是：d=a√h2+k2+l2其中，a是晶格常数，h、k、l是晶面指数。

这个公式可以用几何方法推导出来，如下图所示：简单立方晶面间距推导在简单立方中，相邻两个原子的距离就是a，所以我们可以用a作为单位长度。

假设我们要求的晶面为(hkl)，它与三个坐标轴的交点分别为A、B、C。

那么，A点的坐标就是(a/h,0,0)，B点的坐标就是(0,a/k,0)，C点的坐标就是(0,0,a/l)。

由于A、B、C三点共线，所以它们满足以下关系：x a/h =ya/k=za/l这个方程就是(hkl)晶面的方程。

我们可以用它来求出任意一点P(x,y,z)到这个晶面的距离d。

为了方便计算，我们取P点为原点(0,0,0)，那么d就等于原点到晶面的垂直距离。

根据点到平面距离的公式，我们有：d=|Ax+By+Cz+D|√A2+B2+C2其中，A、B、C、D是平面方程Ax+By+Cz+D=0的系数。

将(hkl)晶面的方程代入，得到：d=|a/hx+a/ky+a/lz|√(a/h)2+(a/k)2+(a/l)2将P点的坐标(0,0,0)代入，得到：d=a√(h/a)2+(k/a)2+(l/a)2化简后，得到：d=a√h2+k2+l2这就是简单立方晶面间距公式。

面心立方晶面间距公式面心立方是一种常见的金属结构，它在每个顶点和每个面心都有一个原子。

面心立方的晶面间距公式是：d=a√4(h2+k2+l2)其中，a是晶格常数，h、k、l是晶面指数。

这个公式也可以用几何方法推导出来，如下图所示：面心立方晶面间距推导在面心立方中，相邻两个顶点原子的距离是√2a，相邻两个面心原子的距离是a，所以我们可以用a作为单位长度。

第1章习题解答---(部分)

第一章　晶体结构1. ( 黄1.7； ) 写出体心立方和面心立方晶格结构的金属中，最近邻和次近邻的原子数．若立方边长为a ，写出最近邻和次近邻的原子间距. 解：2. 补充题：对由两种原子构成的配位数是4的复式格子，求小原子半径r 与大原子半径R 之比的下限．解：配位数为4， A 为正四面体结构．如图，四个大球的球心为正四面体的四个顶点A、B、 pC、D；小球球心为正四面体的 o中心0 ；它们都相切． DR AB AP ==21Er R AO += B C∴ RrAP AO +=1225.0130sec 4230sec 42)30cos /(42)()(2222222≈−°−=∴°−=°−=−==Rr R R R BE AB R AE ABAP AO Q 即配位数为4， 225.041.0≥>Rr或利用正方体,225.015.1222223≈−=−=R r3. ( 黄1.8； )画出体心立方和面心立方晶格结构的金属在 (100) , (110) , (111) 面上的原子排列. [ 提示：本题为轴矢系统中的Miller 指数，画出平面点阵的平行四边形晶胞 ]解：设体心立方和面心立方晶胞的晶胞常数为a ，则所求晶面平面点阵的二维晶胞如下：( 1 0 0 ) ( 1 1 0 ) ( 1 1 1 ) ● ● ● ● ● ●bcc a ● 2a● ● ● ● 60 o a 2a ● ● 2a● ● ● ● ●fcc a ● a ● ● ● ● ● ● ● ● ● a 2a 2/a 引申讲解一.问题：1.只在立体图上标出晶面（可能对，但不好）．2.只给出平面点阵，无连线、尺度及角度标注（可能对，但不好）．二.原则：尽量理解别人的意思；尽量给别人表示清楚：简明、准确、无歧义．三.本题：设……a ；分别画二维晶胞；标明尺度；非90o 之角最好表示．4. ( 黄1.9； )指出立方晶格（111）面与（100）面，（111）面与（110）面交线的晶向.[ 提示：最好画图说明]解：如右图所示，（111）面即为EBG 面；（100）面为ABCD 面或EFGH 面；（110）面即ABGH 面；（111）面与（100）面的交线，可为EG 线，晶向指数为[1,1,0]；（111）面与（110）面的交线，可为BG 线，晶向指数为[0,1,1]；5. (黄1.3；方3 )试证面心立方的倒格子是体心立方；体心立方的倒格子是面心立方．证明：(1) fcc 的基矢 )(2,)(2,)(2321j i a a k i a a k j a a rr r r r r r r r +=+=+= 原胞体积 341a =Ω相应倒格子基矢 )(2)(2321k j i aa ab r r r r r r ++−π=Ω×π= )(22k j i a b rr r r +−π= )(23k j i ab r r r r −+π=所以面心立方的倒格子是体心立方格子．(2) bcc 的基矢 )(2,)(2,)(2321k j i a a k j i a a k j i a a rr r r r r r r r r r r ++=+−=++−= 原胞体积 321a =Ω相应倒格子基矢 )(2)(2321k j aa ab r r r r r +π=Ω×π= )(22k i a b rr r +π= )(23j i ab r r r +π=所以体心立方的倒格子是面心立方格子．6. ( 黄1.4； ) 证明：倒格子原胞的体积为c v /)2(3π，其中c v 为正格子原胞的体积．ZE H A DF G Y B C X证：倒格子原胞的体积记为∗c v ，由公式CB A BC A C B A rr r r r r r r r )()()(⋅−⋅=××{{}c ccc v a a a a a a a a a a v a a a a a a v b b b v 321131213323321133233321)2(])[(])[()(8)]()[()(8)(*π=⋅×−⋅×⋅×π=×××⋅×π=×⋅=r r r r r r r r r r r r r r rr r r r [解法二]用到一个公式：)()(C B A C B A rr r r r r ×⋅=⋅× ，则有推论：))(())((])()[()]([)()(c b d a d b c a d c b c d b a d c b a d c b a rr r r r r r r r r r r r r r r r r r r r r r ⋅⋅−⋅⋅=⋅−⋅⋅=××⋅=×⋅×本题：323323322323211321321)2()])(())([(2)])()[(()]()][([*π=⋅⋅−⋅⋅π=××⋅=×⋅×⋅=b a b a b a b a b b a a b a b b b a a a v v c c rr r r r r r r r r r r r r r r r rr r 本题易犯的错误及纠正：1. a r 1无定义！×=⋅ab a b r v r r 12. 2a ab a b r r v r r ≠⋅，如j i b a b i a j i b r r r r r rr r r r +=⋅⎩⎨⎧=+=, 而 i a a r r r =2 3. )()]([32211321a a a a a a a rr r r r r r ×≠×⋅7.补充题：有一简单格子，基矢选成)(5.133321k j i a j a i a r r r r r r r r++===、、．其中k j i rr r 、、为笛卡尔坐标系中的单位矢量．证明这种晶格是哪种Bravais 格子？并计算其晶胞体积．解：可选轴矢k a a a c j a b i a a r r r r r s v r r rr 32,3,321321=−−=====；构成立方体；又由3a r可知在体心有格点；且题中所给原胞的体积5.13)(321=×⋅=a a a r r r ；新选晶胞的体积27)(=×⋅=c b a rr r ，故这种晶格必是bcc 格子．晶胞体积＝33＝27．8.补充题：六角晶系的基矢： k c c j a i a b j a i a a r r rr r r r r=+−=+=,223,223求其倒格子基矢.解：六角晶系的平行六面体晶胞即原胞，正格子原胞体积：)3()3(4])223[()223()(2i j j i ca k c j a i a j a i a cb a r r v r r r r r r r r r +⋅+=×+−⋅+=×⋅=Ωc a 223=倒格子基矢： )33(2])223[(34)(2*2j i a k c j a i a ca cb a vr r r r rr r +π=×+−π=×Ωπ= )33(2)]223([34)(2*2j i a j a i a k c ca a cb vr r r r r r r +−π=+×π=×Ωπ= )33(3)]223()223[(34)(2*2k k cj a i a j a i a c a b a c r r r r r r r r r +π=+−×+π=×Ωπ= kc r π=2仍为六角晶胞格子.9.补充题求晶格常数为a 的面心立方和体心立方晶体晶面族)(321h h h 的面间距．解：(1) fcc 的倒格子基矢： )(21k j i a b r r r r ++−π= )(22k j i a b r r r r +−π= )(23k j i a b r r r r −+π=则])()()[(2321231132332211k h h h j h h h i h h h ab h b h b h K h r rr r r r r −++−++−+π=++=)(2)(32)()()(2323121232221232122312132h h h h h h h h h ah h h h h h h h h aK h ++−++π=−++−++−+π=r ∴ )(2)(32323121232221h h h h h h h h h aK d hh ++−−+=π=r (2) bcc 的倒格子基矢：)(21k j a b r r r +π= )(22k i a b rr r +π= )(23j i a b r r r +π=则])()()[(2213132332211k h h j h h i h h ab h b h b h K h r rr r r r r +++++π=++=3231212322212212312328)()()(2h h h h h h h h h ah h h h h h a K h +++++π=+++++π=r ∴ )(22323121232221h h h h h h h h h aK d hh +++++=π=r 10.补充题试找出体心立方和面心立方结构中，格点最密的面和最密的线．解：(1)bcc )(22323121232221h h h h h h h h h aK d hh +++++=π=r 格点最密的面为{1,0,0}及{1,-1,0}，而最密的线为[1,0,0]． (2)fcc )(2)(32323121232221h h h h h h h h h aK d hh ++−++=π=r 格点最密的面为{1,0,0}及{1,1,1}，而最密的线为[1,0,0]．11.补充题对于面心立方晶体，已知晶面族的密勒指数为(hkl )，求对应的原胞坐标系中的面指数(321h h h )，若已知(321h h h )，求对应的(hkl ).解： kac j a b i a a ka c j ab i a a rr r r r r r rr r r r π=π=π====2*,2*,2*;,,基矢和倒格子基矢： )(2,)(2,)(2321j i a a k i a a k j a a rr r r r r r r r +=+=+= ；)(2)(2321k j i a a a b r r r r r r ++−π=Ω×π= )(22k j i a b r r r r +−π= )(23k j i a b r r r r −+π=][2***k l j k i h ac l b k a h K hkl rr r r r r r ++π=++=])()()[(2321231132332211k h h h j h h h i h h h ab h b h b h K h r rr r r r r −++−++−+π=++=)(hkl Q 和)(321h h h 表示同一晶面族，hkl K r ∴∥hK r设h hkl K p K rr 2′=，可解得)](),(),[(1)(321k h l h l k ph h h +++′=(1)因 (hkl )皆为整数，(321h h h )为互质整数，故p ′为整数.再设hkl h K p K rr =，则)](),(),[(1)(321231132h h h h h h h h h phkl −+−+−+=(2)理由同上，p 为整数.由两次所设知2,2=′′=p p K p p K hklhkl rr (1)式和(2)式并保证 (hkl )及(321h h h )都是互质整数，取⎩⎨⎧=′=21p p 或⎩⎨⎧=′=12p p 即为所求．12.补充题 ( 方8 )如X 射线沿简立方瑷胞的OZ 轴负方向入射，求证：当λa l k l =+222 和 2222cos k l k l +−=β时，一级衍射线在YZ 平面内，其中β是衍射光与OZ 轴的夹角．证明： ZβθθYX a (h,k,l )对简立方 d ah k l h k l =++222(1) 设X 射线由OZ 轴的负方向入射，根据布拉格反射条件 2d n h k l sin θλ= (2)2cos 12cossin )(2β+=β=θ∴π=θ+β见图Q (2)式中取n = 1，并将βθcos sin 、分别带入，得代入，得再将222222sin 2k l l a ll k d lk h +=λ+λ=θλ=222222l k a ll k k l la d lk h +=++= 将此式与(1)式比较，可得h =0．(h ,k ,l )是衍射晶面族的密勒指数，h =0表示该晶面族的法线与X 轴垂直，即在YZ 平面内；而入射线又与OZ 轴重合，所以衍射线在YZ 平面内．。

13级固体物理题库

一、填空1. 固体按其微结构的有序程度可分为_______、_______和准晶体。

2. 组成粒子在空间中周期性排列，具有长程有序的固体称为_______；组成粒子在空间中的分布完全无序或仅仅具有短程有序的固体称为_________。

3. 在晶体结构中，所有原子完全等价的晶格称为______________；而晶体结构中，存在两种或两种以上不等价的原子或离子的晶格称为____________。

4晶体结构的最大配位数是____；具有最大配位数的晶体结构包括______________晶体结构和______________晶体结构。

5. 简单立方结构原子的配位数为______；体心立方结构原子的配位数为______。

6．NaCl 结构中存在_____个不等价原子，因此它是_______晶格，它是由氯离子和钠离子各自构成的______________格子套构而成的。

7. 金刚石结构中存在______个不等价原子，因此它是_________晶格，由两个_____________结构的布拉维格子沿空间对角线位移1/4的长度套构而成，晶胞中有_____个碳原子。

8. 以结晶学元胞（单胞）的基矢为坐标轴来表示的晶面指数称为________指数。

9. 满足2,2,1,2,3)0i j ij i j a b i j i j ππδ=⎧⋅===⎨≠⎩r r 当时（，当时关系的123,,b b b r r r 为基矢，由112233h K hb h b h b =++r r r r 构成的点阵，称为_______。

10. 晶格常数为a 的一维单原子链，倒格子基矢的大小为________。

11. 晶格常数为a 的面心立方点阵初基元胞的体积为_______；其第一布里渊区的体积为_______。

12. 晶格常数为a 的体心立方点阵初基元胞的体积为_______；其第一布里渊区的体积为_______。

13. 晶格常数为a 的简立方晶格的(010)面间距为________14. 体心立方的倒点阵是________________点阵，面心立方的倒点阵是________________点阵，简单立方的倒点阵是________________。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1、求晶格常数为a 的面心立方和体心立方晶体晶面族(h 1h 2h 3)的面间距。

2、用波长为1.5405A
的X 光对钽金属粉末作为衍射分析，测得布拉格角大小为序的五条眼射线见下表
已知钽金属为体心结构，求：（1）衍射晶面族的晶面指数；（2）晶格常数a 。

3、有一晶体，平衡时体积为V 0，原子间相互作用势为U 0。

如果相距为r 的两原子相互作用势为n r βα
+=m r -u(r)，证明：（1）体积弹性模量为0
09V mn U K =；（2）求出体心立方结构惰性分子晶体的体积模量。

4、雷纳德-琼斯势为])()[(4)(612r
r r u σσε-=，证明：r=1.12σ时，势能最小，且ε-=）r u (；当r=σ时，0(=）
r u ；说明ε和σ的物理意义。

5、如果离子晶体中离子总得相互作用势能为]4[N )(/02
ρλπεμr e Z r q r u ---=，求晶体的压缩系数，其中λ，ρ为常数，Z 为配位数。

6、设两原子间的互作用能可由n m r r r U βα
+-=)(表述。

若m=2，n=10，而且两原子构
成稳定的分子，其核间距离为m 10103-⨯，离解能为eV 4，试计算：① βα和；② 使该分子分裂所必须的力和当分裂发生时原子核的临界间距；③ 使原子间距比平衡距离减少10%时所需的压力？。