晶面和体心立方晶体
七大晶系详细图解
七大晶系详细图解已知晶体的形态已经超过了四万种,可是万物都会有规律,晶体自然也是有的。
它们都是按七种结晶方式模式发育的,即七大晶系。
晶体即是一种以三维方向发育的的几何体,为了表示三维空间,别离用三、四跟人为添加的轴来表示晶体的长宽高和中心。
三条轴别离用X、Y、Z(U)(Z轴也可叫做“主轴”)来表示,而为了更好表示轴之间的度数,咱们用α、β、γ来表示轴角。
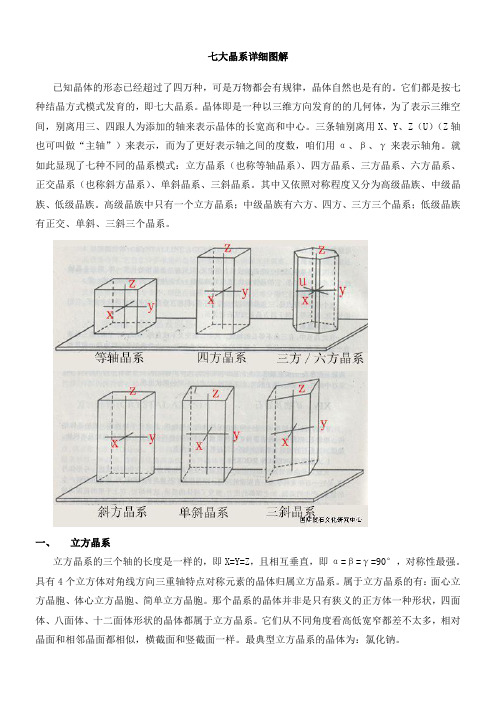
就如此显现了七种不同的晶系模式:立方晶系(也称等轴晶系)、四方晶系、三方晶系、六方晶系、正交晶系(也称斜方晶系)、单斜晶系、三斜晶系。
其中又依照对称程度又分为高级晶族、中级晶族、低级晶族。
高级晶族中只有一个立方晶系;中级晶族有六方、四方、三方三个晶系;低级晶族有正交、单斜、三斜三个晶系。
一、立方晶系立方晶系的三个轴的长度是一样的,即X=Y=Z,且相互垂直,即α=β=γ=90°,对称性最强。
具有4个立方体对角线方向三重轴特点对称元素的晶体归属立方晶系。
属于立方晶系的有:面心立方晶胞、体心立方晶胞、简单立方晶胞。
那个晶系的晶体并非是只有狭义的正方体一种形状,四面体、八面体、十二面体形状的晶体都属于立方晶系。
它们从不同角度看高低宽窄都差不太多,相对晶面和相邻晶面都相似,横截面和竖截面一样。
最典型立方晶系的晶体为:氯化钠。
常见立方晶系晶体模型图:晶体实物图:二、四方晶系四方晶系四方晶系的三条晶轴相互垂直,即α=β=γ=90°。
其中两个水平轴(X轴、Y轴)长度一样,Z轴的长度可长可短,通俗的说:四方晶系的晶体大多是四棱的柱状体,有的是长柱体,有的是短柱体,即其晶胞必具有四方柱的形状。
横截面为正方形,四个柱面是对称的,即相邻和相对的柱面都是一样的,但和顶端不对称。
所有主晶面交角都是90。
特点对称元素为四重轴。
若是Z轴发育,它确实是长柱状乃至针状;若是两个横轴(X轴、Y轴)发育大于Z轴,那么晶体就会呈现四方板状,最有代表的确实是磷酸二氢钠和硫酸镍β了。
1-3常见晶体结构

三、常见晶体结构及其几何特征
2 几何特征
2.3 堆垛密度 又称紧密系数 致密度 简写 它表示原子排列的密集程度。假如把金属晶
体中的原子看成是有一定直径的刚球,则紧密系 数可以用刚球所占空间的体积百分数来表示。
以一个晶胞为例,致密度就等于晶胞中原子 所占体积与晶胞体积之比 即: 致密度 =晶胞中原子所占体积之和/晶胞的体积。
12
A
6
3
54
B
A
于是每两层形成一个周
B
期,即 AB AB 重复的堆积
A
方式,形成六方紧密堆积。
配位数 12 。 ( 同层 6,上下层各 3 )
六方密堆积配位数 12 ,空间利用率为 74.05 % 。
属于六方密堆积的金属有: IIIB,IVB及 Be、 Mg、Tc、Re、Ru、Os 等。
③ 面心立方紧密堆积(Face-centred Cubic clode
3 常见晶体中的重要间隙 3.3 HCP结构 (2)四面体间隙
数量: 12 与原子数比为12:6=2:1 rx /r=0.225
三、常见晶体结构及其几何特征
3 常见晶体中的重要间隙
3.4 总结 根据书中表1-2和1-3:
(1)FCC和HCP都是密排结构。BCC是比较开放的结构,间隙较多, 所以原子半径较小的元素(易形成间隙原子)在BCC金属中的扩散 速率比在FCC、HCP中高得多。
Hcp的堆垛方式为AB,AB,…… 密排面(0001)垂直于C轴。 Fcc的堆垛方式为ABC,ABC,…… 密排面{111}垂直于体对角线。
总结
绪论 ——大家自己看 晶体学基础: 一、空间点阵 阵点: 理想晶体、几何点、周围环境相同 空间点阵:阵点规则、周期、有规律的排列,三维空间 晶胞:具有代表性的 、最小单元、先满足对称性、六个点阵常数(晶格常数) 晶系和空间点阵类型:7各晶系 14个空间点阵 晶体结构和空间点阵的区别 二、晶面指数和晶向指数的标定 步骤: 晶面族和晶向族:位向不同、原子排列相同、晶体学上性质等价 晶带:平行或相交晶带轴晶面的全体 三、常见晶体结构 配位数: 12 8 12 个数 : 4 2 6 堆垛密度:0.74 0.68 0.74 间隙:见表1-3 堆垛方式:FCC ABCABCA………………….
三种晶体结构的最密排晶面和最密排晶向

三种晶体结构的最密排晶面和最密排晶向1.引言1.1 概述晶体是具有长程有序排列的原子、离子或分子的固体物质。
晶体的结构是由最密排列的晶面和晶向构成的。
最密排晶面是指在晶体结构中,原子、离子或分子最紧密地靠近的面,而最密排晶向则指的是在晶体中最紧密地排列的方向。
本文将分析三种不同的晶体结构,探讨它们各自的最密排晶面和最密排晶向。
通过深入研究这些结构的排列方式,可以更好地理解晶体的性质和行为。
第一种晶体结构是立方晶系,也是最简单的晶体结构之一。
它的最密排晶面是(111)晶面,最密排晶向则是[110]晶向。
这些晶面和晶向在晶体中具有紧密的排列,使晶体的结构呈现出高度的对称性。
第二种晶体结构是六方晶系,它相对于立方晶系而言稍复杂一些。
在六方晶系中,最密排晶面是(0001)晶面,最密排晶向是[10-10]晶向。
与立方晶系不同,六方晶系具有六方对称性,呈现出更复杂的晶体结构。
第三种晶体结构是四方晶系,它也是一种常见的晶体结构。
在四方晶系中,最密排晶面是(100)晶面,最密排晶向是[110]晶向。
四方晶系的晶体结构与立方晶系相似,但具有更多的对称性和排列方式。
通过对这三种晶体结构的最密排晶面和最密排晶向进行研究,我们可以更好地理解晶体的基本结构和性质。
这对于材料科学、凝聚态物理和相关领域的研究具有重要意义,同时也有助于开发新材料和改进现有材料的性能。
1.2文章结构文章结构部分的内容可以包括以下几个方面的介绍:1.2 文章结构本文主要分为引言、正文和结论三个部分。
引言部分概述了晶体结构和最密排晶面、最密排晶向的研究背景和重要性,并提出了本文研究的目的和意义。
正文部分分为三个小节,分别介绍了三种晶体结构的最密排晶面和最密排晶向。
每个小节将首先介绍该种晶体结构的一般特点和常见应用,然后详细讨论最密排晶面和最密排晶向的确定方法和规律,并给出具体的实例和数据进行说明。
结论部分对于每种晶体结构的最密排晶面和最密排晶向进行总结和回顾,并指出各种晶体结构最密排晶面和最密排晶向的综合特点和应用前景。
13几种常见的晶体结构

但有些元素晶体和所有化合物晶体,其最小重复单 位(基元)至少包含 2个或 2 个以上的原子,它们的每 一个原子虽然都构成同样的点阵类型(即同样的周期排 列方式),但绘成晶胞时,要绘出基元原子之间位置上 的相互关系,所以是同样的点阵类型的叠加,我们称这 些晶体具有复式晶格。
例如:CsCl晶体是两个原子各自构成简立方点阵后,沿 晶胞对角线方向移动二分之一距离的叠加。
由上述方法定义的晶向和晶面指数有重要意义: 1. 晶轴方向是最重要的方向,晶向指数最简单; 2. 晶面指数最简单的晶面族,晶面间距最大。
三. 晶面间距:晶面间距是指两个相邻的平行晶面间 的垂直距离。以米勒指数表示的晶面间距在晶体结 构的测定中是一个很常用的参数,必须掌握。
可以证明:(见习题)
立方晶系: 四方晶系: 六角晶系:
下图标出了简立方点阵的几组最重要的晶面系的晶面 指数和晶向指数。从中可以明显看出晶面指数最简单 的晶面族面间距最大,它们也是以后经常讨论到的最 重要的晶面。
六角晶系晶面 指数的表示与其它 晶系不同,晶体学 中往往采用四轴定 向的方法,这样的 晶面指数可以明显 地显示出 6 次对称 的特点。
晶面指数小结
的面间距较大,而往往成为晶体的解理面。
(2)用于计算不同晶面族之间的夹角。一般而言,密
勒指数分别为(h1k1l1) 和(h2k2l2)的晶面族的2个平面之间 的夹角的余弦为:
cos
(h12
h1h2 k 1k 2 l l1 2
k12
l12
)
1 2
(h22
k22
l22
)
1 2
在X射线衍射和结晶学中,密勒指数不一定为互质整数, 例如,面心立方中一些平行于(100)的晶面而截a轴 于1/2处的面,其指数为(200),其原因是晶胞并非 是晶体中的最小重复单元。
晶体结构和性质

2.另一种堆积方式是第三层球的突出部分 落在第二层的八面体空隙上。这样,第三 层与第一、第二层都不同而形成 ABCABC…的结构。这种堆积方式可以从
中划出一个立方面心单位来,所以称为面
心立方最密堆积(A1)。
六方最密堆积(A3)图
六方最密堆积(A3)分解图
面 心 立 方 最 密 堆 积 ( 一 ) 图
c
αβ b γ
c a b a
c b a
立方 Cubic a=b=c, ===90°
四方 Tetragonal a=bc, ===90°
正交 Rhombic abc, ===90°
c b a b
三方 Rhombohedral a=b=c, ==90° a=bc, ==90° =120°
两层堆积情况分析 1.在第一层上堆积第二层时,要形成最密堆积, 必须把球放在第二层的空隙上。这样,仅有半数 的三角形空隙放进了球,而另一半空隙上方是第 二层的空隙。 2.第一层上放了球的一半三角形空隙,被4个球 包围,形成四面体空隙;另一半其上方是第二层 球的空隙,被6个球包围,形成八面体空隙。
三层球堆积情况分析 第二层堆积时形成了两种空隙:四面体空隙和 八面体空隙。那么,在堆积第三层时就会产 生两种方式: 1.第三层等径圆球的突出部分落在正四面体空 隙上,其排列方式与第一层相同,但与第二 层错开,形成ABAB…堆积。这种堆积方式可 以从中划出一个六方单位来,所以称为六方 最密堆积(A3)。
c a
c b a
c b a
六方 Hexagonal a=bc, ==90°, =120°
单斜 Monoclinic abc ==90°, 90°
三斜 Triclinic abc ===90°
六、晶体结构的表达及应用
晶面和体心立方晶体
体和四面体间隙的大小。
CHENLI
15
1-3 常见的晶体结构
一、金属晶体结构
(一)三种典型金属晶体结构
1. 面心立方结构
(1)晶胞模型
(2)单胞原子数
(3)原子半径
(4)配位数和致密度
பைடு நூலகம்
(5)原子面密度
(6)重要的晶面和晶向
(7)具有面心立方结构的C典HE型NLI金属
1
1-3 常见的晶体结构
2. 体心立方结构
(1)晶胞模型
(2)单胞原子数
CsCl型晶体结构
NaCl型晶体结构
CHENLI
立方ZnS型晶体结构
10
1-3 常见的晶体结构
(二)AB2型化合物的晶体结构
c
CaF2型晶体结构
a
a
Ti 4+
O2-
TiO2型晶体结构
Si 4+
O2-
-方石英型晶体结构
CHENLI
11
1-3 常见的晶体结构
(三)A2B3型化合物的晶体结构
-Al2O3型晶体结构
A
A
A
A
A
A
A
CHENLI
5
1-3 常见的晶体结构
(三) 晶格间隙
1. 晶格间隙:晶体中未被原子占据的空间 2. 面心立方结构中的晶格间隙 (1)八面体间隙 (2)四面体间隙
CHENLI
6
1-3 常见的晶体结构
3. 体心立方结构中的晶格间隙
(1)八面体间隙
A
(2)四面体间隙
C
F
E
D
体心立方的晶面间距计算

体心立方的晶面间距计算
设简单立方的晶格常数为a,我们都知道,其晶面间距与晶面指数的关系为:
只要知道晶面指数,晶格常数,代入公式计算就行了,不会出错。
但是,面心立方和体心立方却不能直接用这个公式,用了可能就会出错。
例如,我们知道面心立方的(100)晶面间距是a/2,而用上面的公式计算结果是a,这显然是不对的。
体心立方和面心立方的晶面间距应该按照如下方法计算。
面心立方晶体(FCC)晶面间距与点阵常数a之间的关系为:
若h、k、l均为奇数,则
否则
体心立方晶体(BCC)晶面间距与点阵常数a之间的关系:
若h+k+l=偶数,则
否则
例如,分别求体心立方的(100)、(110)、(111)晶面的面间距,并指出晶面间距最大的晶面。
对于面心立方,情况如何呢?我们算一下。
晶体学习题与答案

一、 名词解释(1)阵点;(2)(空间)点阵;(3)晶体结构;(4)晶胞;(5)晶带轴;二、填空(1)晶体中共有 种空间点阵,属于立方晶系的空间点阵有 三种。
(2)对于立方晶系,晶面间距的计算公式为 。
(3){110}晶面族包括 等晶面。
(4){h 1k 1l 1}和{h 2k 2l 2}两晶面的晶带轴指数[u v w]为 。
(5)(110)和(11-0)晶面的交线是 ;包括有[112]和[123]晶向的晶面是 。
三、计算及简答(1)原子间的结合键共有几种?各自有何特点?(2)在立方晶系的晶胞中,画出(111)、(112)、(011)、(123)晶面和[111]、[101]、[111-]晶向.(3)列出六方晶系{101-2} 晶面族中所有晶面的密勒指数,并绘出(101-0)、(112-0)晶面和〔112-0〕晶向。
(4)试证明立方晶系的〔111〕晶向垂直于(111)晶面。
(5)绘图指出面心立方和体心立方晶体的(100)、(110)、及(111)晶面,并求其面间距;试分别指出两种晶体中,哪一种晶面的面间距最大?(6)在立方晶系中,(1-10)、(3-11)、(1-3-2)晶面是否属于同一晶带?如果是,请指出其晶带轴;并指出属于该晶带的任一其他晶面.(7)写出立方晶系的{111}、{123}晶面族和〈112>晶向族中的全部等价晶面和晶向的具体指数。
(8)计算立方晶系中(111)和〔111-〕两晶面间的夹角。
(9)若采用四轴坐标系标定六方晶体的晶向指数,应该有什么约束条件?为什么?答 案二、填空(1)14 简单、体心、面心(2)222hkl d h k l =++(3) (110)、(101)、(011)、(1-10)、(1-01) 、(01-1)(4)1122k l u k l =;1122l h v l h =;1122h k w h k = (5)〔001〕 (111-)三、简答及计算(1)略(2)(3){101-2}晶面的密勒指数为(101-2)、(1-012)、(01-12)、(011-2)、(1-102)、(11-02)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-3 常见的晶体结构
二、离子晶体结构 (一)AB型化合物的晶体结构
CsCl型晶体结构
NaCl型晶体结构
立方ZnS型晶体结构
1-3 常见的晶体结构
(二)AB2型化合物的晶体结构
c
CaF2型晶体结构
a
a
Ti 4+
O2-
TiO2型晶体结构
Si 4+
O2-
-方石英型晶体结构
1-3 常见的晶体结构
(三)A2B3型化合物的晶体结构
-Al2O3型晶体结构
1-3 常见的晶体结构
三、共价晶体(原子晶体)结构
a
b
金刚石型晶体结构(配位数为4)
a — 共价键; b — 晶胞
1-3 常见的晶体结构
三、共价晶体(原子晶体)结构
As、Sb、Bi的晶体结构(配位数为3)
Se和Te的晶体结构(配位数为2)
1-3 常见的晶体结构
思考题: 1. 何谓金属的多晶型性? 2. 分别计算面心立方和体心立方结构中八面
1-3 常见的晶体结构
3. 密排六方结构
(1)晶胞模型 (2)单胞原子数 (3)原子半径 (4)配位数和致密度 (5)原子面密度 (6)重要的晶面和晶向 (7)具有密排六方结构的典型金属
1-3 常见的晶体结构
思考题: 1. 分别画出面心立方、体心立方、密排六方
晶胞,并分别计算面心立方、体心立方、密排 六方晶体的致密度。
1-3 常见的晶体结构
3. 体心立方结构中的晶格间隙源自(1)八面体间隙A
(2)四面体间隙
C
F
E
D
B
1-3 常见的晶体结构
4.密排六方结构中的晶格间隙 (1)八面体间隙 (2)四面体间隙
1-3 常见的晶体结构
(四) 多晶型性与同素异构转变
1. 多晶型性(同素异构性) 2. 铁的多晶型性 3. 同素异构转变
2. 分别计算面心立方晶体{111}晶面和体心 立方晶体{110}晶面原子面密度。
1-3 常见的晶体结构
(二) 金属晶体中的原子堆垛方式
刚球密堆模型 面心立方晶体的堆垛顺序 密排六方晶体的堆垛顺序
A
A
A
A
A
A
A
1-3 常见的晶体结构
(三) 晶格间隙
1. 晶格间隙:晶体中未被原子占据的空间 2. 面心立方结构中的晶格间隙 (1)八面体间隙 (2)四面体间隙
1-3 常见的晶体结构
一、金属晶体结构 (一)三种典型金属晶体结构
1. 面心立方结构 (1)晶胞模型 (2)单胞原子数 (3)原子半径 (4)配位数和致密度 (5)原子面密度 (6)重要的晶面和晶向 (7)具有面心立方结构的典型金属
1-3 常见的晶体结构
2. 体心立方结构
(1)晶胞模型 (2)单胞原子数 (3)原子半径 (4)配位数和致密度 (5)原子面密度 (6)重要的晶面和晶向 (7)具有体心立方结构的典型金属
