数字信号处理习题课
数字信号处理1-5章习题课
+∞
x(n) = xa (nTs ) 1 jw X (e ) = Ts w 2π ∑ X a j T − T l = −∞ s s
+∞
w = ΩTs 1 Fs = Ts
l
Fs: the sampling frequency, sam/sec
Charpter1-6 exercise(补充内容)
z = a −1
x(n)=(a-n-an)u(-n-1)
Charpter1-6 exercise(补充内容)
(3) 收敛域|a|<|z|<|a-1|
x(n)是双边序列。 根据被积函数F(z)， 按n≥0和n<0两 情况分别求x(n)。 n≥0时， c内极点z=a x(n)=Res［F(z), a］=an n<0时， c内极点有二个， 其中z=0是n阶极点， 改求c外极点留数， c外极点只有z=a-1， 因此 x(n)=-Res［F(z), a-1］=a-n 最后将x(n)表示为 an n≥0 x(n)= x(n)=a|n| a-n n<0
Charpter1-6 exercise(补充内容) 有限长序列： ∞ n1<0， n2≤0时， 0≤z＜∞ 双边Z变换 X ( z ) = ∑ x ( n ) z − n n1<0， n2>0时， 0<z＜∞ n =−∞ n1≥0， n2>0时， 0<z≤∞ ∞ 单边Z变换 X ( z ) = ∑ x ( n ) z − n 右序列： n =0 收敛域为Rx- <|z|<∞
Charpter1-6 exercise(补充内容)
第2章 离散时间信号与系统
时域离散信号 时域离散系统 卷积 差分方程
数字信号处理课后习题答案完整版
数字信号处理课后习题答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】数字信号处理（姚天任江太辉）第三版课后习题答案第二章判断下列序列是否是周期序列。
若是，请确定它的最小周期。
（1）x(n)=Acos(685ππ+n )（2）x(n)=)8(π-ne j（3）x(n)=Asin(343ππ+n )解 (1)对照正弦型序列的一般公式x(n)=Acos(ϕω+n )，得出=ω85π。
因此5162=ωπ是有理数，所以是周期序列。
最小周期等于N=)5(16516取k k =。
（2）对照复指数序列的一般公式x(n)=exp[ωσj +]n,得出81=ω。
因此πωπ162=是无理数，所以不是周期序列。
（3）对照正弦型序列的一般公式x(n)=Acos(ϕω+n )，又x(n)=Asin(343ππ+n )＝Acos(-2π343ππ-n )＝Acos(6143-n π)，得出=ω43π。
因此382=ωπ是有理数，所以是周期序列。
最小周期等于N=)3(838取k k =在图中，x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n)，并画出y(n)的图形。
解 利用线性卷积公式y(n)=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法，计算y(n)的每一个取样值。
(a) y(0)=x(O)h(0)=1y(l)=x(O)h(1)+x(1)h(O)=3y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n ≥2 (b) x(n)=2δ(n)-δ(n-1)h(n)=-δ(n)+2δ(n-1)+ δ(n-2)y(n)=-2δ(n)+5δ(n-1)= δ(n-3) (c) y(n)=∑∞-∞=--k kn k n u k u a)()(=∑∞-∞=-k kn a=aa n --+111u(n) 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)=λn u(n)*u(n)解：(1) y(n)=∑∞-∞=-k k n u k u )()(=∑∞=-0)()(k k n u k u =(n+1),n ≥0即y(n)=(n+1)u(n) (2) y(n)=∑∞-∞=-k k k n u k u )()(λ=∑∞=-0)()(k kk n u k u λ=λλ--+111n ,n ≥0即y(n)=λλ--+111n u(n)图所示的是单位取样响应分别为h 1(n)和h 2(n)的两个线性非移变系统的级联，已知x(n)=u(n), h 1(n)=δ(n)-δ(n-4), h 2(n)=a n u(n),|a|<1,求系统的输出y(n). 解 ω(n)=x(n)*h 1(n) =∑∞-∞=k k u )([δ(n-k)-δ(n-k-4)]=u(n)-u(n-4)y(n)=ω(n)*h 2(n) =∑∞-∞=k kk u a )([u(n-k)-u(n-k-4)]=∑∞-=3n k ka,n ≥3已知一个线性非移变系统的单位取样响应为h(n)=a n -u(-n),0<a<1 用直接计算线性卷积的方法，求系统的单位阶跃响应。
数字信号处理习题及参考解答
目录习题一 (3)习题二 (26)习题三 (40)习题四 (61)习题五 (83)习题一1.1序列)(n x 如图T1.1所示，用延迟的单位采样序列加权和表示出这个序列。
图 T1.1 习题1.1图【解答】 任一数字序列都可表达为)()()(k n k x n x k -=∑∞-∞=δ所以图T1-1信号可表达为)3(2)1(3)()3(2)(-+-+-+-=n n n n n x δδδδ1.2 分别绘出以下各序列的图形： （1）)(2)(1n u n x n =（2）)(21)(2n u n x n⎪⎭⎫⎝⎛=（3）()3()2()nx n u n =-（4）)(21)(4n u n x n⎪⎭⎫⎝⎛-=【解答】 用MATLAB 得到的各序列图形如图T1.2所示。
图T1.2习题1.2解答1.3 判断下列每个序列是否是周期性的；若是周期性的，试确定其周期。
（1）⎪⎭⎫ ⎝⎛-=873cos )(ππn A n x（2）⎪⎭⎫⎝⎛=n A n x 313sin )(π（3）⎪⎭⎫⎝⎛-=n j e n x 6)(π（4）{}{}/12/18()Re Im jn jn x n e e ππ=+（5）16()cos(/17)jnx n e n ππ=【解答】（1）因为730πω=，而31473220==ππωπ，这是一有理数。
所以)(n x 是周期的，周期为14。
（2）因为3130πω=，而136313220==ππωπ，也为有理数。
所以)(n x 是周期的，周期为6。
（3）注意此序列的10=ω，πωπ220=，是无理数，所以)(n x 是非周期的。
（4）实际上()cos(/12)sin(/18)x n n n ππ=+因此)(n x 有两个频率分量，即1201πω=，1802πω=，而 24122201==ππωπ；02223618πππω==都是有理数，所以)(n x 是两个周期信号之和，第一个周期信号的周期241=N ，第二个周期信号的周期362=N ，因此)(n x 的周期是这两个周期的最小公倍数，即72123624)36,24gcd(3624),gcd(2121=⋅=⋅=⋅=N N N N N（5）()x n 是两个周期序列的乘积，其中132N =，234N =，所以该序列的周期是121232343234544gcd(,)gcd(32,34)2N N N N N ⋅⋅⋅====1.4 已知序列)]6()()[6()(---=n u n u n n x ，画出下面序列的示意图。
数字信号处理课后习题答案(全)1-7章
x(n)=－δ(n+2)+δ(n－1)+2δ(n－3)
h(n)=2δ(n)+δ(n－1)+ δ(n－2)
由于
x(n)*δ(n)=x(n)
1
x(n)*Aδ(n－k)=Ax(n－k)
2
故
第 1 章 时域离散信号和时域离散系统
y(n)=x(n)*h(n)
=x(n)*［2δ(n)+δ(n－1)+ δ(n－2) 1 2
（5） 系统是因果系统， 因为系统的输出不取决于x(n)的未来值。 如果
|x(n)|≤M, 则|y(n)|=|ex(n)|≤e|x(n)|≤eM，
7． 设线性时不变系统的单位脉冲响应h(n)和输入序列x(n)如题7图所示，
要求画出y(n)输出的波形。
解： 解法（一）采用列表法。
y(n)=x(n)*h(n)=
0≤m≤3
－4≤m≤n
非零区间如下:
第 1 章 时域离散信号和时域离散系统
根据非零区间， 将n分成四种情况求解： ① n<0时， y(n)=0
② 0≤n≤3时， y(n)= ③ 4≤n≤7时， y(n)= ④ n>7时， y(n)=0
1=n+1
n
1=8－m n0
3
mn4
第 1 章 时域离散信号和时域离散系统
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器， 延时器是线性非时变系统， 下面证明。 令输入为
输出为
x(n－n1)
y′(n)=x(n－n1－n0) y(n－n1)=x(n－n1－n0)=y′(n) 故延时器是非时变系统。 由于
T［ax1(n)+bx2(n)］=ax1(n－n0)+bx2(n－n0) =aT［x1(n)］+bT［x2(n)］
数字信号处理习题及答案解析
==============================绪论==============================1. A/D 8bit 5V 00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章 时域离散时间信号与系统==================1.①写出图示序列的表达式答：3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用δ(n) 表示y (n )={2,7,19,28,29,15}2. ①求下列周期)54sin()8sin()4()51cos()3()54sin()2()8sin()1(n n n n n ππππ-②判断下面的序列是否是周期的; 若是周期的， 确定其周期。
（1）A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= （2）)81(j e )(π-=n n x 解： （1） 因为ω=73π, 所以314π2=ω, 这是有理数， 因此是周期序列， 周期T =14。
（2） 因为ω=81, 所以ωπ2=16π, 这是无理数， 因此是非周期序列。
③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。
3.加法乘法序列{2，3，2，1}与序列{2，3，5，2，1}相加为__{4，6，7，3，1}__，相乘为___{4，9，10，2} 。
移位翻转：①已知x(n)波形，画出x(-n)的波形图。
②尺度变换：已知x(n)波形，画出x(2n)及x(n/2)波形图。
卷积和：①h(n)*求x(n)，其他02n 0n 3，h(n)其他03n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤= }23,4,7,4，23{0,h(n)*答案：x(n)=②已知x (n )={1,2,4,3},h (n )={2,3,5}, 求y (n )=x (n )*h (n )x (m )={1,2,4,3},h (m )={2,3,5}，则h (-m )={5,3,2}(Step1:翻转)解得y (n )={2,7,19,28,29,15}③(n)x *(n)x 3)，求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=}{1,4,6,5,2答案：x(n)=4.如果输入信号为，求下述系统的输出信号。
数字信号处理_课后习题答案
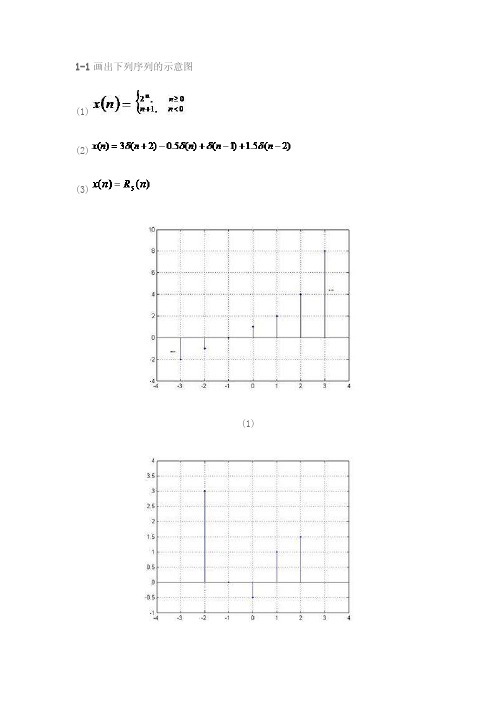
1-1画出下列序列的示意图(1)(2)(3)(1)(2)(3)1-2已知序列x(n)的图形如图1.41，试画出下列序列的示意图。
图1.41 信号x(n)的波形(1) (2)(3) (4)(5) (6)(修正：n=4处的值为0，不是3）（修正：应该再向右移4个采样点）1-3判断下列序列是否满足周期性，若满足求其基本周期(1)解：非周期序列;(2)解：为周期序列，基本周期N=5;(3)解：，，取为周期序列，基本周期。
(4)解：其中，为常数，取，，取则为周期序列，基本周期N=40。
1-4 判断下列系统是否为线性的？是否为移不变的？(1)非线性移不变系统(2) 非线性移变系统（修正：线性移变系统）(3) 非线性移不变系统(4) 线性移不变系统(5) 线性移不变系统（修正：线性移变系统）1-5判断下列系统是否为因果的？是否为稳定的？(1) ，其中因果非稳定系统(2) 非因果稳定系统(3) 非因果稳定系统(4) 非因果非稳定系统(5) 因果稳定系统1-6已知线性移不变系统的输入为x(n)，系统的单位脉冲响应为h(n)，试求系统的输出y(n)及其示意图(1)(2)(3)解：（1）（2）（3）1-7若采样信号m(t)的采样频率fs=1500Hz，下列信号经m(t)采样后哪些信号不失真？(1)(2)(3)解：(1)采样不失真(2)采样不失真(3)，采样失真1-8已知,采样信号的采样周期为。
(1) 的截止模拟角频率是多少？(2)将进行A/D采样后，的数字角频率与的模拟角频率的关系如何？(3)若，求的数字截止角频率。
解：(1)(2)(3)1-9计算下列序列的Z变换，并标明收敛域。
(1) (2)(3) (4)(5)解：(1)(2)(3)(4) ，，收敛域不存在(5)1-10利用Z变换性质求下列序列的Z变换。
(1)(2)(3)(4)解：(1) ,(2) ,(3),(4) , 1-11利用Z变换性质求下列序列的卷积和。
(1)(2)(3)(4)(5)(6)解：(1) ，,，,(2) ,，,(3) , ，,(4) ，,(5) ,，，(6) ，，，1-12利用的自相关序列定义为，试用的Z 变换来表示的Z变换。
数字信号处理习题课
M=log2N
练习题
1、根据基2FFT算法，可将2048点的DFT分解成 级蝶形运算，每一
级包含 24点DFT的复加次数是
是
；
3、若直接计算N点DFT,需要的复乘次数和复加次数分别是
4、课后第1题
、
;
5、试比较直接计算N点DFT与基2FFT快速算法的运算量
第五章 时域离散系统的网络结构
)
A. x((n 2))4 R4 (n)
B. x((n 2))4 R4 (n)
C. x((n 2))4 R4 (n) D.以上答案都不对
6、有限长序列x(n)的8点DFT为X（k），则X（k）=
;
7、求序列R3(n)和 R5(n)长度为8的循环卷积波形 x1(n) R3(n) R5(n) ，并说明序列 x1(n) 与序列 x2 (n) R3(n) R5 (n) 波形是否相同。
用循环卷积实现线性卷积，则循环卷积的长度至少应等于( )
A.20点 B.21点 C.22点 D.23点
3、序列的Z变换和DFT的关系是( )
A.序列的N点DFT是x(n)在单位圆上的Z变换
B.序列的N点DFT是x(n)的Z变换在单位圆上N点采样
C.序列的N点DFT是x(n)的Z变换在单位圆上N点的等间隔采样
D.以上都不对。
4、下面描述中最适合离散傅立叶变换DFT的是（ ）
A．时域为离散序列，频域也为离散序列
B．时域为离散有限长序列，频域也为离散有限长序列
C．时域为离散无限长序列，频域为连续周期信号
D．时域为离散周期序列，频域也为离散周期序列
5、已知序列 x(n) {5,4,3,1}，其循环移位 x((n 2))4 R4 (n) 是(
数字信号处理习题
习题课第三章
3-17：x1(n)=R5(n), X1(ejw)=DTFT[x1(n)],幅频，相频特性
已知是50点的有限长序列，非零值范围为是15点的有限长序列，非零值范围，对两序列做50点圆周卷积，即试问，y(n)中哪个n 值范围对应于的结果。
)(1n x )
(2n x 49
0≤≤n 19n 5≤≤)
())(()()()()(5050249
0121n R m n x m x n x n x n y m −=Θ=∑=)()(21n x n x ∗
•要求会用圆卷积代替线性卷积，因为圆卷积可以用快速算法实现
•两序列线性卷积长度分别等于N1，N2
•起始非零点为两序列各自非零点之和；终点非零值点位两序列各自非零点终点序号之和
•这里就是5-68（64个点）为线性卷积结果的非零点
•这里做50点的圆卷积，就是对这64个点做以周期为50的延拓，所以必然有重合相加点，不等于线性卷积结构。
数字信号处理课后习题答案-第六章习题与答案
1．、2． 用冲激响应不变法将以下 )(s H a变换为变换为 )(z H ，抽样周期为T 。
为任意正整数 ,)()( )2()()()1(022n s s As H b a s as s H na a -=+++=分析：①冲激响应不变法满足)()()(nT h t h n h a nTt a===，T 为抽样间隔。
这种变换法必须)(s H a 先用部分分式展开。
②第（②第（22）小题要复习拉普拉斯变换公式1!][+=n n S n t L ,na n t s a S S As H t u n t Ae t h )()()()!1()(010-=⇔-=-，可求出可求出 )()()(kT Th t Th k h a kTt a===，|又 dz z dX z k kx )()(-⇔，则可递推求解。
解: (1)22111()()2a s a H s s a b s a jb s a jb ⎡⎤+==+⎢⎥+++++-⎣⎦[])( 21)()()(t u e e t h tjb a t jb a a --+-+= 由冲激响应不变法可得：由冲激响应不变法可得：由冲激响应不变法可得：[]()()()() ()2a jb nT a jb nT a T h n Th nT e e u n -+--==+ 11011() () 211naT jbT aT jbT n T H z h n z e e z e e z ∞------=⎡⎤==+⎢⎥--⎣⎦∑ 2211cos 21cos 1 ------+--⋅=z e bT z e bT z e T aT aT aT(2) 先引用拉氏变换的结论[]1!+=n n s n t L 可得：可得： n a s s As H )()(0-=))()!1()(10t u n t Ae t h n t s a -=-则 )()!1()()()(10k u n kT Ae T Tk Th k h n kT s a -⋅==- dzz dX zk kx az k u a ZZk )()( , 11)( 1-−→←-−→←-且按)11()()!1( )()!1( )()(111111000--∞=---∞=----=-==∑∑ze dz d z n AT e z k n T TA z k h z H T s n n kkT s n n k k可得⎪⎪⎩⎪⎪⎨⎧=-=-=•••---,3,2)1(1,1)(111000n z e z e AT n z e ATz H n T s T S n T s ，可以递推求得：2. 已知模拟二阶巴特沃思低通滤波器的归一化系统函数为：2'4142136.111)(s s s H a ++=而而3dB 截止频率为50Hz 的模拟滤波器，需将归一化的)('s H a 中的s 变量用502⨯πs 来代替424'108696044.928830.444108696044.9)100()(⨯++⨯==s s s H s H a a π：设系统抽样频率为设系统抽样频率为Hz f s 500=，要求从这一低通模拟滤波器设计一个低通数字滤波器，采用阶跃响应不变法。
数字信号处理_第一章_习题
解:
画
一个[- , ]周期频谱图
画
一个[- , ]周期频谱图
解:
解:
解:
习题1-2
解:
习题1-21
解:
讨论系数求解
习题1-21
解:
若
留数法或者线性加权特性求出
若
作业(1-6) 例: 已知抽取器的输入和输出关系为 y[k]=x[Mk]
试判断该离散系统是否为时不变系统？
解：输入序列x[k]产生的输出序列y[k]为 y[k]=T{ x[k]}= x[Mk] y[k-n]=x[M(k-n)] 输入序列x[k-n]产生的输出序列为 T{x[k-n]}= x[Mk-n] 由于 x[Mk-n] y[k-n]故该离散系统是时变系 统。
受频率响
应幅度|H(ej ) | 加 权 影 响 , 而 输 出 的
则为输入相位与相系位统响应相位之和。
解: 系统频响
习题1-25
举例
已知系统函数: 如果输入序列为: 则系统的稳态输出y[k]:
信号离散化过程中频谱分析或者频谱变化规律
采样Ts
? 周期化
作业 1-27
解:
周期为2
解:
周期为2
习题1-12
解:
书14页
习题1-12
解:
书14页
补充(第2章内容)
习题1-12
解:
取一周期主值
解:
1 -
习题1-14
因为X(ej )是偶函数，公式简化为: 若k=0
解: 1
若
-
习题1-14
Hale Waihona Puke 解: 1习题1-14
-
-0.5
0.5
《信号与系统》(第2版)书161
清华大学数字信号处理课件--数字信号习题课3共46页
综上所得，第一个和第三个序列满足 X%(k) 0 k2,4,...
课件
16
8. 下图表示一个5点序列 x ( n ) 。 （1）试画出 x(n)x(n)；
（2）试画出 x ( n )⑤ x ( n ) ； （3）试画出x ( n ) ⑩ x ( n ) ；
1 2aej1 2(2N ke0)(2e(j1 2e(2N 2k 0)ee2j1 2)(2N k0))
j0N j0N j0N
ej1 2(2N ke0)(2e(j1 2e(2N 2k 0)ee2j1 2()2N k0))RN(k)
1 2a sin ( siN n (k 0 2 N 1 2 )0)ej N kjN 2 1 0课 件sin ( siN n (k 0 2 N 1 2 )0)ej N kjN 2 1 0 R N 8(k)
n0
N1
j2nk
x(n)e N RN(k)
n0
N1(nn0)ej2N nkRN(k) n0
ej2Nn0kRN(k)
课件
10
6. 如图P3-6（a）画出了几个周期序列 x%( n ) ，这 些序列可以表示成傅里叶级数
x % (n)1N 1X % (k)ej(2/N )nk
Nk 0
（1）哪些序列能够通过选择时间原点使所有的
3．设
x(n)n0,1,
0n4 其他n
h(n)R 4(n2)
令 x% (n)x((n))6，h% (n)h((n))6，
试求 x%( n ) 与 h%( n ) 的周期卷积并作图。
解：
N1
y% (n)x% (m)h% (nm)
m0
课件
数字信号处理课后习题Ch4
= ( n−2 α )π sin[( n − α ) wc ] sin[( n − α ) w0] 因为 h(n)=hd (n)W R (n)= hd(n) R N (n) 所以（1）当 N 为奇数时 h（n）= { (0 ≤ n ≤ N − 1) ; 0 , 其他 （2）当 N 为偶数时 h（n）的表达式与 N 为奇数时相同 （3）若采用汉明窗设计 h(n)= h d (n)W(n) = ( n−2 α )π sin[( n − α ) wc ] sin[( n − α ) w0] [0.54-0.46cos (
N ⎧ 2 1 ⎪ H (ω ) = b ( n ) c o s [ω ( n − )] ∑ ⎪ 2 n =1 ∴ ⎨ ⎪ N b (n ) = 2 h ( − 1 + n) ⎪ 2 ⎩
∴ （1）当 N 为奇数时
2
sinωc (n − α ) ⎧ RN (n), 0 ≤ n ≤ N − 1 ⎪2cosω0 (n-α ) π (n − α ) h( n) = ⎨ ⎪0, 其他 ⎩
（2）当 N 为偶数时 h(n)的表达式与 N 为奇数时的相同； （3）若用汉明窗设计
h( n) = hd (n)ω (n) = 2 cos ω0 ( n − α ) sin ωc ( n − α ) 2π n [0.54 − 0.46 cos( )]RN (n) π (n − α ) N −1
(1 ).h d ( n ) = =
1 2π
∫
2π 0
H d (e
jω
)e
jn ω
dω
1 π + ω c − j ( ω − π ) α jn ω e e dω 2 π ∫π − ω c π +ωc 1 = e jπ α ∫ e j ( n −α )ω d ω π −ω c 2π 1 1 = e jπ α e j ( n − α ) ω 2π j ( n − α ) 1 e jπ α [e = 2π j ( n − α )
数字信号处理习题及解答
数字信号处理习题及解答
第一章 离散时间信号与离散时间系统
4 解答
数字信号处理习题及解答
第二章 Z变换及离散时间系统分析 1
数字信号处理习题及解答
第二章 Z变换及离散时间系统分析 1 解答
数字信号处理习题及解答
第二章 Z变换及离散时间系统分析 1 解答
数字信号处理习题及解答
第二章 Z变换及离散时间系统分析 2
7
(1) X(ej0) x(n)6
n3
(2)
πX (ej)d x(0 )2π4π
π
7
(3) X (ejπ) x(n)ejn ( 1 )nx(n)2
n
n 3
数字信号处理习题及解答
第三章 信号的傅里叶变换 2 试求如下序列的傅里叶变换： (1) x1(n)=δ(n－3)
（2） x2(n)1 2δ(n1)δ(n)1 2δ(n1)
11 a 2 ac 2ac o o s s
F[x T o(n) ]jIm X(e [j]jIm 1a [1 ej]jIm 1a [1 ej1 1 a ae ejj ]
1a 2a s2a i cno s
数字信号处理习题及解答
第三章 信号的傅里叶变换 4 已知长度为N=10的两个有限长序列：
1 0≤ x1(n)0 5≤
故系统是非时变系统。 由于
T［ax1(n)+bx2(n)］=［ax1(n)+bx2(n)］2 ≠aT［x1(n)］+bT［x2(n)］ =ax21(n)+bx22(n)
因此系统是非线性系统。
数字信号处理习题及解答
第一章 离散时间信号与离散时间系统
2 给定下述系统的差分方程， 试判定系统是否是因果稳定系统， 并说明理由。
数字信号处理习题课内容
数字信号处理教程课后习题及答案第一章 离散时间信号与系统1 .直接计算下面两个序列的卷积和)n (h *)n (x )n (y =请用公式表示。
分析：①注意卷积和公式中求和式中是哑变量m （ n 看作参量）， 结果)(n y 中变量是 n ,; )()()()()(∑∑∞-∞=∞-∞=-=-=m m m n x m h m n h m x n y②分为四步 （1）翻褶（ -m ），（2）移位（ n ）,（3）相乘，; )( )( 4n y n n y n 值的，如此可求得所有值的）相加，求得一个（ ③ 围的不同的不同时间段上求和范一定要注意某些题中在 n00 , 01()0 , ,()0,n n n a n N h n n n n x n n n β-⎧≤≤-=⎨⎩⎧≤⎪=⎨<⎪⎩其他如此题所示，因而要分段求解。
2 .已知线性移不变系统的输入为)n (x ,系统的单位抽样响应 为)n (h ,试求系统的输出)n (y ,并画图。
)(5.0)(,)1(2 )()4()(5.0)(,)2( )()3()()(,)( )()2()()(,)( )()1(3435n u n h n u n x n R n h n n x n R n h n R n x n R n h n n x n n n =--==-=====δδ分析：①如果是因果序列)(n y 可表示成)(n y ={)0(y ，)1(y ，)2(y ……}，例如小题（2）为)(n y ={1，2，3，3，2，1} ;②)()(*)( , )()(*)(m n x n x m n n x n x n -=-=δδ ; ③卷积和求解时，n 的分段处理。
()∑∑∑+-=+-=--+===-=-+≥nN n m m nn nN n m mn n m nn m m n h m x n y N n n 111N -00)()()( , 1)3(αββααβ全重叠时当()()()()βααβαβαβαββααβαβαβ==≠--=--=---+++--,)(,100111n n N N n N n n N n n nN n y ∑∞-∞=-==m m n h m x n h n x n y )()()(*)()(:解0)()1(0=<n y n n 时当, 1)2(00部分重叠时当-+≤≤N n n n ()∑∑∑==--===-=nn m mnn n n m mn n m nn m m n h m x n y 0)()()(αββααβ()()βαβαβαβααβαβαβ≠--=--=-+-++-,10111n n n n n n n n())(,1)(00βαα=-+=-n n n y n n3 .已知 10,)1()(<<--=-a n u a n h n ，通过直接计算卷积和的办法，试确定单位抽样响应为 )(n h 的线性移不变系统的阶跃响应。
数字信号处理课后习题Ch1
数字信号处理课后习题详解第一章1.1 试画出正弦序列sin(16πn /5)的波形，它是不是一个周期序列？若是，其周期长度是多少？解：matlab 环境下实现源代码如下： n=[0:15]; y=sin(16*pi*n/5);stem(n,y); xlabel('n'); ylabel('x(n)') 图形如下图所示。
2251685p q πππβ===，取k =p ，则周期N =p =5，即sin(16πn /5)是一个周期序列，周期长度为5；图中也可以看出这点。
1.2 判断下列序列是否是周期序列，若是，确定其周期长度。
(1) 3()cos(74x n n ππ=−解：2214337p q πππβ===∵ p ，q 是互为质数的整数，取k =q 则周期N =p =14∴周期长度为14 (2) 7cos()4sin()(nnn x ππ−=解：1284N ππ== 22147N ππ==∵N 1，N 2最小公倍数为56 ∴其周期长度为561.3 试画出如下序列的波形(1) x(n)=3δ(n+3)+2δ(n+1)-4δ(n-1)+2δ(n-2) (2)x(n)= 0.5n R 5(n)解：(1)(2)1.4 今对三个正弦信号)2cos()(1t t x a π=、)6cos()(2t t x a π−=、)10cos()(3t t x a π=进行理想采样，采样频率为π8=Ωs ，求这三个采样输出序列，比较其结果。
画出x a 1(t )、x a 2(t )、x a 3(t )的波形及采样点位置并解释频谱混叠现象。
解：matlab 环境下实现源代码如下：t=-1:0.01:1; x1=cos(2*pi*t); x2=-cos(6*pi*t); x3=cos(10*pi*t); t2=-1:0.25:1; y1=cos(2*pi* t2);y2=-cos(6*pi* t2);y3=cos(10*pi* t2);subplot(311)plot(t,x1);xlabel('t');ylabel('Xa1(t)') holdstem(t2, y1)subplot(312)plot(t,x2);xlabel('t');ylabel('Xa2(t)') holdstem(t2, y2)subplot(313)holdstem(t2, y3)plot(t,x3);xlabel('t');ylabel('Xa3(t)') 三个信号波形已知πω8=，则4182,42===πππωs T 。
数字信号处理课后习题答案 全全全
1
1 >
. . z
z
(3) , | | 0.5
1 0.5
1
1 <
. . z
z
(4)
, | | 0
1 0.5
1 (0.5 )
1
1 10
>
.
.
.
.
z
z
z
1.8 (1) ) , 0
1
( ) (1 2
1 3 3
3.014 2.91 1.755 0.3195
0.3318 0.9954 0.9954 0.3318
1 0.9658 0.5827 0.1060
z z z
z z z
z z z
z z z
. . .
. . .
. . .
. . .
. + .
=
= . . +
= . . . +
..
.
..
. π
2.13
0,1,2, , 1
( ) ( )
= .
=
k N
Y rk X k
..
2.14
Y(k) = X ((k)) R (k) k = 0,1, ,rN .1 N rN ..
2.15 (1) x(n) a R (n) N
= n y(n) b R (n) N
= n
(2) x(n) =δ (n) y(n) = Nδ (n)
2.16 ( )
1
1 a R N
a N
n
. N
数字信号处理习题课
第三章 离散傅里叶变换D F TD F T 定义D F T 性质（循环移位、循环卷积）D F T 应用计算线性卷积信号谱分析1、序列X 1( n )的长度为4，序列X 2（n ）的长度为3，则它们线性卷积的长度和五点循环卷积的长度分别是（ ）A . 5, 5B . 6, 5C . 6, 6D . 7, 52、已知序列 x (n )的为10点，系统的单位脉冲响应 为12点，若要用循环卷积实现线性卷积，则循环卷积的长度至少应等于( )A .20点B .21点C .22点D .23点3、序列的Z 变换和D F T 的关系是( )A .序列的N 点D F T 是x (n )在单位圆上的Z 变换B .序列的N 点D F T 是x (n )的Z 变换在单位圆上N 点采样C .序列的N 点D F T 是x (n )的Z 变换在单位圆上N 点的等间隔采样D .以上都不对。
4、下面描述中最适合离散傅立叶变换D F T 的是（ ）A ．时域为离散序列，频域也为离散序列B ．时域为离散有限长序列，频域也为离散有限长序列C ．时域为离散无限长序列，频域为连续周期信号D ．时域为离散周期序列，频域也为离散周期序列5、已知序列}1,3,4,5{)(-=n x ，其循环移位)())2((44n R n x -是( )A . )())2((44n R n x -B .)())2((44n R n x -C . )())2((44n R n x -D .以上答案都不对6、有限长序列x (n )的8点D F T 为X （k ），则X （k ）= ;7、求序列R 3(n )和 R 5(n )长度为8的循环卷积波形 )()()(531n R n R n x ⊗= ，并说明序列)(1n x 与序列 )()()(532n R n R n x *=波形是否相同。
8、例题3.4.2与课后16题9、已知序列x (n )的32点D F T 为X (k ),则X (k )的隐含周期是（ ）第四章 快速傅里叶变换F F T• 直接计算N 点D F T 的运算量（复乘和复加）• 基2—F F T 快速算法的运算量• 基2—F F T 快速算法的重要结论把N 点D F T 分解成M 级蝶形运算，每一级包含N /2个蝶形 M =l o g 2N练 习 题1、根据基2F F T 算法，可将2048点的D F T 分解成 级蝶形运算，每一级包含 个蝶形；2、用基2F F T 快速算法计算1024点D F T 的复加次数是 ；复乘次数是 ；3、若直接计算N 点D F T ,需要的复乘次数和复加次数分别是 、 ;4、课后第1题5、试比较直接计算N 点D F T 与基2F F T 快速算法的运算量第五章 时域离散系统的网络结构• I I R 系统网络结构直接型、级联型、并联型• F I R 系统网络结构 直接型、频率采样结构练 习 题1、已知系统的信号流图，写出系统函数表达式3、设数字滤波器的差分方程为()()()()()2615)2(156---+-+-+=n y n y n x n x n x n y画出该滤波器的直接型、级联型和并联型结构。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
所以：
1 1 1 a ( z z 1 ) a (z z ) 2j 2j H I ( z) 2 1 1 a a ( z z ) (1 az1 )(1 az)
两个极点：
z1 a, z2 a 1
FTxo (n) j Im X (e j )
j 2 ) | cos{ n arg[H (e 3 )]} 3
2
H (e
j
2 3
) 1 0.8e
1
2 j3
3.2
所以y(n) 最大值：
y(n) max 20 3.2 64
例5 设序列x(n) 为：
mn nm u(n n0 N )
0
n1n n1n
0
N u(n n0 ) ( ) u(n n0 N )( )
线性卷积的计算方法：
1、图解法 适用于有限长和无限长序列卷积的计算
2、利用单位采样序列的选择性 适用于非零值有限的卷积的计算
解答：题意分析：该题考查的是对系统时域性质的掌握情况， 已知系统的输入输出关系，按照定义判断即可。
(1) 线性
定义
T [ax1 (n) bx2 (n)] aTx1 (n) bTx2 (n) ay1 (n) by2 (n)
输入线性组合的响应 输入响应的线性组合
系统对输入线性组合的响应等于对输入响应的线性组合
x ( m)
n n
0
m n0
0
n 1n n 1 n ( )
0
-N+n0
n0
m
x ( m)
y(n)
n n0
m n0
1 (n n )
0
n
n n0
( )
n0
N+n0
m
（3 ） n n0 N 时，全重叠。即：
（3）根据FT与ZT关系，得：
H ( e j ) H ( z ) z e j 1 1 0.8e j 0.64e 2 j
画出滤波器的幅频特性，知是带通滤波器 （4）y(n)及其最大值
LTI 系统的正弦稳态响应
y (n) 20 | H (e
其中：
2 j 3
两者相等，故为线性系统
（2）时不变性 定义
T [ x(n k )] y(n k )
对输入的移位 对响应的移位
nk nk
T [ x(n k )]
m
x(m k ) x(m) x(m)
m k m m
n
y (n k )
信号与系统分析
时域分析：信号和系统的性质；LTI系统的输入、输出关系 变换域分析：信号和系统的性质；LTI系统的输入、输出关 系、频率特性分析（DTFT、ZT、DFT） 例1：判断系统：
T x(n)
m
x ( m)
n
的（1）线性；（2）时变性；（3）因果性；（4）稳定性 解题步骤： 1、题意分析（已知、求解的问题） 3、求解（知识的运用） 2、知识点
y(n) 0.8 y(n 1) 0.64 y(n 2) x(n)
（1）求H(z)，画出零极点图；
（2）标出H(z)的ROC，并判断稳定性，说明理由； （3）求系统的频率响应，画出幅频特性示意图，并指出滤 波特性
2 （4）设 x ( n ) 20 cos( n )，求y(n) 最大值 3
已知序列的傅里叶变换，求原序列，一般采用ZT求解。
1 j j a (e e ) a sin 2j j H I (e ) 2 1 a 2a cos 1 a 2 a(e j e j )
ZT与FT的关系：
H (e j ) H ( z) z e j
n
故为因果系统（ n 0 时，h(n) 0 ）
(4) 稳定性
定义：有界输入产生有界输出（BIBO）的系统。 方法1：设 x(m) M ，则:
y(n) T [ x(n)]
故为不稳定系统。
m
x(m) M M
m
n
n
方法2：
m
h( n)
1、n≥1时，围线内有单极点a
z 2 1 1 n n 1 h(n) Re s[ F ( z), a] z ( z a) a 1 za 2 2( z a)( z a )
2、n 0 时，围线内有两个单极点 z1 0, z2 a,
ho (n) Re sF ( z), a Re sF ( z),0 0
m
u ( n)
m
1
为非稳定系统
注：只有LSI系统的因果性和稳定性可通过其h(n)判定。
例2 P75
No1.21
已知：
n n0 0 n N 1 n 0 n N 1 h( n) x ( n) 0 其他 0 其他
h(n)是实因果序列，且为指数序列，所以：
h(0) 1
a n n 1 h(n) 1 n 0 a n u ( n) 0 n 1
H (e ) a e
j n 0
n jn
1 1 ae j
例4 已知一因果LTI系统，用差分方程表示为：
0
1 n0 m n u (m n0 )u (n m) 0，其他 1 n0 m n N u (m n0 )u (n m N ) 0，其他
带入上式：
y(n)
m
m n0
nm
u(n n0 )
0
m
令分子、分母分别为零，得系统零、极点：
p1,2 0
4 1 j 3 4 1 j 3 z1 , z2 5 2 5 2
z1, 2
4 1 j 3 0.8 5 2
（2） 系统函数ROC与系统性质的关系
因果系统，系统函数的ROC必包括无穷远点，故：
z 0.8
ROC包含单位圆，系统稳定。
y ( n)
mn N
1 N
n
n n0
方法2 利用单位阶跃序列u(n)
单位阶跃序列的乘积具有选择性
u (n n0 ) n0 m n u (m n0 )u (n m) 0，其他
步骤1、将已知序列用单位阶跃序列u(n)表示
n n0 , n0 n x ( n) n n0 u (n n0 ) 0 n n0
y ( n)
mn N n
x ( m ) h ( n m)
m n0
n
x ( m)
mn N
0
nm
n0
N+n0
n n
mn N
m ( / ) n n0 N
n
m
N 1
n 1 n0
n n0
( )
( )
m
mn nm u(n m) u(n m N ) u ( m n ) 0
0
m
mn m u ( m n ) u (n m) 0
0
又：
m
mn m u ( m n ) u (n m N ) 0
解答：LTI系统的差分方程与系统函数的关系；系统函数与 频率响应的关系；系统的Z域分析；正弦稳态响应。
（1） LTI系统函数与差分方程的关系；ZT的性质
对差分方程两边取ZT：
Y ( z) 0.8z 1Y ( z) 0.64z 2Y ( z) X ( z)
Y ( z) 1 z2 H ( z) 2 1 2 X ( z ) 1 0.8z 0.64z z 0.8z 0.64
n ,0 n N h( n ) n u (n) u(n N ) 0 其他
步骤2、变量代换
x(m) mn0 u(m n0 )
h(m) m u(m) u(m N )
步骤3、将h(m)翻褶
h(m) m u(m) u(m N )
试求 y(n) x(n) h(n) 。
题意分析 ：考察线性卷积的计算。一般需要根据序列的起始 点和结束点进行分段讨论；注意相加的范围不要弄错。
方法1 图解法
y ( n ) x ( n ) h ( n)
m
x(m)h(n m)
mn nm
0
并移位：
h(n m) nm u(n m) u(n m N )
步骤4、带入公式计算
y ( n ) x ( n ) h ( n)
m
x(m)h(n m)
y ( n ) x ( n ) h ( n)
m
x(m)h(n m)
j
a 1
求序列h(n)及其傅里叶变换。
解：FT的共轭对称性；ZT与FT的关系；Z逆变换的求解
FTxo (n) j Im X (e j )
若表达式中包含正弦（余弦）信号，利用欧拉公式代换:
1 j j 1 j sin (e e ), cos (e e j ) 2j 2 1 j j a (e e ) a sin 2j j H I (e ) 2 1 a 2a cos 1 a 2 a(e j e j )
x ( m)
nk