振动加速度总级计算公式
振动加速度计算公式

振动加速度计算公式
振动是物体在固定点或轴线周围做有规律地往复运动。
振动加速度是描述物体振动情况的一个物理量,表示单位时间内物体所获得的速度变化量。
首先,简谐振动的运动方程可以表示为:
x = Acos(ωt + φ)
其中,x为物体的位移,A为振幅,ω为角频率,t为时间,φ为相位常数。
其次,速度是位移对时间的导数,即
v = dx/dt = -Aωsin(ωt + φ)
再次,加速度是速度对时间的导数,即
a = dv/dt = -Aω^2cos(ωt + φ)
根据上述推导,振动加速度计算公式为:
a = -Aω^2cos(ωt + φ)
在上述公式中,A表示振幅,ω表示角频率,t表示时间,φ表示相位常数。
振幅决定了振动的幅度大小,角频率则影响振动的周期,相位常数则决定了振动的起始位置。
此外,还有一种计算振动加速度的方法是使用泰勒级数。
泰勒级数是一种将函数在其中一点展开成无穷级数的方法,通过求取一定阶数的导数来逼近其中一函数的值。
对于振动加速度,可以使用泰勒级数展开cos函数来计算。
根据泰勒
级数展开可得到:
cos(x) = 1 - (x^2/2!) + (x^4/4!) - (x^6/6!) + ...
通过对cos(x)函数进行泰勒级数展开,并截取一定阶数的项,可以
计算出振动加速度的近似值。
综上所述,振动加速度的计算公式可以根据物体振动特性得出,根据
简谐振动的运动方程和泰勒级数展开可以求得振动加速度的精确或近似值。
这些计算方法能够帮助我们更好地理解和描述振动现象。
振动计算力学公式

振动计算力学公式一、简谐振动(Simple Harmonic Motion)简谐振动指的是一个物体在一个平衡位置附近做低幅度的周期性振动。
简谐振动的一些重要的力学公式如下:1. 位移(Displacement):x = A * cos(ωt + φ)其中,x表示位移,A表示振幅,ω表示角频率,t表示时间,φ表示相位。
2. 速度(Velocity):v = -A * ω * sin(ωt + φ)其中,v表示速度。
3. 加速度(Acceleration):a = -A * ω^2 * cos(ωt + φ)其中,a表示加速度。
4. 动能(Kinetic Energy):K = 0.5 * m * v^2其中,K表示动能,m表示质量。
5. 势能(Potential Energy):P = 0.5 * k * x^2其中,P表示势能,k表示弹性系数。
6. 总机械能(Total Mechanical Energy):E = K + P其中,E表示总机械能。
7. 振动周期(Vibration Period):T = 2π/ω其中,T表示振动周期。
二、阻尼振动(Damped Vibration)阻尼振动指的是振动过程中受到了阻尼力的影响,导致振幅逐渐减小。
阻尼振动的一些重要的力学公式如下:1. 位移(Displacement):x = A * e^(-βt) * cos(ωdt + φ)其中,x表示位移,A表示振幅,β表示阻尼系数,ωd表示阻尼角频率,t表示时间,φ表示相位。
2. 速度(Velocity):v = -A * β * e^(-βt) * cos(ωdt + φ) - A * ωd * e^(-βt) * sin(ωdt + φ)其中,v表示速度。
3. 加速度(Acceleration):a = A * (β^2 * e^(-βt) *cos(ωdt + φ) + 2β * ωd * e^(-βt) * sin(ωdt + φ)) - A *ωd^2 * e^(-βt) * cos(ωdt + φ)其中,a表示加速度。
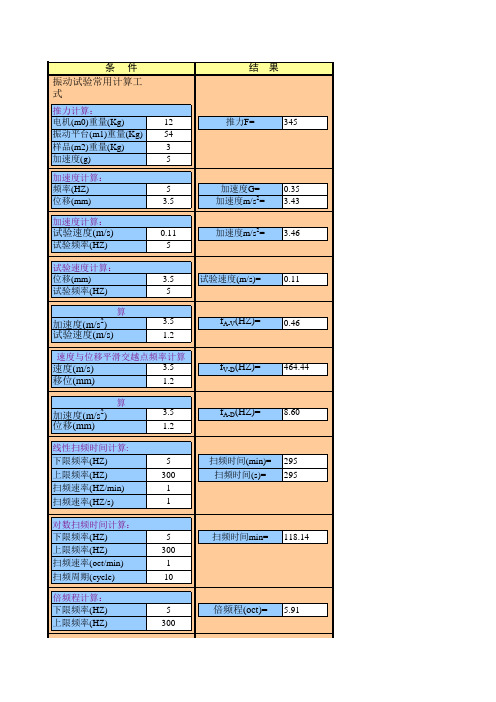
振动试验常用工式计算
0.35 3.43 3.46
试验速度(m/s)
试验频率(HZ) 试验速度计算: 位移(mm) 试验频率(HZ)
3.5 5
试验速度(m/s)=
Байду номын сангаас
0.11
加速度与速度平滑交越点频率计算 3.5 加速度(m/s2) 试验速度(m/s) 1.2 速度与位移平滑交越点频率计算 3.5 1.2
fA-V(HZ)=
fA-D(HZ)=
8.60
5 300 1 1
扫频时间(min)= 扫频时间(s)=
295 295
5 300 1 10
扫频时间min=
118.14
5 300
倍频程(oct)=
5.91
下限频率(HZ) 上限频率(HZ) 扫频时间(min) 功率(W) 阻抗(Ω )
5 300 5.9 0.005 32
扫频速率(oct/min)= 1.00
条 件 振动试验常用计算工式
推力计算: 电机(m0)重量(Kg) 振动平台(m1)重量(Kg) 样品(m2)重量(Kg) 加速度(g) 加速度计算: 频率(HZ) 位移(mm) 加速度计算: 12 54 3 5 5 3.5 0.11 5
结
果
推力F=
345
加速度G= 2 加速度m/s = 加速度m/s =
喇叭寿命试验电压计算:
电压V= 0.40
0.46
速度(m/s) 移位(mm)
fV-D(HZ)=
464.44
加速度与位移平滑交越点频率计算 3.5 加速度(m/s2) 位移(mm) 1.2 线性扫频时间计算: 下限频率(HZ) 上限频率(HZ) 扫频速率(HZ/min) 扫频速率(HZ/s) 对数扫频时间计算: 下限频率(HZ) 上限频率(HZ) 扫频速率(oct/min) 扫频周期(cycle) 倍频程计算: 下限频率(HZ) 上限频率(HZ) 扫频速率计算:
振动加速度计算公式

振动加速度计算公式在一维简谐振动中,振动加速度与位移和时间的关系可以由如下公式描述:a(t)=-ω²x(t)其中,a(t)表示物体在时刻t的振动加速度,x(t)表示物体在时刻t 的位移,ω表示振动的角频率。
这个公式的推导基于牛顿第二定律以及简谐振动的基本假设。
根据牛顿第二定律,物体受到的合力F与物体的质量m和加速度a的关系为:F = ma在简谐振动中,振动物体只受到恢复力F = -kx的作用,其中k是物体的弹性系数。
将恢复力代入牛顿第二定律中,得到:-mω²x = ma两边除以m,得到:ω²x=-a移项后得到振动加速度的计算公式:a=-ω²x其中,负号表示振动加速度的方向与位移方向相反。
由于振动加速度的数值与物体的位移成正比,所以振动加速度的大小与位移大小呈非线性关系。
当物体位移达到最大值时,振动加速度为零;当物体位移为零时,振动加速度达到最大值。
对于其他类型的振动,如二维和三维振动,振动加速度的计算公式也可以根据具体情况进行推导。
在这些情况下,振动加速度的计算公式通常包含物体的质量、位移、速度以及加速度的各个分量。
振动加速度计算公式的应用非常广泛。
例如,在工程领域中,振动加速度常用于分析和设计各种振动系统,如机械结构、传动系统和软件系统等。
通过计算和测量振动加速度,我们可以评估系统的稳定性、响应特性以及可能的故障和损坏情况。
此外,在物理学和材料科学中,振动加速度的计算公式也被用于研究材料的弹性特性、声学特性和磁学特性等。
总结起来,振动加速度计算公式是描述物体振动过程中加速度变化的数学公式。
它在物理学和工程领域中有着广泛的应用,对于分析振动系统并评估系统的性能和稳定性非常重要。
振动位移,速度,加速度公式

振动位移,速度,加速度公式
速度公式:vt=v0+at①
位移公式:s=v0t+at2②
速度位移关系式:-=2as③
平均速度公式:=④
=(v0+vt)⑤
=⑥
位移差公式:△s=aT2⑦
公式说明:(1)以上公式除④式之外,其它公式只适用于匀变速直线运动。
(2)公式⑥指的是在匀变速直线运动中,某一段时间的平均速度之值恰好等于这段时间中间时刻的速度,这样就在平均速度与速度之间建立了一个联系。
6.对于初速度为零的匀加速直线运动有下列规律成立:
(1).1T秒末、2T秒末、3T秒末…nT秒末的速度之比
为:1:2:3:…:n。
(2).1T秒内、2T秒内、3T秒内…nT秒内的位移之比
为:12:22:32:…:n2。
(3).第1T秒内、第2T秒内、第3T秒内…第nT秒内的位移之比为:1:3:5:…:(2n-1)。
(4).第1T秒内、第2T秒内、第3T秒内…第nT秒内的平均速度之比为:1:3:5:…:(2n-1)。
grms计算公式和原理

振动台在使用中经常运用的公式1、 求推力(F )的公式F=(m 0+m 1+m 2+ ……)A …………………………公式(1) 式中:F —推力(激振力)(N )m 0—振动台运动部分有效质量(kg ) m 1—辅助台面质量(kg )m 2—试件(包括夹具、安装螺钉)质量(kg )A — 试验加速度(m/s 2)2、 加速度(A )、速度(V )、位移(D )三个振动参数的互换运算公式 2.1 A=ωv ……………………………………………………公式(2) 式中:A —试验加速度(m/s 2)V —试验速度(m/s ) ω=2πf (角速度) 其中f 为试验频率(Hz )V=ωD ×10-3 ………………………………………………公式(3) 式中:V 和ω与“”中同义D —位移(mm 0-p )单峰值2.3 A=ω2D ×10-3 ………………………………………………公式(4) 式中:A 、D 和ω与“”,“”中同义 公式(4)亦可简化为:A=D f ⨯2502式中:A 和D 与“”中同义,但A 的单位为g1g=9.8m/s 2所以: A ≈D f ⨯252,这时A 的单位为m/s 2 定振级扫频试验平滑交越点频率的计算公式 加速度与速度平滑交越点频率的计算公式f A-V =VA28.6 ………………………………………公式(5)式中:f A-V —加速度与速度平滑交越点频率(Hz )(A 和V 与前面同义)。
速度与位移平滑交越点频率的计算公式DV f DV 28.6103⨯=- …………………………………公式(6) 式中:D V f -—加速度与速度平滑交越点频率(Hz )(V 和D 与前面同义)。
加速度与位移平滑交越点频率的计算公式f A-D =DA ⨯⨯23)2(10π ……………………………………公式(7)式中:f A-D — 加速度与位移平滑交越点频率(Hz ),(A 和D 与前面同义)。
振幅、加速度、振动频率三者的关系式

振幅、加速度、振动频率三者的关系式在低频范围内,振动强度与位移成正比,而在中频范围内,振动强度与速度成正比。
在高频范围内,振动强度与加速度成正比。
这是因为频率低意味着振动体在单位时间内振动的次数少,过程时间长,速度和加速度的数值相对较小且变化量更小,因此振动位移能够更清晰地反映出振动强度的大小。
而频率高,意味着振动次数多,过程短,速度和尤其是加速度的数值及变化量大,因此振动强度与振动加速度成正比。
也可以认为,振动位移具体地反映了间隙的大小,振动速度反映了能量的大小,振动加速度反映了冲击力的大小。
振动加速度的量值是单峰值,单位是重力加速度[g]或米/秒平方[m/s2],1[g]=9.81[m/s2]。
最大加速度不可大于20g,最大振幅不可大于5mm。
根据公式最大加速度=0.002×f2(频率Hz的平方)×D(振幅p-pmm),可以举例说明:10Hz最大加速度=0.002×10*10×5=1g。
在任何频率下,最大加速度不可大于20g,最大振幅不可大于5mm。
根据公式最大振幅=20/(0.002×f2),可以举例说明:100Hz最大振幅=20/(0.002×100*100)=1mm。
在任何频率下,振幅不可大于5mm。
加速度与振幅之间可以通过公式1g=9.8m/s2A=1/2×0.002*F2*D进行换算。
其中,A表示加速度(g),F表示频率(Hz),D表示位移量(mm)。
举例来说,当13.2Hz振幅为1mm时,加速度为7m/s2A=0.002X(2X2)X1A=0.002X4X1A=0.008g。
可以通过单位转换1g=9.81m/s2A=0. m/s2来得到2Hz频率时的加速度,即0.m/s。
以上公式可以根据对应的参数输入进行计算,得到所需的结果。
振动试验常用公式

振动试验常用公式集团标准化工作小组 #Q8QGGQT-GX8G08Q8-GNQGJ8-MHHGN#振动台在使用中经常运用的公式1、求推力(F )的公式F=(m 0+m 1+m 2+ ……)A …………………………公式(1) 式中:F —推力(激振力)(N )m 0—振动台运动部分有效质量(kg ) m 1—辅助台面质量(kg )m 2—试件(包括夹具、安装螺钉)质量(kg )A —试验加速度(m/s 2)2、加速度(A )、速度(V )、位移(D )三个振动参数的互换运算公式 A=ωv ……………………………………………………公式(2) 式中:A —试验加速度(m/s 2)V —试验速度(m/s ) ω=2πf (角速度) 其中f 为试验频率(Hz )V=ωD ×10-3 ………………………………………………公式(3) 式中:V 和ω与“”中同义D —位移(mm 0-p )单峰值A=ω2D ×10-3 ………………………………………………公式(4) 式中:A 、D 和ω与“”,“”中同义 公式(4)亦可简化为:A=D f 2502式中:A 和D 与“”中同义,但A 的单位为g1g=s 2所以: A ≈D f ⨯252,这时A 的单位为m/s 2 定振级扫频试验平滑交越点频率的计算公式 加速度与速度平滑交越点频率的计算公式f A-V =VA28.6 ………………………………………公式(5) 式中:f A-V —加速度与速度平滑交越点频率(Hz )(A 和V 与前面同义)。
速度与位移平滑交越点频率的计算公式DV f DV 28.6103⨯=- …………………………………公式(6) 式中:D V f -—加速度与速度平滑交越点频率(Hz )(V 和D 与前面同义)。
加速度与位移平滑交越点频率的计算公式f A-D =DA ⨯⨯23)2(10π ……………………………………公式(7)式中:f A-D — 加速度与位移平滑交越点频率(Hz ),(A 和D 与前面同义)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
振动加速度总级计算公式
振动加速度总级的计算公式
1. 振动加速度公式
振动加速度(a)是指物体在振动运动中,单位时间内速度的增量。
它可以通过以下公式进行计算:
a = ω^2 * x
其中,a表示振动加速度,ω表示角频率, x表示位移。
2. 振动加速度总级公式
若系统中存在多个振动源,且相互独立且方向相同,则振动加速
度的总级(A)可以通过以下公式进行计算:
A = √(a1^2 + a2^2 + … + an^2)
其中,A表示振动加速度总级,a1, a2, …, an分别表示各个振动源的加速度。
示例解释
假设有一个机械系统中,有两个独立的振动源,分别产生的振动
加速度为a1 = 5 m/s^2和a2 = 3 m/s^2。
根据振动加速度总级公式,我们可以计算出振动加速度的总级为:
A = √(5^2 + 3^2) = √(25 + 9) = √34 ≈ m/s^2
因此,机械系统的振动加速度总级为约 m/s^2。
这个示例说明了当系统中存在多个独立的振动源时,我们可以使用振动加速度总级公式来计算系统的总体振动加速度。
通过将各个振动源的加速度平方相加,再进行开方运算,我们可以得到系统的振动加速度总级。
以上是关于“振动加速度总级”的计算公式及示例解释。
通过这些公式,我们可以更好地理解和计算系统的振动加速度总级,从而对系统的振动性质进行分析和评估。
