线段和角的模型-初中数学常见的模型方法专题
初中数学几何模型

全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型:说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是°、°、°、°及有一个角是°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇度旋度,造等边三角形遇度旋度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋度,造中心对称说明:IS 8模型变形BEFcEB说明:说明:nnnnnnnnnnnnnnnnnnnnnnn nnnnn口叩皿皿皿皿皿中点模型 边构诗中{fflt 逢阳点闵iS 中幽城 几何最值模型 VH *h 轴对称模型 对称最值 线mi 差模型 fflftffw 同侧"异侧两蜒段之利罐短视它 同侧、异删芮线投之羞媪小槐型 四边形周怏垠小根地 三角形眉长 必小檢哩三线穀之和 她知爬制过桥模取旋转最值说明:找到与所要求最值相关成三角形的两个定长线段,定长线段的和为最大值,定长线段的差为最小值。
简拼模型三角形j四边形E 面积等分说明:说明:3045602说明:ACOCOAA 模型一:手拉手模型-旋转型全等<2)等濮的AA Mfr=血°拟述°均为等媵直甬M 册A 结险(DA (UCtAO^l>j 超乙他»③。
E 平分£忖了儿(1)―况> Sfr :LDW 牛底皿力能转至右囲检置A 皓论:> 右图中①bOCWMe\QAC AOSD 』 >⑨延氏M 交购于点G 必肖5氏-LBOA⑵特燥惜况>条件m 3MB ,厶伽■剜,将AXD 龍讳至右團位蛊a gife :右gcp fflAfJCD^iOJ^AC?JCiM£33②延长M 交加于点瓦愁有3EC -LUGA f BD 000B (5)-—--——=—-=tan ZlfX D®ACOCOA 3f^SDLAC.灘接也JC >临加*†g ・a+o>s ⑥矢"訐c&J 冊哒相垂直的四嬷)<3)任翦腰三角晤†辭,。
初中几何48个模型及题型讲解

初中几何48个模型及题型讲解一、直线和角1. 平行线和垂直线的性质平行线的性质包括对应角相等、内错角相等、同旁内角相等,垂直线的性质包括互补角相等、邻补角相等等等。
2. 直线的夹角与邻角两条直线之间的夹角等于它的补角,夹角的补角叫相邻角。
3. 同位角与对顶角同位角相等、对顶角相等。
4. 角的大小关系锐角、直角、钝角的大小关系。
5. 角和角度角的性质包括平分角等。
6. 角的运算法则相等角相加还是相等角;补角与角补加为90°。
7. 顶角和底角的性质同位角相等、顶底角相等。
二、等腰三角形、等边三角形1. 等腰三角形的性质两底角相等,两底边相等等。
2. 等边三角形的性质三边相等、三角也相等等等三、全等三角形1. 全等三角形的基本判定条件AAA、SAS、SSS、ASA四种判定条件。
2. 全等三角形的性质全等三角形的对应边和对应角相等等等。
四、相似三角形1. 相似三角形的基本判定条件AA、SAS、SSS、AAS四种判定条件。
2. 相似三角形的性质相似三角形的对应边成比例,对应角相等等等。
五、直角三角形1. 直角三角形的性质勾股定理、边角关系、三边关系等。
2. 解直角三角形的基本方法利用三角函数解决实际问题等。
六、三角形的面积1. 三角形的面积计算公式面积公式S=1/2×底×高等。
2. 多边形的面积计算公式正多边形、梯形、平行四边形、菱形等多边形的面积公式。
七、四边形1. 平行四边形的性质对角线互相平分等。
2. 矩形的性质对角相等、对边相等等。
3. 菱形的性质对角相等、对边相等、对角平分等。
4. 正方形的性质矩形和菱形的结合。
五、圆1. 圆的基本概念圆心、圆周、半径、直径等。
2. 圆的周长和面积周长C=2πr,面积S=πr^2等。
3. 圆中角和弧的关系圆心角、圆周角、同弧对应角等。
4. 切线与切点切线与圆相切于一个点等。
六、坐标系1. 直角坐标系和平面直角坐标系横坐标和纵坐标等。
初中数学常用几何模型及构造方法大全

初中数学常用几何模型及构造方法大全初中数学中常用的几何模型有点线面体等,下面是一些具体的模型及其构造方法的介绍。
1.点:点是最基本的几何模型,没有大小和形状,通常用字母表示,如点A。
构造一个点的方法是利用直尺和量角器可以在纸上画出一个点。
2.线段:线段是由两个点A、B确定的一段有限长度的直线。
构造一个线段的方法是使用直尺在纸上连接两个点A、B。
3.直线:直线是不限长度的连续的直线,由无数个点连成。
构造一条直线的方法是使用直尺和铅笔,通过两个点A、B可以画出一条直线。
4.射线:射线是起始点A和其中一点B组成的,且延伸方向上没有终点的线段,A点称为射线的起点。
构造一个射线的方法是先画一个点A,然后通过这个点再延伸一段。
5.角:角是由两条射线共享一个端点所组成的图形,其中这个端点称为角的顶点,两条射线称为角的腿。
构造一个角的方法是先画出射线,然后再画出另一条射线与之相交,两射线的交点即为角的顶点。
6.平行线:平行线是在同一个平面上永远不会相交的直线。
构造平行线的方法是使用直尺和量角器,通过已知的一条直线上的一点和一条角度相等的直线可以画出平行线。
7.相交线:相交线是在同一个平面上交叉的直线。
构造相交线的方法是使用直尺和量角器,在纸上画出两条直线,交点即为相交线的点。
8.三角形:三角形是由三条线段组成的图形。
构造一个三角形的方法是使用直尺和量角器,先画出一个线段作为一条边,再使用量角器构造两条角度相等的线段作为其它两边。
9.直角三角形:直角三角形是一个角为90度的三角形。
构造直角三角形的方法是使用直尺和量角器,首先画出一条线段,然后构造一个90度的角作为其中一条边。
10.等边三角形:等边三角形是三边相等的三角形。
构造等边三角形的方法是使用直尺和量角器,首先画出一条线段作为其中一条边,然后通过量角器构造另外两条边,使得三边相等。
除了以上列举的几何模型,还有圆、四边形、多边形等,它们的构造方法有一些特定的规则,可以通过直尺、圆规和量角器等几何工具进行构造。
2024年中考数学几何模型归纳(全国通用):01 双中点(线段)模型与双角平分线(角)模型(学生版)

专题01.双中点(线段)模型与双角平分线(角)模型线段与角度是初中几何的入门知识,虽然难度不高,但重要性是不言而喻的。
这类模型通常由问题出发,先由线段(角度)和差确定解题方向,然后辅以线段中点(角平分线)来解决。
但是,对于有公共部分的线段双中点模型和双角平分线模型,可以写出的线段(角度)和差种类较多,这就增加了思考的难度。
模型1.线段的双中点模型图1图21)双中点模型(两线段无公共部分)条件:如图1,已知A 、B 、C 三点共线,D 、E 分别为AB 、BC 中点,结论:12DE AC .2)双中点模型(两线段有公共部分)条件:如图2,已知A 、B 、C 三点共线,D 、E 分别为AB 、BC 中点,结论:12DE AC ...A .20ACB .DC 例3.(2022秋·湖北咸宁·七年级统考期末)1例5.(2022秋·山东青岛·七年级校考期末)直线(1)若20AB cm ,求MN 的长;(2)初步感知:(1)如图1,点C 在线段AB 上,若2k ,则AC __________;若3AC BC ,则k例9.(2022·贵州铜仁·七年级期末)如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.(1)求线段MN的长度.(2)根据第(1)题的计算过程和结果,设AC=a,BC=b,其他条件不变,求MN的长度.(3)动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB 向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动.设点P的运动时间为t(s).当C、P、Q三点中,有一点恰好是以另外两点为端点的线段的中点时,直接写出时间t.模型2.双角平分线模型图1图2图31)双角平分线模型(两个角无公共部分)条件:如图1,已知:OD 、OE 分别平分∠AOB 、∠BOC ;结论:12DOE AOC .2)双角平分线模型(两个角有公共部分)条件:如图1,已知:OD 、OE 分别平分∠AOB 、∠BOC ;结论:12DOE AOC .3)拓展模型:双角平分线模型(三个角围成一个周角)条件:如图3,已知∠AOB +∠BOC+∠AOC=360°,OP 1平分∠AOC 、OP 2平分∠BOC ;结论:1211802POP AOB .A .70 B .100例2.(2023秋·福建福州·七年级统考期末)如图,已知射线,BOC OF 平分AOB ,以下四个结论:③AOD BOC ;④EOF例3.(2023·河南·七年级校联考期末)如图,22OA OB 、分别是1AOM 和MOB 分别是1n A OM 和1n MOB 的平分线,则例4.(2022秋·山西太原·七年级统考期末)图,的内部,OE 是∠AOB 的一条三等分线.请从A .当∠BOC =30°时,∠EOD 的度数为B .当∠BOC =α°时,∠EOD 的度数为例5.(2023·江苏无锡·七年级校考期末)解答题:别平分AOB 、AOC ,求 °<180n m ,OD 、OE 分别平分例6.(2022秋·河南商丘·七年级统考期末)综合与探究:如图1,在AOB 的内部画射线OC ,射线OC 把AOB 分成两个角,分别为AOC 和BOC ,若这两个角中有一个角是另外一个角的2倍,则称射线OC 为AOB 的“3等分线”.(1)若90AOB ,射线OC 为AOB 的“3等分线”,则AOC 的度数为__________.(2)如图2,已知60AOB ,过点O 在AOB 外部作射线OP .若,,OA OP OB 三条射线中,一条射线恰好是以另外两条射线为角的“3等分线”,求AOP 的度数(180AOP ).例9.(2022·四川·成都市七年级期末)如图所示:点P 是直线AB 上一点,∠CPD 是直角,PE 平分∠BPC .(1)如图1,若∠APC =40°,求∠DPE 的度数;(2)如图1,若∠APC = ,直接写出∠DPE 的度数(用含 的代数式表示);(3)保持题目条件不变,将图1中的∠CPD 按顺时针方向旋转至图2所示的位置,探究∠APC 和∠DPE 的度数之间的关系,写出你的结论,并说明理由.A .①②③B .③④C .①②④A .20225102 B .20235102 C .20225102 D .20235102A .30B .25 7.(2023秋·山西大同·七年级统考期末)在别为AOC 和BOC ,若AOC 60AOB ,射线OC 为AOB①在图1的情况下,在DBC 内作DBF ②在旋转过程中,若BM 平分DBA ,BN ③在旋转过程中,两块三角板的边所在直线夹角成④DBC ABE 的角度恒为105 .其中正确的结论个数为(A .1个B .2个11.(2022秋·四川巴中·七年级统考期末)如图:数轴上点713.(2023春·四川达州·七年级校考阶段练习)D 、E 分别为线段AB BC 、中点,直线14.(2023秋·福建福州·七年级校考期末)已知线段QD16.(2023秋·福建福州·七年级校考期末)已知有理数MP 时,NP ;(1)若点P在线段AB上运动,当7AB ,点P以1cm/s (2)【拓展与延伸】已知线段10cm3cm/s的速度从点B出发,先向点A方向运动,到达点(1)根据题意,小明求得MN ______于是他先将题中的条件一般化,并开始深入探究.设AB a=,C是线段AB上任意一点(不与点(1)如图1,求证:AOB EOB DOE ;(2)如图2,作OF 平分AOB (3)如图3,在(2)的条件下,当90AOD 时,作射线OA 的反向延长线AOH AOE ,反向延长射线OE 得到射线OQ ,射线OP 在HOQ 内部,26BOC DOF ,5271GOH POQ EOF ,求BOP 的度数.(2)若将(1)中的条件“ON 平分BOC ,OM 平分且AOB ,求AOM BON 的度数;(3)如图2,若ON 、OC 在AOB 的外部时,ON 时,猜想:MON 与 的大小有关系吗?如果没有,指出结论并说明理由.232023··(1)如图1,当OB ,OC 重合时,求EOF 的度数;EOF 的度数;(3)当AOB 和COD 的位置如图325.(2023·江苏七年级课时练习)(理解新知)如图①,点M在线段AB上,图中共有三条线段AB、AM和BM,若其中有一条线段的长度是另外一条线段长度的2倍,则称点M是线段AB的“奇妙点”,(1)线段的中点这条线段的“奇妙点”(填“是”或“不是”)为何值时,26.(2022·广东茂名·七年级期末)已知:∠AOB =60°,∠COD =90°,OM 、ON 分别平分∠AOC 、∠BOD .(1)如图1,OC 在∠AOB 内部时,∠AOD +∠BOC =,∠BOD ﹣∠AOC =;(2)如图2,OC 在∠AOB 内部时,求∠MON 的度数;(3)如图3,∠AOB ,∠COD 的边OA 、OD 在同一直线上,将∠AOB 绕点O 以每秒3°的速度逆时针旋转直至OB 边第一次与OD 边重合为止,整个运动过程时间记为t 秒.若∠MON =5∠BOC 时,求出对应的t 值及∠AOD 的度数.27.(2023·江苏·七年级专题练习)如图1,射线OC 在AOB 的内部,图中共有3个角:AOB 、AOC 、BOC ,若其中有一个角的度数是另一个角度数的两倍,则称射线OC 是AOB 的“定分线”.(1)一个角的平分线_________这个角的“定分线”;(填“是”或“不是”)(2)如图2,若MPN a ,且射线PQ 是MPN 的“定分线”,则MPQ ________(用含a 的代数式表示出所有可能的结果);(3)如图2,若MPN =48°,且射线PQ 绕点P 从PN 位置开始,以每秒8°的速度逆时针旋转,当PQ 与PN 成90°时停止旋转,旋转的时间为t 秒;同时射线PM 绕点P 以每秒4°的速度逆时针旋转,并与PQ 同时停止.当PQ 是MPN 的“定分线”时,求t 的值.。
初中数学几何图形构造方法梳理

初中数学几何图形构造方法梳理几何图形构造方法梳理在初中数学学习中,几何图形构造是一个重要的部分,它涉及到直线、角度、三角形、四边形等各种图形的构造方法。
本文将梳理一些常见的初中数学几何图形构造方法,帮助学生更好地理解和掌握这些内容。
一、直线图形的构造方法1. 画线段:给定两个不同的点A和B,我们可以使用直尺在点A和B之间画一条直线段AB。
2. 画射线:给定一个起点A和一个方向,我们可以使用直尺在起点A开始,按照给定的方向延伸出一条射线。
3. 画平行线:给定一条直线L和一个点P,在点P处画一条与直线L平行的直线。
4. 画垂直线:给定一条直线L和一个点P,在点P处画一条与直线L垂直的直线。
二、角度的构造方法1. 画角:给定两条射线,将它们的起点重合,通过尺规作图的方法,可以构造出一个特定的角。
2. 以角的顶点为中心,以确定的角度为半径,画弧:给定一个角的顶点O和一个角度a,我们可以使用尺规作图的方法,在以O为中心,以a为半径的圆上选择一点P,然后连接OP,即可得到一个角为a的角。
3. 画平分线:给定一个角,我们可以使用尺规作图的方法,构造出这个角的平分线,即将这个角平分为两个相等的角。
4. 画垂线:给定一条直线L和一个点P,在点P处画一条与直线L垂直的直线。
三、三角形的构造方法1. 画等边三角形:给定一个边长,我们可以使用尺规作图的方法,构造一个边长相等的等边三角形。
2. 画等腰三角形:给定一个底边和两个底角,我们可以使用尺规作图的方法,构造一个具有底边和底角相等的等腰三角形。
3. 画直角三角形:给定一个直角,我们可以使用尺规作图的方法,在直角的一边上任选一点,然后以这个点为顶点,直角的两条边为另外两边,构造一个直角三角形。
4. 画任意三角形:给定三条边长a、b、c,我们可以使用尺规作图的方法,构造一个具有边长分别为a、b、c的任意三角形。
四、四边形的构造方法1. 画平行四边形:给定两条平行线L1和L2,以及一个点P,我们可以使用尺规作图的方法,在点P处作出一条与L1平行的线段,然后再以该线段为边作出一条与L2平行的线段,连接两个线段的两个端点,即可得到一个平行四边形。
初中数学必背几何模型
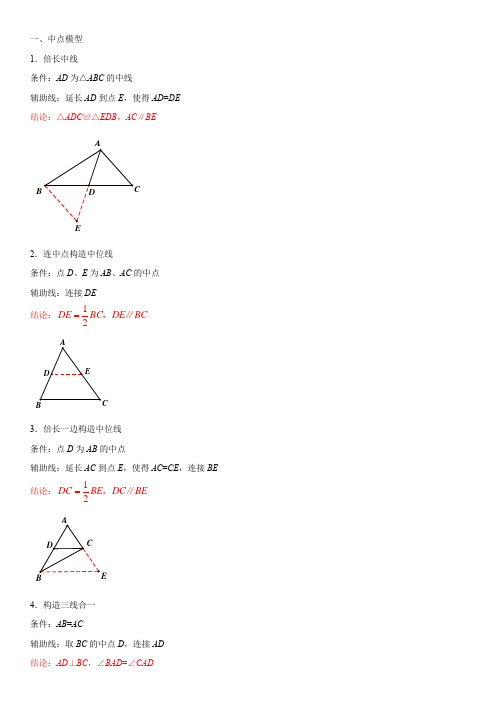
一、中点模型1.倍长中线条件:AD 为△ABC 的中线辅助线:延长AD 到点E ,使得AD =DE结论:△ADC ≌△EDB ,AC ∥BE2.连中点构造中位线条件:点D 、E 为AB 、AC 的中点辅助线:连接DE 结论:12DE BC DE BC =,∥3.倍长一边构造中位线条件:点D 为AB 的中点辅助线:延长AC 到点E ,使得AC =CE ,连接BE 结论:12DC BE DC BE =,∥4.构造三线合一条件:AB =AC辅助线:取BC 的中点D ,连接AD结论:AD ⊥BC ,∠BAD =∠CADB5.构造斜边中线条件:∠ABC =90°辅助线:取AC 的中点D ,连接BD 结论:12BD AC AD CD ===二、角平分线模型6.往角两边作垂线条件:AD 平分∠BAC辅助线:过点D 作AB 、AC 的垂线,垂足分别为E 、F结论:△ADE ≌△ADF7.在角的两边截取等长线段条件:AD 平分∠BAC辅助线:在AB 、AC 上取点E 、F ,满足AE =AF ,连接DE 、DF 结论:△ADE ≌△ADF8.过角平分线上一点作垂线条件:AD 平分∠BAC辅助线:过点D 作EF ⊥AD ,交AB 、AC 于点E 、FD CBB CCC结论:△ADE ≌△ADF三、双角平分线模型9.内内模型条件:BD 、CD 平分∠ABC 、∠ACB 结论:1902D A ∠=︒+∠10.内外模型条件:BD 、CD 平分∠ABC 、∠ACE 结论:12D A ∠=∠11.外外模型条件:BD 、CD 平分∠CBE 、∠BCF 结论:1902D A ∠=︒-∠四、平行线模型12.猪蹄模型CA BCC ED条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠B +∠D =∠BED13.铅笔头模型条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠B +∠D +∠BED =360°14.鸟头模型条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠D +∠BED =∠B15.平行线+角平分线模型条件:AB ∥CD ,CE 平分∠ACD结论:AC =AE五、等积模型16.等底等高条件:AD ∥BCFAFBC结论:ABC DBC S S =,ADB ADC S S =17.等高模型条件:B 、C 、D 共线结论:::ABD ADC S S BD CD =18.等底模型条件:AE 、DE 为△ABC 、△DBC 边BC 上的高结论:::ABC DBC S S AE DE =六、对称半角模型19.对称半角模型-含45°角的三角形条件:∠BAC =45°,AD ⊥BC辅助线:作点D 关于AB 的对称点E ,关于AC 的对称点F , 连接AE 、AF 、BE 、CF 、EF结论:△AEF 是等腰直角三角形20.对称半角模型-含30°角的三角形B CB C DED条件:∠BAC =30°,AD ⊥BC辅助线:作点D 关于AB 的对称点E ,关于AC 的对称点F , 连接AE 、AF 、BE 、CF 、EF结论:△AEF 是等边三角形七、旋转半角模型21.旋转半角模型-等腰直角三角形条件:AB =AC ,∠BAC =90°,∠MAN =45°辅助线:将△ABM 绕点A 逆时针旋转90°,得到△ACM ' 结论:ANM ANM '≌,222BM CN MN +=22.旋转半角模型-等边三角形条件:△ABC 是等边三角形,BD =CD ,∠BDC =120°, ∠MDN =60°辅助线:将△BDM 绕点D 顺时针旋转120°,得到△DCM ' 结论:NDM NDM '≌,BM CN MN +=23.旋转半角模型-正方形条件:正方形ABCD ,∠MAN =45°,FEAM'M CAB辅助线:将△ABM 绕点A 逆时针旋转90°,得到△ADM ' 结论:NAM NAM '≌,BM DN MN +=八、自旋转模型24.自旋转模型-等边三角形条件:△ABC 是等边三角形,点P 为其内任意一点辅助线:将△BAP 绕点B 顺时针旋转60°,得到△BCP ' 结论:△BPP '是等边三角形25.自旋转模型-等腰直角三角形条件:△ABC 中,∠BAC =90°,AB =AC ,点P 为△ABC 内任 意一点辅助线:将△BAP 绕点A 逆时针旋转90°,得到△ACP ' 结论:△APP '是等腰直角三角形26.自旋转模型-等腰三角形条件:△ABC 中,AB =AC ,点P 为△ABC 内任意一点,∠BAC =α 辅助线:将△BAP 绕点A 逆时针旋转α,得到△ACP ' 结论:△APP '是等腰三角形M'DNCBAB九、手拉手模型29.手拉手模型-等边三角形条件:△ABC和△CDE都是等边三角形结论:△ACE≌△BCD27.手拉手模型-等腰直角三角形条件:△ABC和△CDE都是等腰直角三角形结论:△ACE≌△BCD,AE⊥BDEE28.手拉手模型-等腰三角形条件:△ABC 和△CDE 都是等腰三角形,CA =CB , CD =CE ,且∠ACB =∠DCE结论:△ACE ≌△BCD30.手拉手模型-正方形条件:四边形ABCD 和AEFH 都是正方形结论:△ABE ≌△ADH ,BE ⊥DH十、最短路程模型31.直线同侧两线段之和最小(将军饮马)条件:点A 、B 在直线l 同侧,点P 为l 上一点辅助线:作点A 关于直线l 的对称点A ',连接A 'B 结论:点P 为A 'B 和l 交点时,AP +BP 最小C32.直线异侧两线段之差最小条件:点A 、B 在直线l 异侧,点P 为l 上一点辅助线:作线段AB 的垂直平分线m结论:点P 为m 和l 交点时,|AP -BP |最小33.直线同侧两线段之差最小条件:点A 、B 在直线l 同侧,点P 为l 上一点辅助线:作线段AB 的垂直平分线m结论:点P 为m 和l 交点时,|AP -BP |最小34.过桥模型(将军饮马)条件:A 、B 为定点,l 1∥l 2,MN 为定长线段且MN ⊥l 1 辅助线:将点A 向上平移MN 的长度得到A ',连接A 'B 结论:点N 为A 'B 与l 1交点时,AM +MN +BN 最小35.四边形周长最小(将军饮马)条件:A 、B 为定点,M 、N 为角两边上的动点辅助线:作点A 、B 关于角两边的对称点A '、B ',连接 lAlAll 1l 2A'B'结论:M、N为A'B'与角两边交点时,四边形ABMN的周长最小B'36.三角形周长最小(将军饮马)条件:A为定点,B、C为角两边上的动点辅助线:作点A关于角两边的对称点A'、A",连接A'A"结论:B、C为A'A"与角两边交点时,△ABC的周长最小37.旋转类最短路程模型条件:线段OA=a,OB=b(a>b),OB绕点O在平面内旋转结论:点B与点N重合时,AB最小;点B与点M重合时,AB最大十一、基本相似模型38.A字型条件:BC∥DE结论:△ABC∽△ADE条件:∠ABC =∠ADE结论:△ABC ∽△ADE39.8字型条件:AB ∥CD结论:△AOB ∽△DOC条件:∠BAO =∠DCO结论:△AOB ∽△COD40.母子型条件:△ABC 中,∠ACB =90°,CD ⊥AB结论:△ABC ∽△ACD ∽△CBD41.一线三等角模型条件:∠B =∠D =∠ACE结论:△ABC ∽△CDECBCC A42.手拉手相似模型条件:△ABC ∽△ADE结论:△ACE ∽△ABD十二、对角互补模型43.对角互补模型-90°全等型条件:∠AOB =∠DCE =90°,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,OD +OEOC ,212OECD S OC 四边形CB ACE AB D CDD44.对角互补模型-120°全等型条件:∠AOB =120°,∠DCE =60°,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,OD +OE =OC ,24OECD S =四边形45.对角互补模型-任意角全等型条件:∠AOB =2α,∠DCE =180°-2α,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,2cos OD OE OC α+=⋅, 2sin cos OEC OCD S S OC αα+=⋅46.邻边相等的对角互补模型条件:四边形ABCD 中,AB =AD ,∠ABC +∠ADC =180°D BAN E OB辅助线:延长CD 到E ,使得DE =BC ,连接AE结论:△ABC ≌△ADE ,CA 平分∠BCD十三、隐圆模型47.动点定长模型条件:AB =AC =AP ,点P 为动点结论:点B 、C 、P 三点共圆,点A 为圆心,AB 为半径48.直角圆周角模型条件:点C 为动点,∠ACB =90°结论:点A 、B 、C 三点共圆,线段AB 的中点为圆心,线段 AB 为直径49.定弦定长模型条件:点P 为动点,固定线段AB 所对的动角∠APB 为定值 结论:点A 、B 、P 三点共圆,线段AB 和BP 的中垂线的交点 为圆心BA50.四点共圆模型①条件:点A 、C 为动点,∠BAD +∠BCD =180°结论:点A 、B 、C 、D 四点共圆,线段AB 和BC 的中垂线的 交点为圆心当∠BAD =∠BCD =90°,BD 为直径51.四点共圆模型②条件:线段AB 为固定长度,点D 为动点,∠C =∠D结论:点A 、B 、C 、D 四点共圆,线段AB 和BC 的中垂线的 交点为圆心CCA当∠C=∠D=90°,AB为直径。
初中数学几何模型大全+经典题型(含答案)

初中数学几何模型大全+经典题型(含答案)全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明:通过对称进行等量代换,转换成两点间距离及点到直线距离。
初中数学三角形全等常用几何模型及构造方法大全初二

初二数学三角形全等常用几何模型及构造方法大全掌握它轻松搞定全等题!全等是初中数学中非常重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省不少时间,这次整理了常用的各大模型,一定要认真掌握~全等变换类型:(一)平移全等:平行等线段(平行四边形)(二)对称全等模型:角平分线或垂直或半角1:角平分线模型;2:对称半角模型;(三)旋转全等模型:相邻等线段绕公共顶点旋转1.旋转半角模型2.自旋转模型3.共旋转模型4.中点旋转如图,在△ABC的边上取两点D、E,且BD=CE,求证:AB+AC>AD+AE分析:将△ACE平移使EC与BD重合。
B\D,上方交点,左右两个三角形,两边和大于第三边!1:角平分线模型:说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
2:对称半角模型说明:上图依次是45°、30°、 45+ °、对称(翻折)15°+30°直角三角形对称(翻折) 30+60+90直角三角形对称(翻折)翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
1.半角:有一个角含1/2角及相邻线段2.自旋转:有一对相邻等线段,需要构造旋转全等3.共旋转:有两对相邻等线段,直接寻找旋转全等(共顶点)4.中点旋转:倍长中点相关线段转换成旋转全等问题(专题七)1、旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
2、自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称3、共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
(接上------共旋转模型)模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形混用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
根据前面的结果解答即可.
【详解】解: 分别是 的中点,
分别是 的中点
又
∵ ,
∴ 在点 的右边,
如图示:
分别是 的中点,
又
只要满足点 在线段 所在直线上,点 分别是 的中点.那么 就等于 的一半
【点睛】本题主要是线段中点的运用,熟悉相关性质是解题的关键.
【点睛】考查了两点间的距离,利用了等分点等分线段的性质,线段的和差.
变式8
9.如图,线段AB=20,BC=15,点M是AC的中点.
(1)求线段AM的长度;
(2)在CB上取一点N,使得CN:NB=2:3.求MN的长.
【答案】(1) ;(2)
【解析】
【分析】(1)根据图示知AM= AC,AC=AB﹣BC;
①图中的点D,P,C,E都是动点;
②AD BE;
③AB=2DE;
④当AC=BC时,点P与点C重合.
其中正确的是____________.(把你认为正确结论的序号都填上)
【答案】①③④
【解析】
【分析】①由题意可知随着C的运动,D、P、E都在动,故正确;
②可以推得当C点在AB中点左边(不含中点)运动时,AC<BC,故错误;
(2)由2平分两个点组成的线段,得到左边的点为2-距离的一半,从而可求得答案;
(3)设点C表示的数为x,分三种情况讨论:①点C在A的左侧,②点C在A和B之间,③点C在B的右侧.
(4)先求出每两条相邻折痕的距离,进一步得到最左端的折痕和最右端的折痕与数轴的交点表示的数,即可求得答案.
【详解】解:(1)(﹣1+5)÷2=4÷2=2.
③由题意及中点的性质可知正确;
④由题意,当AC=BC时,C为DE中点,根据已知,P也为DE中点,所以点P与点C重合.
【详解】解:①∵点C是线段AB上的一个动点(不与A,B重合),点D,E,P分别是线段AC,BC,DE的中点,∴D、E随着C的运动而运动,点P随着D、E的运动而运动,因此,随着C的运动,D、P、E都在动,∴本选项正确;
变式2
3.如图,点C是线段AB的中点,点D是线段CB上任意一点,则下列表示线段关系的式子不正确的是( )
A. AB=2AC
B. AC+CD+DB=AB
C.CD=AD- AB
D.AD= (CD+AB)
【答案】D
【解析】
【详解】解:A、由点C是线段AB的中点,则AB=2AC,正确,不符合题意;B、AC+CD+DB=AB,正确,不符合题意;C、由点C是线段AB的中点,则AC= AB,CD=AD-AC=AD- AB,正确,不符合题意;D、AD=AC+CD= AB+CD,不正确,符合题意.故选D.
【详解】(1) , 同向运动
由题意得 ,
∴ 和 两条线段的中点相距
(2) , 反向运动
由题意得 ,
∴ 和 两条线段的中点相距
故答案为: 和 两条线段的中点相距2或6个单位.
【点睛】本题考查了线段的长度问题,掌握中点平分线段长度是解题的关键.
例题2
12.如图,点M在线段AN的延长线上,且线段MN=20,第一次操作:分别取线段AM和AN的中点 ;第二次操作:分别取线段 和 的中点 ;第三次操作:分别取线段 和 的中点 ;……连续这样操作10次,则每次的两个中点所形成的所有线段之和 ( )
A. B. C. D.
【答案】A
【解析】
【分析】根据 , 分别为 的中点,求出 的长度,再由 的长度求出 的长度,找到 的规律即可求出 的值.
【详解】解:∵ , 分别为 的中点,
∴ ,
∵ 分别为 的中点,
∴ ,
根据规律得到 ,
∴ ,故选A.
【点睛】本题是对线段规律性问题的考查,准确根据题意找出规律是解决本题的关键,相对较难.
(4)如图2,若将此纸条沿A、B两处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折 次后,再将其展开,求最左端的折痕与数轴的交点表示的数.(用含 的代数式表示)
【答案】(1)2;(2) ; (3)2或10;(4) .
【解析】
【分析】(1)找出5表示的点与﹣1表示的点组成线段的中点表示数,然后结合数轴即可求得答案;
线段和角的模型
模型一 线段分点模型
1、单中点模型:
如图,P是线段AB的中点,则:
2、双中点模型
(1)线段上 双中点
如图,点C为线段AB上任意一点,P1,P2分别为AC,BC中点,则
(2)线段延长线上的双中点模型
线段双中点模型总结:一点把线段分成三条线段,任意两线段中点之间长度等于第三条线段长度的一半.
变式3
4.如图,工作流程线上A、B、C、D处各有一名工人,且AB=BC=CD=1,现在工作流程线上安放一个工具箱,使4个人到工具箱的距离之和为最短,则工具箱安放的位置()
A.线段BC的任意一点处
B.只能是A或D处
C.只能是线段BC的中点E处
D.线段AB或CD内的任意一点处
【答案】A
【解析】
【详解】要想4个人到工具箱的距离之和最短,据图可知:位置在A与B之间时,距离之和 位置在B与C之间时,距离之和 位置在C与D之间时,距离之和 则工具箱在B与C之间时,距离之和最短.
【分析】(1)先求解 再利用中点的含义求解 再利用线段的差可得答案;
(2)先利用含 的代数式 再利用中点的含义,用含 的代数式 再利用线段的差可得答案;
(3)先利用含 的代数式 再利用中点的含义,用含 的代数式 再利用线段的差可得答案;
(4)由(1)(2)(3)总结出结论即可.
【详解】解:(1) , 分别是 的中点,
故选A.
变式4
5.C为线段 上任意一点, 分别是 的中点,若 ,则 的长是( ).
A. B. C. D.
【答案】D
【解析】
【分析】先画好符合题意的图形,再证明 再利用线段的和可得答案.
【详解】解:如图,
分别是 的中点,
故选:
【点睛】本题考查的是线段中点的含义,线段的和差关系,掌握线段的和差与中点的定义是解题的关键.
∴AE= AC= cm,
∴DE=AE-AD= -12=4.5cm,
∴DE=4.5cm.
【点睛】本题考查两点间距离,线段中点的定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
变式7
8.如图M、N把线段AB三等分,C为NB的中点,且CM=6cm,则AB=_____cm.
【答案】12
【解析】
【答案】4.5cm
【解析】
【分析】根据中点的定义求出AD,根据已知可求BC=9,进一步由AC=AB+BC求得AC,再根据中点的定义求得AE,再根据DE=AE-AD即可求解.
【详解】∵AB=24cm,D是AB中点,
∴AD= AB=12cm,
∵BC= AB,
∴BC=9,AC=AB+BC=33cm,
∵E是AC中点,
(2) , 分别是 的中点,
(3) , 分别是 的中点,
(4)由(1)(2)(3)的结果中可得:线段 的长度等于线段 的一半,与 点的位置无关.
【点睛】本题考查的是线段的中点的含义,线段的和差关系,掌握利用线段的中点及线段的和差关系求解线段的长度是解题的关键.
变式1
2.已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN的长度是()
【解析】
【分析】根据题意,得第一次跳动到OA的中点A1处,即在离原点的长度为 ×4,第二次从A1点跳动到A2处,即在离原点的长度为( )2×4,找到跳动n次的规律即可.
【详解】由于OA=4,所以第一次跳动到OA的中点A1处时,1= OA= ×4=2,
同理第二次从A1点跳动到A2处,离原点的( )2×4处,
模型二 线段的折叠与动点问题
例题1
11.已知 , 为数轴上从原点 出发的两个动点,点 每秒1个单位,点 的速度为点 的2倍,则当运动时间为4秒时, 和 两条线段的中点相距________个单位.
【答案】2或6
【解析】
【分析】分两种情况:(1) , 同向运动;(2) , 反向运动,根据中点平分线段长度进行求解即可.
同理跳动n次后,离原点的长度为( )n×4= ,
则2020次跳动后的点与 点的距离是
故选:A.
【点睛】本题是一道找规律的题目,考查了两点间的距离,根据题意表示出各个点跳动的规律是解题关键.
变式2
14.如图,点C是线段AB上的一个动点(不与A,B重合),点D,E,P分别是线段AC,BC,DE的中点,下列结论:
(2)根据已知条件求得CN=6,然后根据图示知MN=MC+NC.
【详解】解:(1)线段AB=20,BC=15,
∴AC=AB﹣BC=20﹣15=5.
又∵点M是AC的中点.
∴AM= AC= ×5= ,即线段AM的长度是 .
(2)∵BC=15,CN:NB=2:3,
∴CN= BC= ×15=6.
又∵点M是AC的中点,AC=5,
变式5
6.已知点 是线段 的中点,点 是线段 的中点,那么线段 的比值是_______.
【答案】
【解析】
【分析】根据题意易得 , ,然后直接进行比值即可.
【详解】解:由题意得
, ,
∴ .
【点睛】本题主要考查比值及化简比,熟练掌握求比值和化简比的方法是解题的关键.
变式6
7.如图,已知 、 、 三点在同一直线上, cm, , 是 的中点, 是 的中点,则 的长______.
∴MC= AC= ,
∴MN=MC+NC= ,即MN的长度是 .
【点睛】本题考查了两点间的距离,利用了线段的和差,线段中点的定义,熟练掌握线段中点的定义是解答本题的关键.
