双代号网络图绘制中的虚箭线判定
双代号网络图中虚箭线的几种常见用法辨析-文档资料

双代号网络图中虚箭线的几种常见用法辨析-文档资料
双代号网络图中虚箭线的几种常见用法辨析
1 虚箭线运用的几种常用情况
(1)网络计划中涉及交替工序,交替工序的画法如图1所示。
(2)两个工序有共同的起始点事件和终点事件,如图2(1)所示,此时需要添加虚箭线,如图2(2)所示。
(3)某两个工序除了有共同的紧后工序外,这两个工序还有其他紧后工序,这是虚箭线运用过程中的重点与难点所在。
本文予以重点分析。
1)两个工序除具有共同的紧后工序以外,其中一个还有其他紧后工序,此时用到一条虚箭线,如图3所示,A、B有共同的紧后工序D,除此之外,A还有其他紧后工序C,此时,运用一条虚箭线即可清晰表明工序间的逻辑关系。
2)两个工序除具有共同的紧后工序以外,还各自都有其他紧后工序,此时用到两条虚箭线,如图4所示,A、C有共同的紧后工序D,除此之外,A还有其他紧后工序B,C还有其他紧后工序E,此时会用到两条虚箭线。
2 实例分析
例如,已知如表3所示资料,要求绘制网络图(本例选自清华大学出版社,胡运权主编的《运筹学习题集》P104)。
第1步,从表3中找出具有共同紧后工序的工序。
项目管理单双代号网络图
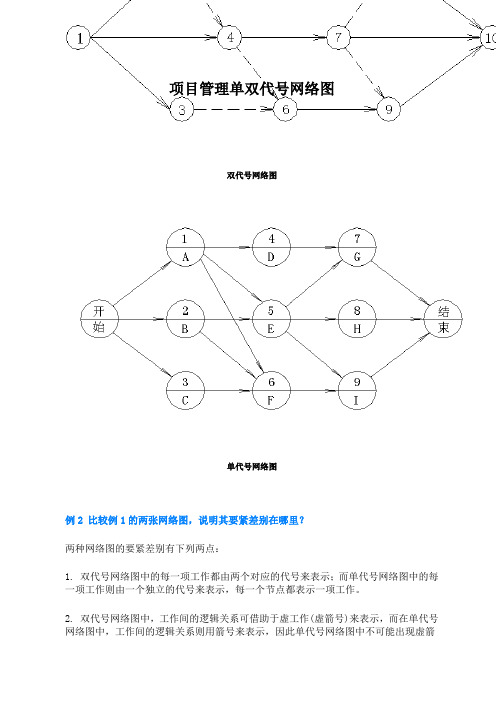
项目管理单双代号网络图双代号网络图单代号网络图例2 比较例1的两张网络图,说明其要紧差别在哪里?两种网络图的要紧差别有下列两点:1. 双代号网络图中的每一项工作都由两个对应的代号来表示;而单代号网络图中的每一项工作则由一个独立的代号来表示,每一个节点都表示一项工作。
2. 双代号网络图中,工作间的逻辑关系可借助于虚工作(虚箭号)来表示,而在单代号网络图中,工作间的逻辑关系则用箭号来表示,因此单代号网络图中不可能出现虚箭号。
一幅单代号网络图中,只会出现两个虚设的工作节点,那就是表示计划开始的虚工作节点与表示计划结束的虚工作节点。
例3 下图为一单号网络图,网络图各圆圈中横线上边的数字是工作代号,横线下边的数字是工作持续时间。
试用图上计算法计算各工作的最早可能开始时间ES i、最迟务必开始时间LS i、总时差TF i与局部时差FF i,标记出关键线路并确定总工期。
解:根据题意用图算法推算出的各工作时间参数,见上图,关键线路用粗箭号表示。
该网络图的计划总工期为11天。
例4 某工程的单代号网络如下图所示。
试用表上计算法求出网络图中各工作的ES i、EF、LS i、LF i、TF i、与FF i;确定关键工作并在图上说明关键线路;确定计划总工期(注:i下图中圆圈内横线上边为工作代号,横线下边为工作持续时间)。
解:用表算法推算了各工作的时间参数见下表。
该网络图的关键线路共有3条,它们分别为:计划总工期为19天。
一、网络计划技术基本概念二、网络图的绘制:知识点总结与归纳三、网络计划时间参数的计算(一)、网络计划时间参数的概念4.计算工作的总时差工作的总时差等于该工作最迟完成时间与最早完成时间之差,或者该工作最迟开始时间与最早开始时间之差。
5.计算工作的自由时差工作自由时差的计算应按下列两种情况分别考虑:(1)关于有紧后工作的工作,其自由时差等于本工作之紧后工作最早开始时间减本工作最早完成时间所得之差的最小值。
(2)关于无紧后工作的工作,也就是以网络计划终点节点为完成节点的工作,其自由时差等于计划工期与本工作最早完成时间之差。
双代号网络图

工序名称
支模板
绑钢筋
持续时间
4天
4天
工序名称和持续时间标注法
5、本工序、紧前工序、紧后工序、平行工序 紧靠本工序之前的工序称为紧前工序,紧
靠本工序之后的工序称为紧后工序。
本工序、紧前工序、紧后工序应连续施工, 箭线也应连续画出。与本工序平行的工序称为 平行工序,箭线与本工序箭线平行画出。
支模板
支模板
1 支同工模1工种种的2的工连作续,作与支业横模情道2 况图,画该法法接便近于,检也查是
按 施
工地常用的一种方法
工 过
绑钢筋1
3
4 绑钢筋2
程
浇混凝土1
5 浇混凝土2 6
2.按施工段排列 (或流水段法)
该法是把同施工段上的各项工作排在同 一条水平方向上。该法能直观地反映工 程分段施工的特点,突出表现工作面的 连续作业情况。
逻辑关系。 1)避免出现节点相同的工作
2)保证网络图只有一个起点节点和一个终 点起点
3)正确表达工作间的逻辑关系。采用增加 虚箭线,不增加节点方法表达工作间的逻辑 关系。
(3)双代号网络图绘制图中1的2-1断1 路虚法箭线所(虚谓工断作路)示法意是图指采用虚箭线在线路 上隔断无逻辑关a)系有多的余各工项作工的作虚,箭使线其满b)无足多工余作工逻作辑实关箭系线要求的一种绘 图方法。
网络图是一种有向图,是沿着箭头指引方向前进的。
1
2
3
4
5
图3-21 双向箭头的错误
7、在网络图中尽量避免使用反向箭线,反向箭线可能造成循 环线路。
1
2
3
4
5
6
3
7
8
×
• 8.绘制网络图时,箭线不宜交叉;当交叉 • 不可避免时,可用过桥法或指向法。
双代号网络图中常见的逻辑关系及其表示方法

双代号网络图中常见的逻辑关系及其表示方法双代号网络图的绘制1,各种逻辑关系的正确表示方法各工作间的逻辑关系,既包括客观上的由工艺所决定的工作上的先后顺序关系,也包括施工组织所要求的工作之间相互制约、相互依赖的关系。
逻辑关系表达得是否正确,是网络图能否反映工程实际情况的关键,而且逻辑关系搞错,图中各项工作参数的计算以及关键线路和工程工期都将随之发生错误。
,1,工艺顺序所谓工艺顺序,就是工艺之间内在的先后顺序。
如某一现浇钢筋混凝土柱的施工,必须在绑扎完柱子钢筋和支完模板以后,才能浇筑混凝土。
,2,组织顺序所谓组织顺序,是网络计划人员在施工方案的基础上,根据工程对象所处的时间、空间以及资源供应等客观条件所确定的工作展开顺序。
如同一施工过程,有A,B,C三个施工段,是先施工A,还是先施工B或C,或是同时施工其中的两个或三个施工段,某些不存在工艺制约关系的施工过程,如屋面防水工程与门窗工程,二者之中先施工其中某项,还是同时进行,都要根据施工的具体条件(如工期要求、人力及材料等资源供应条件来确定。
在绘制网络图时,应特别注意虚箭线的使用。
在某些情况下,必须借助虚箭线才能正确表达工作之间的逻辑关系,如表12-l中的第10种和第12种情况。
表12-l 给出了常见逻辑关系及其表示方法。
表12-1 双代号网络图中常见的逻辑关系及其表示方法序号工作间逻辑关系表示方法A,B,C无紧前工作,即工作A,B,C均1 为计划的第一项工作,且平行进行2 A完成后,B,C,D才能开始3 A,B,C均完成后,D才能开始4 A,B均完成后,C,D才能开始A完成后,D才能开始,A,B均完成5 后E才能开始,A,B,C均完成后,E才能开始6 A与D同时开始,B为A的紧后工作A,B均完成后,D才开始,A,B,C均7 完成后,E才开始,D,E完成后,F 才开始A结束后,B,C,D才开始,B,C,D结8 束后,E才开始A,B完成后,D才能开始,B,C完成9 后,E才能开始工作A,B分为三个施工阶段,分段流10 水施工,a完成后进行a,b;a完成1212 后进行a;a,b完成后进行b3 321A,B均完成后,C才能开始,A,B分为a,a, a和b,b,b3三个1231211 施工段,C分为c,c,c3,A, B,12C分三段作业交叉进行A,B,C为最后三项工作,即A,B,12 C无紧后作业2,双代号网络图的绘制规则绘制双代号网络图,必须遵守一定的基本规则,才能明确地表达出工作的内容,准确地表达出工作间的逻辑关系,并且使所绘出的图易于识读和操作。
双代号网络图绘制规则

双代号网络计划绘制一般规定:
• 1、双代号网络计划图中,每一条箭线表示一 项 工作。箭线的箭尾节点 表示工作的开始,箭头节点表示该工作结束。在非时标网络图中,箭线 长度不直接反映该工作所占用时间长短。箭线宜画成水平直线,也可画 成折线或斜线。水平直线投影的方向应自左向右,表示工作的前进方向 。
示的,与其所代表的时间值相对应。
• (2)节点的中心线必须对准时标的刻度线。 • (3)虚工作必须以垂直虚箭线表示,有时差时加波型线表示。 • (4)时标网络计划宜按最早时间编制,不宜按最迟时间编制。 • (5)时标网络计划编制前,必须先绘制无时标网络计划。
• 5、关键线路
• (1)关键线路是自始至终全部由关键工作组成的线路,关键线路上 总的工作持续时间最长的线路。时标网络计划中关键线路自始至终不 出现波型线的线路。可有多条
• 暗桥法
• 指向法
• 7、双代号网络图中应只有一个起点节点;在不分期完成任务的网络 图中,应只有一个终点节点;其他节点均应是中间节点
双代号时标网络计划
• 1、双代号网络计划是以时间坐标为尺度编制的双代号网络计划。 ……….
• 2、时标网络计划绘制在时标计划表上的。时标的时间单位是根据需 要,在编制网络计划之前确定的,可以是天、周、月等,时间可标注 在底部或顶部,时标的单位必须注明。必要时可以在顶部时标之上或 底部时标之下加注日历的对应时间。时标计划表中部的刻度线宜为细 线。
• 5、当双代号网络图的某些结点有多条内项线或多条外项线时,在不 违反“一项工作应只有唯一的一条箭线和相应的一对结点编号”的规 定前提下,可使用母线法绘制。当箭线线型不同时,可在母线上引出 的支线上标出。
母线表示方法
• 母线表示方法
双代号网络图绘制

A
(1)箭线 在双代号网络中,箭线表示工作,箭尾表示工作的开始,箭头表示工作
的完成。工作通常可以分为两种:
1)需要消耗时间和资源的工作
这类工作称为实工作,在网络图中用实箭线表示,一般在箭线的上方标
出工作的名称,在箭线的下方标出工作的持续时间。
工作名称 持续时间
2)既不消耗时间,也不消耗资源的工作 这类工作称为虚工作,在网络图中用虚箭线表示。虚工作是虚设的,只 表示相邻工作之间的逻辑关系。
双代号网络图
网络图的绘制主要是依据项目工作关系表,通过网络图的形 式将项目工作关系表达出来。
网络图的分类
双代号非时标网络图 双代号网络图
网络图
单代号网络图
双代号时标网络图 普通单代号网络图 单代号搭接网络图
双代号网络图定义
双代号网络图由箭线、节点、线路三个基本要素所组成,其中每一项工 作都用一根箭线和两个节点来表示,“双代号”即由此而来。
工作名称
(2)节点
节点的主要作用是联结箭线。每个节点都编以号码,箭线的箭尾节点和箭
头节点Байду номын сангаас是每一工作的起点和终点。
4
A
5
7
B
8
(3)线路 从起点节点开始,沿着箭线的方向连续通过一系列箭线与节点,最后到 达终点节点的通路称为线路。每一条线路都有自己确定的完成时间,它等 于该线路上各项工作持续时间总和,也是完成这条线路上所有工作的计划 工期,该工期也可称为路长。
2 A 1 3 D 3
C 5
4
8
G 5
F
B
4
6
E 5 8
根据路长的大小,线路可分为关键线路、次关键线路和非关键线路。
网络计划技术之双代号网络

实例分析和经验教训总结
实例分析:某公司在实施一个软件开发项目时,采用了 双代号网络进行项目进度管理,并通过成本估算和控制 措施,成功地将项目成本控制在预算范围内。 重视历史数据的收集和分析,为成本估算提供可靠依据 。
加强团队沟通和协作,形成全员参与成本控制的良好氛 围。
经验教训总结
制定切实可行的成本计划和控制措施,确保项目的经济 效益。
应急处理方案制定和执行情况回顾
制定应急处理方案
针对识别出的风险事件, 制定相应的应急处理方案, 明确应对措施、责任人和 资源需求。
应急演练
定期组织应急演练,提高 团队的应急响应能力和协 同配合水平。
执行情况回顾
对应急处理方案的执行情 况进行定期回顾和总结, 评估其有效性和可行性, 不断完善和优化方案。
目录
CONTENTS
01
双代号网络基本概念与原理
BIG DATA EMPOWERS TO CREATE A NEW
ERA
双代号网络定义及特点
定义
双代号网络是一种用箭线和节点 表示工作及其逻辑关系的网络图 ,其中箭线表示工作,节点表示 工作的开始或结束。
特点
双代号网络能够清晰地表达工作 之间的逻辑关系,便于进行时间 参数的计算和优化。
敏感性分析
通过改变网络计划中的某 些参数,观察其对整体计 划的影响,从而识别出关 键风险因素。
风险防范策略和措施
风险规避
通过调整网络计划,避免高风险事件的发生。
风险转移
通过保险、合同等方式将部分风险转移给第 三方。
风险减轻
采取相应措施,降低风险事件发生的概率或 减轻其后果。
风险接受
对于某些无法避免且后果较轻的风险,可以 选择接受并准备相应的应对措施。
项目管理工具--箭线图法

项目管理工具--箭线图法什么是箭线图法箭线图法又称矢线图法或双代号网络图法(Activity-On-Arrow,AOA)是计划评审法在质量管理中的具体运用,使质量管理的计划安排具有时间进度内容的一种方法。
它有利于从全局出发、统筹安排、抓住关键线路,集中力量,按时和提前完成计划。
是网络图在质量管理中的应用。
箭线图法用箭线表示活动,活动之间用节点(称作“事件”)连接,只能表示结束——开始关系,每个活动必须用唯一的紧前事件和唯一的紧后事件描述;紧前事件编号要小于紧后事件编号;每一个事件必须有唯一的事件号。
虽比顺序图法较少使用,但在某些应用领域仍是一种可供选择的方法。
箭线图法仅利用“结束——开始”关系以及用虚工作线表示活动间逻辑关系。
箭线图法可手编也可在计算机上实现。
明确箭线图的应用范围(1)交货期管理。
(2)新产品开发日程计划的制定和改善。
(3)试产阶段计划的制定及管理。
(4)量产阶段计划的制定及管理。
(5)较复杂活动的筹办及计划的管理。
双代号网络图的组成(一)节点双代号网络图中节点表示工作之间的联结,它不占用任何时间和资源,只表示指向节点的工作全部完成后,该节点后面的工作才能开始这件事。
因此节点只是一个“瞬间”,被称为事件。
(二)工作任何一项计划,都包含许多待完成的工作。
在双代号网络图中,工作是用箭线表示的。
箭尾表示工作的开始,箭头表示工作的完成。
对于某项工作来说,紧排在其前面的工作,称为该工作的紧前工作,紧接在其后面的工作称为该工作的紧后工作,和它同时进行的工作称为平行工作。
(三)虚工作(逻辑箭线)虚工作是一项虚拟的工作,实际并不存在。
它仅用来表示工作之间的先后顺序,无工作名称,既不消耗时间,也不消耗资源。
用虚箭线表示虚工作,其持续时间为0。
如图所示,为虚工作的两种表达方法。
在用实箭线表示时,需要标注持续时间为0。
(四)网络图的绘制在绘制网络图前,根据第一章所讲述的工作分解结构方法和项目管理的需要,将项目分解为网络计划的基本组成单元—工作(或工序),并确定各工作的持续时间,确定网络计划中各项工作的先后顺序,工作间的逻辑关系分为工艺关系和组织关系,据此绘制网络计划图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双代号网络图绘制中的虚箭线判定——存在、指向及数目
在双代号网络图的绘制中,经常需要引入虚箭线(表示虚工作)。
但对虚箭线的准确判定与正确绘制却比较复杂。
对此,本文在对虚箭线的应用情况进行归纳的基础上,分别给出了由绘图关系要求而需引入及由逻辑关系要求而需引入的虚箭线的存在、指向及数目的判定准则。
1、虚箭线应用归纳
虚箭线在双代号网络图中的应用可以从网络逻辑关系要求及绘图关系要求两个方面进行归纳。
如图1所示:
2、绘图关系要求的虚箭线
2.1绘图关系要求
绘图关系要求,是指在双代号网络图的绘制过程中,必须保证一对代号最多只能代表一项工作。
也就是说,在双代号网络图的绘制中,不能出现多项工作重号的现象。
可以多项工作共用一个开始节点(称该节点为分枝节点)或共用一个完成节点(称该节点为汇集节点),但不能多项工作共用同一对开始及完成节点。
2.2绘图关系要求的虚箭线判定
相比由逻辑关系要求的虚箭线,由绘图关系要求的虚箭线的判定(存在、指向及数目)比较简单。
归纳如下:绘图关系要求的虚箭线判定准则——
存在判定:当有n(n≥2)项工作同时开始并且同时完成时,存在虚箭线,亦即需要引入虚箭线。
指向判定:虚箭线与引入前的工作的方向保持一致,亦即从增加的节点指向共同的完成节点。
数目判定:当有n(n≥2)项工作同时开始并且同时完成时,需引入(n-1)条虚箭线。
3、逻辑关系要求的虚箭线
3.1逻辑关系要求
逻辑关系要求,是指用虚箭线来反映工作之间的逻辑关系。
如图1所示,由逻辑关系而引入虚箭线的情况比较复杂,包括工作间的逻辑联系关系与逻辑断路关系,也还包括一项工程内工作之间的逻辑联系和多项工程间工作之间的逻辑联系。
因此,由逻辑关系要求而引入的虚箭线判定是虚箭线应用的难点。
3.2工作间逻辑关系分析
工作间的逻辑关系包括工艺关系和组织关系两种。
工艺关系是指根据已确定的施工方法,由于工艺过程的技术要求而使得执行各项工作的前后次序受到严格的制约。
组织关系是指在施工过程中,根据施工场地的空间限制、施工时间以及施工设备和其它资源等客观条件,由管理人员通过组织决策确定的逻辑关系。
从工艺关系看,一项工作能否开始,必备两个条件:其一,要有相应的施工队;其二,要有相应的施工段。
在实际施工中,除必须满足工艺关系要求外,还要求工作的开展要满足组织关系的要求。
如,在流水施工组织中,为满足施工过程的“连续性”原则要求,某专业队能否投入施工除工艺关系上的两个必备条件需得到满足外,还需满足组织关系上的流水步距的要求。
3.3逻辑关系要求的虚箭线判定
在双代号网络图的绘制中,由逻辑关系要求而引入虚箭线的情况虽然比较复杂,但还是有规律可循。
逻辑关系要求的虚箭线判定准则——
存在判定:两项工作既有相同的、又有不同的紧后工作时,存在虚箭线,亦即需要引入虚箭线。
指向判定:虚箭线应从具有不同紧后工作的工作之完成节点指向相同紧后工作的开始节点。
数目判定:当两项工作中只有一项工作具有不同的紧后工作时,则只有一条虚箭线;当两项工作分别具有不同的紧后工作时,则有两条虚箭线。
需要注意的是,在虚箭线数目判定时,若两项工作中只有一项工作具有不同的紧后工作时,不论不同的紧后工作有多少项,都只需引入一条虚箭线;而当两项工作分别具有不同的紧后工作时,也不论不同的紧后工作有多少项,都只需要引入两条虚箭线即可表达清楚相应的逻辑关系。
4、虚箭线应用示例
以下以分段作业为例介绍虚箭线的应用。
分段作业是将工程对象从空间上进行施工段数m的划分和从工艺上进行施工过程数n的划分,再从时间上进行流水节拍ti的确定(对分段流水作业尚需确定流水步距K),然后按照施工段的组织顺序和施工过程的工艺顺序组织施工。
按照专业队的施工是否连续,分段作业可分为普通分段作业(不要求各专业队在各施工段上连续施工)和分段流水作业(要求各专业队在各施工段上连续施工)。
典型分段作业的施工组织如表1所示。
表1所示施工组织表示整个工程分为四个施工段(m=4),每一施工段都有A、B、C、D四个施工过程(n=4)。
在绘制普通分段作业双代号网络图前,可先进行虚箭线判定。
根据逻辑关系要求的虚箭线判定准则,对表1所示的“m×n”的施工组织用双代号网络图表示时的虚箭线判定如表2所示。
根据“表2”的虚箭线判定结果,可快捷而准确地绘制出普通分段作业的双代号网络图,见图2.
可以证明(作者有另文介绍,在此不再赘述),在普通分段作业双代号网络图中的虚箭线数目为:
式中:QDA1为虚箭线数(QuantityofDummyArrows);m为施工段数;n为施工过程数(工序数、施工队数)。
如:对图2所示“m×n=4×4”的普通分段作业施工组织,用式(1)计算虚箭线数为:QDA1=3(4-1)×(4-1)-4×4+1=12条,与“表1”的虚箭线判定结果一致。
需要注意的是:式(1)仅能用于计算由逻辑关系要求而引入的虚箭线数目且式(1)成立的条件为m和n皆大于等于2且不同时等于2.例如,当m和n同时等于2时,由式(1)得到虚箭线数QDA1为0,但在绘图时,会因“1虚箭线应用情况归纳”的“绘图关系”要求引入一条虚箭线。
如图3所示。
进一步地,在普通分段作业双代号网络图的逻辑关系中引入流水步距K———指工艺上相邻的专业队相继投入施工的开始时间的间隔,即可构成分段流水作业网络图,且“m×n”施工组织的分段流水作业网络图中的虚箭线数为:
式中符号意义同式(1)。
与式(1)不同的是,对“m×n=2×2”的流水施工组织,式(2)成立(此时将流水步距KAB 视为一项工作)。
5、结语
通过以上分析可见,在绘制双代号网络图时,先进行虚箭线的判定将使网络图的绘制快捷而准确;通过对分段作业施工组织(“m×n施工组织”)的虚箭线判定与虚箭线数判定与计算可见,不论双代号网络的图形复杂程度如何,虚箭线的存在、指向及数目均可依“准则”进行判定。
掌握了这些规律,双代号网络图的绘制也就迎刃而解且十分方便图形的检查。
参考文献
[1]中国建筑学会建筑统筹管理分会。
工程网络计划技术规程教程[M].北京:中国建筑工业出版社,2000.
[2]邬晓光。
工程进度监理[M].北京:人民交通出版社,1999.
[3]许立山,刘敏。
水运工程进度控制[M].北京:国防工业出版社,1995.
碧森尤信作者:张玉强,彭在萍。
