第11讲 电偶极子
电磁学02-电偶极子

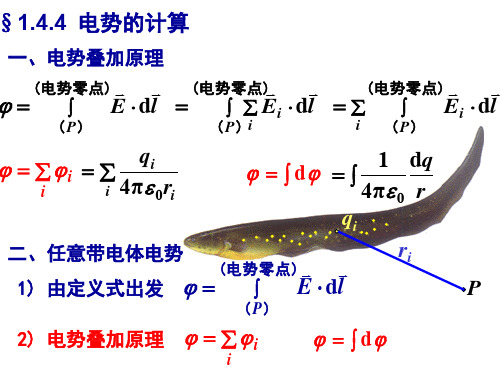
dS⊥电场线实例-OH H+*电多极子和分布在小区域内的电荷•除电偶极子外,还有电四极子、电八极子等。
–E 电单极子~r -2(点电荷可以称为“电单极子”)–E 电偶极子~r -3–E 电四极子~r -4……•分布在小区域内的电荷可以看成是点电荷(电单极子)、电偶极子、电四极子等电多极子的组和,以进行不同近似度的分析:•在后续课程的电场理论中,会出现将场函数进行幂级数展开的分析方法,形象的说,这种方法就相当于把小区域内的电荷分解成多极子的组合。
∑∑∑...电四极子+电偶极子+电单极子+实际电荷分布=§2.2 导体和电介质--物质的电学特性•物质分类•物质的电效应物质的分类•为了研究和总结各种物质的电性质,需要进行分类。
一般是按照物质的不同种类分别描述和研究其电性能。
一般将物质分为三种:导体绝缘体半导体–不同种类的物质,其原子、分子的电荷分布和运动机制各不相同。
•下面将按照另一个角度,按照能量转换的不同形式进行分类,对物质的电性能进行分类总结。
电学-机械性质介电效应介电效应磁片电容(绝缘介质影响电场分布)压电效应压电效应(介质受压缩形变,产生电压)电致伸缩效应电致伸缩效应石英振荡器石英钟(介质在电场作用下发生机械伸缩)导电效应导电效应电线(导体可导通电流)光电效应光电效应半导体硅(光照物质产生电压)激光笔电致发光电致发光半导体发(电压加于物质产生光)电光效应电光效应(电场改变物质的光性能)液晶显示器•电学-热学性质热致电阻变化热致电阻变化冰箱温度传感器(半导体或导体热敏电阻)……热电效应热电效应(导体的热生电动势)热电偶(测温度)电热效应电热效应电热壶(导体导电产生焦耳热)热释电效应热释电效应(绝缘体受热产生电压)人体红外探测器红外摄像器§2.3 电流场的描述•电流和电流密度•电流与电荷运动•电流的模型•电流场•电流密度的通量I电流密度矢量构成的矢量场叫电流场。
电流场可以形象的用电流线表示。
物理 电磁学 第11讲 电势叠加原理及电势的计算
d
Q
Q
4π 0 2 x 2
dq
2
1
d
Q
Q
4π 0 x
2
dq
2
2
1
讨论
当 x = 0 时, 盘
R 0
Q 2π d 2 πR 4 π 0 x
2
2
2
1 2 R 0 2
盘0
Q 2π 0 R
O
Q1 ( r R ) 1 4 π R 0 1 1 Q1 ( r R ) 1 4 π 0 r
Q2 ( r R ) 2 4 π R 0 2 2 Q2 ( r R ) 2 4 π 0 r
Q2
区域 r < R1 R1 < r < R2 r > R2
dq 4πr dr
2
内
2
A d
2 2 R2 R1 2 0
2. 求 B
R2 dq R1 4 π 0 r
R2 R1
4πr dr 4π 0 r
外
R1 O
rB rA A
r
B
q内 B B外 B内 4π 0 rB 4 3 2 2 3 R2 rB π rB R1 2 0 4π 0 rB 3 3 2 2 2 R1 3 R r 2 B 6 0 r B
R2 dq rB 4 π 0 r
R2
2 2 B 3 R2 rB 6 0 rB
当 R1 = 0 时,均匀带电球体内
第11讲_SPP的激发与表征

研究生课程纳米光学(Nano-Optics)第11讲:等离子体(III)——SPP的激发与表征董国艳中国科学院大学材料科学与光电技术学院课本:S.Maier,Plasmonics:Fundamentals and Applications,Chap.3&4回想前面的课程:可以通过光照射平的金属表面激发SPP吗?由于SPP位于金属表面,我们怎么能观察或检测呢?2本讲内容1.SPP 激发−−−−−−2.SPP 的表征−−−−3棱镜耦合通过高度集中的光束激发光栅耦合散射激发近场激发其它耦合方法近场显微镜泄漏辐射显微镜荧光成像散射光成像4•激发SPP,入射光波矢应该满足:k x inc =βSPP (被称为“相位匹配条件”)conservation:守恒,momentum:动量光子动量:P =ħk为什么呢?——光子的横向动量守恒!1.SPP 激发约化普朗克常数:ћ=h/(2π)h=6.63×10-34 J·s5k x inc =εd sin θ=εdintersection:交叉grazing incidence :掠入射•可以只是通过光照射在平的金属表面激发吗?入射波矢的x 分量:βor k xωωspLight line for θ<90ºωcLight line for 掠入射(θ=90º)ωk inc cSPP 色散总位于light line 的底部!(约束模)没有交集的色散曲线→无耦合进的光&无耦合出的SPP(∴约束场)因此,必须采用某些“技巧”来增大k x inc 与βSPP 匹配。
θωεθsin csin inc xinc dk k ==6全反射中的倏逝波22022exp[()]i tx z E E i k x k z e ω-=+()212121222222xx z k k n n k k k -=-=()()122121122121212sin sin i n n k i k k n n -=-=12211221sin sin 2sin sin i i i i k c c -=-=λπi 1i’1i 2n 1n 2k 1k’1k 2xz由边界条件,折射波的表达式122c z z i i k k i κ>=当,发生全内反射,为纯虚数,令n 1>n 22202202exp[()]exp[()]z x E E i k r t E e i k x t κωω-=⋅-=-全反射情况下,入射波的能量是穿透介质2内一定深度后逐渐反射的。
偶极子1解读

偶极子[编辑]维基百科,自由的百科全书(重定向自偶极矩)地球磁场可以近似为一个磁偶极子的磁场。
但是,图内的N 和S 符号分别标示地球的地理北极和地理南极。
这标示法很容易引起困惑。
实际而言,地球的磁偶极矩的方向,是从地球位于地理北极附近的地磁北极,指向位于地理南极附近的地磁南极;而磁偶极子的方向则是从指南极指向指北极。
电极偶子的等值线图。
等值曲面清楚地区分于图内。
在电磁学里,有两种偶极子(dipole):电偶极子是两个分隔一段距离,电量相等,正负相反的电荷。
磁偶极子是一圈封闭循环的电流,例如一个有常定电流运行的线圈,称为载流回路。
偶极子的性质可以用它的偶极矩描述。
电偶极矩()由负电荷指向正电荷,大小等于正电荷量乘以正负电荷之间的距离。
磁偶极矩()的方向,根据右手法则,是大拇指从载流回路的平面指出的方向,而其它拇指则指向电流运行方向,磁偶极矩的大小等于电流乘以线圈面积。
除了载流回路以外,电子和许多基本粒子都拥有磁偶极矩。
它们都会产生磁场,与一个非常小的载流回路产生的磁场完全相同。
但是,现时大多数的科学观点认为这个磁偶极矩是电子的自然性质,而非由载流回路生成。
永久磁铁的磁偶极矩来自于电子内禀的磁偶极矩。
长条形的永久磁铁称为条形磁铁,其两端称为指北极和指南极,其磁偶极矩的方向是由指南极朝向指北极。
这常规与地球的磁偶极矩恰巧相反:地球的磁偶极矩的方向是从地球的地磁北极指向地磁南极。
地磁北极位于北极附近,实际上是指南极,会吸引磁铁的指北极;而地磁南极位于南极附近,实际上是指北极,会吸引磁铁的指南极。
罗盘磁针的指北极会指向地磁北极;条形磁铁可以当作罗盘使用,条形磁铁的指北极会指向地磁北极。
根据当前的观察结果,磁偶极子产生的机制只有两种,载流回路和量子力学自旋。
科学家从未在实验里找到任何磁单极子存在的证据。
物理偶极子、点偶极子、近似偶极子[编辑]分开有限距离的两个异性电荷的电场线。
有限直径的载流循环的磁场线。
任意点偶极子(电偶极子、磁偶极子、声偶极子等等)的场线。
第11章电势1

上海大学物理系张金仓第五讲q PC PC ∫∫11012rd E q A p P Cr v ⋅=∫21012对单位正电荷而言,有:称为电场强度E 沿任意路径C 的线积分意义:在电场力作用下移动单位正电荷电场力所作的功!二、静止点电荷电场线积分q ∫∫⋅=⋅2121304p P Cp P C rd r rq r d E r r r v πε1、静止点电荷的电场中,电场强度的线积分(对单位正电荷所作的功!)只与积分路经的起点和终点位置有关,而与积分路径无关;2、推广一:对点电荷系,由于合力的功等于分力功之和,故总电场强度的线积分也具有同样特点;3、推广二:对连续带电体,总电场强度的线积分也具有同样特点;)11(421021r r q r d E p PC −=⋅∫πεr v三、静电场的保守性=⋅∫Cr d E r r 静电场的环路定理ab cd对任何静电场,电场强度的线积分(对单位正电荷所作的功!)只与积分路经的起点和终点位置有关,而与积分路径无关——静电场是一保守力场!!!与路径无关r d E 积分即:21p P C rv ⋅∫表述:静电场中电场强度沿任一闭合路径的线积分等于零。
四、静电场的环路定理qrd E U p P r v ⋅=−=∫212112ϕϕ物理意义:有限大带电体无限远处为电势零点 对正电荷,电势高意味着电势能高,对负电荷则相反;二、电势rd E U p P r v ⋅=−=∫212112ϕϕrd E p PP P r v ⋅=−=∫0ϕϕϕ意义:场中某一点P的电势,在数值上等于把单位正电荷自P点移动到电势零点P0处电场力所作的功。
rd E U p P r v ⋅=−=∫212112ϕϕ三、电势与电势差的关系rd E p PP P rv ⋅=−=∫00ϕϕϕ四、电场力的功rd E q q U q A p P r v ⋅=−==∫21021012012)(ϕϕ电势为五、点电荷的电势分布q+1P 1r 2r 2P rv r d r rr +rd r θFrE r 0q C P )11(44210302121r r qrd r rqr d E p P p P P −=⋅=⋅=∫∫πεπεϕr r rv 选择无限远处为电势零点,距静止点电荷为r 处电场中的电势:),(4210∞===r r r rq πεϕ+Vr014q V rπε=q >Vr014q V rπε=q <- q >0电势是正的愈远愈小。
第十一章 电磁学 恒定磁场 Ma 2016

0 qnS d lv er dB 4 r2
d B 0 qv er B d N 4 r 2 方向根据右手螺旋法则, B 垂直 v 、 正, B 为 v r 的方向;q为负, B 与
q
+
r B
v
q-
q为 r组成的平面。 v r 相反。
μ0 I B (cos θ1 cos θ 2 ) 4πr0
0 π
2
I
无限长载流长直导线的磁场
θ1 θ2
μ0 I B 2πr0
注意用右手螺旋关系判断方向。 半无限长载流长直导线的磁场
1
r0
P
θ1 θ2
2 π
μ0 I B 4πr0
I
r0
P
大学物理 电磁学
2、载流圆线圈轴线上的磁场 真空中,半径为R的载流导线,通有电流I,称圆电流。求其 轴线上一点 P的磁感强度的方向和大小
1、5 点 : dB 0
7
6 5
Idl
R
×
× 3
3、7点 : dB
0 Idl 4 π R2
4
2、4、6、8 点 :
dB
0 Idl
4π R
2
sin 45
0
大学物理 电磁学
3. 毕—萨定律应用举例
dB 的方向均
沿x 轴负方向
(1) 载流长直导线的磁场
z
dz
解
2
dB
大学物理 电磁学
磁现象与电现象有没有联系?
静电场 ?
静止的电荷 运动的电荷
1820年奥斯特:发现电流的磁效应
N
电偶极子名词解释

电偶极子名词解释
电偶极子是常见的物理学概念,指的是在一个物体中两个带电物质分别集中在不同位置形成的电荷对,这两个带电物质分别被称为电荷。
电偶极子可以用来描述一个复杂的分布电荷体系的整体电荷态。
以下是关于电偶极子的详细解释:
1. 什么是电偶极子?
正电荷和负电荷分别位于空间中的两个不同位置,两电荷之间的连线称为电偶极子轴线。
电偶极子的大小通常用电荷大小的乘积与电荷的距离之积来表示,即q*d。
其中,q为电荷大小,d为电荷间距离。
2. 电偶极子的具体特点?
在电场中,电子会同时受到正电荷和负电荷的吸引作用,由此产生了一个力矩,使电偶极子朝向电场的方向旋转。
电偶极子的旋转方向受到电场方向的影响。
如果电场方向与电偶极子轴线平行,则不会发生旋转。
3. 电偶极子有哪些应用?
电偶极子常用于描述电场中的分布电荷,例如在大分子中,不同的原子核质子和电子云之间就会形成电偶极子。
此外,电偶极子也常用于天文学,它可以用来描述恒星的星风。
总之,电偶极子既是一种抽象的物理概念,也是一种世界上常见的物理现象。
在日常生活和科学研究中,电偶极子以其独特的特点和多样的应用引起了人们的广泛关注。
因此,深入了解电偶极子的特性和应用具有重要意义。
电偶极子与电场分布

电偶极子在材料科学中的 定义和性质
电偶极子在材料科学中的 作用和影响
电偶极子在材料科学中的 研究方法和技术
电偶极子在材料科学中的 实际应用案例和效果
感谢您的观看
汇报人:XX
电偶极子的极化 强度与电场强度 成正比
电偶极子的极化 强度与电场频率 成正比
电偶极子的极化 强度与电场方向 有关
电偶极子的极化 强度与电偶极子 的形状和尺寸有 关
4
电偶极子在电场中的相 互作用
电偶极子间的相互作用力
电偶极子:由两个等量异号电荷组成的系统 电场分布:电偶极子在电场中会产生电场分布 相互作用力:电偶极子间的相互作用力与电场分布有关 计算方法:可以通过计算电偶极子间的电势差来获得相互作用力
平方成反比
电偶极子的电 场力:与距离 的平方成反比, 方向指向电偶
极子的中心
电偶极子的电场强度
电偶极子的电场强度与距离的关系:随着距离的增加,电场强度逐渐减小
电偶极子的电场强度与角度的关系:随着角度的增加,电场强度逐渐减小
电偶极子的电场强度与电偶极子长度的关系:随着电偶极子长度的增加,电场强度逐 渐增大 电偶极子的电场强度与电偶极子形状的关系:电偶极子的形状对电场强度有影响,如 针状电偶极子的电场强度较大,而球状电偶极子的电场强度较小。
电偶极子在电子学中的发展趋势和 前景
电偶极子在电磁学中的应用
电偶极子在电场中的作用:产 生电场,影响电荷运动
电偶极子在电磁波中的应用: 产生电磁波,影响电磁波传播
电偶极子在电磁学中的理论研 究:电偶极子模型,电偶极子 场方程
电偶极子在电磁学实验中的应 用:电偶极子天线,电偶极子 滤波器
电偶极子在材料科学中的应用
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题选讲
1. 已知两杆电荷线密度为λ, 长度为L, 相距L . 求两带 电直杆间的电场力. 解:(1)距离原点x处取元电荷dq = λdx,在x轴上 距离原点为a (a > L)的空间点形成的场强为 dx
dE
dx
4 0 ( a x )
2
L 0
0
x L
2
2L a 3L
a点的总场强为
电偶极子
电偶极子是一种常见的带电结构。 所有有极分子都属于电偶极子。
1 基本概念
电偶极子:等量异号电荷+q、-q,相距为l,l 相较 于场点距离很小. 电偶极子的轴:从-q 指向+q 的矢量 l
电偶极矩(electric moment) : p e q l
l
-q
+q
-1 -1
CH3
4 0 r
kR
4 2
4 0 r
3. 如图所示的绝缘细线上均匀分布着线密度为λ的正 电荷, 两直导线的长度和半圆环的半径都等于R。试 求环中心O点处的场强和电势。 解:(1) 在x处取电荷元dq=λdx。 在O点的场强为
dE
dx
பைடு நூலகம்dx
2R
4 0 x
2
x
8 0 R
CD段在O点的场强 E d E R 同样可求AB段在O点的场强 E 而BC段在O点的场强易求,为
CH2
OH
O
C
O
?
?
+2
CO2分子不是电偶极子 酒精分子是电偶极子 水分子是电偶极子
2 电偶极子在均匀电场中所受的和力与和力矩 受力分析
F F F 0
q
l 2
M F
l 2
o
sin F qE
p ql
sin F
E
F qE
3L 2L
2 1 1 4 2 dx ln L 4 0 x L x 4 0 3
2. 如图所示,半径R的非金属球体内,电荷体密度 为ρ = k r,式中k为大于零的常量,求: (1)球体内任意一点的场强E1(r); (2)球体外任意一点的场强E2(r)。
p 4 0 y
3
y
B
r
A点(y = 0)
Ey 0
q
Ex
2p 4 0 x
3
O l
q
A
x
如何理解带电球面内的场强为0 ?
E 0
E
q 4 0 r
2
ˆ r
过P点作圆锥 则在球面上截出两电荷元
d q1 d S 1 dq2 dS 2
dE1
4 0 x
CD段在O点的总电势为
U CD
dU
2R R
dx
4 0 x
4 0
ln 2
AB段在O点的电势与CD段相同,即UAB = UCD。 CD段在O点的总电势为 则O点的总电势为
U U
AB
U BC
dU
R
0
dl
4 0 R
4 0
U BC U CD
q
矢量式 M p e E p 可见: e E力矩最大;pe / / E力矩最小。
q lE sin
力矩总是使电矩 pe 转向 E 的方向,以达到稳定状态
例题1
求电偶极子电场中任一点P 的电势.
解: 由叠加原理
U P U1 U 2
若 r l
q 4 0 r1
q 4 0 r2
q ( r2 r1 ) 4 0 r1 r2
2
r2 r1 l co s
r1 r2 r
y
P ( x, y )
U
2
q 4 0
2
l co s r
2
2
其中 r x y co s
U 1 4 0
2
x x y
2
3
r2
2
px ( x y )2
2
q
O
r r 1
q
x
l
例题2
计算电偶极子电场中任一点的场强。
1
2
解:U U ( x , y )
U x
px
2 3 2
4 0 ( x y )
p 3x
2 5
Ex
4 0 ( x 2 y 2 )
[
2 2
1 (x y )
2 3 2
]
Ey
U y
p
3 xy
5 2
4 0 ( x 2 y 2 )
Ex
p
4 0 ( x 2 y 2 )
[
3x
2 5 2
2
1 (x y )
2 3 2
]
Ey
p
2
3 xy
2 5 2
4 0 ( x y )
B点(x = 0)
Ex
Ey 0
2 0
ln 2
4 0
P
dq 1
dq 2
d q 1 在P点场强
dS1
4 0 r1
2
4 0
d
方向 如图
dq 2
在P点场强
dE 2
dS 2
4 0 r2
2
4 0
d
方向 如图
dE1 dE 2
立体角示意图
立体角:物体在一个以观测点为球心的球面上的投影面积与半径平方的比值。 平面角:圆的弧长与半径的比值。
E
dx
4 0 a x
(2)距离原点x(2L < x <3L)处取电荷元dq = λdx, 其所受电场力为
1 1 dF Edq dx 4 0 x L x 则右侧棒受到的合力为
F
1 1 4 0 a L a
dx
二者方向相反, 8 0 R 大小相等。
2 0 R
4 0 x
2
E
dE
y
2
2 0
Rd
4 0 R
2
co s
所以O点的场强为: E
2 0 R
ˆ j
(2) CD段上,在x处取电荷元dq=λdx。在O点的电 dx 势为 dU
解: 取同心球面为高斯面
电通量 e E 4 r
r
2
kr
r R
q k r 4 r d r k r
2 0
r
4
由高斯定理得: E
R
k r
4 2
4 0 r
kr
2
R
4 0
k R
4 2
r R
2 4 q k r 4 r d r k R E 0
