对数函数及定义域 知识点
对数函数的定义域专题复习讲义(解析版)

对数函数的定义域解题策略:函数定义域(是使解析式有意义的自变量的取值集合) 一般有以下几种问题:①已知函数解析式,求函数的定义域;②在实际问题中,函数的定义域的求解除要考虑解析式有意义外,还应考虑使实际问题有意义;③已知()f x 的定义域求[()]f g x 的定义域或已知[()]f g x 的定义域求()f x 的定义域. 2. 求函数定义域的常用方法技巧( 1) 根据解析式要求如偶次根式的被开方式大于零,分母不能为零. ( 2) 根据实际问题的要求确定自变量的范围.( 3) 复合函数的定义域: 若已知()f x 的定义域为[,]a b ,其复合函数[()]f g x 的定义域由不等式()b a g x ≤≤解出即可.3.求对数型函数定义域的方法同前面讲到的求的一般函数定义域的方法一样,但应特别注意的是:真数大于零、底数大于零且不等于1.典例精析:考点一 具体函数的定义域【例1】若对数()()21log 62a a --有意义,则实数a 的取值范围为( ) A .(-∞,3) B .1(,3)2 C .1(,1)2∪(1,+∞)D .1(,1)2∪(1,3) 【解析】由已知,得3620112103222111a a a a a a a <⎧->⎧⎪⎪⎪->⇒>⇒<<⎨⎨⎪⎪-≠⎩≠⎪⎩且1a ≠,故选:D .【例2】函数()22log 6y x x =--的定义域为 ( )A .()2,3-B .()3,2-C .()(),32,-∞-+∞D .()(),23,-∞-+∞【解析】函数()22log 6y x x =--的定义域为:260x x -->,即3x >或2x <-,所以定义域为:()(),23,-∞-+∞.故选:D.:变式1:函数()21log 4xf x x -=-的定义域为( ) A .()1,4 B .[)1,4 C .()(),14,-∞⋃+∞ D .(](),14,-∞⋃+∞【解析】由题意得104xx ->-,即()()140x x --<,解得14x <<.故选:A .变式2:函数1(1)y ln x =-的定义域为( )A .(1,)+∞B .[1,)+∞C .(1,2)(2⋃,)+∞D .(1,2)[3,)+∞【解析】解:要使函数1(1)y ln x =-有意义则(1)010ln x x -≠⎧⎨->⎩解得1x >且2x ≠∴函数1(1)y ln x =-的定义域为(1,2)(2⋃,)+∞故选:C .【例3】函数()lg(2)f x x =-的定义域是( )A .(,2)-∞B .[0,2)C .[0,2]D .[0,)+∞【解析】由题意,有200x x ->⎧⎨≥⎩,解得02x ≤<.∴函数定义域为[0,2).故选:B.变式1:函数()(1)f x ln x =+的定义域为( )A .(2,)+∞B .(1-,2)(2⋃,)+∞C .(1,2)-D .(1-,2]【解析】:由题意得:2010x x ->⎧⎨+>⎩,解得:12x -<<,故选:C .变式2:函数y =( )A .(4,1)--B .(4,1)-C .(1,1)-D .(1-,1]【解析】解:由题意知,函数y =210340x x x +>⎧⎨--+>⎩,解得11x -<<,故选:C .变式3:()22log 4y x =--的定义域是( ) A .(2,0)(1,2)- B .(2,0](1,2)-⋃ C .(2,0)[1,2)-⋃ D .[2,0][1,2]-⋃【解析】要使函数有意义,则21022040x xx x -⎧≥⎪⎪⎨≠⎪⎪->⎩, 解得20x -<<或12x ≤<,所以函数的定义域为(2,0)[1,2)-⋃.故选:C .变式4:函数3()log (21)xf x x =-的定义域是( ) A .1,12⎛⎤ ⎥⎝⎦B .1,12⎡⎤⎢⎥⎣⎦C .(1,)+∞D .1(,1)2【解析】由已知得1021>0x x ->⎧⎨-⎩,解得112x <<,所以函数()f x 的定义域为112⎛⎫⎪⎝⎭,,故选:D变式5:函数(2)y x =-的定义域为( )A .(0,2)B .[0,2)C .(0,2]D .[0,2]【解析】解:要使原函数有意义,则200x x ->⎧⎨⎩,解得:02x <.所以原函数的定义域为[0,2). 故选:B .变式6:函数()ln 1x f x -=)A .(]1,2B .[]1,4C .()1,4D .[]2,4【解析】对于函数()f x =有1040x x ->⎧⎨->⎩,解得14x <<.因此,函数()f x =的定义域为()1,4.故选:C.【例4】函数()f x)A.12x x⎧⎫>-⎨⎬⎩⎭B.12x x⎧⎫-<<⎨⎬⎩⎭C.12x x⎧⎫-<≤⎨⎬⎩⎭D.{}0x x≥【解析】因为()f x()12log210x+≥,即()1122log21log1x+≥,所以0211x<+≤,解得12x-<≤,即函数的定义域为12x x⎧⎫-<≤⎨⎬⎩⎭,故选:C变式1:函数y=()A.[1,)+∞B.3(,)4+∞C.3(,1]4D.(-∞,1]【解析】函数y=0.5log(43)0{|}430xxx-⎧⎨->⎩,即431{|}34xxx-⎧⎪⎨>⎪⎩,解得3{|1}4x x<.故选:C.变式2:函数y=__________.【解析】由411x-≥可得222x≥,得12x≥.所以函数y=1[,)2+∞.【例5】函数()00.5log21y x=-⎡⎤⎣⎦的定义域为()A.1,12⎛⎫⎪⎝⎭B.1,2⎛⎫+∞⎪⎝⎭C.()1,+∞D.()1,11,2⎛⎫+∞⎪⎝⎭【解析】要使函数有意义,只需()0.5log210x-≠,即210211xx->⎧⎨-≠⎩,解得112x<<或1x>.故选:D .变式1:函数20()(54)lg(43)x f x x x =+-+的定义域为 【解析】若要使函数有意义,则lg(43)0430540x x x +≠⎧⎪+>⎨⎪-≠⎩,解得34x >-且12x ≠-,45x ≠,所以该函数的定义域为31144,,,42255⎛⎫⎛⎫⎛⎫--⋃-⋃+∞ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.【例6】函数12y x=-的定义域为 【解析】若要使函数有意义,则22010x x ⎧-≠⎪⎨-≥⎪⎩,解得1≥x 或1x ≤-且2x ≠±,所以该函数的定义域为][)()(,2)(2,11,22,-∞-⋃--⋃⋃+∞;变式1:函数2()f x =的定义域为【解析】若要使函数有意义,则2210log (1)010x x x ⎧--≥⎪-≠⎨⎪->⎩,解得3x ≥,所以该函数的定义域为[)3,+∞;考点二 抽象函数的定义域【例7】若函数(1)f x +的定义域为[0 1],,则(lg )f x 的定义域为( ) A .[10 100],B .[1 2],C .[0 1],D .[0 lg2], 【解析】因为函数(1)f x +的定义域为[0 1],,所以112x ≤+≤,所以1lg 2x ≤≤, 解得:10100x ≤≤,所以(lg )f x 的定义域为[10 100],,故选:A.变式1:已知函数(2)x y f =的定义域是[]1,1-,则函数3(log )f x 的定义域是( )A .[]1,1-B .1,33⎡⎤⎢⎥⎣⎦C .[]1,3 D.【解析】由[]1,1x ∈-,得1,222x⎡⎤∈⎢⎥⎣⎦,所以31log ,22x ⎡⎤∈⎢⎥⎣⎦,所以x ⎤∈⎦.故选:D.考点三 逆用函数的定义域【例8】若函数()lg 1y ax =+的定义域为(),1-∞,则a =( ) A .1 B .-1 C .2D .无法确定【解析】函数()lg 1y ax =+的定义域为(),1-∞,则10ax +>的解集为(),1-∞, 即0a <,且10ax +=的根11a-=,故1a =-.故选:B.【例9】若函数()2()log 1a f x x ax =-+的定义域为R ,则实数a 取值范围是( ) A .(0,1) B .(0,1)(1,2) C .(1,2) D .[2,)+∞【解析】()2log 1a y x ax =-+的定义域为R ;210x ax ∴-+>的解集为R ;∴240a ∆=-<;22a ∴-<<;又0a >且1a ≠;01a ∴<<或12a <<; ∴实数a 的取值范围是()()0,11,2.故选:B .变式1:已知函数()2lg 1y kx kx =-+的定义域为R ,则实数k 的取值范围是__________. 【解析】由题意可知,kx 2﹣kx +1>0恒成立,当k =0时,1>0恒成立, 当k ≠0时,240k k k ⎧⎨∆=-⎩><,解可得,0<k <4,综上可得,k 的范围[0,4).【例10】若2()log (log )a a f x x x =-+对任意1(0,)2x ∈恒有意义,则实数a 的范围 .【解析】要使函数()f x 有意义,则当意1(0,)2x ∈时,2log 0a x x -+>恒成立,即2log a x x >.若1a >时,当1(0,)2x ∈时log 0a x <,此时不成立.若01a <<,当1(0,)2x ∈时,作出函数log a y x =和2y x =的图象,当12x =时,11log 24a =,得1412a =,即116a =,∴若2()log (log )a a f x x x =-+对任意1(0,)2x ∈恒有意义, 则1116a <,即实数a 的范围是1[,1)16.故答案为:1[,1)16.变式1:()(42)xf x lg k =-在(-∞,2]上有意义,则实数k 的取值范围是 .【解析】由题意函数(42)x k -在(-∞,2]上,恒为正值, 即:(42)0x k ->恒成立,42x k <,因为2x 在(-∞,2]上是增函数,所以1k < 故答案:(,1)-∞【例11】已知函数()()2lg 21f x ax x =++.(1)若函数()f x 的值域为R ,求实数a 的取值范围; (2)若函数()f x 的定义域为R ,求实数a 的取值范围.【解析】(1)∵()f x 的值域为R ,∴要求221u ax x =++的值域包含()0,∞+. 当0a <时,显然不可能;当0a =时,21u x R =+∈成立; 当0a >时,若221u ax x =++的值域包含()0,∞+, 则440a ∆=-≥,解得01a <≤. 综上所述,可知a 的取值范围是01a ≤≤.(2)由题意,知221u ax x =++的值恒为正,∴0440a a >⎧⎨∆=-<⎩,解得1a >,故a 的取值范围是1a >.巩固训练:1、已知对数式()12log 4a a+-(a ∈Z )有意义,则a 的取值范围为( ) A .()1,4- B .()()1,00,4-⋃ C .{}1,2,3 D .{}0,1,2,3【解析】由题意可知:101110244a a a a a a⎧⎪+>>-⎧⎪⎪+≠⇔≠⎨⎨⎪⎪<⎩⎪>-⎩,解之得:14a -<<且0a ≠.∵a ∈Z ,∴a 的取值范围为{}1,2,3.故选:C.2、函数(1)log (164)xx y +=-的定义域是【解析】要使函数有意义需,10111640x x x +>⎧⎪+≠⎨⎪->⎩,解得12x -<<且0x ≠,即10x -<<或02x <<,所以函数(1)log (164)xx y +=-的定义域是(1,0)(0,2)-.3、函数(2)y lg x =-的定义域是( ) A .(2,)+∞B .(1,)+∞C .[1,)+∞D .[2,)+∞【解析】函数2log (2)y x =-有意义,必须20x ->,即:2x >,故选:A .4、函数()(31)f x lg x =++的定义域是( ) A .1(3-,)+∞B .[2-,1)3C .1(3-,2]D .(-∞,2]【解析】要使函数有意义,则20310x x -⎧⎨+>⎩,即213x x ⎧⎪⎨>-⎪⎩,∴123x -<,即函数的定义域为1(3-,2],故选:C .5、函数2()log (62)f x x =-的定义域是( )A .{|3}x x >B .{|43}x x -<<C .{|4}x x >-D .{|43}x x -<【解析】对于2log (62)x -,得出620x ->3x ∴<40x +4x ∴-∴函数2()log (62)f x x =-的定义域是{|43}x x -<故选:D .6、函数1y x=+的定义域是( ) A .[1,0)(0,1)- B .[1,0)(0,1]-⋃ C .(1,0)(0,1)-D .(1,0)(0,1]-⋃【解析】由题意得10,10,0,x x x ->⎧⎪+>⎨⎪≠⎩解得10x -<<或01x <<.所以原函数的定义域为(1,0)(0,1)-.故选:C.7、函数()f x ( ) A .(0,2)B .(0,1)(1⋃,2)C .(0,2]D .(0,1)(1⋃,2]【解析】要使函数()f x 有意义,只需要2000x x lgx -⎧⎪>⎨⎪≠⎩,解得01x <<或12x <,所以定义域为(0,1)(1⋃,2]. 故选:D .8、函数y =的定义域是【解析】(1)要使函数有意义需,2400lg 30x x x ⎧-≥⎪>⎨⎪+≠⎩,解得2x ≥,所以函数lg 3y x =+的定义域是[2,)+∞;9、()f x 的定义域 .【解析】()f x =的定义域为1310log (1)0x x ->⎧⎪⎨-⎪⎩,解得12x <.故答案为:(1,2].10、已知函数()f x 的定义域为M ,()(1)g x ln x =+的定义域为N ,则()(RMN =⋃ )A .{|1}x x <B .{|1}x x -C .∅D .(|11}x x -<【解析】因为函数()f x ={|11}M x x =-<<;()(1)g x ln x =+的定义域为{|1}N x x =>-,所以{|1}RN x x =-(){|11}{|1}{|1}R MN x x x x x x =-<<-=<.故选:A .11、已知函数()()()log 2log 2a a f x x x =+--,(0a >且1)a ≠. (1)求()f x 的定义域; (2)判断并证明()f x 的奇偶性; (3)求满足()0f x ≤的实数x 的取值范围. 【解析】(1)()()()log 2log 2a a f x x x =+--,要使函数有意义可得2020x x +>⎧⎨->⎩,解得22x -<<,所以函数的定义域为()2,2-,(2)由(1)可知,函数的定义域关于原点对称,()()()()log 2log 2a a f x x x f x -=--+=-,所以函数为奇函数, (3)由()0f x ≤,则()()log 2log 2a a x x +≤-,当1a >时,可得22x x +≤-,解得0x ≤,此时实数x 的取值范围为(],0-∞,第 11 页 共 12 页当01a <<时,可得22x x +≥-,解得0x ≥,此时实数x 的取值范围为[)0,+∞.12、已知函数()()22log 1f x x ax =-+. (1)若()f x 的定义域,值域都是R ,求a 的值;(2)当2a =时,讨论()f x 在区间[]0b ,上的值域.【解析】(1)因为()f x 的定义域是R ,所以210x ax -+>在实数集上恒成立, 故一元二次方程210x ax -+=的根的判别式22404a a ∆=-<⇒<;()f x 的值域是R ,说明21y x ax =-+能取遍所有的正实数,因此一元二次方程210x ax -+=的根的判别式22404a a ∆=-≥⇒≥,显然这与刚得到24a <矛盾,故不存在这样的实数a ;(2)因为2a =,所以()()()2222log 21log 1f x x x x =-+=-,函数的定义域为不等于1的全体实数,故区间[]0b ,的右端点不能等于1,即0b >且1b ≠,显然函数在(,1)-∞上单调递减,在(1,)+∞上单调递增.当01b <<时,函数在[]0b ,上是减函数,故函数的最大值为()20log 10f ==,函数的最小值为:()()22log 21f b b b =-+,因此函数的值域为:()22[log 21,0]b b -+; 当12b <≤,函数没有单调性,故函数的最大值为()20log 10f ==,而1x ≠,所以函数的值域为(,0]-∞;当2b >时,函数的最大值为:()()22log 21f b b b =-+,而1x ≠,所以函数的值域为: ()22(,log 21]b b -∞-+.第12 页共12 页。
高三:对数与对数函数

这时f(x)=log4(-x2+2x+3).
由-x2+2x+3>0得-1<x<3,即函数定义域为(-1,3). 令g(x)=-x2+2x+3. 则g(x)在(-1,1)上单调递增,在(1,3)上单调递减. 又y=log4x在(0,+∞)上单调递增,
所以f(x)的单调递增区间是(-1,1),单调递减区间是
则f(a2)+f(b2)=________. 解析:由f(ab)=1得ab=10,于是f(a2)+f(b2)=lg a2 +lg b2=2(lg a+lg b)=2lg(ab)=2lg 10=2. 答案:2
1.在运用性质logaMn=nlogaM时,要特别注意条件,在
无M>0的条件下应为logaMn=nloga|M|(n∈N*,且n为偶数).
1 4 3 1 = ×(5lg 2-2lg 7)- × lg 2+ (lg 5+2lg 7) 2 3 2 2 5 1 = lg 2-lg 7-2lg 2+ lg 5+lg 7 2 2 1 1 1 1 = lg 2+ lg 5= lg(2×5)= . 2 2 2 2
(2)由 2a=5b=m 得 a=log2m,b=log5m, 1 1 ∴a+b=logm2+logm5=logm10. 1 1 ∵a+b=2, ∴logm10=2,即 m2=10. 解得 m= 10(∵m>0).
A.0,
(
B. 2 ,1 2
)
2 2
C.(1, 2)
D.( 2,2)
[自主解答]
(1)由1-x>0,知x<1,排除选项A、
B;设t=1-x(x<1),因为t=1-x为减函数,而y=ln t 为增函数,所以y=ln(1-x)为减函数,可排除D选C.
对数与对数函数知识点及例题讲解

对数与对数函数1.对数(1)对数的定义:)对数的定义:如果a b =N (a >0,a ≠1),那么b 叫做以a 为底N 的对数,记作log a N =b . (2)指数式与对数式的关系:a b =N Ûlog a N =b (a >0,a ≠1,N >0).两个式子表示的a 、b 、N 三个数之间的关系是一样的,并且可以互化. (3)对数运算性质: ①log a (MN )=log a M +log a N . ②log a NM =log a M -log a N . ③log a M n =n log a M .(M >0,N >0,a >0,a ≠1)④对数换底公式:log b N =bNN a a log log log (a >0,a ≠1,b >0,b ≠1,N >0). 2.对数函数(1)对数函数的定义)对数函数的定义函数y =log a x (a >0,a ≠1)叫做对数函数,其中x 是自变量,函数的定义域是(0,+∞). 注意:真数式子没根号那就只要求真数式大于零,如果有根号,要求真数大于零还要保证根号里的式子大于零,底数则要大于0且不为1 对数函数的底数为什么要大于0且不为1呢?在一个普通对数式里在一个普通对数式里 a<0,或=1 的时候是会有相应b 的值的。
但是,根据对数定义: : loglog a a=1;如果a=1或=0那么log a a 就可以等于一切实数(比如log 1 1也可以等于2,3,4,5,等等)第二,根据定义运算公式:log a M^n = nlog a M 如果a<0,那么这个等式两边就不会成立 (比如,log (-2) 4^(-2) 就不等于(-2)*log (-2) 4;一个等于1/16,另一个等于-1/16) (2)对数函数的图象)对数函数的图象O xyy = l o g x a > Oxy<a <a y = l o g x a 1111( ())底数互为倒数的两个对数函数的图象关于x 轴对称. (3)对数函数的性质: ①定义域:(0,+∞). ②值域:R . ③过点(1,0),即当x =1时,y =0. ④当a >1时,在(0,+∞)上是增函数;当0<a <1时,在(0,+∞)上是减函数. 基础例题1.函数f (x )=|log 2x |的图象是的图象是1 1 1-1 1111 1 xxxxy y y y O OOOA BC D解析:f (x )=îíì<<-³.10,log ,1,log 22x x x x答案:A 2.若f --1(x )为函数f (x )=lg (x +1)的反函数,则f --1(x )的值域为___________________. 解析:f -1(x )的值域为f (x )=lg (x +1)的定义域.由f (x )=lg (x +1)的定义域为(-1,+∞),∴f --1(x )的值域为(-1,+∞). 答案:(-1,+∞)∞)3.已知f (x )的定义域为[0,1],则函数y =f [log 21(3-x )]的定义域是__________. 解析:由0≤log 21(3-x )≤1Þlog 211≤log 21(3-x )≤log 2121Þ21≤3-x ≤1Þ2≤x ≤25. 答案:[2,25]4.若log x7y=z ,则x 、y 、z 之间满足之间满足A.y 7=x zB.y =x 7zC.y =7x zD.y =z x解析:由logx 7y=z Þx z=7y Þx 7z=y ,即y =x 7z. 答案:B 5.已知1<m <n ,令a =(log n m )2,b =log n m 2,c =log n (log n m ),则,则A.a <b <cB.a <c <bC.b <a <cD.c <a <b解析:∵1<m <n ,∴0<log n m <1. ∴log n (log n m )<0. 答案:D 6.若函数f (x )=log a x (0<a <1)在区间[a ,2a ]上的最大值是最小值的3倍,则a 等于等于 A.42 B.22 C.41 D.21解析:∵0<a <1,∴f (x )=log a x 是减函数.∴log a a =3·log a 2a . ∴log a 2a =31.∴1+log a 2=31.∴log a 2=-32.∴a =42. 答案:A 7.函数y =log 2|ax -1|(a ≠0)的对称轴方程是x =-2,那么a 等于A. 21 B.-21 C.2 D.-2 解析:y =log 2|ax -1|=log 2|a (x -a1)|,对称轴为x =a1,由a1=-2 得a =-21. 答案:B 注意:此题还可用特殊值法解决,如利用f (0)=f (-4), 可得0=log 2|-4a -1|.∴|4a +1|=1.∴4a +1=1或4a +1=-1. ∵a ≠0,∴a =-21. 8.函数f (x )=log 2|x |,g (x )=-x 2+2,则f (x )·g (x )的图象只可能是能是OxyOxyOxyOxyABC D解析:∵f (x )与g (x )都是偶函数,∴f (x )·g (x )也是偶函数,)111-1O xy注意:研究函数的性质时,利用图象会更直观. 【例3】 已知f (x )=log 31[3-(x -1)2],求f (x )的值域及单调区间. 解:∵真数3-(x -1)2≤3,∴log 31[3-(x -1)2]≥log 313=-1,即f (x )的值域是[-1,+∞).又3-(x -1)2>0,得1-3<x <1+3,∴x ∈(1-3,1]时,]时,3-(x -1)2单调递增,从而f (x )单调递减;x ∈[1,1+3)时,f (x )单调递增. 注意:讨论复合函数的单调性要注意定义域. 【例4】已知y =log a (3-ax )在[0,2]上是x 的减函数,求a 的取值范围. 解:∵a >0且a ≠1,∴t =3-ax 为减函数.依题意a >1,又t =3-ax 在[0,2]上应有t >0,∴3-2a >0.∴a <23.故1<a <23. 【例5】设函数f (x )=lg (1-x ),g (x )=lg (1+x ),在f (x )和)和 g (x )的公共定义域内比较|f (x )|与|g (x )|的大小. 解:f (x )、g (x )的公共定义域为(-1,1). |f (x )|-|g (x )|=|lg (1-x )|-|lg (1+x )|. (1)当0<x <1时,|lg (1-x )|-|lg (1+x )|=-lg (1-x 2)>0; (2)当x =0时,|lg (1-x )|-|lg (1+x )|=0;(3)当-1<x <0时,|lg (1-x )|-|lg (1+x )|=lg (1-x 2)<0. 综上所述,当0<x <1时,|f (x )|>|g (x )|;当x =0时,|f (x )|=|g (x )|;当-1<x <0时,|f (x )|<|g (x )|. 【例6】 求函数y =2lg (x -2)-lg (x -3)的最小值. 解:定义域为x >3,原函数为y =lg 3)2(2--x x . 又∵3)2(2--x x x =3442-+-x x x =31)3(2)3(2-+-+-x x x =(x -3)+31-x +2≥4, ∴当x =4时,y min =lg4. 【例7】 (2003年北京宣武第二次模拟考试)在f 1(x )=x 21,f 2(x )=x 2,f 3(x )=2x ,f 4(x )=log 21x 四个函数中,x 1>x 2>1时,能使21[f(x 1)+f (x 2)]<f (221x xx x +)成立的函数是)成立的函数是A.f 1(x )=x 21B.f 2(x )=x 2C.f 3(x )=2xD.f 4(x )=log 21x解析:由图形可直观得到:只有f 1(x )=x 21为“上凸”的函数. 答案:A 探究创新1.若f (x )=x 2-x +b ,且f (log 2a )=b ,log 2[f (a )]=2(a ≠1). (1)求f (log 2x )的最小值及对应的x 值;值;(2)x 取何值时,f (log 2x )>f (1)且log 2[f (x )]<f (1)?)? 解:(1)∵f (x )=x 2-x +b ,∴f (log 2a )=log 22a -log 2a +b . 由已知有log 22a -log 2a +b =b ,∴(log 2a -1)log 2a =0. ∵a ≠1,∴log 2a =1.∴a =2.又log 2[f (a )]=2,∴f (a )=4. ∴a 2-a +b =4,b =4-a 2+a =2.故f (x )=x 2-x +2,127m +m -+m )-+m+2m ≥+xm+2m )+x m ≥2m (当且仅当=xm ,即=m 时等号成立)+x m +2m )=4m ,即4m ≥≥169. 可以首先将它们与零比较,分出正负;正数通常都再与1比较分出大于1还是小于1,然后在各类中间两两相比较. 3.在给定条件下,求字母的取值范围是常见题型,要重视不等式知识及函数单调性在这类问题上的应用. 。
对数函数及其性质知识点总结经典讲义

对数函数及其性质知识点总结经典讲义对数函数是指以一些正数b为底的函数,表示为logb(x),其中x为自变量,b为底数。
对数函数是指数函数的逆运算,可以用于解决指数方程和指数不等式问题。
对数函数的一些重要性质如下:1.对数函数的定义域是正实数集R+。
2.对数函数的值域是实数集R。
3.对数函数的自变量必须大于0,即x>0。
4.底数b必须大于0且不等于1,即b>0,b≠15.对数函数的图像在直线y=x左侧,与x轴交于点(1,0)。
6. 对数函数是单调递增函数,即当自变量x1 > x2时,有logb(x1) > logb(x2)。
7. 对数函数的特殊值:logb(1) = 0,logb(b) = 18. 对数函数的运算规则:logb(x·y) = logb(x) + logb(y),logb(x/y) = logb(x) - logb(y),logb(x^n) = n·logb(x),其中x、y 为正实数,n为任意实数。
9. 对数函数的函数性质:logb(1/x) = -logb(x),logb√x =(1/2)·logb(x)。
10. 对数函数的性质:logb(m/n) = logb(m) - logb(n),logb(m^n) = n·logb(m),logb(m) = (logc(m))/(logc(b)),其中b、c为正实数,m、n为正实数。
11. 对数函数的解析式:logb(x) = logc(x)/logc(b),其中c为任意正实数,c ≠ 112. 对数函数的性质:logb(x) = 1/(logx(b))。
13. 对数函数与指数函数的关系:y = logb(x)是函数y = b^x的反函数,两者互为反函数。
对数函数在数学、科学和工程等领域中具有广泛的应用。
它可以用于求解指数方程和指数不等式,简化复杂的计算和求解过程。
在数学中,对数函数是指数函数的重要补充,它们互为反函数,可以相互转化,应用更加灵活。
log函数的知识点和公式

log函数是一种常见的对数函数,它的知识点包括以下几个方面:
1.定义:log(x)表示以某个底数(base)为基准的对数函数,其中x为函数的自变量,base为函数的底数。
2.符号:在数学中,常用的底数为10,表示为log10();在计算机科学中,常用的底数为2,表示为log2()。
3.性质:log(x)是一个单调递增函数,其定义域为正实数集合(0, +∞),值域为实数集合(-∞, +∞)。
4.运算律:log函数具有以下运算律:(1) log(ab) = log(a) + log(b),其中a和b为正实数;(2) log(a/b) = log(a) - log(b),其中a和b为正实数;(3) log(a^n) = nlog(a),其中a为正实数,n为正整数。
5.应用:log函数在数学、物理学、工程学、计算机科学等领域都有广泛应用,如自然对数的计算、信号处理、图像压缩、网络优化等。
关于log函数的公式,以下是一些常见的log函数公式:
1.自然对数公式:log(a) = ln(a)/ln(e),其中ln(e)表示自然对数的底数,约等于1.4142。
2.对数恒等式:log(a^b) = b/log(a),其中a和b为正实数。
3.对数换底公式:log(a) = log(b)/log(c),其中a、b、c为正实数,且b和c不等于1。
4.对数与指数的关系:log(a^b) = b/log(a),其中a和b为正实数。
5.对数函数的求导:设y = log(x),则y' = 1/(xln(x)),其中x为正实数。
对数函数知识点总结
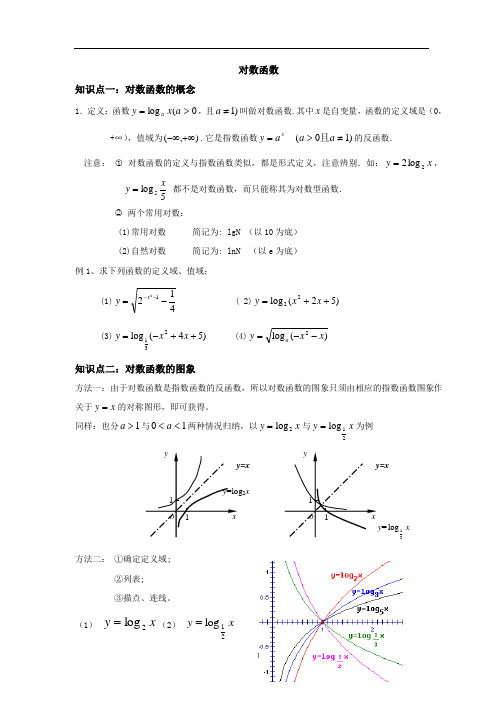
对数函数知识点一:对数函数的概念1.定义:函数0(log >=a x y a ,且)1≠a 叫做对数函数.其中x 是自变量,函数的定义域是(0,+∞),值域为),(+∞-∞.它是指数函数xa y = )10(≠>a a 且的反函数.注意: ○1 对数函数的定义与指数函数类似,都是形式定义,注意辨别.如:x y 2log 2=,5log 5xy = 都不是对数函数,而只能称其为对数型函数. ○2 两个常用对数: (1)常用对数 简记为: lgN (以10为底) (2)自然对数 简记为: lnN (以e 为底)例1、求下列函数的定义域、值域:(1)41212-=--xy ( 2))52(log 22++=x x y (3))54(log 231++-=x x y (4))(log 2x x y a --=知识点二:对数函数的图象方法一:由于对数函数是指数函数的反函数,所以对数函数的图象只须由相应的指数函数图象作关于x y =的对称图形,即可获得。
同样:也分1>a 与10<<a 两种情况归纳,以x y 2log =与x y 21log =为例方法二: ①确定定义域; ②列表; ③描点、连线。
(1)x y 2log =(2) x y 21log =y=x o 11 yxy =log 2x o 11 yxy=xy =x 21log(3)x y 3log =(4) x y 31log =思考:函数x y 2log =与y =3log x 与y对函数的相同性质和不同性质. 相同性质: 不同性质:例2、作出下列对数函数的图象:知识点三:对数函数的性质由对数函数的图象,观察得出对数函数的性质.思考:底数a 是如何影响函数x y a log =的.(学生独立思考,师生共同总结)规律:在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大. 例3、比较下列各组数中两个值的大小:⑴ 5.8log ,4.3log 22; ⑵7.2log ,8.1log 3.03.0; ⑶)1,0(9.5log ,1.5log ≠>a a a a . 变式训练:(1)若3log 3log n m <,求n m 和的关系。
知识讲解_对数函数及其性质_基础

对数函数及其性质【学习目标】1.理解对数函数的概念,体会对数函数是一类很重要的函数模型;2.探索对数函数的单调性与特殊点,掌握对数函数的性质,会进行同底对数和不同底对数大小的比较;3.了解反函数的概念,知道指数函数xy a =与对数函数log a y x =互为反函数()0,1a a >≠.【要点梳理】要点一、对数函数的概念1.函数y=log a x(a>0,a≠1)叫做对数函数.其中x 是自变量,函数的定义域是()0,+∞,值域为R . 2.判断一个函数是对数函数是形如log (0,1)a y x a a =>≠且的形式,即必须满足以下条件: (1)系数为1;(2)底数为大于0且不等于1的常数; (3)对数的真数仅有自变量x . 要点诠释: (1)只有形如y=log a x(a>0,a≠1)的函数才叫做对数函数,像log (1),2log ,log 3a a a y x y x y x =+==+等函数,它们是由对数函数变化得到的,都不是对数函数。
(2)求对数函数的定义域时应注意:①对数函数的真数要求大于零,底数大于零且不等于1;②对含有字母的式子要注意分类讨论。
要点诠释:关于对数式log a N 的符问题,既受a 的制约又受N 的制约,两种因素交织在一起,应用时经常出错.下面介绍一种简单记忆方法,供同学们学习时参考.以1为分界点,当a ,N 同侧时,log a N>0;当a ,N 异侧时,log a N<0. 要点三、底数对对数函数图象的影响 1.底数制约着图象的升降. 如图要点诠释:由于底数的取值范围制约着对数函数图象的升降(即函数的单调性),因此在解与对数函数单调性有关的问题时,必须考虑底数是大于1还是小于1,不要忽略.2.底数变化与图象变化的规律在同一坐标系内,当a>1时,随a 的增大,对数函数的图像愈靠近x 轴;当0<a<1时,对数函数的图象随a 的增大而远离x 轴.(见下图)要点四、反函数 1.反函数的定义设,A B 分别为函数()y f x =的定义域和值域,如果由函数()y f x =所解得的()x y ϕ=也是一个函数(即对任意的一个y B ∈,都有唯一的x A ∈与之对应),那么就称函数()x y ϕ=是函数()y f x =的反函数,记作1()x fy -=,在1()x f y -=中,y 是自变量,x 是y 的函数,习惯上改写成1()y f x -=(,x B y A ∈∈)的形式.函数1()x fy -=(,y B x A ∈∈)与函数1()y f x -=(,x B y A ∈∈)为同一函数,因为自变量的取值范围即定义域都是B ,对应法则都为1f-.由定义可以看出,函数()y f x =的定义域A 正好是它的反函数1()y f x -=的值域;函数()y f x =的值域B 正好是它的反函数1()y fx -=的定义域.要点诠释:并不是每个函数都有反函数,有些函数没有反函数,如2y x =.一般说来,单调函数有反函数. 2.反函数的性质(1)互为反函数的两个函数的图象关于直线y x =对称.(2)若函数()y f x =图象上有一点(),a b ,则(),b a 必在其反函数图象上,反之,若(),b a 在反函数图象上,则(),a b 必在原函数图象上.【典型例题】类型一、对数函数的概念例1.下列函数中,哪些是对数函数? (1)log 0,1)ay a a =>≠;(2)2log 2;y x =+ (3)28log (1)y x =+;(4)log 6(0,1)x y x x =>≠; (5)6log y x =.【答案】(5) 【解析】(1)中真数不是自变量x ,不是对数函数. (2)中对数式后加2,所以不是对数函数.(3)中真数为1x +,不是x ,系数不为1,故不是对数函数. (4)中底数是自变量x ,二非常数,所以不是对数函数.(5)中底数是6,真数为x ,符合对数函数的定义,故是对数函数.【总结升华】已知所给函数中有些形似对数函数,解答本题需根据对数函数的定义寻找满足的条件. 类型二、对数函数的定义域求含有对数函数的复合函数的定义域、值域,其方法与一般函数的定义域、值域的求法类似,但要注意对数函数本身的性质(如定义域、值域及单调性)在解题中的重要作用.例2. 求下列函数的定义域:(1)2log a y x =; (2)log (4-)(01)a y x a a =>≠且.【答案】(1){|0}x x ≠;(2){|4}x x <.【解析】由对数函数的定义知:20x >,40x ->,解出不等式就可求出定义域.(1)因为20x >,即0x ≠,所以函数2log {|0}a y x x x =≠的定义域为;(2)因为40x ->,即4x <,所以函数log (4-){|4}a y x x x =<的定义域为.【总结升华】与对数函数有关的复合函数的定义域:求定义域时,要考虑到真数大于0,底数大于0,且不等于1.若底数和真数中都含有变量,或式子中含有分式、根式等,在解答问题时需要保证各个方面都有意义.一般地,判断类似于log ()a y f x =的定义域时,应首先保证()0f x >.举一反三:【变式1】求函数y =.【答案】(1,23) (23,2] 【解析】因为121210log (1)0log (1)1x x x ⎧⎪->⎪⎪-≥⎨⎪⎪-≠⎪⎩, 所以101132x x x ⎧⎪>⎪<-≤⎨⎪⎪≠⎩,所以函数的定义域为(1,23) (23,2].类型三、对数函数的单调性及其应用利用函数的单调性可以:①比较大小;②解不等式;③判断单调性;④求单调区间;⑤求值域和最值.要求同学们:一是牢固掌握对数函数的单调性;二是理解和掌握复合函数的单调性规律;三是树立定义域优先的观念.例3. 比较下列各组数中的两个值大小: (1)33log 3.6,log 8.9;(2)0.20.2log 1.9,log 3.5; (3)2log 5与7log 5; (4) 3log 5与6log 4.(5)log 4.2,log 4.8a a (01a a >≠且).【思路点拨】利用函数的单调性比较函数值大小。
对数函数的定义与性质

对数函数的定义与性质对数函数是数学中一种常见的特殊函数,它在很多领域都有着重要的应用。
在本文中,我们将探讨对数函数的定义与一些基本性质。
一、对数函数的定义对数函数是指以某个常数为底数的对数函数。
通常用log表示。
对于任何正数x和正数a(a≠1),对数函数可以用以下公式表示:y = logₐx其中,a表示底数,x表示真数,y表示以a为底x的对数。
二、常见的对数函数1. 自然对数函数:当底数a取自然常数e(e≈2.71828)时,对数函数称为自然对数函数。
自然对数函数的常用记法为ln,即y = lnx。
2. 以10为底的对数函数:当底数a取10时,对数函数称为常用对数函数。
常用对数函数用log表示,即y = log₁₀x。
三、对数函数的性质对数函数具有以下几个基本性质:1. 定义域和值域:对于底数a大于1的对数函数,其定义域为正实数集(0,+∞),值域为实数集。
对于底数a等于1的对数函数,其定义域为正实数集(0,+∞),值域为空集。
2. 单调性:对数函数在定义域内是严格递增函数。
当底数a大于1时,对数函数随着真数的增大而增大;当底数a在0和1之间时,对数函数随着真数的增大而减小。
3. 对数的运算性质:(1)对数乘法公式:logₐ(x·y) = logₐx + logₐy。
即对数函数中两个数的积等于对数函数中各自对应数的对数之和。
(2)对数除法公式:logₐ(x/y) = logₐx - logₐy。
即对数函数中两个数的商等于对数函数中各自对应数的对数之差。
(3)对数的幂运算公式:logₐ(b^x) = x·logₐb。
即对数函数中一个数的指数幂等于对数函数中该数对应底数的对数乘以指数。
4. 特殊值:(1)对于底数a大于1的对数函数,当真数x等于1时,对数函数的值为0,即logₐ1 = 0。
(2)对于底数a大于1的对数函数,当真数x等于底数a时,对数函数的值为1,即logₐa = 1。
