考研数学两个重要极限64页PPT
合集下载
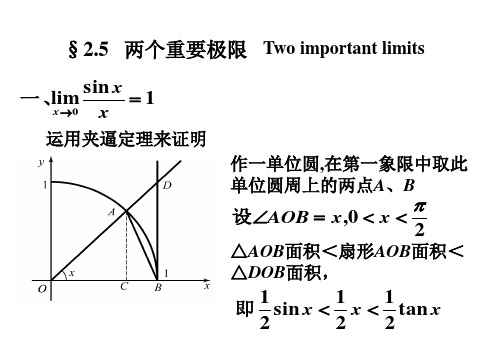
2.5两个重要极限
例5 求 lim e x 1 . x0 x
解 令u ex 1,则x ln(1 u),当x 0时, u 0, 有
ex 1
u
1
lim
lim
lim
1
x0 x
u0 ln(1 u) u0 1 ln(1 u)
u
练习
7.lim n
1+
1 n
n1
1
8.lim 1 2 x x x0
9.lim x
1 2
练习
1.lim tan x x0 x
1 cos x
2.lim x0
x2
x sin 2x 3.lim
x0 x sin 2 x
sin5( x a ) 4.lim
xa x a
5.lim x0
1 x
sin
x+x
sin
1 x
6.lim x
1 x
sin
x+x
sin
1 x
二 、lim(1 1 )x e
2
22
当0 x ,有 cos x sin x 1
2
x
由sin x,cos x的奇偶性知
当0 x ,有 cos x sin x 1
2
x
由夹逼定理得 lim sin x 1 x0 x
我们不难证得: lim x 1
x0 sin x
例1 求 lim sinax (a为 非 零 常 数)
x
x2
x2
例3 求 lim(1 1 )3x .
解
x
lim(1
x
x 1 )3x x
lxim(1
1 x
)
x
3
lxim(1
1-6 两个重要极限

n n2 1 n2 2
n2 n
2.单调有界准则
如果数列 xn满足条件 x1 x2 xn xn1 , 单调增加 x1 x2 xn xn1 , 单调减少
单调数列
几何解释:
x1 x2 x3xn xn1 A M
x
二、两个重要极限
证:
当
x(0,
π 2
)
时,
△AOB 的面积< 圆扇形AOB的面积
•
7、最具挑战性的挑战莫过于提升自我 。。20 20年12 月上午 12时31 分20.1 2.1000: 31Dece mber 10, 2020
•
8、业余生活要有意义,不要越轨。20 20年12 月10日 星期四 12时31 分35秒 00:31:3 510 December 2020
•
9、一个人即使已登上顶峰,也仍要自 强不息 。上午 12时31 分35秒 上午12 时31分 00:31:3 520.12. 10
x0 x
(2) lim sin 5x x0 sin 8x
(4) lim
x0
1
cos x2
x
arcsin x
(5) lim
x0
x
(3) lim tan x x0 x
(6) lim sin x x x
说明:1. 以下结论也可直接作为公式使用
lim tan u 1 u0 u lim arcsin u 1 u0 u
• 10、你要做多大的事情,就该承受多大的压力。12/10/
2020 12:31:35 AM00:31:352020/12/10
• 11、自己要先看得起自己,别人才会看得起你。12/10/
谢 谢 大 家 2020 12:31 AM12/10/2020 12:31 AM20.12.1020.12.10
24两个重要极限精品PPT课件

lim
(x) 0 (x)
1
(0) 0
(2)
lim ( 1 1 ) ( x) e
( x)
(x)
(1 )
1
或 lim (1 ( x))( x) e ( x)0
lim ( 1 1 ) (x) e1
( x)
(x)
提问与解答环节
Questions And Answers
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
u
1 (x)
k
1
例7:求lim(1 3 )x
x
x
1
e . 解:原式
lim(1 Hale Waihona Puke 3)x 3
3
[lim(1
3
)
x 3
]3
3
x
x
x
x
1
例8 : 求 lim 1 2x x x0
解:
原式 lim
1 (2x)
(
1 2x
)(
2
)
x0
e . [lim
1 2x
] (
1 2x
)
-2
2
x0
例9:求 lim(1 1 )x2
0
解:
原式
lim sin 5x x0 5x
5 2
5 sin 5x lim
2 x0 5x
5 2
例2.
求
tan x lim .
x0 x
(0) 0
解: 原式 lim sin x 1 x0 x cos x
lim sin x lim 1 x0 x x0 cos x
1
(x) 0 (x)
1
(0) 0
(2)
lim ( 1 1 ) ( x) e
( x)
(x)
(1 )
1
或 lim (1 ( x))( x) e ( x)0
lim ( 1 1 ) (x) e1
( x)
(x)
提问与解答环节
Questions And Answers
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
u
1 (x)
k
1
例7:求lim(1 3 )x
x
x
1
e . 解:原式
lim(1 Hale Waihona Puke 3)x 3
3
[lim(1
3
)
x 3
]3
3
x
x
x
x
1
例8 : 求 lim 1 2x x x0
解:
原式 lim
1 (2x)
(
1 2x
)(
2
)
x0
e . [lim
1 2x
] (
1 2x
)
-2
2
x0
例9:求 lim(1 1 )x2
0
解:
原式
lim sin 5x x0 5x
5 2
5 sin 5x lim
2 x0 5x
5 2
例2.
求
tan x lim .
x0 x
(0) 0
解: 原式 lim sin x 1 x0 x cos x
lim sin x lim 1 x0 x x0 cos x
1
考研高数总复习函数的极限(讲义)PPT课件

无穷小是函数极限的必要条件,即如果函数在某点的极限存在,那么函数在该点的值必定是无穷小。
无穷小与函数极限的关系是相互依存的,无穷小是函数极限的一种表现形式,而函数极限又是无穷小的 一种表现形式。
无穷小在求极限中的应用
利用无穷小的性质,可以将复杂的函数极限转化为简单的无穷小量,从而 简化计算过程。
在求函数极限时,可以利用等价无穷小替换,将复杂的函数表达式替换为 简单的无穷小量,从而得到更易处理的极限表达式。
利用极限的四则运算法则,消去零因子,化 简函数形式,再求极限。
利用两个重要极限求解
利用重要极限$lim_{x to 0} frac{sin x}{x} = 1$求解:当函数 形式为$frac{sin x}{x}$时,可以利用此重要极限求解。
利用重要极限$lim_{x to infty} frac{1}{x} = 0$求解:当函数 形式为$frac{1}{x}$时,可以利用此重要极限求解。
考研高数总复习函数的极限(讲义 )ppt课件
contents
目录
• 函数极限的基本概念 • 函数极限的求解方法 • 函数极限的应用 • 函数极限的深入理解 • 总结与展望
01 函数极限的基本概念
函数极限的定义
1 2
函数极限的定义
当自变量趋近某一特定值时,函数值的变化趋势。
函数极限的表示方法
lim f(x) = A,表示当x趋近于某个值时,f(x)趋 近于A。
THANKS FOR WATCHING
感谢您的观看
在物理学中,函数极限被用来描述物体运动的速度、加速度等概念;在 工程中,函数极限被用来描述信号的变化趋势;在经济中,函数极限被
用来描述市场的变化趋势。
通过对函数极限的学习,我们可以更好地理解和应用这些概念,为未来 的学习和工作打下坚实的基础。
无穷小与函数极限的关系是相互依存的,无穷小是函数极限的一种表现形式,而函数极限又是无穷小的 一种表现形式。
无穷小在求极限中的应用
利用无穷小的性质,可以将复杂的函数极限转化为简单的无穷小量,从而 简化计算过程。
在求函数极限时,可以利用等价无穷小替换,将复杂的函数表达式替换为 简单的无穷小量,从而得到更易处理的极限表达式。
利用极限的四则运算法则,消去零因子,化 简函数形式,再求极限。
利用两个重要极限求解
利用重要极限$lim_{x to 0} frac{sin x}{x} = 1$求解:当函数 形式为$frac{sin x}{x}$时,可以利用此重要极限求解。
利用重要极限$lim_{x to infty} frac{1}{x} = 0$求解:当函数 形式为$frac{1}{x}$时,可以利用此重要极限求解。
考研高数总复习函数的极限(讲义 )ppt课件
contents
目录
• 函数极限的基本概念 • 函数极限的求解方法 • 函数极限的应用 • 函数极限的深入理解 • 总结与展望
01 函数极限的基本概念
函数极限的定义
1 2
函数极限的定义
当自变量趋近某一特定值时,函数值的变化趋势。
函数极限的表示方法
lim f(x) = A,表示当x趋近于某个值时,f(x)趋 近于A。
THANKS FOR WATCHING
感谢您的观看
在物理学中,函数极限被用来描述物体运动的速度、加速度等概念;在 工程中,函数极限被用来描述信号的变化趋势;在经济中,函数极限被
用来描述市场的变化趋势。
通过对函数极限的学习,我们可以更好地理解和应用这些概念,为未来 的学习和工作打下坚实的基础。
极限存在准则与两个重要极限资料

1
(1
1 )(1
2 )(1
n1 )
2! n
n! n n
n
xn
11
1 2!
1 n!
11
1 2
1 2n1
3
1 2n1
3,
{xn}是有界的; 单调上升有上界必有极限
lim n
xn
存在.
记为 lim(1 1)n e
n
n
(e 2.718281828459045) 无理数
12 23
n1 n
2 1 2, n
{ xn}是有上界的;
因此, 利用单调有界数列必收敛准则即得结论.
15
2.5 极限存在准则 两个重要极限
例 证明数列 xn 3 3 3
(n重根式)的极限存在.
证 (1) 显然 xn1 xn ,
{xn}是单调增加的; (2) x1 3 3, 假定 xk 3,
1.
8
2.5 极限存在准则 两个重要极限
0
例 lim x 0 lim
x
lim sin x 1 lim x 1
x0 x
x0 sin x
cos x 1.
x0 tan x x0 sin x
例
sin3 3 lim x0 3x
x
0
0
1 3
lxim0
sin
3
3
x
x
3
n
an
bn
cn ,求 lim n
xn .
解 法一 由于 a xn a n 3
1
以及 lima a, lim a n 3 lim a 3n a 1
第1-6讲 极限4(两个重要极限)
2
x
=
1
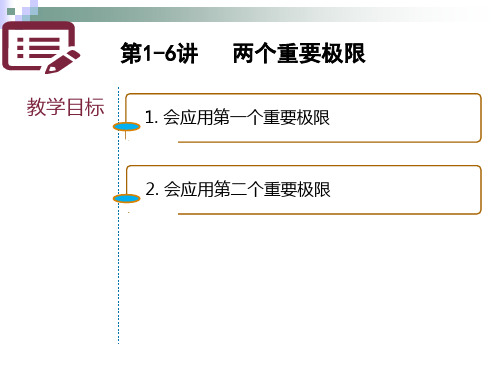
sin lim(
2 )2
2 x→0 x
2
=1 2
练一练
1. lim sin x = _____ ; x→0 x
1
3. lim x sin = ____ ;
x→0
x
2. lim sin x = _____ ; x→ x
1
4. lim x sin = ____ .
x→
x
第一个 重要极限
注 (1) 1 型
例1 求lim tan x x→0 x
解 lim tan x = lim( sin x 1 )
x→0 x
x→0 x cos x
= lim sin x lim 1 x→0 x x→0 cos x
= 11 = 1
例2 求 lim sin 2x x→0 x
解
sin 2x lim
= lim 2sin 2x = 2lim sin 2x
x→
x
lim 2 x
x→ x = e2
例6 求 lim(1 − 2 )3x
x→
x
解
= e lim(1 − 2 )3x
x→
x
lim (− 2 )3x x→ x
= e−6
1
例7 求 lim(1 + 2 x) x x→0
解
1
lim(1+2x) x
lim 2x 1
= e x→0
x
= e2
x→0
内容小结
两个重要极限
(2) lim (1+ 1 )Δ =e
x →(.)
Δ
∆即可表示自变量x, 也可表示x的函数.
(只要lim 1 = 0) x→(.)
1.4两个重要极限
x
于是
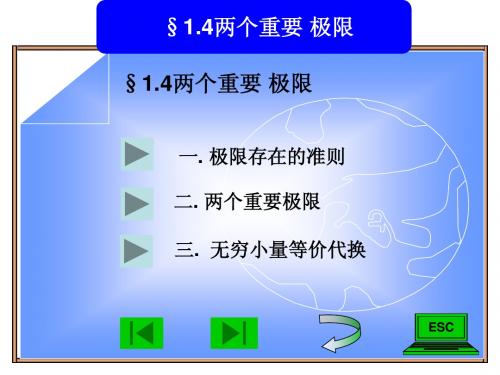
3 x lim (1 + ) = lim(1 + t ) t = lim[(1 + t ) t ]3= [lim(1 + t ) t ]3 = e 3 x →∞ t →0 t →0 t →0 x x 3 x 3 3 3 或 lim(1 + ) = [lim(1 + ) ] = e3 x →∞ x →∞ x x
π
ESC
一. 极限的四则运算法则 二.第一个重要 极限 第一个重要
x 1 2 cos 另一方面, x = 1 − 2 sin > 1 − x ,于是有 另一方面, 2 2 1 2 sin x 1 − x < cos x < <1. 2 x
2
1 2 由准则Ⅰ 因为 lim (1 − x ) = 1 ,由准则Ⅰ可得 x →0 2 sin x =1. lim x →0 x
n →∞
ESC
二.第一个重要 极限 第一个重要
sin x =1 1. lim x→0 x
(1.4.1)
证 因为 sin( − x) = − sin x = sin x ,所以 −x −x x 由正值趋于零的情形. 只讨论 x 由正值趋于零的情形. 作单位园O 作单位园O, 设圆心角 ∠AOB = x ,延长 OB交过 A点的切线于于 D , 面积< 则 ∆AOB 面积<扇形 AOB 面积< 面积. 面积< ∆AOD 面积.即 ESC
ESC
一. 极限的四则运算法则 二.第二个重要 极限 第二个重要
lim x 2. x→∞(1+ 1)x = e
表1
(1.4.7)
1 x x → ∞ 时 (1 + ) 之值的变化情况 x
两个重要极限

x0
x0 tan 2x 2
(3) lim
x sin
x
1 sin x lim x
x0 x sin x x0 1 sin x
11 0 11
x
高等数学 advanced math 两个重要极限 (Two important limits)
例4 求 lim sin(x2 9)
x3 x 3
解:lim sin(x2 9)
按前面所述的资金现值计算方法知
该股票筹得资金的现值为P(1-F),等于各年股利按普通 股成本K贴现的现值和,即
P(1
F)
D 1 K
D(1 G) (1 K )2
D(1 G)2 (1 K )3
高等数学 advanced math 两个重要极限 (Two important limits)
试利用数学方法计算股票筹资成本K
案例【圆的面积】
为了求圆面积,可以先作圆 的内接正四边形,其面积记
作A4 ;又作圆的内接正六边 形,其面积记作A6;如此循
环下去,当圆的内接正多边 形的边数不断增加时,其相 应的面积与圆的面积就越来
越接近,当边数n无限增大时 播放
,圆的内接正多边形的面积 就是圆的面积
高等数学 advanced math 两个重要极限 (Two important limits)
x3 x 3
lim
x3
s
in(x2 x2 9
9)
(
x
3)
sin(x2 9)
lim x3
x2 9
lim (x 3) x3
6
高等数学 advanced math 两个重要极限 (Two important limits)
