两个重要极限
两个重要极限的证明

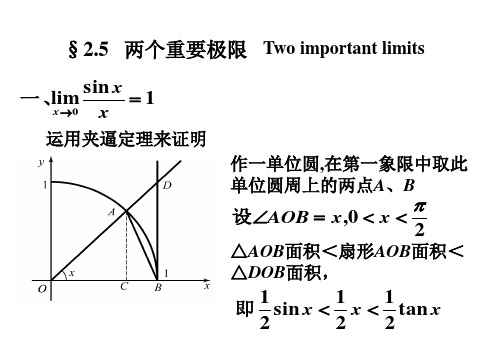
两个重要的极限1.证明:0sin lim 1x x x→= 证明:如图(a )作单位圆。
当0<x<2π时,显然有ΔOAD 面积<扇形OAD 面积<ΔOAB 面积。
即111sin 222x x <<tgx ,sinx<x<tgx 。
除以sinx ,得到11sin cos x x x<< 或sin 1cos x x x >>。
(1) 由偶函数性质,上式对02x π-<<时也成立。
故(1)式对一切满足不等式0||2x π<<的x 都成立。
由0lim x →cosx=1及函数极限的迫敛性定理立刻可得0lim x →sin 1x x=。
函数f(x)=sin x x的图象如图(b )所示。
2.证明:1lim(1)n n n →∞+存在。
证明:先建立一个不等式,设b>a>0,于是对任一自然数n 有 11(1)n n n b a n b b a++-<+-或11(1)()n n n b a n b b a ++-<+-,整理后得不等式1[(1)]n n a b n a nb +>+-。
(1) 令a=1+11n +,b=1+1n ,将它们代入(1)。
由于11(1)(1)(1)(1)11n a nb n n n n +-=++-+=+, 故有111(1)(1)1n n n n ++>++,这就是说1{(1)}n n+为递增数列。
再令a=1,b=1+12n代入(1)。
由于11(1)(1)(1)22n a nb n n n +-=+-+=,故有111(1)22n n >+,12(1)2n n >+。
不等式两端平方后有214(1)2n n >+,它对一切自然数n 成立。
联系数列的单调性,由此又推得数列1{(1)}n n +是有界的。
于是由单调有界定理知道极限1lim(1)n n n→∞+是存在的。
2.5两个重要极限
例5 求 lim e x 1 . x0 x
解 令u ex 1,则x ln(1 u),当x 0时, u 0, 有
ex 1
u
1
lim
lim
lim
1
x0 x
u0 ln(1 u) u0 1 ln(1 u)
u
练习
7.lim n
1+
1 n
n1
1
8.lim 1 2 x x x0
9.lim x
1 2
练习
1.lim tan x x0 x
1 cos x
2.lim x0
x2
x sin 2x 3.lim
x0 x sin 2 x
sin5( x a ) 4.lim
xa x a
5.lim x0
1 x
sin
x+x
sin
1 x
6.lim x
1 x
sin
x+x
sin
1 x
二 、lim(1 1 )x e
2
22
当0 x ,有 cos x sin x 1
2
x
由sin x,cos x的奇偶性知
当0 x ,有 cos x sin x 1
2
x
由夹逼定理得 lim sin x 1 x0 x
我们不难证得: lim x 1
x0 sin x
例1 求 lim sinax (a为 非 零 常 数)
x
x2
x2
例3 求 lim(1 1 )3x .
解
x
lim(1
x
x 1 )3x x
lxim(1
1 x
)
x
3
lxim(1
两个重要极限

两边夹定理可知, lim | sin x | 0 , 从而 lim sin x 0.
图 2.13 例6.2 证明 lim cos x 1.
x 0
2 x x x 证 当 x 在 0 附近,即当 | x | 时, 由半角公式知 0 1 cos x 2 sin 2 2( )2 . 2 2 2 2
36
1 n 重要极限二: lim (1 ) e. n n 1 n 我们可以利用单调有界数列必有极限来证明 lim (1 ) 的存在性。 n n 1 n 证 设 f (n) (1 ) . 先证 f (n) 单调增加。事实上,由二项式展开有 n 1 n n 1 n( n 1) 1 n( n 1)(n 2) 1 f ( n) (1 ) 1 2 3 n 1! n 2! n 3! n n( n 1)(n 2)...(n n 1) 1 ﹢ n n! n 1 1 1 1 1 2 1 (1 ) (1 )(1 ) 1! 2! n 3! n n 1 1 2 n 1 (1 )(1 )(1 ). 同理有 n! n n n 1 n 1 1 1 1 1 2 1 f (n 1) (1 ) 1 (1 ) (1 )(1 ) n 1 1! 2! n 1 3! n 1 n 1 1 1 2 n 1 (1 )(1 )(1 ) n! n 1 n 1 n 1
n
例 6.13
求 lim
sin x . sin x sin(x) lim 2 2 x x ( x x)(x)
lim 例 6.14
2 2 sin( x) lim 1 . x x x x 2 2
例 6.8
两个重要极限

高等数学 两个重要极限 (Two important limits)
advanced mathematics
sin x 1. lim =1 x0 x
1 0.75 0.5 0.25
f ( x)
5
s i nx x
10 15
-15
-10
-5
o
-0.25 -0.5
高等数学 两个重要极限 (Two important limits)
例10
解
求极限
2x 3 x lim( ) . x 2 x 1
2x 3 x 2 l i m( ) l i m(1 )x x 2 x 1 x 2x 1
2 x 1 2 x 2 2 x 1
2 lim(1 ) x 2x 1
2 lim(1 ) x 2x 1
2 x 1 1 2 2
e
2x x 2 x 1 lim
e.
2 (1 ) 2x 1 lim 1 x 2 2 (1 ) 2x 1
2 x 1 2
e.
高等数学
advanced mathematics
3 1 另解: 2x 3 x 2x )x l i m( ) l i m( x 2 x 1 x 1 1 2x 3 x 3 x l i m(1 ) (1 ) x 2x 2 x lim x 1 x 1 x l i m(1 ) (1 ) x 2x 2x
4x 1 5 x
解
4 2 (2)求 lim(1 ) x 3x 3x 3x 4 2 4 4 2 e2 lim(1 ) lim(1 ) x x 3x 3x
e .3 x
第五节 两个重要极限

类型5: 幂指式的极限,先利用幂的有关运 算把式子变换成含有标准式,再用公式
求.
练习
3 x 2x 求 lim( ) . x 2 x
极限的常用计算方法
1.代入法
x 4 3x 8 lim 2 x 2 x x 3
0 2.多项式的 型,分子分母同时分解, 0 约掉同为无穷小的公因
第5节 两个重要极限
sin x 1. lim 1. x 0 x
sin x 观察函数 当 x 0时的变化趋势 . x
y sin x x
sin x 重要极限lim 1的使用要求: x 0 x
1、式中含有三角函数的分式; 2、分母与正玄函数的角变量相同; 3、角变量趋近于0. sin x 重要极限lim 1的推广(类型四) : x 0 x 公式 要求
x
1 2
例5
计算li m 1 x .
x 0 2 x
解 方法1 令 u = -x,因为 x 0 时 u 0,
( 所以 l i m 1 x l i m 1 u)
x 0 2 x u0
2 u
lim
u0
1
(1 u)
1 . 2 2 1 e u
x 0
2 5 x
答案: e
6
有时,所给函数在自变量的某个趋向 下,底的极限为1,指数的极限为无穷,
人们称这类极限为1 ”型未定式. “
1 重要极限lim 1 e的使用要求: x x
(1)幂指式的底是由1与一个接近于0的变量和 (2)底中的变量与指数间互为倒数.
sin x x 0 lim lim 1 ( 型) x 0 x 0 sin x x 0 sin 推广: lim lim 1(上下一致) 0 0 sin
两个重要的极限

例7 求 解 令 arcsin x t ,则 且 x 0时,t 0
arcsin x lim x 0 x
x sin t
arcsin x t lim lim 1 x 0 t 0 sin t x
(2)
定义
1 x lim (1 ) e x x 1 n lim (1 ) e n n
arccot x 3、 lim __________. x 0 x
4、 lim x cot 3 x __________.
x 0
sin x 5、 lim __________. x 2 x
6、 lim (1 x ) _________.
x 0
1 x
1 x 2x 7、 lim ( ) _________. x x 1 x 8、 lim (1 ) _________. x x
xn 是单调递增的 ;
1 1 1 1 xn 1 1 1 1 n 1 2! n! 2 2 1 3 n 1 3, xn 是有界的; 2 1 n lim x n 存在. 记为 lim (1 ) e (e 2.71828) n n n2例5 求 解Fra biblioteklim
x 0
tan x sin x lim x 0 x3
tan x sin x tan x(1 cos x) 1 sin x 1 cos x lim lim ( ) 3 3 2 x 0 x 0 x x cos x x x
1 sin x 1 cos x 1 (lim )( lim )( lim ) 2 x 0 cos x x 0 x 0 x 2 x
sin口 lim (口代表同样的变量 1 口0 口
两个重要极限公式

两个重要极限公式
两个重要极限公式:极限是微积分中的基础概念,它指的是变量在一定的变化过程中,从总的来说逐渐稳定的这样一种变化趋势以及所趋向的值(极限值)。
1、第一个重要极限的公式:
lim sinx / x = 1 (x->0)当x→0时,sin / x的极限等于1。
特别注意的是x→∞时,1 / x是无穷小,根据无穷小的性质得到的极限是0。
2、第二个重要极限的公式:
lim (1+1/x) ^x = e(x→∞)当x →∞时,(1+1/x)^x的极限等于e;或当x →0 时,(1+x)^(1/x)的极限等于e。
极限的求法
连续初等函数,在定义域范围内求极限,可以将该点直接代入得极限值,因为连续函数的极限值就等于在该点的函数值。
利用恒等变形消去零因子(针对于0/0型)
利用无穷大与无穷小的关系求极限。
利用无穷小的性质求极限。
利用等价无穷小替换求极限,可以将原式化简计算。
利用两个极限存在准则,求极限,有的题目也可以考虑用放大缩小,再用夹逼定理的方法求极限。
两个重要极限-重要极限

两个重要极限-重要极限
1、无穷小
如果f(x)在x→x0时的极限为0,则称f(x)为x→x0时的无穷小。
在x趋于x0的同一变化过程中,f(x)有极限的充要条件为f(x)=A+α(α为无穷小)。
2、无穷大
如果f(x)是无穷小,则1/f(x)为无穷大,反之亦然。
3、极限运算法则
(1)有限个无穷小的和(或乘积)也是无穷小。
(2)有界函数和无穷小的乘积是无穷小。
(3)两个函数的和(或乘积)的极限等于两个函数的极限的和(或乘积),当然,比值也如此,只是需要额外要求分母上的极限不能为0。
(3‘)函数的n次幂的极限等于函数的极限的n次幂(n为正整数)。
(4)如果函数A(x)≥B(x),则A的极限也大于等于B的极限。
4、极限存在准则
(1)设数列X处于两个数列之间,即Yn≤Xn≤Zn,如果数列Y和Z 都有极限为a,则X也有极限为a。
(1’)设函数f(x),在x0的某去心邻域内有g(x)≤f(x)≤h(x),如果g和h都有极限为A,则f(x)也有极限为A。
上述两条准则统称为夹逼准则。
(2)单调有界数列必有极限。
(3)柯西极限存在准则。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
=
=e
例题4求
解: =
= =
=
例题5求
解: = = = =
练习:求
教学步骤及教学内容
时间分配
四,课堂练习
五,课堂小结
1.第一个重要极限:
2.第二个重要极限:
作业布置
课后反思
准则1如果数列 及 满足下列条件:
(1) ,(2)
那么数列 的极限存在,且 。
准则2单调有界数列必有极限
例 求
解:
而
所以原式极限为1。
二.新课讲解
1.第一个重要极限:
教学步骤及教学内容
时间分配
注:(1)这个重要极限主要解决含有三角函数的 型的极限。
(2)公式形象的记为: ()表示同一个代数式
2.第二个重要极限:
授课课题
两个重要极限
教学
目标和要求
掌握两个极限的存在准则,并会利用它们求极限,
掌握利用两个重要极限求极限的方法
教学
重点和难点
利用两个重要极限求极限
特别是利用第二重要极限求极限的方法
教学方法
案例分析法
教学手段
板书
授课时间
第3周
课时累计
1-2
教 学 过 程
教学步骤及教学内容
时间分配
一,新课引入
1.下面我们来介绍极限存在的两个准则:
也可以写为:
注:(1)公式形象记忆为:
(2)此极限主要解决 型幂指函数的极限。
三.例题讲解
例1(1)求
解:原式= = =1
(2)求
解:原式= = =练习来自求例2(1)求 (2)
解:(1)原式
(2)令arcsinx=t,则x=sint,当 时, 。
所以 = =1
练习:
教学步骤及教学内容
时间分配
例题3求
