画三视图 注意三点
三视图的重点掌握

三视图课堂重点
第一点:画三视图时,三个视图都要放在正确的位置,并且注意主视图与俯视图的长对正,主视图
与左视图的高对齐,左视图与俯视图的宽相
等。
第二点:本节有三组练习题,它们分别考察
(1)画三视图(注意画图时要遵循的原则,三
点:主视图与俯视图的长对正,主视图与左
视图的高对齐,左视图与俯视图的宽相等,
除此之外,还要注意画图时虚线与实线的选
择)。
(2)由三视图想立体形状
(3)由三视图想立体形状并画出展开图(怎
么画出展开图,就是把每一个面都拆出来,
所有的面由上中下的顺序来摆放好)
第三点:三组练习的训练让同学们自己去实践画图,再给出一个正确的答案让同学进一步的掌
握怎么画一个立体几何图形的三视图和怎
么由三视图想立体形状并画出它的展开图。
画三视图 注意三点
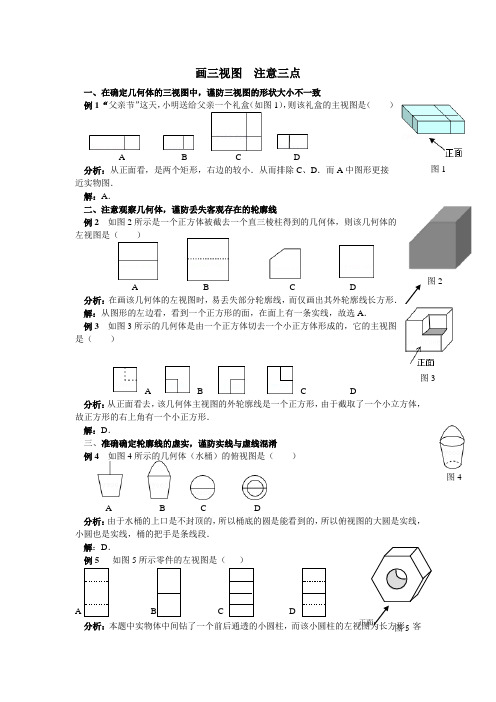
图4画三视图注意三点一、在确定几何体的三视图中,谨防三视图的形状大小不一致例1 “父亲节”这天,小明送给父亲一个礼盒(如图1),则该礼盒的主视图是()A B C D分析:从正面看,是两个矩形,右边的较小.从而排除C、D.而A中图形更接近实物图.解:A.二、注意观察几何体,谨防丢失客观存在的轮廓线例2 如图2所示是一个正方体被截去一个直三棱柱得到的几何体,则该几何体的左视图是()A B C D分析:在画该几何体的左视图时,易丢失部分轮廓线,而仅画出其外轮廓线长方形.解:从图形的左边看,看到一个正方形的面,在面上有一条实线,故选A.例3 如图3所示的几何体是由一个正方体切去一个小正方体形成的,它的主视图是()A B C D分析:从正面看去,该几何体主视图的外轮廓线是一个正方形,由于截取了一个小立方体,故正方形的右上角有一个小正方形.解:D.三、准确确定轮廓线的虚实,谨防实线与虚线混淆例4 如图4所示的几何体(水桶)的俯视图是()A B C D分析:由于水桶的上口是不封顶的,所以桶底的圆是能看到的,所以俯视图的大圆是实线,小圆也是实线,桶的把手是条线段.解:D.例5 如图5所示零件的左视图是()B C D分析:本题中实物体中间钻了一个前后通透的小圆柱,而该小圆柱的左视图为长方形,客图1图2图3图5正面观存在,但看不到,故用虚线. 在画视图时,..........................首先观察物体,画出视图的外轮廓线,然后将视图补充完整,看得见部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线........................................解:D.。
基本形体的三视图面上的点和线

曲面立体三视图分析
曲面立体的投影特性
曲面立体在三视图中的投影具有积聚性、类似性和真实性等特性。
曲面立体表面上的点和线
通过分析曲面立体表面上的点和线的投影,可以确定它们在空间中 的位置。
截交线和相贯线的分析
截交线和相贯线是曲面立体三视图中的重要内容,通过分析它们的 形状和位置关系,可以深入了解形体的结构。
三视图基本概念
01
主视图:从正面方向观察 物体所得到的视图,反映 物体的主要形状和特征。
02
03
俯视图:从上面方向观察 物体所得到的视图,反映 物体的顶部形状和特征。
左视图:从左面方向观察 物体所得到的视图,反映 物体的左侧形状和特征。
04
三个视图之间的投影关 系:长对正、高平齐、 宽相等。
02
感观看
正投影面(V面)
01
反映形体的上下、左右位置关系;
水平投影面(H面)
02
反映形体的前后、左右位置关系;
侧投影面(W面)
03
反映形体的上下、前后位置关系。
线的可见性判断
重影点中,离观察者远的点不可见,应用虚线表示;
当空间两直线段在某一投影面上的投影重合时,需判断其可见性。若两线段在同一方向上的投影不重 合,则重影点中离观察者远的点不可见;若两线段在同一方向上的投影重合,则应根据其他投影或空 间几何条件来判断可见性。
确定主视图方向
选择最能反映形体特征的方向作为主视图方向。
绘制三视图
根据形体在主视图、俯视图和左视图上的投影, 分别绘制出三个视图。
检查视图正确性
检查三个视图是否满足“长对正、高平齐、宽相 等”的投影规律,确保视图正确。
实例二:曲面立体三视图绘制
机械制图课程--三视图的画法

正视图
圆柱,圆锥三视图
侧视图
正视图
侧视图
·
俯视图
俯视图
老师提示:画锥体的三视图要注意!
正视图
球的三视图
侧视图
俯视图
老师提示:画三视图要认真准确
何 体 的
画 出 下
练 习
三列一
视基:
图本
几
长方体
圆台
六棱锥
正视图
侧视图
长方体
俯视图
长方体
正视图
侧视图
圆台
俯视图
圆台
六棱锥的三视图
六棱锥 小结:若相邻的两平面的相 交,表面的交线是它们的分 界线,在三视图中,分界线 和可见轮廓线都用实线画出。
B. 21m2 D. 34m2
例7. 图10是一块带有圆形空洞和方形 空洞的小木板,则下列物体中既可以堵 住圆形空洞,又可以堵住方形空洞的是 ()
2 3
5
2
4
D A
B
C
主讲:刘玲珑
从上面看到的图
从左边看到的图
三视图:我们从不同的 方向观察同一物体时, 可能看到不同的图形。 其中,把从正面看到的 图叫做正视图,从左面 看到的图叫做侧视图, 从上面看到的图叫做俯 视图。三者统称三视图。
从正面看到的图
正视图
侧视图
俯视图
俯视图方向
侧视图方向
高平齐,
正视图
长
俯视图
长对正,
高
侧视图
正视图方向
宽 宽相等.
画 一 个 物 体 的 三视图时,正视图 ,侧视图,俯视图
所画的位置如图 所示,且要符合如 下原则:
俯视图方向
三视图的作图步骤
侧视图方向
三视图的绘制规则与技巧

三视图的绘制规则与技巧三视图是制图中最常用的一种图形表达方式,广泛应用于建筑设计、工程制图以及产品设计等领域。
它通过正面、俯视和侧面三个视角来展示物体的外观和结构,为观察者提供了全方位的信息。
然而,要绘制出清晰准确的三视图并不容易,需要遵循一定的规则和技巧。
首先,三视图的绘制需要准确的测量数据。
在开始绘制前,我们需要使用测量工具(如尺子、量角器等)对物体的各个尺寸进行测量,并记录下来。
这些尺寸包括长度、宽度、高度等,它们是绘制三视图的基础数据。
其次,三视图的绘制需要遵循一定的比例尺。
比例尺是指图纸上物体尺寸与实际尺寸之间的比例关系。
通常,我们使用1:1、1:10或1:100等比例尺来绘制三视图。
选择合适的比例尺可以使绘制的图形更加清晰易懂。
在绘制三视图时,我们需要注意视角的选择。
正面视图是指从物体的正面观察,俯视图是指从物体的上方观察,侧面视图是指从物体的侧面观察。
这三个视角需要同时绘制,以展示物体的各个方面。
在选择视角时,我们要考虑到物体的主要特征和表现形式,选择最能表达物体特点的视角进行绘制。
另外,绘制三视图时需要注意投影的规则。
投影是指将三维物体的形状和尺寸投影到二维平面上。
根据投影的方法不同,可以分为正投影和透视投影两种。
在绘制三视图时,我们通常使用正投影,即将物体的各个面按照垂直于投影平面的方向投影到平面上。
这样可以保持物体各个面的形状和尺寸不变,使观察者能够清晰地看到物体的外观。
此外,绘制三视图还需要注意线条的粗细和颜色的选择。
线条的粗细可以通过调整画笔的压力来实现,粗细不一的线条可以突出物体的主次关系。
而颜色的选择可以根据物体的材质和用途来决定,不同的颜色可以使物体的特点更加突出。
最后,绘制三视图需要耐心和细心。
绘制三视图是一项繁琐的工作,需要耐心地绘制每一条线条、每一个细节。
同时,要细心地检查绘制的结果,确保没有错误和遗漏。
只有经过认真细致的绘制,才能得到准确、清晰的三视图。
总之,三视图的绘制是一项需要技巧和规则的工作。
点的三面投影规律
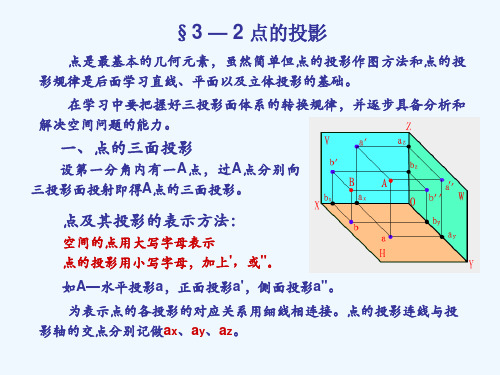
点的位置有如下说法:
1.空间的点,如图中的A点 2.投影面上的点,即位于V、H 或W投影面上,如B点 投影面上的点的三个坐标中有一个为0
点在V面上 —— Y坐标为0 在H面上 —— Z坐标为0 在W面上 —— X坐标为0
当点位于H面、W面以及Y轴上时, 要注意分析点的各个投影的位置。
三、点的三面投影规律
五、重影点及其可见性
判别图中各点的可见性 1.从图中可看出A、B在H面上的投影重合,为水平重影点。由于A
点的Z坐标比B点的Z坐标大故B点的水平投影不可见。 2.C、D两点在V面重影,因D点的Y坐标小故D点的正面投影不可见。
例:已知点A(40、15、30)求作A点的直观图。 由于直观图具有一定的空间效果,因此在分析问题时常需要绘制 这样的图形 三投影面体系直观图 作图步骤:
点的三面投影规律为:
1.点的正面投影与水平投影的连线垂直于OX轴,即a' a⊥o x 2.点的正面投影与侧面投影的连线垂直于OZ轴,即a'a''⊥o z 3.点的水平投影与侧面投影具有相同的Y坐标,即a ax=a'' az 根据上述规律就可准确作出点的三面投影图。
三、点的三面投影规律
例 1. 已知点 A ( 30 、 15 、 25 )求作 A 点的三面 投影。
作图步骤:
1.分别在X、Y、Z轴上量取 A点的坐标30、15和25, 得ax、ayh、ayw和az点
2.过ax、ayh、ayw和az 点作A点投影的连线 3.各连线的交点即为 所求
三、点的三面投影规律
例2: 已知B(40、30、0)作出B点的三面投影。 问题:根据B点的坐标分析B点的位置。 因B点的坐标(40、30、0)中Z坐标为0,故B点位于H面上。
三视图复原技巧

当物体某部分被其他部分遮挡时,需要在视图中进行相应的处理,如使用虚线表示被遮挡部分的轮廓。
处理遮挡关系
在复原三视图时,应注意细节部分的处理,如倒角、圆角、螺纹等。这些细节部分对于准确表达物体形状至关重要。
注意细节处理
在三视图中,各视图之间的比例关系应保持以确定长方体的宽度。
根据三个视图的信息,可以绘制出长方体的三维图。
主视图通常显示圆柱体的一个端面,呈现为一个圆。通过主视图可以确定圆的直径。
确定主视图
确定俯视图
确定左视图
绘制三维图
俯视图也显示圆柱体的上面,呈现为一个圆。这个圆应该与主视图的圆大小和位置一致。
左视图显示圆柱体的侧面,呈现为一个矩形。矩形的长度应该等于圆的直径,高度等于圆柱体的高度。
主视图
从物体的正面看去的视图,反映物体的主要形状和特征。
俯视图
从物体的上面看去的视图,反映物体的水平投影和上下位置关系。
左视图
从物体的左侧看去的视图,反映物体的左侧形状和左右位置关系。
02
CHAPTER
三视图复原步骤
仔细分析三视图中的每一个视图,理解其表达的空间形状和位置关系。
注意视图中的图线、符号等细节信息,特别是虚线和实线的含义。
根据三个视图的信息,可以绘制出圆柱体的三维图。
确定主视图
主视图通常显示圆锥体的一个侧面,呈现为一个等腰三角形。通过主视图可以确定圆锥体的高度和底面的直径。
确定俯视图
俯视图显示圆锥体的底面,呈现为一个圆。这个圆应该与主视图中三角形的底边大小和位置一致。
确定左视图
左视图也显示圆锥体的一个侧面,呈现为一个直角三角形。直角三角形的直角边应该等于圆的直径,斜边等于圆锥体的母线长。
三视图教学反思 三视图课后反思

三视图教学反思三视图课后反思《三视图》教学反思篇一这周学习的是三视图,主要培养学生的空间想象力。
学生对这部分知识感兴趣,特别是男生反应较快,而有些平时表现较好的女生却有些糊涂。
教学重点是能识别简单几何体的三个视图,会画常见几何体及简单组合几何体的三视图。
现以自己对教材的理解及上课后的感受提出对本节教学的几点建议:1、画三视图时,主视图画在左上方,它反映物体的长和高,左视图画在右上方,与主视图平高,它反映的是物体的宽和高,俯视图画在左下方,与主视图同宽,它反映的是物体的长和宽。
2、在画视图是,看的见部分的轮廓线要画成实线,看不见部分的轮廓线画成虚线;也可以说,被面遮住的棱画成虚线,被棱遮住的棱不画。
3、看到几个面就画几个面,面是由棱组成。
本节课的感受:学生画一些组合体的三视图有困难,特别是由三视图想象出立体图形,对学生提出了更高的要求。
因此,要让学生熟悉一些常见的物体的三视图,如:柱体、锥体、圆台、常见的组合体(特别是积木)。
逐步培养学生的空间想象力。
《三视图》教学反思篇二一、设计的初衷《三视图》在教学内容中,是比较抽象并且难以理解的,然而三视图在工业设计中又是表达与交流设计构思、设计方案的一种常用的工程技术语言。
学生不但要学会识读三视图,而且还要学会绘制简单的三视图,并且在今后的设计实践中,能够运用三视图来表达自己的设计构思,与他人交流设计方案,从而获得全面的评价,优化设计方案。
于是针对此教学内容,如何进行有效的教学;以及在教学中常遇到的一些问题,有哪些可供参考的解决办法,我进行了尝试性教学实践。
1. 课题引入方面:采用问题情景设置的方法:学生喜爱打篮球,而用直尺测算出篮球的表面积是学生平时不会想到或实践过的问题。
这样激起了学生的好奇心和想解决问题的兴趣。
问题提出来后,学生积极思考,想出了许多办法。
而解决这个问题的关键是能否利用墙面与地面相互垂直这一条件。
目的是打开学生空间想象能力。
而空间想象能力是学好三视图,理解三视图以及绘制三视图的必备能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图
4
画三视图
注意三点
房延华
一、在确定几何体的三视图中,谨防三视图的形状大小不一致
例1 “父亲节”这天,小明送给父亲一个礼盒
(如图1),则该礼盒的主视图是( )
A B C D
分析:从正面看,是两个矩形,右边的较小.从而排除C 、D .而A 中图形更接
近实物图.
解:A .
二、注意观察几何体,谨防丢失客观存在的轮廓线
例2 如图2所示是一个正方体被截去一个直三棱柱得到的几何体,则该几何体的左视图是( )
A B C D
分析:在画该几何体的左视图时,易丢失部分轮廓线,而仅画出其外轮廓线长方形. 解:从图形的左边看,看到一个正方形的面,在面上有一条实线,故选A .
例3 如图3所示的几何体是由一个正方体切去一个小正方体形成的,它的主视图是( )
A B C D 分析:从正面看去,该几何体主视图的外轮廓线是一个正方形,由于截取了一个小立方体,故正方形的右上角有一个小正方形.
解:D .
三、准确确定轮廓线的虚实,谨防实线与虚线混淆
例4 如图4所示的几何体(水桶)的俯视图是( )
A B C D
分析:由于水桶的上口是不封顶的,所以桶底的圆是能看到的,所以俯视图的大圆是实线,小圆也是实线,桶的把手是条线段.
解:D .
例5 如图5所示零件的左视图是( )
图1 图2
图3 图5 正面
A B C D
分析:本题中实物体中间钻了一个前后通透的小圆柱,而该小圆柱的左视图为长方形,客
观存在,但看不到,故用虚线. 在画视图时,
....................
......首先观察物体,画出视图的外轮廓线,然后将
视图补充完整,看得见部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线........................................
解:D.。
