运用插值法计算实际利率
插值法怎么估利率计算公式

插值法怎么估利率计算公式插值法是一种常用的数值分析方法,用于在已知数据点之间估计未知数据点的数值。
在金融领域中,利率是一个非常重要的指标,对于投资和贷款都有着重要的影响。
因此,利率的估计和预测对于金融市场的参与者来说至关重要。
在本文中,我们将介绍如何使用插值法来估计利率,并给出相应的计算公式。
首先,让我们简要回顾一下插值法的基本原理。
插值法是一种利用已知数据点来估计未知数据点的数值的方法。
在金融领域中,我们通常会遇到一些已知的利率数据点,比如一年期、两年期、五年期等不同期限的利率。
我们可以使用这些已知的利率数据点来估计其他期限的利率,从而得到一个完整的利率曲线。
在金融市场中,利率曲线通常是非线性的,并且在不同期限上可能有着不同的形状。
因此,我们需要使用一种灵活的插值方法来估计利率曲线上任意期限的利率。
在这里,我们将介绍一种常用的插值方法——样条插值法。
样条插值法是一种利用分段低次多项式来逼近已知数据点的方法。
在利率曲线的估计中,我们可以使用样条插值法来逼近不同期限上的利率数据点,从而得到一个平滑的利率曲线。
具体来说,我们可以将利率曲线分成若干段,并在每一段上使用低次多项式来逼近已知的利率数据点。
通过这种方法,我们可以得到一个连续且光滑的利率曲线,从而可以方便地估计任意期限上的利率。
接下来,让我们来介绍如何使用样条插值法来估计利率曲线。
假设我们已经有了一些已知的利率数据点,比如一年期、两年期、五年期等不同期限的利率。
我们可以先将这些数据点按照期限的大小进行排序,并将它们分成若干段。
然后,在每一段上使用低次多项式来逼近已知的利率数据点,从而得到一个平滑的利率曲线。
在实际计算中,我们可以使用一些常见的低次多项式来进行插值,比如线性插值、二次插值、三次插值等。
这些插值方法都有各自的优缺点,我们可以根据实际情况来选择合适的插值方法。
在金融市场中,通常会使用三次样条插值来估计利率曲线,因为它可以得到一个光滑且具有良好数学性质的曲线。
财务管理插值法公式是什么

财务管理插值法公式是什么学习财务管理的同学对于插值法应该不陌生,这插值法是有什么公式的呢?小编为你带来了“财务管理插值法”的相关知识,这其中也许就有你需要的。
什么是插值法插值法又称“内插法”,是利用函数f (x)在某区间中已知的若干点的函数值,作出适当的特定函数,在区间的其他点上用这特定函数的值作为函数f (x)的近似值,这种方法称为插值法。
如果这特定函数是多项式,就称它为插值多项式。
插值法计算实际利率20×0年1月1日,XYZ公司支付价款l 000元(含交易费用)从活跃市场上购入某公司5年期债券,面值1 250元,票面利率4.72%,按年支付利息(即每年59元),本金最后一次支付。
合同约定,该债券的发行方在遇到特定情况时可以将债券赎回,且不需要为提前赎回支付额外款项。
XYZ公司在购买该债券时,预计发行方不会提前赎回。
XYZ公司将购入的该公司债券划分为持有至到期投资,且不考虑所得税、减值损失等因素。
XYZ公司在初始确认时首先应计算确定该债券的实际利率,设该债券的实际利率为r,则可列出如下等式:59×(1+r)^1+59×(1+r)^2+59×(1+r)^3+59×(1+r)^4+(59+1 250)×(1+r)^5=1000(元)(1)上式变形为:59×(1+r)^1+59×(1+r)^2+59×(1+r)^3+59×(1+r)^4+59×(1 +r)^5+1250×(1+r)^5=1000(元)(2)2式写作:59×(P/A,r,5)+1250×(P/F,r,5)=1000 (3)(P/A,r,5)是利率为r,期限为5的年金现值系数;(P/F,r,5)是利率为r,期限为5的复利现值系数。
现值系数可通过查表求得。
当r=9%时,(P/A,9%,5)=3.8897,(P/F,9%,5)=0.6499 代入3式得到59×3.8897+1250×0.6499=229.4923+812.375=1041.8673>1 000当r=12%时,(P/A,12%,5)=3.6048,(P/F,12%,5)=0.5674代入3式得到59×3.6048+1250×0.5674=212.6832+709.25=921.9332<1000 采用插值法,计算r按比例法原理: 1041.8673 9%1000.0000 r921.9332 12%(1041.8673-1000)/(1041.8673-921.9332)=(9%-r)/(9%-12%)解之得,r=10%Lagrange插值Lagrange插值是n次多项式插值,其成功地用构造插值基函数的方法解决了求n次多项式插值函数问题。
求实际利率是要用内插法

求实际利率是要用内插法(又叫插值法)计算的。
“内插法”的原理是根据比例关系建立一个方程,然后,解方程计算得出所要求的数据。
例如:假设与A1对应的数据是B1,与A2对应的数据是B2,现在已知与A对应的数据是B,A介于A1和A2之间,则可以按照(A1-A)/(A1-A2)=(B1-B)/(B1-B2)计算得出A的数值,会计考试时如用到年金现值系数及其他系数时,会给出相关的系数表,再直接用内插法求出实际利率。
建议你学习一下财务成本管理的相关内容。
以教材35页的例题2-5为例:
59×(1+r)^-1+59×(1+r)^-2+59×(1+r)^-3+59×(1+r)^-4+(59+1250)×(1+r)^-5=1000(元)这个计算式可以转变为59×(P/A,r,5)+1250×(P/F,r,5)=1000
当r=9%时,59×3.8897+1250×0.6499=229.4923+812.375=1041.8673>1 000元当r=12%时,59×3.6048+1250×0.5674=212.6832+709.25=921.9332<1000元因此,
现值利率
1041.8673 9%
1000 r
921.9332 12%
(1041.8673-1000)/(1041.8673-921.9332)=(9%-r)/(9%-12%)
解之得,r=10%。
插值法例题计算过程

插值法例题计算过程(实用版)目录一、插值法简介二、插值法例题计算过程1.公式变形2.计算过程3.结论正文一、插值法简介插值法是一种求解未知数值的方法,通常用于预测和推断。
在财务管理中,插值法常用于计算实际利率、股票价格和债券价格等。
插值法的核心思想是根据已知的数据点,通过数学模型估算出未知数据点的值。
二、插值法例题计算过程假设有一个财务问题,需要计算一个项目的净现值(NPV)。
已知该项目在不同折现率下的净现值如下:- 当折现率为 12% 时,净现值为 116530- 当折现率为 i 时,净现值为 120000- 当折现率为 10% 时,净现值为 121765为了计算项目的实际利率,我们可以使用插值法。
首先,我们需要将公式进行变形,以便于理解和计算。
变形后的公式如下:(i-12%) / (10%-12%) = (120000-116530) / (121765-116530)接下来,我们可以按照以下步骤进行计算:1.将已知的数值代入公式中,得到:(i-12%) / (10%-12%) = 3470 / 52352.对公式进行化简,得到:(i-12%) / (10%-12%) = 0.66023.解方程,得到:i = 12% + 0.6602 * (10%-12%)i = 12% + 0.6602 * (-2%)i = 12% - 1.3204%i = 10.68%因此,该项目的实际利率为 10.68%。
通过以上计算过程,我们可以看到插值法在计算实际利率方面的应用。
在实际应用中,插值法还可以用于计算其他财务指标,如股票价格、债券价格等。
债券实际利率插值法的计算过程

债券实际利率插值法的计算过程第一步:收集市场数据首先,我们需要收集到期时间相似的债券的市场利率。
这些债券通常被称为基准债券或参考债券。
我们需要至少收集两个基准债券的市场利率,但最好收集三个或更多的债券,以确保计算结果的准确性。
第二步:计算每个基准债券的价格将每个基准债券的市场利率和到期时间带入债券定价模型,计算出每个基准债券的价格。
债券定价模型的具体选择可以根据实际情况而定,通常使用的模型包括贴现现金流模型和折现债券模型。
第三步:确定待估计债券价格计算待估计债券的市场利率对应的价格。
同样,我们可以使用债券定价模型来计算待估计债券的价格。
第四步:建立价格与利率之间的关系以基准债券的收益率为横坐标,基准债券的价格为纵坐标,建立一个价格与利率之间的关系图表。
可以绘制一条或多条拟合曲线,以观察价格与利率之间的趋势关系。
第五步:插值计算实际利率在建立的价格与利率关系的图表中,根据待估计债券的价格,找到对应的点。
然后,根据该点在图表中所处的位置,使用插值方法计算出待估计债券的实际利率。
常用的插值方法包括线性插值和二次插值。
线性插值将待估计点与其前后两个已知点之间进行直线插值。
二次插值则会根据待估计点附近的三个已知点计算出二次曲线,再根据二次曲线插值计算待估计点的实际利率。
第六步:检验计算结果计算得出待估计债券的实际利率后,可以将其代入债券定价模型中,计算出该利率对应的债券价格。
与实际市场价格进行对比,检验计算结果的准确性。
注意事项:1.在选择基准债券时,应选择到期时间与待估计债券相似的债券,以确保插值结果的准确性。
2.绘制价格与利率之间的关系时,应将基准债券的到期时间作为横坐标,以保持一致。
3.在进行插值计算时,要注意选择适当的插值方法以及控制误差范围,以确保计算结果的可靠性。
债券实际利率插值法是一种常用的债券定价方法,可以帮助投资者评估债券的实际收益率。
通过收集市场数据、建立价格与利率之间的关系,以及进行插值计算,投资者可以更准确地了解债券的收益情况,并做出相应的投资决策。
插值法计算实际利率

插值法计算实际利率20×0年1月1日,XYZ公司支付价款l 000元(含交易费用)从活跃市场上购入某公司5年期债券,面值1 250元,票面利率4.72%,按年支付利息(即每年59元),本金最后一次支付。
合同约定,该债券的发行方在遇到特定情况时可以将债券赎回,且不需要为提前赎回支付额外款项。
XYZ公司在购买该债券时,预计发行方不会提前赎回。
XYZ公司将购入的该公司债券划分为持有至到期投资,且不考虑所得税、减值损失等因素。
XYZ公司在初始确认时首先应计算确定该债券的实际利率,设该债券的实际利率为r,则可列出如下等式:59×(1+r)-1+59×(1+r)-2+59×(1+r)-3+59×(1+r)-4+(59+1250)×(1+r)-5=1000(元)(1)上式变形为:59×(1+r)-1+59×(1+r)-2+59×(1+r)-3+59×(1+r)-4+59×(1+r)-5+1250×(1+r)-5=1000(元)(2)2式写作:59×(P/A,r,5)+1250×(P/F,r,5)=1000 (3)(P/A,r,5)是利率为r,期限为5的年金现值系数;(P/F,r,5)是利率为r,期限为5的复利现值系数。
现值系数可通过查表求得。
当r=9%时,(P/A,9%,5)=3.8897,(P/F,9%,5)=0.6499代入3式得到59×3.8897+1250×0.6499=229.4923+812.375=1041.8673>1 000当r=12%时,(P/A,12%,5)=3.6048,(P/F,12%,5)=0.5674代入3式得到59×3.6048+1250×0.5674=212.6832+709.25=921.9332<1000采用插值法,计算r按比例法原理: 1041.8673 9%1000.0000 r921.9332 12%(1041.8673-1000)/(1041.8673-921.9332)=(9%-r)/(9%-12%)解之得,r=10%备注:此处要用到两个表:《年金现值系数表》、《复利现值系数表》题中的3.8897和3.6048是查《年金现值系数表》得来的,i=9%和12%,n=5;0.6499和0.5674是查《复利现值系数表》得来的,i=9%和12%,n=5假设两个实际利率的目的在于,确定现值1000在两个利率对应现值的范围内。
用插值法计算实际利率的excel模拟,CPA持有至到期投资例题2-5
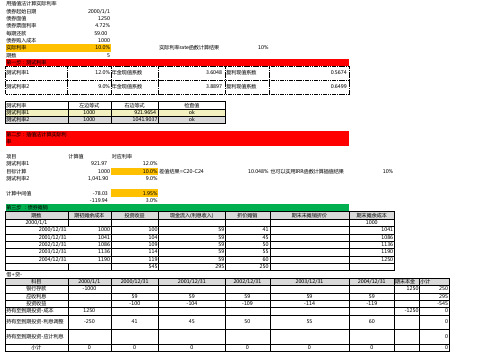
0.5674 0.6499
对应利率 921.97 1000 1,041.90 -78.03 -119.94 12.0% 10.0% 差值结果=C20-C24 9.0% 1.95% 3.0% 投资收益 100 104 109 114 119 545 2000-12-31 59 -100 2001-12-31 59 -104 45 0 现金流入(利息收入) 59 59 59 59 59 295 折价摊销 41 45 50 55 60 250 2002-12-31 59 -109 50 0 2003-12-31 59 -114 55 0 期末未摊销折价 期末摊余成本 1000 1041 1086 1136 1190 1250 10.048% 也可以实用IRR函数计算插值结果 10%
2000-1-1 1250 4.72% 59.00 1000 10.0% 5 12.0% 年金现值系数 9.0% 年金现值系数 左边等式 1000 1000 右边等式 921.9654 1041.9037
实际利率rate函数计算结果
10%
3.6048 复利现值系数 3.8897 复利现值系数 检查值 ok ok
插值法计算实际利率

20×0年1月1日,XYZ公司支付价款l 000元(含交易费用)从活跃市场上购入某公司5年期债券,面值1 250元,票面利率%,按年支付利息(即每年59元),本金最后一次支付。
合同约定,该债券的发行方在遇到特定情况时可以将债券赎回,且不需要为提前赎回支付额外款项。
XYZ公司在购买该债券时,预计发行方不会提前赎回。
XYZ公司将购入的该公司债券划分为持有至到期投资,且不考虑所得税、减值损失等因素。
XYZ公司在初始确认时首先应计算确定该债券的实际利率,设该债券的实际利率为r,则可列出如下等式:59×(1+r)-1+59×(1+r)-2+59×(1+r)-3+59×(1+r)-4+(59+1250)×(1+r)-5=1000(元)(1)上式变形为:59×(1+r)-1+59×(1+r)-2+59×(1+r)-3+59×(1+r)-4+59×(1+r)-5+1250×(1+r)-5=1000(元)(2)2式写作:59×(P/A,r,5)+1250×(P/F,r,5)=1000 (3)(P/A,r,5)是利率为r,期限为5的年金现值系数;(P/F,r,5)是利率为r,期限为5的复利现值系数。
现值系数可通过查表求得。
当r=9%时,(P/A,9%,5)=,(P/F,9%,5)=代入3式得到59×+1250×=+=>1 000当r=12%时,(P/A,12%,5)=,(P/F,12%,5)=代入3式得到59×+1250×=+=<1000采用插值法,计算r按比例法原理:9%r12% /解之得,r=10%备注:此处要用到两个表:《年金现值系数表》、《复利现值系数表》题中的和是查《年金现值系数表》得来的,i=9%和12%,n=5;和是查《复利现值系数表》得来的,i=9%和12%,n=5假设两个实际利率的目的在于,确定现值1000在两个利率对应现值的范围内。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运用插值法计算实际利率
阎震
学校:大连工业大学学院:机械工程与自动化学院
专业:机械工程学号:1304100115
摘要:在现实生活中需要解决实际利率的问题。
其中就运用到了插值法插值法计算实际利率,其原理是根据比例关系建立一个方程,然后解方程,计算得出所要求的数据。
插值法是函数逼近的一种重要方法,是数值计算的基本课题。
关键词: 计算实际利率计算方法插值法
Using the interpolation method to calculate the real interest rate
Yan Zhen
School: Dalian Polytechnic University
Institute: School of mechanical engineering
Major: mechanical engineering Student number: 1304100115 Abstract:In real life need to solve the problem of real interest rates. Which is applied to the interpolation method of interpolation method to calculate the real interest rate, its principle is to establish an equation, according to the proportion relationship equation, then calculates the required data. Interpolation is a kind of important method, the approximation of function is a basic subject of numerical calculation.
Key word:To calculate the real interest rate Calculation method Interpolation method
引言
随着科技飞速的发展,人类遇到的问题越来越多,其中就包括了一些大公司都会遇到的问题就是实际利率的问题,而本文就是运用插值法来帮助我们解决实际中的利率问题,这样可以帮助该公司解决很大的问题,从而对该公司未来的发展都会有很大的好处。
而且运用计算方法中的插值法计算出来的实际利率与真正的值很接近,所以很大程度帮助了公司的发展。
插值法计算实际利率
模型建立
2000年1月1日,ABC公司支付价款120000元(含交易费用),从活跃市场上购入某公司5年期债券,面值180000元,票面利率5%,按年支付利息(即每年9000元),本金最后一次支付。
合同约定,该债券的发行方在遇到特定情况时可以将债券赎回,且不需要为提前赎回支付额外款项。
XYZ公司在购买该债券时,预计发行方不会提前赎回。
ABC公司将购入的该公司债券划分为持有至到期投资,且不考虑所得税、减值损失等因素。
为此,XYZ公司在初始确认时先计算确定该债券的实际利率。
方法流程
设该债券的实际利率为r,则可列出如下等式:
9000×(1+r)-1+9000×(1+r)-2+9000×(1+r)-3+9000×(1+r)-4+(9000+180000)×(1+r)-5=120000元
但是如果计算利率r先假设两个实际利率a和b,那么这两个利率的对应值为A和B,实际利率是直线a、b上的一个点,这个点的对应值是120000,则有方程:(a-r)/(A-120000)=(b-r)/(B-120000)。
假设实际利率是13%,则有9000×3.5172+180000×
0.5428=31631654.8+97704=129358.8.
假设实际利率是15%,则有9000×3.3522+180000×
0.4972=30169.8+89496=119665.8.
(0.13-r)/9358.8=(0.15-r)/(-334.2),解得:r=14.93%.
结果及分析
解得:r=14.93%. 该结果与实际结果误差很小。
结论
从上面这个例子就可以看出通过该方法计算出来的利率与实际利率误差很小,而且计算方面来说不需要大量的运算就可以计算出与实际值非常近似的值。
所以该计算方法是非常实用的。
参考文献:
1.百度文库:/
2.百度翻译
3. 唐东升;;应付债券实际利率与实际利息的计算[J];知识经济;2009年09期。
