第二章 第五节 函数的图像
合集下载
2.5反馈控制系统的传递函数
第五节 反馈控制系统的传递函数
一、系统的开环传递函数
闭环控制 R(s) 系统的典型
结构：
开环传递函数：
E(s)
_ G1(s)
B(s)
D(s)
+
C(s) G2(s)
H(s)
系统反馈量与误差信号的比值
Gk(s)=
B(s) E(s)
=G1(s)G2(s)H
(s)=G(s)H(s)
第五节 反馈控制系统的传递函数
求
DR(s()s) +_
_G3 G1
C(s)
H1
D(s) G1G2
G2G1 - H1
1+G1G2H1
D(s)
_
G2
C(s+)
C(s) G3
- -1
H-(21+H2/G1)
H2 /G1
解:
D(s) 系+统传G递3 函数为：
C(s)
R(s) = 0
H1
结 变构换图为CD((ss))= 1+G1GGG22H3(11++G-G21GGG32H1H21+- )GH21G2-1G3
解1+: 1RERG+1(G+(G(s1sDs)GG1)1)G(G=21s-GG21)2GH+32=GH3G13H0111HG2+2/2GGG结H121=1G构+1G2-+H图HG21G1变1+GG3GHG换122GH12G+为21G3G+H-：G13G2E2G(2sG)3H3 2
第五节 反馈控制系统的传递函数
B(s) H(s)
第五节 反馈控制系统的传递函数
2．扰动信号D(s)作用
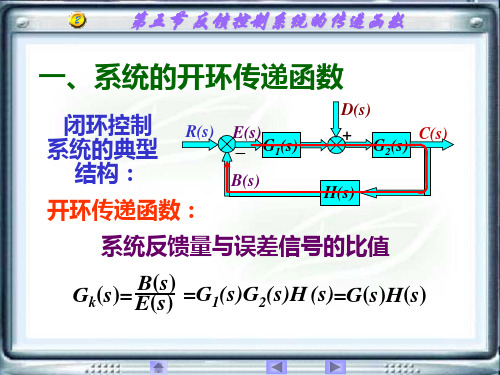
一、系统的开环传递函数
闭环控制 R(s) 系统的典型
结构：
开环传递函数：
E(s)
_ G1(s)
B(s)
D(s)
+
C(s) G2(s)
H(s)
系统反馈量与误差信号的比值
Gk(s)=
B(s) E(s)
=G1(s)G2(s)H
(s)=G(s)H(s)
第五节 反馈控制系统的传递函数
求
DR(s()s) +_
_G3 G1
C(s)
H1
D(s) G1G2
G2G1 - H1
1+G1G2H1
D(s)
_
G2
C(s+)
C(s) G3
- -1
H-(21+H2/G1)
H2 /G1
解:
D(s) 系+统传G递3 函数为：
C(s)
R(s) = 0
H1
结 变构换图为CD((ss))= 1+G1GGG22H3(11++G-G21GGG32H1H21+- )GH21G2-1G3
解1+: 1RERG+1(G+(G(s1sDs)GG1)1)G(G=21s-GG21)2GH+32=GH3G13H0111HG2+2/2GGG结H121=1G构+1G2-+H图HG21G1变1+GG3GHG换122GH12G+为21G3G+H-：G13G2E2G(2sG)3H3 2
第五节 反馈控制系统的传递函数
B(s) H(s)
第五节 反馈控制系统的传递函数
2．扰动信号D(s)作用
高考数学《函数的图像》PPT复习课件
19
作出下列函数的图象： (1)y＝12|x|；(2)y＝|log2(x＋1)|； (3)y＝2xx－－11；(4)y＝x2－2|x|－1.
20
[解] (1)先作出 y＝12x的图象，保留 y＝12x图象中 x≥0 的部分， 再作出 y＝12x的图象中 x＞0 部分关于 y 轴的对称部分，即得 y＝12|x| 的图象，如图①实线部分．
8
(4)翻转变换
①y＝f(x)的图象―x―轴x―轴下―及方―上部―方分―部翻―分折――不到―变上―方→y＝ |f(x)|
的
图象；
②y＝f(x)的图象―原―y轴y―轴左―右侧―侧―部部―分分―去翻―掉折―，―到右―左侧―侧不―变→y＝ f(|x|)
的图象．
9
[常用结论] 1．关于对称的三个重要结论 (1)函数 y＝f(x)与 y＝f(2a－x)的图象关于直线 x＝a 对称． (2)函数 y＝f(x)与 y＝2b－f(2a－x)的图象关于点(a，b)中心对称． (3)若函数 y＝f(x)的定义域内任意自变量 x 满足：f(a＋x)＝f(a－x)， 则函数 y＝f(x)的图象关于直线 x＝a 对称．
A
B
C
D
29
(1)D
(2)B
(3)A
[(1)∵f(－x)
＝cossi－n－x＋x－－xx2
＝－csoins
x＋x x＋x2
＝－f(x)，
∴f(x)是奇函数．又∵f(π)＝csoins ππ＋＋ππ2＝－1π＋π2＞0，∴选 D.
(2)当 x＝0 时，－f(2－x)＝－f(2)＝－1；当 x＝1 时，－f(2－x)＝
高考数学《函数的图像》PPT复习 课件
[最新考纲] 1.在实际情境中，会根据不同的需要选择恰当的方 法(如图象法、列表法、解析法)表示函数.2.会运用基本初等函数的图 象分析函数的性质，并运用函数的图象解简单的方程(不等式)问题．
作出下列函数的图象： (1)y＝12|x|；(2)y＝|log2(x＋1)|； (3)y＝2xx－－11；(4)y＝x2－2|x|－1.
20
[解] (1)先作出 y＝12x的图象，保留 y＝12x图象中 x≥0 的部分， 再作出 y＝12x的图象中 x＞0 部分关于 y 轴的对称部分，即得 y＝12|x| 的图象，如图①实线部分．
8
(4)翻转变换
①y＝f(x)的图象―x―轴x―轴下―及方―上部―方分―部翻―分折――不到―变上―方→y＝ |f(x)|
的
图象；
②y＝f(x)的图象―原―y轴y―轴左―右侧―侧―部部―分分―去翻―掉折―，―到右―左侧―侧不―变→y＝ f(|x|)
的图象．
9
[常用结论] 1．关于对称的三个重要结论 (1)函数 y＝f(x)与 y＝f(2a－x)的图象关于直线 x＝a 对称． (2)函数 y＝f(x)与 y＝2b－f(2a－x)的图象关于点(a，b)中心对称． (3)若函数 y＝f(x)的定义域内任意自变量 x 满足：f(a＋x)＝f(a－x)， 则函数 y＝f(x)的图象关于直线 x＝a 对称．
A
B
C
D
29
(1)D
(2)B
(3)A
[(1)∵f(－x)
＝cossi－n－x＋x－－xx2
＝－csoins
x＋x x＋x2
＝－f(x)，
∴f(x)是奇函数．又∵f(π)＝csoins ππ＋＋ππ2＝－1π＋π2＞0，∴选 D.
(2)当 x＝0 时，－f(2－x)＝－f(2)＝－1；当 x＝1 时，－f(2－x)＝
高考数学《函数的图像》PPT复习 课件
[最新考纲] 1.在实际情境中，会根据不同的需要选择恰当的方 法(如图象法、列表法、解析法)表示函数.2.会运用基本初等函数的图 象分析函数的性质，并运用函数的图象解简单的方程(不等式)问题．
北师大版高中数学必修一第二章 函数第五节简单的幂函数之函数的奇偶性说课课件(共22张PPT)
教材分析 教学重点、难点
教法、学法
学情分析 教学目标
教学过程
教学反思
板书设计
教材分析
奇偶性是函数的一条重要性质，教材从学 生熟悉的函数入手，从特殊到一般，从具体到 抽象，注重信息技术的应用，比较系统地介绍 了函数的奇偶性。从知识结构看，它既是函数 概念的拓展和深化，又是后续研究指数函数、 对数函数、幂函数、三角函数的基础。因此， 本节课起着承上启下的重要作用
指导观察、形成概念
考察下列函数：
f (x) x2
思考1:观察这个函数的图象，并讨论有何特征？
思考2:对于上述函数，f(1)与f(-1)，f(2)与f(-2)有什么
关系？ 12
f(a)与f1(0 -a)f呢x =？x2
8
思考3:怎样定义偶函数？ 6
思考4:函数 f (x) x2 , x [3, 2] 偶函数吗？ 4
f(x)≠0
若f(-x)/f(x)=-1，则f(x)为奇函数；
若f(-x)/f(x)=1，则f(x)为偶函数。
完成“函数奇偶性”概念的第三 个层次。
讲练结合，巩固新知
例. 利用定义判断下列函数的奇偶性
f (x) x3 2x
练习：利用定义判断下列函数的奇偶性
(1)f (x) x 1 (2)f (x) x2 -1
f (x) x -2
(1)f (x) x3 , x [1,1]
(2)f (x) x3 , x [1,1) -4
(3)f (x) x3, x [2,1) [1,2]-6
-8
强化定义，深化内涵
对奇函数、偶函数定义的说明: (1)如果一个函数f(x)是奇函数或偶函数,那么
我们就说函数f(x) 具有奇偶性。 (2)函数具有奇偶性的前提是：定义域关于原点对称。 (3)若f(x)为奇函数, 则对于定义域中的任意x,
函数图像总结
函数图像总结函数图像是指函数在直角坐标系中的图形表示。
通过观察函数图像，可以了解函数的基本特征和性质。
下面我将对常见的函数图像进行总结。
一、一次函数图像：一次函数的一般形式为y = kx + b，其中k为斜率，b为截距。
当k>0时，函数图像呈现正斜率，向右上方倾斜；当k<0时，函数图像呈现负斜率，向右下方倾斜；当k=0时，函数图像为水平直线；当b>0时，函数图像在y轴上方截距b的位置；当b<0时，函数图像在y轴下方截距-b的位置。
二、二次函数图像：二次函数的一般形式为y = ax^2 + bx + c，其中a决定了函数的开口方向和开口大小，b决定了函数图像的对称轴位置，c决定了函数图像与y轴的交点。
当a>0时，函数图像向上开口；当a<0时，函数图像向下开口；当b=0时，函数图像的对称轴为y轴；当b>0时，函数图像的对称轴在原点的右侧；当b<0时，函数图像的对称轴在原点的左侧。
三、指数函数图像：指数函数的一般形式为y = a^x，其中a为底数。
当底数a>1时，函数图像呈现增长趋势，向上凸起；当0<a<1时，函数图像呈现递减趋势，向下凹陷；当a=1时，函数图像为水平直线。
四、对数函数图像：对数函数的一般形式为y = loga(x)，其中a为底数。
当底数a>1时，函数图像呈现增长趋势，向右上方倾斜；当0<a<1时，函数图像呈现递减趋势，向右下方倾斜；当a=1时，函数图像为y轴。
五、三角函数图像：常见的三角函数包括正弦函数、余弦函数、正切函数等。
正弦函数的图像呈现周期性的波形，振动范围在[-1,1]之间；余弦函数的图像也呈现周期性的波形，振动范围也在[-1,1]之间；正切函数的图像在某些点上发生突变，振动范围在整个坐标轴上。
总结以上几种函数图像，可以根据函数的数学表达式和特点来推测图像的形状和性质，进而帮助解决与函数相关的问题。
第二章第五节《水循环》苏科版物理八年级上册(共17张PPT)
非洲草原上的斑马常常为寻找水源而四处奔波
京杭大运河是南北航运的“黄金水道”
水循环伴随着水的物态变化过程，熔化、凝固、汽化、液化、升华、凝华都是物态变化的具体形式。
同时，随着人口和经济的快速增长，水污染日益加剧，因此可利用的淡水资源正面临危机
水循环伴随着水的物态变化过程，熔化、凝固、汽化、液化、升华、凝华都是物态变化的具体形式。
而可利用的淡水，只占地球上淡水资源的10%还不到!这说明，地球上的水虽然很多，但可利用的淡水却很少。
地球上淡水主要来自降雨、降雪、冰川和地下水，他们的总和仅约占地球总水量的3%；
请大家观察图2-41 水循环示意图，填写空格中所经历的物态变化
而可利用的淡水，只占地球上淡水资源的10%还不到!这说明，地球上的水虽然很多，但可利用的淡水却很少。
京杭大运河是南北航运的“黄金水道”
水循环伴随着水的物态变化过程，熔化、凝固、汽化、液化、升华、凝华都是物态变化的具体形式。 地球表面的71%被水覆盖着，这说明地球拥有大量的水，而且，水即使变成水蒸气上升到天空，他最终还是会回到地球表面，那么，为什么人类还会面临“水荒”呢？
而可利用的淡水，只占地球上淡水资源的10%还不到!这说明，地球上的水虽然很多，但可利用的淡水却很少。 非洲草原上的斑马常常为寻找水源而四处奔波 地球上淡水主要来自降雨、降雪、冰川和地下水，他们的总和仅约占地球总水量的3%； 非洲草原上的斑马常常为寻找水源而四处奔波
京杭大运河是南北航运的“黄金水道”
地球上淡水主要来自降雨、降雪、冰川和地下水，他们的总和仅约占地球总水量的3%； 非洲草原上的斑马常常为寻找水源而四处奔波 非洲草原上的斑马常常为寻找水源而四处奔波 京杭大运河是南北航运的“黄金水道” 京杭大运河是南北航运的“黄金水道” 非洲草原上的斑马常常为寻找水源而四处奔波 而可利用的淡水，只占地球上淡水资源的10%还不到!这说明，地球上的水虽然很多，但可利用的淡水却很少。 宏伟的三峡工程利用水来发电 水循环伴随着水的物态变化过程，熔化、凝固、汽化、液化、升华、凝华都是物态变化的具体形式。 地球上淡水主要来自降雨、降雪、冰川和地下水，他们的总和仅约占地球总水量的3%； 请大家观察图2-41 水循环示意图，填写空格中所经历的物态变化
京杭大运河是南北航运的“黄金水道”
水循环伴随着水的物态变化过程，熔化、凝固、汽化、液化、升华、凝华都是物态变化的具体形式。
同时，随着人口和经济的快速增长，水污染日益加剧，因此可利用的淡水资源正面临危机
水循环伴随着水的物态变化过程，熔化、凝固、汽化、液化、升华、凝华都是物态变化的具体形式。
而可利用的淡水，只占地球上淡水资源的10%还不到!这说明，地球上的水虽然很多，但可利用的淡水却很少。
地球上淡水主要来自降雨、降雪、冰川和地下水，他们的总和仅约占地球总水量的3%；
请大家观察图2-41 水循环示意图，填写空格中所经历的物态变化
而可利用的淡水，只占地球上淡水资源的10%还不到!这说明，地球上的水虽然很多，但可利用的淡水却很少。
京杭大运河是南北航运的“黄金水道”
水循环伴随着水的物态变化过程，熔化、凝固、汽化、液化、升华、凝华都是物态变化的具体形式。 地球表面的71%被水覆盖着，这说明地球拥有大量的水，而且，水即使变成水蒸气上升到天空，他最终还是会回到地球表面，那么，为什么人类还会面临“水荒”呢？
而可利用的淡水，只占地球上淡水资源的10%还不到!这说明，地球上的水虽然很多，但可利用的淡水却很少。 非洲草原上的斑马常常为寻找水源而四处奔波 地球上淡水主要来自降雨、降雪、冰川和地下水，他们的总和仅约占地球总水量的3%； 非洲草原上的斑马常常为寻找水源而四处奔波
京杭大运河是南北航运的“黄金水道”
地球上淡水主要来自降雨、降雪、冰川和地下水，他们的总和仅约占地球总水量的3%； 非洲草原上的斑马常常为寻找水源而四处奔波 非洲草原上的斑马常常为寻找水源而四处奔波 京杭大运河是南北航运的“黄金水道” 京杭大运河是南北航运的“黄金水道” 非洲草原上的斑马常常为寻找水源而四处奔波 而可利用的淡水，只占地球上淡水资源的10%还不到!这说明，地球上的水虽然很多，但可利用的淡水却很少。 宏伟的三峡工程利用水来发电 水循环伴随着水的物态变化过程，熔化、凝固、汽化、液化、升华、凝华都是物态变化的具体形式。 地球上淡水主要来自降雨、降雪、冰川和地下水，他们的总和仅约占地球总水量的3%； 请大家观察图2-41 水循环示意图，填写空格中所经历的物态变化
函数图像ppt课件
03
描点法
根据函数表达式，在坐标 系中逐个描出对应的点(x, y)，然后用平滑的曲线将 这些点连接起来。
计算法
利用数学软件或计算器， 输入函数表达式，自动生 成函数图像。
表格法
根据函数表达式和已知数 据，制作表格，然后在坐 标系中根据表格数据绘制 出函数图像。
函数图像的观察与分析
观察图像形状
通过观察函数的图像，可以初 步判断函数的类型（如一次函 数、二次函数、三角函数等）
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
06
复合函数的图像
复合函数的定义与性质
总结词
理解复合函数的定义与性质是绘制和分 析其图像的基础。
VS
详细描述
复合函数是由两个或多个函数的组合而成 的函数。它具有一些特殊的性质，如复合 函数的导数、极限等。了解这些性质有助 于更好地绘制和分析复合函数的图像。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
03
二次函数的图像
二次函数的定义与性质
总结词
二次函数的定义、性质和 表达式
二次函数的定义
二次函数是指形式为 y=ax^2+bx+c（其中a、 b、c为常数，且a≠0）的 函数。
二次函数的性质
二次函数具有开口方向、 顶点、对称轴等性质，这 些性质决定了函数图像的 形状和位置。
复合函数图像的绘制
总结词
掌握绘制复合函数图像的方法是理解其性质 和应用的必要手段。
详细描述
绘制复合函数图像需要使用数学软件或绘图 工具，如Matlab、GeoGebra等。在绘制 过程中，需要注意函数的定义域、值域以及 函数的单调性、奇偶性等性质。
微分几何第二章曲面论第五节曲面论的基本定理
l ij p l p k rl ij pk rl ij L pk n l u p l p
Lij pl k n ( Lij Lkp g )rl u l p
l ij p l p k rl ij pk rl ij L pk n l u p l p
l ij
移项得：
l ik pl p l p l ( L L L L ) g ( ) (1) ij kp ik jp ij pk ik pj k j u p p u L Lik ij p p ( L ( 2) ij L pk ) u k u j ik pj p l l p l p l 令 Rijk k ik ( ij pk ik pj ) j u u p l pl R ( L L L L ) g 则(1)式变为： ijk ij kp ik jp l ij l ij
II Ldu2 2 Mdudv Ndv2
L11du1du1 L12du1du2 L21du2du1 L22du2du2
Lij dui du j ,
i, j
a b a 注意： b ,
a b a b ,
,
a b a b , ,
2 1
曲面的基本方程为：
k r ij ij rk Lij n k kj ni Lik g r j j ,k
Gauss 方程
( i , j 1,2)
Weingarten方程
5.2 曲面的黎曼曲率张量和G-C-M公式
1. G C M公式
仿射标架{ P; r1 , r2 , n} r11 , r12 r21 , r22 , 即r ( i , j 1,2) ij n1 , n2 , 即n ( i 1,2) i 可表为r1 , r2 , n的线性组合.
Lij pl k n ( Lij Lkp g )rl u l p
l ij p l p k rl ij pk rl ij L pk n l u p l p
l ij
移项得：
l ik pl p l p l ( L L L L ) g ( ) (1) ij kp ik jp ij pk ik pj k j u p p u L Lik ij p p ( L ( 2) ij L pk ) u k u j ik pj p l l p l p l 令 Rijk k ik ( ij pk ik pj ) j u u p l pl R ( L L L L ) g 则(1)式变为： ijk ij kp ik jp l ij l ij
II Ldu2 2 Mdudv Ndv2
L11du1du1 L12du1du2 L21du2du1 L22du2du2
Lij dui du j ,
i, j
a b a 注意： b ,
a b a b ,
,
a b a b , ,
2 1
曲面的基本方程为：
k r ij ij rk Lij n k kj ni Lik g r j j ,k
Gauss 方程
( i , j 1,2)
Weingarten方程
5.2 曲面的黎曼曲率张量和G-C-M公式
1. G C M公式
仿射标架{ P; r1 , r2 , n} r11 , r12 r21 , r22 , 即r ( i , j 1,2) ij n1 , n2 , 即n ( i 1,2) i 可表为r1 , r2 , n的线性组合.
北师版高考总复习一轮理科数精品课 第2章 函数的概念与性质 第5节 指数与指数函数
对点训练2(2021陕西西安一中月考)若函数y=ax+b-1(a>0,且a≠1)的图像经
过第二、三、四象限,一定有(
A.0<a<1且b<0
B.a>1且b>0
C.0<a<1且b>0
D.a>1且b<0
)
答案:A
解析:如图所示,从图像上看出其是一个减函数,则0<a<1;
图像与y轴的交点在y轴的负半轴上(纵截距小于零),
x
x
,
≤
1
.
2
1
4 +1
≤
1
,
2
1
,若-6≤f(x)≤0,则实数
考向3.指数函数性质的综合应用
典例突破
例6.(1)已知函数f(x)=2|2x-m|(m为常数),若f(x)在区间[2,+∞)上是递增的,则m
的取值范围是
(2)函数f(x)=4x-2x+1的递增区间是
.
.
答案:(1)(-∞,4]
(2)[0,+∞)
会指数函数是一类重要的函数模型.
衍生考点
核心素养
1.指数幂的运算
2.指数函数的图 1.直观想象
像及应用
2.逻辑推理
3.指数函数的性 3.数学运算
质及应用
强基础 增分策略
1.根式
(1)根式的概念
xn=a⇒
x=
n
(为奇数,且 > 1,∈N * ),
= ± ( > 0,为偶数,且 > 1,∈N* ).
当x<0时,3x<2x<1,又f(x)在(-∞,1)上是减少的,∴f(bx)<f(cx).
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
返回
返回
[考题范例] (2011· 天津高考)对实数a和b，定义运算“⊗”：a⊗b＝
a，a－b≤1， b，a－b＞1.
设函数f(x)＝(x2－2)⊗(x－1)，x∈R.若函数y＝ )
f(x)－c的图像与x轴恰有两个公共点，则实数c的取值范围是( A．(－1,1]∪(2，＋∞) C．(－∞，－2)∪(1,2] B．(－2，－1]∪(1,2] D．[－2，－1]
返回
[巧妙运用] 依题意可得
x2－2，－1≤x≤2， f(x)＝ x－1，x＜－1或x＞2，
作出其示意图如图所示． 由数形结合知， 实数c需有1＜c≤2或－2＜c≤－1.
答案：B
返回
[题后悟道] 解答本题利用了数形结合思想，属于“以形助数”，是 指把某些抽象的数学问题直观化、生动化，能够变抽象思
返回
3．(2011· 沈阳六校联考)函数y＝2x－x2的图像大致是(
)
返回
解析：画出函数y＝2x，y＝x2的图像可知两个函数图像 有三个交点，所以函数y＝2x－x2的图像与x轴有三个
交点，故排除B、C；当x很小时2x－x2<0，排除D.
答案： A
返回
[冲关锦囊] “看图说话”常用的方法有 (1)定性分析法：通过对问题进行定性的分析，从而得出图像
答案： B
返回
4．(教材习题改编)为了得到函数y＝2x－3的图像，只需 把函数y＝2x的图像上所有的点向______平移______ 个单位长度． 答案：右 3
返回
5．若关于x的方程|x|＝a－x只有一个解，则实数a的
取值范围是________．
解析：由题意知，a＝|x|＋x
2x，x≥0， 令y＝|x|＋x＝ 0，x＜0，
D．④③①②
返回
解析：第一个图像过点(0,0)，与④对应； k 第二个图像为反比例函数图像，表达式为y＝x，③y＝x－1恰好 符合，∴第二个图象对应③； 第三个图像为指数函数图像，表达式为y＝ax，且a>1，
返回
①y＝2x恰好符合， ∴第三个图像对应①； 第四个图像为对数函数图像，表达式为y＝logax，且 a>1，②y＝log2x恰好符合，∴第四个图象对应②. ∴四个函数图像与函数序号的对应顺序为④③①②. 答案：D
第 二 章
抓 基 础
第 五 节 函 数 的 图 像
函 数、 导 数 及 其 应 用
明 考 向
教 你 一 招
提 能 力
我 来 演 练
返回
[备考方向要明了] 考 什 么 会运用函数图像理解和研究函数的性质
返回
怎 么 考 1.函数的图像是近几年高考的热点； 2.运用函数的图像研究函数的性质(单调性、奇偶性、最值)、 图像的变换、图像的运用(方程的解、函数的零点、不等 式的解、求参数值)等问题是重点，也是难点； 3.题型以选择题和填空题为主.
返回
返回
一、利用描点法作函数图像 其基本步骤是列表、描点、连线，首先：①确定函数 的定义域；②化简函数解析式；③讨论函数的性质(奇偶性、
单调性、周期性)；其次：列表(尤其注意特殊点、零点、
最大值点、最小值点、与坐标轴的交点)，最后：描点，连 线．
返回
二、利用基本函数的图像作图 1．平移变换 (1)水平平移：y＝f(x±a)(a>0)的图像，可由y＝f(x)的图像 向 左 (＋)或向 右 (－)平移 a个 单位而得到．
图像如右图所示： 观察图像可知要使a＝|x|＋x只有一解，则只需a>0.
答案： (0，＋∞)
返回
函数图像是高考的必考内容，其中作图、识图、用图 也是学生必须掌握的内容． (1)作图一般有两种方法：描点法、图像变换法．特别是 图像变换法，有平移变换、伸缩变换和对称变换，要 记住它们的变换规律．
返回
(2)识图时，要留意它们的变化趋势，与坐标轴的交点及 一些特殊点，特别是对称性、周期性等特点，应引起 足够的重视． (3)用图，主要是数形结合思想的应用.
(4)要得到y＝|f(x)|的图像，可将y＝f(x)的图像在x轴下方的
部分以 x轴 为对称轴翻折到x轴上方，其余部分不变． (5)要得到y＝f(|x|)的图像，可将y＝f(x)，x≥0的部分作出， 再利用偶函数的图像关于 y轴 的对称性，作出x＜0时的 图像． 返回
3．伸缩变换 (1)y＝Af(x)(A>0)的图像，可将y＝f(x)图像上所有点的纵坐 标变为 原来的A倍 ，横坐标不变而得到． (2)y＝f(ax)(a>0)的图像，可将y＝f(x)图像上所有点的横坐 1 标变为 原来的 a 倍 ，纵坐标不变而得到．
的图像恰有3个不同的公共点．
返回
[冲关锦囊] 1．函数图像形象地显示了函数的性质(如单调性、奇偶 性、最值等)，为研究数量关系问题提供了“形”的直 观性，因此常用函数的图像研究函数的性质． 2．有些不等式问题常转化为两函数图像的上、下关系
来解．
3．方程解的个数常转化为两熟悉的函数图像的交点个 数问题来求解． 返回
(2)竖直平移：y＝f(x)±b(b>0)的图像，可由y＝f(x)的图像
向 上 (＋)或向 下 (－)平移 b个 单位而得到．
返回
2．对称变换 (1)y＝f(－x)与y＝f(x)的图像关于 y轴 对称． (2)y＝－f(x)与y＝f(x)的图像关于 x轴 对称． (3)y＝－f(－x)与y＝f(x)的图像关于 原点 对称．
维为形象思维，揭示数学问题的本质．本题首先作出f(x)
的图象，观察图像上、下平移后与x轴交点情况确定c的范 围，应注意c的端点值．
返回
点击此图进入
返回
的上升(或下降)的趋势，利用这一特征分析解决问题．
(2)定量计算法：通过定量的计算来分析解决问题． (3)函数模型法：由所提供的图像特征，联想相关函数模型， 利用这一函数模型来分析解决问题.
返回
[精析考题] [例3] (2011· 新课标全国卷)已知函数y＝f(x)的周期为2， 当x∈[－1,1]时f(x)＝x2，那么函数y＝f(x)的图像与函数y
返回
1．一次函数f(x)的图像过点A(0,1)和B(1,2)，则下列
各点在函数f(x)的图像上的是 A．(2,2) C．(3,2) B．(－1,1) D．(2,3) ( )
返回
解析：一次函数f(x)的图像过点A(0,1)，B(1,2)，则f(x)
＝x＋1，代入验证D满足条件． 答案：D
返回
2．函数y＝x|x|的图像大致是
返回
[巧练模拟]—————(课堂突破保分题，分分必保！)
4 ． (2011· 海 交 大 附 中 月 考 ) 已 知 函 数 f(x) ＝ 上
2－x－1，x≤0， fx－1，x>0，
若方程 f(x)＝x＋a 有且只有两个不 ( )
相等的实数根，则实数 a 的取值范围为 A．(－∞，0] C．(－∞，1) B．[0,1) D．[0，＋∞)
返回
解析：当x>0时，因为f(x)＝f(x－1)，所 以当x>0时，f(x)是以1为周期的函数，又 当0<x≤1时，x－1≤0，所以f(x)＝f(x－1) ＝2
1－x
1 －1＝2·2 x－1.方程f(x)＝x＋a的根的个数可看成
是两个函数y＝f(x)与y＝x＋a的图像的交点个数，画出函 数的图像，如图，由图像可知，实数a的取值范围是(－ ∞，1)．
返回
[精析考题]
[例2] (2011· 陕西高考)设函数f(x)(x∈R)满足f(－x)＝ f(x)，f(x＋2)＝f(x)，则y＝f(x)的图像可能是 ( )
返回
[自主解答]
表达式“f(x)＝f(－x)”，说明函数是偶函
数，表达式“f(x＋2)＝f(x)”，说明函数的周期是2，
再结合选项图像不难看出正确选课堂突破保分题，分分必保！)
2．(2012· 临沂一模)已知函数：①y＝2x；②y＝log2x； ③y＝x ；④y＝ x .则下列函数图像(在第一象限部分)从左 到右依次与函数序号的正确对应顺序是 ( )
－1
1 2
返回
A．②①③④
B．②③①④
C．④①③②
＝|lg x|的图像的交点共有
A．10个 C．8个 B．9个 D．1个
(
)
返回
[自主解答]
根据f(x)的性质及f(x)在[－1,1]上的解析式
可作图如下：
可验证当x＝10时，y＝|lg 10|＝1；0<x<10时，|lg x|<1； x>10时|lg x|>1. 结合图像知y＝f(x)与y＝|lg x|的图像交点共有10个． [答案] A
x≥0， 图像如图③. x<0.
返回
[巧练模拟]——————(课堂突破保分题，分分必保！)
1．分别画出下列函数的图像： (1)y＝|x－2|(x＋1)；
1|x| (2)y＝2 .
返回
x2－x－2，x≥2， 解：(1)∵y＝|x－2|(x＋1)＝ －x2＋x＋2，x<2.
返回
返回
[精析考题] [例1] 分别画出下列函数的图像： (1)y＝|lg x|；
(2)y＝2x＋2
(3)y＝x2－2|x|－1.
返回
[自主解答]
lg x， (1)y＝ －lg x，
x≥1， 图像如图①. 0<x<1.
(2)将y＝2x的图象向左平移2个单位．图像如图②.
x2－2x－1， (3)y＝ 2 x ＋2x－1，
答案：C 返回
5．(2012· 沈阳模拟)已知直线y＝mx(m∈R)与函数f(x)＝ 1x 2－2 ，x≤0， 1x2＋1，x>0 2 的图像恰有3个不同的公共点，
则实数m的取值范围是________．