高考数学(文)二轮专题复习课件:第1部分 专题八 选考系列4-4、4-5 1-8-2
合集下载
高考数学文科二轮(通用版)复习课件:第一部分 专题八 选考部分 第1讲

2.已知圆 C 的极坐标方程为 ρ +2
2
π 2ρ sinθ-4-4=0,求圆 C 的半径.
突破点拨 将曲线的极坐标方程化为直角坐标方程,进而利用圆方程的特征配方求半径.
解析:以极坐标系的极点为平面直角坐标的原点 O,极轴为 x 轴的正半轴,建立 直角坐标系 xOy. 圆 C 的极坐标方程为 ρ +2
→ 分析t的限制条件,看转化前后x,y的范围是否一致 解题 ④普通方程化参数方程: 模板 分析方程Fx,y=0的特征 → 确定一个关系式x=ftt为参数
x=ft → 将x=ft代入Fx,y=0 → 求出y=φt → 整理得 y=φt
→ 分析x与ft的一致性
第一部分
核心专题突破
专题八 选考部分
2017考点解读
பைடு நூலகம்高频考 点
• 1.坐标系与参数方程部分: • 坐标系与参数方程是高考选考内容之一,高 考对本讲内容的考查主要是:(1)直线与圆的 极坐标方程以及极坐标与直角坐标的互化; (2)直线、圆与圆锥曲线的参数方程以及参数 方程与普通方程的互化.
• 2.不等式选讲部分: • 本部分主要考查绝对值不等式的解法,求含 绝对值的函数的值域及求含参数的绝对值不 等式中参数的取值范围,不等式的证明等, 结合集合的运算、函数的图象和性质、恒成 立问题及基本不等式、绝对值不等式的应用 成为命题的热点,主要考查学生的基本运算 能力与推理论证能力以及数形结合思想、分 类讨论思想等.
2
2ρ
2 2 -4=0, sin θ - cos θ 2 2
化简,得 ρ2+2ρsin θ-2ρcos θ-4=0. 则圆 C 的直角坐标方程为 x2+y2-2x+2y-4=0, 即(x-1)2+(y+1)2=6, 所以圆 C 的半径为 6.
高考数学二轮复习专题八选考4系列选讲8.2不等式选讲课件理

2021/12/11
第二十四页,共三十二页。
考点三 不等式的证明 定理 1:设 a,b∈R,则 a2+b2≥2ab.当且仅当 a=b 时,等 号成立. 定理 2:如果 a,b 为正数,则a+2 b≥ ab,当且仅当 a=b 时,等号成立.
定理 3:如果 a,b,c 为正数,则a+3b+c≥3 abc,当且仅当 a=b=c 时,等号成立.
2021/12/11
第十三页,共三十二页。
考点二 含绝对值不等式的综合问题 1.定理 1:如果 a,b 是实数,则|a+b|≤|a|+|b|,当且仅当 ab≥0 时,等号成立. 2.定理 2:如果 a,b,c 是实数,那么|a-c|≤|a-b|+|b- c|,当且仅当(a-b)(b-c)≥0 时,等号成立.
2021/12/11
第十六页,共三十二页。
角度 2:含绝对值不等式的恒成立问题
2021/12/11
第十七页,共三十二页。
[解] (1)由题意得,当 a=2018 时,
f(x)=220x-182,01x<8,20x1≥8,2018, 因为 f(x)在[2018,+∞)上单调递增,所以 f(x)的值域为[2018, +∞). (2)由 g(x)=|x+1|,不等式 g(x)-2>x-f(x)恒成立,知|x+1| +|x-a|>2 恒成立,即(|x+1|+|x-a|)min>2. 而|x+1|+|x-a|≥|(x+1)-(x-a)|=|1+a|, 所以|1+a|>2,解得 a>1 或 a<-3.
2021/12/11
第二十一页,共三十二页。
(2)f(x)=|x+4|=x0+x=4x->- 4,4, -4-xx<-4,
∴不等式 f(x)>1-12x 等价于
2015年人教A版高三数学(文)二轮复习课件 选修4-4

的普通方程.
解 椭圆的普通方程为2x52 +y92=1, 左焦点为(-4,0),直线xy= =1-+4t+,2t, (t 为参数)的普通方程为 2x-y-6=0, 所求直线方程为 y=-12(x+4), 即 x+2y+4=0.
热点二 曲线的极坐标方程的应用
【 例 2 】 在 直 角 坐 标 系 xOy 中 , 曲 线 C1 的 参 数 方 程 为
求|AB|.
解 (1)设 P(x,y),则由条件知 M2x,2y,由于 M 点在 C1 上,
所以22xy==22c+os2sαi,n α,
即xy= =44c+os4sαi,n α.
从而 C2 的参数方程为xy= =44c+os4sαi,n α (α 为参数).
(2)曲线 C1 的极坐标方程为 ρ=4sin θ,曲线 C2 的极坐标方程为 ρ=8sin θ.射线 θ=π3与 C1 的交点 A 的极径为 ρ1=4sinπ3=2 3, 射线 θ=π3与 C2 的交点 B 的极径为 ρ2=8sinπ3=4 3.所以|AB|= |ρ2-ρ1|=2 3. 规律方法 解决这类问题一般有两种思路,一是将极坐标方程 化为直角坐标方程,求出交点的直角坐标,再将其化为极坐标; 二是将曲线的极坐标方程联立,根据限制条件求出极坐标.要 注意题目所给的限制条件及隐含条件.
•高考定位 坐标系与参数方程是新课标选考内 容之一,高考对本讲内容的考查主要是:(1)直
线与圆的极坐标方程以及极坐标与直角坐标的 互化;(2)直线、圆与圆锥曲线的参数方程以及 参数方程与普通方程的互化.
热点一 极坐标方程和参数方程 【例 1】 以直角坐标系的原点 O 为极点,x 轴的正半轴为极 轴.已知点 P 的直角坐标为(1,-5),点 M 的极坐标为4,π2, 若直线 l 过点 P,且倾斜角为π3,圆 C 以 M 为圆心、4 为半径. (1)求直线 l 关于 t 的参数方程和圆 C 的极坐标方程; (2)试判定直线 l 和圆 C 的位置关系.
高中总复习二轮文科数学精品课件 专题8 选修4系列 8.1 坐标系与参数方程(选修4—4)
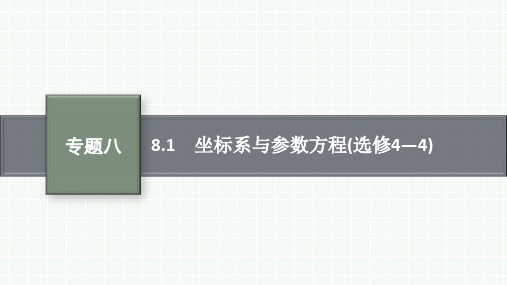
(t为参数),
= 3
以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标
方程为ρ=6cos θ.
(1)求直线l的极坐标方程和曲线C1的直角坐标方程;
π
(2)若曲线C2的极坐标方程为θ= (ρ∈R),曲线C2与直线l的交点为A,与曲线
6
C1异于极点的交点为B,求|AB|.
解:(1)因为直线 l 的参数方程为
5
∴- 3 ≤4m≤10,即-12 ≤m≤2.
∴m 的取值范围为
19 5
- ,
12 2
.
题后反思 1.将参数方程化为普通方程的过程就是消去参数的过程,常用的
消参方法有代入消参、加减消参和三角恒等式消参等,往往需要对参数方
程进行变形,为消去参数创造条件.
2.若极坐标系的极点与直角坐标系的原点重合,极轴与x轴正半轴重合,两
坐标、参数方程与普通方程的互化;
参数方程及其应用;极坐标方程与参
数方程的综合应用.
高频考点•探究突破
命题热点一
求直线或曲线的极坐标方程和参数方程
【思考】 如何求直线、曲线的极坐标方程和参数方程?
例1在直角坐标系xOy中,☉C的圆心为C(2,1),半径为1.
(1)写出☉C的一个参数方程;
(2)过点F(4,1)作☉C的两条切线,以坐标原点为极点,x轴正半轴为极轴建立
.
题后反思 对于极坐标和参数方程的问题,既可以通过极坐标和参数方程来
解决,也可以通过直角坐标解决,但大多数情况下,把极坐标问题转化为直
角坐标问题,把参数方程转化为普通方程更有利于在一个熟悉的环境下解
决问题.这样可以减少由于对极坐标和参数方程理解不到位造成的错误.
= 2- 3,
= 3
以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标
方程为ρ=6cos θ.
(1)求直线l的极坐标方程和曲线C1的直角坐标方程;
π
(2)若曲线C2的极坐标方程为θ= (ρ∈R),曲线C2与直线l的交点为A,与曲线
6
C1异于极点的交点为B,求|AB|.
解:(1)因为直线 l 的参数方程为
5
∴- 3 ≤4m≤10,即-12 ≤m≤2.
∴m 的取值范围为
19 5
- ,
12 2
.
题后反思 1.将参数方程化为普通方程的过程就是消去参数的过程,常用的
消参方法有代入消参、加减消参和三角恒等式消参等,往往需要对参数方
程进行变形,为消去参数创造条件.
2.若极坐标系的极点与直角坐标系的原点重合,极轴与x轴正半轴重合,两
坐标、参数方程与普通方程的互化;
参数方程及其应用;极坐标方程与参
数方程的综合应用.
高频考点•探究突破
命题热点一
求直线或曲线的极坐标方程和参数方程
【思考】 如何求直线、曲线的极坐标方程和参数方程?
例1在直角坐标系xOy中,☉C的圆心为C(2,1),半径为1.
(1)写出☉C的一个参数方程;
(2)过点F(4,1)作☉C的两条切线,以坐标原点为极点,x轴正半轴为极轴建立
.
题后反思 对于极坐标和参数方程的问题,既可以通过极坐标和参数方程来
解决,也可以通过直角坐标解决,但大多数情况下,把极坐标问题转化为直
角坐标问题,把参数方程转化为普通方程更有利于在一个熟悉的环境下解
决问题.这样可以减少由于对极坐标和参数方程理解不到位造成的错误.
= 2- 3,
2016高考数学文科二轮复习课件:专题8选修4系列(选考)

解析: 因为 x=ρcosθ, y=ρsinθ, 且 y=1-x, 所以 ρsinθ=1-ρcosθ, 1 所以 ρ(sinθ+cosθ)=1,ρ= .又 0≤x≤1,所以 0≤y≤1,所 sinθ+cosθ π 以点(x,y)都在第一象限及坐标轴的正半轴上,则 0≤θ≤2. 答案:A
2.(2015· 天津卷)如图,在圆 O 中,M,N 是弦 AB 的三等分点, 弦 CD,CE 分别经过点 M,N.若 CM=2,MD=4,CN=3,则线段 NE 的长为( ) 8 A.3 B.3 10 5 C. 3 D.2
6.直线的极坐标方程 若直线过点 M(ρ0,θ0),且极轴到此直线的角为 α,则它的方程为 ρsin(θ-α)=ρ0sin(θ0-α). 几个特殊位置的直线的极坐标方程 (1)直线过极点:θ=α; (2)直线过点 M(a,0)且垂直于极轴:ρcosθ=a; π (3)直线过点 Mb,2且平行于极轴:ρsinθ=b.
解析:设 MA=t,则 MB=2t,根据圆的相交弦定理 MC· MD= MA· MB,得 8=2t2,所以 t=2,所以 MA=MN=NB=2,又 NA· NB= 8 NE· NC,所以 4×2=3×NE,所以 NE=3.故选 A. 答案:A
π 3.在平面直角坐标系中,倾斜角为4的直线 l 与曲线 C: x=2+cosα, (α 为参数)交于 A,B 两点,且|AB|=2.以坐标原点 O y = 1 + sin α 为极点,x 轴正半轴为极轴建立极坐标系,则直线 l 的极坐标方程是 __________.
5.直角坐标与极坐标的互化
把直角坐标系的原点作为极点,x 轴正半轴作为极轴,且在两坐 标系中取相同的长度单位. 设 M 是平面内的任意一点, 它的直角坐标、 2 2 2 ρ = x + y , x = ρcosθ , 极坐标分别为(x,y)和(ρ,θ)则 y y = ρ sin θ , tanθ=xx≠0.
高考数学二轮复习 专题八 选考4系列选讲 2.8.1 坐标系与参数方程课件 理

值范围.
2021/12/13
第二十八页,共四十三页。
[解] (1)由已知得直线 l 经过的定点是 P(3,4),而圆 C 的圆 心是 C(1,-1),
所以,当直线 l 经过圆 C 的圆心时,直线 l 的斜率为 k=52. (2)解法一:由圆 C 的参数方程xy= =1-+12+co2ssθin,θ, 得圆 C 的 圆心是 C(1,-1),半径为 2.
2021/12/13
第二十一页,共四十三页。
[解] (1)曲线 C 的普通方程为x92+y2=1. 当 a=-1 时,直线 l 的普通方程为 x+4y-3=0.
x+4y-3=0, 由x92+y2=1 解得xy= =30, 或xy= =22-4522. 15, 从而 C 与 l 的交点坐标为(3,0),-2215,2245.
2021/12/13
第三十四页,共四十三页。
2021/12/13
第三十五页,共四十三页。
[解] (1)由xy= =3-+5+2si2nctost, 消去参数 t,得(x+5)2+(y- 3)2=2,
所以圆 C 的普通方程为(x+5)2+(y-3)2=2. 由 ρcosθ+π4=- 2,得 ρcosθ-ρsinθ=-2. 可得直线 l 的直角坐标方程为 x-y+2=0.
2021/12/13
第二十五页,共四十三页。
所以①有两个解,设为 t1,t2,则 t1+t2=0. 又由①得 t1+t2=421c+os3αc+oss2iαnα, 故 2cosα+sinα=0,于是直线 l 的斜率 k=tanα=-2.
2021/12/13
第二十六页,共四十三页。
解决参数方程问题的 3 个要点 (1)把参数方程化为普通方程,需要根据其结构特征,选取适 当的消参方法.
2021/12/13
第二十八页,共四十三页。
[解] (1)由已知得直线 l 经过的定点是 P(3,4),而圆 C 的圆 心是 C(1,-1),
所以,当直线 l 经过圆 C 的圆心时,直线 l 的斜率为 k=52. (2)解法一:由圆 C 的参数方程xy= =1-+12+co2ssθin,θ, 得圆 C 的 圆心是 C(1,-1),半径为 2.
2021/12/13
第二十一页,共四十三页。
[解] (1)曲线 C 的普通方程为x92+y2=1. 当 a=-1 时,直线 l 的普通方程为 x+4y-3=0.
x+4y-3=0, 由x92+y2=1 解得xy= =30, 或xy= =22-4522. 15, 从而 C 与 l 的交点坐标为(3,0),-2215,2245.
2021/12/13
第三十四页,共四十三页。
2021/12/13
第三十五页,共四十三页。
[解] (1)由xy= =3-+5+2si2nctost, 消去参数 t,得(x+5)2+(y- 3)2=2,
所以圆 C 的普通方程为(x+5)2+(y-3)2=2. 由 ρcosθ+π4=- 2,得 ρcosθ-ρsinθ=-2. 可得直线 l 的直角坐标方程为 x-y+2=0.
2021/12/13
第二十五页,共四十三页。
所以①有两个解,设为 t1,t2,则 t1+t2=0. 又由①得 t1+t2=421c+os3αc+oss2iαnα, 故 2cosα+sinα=0,于是直线 l 的斜率 k=tanα=-2.
2021/12/13
第二十六页,共四十三页。
解决参数方程问题的 3 个要点 (1)把参数方程化为普通方程,需要根据其结构特征,选取适 当的消参方法.
教育课件完美版高考数学大二轮复习精品文理通用课件:第1部分 专题8 选修系列 第1讲

(2)l 的参数方程为xy==t-cosα2,+tsinα, (t 为参数,π4<α<34π).
设 A,B,P 对应的参数分别为 tA,tB,tP,则 tP=tA+2 tB,且 tA,tB 满足 t2-2 2
tsinα+1=0.
于是 tA+tB=2 2sinα,tP= 2sinα. 又点 P 的坐标(x,y)满足xy==t-Pcos2α+,tPsinα.
经检验,当 k=0 时,l1 与 C2 没有公共点;当 k=-43时,l1 与 C2 只有一个公共 点,l2 与 C2 有两个公共点.
当 l2 与 C2 只有一个公共点时,A 到 l2 所在直线的距离为 2, 所以 |kk+2+2|1=2,故 k=0 或 k=43. 经检验,当 k=0 时,l1 与 C2 没有公共点;当 k=43时,l2 与 C2 没有公共点. 综上可得,k=-43,C1 的方程为:y=-43|x|+2.
所以点
P
x= 的轨迹的参数方程是
22sin2α,
y=-
22-
2 2 cos2α
(α 为参数,π4<α<34π).
4.(2018·江苏卷,21C)在极坐标系中,直线 l 的方程为 ρsinπ6-θ =2,曲线 C
的方程为 ρ=4cosθ,求直线 l 被曲线 C 截得的弦长.
[解析] 因为曲线 C 的极坐标方程为 ρ=4cos θ, 所以曲线 C 是圆心为(2,0),直径为 4 的圆. 因为直线 l 的极坐标方程为 ρsinπ6-θ=2, 则直线 l 过 A(4,0),倾斜角为π6,所以 A 为直线 l 与圆 C 的一个交点. 设另一个交点为 B,则∠OAB=π6. 连结 OB,因为 OA 为直径,从而∠OBA=π2,所以 AB=4cosπ6=2 3. 因此,直线 l 被曲线 C 截得的弦长为 2 3.
高考数学二轮复习重点保分专题八选修45不等式选讲课件文

所以a2+b2+c2≥ab+bc+ca=ab+abbcc+ca=1a+1b+1c, 当且仅当a=b=c=1时,等号成立. 所以1a+1b+1c≤a2+b2+c2. (2)因为a,b,c为正数且abc=1, 故有(a+b)3+(b+c)3+(c+a)3
≥33 a+b3b+c3c+a3=3(a+b)(b+c)(c+a)
分析法
12/11/2021
考点(一) 含绝对值不等式的解法 [典例] (2019·昆明诊断测试)已知函数f(x)=|2x+1|-|x-1|. (1)求不等式f(x)>1的解集; (2)若不等式f(x)<x2+x+m的解集为R ,求实数m的取值范 围.
12/11/2021
[解] (1)原不等式等价于|2x+1|-|x-1|>1,
-x2-2x-2,x<-12, g(x)=-x2+2x,-12≤x≤1,
-x2+2,x>1, 作出其图象如图所示,由图象知g(x)max=1. 所以m>1,即m的取值范围为(1,+∞).
12/11/2021
[解题方略] 解不含参数的绝对值不等式的基本思想是去掉绝对值.一 般步骤是:求零点(确定每个绝对值的零点),定区间(按零点将 数轴分成几段),去绝对值(去掉原不等式中各个绝对值的符 号),解不等式(解去掉绝对值符号后的不等式),取并集(对自变 量x分类,最后必须取所有分类结果的并集).
12/11/2021
[对点训练] (2018·全国卷Ⅱ)设函数f(x)=5-|x+a|-|x-2|. (1)当a=1时,求不等式f(x)≥0的解集; (2)若f(x)≤1,求a的取值范围.
12/11/2021
2x+4,x<-1, 解:(1)当a=1时,f(x)=2,-1≤x≤2,
≥33 a+b3b+c3c+a3=3(a+b)(b+c)(c+a)
分析法
12/11/2021
考点(一) 含绝对值不等式的解法 [典例] (2019·昆明诊断测试)已知函数f(x)=|2x+1|-|x-1|. (1)求不等式f(x)>1的解集; (2)若不等式f(x)<x2+x+m的解集为R ,求实数m的取值范 围.
12/11/2021
[解] (1)原不等式等价于|2x+1|-|x-1|>1,
-x2-2x-2,x<-12, g(x)=-x2+2x,-12≤x≤1,
-x2+2,x>1, 作出其图象如图所示,由图象知g(x)max=1. 所以m>1,即m的取值范围为(1,+∞).
12/11/2021
[解题方略] 解不含参数的绝对值不等式的基本思想是去掉绝对值.一 般步骤是:求零点(确定每个绝对值的零点),定区间(按零点将 数轴分成几段),去绝对值(去掉原不等式中各个绝对值的符 号),解不等式(解去掉绝对值符号后的不等式),取并集(对自变 量x分类,最后必须取所有分类结果的并集).
12/11/2021
[对点训练] (2018·全国卷Ⅱ)设函数f(x)=5-|x+a|-|x-2|. (1)当a=1时,求不等式f(x)≥0的解集; (2)若f(x)≤1,求a的取值范围.
12/11/2021
2x+4,x<-1, 解:(1)当a=1时,f(x)=2,-1≤x≤2,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[ 自我挑战] 2.(2017· 高考全国卷Ⅱ)已知 a>0,b>0,a3+b3=2,证明: (1)(a+b)(a5+b5)≥4; (2)a+b≤2.
证明:(1)(a+b)(a5+b5)=a6+ab5+a5b+b6 =(a3+b3)2-2a3b3+ab(a4+b4)=4+ab(a2-b2)2≥4. (2)证明:因为(a+b)3=a3+3a2b+3ab2+b3=2+3ab(a+b)≤2 3a+b2 3a+b3 + 4 (a+b)=2+ 4 , 所以(a+b)3≤8,因此 a+b≤2.
于是 a=3.
1.用零点区分法解绝对值不等式的步骤: (1)求零点;(2)划区间、去绝对值号;(3)分别解去掉绝对值的 不等式;(4)取每个结果的并集,注意在分段时不要遗漏区间的端 点值. 2.用图象法、数形结合可以求解含有绝对值的不等式,使得 代数问题几何化,既通俗易懂,又简洁直观,是一种较好的方法.
a+b+c 3 定理 3:如果 a,b,c 为正数,则 3 ≥ abc,当且仅当 a=b=c 时,等号成立. 定理 4:(一般形式的算术—几何平均不等式)如果 a1、a2、…、 a1+a2+…+an n an 为 n 个正数, 则 ≥ a1a2…an, 当且仅当 a1=a2=… n =an 时,等号成立.
2.|ax+b|≤c(c>0)和|ax+b|≥c(c>0)型不等式的解法: (1)|ax+b|≤c⇔-c≤ax+b≤c; (2)|ax+b|≥c⇔ax+b≥c 或 ax+b≤-c. 3.基本不等式 定理 1:设 a,b∈R,则 a2+b2≥2ab.当且仅当 a=b 时,等号 成立. a+b 定理 2:如果 a,b 为正数,则 2 ≥ ab,当且仅当 a=b 时, 等号成立.
1.不等式的证明常利用综合法、分析法、反证法、放缩法、 基本不等式和柯西不等式等,要根据题目特点灵活选用方法. 2.证明含绝对值的不等式主要有以下三种方法: (1)利用绝对值的定义去掉绝对值符号,转化为普通不等式再 证明; (2)利用三角不等式||a|-|b||≤|a± b|≤|a|+|b|进行证明; (3)转化为函数问题,利用数形结合进行证明.
[ 自我挑战] 1.已知函数 f(x)=|x-2|-|x-5|. (1)证明:-3≤f(x)≤3; (2)求不等式 f(x)≥x2-8x+15 的解集.
ቤተ መጻሕፍቲ ባይዱ
解:(1)证明:f(x)=|x-2|-|x-5| -3,x≤2, =2x-7,2<x<5, 3,x≥5. 当 2<x<5 时,4<2x<10,∴-3<2x-7<3. 所以-3≤f(x)≤3.
4.柯西不等式 (1)设 a,b,c,d 为实数,则(a2+b2)(c2+d2)≥(ac+bd)2,当 且仅当 ad=bc 时等号成立. n 2 n 2 n (2)若 ai,bi(i∈N )为实数,则( ∑ ai )( ∑ bi )≥( ∑ aibi)2,当 i = 1 i =1 i=1
*
且仅当 bi=0(i=1,2, …, n)或存在一个数 k, 使得 ai=kbi(i=1,2, …, n)时,等号成立. (3)柯西不等式的向量形式:设 α,β 为平面上的两个向量,则 |a|· |β|≥|α·β|,当且仅当这两个向量同向或反向时等号成立.
(2)由(1)可知, 当 x≤2 时,f(x)≥x2-8x+15 的解集为空集; 当 2<x<5 时,f(x)≥x2-8x+15 的解集为{x|5- 3≤x<5}; 当 x≥5 时,f(x)≥x2-8x+15 的解集为{x|5≤x≤6}. 综上,不等式 f(x)≥x2-8x+15 的解集为{x|5- 3≤x≤6}.
毕业论文答辩模板
G R A D U AT I O N T H E S I S
汇报人:安妮
专题八
选考系列(4-4、4-5)
解题必备
解题方略
走进高考
限时规范训练
考点二
不等式选讲
1.绝对值三角不等式 定理 1:如果 a,b 是实数,则|a+b|≤|a|+|b|,当且仅当 ab≥0 时,等号成立. 定理 2:如果 a,b,c 是实数,那么|a-c|≤|a-b|+|b-c|,当 且仅当(a-b)(b-c)≥0 时,等号成立.
类型一 绝对值不等式的解法 [典例 1] (2017· 安徽合肥高三质量检测)已知函数 f(x)=|x-a|, 其中 a>1. (1)当 a=2 时,求不等式 f(x)≥4-|x-4|的解集; (2) 已 知 关 于 x 的 不 等 式 |f(2x + a) - 2f(x)|≤2 的 解 集 为 {x|1≤x≤2},求 a 的值.
(2)记 h(x)=f(2x+a)-2f(x), -2a,x≤0, 则 h(x)=4x-2a,0<x<a, 2a,x≥a. a-1 a+1 由|h(x)|≤2,解得 2 ≤x≤ 2 . 又已知|h(x)|≤2 的解集为{x|1≤x≤2}, a-1=1, 2 所以 a+1 =2 , 2
类型二 不等式的证明 [典例 2] 1 1 设 a>0,b>0,且 a+b=a+b,证明:(1)a+b≥2;
(2)a2+a<2 与 b2+b<2 不可能同时成立.
1 1 a+b 解:证明:由 a+b=a+b= ab ,a>0,b>0,得 ab=1. (1)由基本不等式及 ab=1,有 a+b≥2 ab=2,即 a+b≥2. (2)假设 a2+a<2 与 b2+b<2 同时成立,则由 a2+a<2 及 a >0 得 0<a<1; 同理, 0<b<1, 从而 ab<1, 这与 ab=1 矛盾. 故 a2+a<2 与 b2+b<2 不可能同时成立.
-2x+6,x≤2, 解:(1)当 a=2 时,f(x)+|x-4|=2,2<x<4, 2x-6,x≥4. 当 x≤2 时,由 f(x)≥4-|x-4| 得-2x+6≥4, 解得 x≤1; 当 2<x<4 时,f(x)≥4-|x-4|无解; 当 x≥4 时,由 f(x)≥4-|x-4|得 2x-6≥4,解得 x≥5; 所以 f(x)≥4-|x-4|的解集为{x|x≤1 或 x≥5}.
