第2章 变压器的运行分析
第2章 变压器的运行原理和特性

仅
E U 20 2
Y,d接线 D,y接线
U 1N k 3U 2 N
k
3U1N U2N
由于 R m R1 , X m X 1 ,所以有时忽略漏阻抗,空载等效电路只是一 个Z m元件的电路。在 U1一定的情况下,I 0大小取决于Z m的大小。从运行角度 讲,希望 I 0 越小越好,所以变压器常采用高导磁材料,增大 Z m,减小 I 0 , 提高运行效率和功率因数。
使
用
1 与 I 0成线性关系; 1)性质上: 0 与 I 0 成非线性关系;
– 变压器各电磁量正方向
• 由于变压器中各个电磁量的大小和方向都随时间以 电源频率交变的,为了用代数式确切的表达这些量 的瞬时值,必须选定各电磁量的正方向,才能列式 子。 • 当某一时刻某一电磁量的瞬时值为正时,说明它与 实际方向一致; 当某一时刻某一电磁量的瞬时值为负时,说明它与 实际方向相反。 • 注:正方向是人为规定的有任选性,而各电磁量的 实际方向则由电磁定律决定。
习
(2)二次侧电动势平衡方程
U1
I 0
0
) (I 2
用
E U 20 2
(3)变比
U 1
U2
E 1
使
E 1
1
E 2
U 20
u2
仅
对三相变压器,变比为一、二次侧的相电动势之比,近似为 额定相电压之比,具体为 Y,d接线
U1N k 3U 2 N
8
供
22
仅
F F F 1 2 0 N I 或 N1 I 1 2 2 N1 I 0 N I I ( 2 ) I I ( 2 ) I I 用电流形式表示 I 2 0 0 1L 1 0 N1 k
第二章 电力变压器及运行

三、变压器的主要技术参数
• 1.额定容量SN • 变压器额定容量是指变压器额定情况下的视在功率,单位用VA、 kVA或MVA表示,并采用R8或R10容量系列。 • 2.额定电压U1N/U2N • U1N是一次侧额定电压。U2N是二次侧额定电压,即当一次侧施 加额定电压U1N时,二次侧开路时的电压。对三相变压器,额定电 压均指线电压,单位用V或kV表示。 • 3.额定电流I1N/I2N • 由发热条件决定的允许变压器一、二次绕组长期通过的最大电 流。对三相变压器,额定电流均指线电流,单位用A或kA。 • 4.短路阻抗Zk • 在额定频率及参考温度下,给变压器的一对绕组施加一短路 电压(即使得该绕组电流达到额定值时的电压),将另一个绕组短 路,其他绕组开路,此时所求得的该绕组端子之间的等效阻抗就是 变压器的短路阻抗。
• 主变压器型式及相关参数 • (1)变压器型式:三相式、强迫油循环、强迫风冷、双 线圈铜绕组无激磁调压油浸式低损耗升压变压器、户外式; • • • • • • • (2)型号:SFP10-780000/220; (3)系统最高工作电压(高压侧/低压侧):252kV/23kV; (4)额定容量:780MVA; (5)额定电压(高压侧/低压侧): 242/22kV; (6)额定电流(高压侧/低压侧): 1861/20470A; (7)空载电流:≤0.2%; (8)阻抗电压:20%(允许偏差:<±5%);
• • • • • • • • •
四、变压器的连接组标号
• 1.三相绕组的连接方法 • (1)星形连接法;(2)顺序三角形连接; (3)逆序三 角形连接。
2.三相变压器的连接组标号
(1) Y,y0连接组标号
(2) Y,d11连接组标号
五、变压器的冷却方式
第二章 变压器的运行原理

Electric Machinery
本章节重点和难点: 重点: (1)变压器空载运行时磁动势、电动势平衡关系,等值电路和相 量图; (2)变压器负载运行时磁动势、电动势平衡关系,等值电路和相 量图; (3)绕组折算前后的电磁关系; (4)变压器空载实验和短路实验,变压器各参数的物理意义; (5)变压器的运行特性。 难点: (1)变压器绕组折算的概念和方法; (2)变压器的等值电路和相量图; (3)励磁阻抗Zm与漏阻抗Z1的区别; (4)励磁电流与铁芯饱和程度的关系; (5)参数测定、标么值。
空载损耗约占额定容量的(0.2~1)%,随 容量的增大而减小。这一数值并不大,但因为 电力变压器在电力系统中用量很大,且常年接 在电网上,因而减少空载损耗具有重要的经济 意义。工程上为减少空载损耗,改进设计结构 的方向是采用优质铁磁材料:优质硅钢片、激 光化硅钢片或应用非晶态合金。
Electric Machinery
漏电动势 : E1
2 2
fN 1 1
2 fN 1 1
Electric Machinery
E 1 j 2 f
N 1 1
I 0 j 2 fL 1 I 0 j I 0 x 1
I0
x 1 2 f
N1
2
为一次侧漏抗,反映漏磁通的作用。
电机学:变压器第二章变压器的运行分析 04
用一台副绕组匝数等于原绕组匝数的假想变压器来模拟实际变压器,假想变压器与实际变压器在物理情况上是等效的。
2)3) 有功和无功损耗不变。
2I实际上的二次侧绕组各物理量称为实际值或折合前的值。
折合后,二次侧各物理量的值称为其折合到一次绕组的折合值。
当把副边各物理量归算到原边时,凡是单位为伏的物理量(电动势、电压等)的归算值等于其原来的数值乘以k;凡是单位为欧姆的物理量(电阻、电抗、阻抗等)的归算值等于其原来的数值乘以k2;电流的归算值等于原来数值乘以1/k。
参数意义220/110V,1R m E 0I 2I ′ U 2I简化等效电路R k 、X k 、Z k 分别称为短路电阻、短路电抗和短路阻抗,是二次侧短路时从简化等效电路一次侧端口看进去的电阻、电抗和阻抗。
R k =R 1+2R ′, X k =X 1+2X ′ Z k =R k +j X k应用基本方程式作出的相量图在理论上是有意义的,但实际应用较为困难。
因为,对已经制造好的变压器,很难用实验方法把原、副绕组的漏电抗x 1和x 2分开。
因此,在分析负载方面的问题时,常根据简化等效电路来画相量图。
短路阻抗的电压降落一个三角形ABC ,称为漏阻抗三角形。
对于给定的一台变压器,不同负载下的这个三角形,它的形状是相似的,三角形的大小与负载电流成正比。
在额定电流时三角形,叫做短路三角形。
讨论:变压器的运行分析感性负载时的简化相量图2U ′− 21I I ′−= 2ϕ 1kI r kx I j 1 1U ABC()()1111111121111210211220m2211P U I E I R jX I E I I RE I I I R I R E I I R =⎡⎤=−++⎣⎦=−+′=−−+′′=++ i i i i i()em 222222222222P E I U I R jX I U I I R ′′=′′′′′⎡⎤=++⎣⎦′′′′=+ i i i 有功功率平衡关系,无功功率平衡关系例题一台额定频率为60Hz的电力变压器,接于频率等于50Hz,电压等于变压器5/6倍额定电压的电网上运行,试分析此时变压器的磁路饱和程度、励磁电抗、励磁电流、漏电抗以及铁耗的变化趋势。
第二部分 变压器 第二章 变压器

四、变压器铭牌: 用以标明该设备的额定数据和使用条件。 额定值:保证设备能正常工作,且能保证一
定寿命而规定的某量的限额。
1、额定容量: S N
视在功率,伏安,千伏安,兆伏安。 在稳定负载和额定使用条件下,加额定电压, 额定频率时能输出额定电流而不超过温升限值 的容量。对 三相变压器指三相容量之和。
(无功分量)
铁耗电流 IFe :产生损耗
故
Im I IFe
(有功分量)
附:1、磁化电流波形分析(磁化曲线) 2、激磁电流波形分析(考虑磁滞损耗) 3、向量图
3、感应电势与激磁电流的关系: 主磁通所感应的电势与产生主磁通的磁化电流的
关系为: N1i m
e1
N1
d
dt
三、变压器的结构:
器身:铁心、绕组、绝缘和出线装置; 油箱; 冷却装置; 保护装置 (一)、铁芯:磁路部分。 含硅量高的(0.35~0.5mm)厚硅钢片迭压而成。 (为减少磁滞,涡流损耗)分为铁芯柱和铁轭两部分 结构的基本形式有芯式和壳式两种。
单相心式变压器
单相壳式 变压器
(二)绕组:电路部分。 高压绕组,低压绕组
U1
I1
F1
N1 I1
E1
I0
Zm
I 2 F2 N 2 I2
E2
2 E 2
I 2R2
U2 I2 Z L
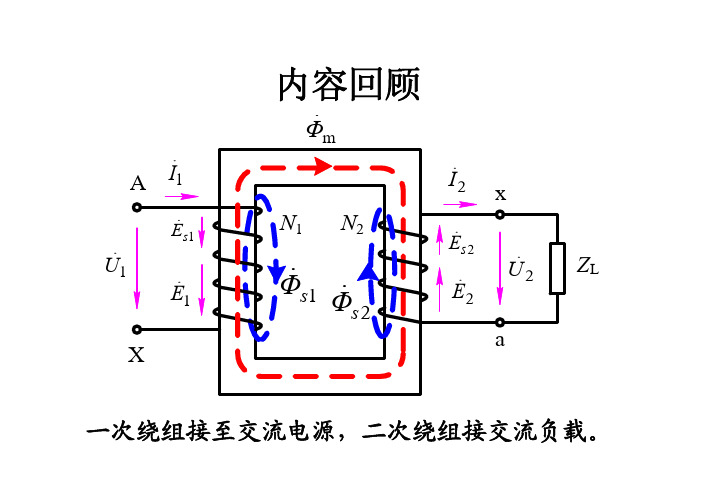
2、磁动势平衡关系: 负载时建立主磁通的磁动势为 F1 F2 空由载空时载建到立负主 载磁,通电的源磁电动压势不为变,F0主磁通基本不变,
第2章 变压器的基本作用原理与理论分析

3、油枕 4、高低压绝缘套管 5、油标` 6、起吊孔
1、油箱
2、散热管
7、铭牌
18
大型电力变压器
19
五、变压器的额定值
1 额定容量S N (kVA) : 、
指铭牌规定的额定使用条件下所能输出的视在功率。
2 额定电流I1N 和I 2 N ( A) : 、
指在额定容量下,允许长期通过的额定电流。在三相 变压器中指的是线电流
铁轭
铁芯柱
铁芯叠片
装配实物
11
铁芯各种截面
充分利用空间
提高变压器容量
减小体积。
12
㈡、绕组
变压器的电路,一般用绝缘铜线或铝线绕制而成。
按照绕组在铁芯中的排列方法分为:铁芯式和铁壳式两类 按照变压器绕组的基本形式分为:同芯式和交叠式两种.
1、铁芯式:
(1)、每个铁芯柱上都套有
高压绕组和低乐绕组。为了绝
3 额定电压U1N 和U 2 N (kV ) : 、
指长期运行时所能承受的工作电压( 线电压)
U1N是指加在一次侧的额定 电压,U 2 N 是指一次侧加 U1N时二次的开路电压对三相变压器指的是线 . 电压.
20
三者关系:
单相 : S 三相 : S
N N
U 1 N I1 N U 2 N I 2 N 3U1N I1N 3U 2 N I 2 N
同理,二次侧感应电动势也有同样的结论。
则:
e2 N 2 d 0 2fN 2 m sin(t 90 0 ) E2 m sin(t 90 0 ) dt
有效值: E2 4.44 fN2m
相量:
E2 j 4.44 fN2m
25
⒉ E1﹑E2在时间相位上滞后于磁通 0 900. 其波形图和相量图如图2—8所示
第2章 变压器的工作原理和运行分析

SN SN ,I 2 N 3U 1 N 3U 2 N
注意!对于三相系统,额定值都是指线间值。
第二节 变压器空载运行
空载:一次侧绕组接到电源,二次侧绕组开路。 一、电磁现象
u1
Φm
i0
Φ 1σ
e1 e1σ
N1
N2
e2
u20
i
二、参考方向的规定
e
i i
e
e
三、变压原理、电压变比
对于变压器的原边回路,根据电路理论有:
u1 i0 r1 e1 e1
空载时 i0r1 和 e1σ 都很小,如略去不 计,则 u1 = - e1 。设外加电压 u1 按 正弦规律变化,则 e1 、Φ 和e2 也都 按正弦规律变化。 设主磁通 m sin t ,则:
u1
Φm
u1
Φm
e1
e2
ωt 0 180° 360°
现在的问题是,要产生上述大小的主磁通 Φm ,需 要多大(什么样)的激磁电流 Im ?
励磁电流的大小和波形受磁路饱和、磁滞及涡 流的影响。
1、磁路饱和对励磁电流的影响
mm mm
i0 tt
00
i0i0 tt
00
i0 i0
tt
tt
磁路不饱和时,i0 ∝φ,其波形为正弦波。
磁路饱和时,i0与φ 不成线性关系,φ越大,磁路 越饱和,i0/φ比值越大,励磁电流的波形为尖顶波。
六、漏抗 漏电势的电路模型与励磁特性的电路模型类似, 只是漏磁通所经路径主要为空气,磁阻大,磁通量 小,磁路不饱和,因此可以忽略漏磁路的铁耗,即 漏电势的电路模型中的等效电阻为零,即漏电势
第02章_变压器的基本理论

第 2 章 思考题与习题参考答案
2.1 试述变压器空载和负载运行时的电磁过程。
,建立磁动势 F ,由其产生主磁通 Φ 和 答:空载时,原边接交流电源,原绕组中流过交流电流 I 0 0 0
负载: R L = 3Ω , X L = 4Ω 。分别用 T 形等效电路、近似等效电路和简化等效电路计算 I 1 、 I 0 、 I 2 、
U 2 ,并比较三次计算的结果。
解:(1)用 T 形等效电路计算 根据已知参数可得: k =
U 1N 380 = = 1.7273 U 2 N 220
′ = k 2 R2 = 1.7273 2 × 0.035 = 0.104Ω R2 ′ = k 2 RL = 1.7273 2 × 3 = 8.951Ω RL
2.11 试说明变压器等效电路中各参数的物理意义,这些参数是否为常数?
′ 分别为副边一相绕组的电阻和漏电 ′和 X2 答: R1 和 X 1 分别为原边一相绕组的电阻和漏电抗, R2
′ 的大小分别反映了原、副绕组漏磁通的大小。 Rm 是 抗的折算值,上述四个参数为常数,其中 X 1 、 X 2
反映铁心损耗的等效电阻,称为励磁电阻, X m 是反映主磁通大小的电抗,称为励磁电抗,这两个参数 也是一相参数,当电源电压不变时, Rm 和 X m 近似为常数。 2.12 利用 T 形等效电路进行实际问题计算时,算出的一次和二次侧电压、电流、损耗、功率是否 均为实际值,为什么? 答: 一次各物理量数值均为实际值,二次电压、电流是折算值,二次损耗、功率是实际值。因为对 二次绕组进行折算时,是以等效为原则,其中,折算前、后的二次侧损耗、功率是保持不变的。 2.13 变压器空载实验一般在哪侧进行?将电源加在低压侧或高压侧所测得的空载电流、空载电流 百分值、空载功率、励磁阻抗是否相等? 答:空载实验一般在低压侧进行。空载电流不等,高压侧空载电流是低压侧的 1 / k ;空载电流百 分值相等;空载功率相等;励磁阻抗不等,高压侧励磁阻抗是低压侧的 k 倍。 2.14 变压器短路实验一般在哪侧进行?将电源加在低压侧或高压侧所测得的短路电压、短路电压 百分值、短路功率、短路阻抗是否相等? 答:短路实验一般在高压侧进行。短路电压不等,高压侧短路电压是低压侧的 k 倍;短路电压百分 值相等;短路功率相等;短路阻抗不等,高压侧短路阻抗是低压侧的 k 倍。 2.15 为什么可以把变压器的空载损耗看作铁耗?短路损耗看作额定负载时的铜耗? 答:空载试验时外加额定电压,空载损耗包括额定铁损耗和空载铜损耗,由于空载电流很小,空载 铜损耗远远小于额定铁损耗,可忽略,所以空载损耗可看作铁损耗。 短路试验时电流为额定电流,短路损耗包括额定铜损耗和短路时的铁损耗,由于短路电压很低,磁
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 变压器的运行分析
一、例题
例2-1一台三相电力变压器的额定容量kVA S N 750=,额定电压为V U U N N 400/1000/21=,Y Y '联接,已知每相短路电阻Ω=4.1k r ,短路电抗Ω=48.6k x ,该变压器原边接额定电压,副边接三相对称Y 接负载,每相负载阻抗Ω+=07.020.0j z L 。
计算:
(1) 变压器原、副边电流(电压电流没有特别指出为相值时,均为线值);
(2) 副边电压;
(3) 输入及输出的有功功率和无功功率;
(4) 效率。
解
(1) 原、副边电流
变比
253
/4003/100003/3/21===N N U U k 负载阻抗
212.007.020.0=+=j z L ︒29.19/()Ω
()Ω+=='75.431252j z k z L L
忽略0I ,采用简化等值电路计算。
从原边看进去每相总阻抗
()Ω=+++='+'++='+= 67.21/01.13675.4312548.64.1j j jx R jx r z z z L L K k L K 原边电流
()A z U I N 45.4201
.1363/100003/11=== 副边电流
()A kI I 24.106125.422512=⨯==
(2) 副边电压
()V z I U L 7.389212.025.10613322=⨯⨯==
(3) 输入及输出功率
原边功率因数角
︒=67.211ϕ
原边功率因数
93.067.211== Cos Cos ϕ
输入有功功率
()W Cos I U P N 31111108.68393.025.421000033⨯=⨯⨯⨯==
ϕ 输入无功功率
()var 105.271331
111⨯==ϕSin I U P N (落后) 副边功率因数
()
33.0,29.1994.029.19222=====ϕϕϕϕSin Cos Cos L 输出有功功率
()W Cos I U P 32222103.67394.025.10617.38933⨯=⨯⨯⨯==ϕ
输出无功功率
()var 106.236332222⨯==ϕSin I U Q
(4) 效率
46.98108.683106.67333
1
2=⨯⨯==P P η%
例2-2某台三相电力变压器kVA S N 600=,V U U N N 400/1000/21=,D ,y11接法,短路阻抗Ω+=58.1j z K ,副边带Y 接的三相对称负载,每相负载阻抗Ω+=1.03.0j z L ,计算该变压器以下几个量:
(1) 原边电流1I 及其与额定电流N I 1的百分比1β;
(2) 副边电流2I 及其与额定电流N I 2的百分比2β;
(3) 副边电压2U 及其与额定电流N U 2相比降低的百分值;
(4) 变压器输出容量。
解
(1)原边电流计算
变比
3.433/400100003/21===N N U U k
负载阻抗
316.01.03.0=+=j z L 43.18/()Ω
()Ω+=='5.1875.5622j z k z L L
从原边看进去每相总阻抗
()Ω=+++='+'++='+= 84.18/23.5965.1875.56258.1j j jx R jx r z z z L L K k L K
原边电流
()A z U I N 05.2923
.596100003311=⨯== 原边额定电流
()A U S I N N N 64.3410000
31060033
11=⨯⨯== 比值1β
86.8364.3405.29111===
N I I β% (2) 副边电流
副边电流
()A Z U k I k I N 23.72623.596100003.433
112=⨯=== 副边额定电流
()A U S I N N N 05.866400
31060033
22=⨯⨯== 比值2β
86.8305
.86623.726222===
N I I β% (3) 副边电压计算
副边电压 ()A z I U L 47.397316.023.7263322=⨯⨯==
副边电压比额定值降低
()V U U U N 53.247.39740022=-=-=∆
副边电压降低的百分值
63.0400
53.22==∆N U U % (4) 变压器的输出容量
()VA I U S 49995023.72647.39733222=⨯⨯==
即
kVA S 5002≈
例2-3某车间采用如图2-11(a )所示的两台单相变压器串联供机床照明用电。
第I 台变压器额定数据为V kVA 120/240,20,短路阻抗Ω+=25.015.0j z K 。
第II 台变压器额定数据为V kVA 24/120,20,短路阻抗Ω+=06.004.0j z KII 。
负载为电灯,每盏灯为100W(24V)。
当电源电压为240V ,150盏灯照明时,求电流1I ,2I ,3I ,3U ;与无载比较3U 的下降值;总输入和总输出的用功功率;总效率。
图1
解
忽略励磁电流,并折合到第I 台变压器原边进行计算,其等值电路如图2-11(b )所示。
变比
2120
240==I k 524
120==I k
Ω⨯=⨯=-32
104.38150
10024L z 从原边看进去的总阻抗
()49
.015.4104.385206.004.0225.015.03222j j j z z z z L KII KI +=⨯⨯⨯++⨯++="+'+=-()Ω= 73.6/179.4
各个电流值
()A z U I 43.57179
.424011=== ()A I I 86.114212==
()A I I 3.5742513=⨯=
输出电压3U
()V z I U L 05.22104.383.574333=⨯⨯==-
与无载相比,输出电压下降值
()V U U N 95.105.222433=-=-
81324
95.1333==-=∆N N U U U U % 总输入和总输出的有功功率为
(
)W Cos Cos I U P 1368873.643.572401111=⨯⨯== ϕ ()W I U P 126633.57405.22333=⨯==
总效率
51.9213688126631
3===P P η%
例2-4 请用标么值计算例题2-1
解
(1) 原、副边电流
原边阻抗基值
33.133107501000033/3/3
2
2111111=⨯====N N N
N N N N N S U U S U I U z
0105.033
.1334.11===N K K z r r 0486.033.13348.61===
N K K z x x 0486.00105.0j jx r z K K K +=+=
负载阻抗
() 29.19/9333.03281.09375.033
.13307.020.025212=+=+⨯==j j z z k z N L L 从原边看进去的总阻抗
67.21/02.13767.0948.03281.09375.00486.00105.0=+=+++=+=j j j z z z L K 原边电流
98.002
.1111===z U I N
副边电流
98.012==I I
(2) 副边电压
9734.09933.098.022=⨯==L z I U
(3) 输入、输出功率
原边功率因数角
37.093.067.2111===ϕϕϕSin Cos
输入有功功率 911.093.098.011111=⨯⨯==ϕCos I U P
输入无功功率
362.0111==ϕSin I U Q (落后)
副边功率因数
33.094.029.1922===ϕϕSin Cos Cos
副边输出有功功率
897.094.098.09734.02222=⨯⨯==ϕCos I U P
副边输出无功功率
315.033.098.09734.02222=⨯⨯==ϕSin I U Q
46.989846.0911
.0897.012====
P P η% 结果与例题2-1完全相符
二、思考题:
2-1 变压器的正方向和惯例的选择是不可改变的吗?规定不同的正方向对变压器各电磁量之间的实际关系有无影响?教材中一次绕组电路采用电动机惯例,是否意味着变压器的功率总是从一次侧流向二次侧?应该如何判断其实际的功率流向?
2-2 变压器二次绕组开路、一次绕组加额定电压时,虽然一次绕组电阻很小,但一次电流并不大,为什么?m Z 代表什么物理意义?电力变压器不用铁心而用空气心行不行?
2-3 变压器负载运行时引起二次电压变化的原因是什么?电压调整率的大小与这些因素有何关系?二次侧带什么性质负载时,有可能使电压调整率为零?
三、作业
教材p40 2-2, 2-4, 2-6, 2-7, 2-12, 2-14, 2-24,2-29。
