安徽理工大学钢结构第四章题库-精
钢结构习题及参考答案

第二章习题1.钢材的设计强度是根据确定的。
A、比例极限B、弹性极限C、屈服点D、抗拉强度2.钢材的伸长率δ是反映材料的性能指标。
A、承载能力B、抵抗冲击荷载能力C、弹性变形能力D、塑性变形能力3.四种厚度不等的Q345钢钢板,其中钢板设计强度最高。
A、16mmB、20mmC、25mmD、30mm4.钢结构对动力荷载适应性较强,是由于钢材具有。
A、良好的塑性B、高强度和良好的塑性C、良好的韧性D、质地均匀、各向同性5.下列因素中与钢构件发生脆性破坏无直接关系。
A、钢材屈服点的大小B、钢材含碳量C、负温环境D、应力集中6.钢材的疲劳破坏属于破坏。
A、弹性B、塑性C、脆性D、低周高应变7.对钢材的疲劳强度影响不显著的是。
A、应力幅B、应力比C、钢种D、应力循环次数8.吊车梁的受拉下翼缘在下列不同板边的加工情况下,疲劳强度最高的是A、两侧边为轧制边B、两侧边为火焰切割边C、一侧边为轧制边,另一侧边为火焰切割边D、一侧边为刨边,另一侧边为火焰切割边答案1、C2、D3、A4、C5、A6、C7、C8、A第三章习题1.T形连接中,t1=6 mm,t2=12mm,若采用等角角焊缝连接,按构造要求,焊脚尺寸hf 取最合适。
A、4mmB、6mmC、8mmD、10mm2.焊接残余应力对构件的无影响。
A、变形B、静力强度C、疲劳强度D、整体稳定3.摩擦型连接的高强度螺栓在杆轴方向受拉时,承载力。
A、与摩擦面的处理方法有关B、与摩擦面的数量有关C、与螺栓直径有关D、与螺栓的性能等级无关4.在弹性阶段,侧面角焊缝应力沿长度方向的分布为。
A、均匀分布B、一端大、一端小C、两端大、中间小D、两端小、中间大5.以下关于对接焊缝的描述,其中描述错误的是。
A、在钢板厚度相差大于4mm的承受静力荷载的对接连接中,应从板的一侧或两侧做成坡度不大于1:2.5的斜坡,以减少应力集中B、当对接正焊缝的强度低于焊件的强度时,为提高连接的承载力,可改用斜缝C、在钢结构设计中,若板件较厚而受力较小时,可以采用部分焊透的对接焊缝D、当对接焊缝的质量等级为一级或二级时,必须在外观检查的基础上再做无损检测,检测比例为焊缝长度的20%。
钢结构基础第四章课后习题答案
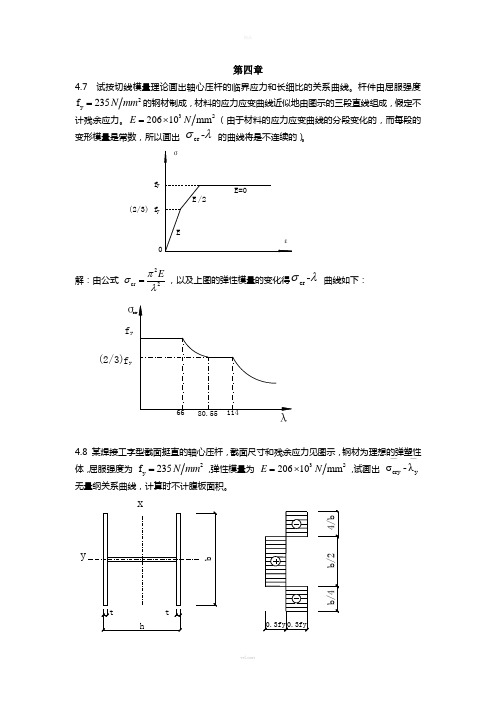
第四章4.7 试按切线模量理论画出轴心压杆的临界应力和长细比的关系曲线。
杆件由屈服强度2y f 235N mm =的钢材制成,材料的应力应变曲线近似地由图示的三段直线组成,假定不计残余应力。
320610mm E N =⨯2(由于材料的应力应变曲线的分段变化的,而每段的变形模量是常数,所以画出 cr -σλ 的曲线将是不连续的)。
解:由公式 2cr 2Eπσλ=,以及上图的弹性模量的变化得cr -σλ 曲线如下:4.8 某焊接工字型截面挺直的轴心压杆,截面尺寸和残余应力见图示,钢材为理想的弹塑性体,屈服强度为 2y f 235N mm =,弹性模量为 320610mm E N =⨯2,试画出 cry y σ-λ——无量纲关系曲线,计算时不计腹板面积。
f yyf (2/3)f y(2/3)f yx解:当 cr 0.30.7y y y f f f σ≤-=, 构件在弹性状态屈曲;当 cr 0.30.7y y y f f f σ>-=时,构件在弹塑性状态屈曲。
因此,屈曲时的截面应力分布如图全截面对y 轴的惯性矩 3212y I tb =,弹性区面积的惯性矩 ()3212ey I t kb =()322232232212212ey cryy y y yI t kb E E E k I tb πππσλλλ=⨯=⨯= 截面的平均应力 2220.50.6(10.3)2y ycr y btf kbt kf k f btσ-⨯⨯==-二者合并得cry y σ-λ——的关系式cry cry342cry σ(0.0273)σ3σ10y λ+-+-= 画图如下4.10 验算图示焊接工字型截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为0.6f yfyλσ0.20.40.60.81.0cryN=1500KN 。
解:已知 N=1500KN ,由支撑体系知对截面强轴弯曲的计算长度 ox =1200cm l ,对弱轴的计算长度 oy =400cm l 。
钢结构基础第四章课后习题答案

第四章4.7 试按切线模量理论画出轴心压杆的临界应力和长细比的关系曲线。
杆件由屈服强度2y f 235N mm =的钢材制成,材料的应力应变曲线近似地由图示的三段直线组成,假定不计残余应力。
320610mm E N =⨯2(由于材料的应力应变曲线的分段变化的,而每段的变形模量是常数,所以画出 cr -σλ 的曲线将是不连续的)。
解:由公式 2cr 2Eπσλ=,以及上图的弹性模量的变化得cr -σλ 曲线如下:4.8 某焊接工字型截面挺直的轴心压杆,截面尺寸和残余应力见图示,钢材为理想的弹塑性体,屈服强度为 2y f 235N mm =,弹性模量为 320610mm E N =⨯2,试画出 cryy σ-λ——无量纲关系曲线,计算时不计腹板面积。
f yyf (2/3)f y(2/3)f yx解:当 cr 0.30.7y y y f f f σ≤-=, 构件在弹性状态屈曲;当 cr 0.30.7y y y f f f σ>-=时,构件在弹塑性状态屈曲。
因此,屈曲时的截面应力分布如图全截面对y 轴的惯性矩 3212y I tb =,弹性区面积的惯性矩 ()3212ey I t kb =()322232232212212ey cryy y y yI t kb E E E k I tb πππσλλλ=⨯=⨯= 截面的平均应力 2220.50.6(10.3)2y ycr y btf kbt kf k f btσ-⨯⨯==-二者合并得cry y σ-λ——的关系式cry cry342cry σ(0.0273)σ3σ10y λ+-+-= 画图如下4.10 验算图示焊接工字型截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为N=1500KN 。
0.6f yfyλσ0.20.40.60.81.0cry解:已知 N=1500KN ,由支撑体系知对截面强轴弯曲的计算长度 ox =1200cm l ,对弱轴的计算长度 oy =400cm l 。
钢结构第四章习题答案

λx = 6000 / 167.936 = 35.7, λ y = 3000 / 56.93 = 52.7 ,均小于 [λ ] = 150 ,刚度满足。
根据 λ
345 查表 4.5(b)和 4.5(c)得绕 X 轴受压稳定系数 φx = 0.9151 235
1
算得绕 Y 轴受压稳定系数 φy = 0.7569
iy:30.6786 mm,
则长细比 λx = 6000 / 197.676 = 30.4, λ y = 3000 / 30.6786 = 97.8 ,刚度满足。 根据 λ
345 查表 4.5(b)得 ϕx 235
= 0.9622,ϕ y = 0.5694
1300 × 103 = 191.9 MPa < f = 205 N / mm 2 ,整体稳定满足。 0.5694 × 11900 型钢截面壁厚较大,局部稳定一般均能满足,此处不再验算。
2
2 4
绕 y 轴名义回转半径: iy =
I y / A = 15849 132
91.20
= 13.2cm ,
绕 y 轴名义长细比: λy = l0y / iy = 7200 绕 y 轴换算长细比: λ0y = 查 ϕ y = 0.785
= 54.5 ,
λy2 + λ12 = 54.52 + 342 = 64.2 < [λ ] = 12
图 4.32 缀板受力
/2
缀板柱所受最大剪力:
V=
Af 85
fy 235
=
9120 × 215 235 = 23068 N 85 235 V1l1 23068 / 2 × 960 = = 42653N a (259.6)
作用于缀板一侧的剪力:
钢结构第四章答案【范本模板】

第四章4。
10验算图示焊接工字形截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为N =1500kN 。
解:由支承条件可知0x 12m l =,0y 4m l =23364x 1150012850025012225012476.610mm 12122I +⎛⎫=⨯⨯+⨯⨯+⨯⨯⨯=⨯ ⎪⎝⎭3364y 5001821225031.310mm 1212I =⨯+⨯⨯⨯=⨯2225012500810000mm A =⨯⨯+⨯=x 21.8cm i ===,y 5.6cm i ===0x x x 12005521.8l i λ===,0y y y 40071.45.6l i λ===,翼缘为火焰切割边的焊接工字钢对两个主轴均为b 类截面,故按y λ查表得=0.747ϕ整体稳定验算:3150010200.8MPa 215MPa 0.74710000N f A ϕ⨯==<=⨯,稳定性满足要求。
4。
13图示一轴心受压缀条柱,两端铰接,柱高为7m 。
承受轴心力设计荷载值N =1300kN ,钢材为Q235。
已知截面采用2[28a ,单个槽钢的几何性质:A =40cm 2,i y =10。
9cm ,i x1=2.33cm ,I x1=218cm 4,y 0=2。
1cm ,缀条采用∟45×5,每个角钢的截面积:A 1=4。
29cm 2。
试验算该柱的整体稳定性是否满足?解:柱为两端铰接,因此柱绕x 、y 轴的计算长度为:0x 0y 7m l l ==224x x10262221840 2.19940.8cm 22b I I A y ⎡⎤⎡⎤⎛⎫⎛⎫=+-=+-=⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦x 11.1cm i === 0x x x 70063.111.1l i λ=== 0y y y 70064.210.9l i λ===0x 65.1λ=== 格构柱截面对两轴均为b 类截面,按长细比较大者验算整体稳定既可。
安徽理工大学钢结构第四章-题库

安徽理工大学钢结构第四章-题库(总18页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第四章轴心受力构件一、选择题1.轴心受力构件应满足正常使用极限状态的( C )要求。
A.变形 B.强度 C.刚度 D.挠度2.轴心受力构件应满足承载能力极限状态的( B )要求。
A.变形 B.强度 C.刚度 D.挠度3.对于轴心受压构件或偏心受压构件,如何保证其满足正常使用极限状态( D )A.要求构件的跨中挠度不得低于设计规范规定的容许挠度B.要求构件的跨中挠度不得超过设计规范规定的容许挠度C.要求构件的长细比不得低于设计规范规定的容许长细比D.要求构件的长细比不得超过设计规范规定的容许长细比4.用Q235钢和Q345钢分别建造一轴心受压柱,两轴心受压柱几何尺寸与边界条件完全一样,在弹性范围内屈曲时,前者临界力与后者临界力之间的关系为( C )A.前者临界力比后者临界力大B.前者临界力比后者临界力小C.等于或接近D.无法比较5.某截面无削弱的热轧型钢实腹式轴心受压柱,设计时应计算( C )A.整体稳定、局部稳定B.强度、整体稳定、长细比C.整体稳定、长细比D.强度、局部稳定、长细比6.在轴心受力构件计算中,验算长细比是为了保证构件满足下列哪项要求( D )A .强度B .整体稳定C .拉、压变形D .刚度7.在下列因素中,对轴心压杆整体稳定承载力影响不大的是( D )A .荷载偏心的大小B .截面残余应力的分布C .构件中初始弯曲的大小D .螺栓孔的局部削弱8.关于残余应力对轴心受压构件承载力的影响,下列说法正确的是( A )A .残余应力对轴压构件的强度承载力无影响,但会降低其稳定承载力B .残余应力对轴压构件的稳定承载力无影响,但会降低其强度承载力C .残余应力对轴压构件的强度和稳定承载力均无影响D .残余应力会降低轴压构件的强度和稳定承载力9.初始弯曲和荷载的初始偏心对轴心受压构件整体稳定承载力的影响为( A )A .初弯曲和初偏心均会降低稳定承载力B .初弯曲和初偏心均不会影响稳定承载力C .初弯曲将会降低稳定承载力,而初偏心将不会影响稳定承载力D .初弯曲将不会影响稳定承载力,而初偏心将会降低稳定承载力10.理想弹性轴心受压构件的临界力与截面惯性矩I 和计算长度0l 的关系为( D )A .与I 成正比,与0l 成正比B .与I 成反比,与0l 成反比C .与I 成反比,与20l 成正比D .与I 成正比,与20l 成反比11.如图所示为轴心受压构件的两种失稳形式,其中( D )A .(a )为弯扭失稳,(b )为扭转失稳B .(a )为弯扭失稳,(b )为弯曲失稳C .(a )为弯曲失稳,(b )为弯扭失稳D .(a )为弯曲失稳,(b )为扭转失稳12.两端铰接轴心受压柱发生弹性失稳时,其它条件相同,轴力分布图如下所示,则各压杆的临界力的关系是( B )A .Nk1>Nk2>Nk3>Nk4B .Nk4>Nk2>Nk3>Nk1C .Nk4>Nk3>Nk2>Nk1D . Nk1>Nk3>Nk2>Nk413.如图所示的轴心受压构件I I x y /≥4,其临界力N cr 为( D )A .π222EI a x /()B .π22EI a x /C .π224EI a y /()D .π22EI a y /14.轴压杆的轴心力分布及支承情况如图所示,验算此杆整体稳定性时,计算长度应取( D )。
钢结构第四章答案

第四章4.10验算图示焊接工字形截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为N=1500kN。
解:由支承条件可知0x 12ml=,0y 4ml=x21.8cmi===,y5.6cmi===0xxx12005521.8liλ===,0yyy40071.45.6liλ===,翼缘为火焰切割边的焊接工字钢对两个主轴均为b类截面,故按yλ查表得=0.747ϕ整体稳定验算:3150010200.8MPa215MPa0.74710000NfAϕ⨯==<=⨯,稳定性满足要求。
4.13图示一轴心受压缀条柱,两端铰接,柱高为7m。
承受轴心力设计荷载值N=1300kN,钢材为Q235。
已知截面采用2[28a,单个槽钢的几何性质:A=40cm2,i y=10.9cm,i x1=2.33cm,I x1=218cm4,y0=2.1cm,缀条采用∟45×5,每个角钢的截面积:A1=4.29cm2。
试验算该柱的整体稳定性是否满足?解:柱为两端铰接,因此柱绕x 、y 轴的计算长度为:0x 0y 7m l l == 格构柱截面对两轴均为b 类截面,按长细比较大者验算整体稳定既可。
由0x 65.1λ=,b 类截面,查附表得0.779ϕ=,整体稳定验算:32130010208.6MPa 215MPa 0.77924010N f A ϕ⨯==<=⨯⨯⨯ 所以该轴心受压的格构柱整体稳定性满足要求。
4.15某压弯格构式缀条柱如图所示,两端铰接,柱高为8m 。
承受压力设计荷载值N =600kN ,弯矩100kN m M =⋅,缀条采用∟45×5,倾角为45°,钢材为Q235,试验算该柱的整体稳定性是否满足? 已知:I22a A=42cm 2,I x =3400cm 4,I y1=225cm 4; [22a A=31.8cm 2,I x =2394cm 4,I y2=158cm 4; ∟45×5 A 1=4.29cm 2。
钢结构第4章习题答案资料

2) 若杆长为6.5m 则 l0 0.7 6.5 4.55m
则
max
lo iy
4.55 4.99
91.2 < [] 150
b类 查表 0.612
N fA 0.612 215 64.28102 845.8kN
3)比较一下 4.8m时 按 λ 336 4.99 67.3 查表0.767
186.7kN
强度: N fA 215 21.6102 464.4kN
(2)Q345
强度: N fA 310 21.6102 669.6kN
刚度:
x
lox ix
36.5 150
y
loy iy
x
127 150
满足
稳定: 型钢构件,局部稳定无需验算
b 88 0.55 0.8 查表, x a y b
(1)几何参数
A 205002 5008 24000
Ix
1 12
8 5003
20 500 2602
2
1.435 109
Iy
1 12
20 5003
2
0.417 109
ix
Ix 244.5 A
iy
Ix 131.8 A
x
lox ix
10103 244.5
40.9
y
loy iy
10103 131.8
75.9
Q345 N=3000kN L=10m
(2)强度:
1
N A
3000 103 24000
125
310
(3)刚度:
x
lox ix
10103 244.5
40.9 150
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 轴心受力构件一、选择题1.轴心受力构件应满足正常使用极限状态的( C )要求。
A .变形B .强度C .刚度D .挠度2.轴心受力构件应满足承载能力极限状态的( B )要求。
A .变形B .强度C .刚度D .挠度3.对于轴心受压构件或偏心受压构件,如何保证其满足正常使用极限状态?( D ) A .要求构件的跨中挠度不得低于设计规范规定的容许挠度B .要求构件的跨中挠度不得超过设计规范规定的容许挠度C .要求构件的长细比不得低于设计规范规定的容许长细比D .要求构件的长细比不得超过设计规范规定的容许长细比4.用Q235钢和Q345钢分别建造一轴心受压柱,两轴心受压柱几何尺寸与边界条件完全 一样,在弹性范围内屈曲时,前者临界力与后者临界力之间的关系为( C )A .前者临界力比后者临界力大B .前者临界力比后者临界力小C .等于或接近D .无法比较5.某截面无削弱的热轧型钢实腹式轴心受压柱,设计时应计算( C )A .整体稳定、局部稳定B .强度、整体稳定、长细比C .整体稳定、长细比D .强度、局部稳定、长细比6.在轴心受力构件计算中,验算长细比是为了保证构件满足下列哪项要求?( D )A .强度B .整体稳定C .拉、压变形D .刚度7.在下列因素中,对轴心压杆整体稳定承载力影响不大的是( D )A .荷载偏心的大小B .截面残余应力的分布C .构件中初始弯曲的大小D .螺栓孔的局部削弱8.关于残余应力对轴心受压构件承载力的影响,下列说法正确的是( A ) A .残余应力对轴压构件的强度承载力无影响,但会降低其稳定承载力B .残余应力对轴压构件的稳定承载力无影响,但会降低其强度承载力C .残余应力对轴压构件的强度和稳定承载力均无影响D .残余应力会降低轴压构件的强度和稳定承载力9.初始弯曲和荷载的初始偏心对轴心受压构件整体稳定承载力的影响为( A ) A .初弯曲和初偏心均会降低稳定承载力B .初弯曲和初偏心均不会影响稳定承载力C .初弯曲将会降低稳定承载力,而初偏心将不会影响稳定承载力D .初弯曲将不会影响稳定承载力,而初偏心将会降低稳定承载力10.理想弹性轴心受压构件的临界力与截面惯性矩I 和计算长度0l 的关系为( D ) A .与I 成正比,与0l 成正比 B .与I 成反比,与0l 成反比C .与I 成反比,与20l 成正比D .与I 成正比,与20l 成反比11.如图所示为轴心受压构件的两种失稳形式,其中( D )A .(a )为弯扭失稳,(b )为扭转失稳B .(a )为弯扭失稳,(b )为弯曲失稳 C .(a )为弯曲失稳,(b )为弯扭失稳 D .(a )为弯曲失稳,(b )为扭转失稳12.两端铰接轴心受压柱发生弹性失稳时,其它条件相同,轴力分布图如下所示,则各压杆的临界力的关系是( B )A .Nk1>Nk2>Nk3>Nk4B .Nk4>Nk2>Nk3>Nk1C .Nk4>Nk3>Nk2>Nk1D . Nk1>Nk3>Nk2>Nk413.如图所示的轴心受压构件I I x y /≥4,其临界力N cr 为( D )A .π222EI a x /()B .π22EI a x /C .π224EI a y /()D .π22EI a y /14.轴压杆的轴心力分布及支承情况如图所示,验算此杆整体稳定性时,计算长度应取( D )。
A .l0x=l/2,l0y=lB .l0x=l ,l0y=lC . l0x=l/2,l0y=l (0.75+0.25N2/N1)D . l0x=l (0.75+0.25N2/N1), l0y=l/215.如图所示焊接组合工字形轴心压杆,一般情况下(当板件不是很薄时)杆件的整体失稳形式是( B )A .绕y 轴的弯扭失稳B .绕y 轴的弯曲失稳C .绕x 轴的弯曲失稳D .绕z 轴的扭转失稳16.单轴对称的轴心受压构件,当绕对称轴失稳时,其整体失稳形式通常是( C )A .弯曲失稳B .扭转失稳C .弯扭失稳D .塑性失稳17.双轴对称工字形截面偏压柱,压力作用在强轴平面内,一旦失稳将会发生( A )A .平面内失稳B .平面外失稳C .可能平面内失稳也可能平面外失稳D .平面内失稳与平面外失稳同时发生18.实腹式偏心受压构件按f W M A N xx x =±=γσ计算强度,它代表的截面应力分布为( C )19.偏心压杆在弯矩作用平面内的整体稳定计算公式)N /N 8.01(W M A N Ex x 1x x mx x -γβ+ϕ≤f 中,W1x 代表( A )。
A .受压较大纤维的毛截面抵抗矩 B .受压较小纤维的毛截面抵抗矩C .受压较大纤维的净截面抵抗矩D .受压较小纤维的净截面抵抗矩 20.实腹式偏心压杆在弯矩作用平面外的整体稳定计算公式f W M A N x1b x tx y ≤ϕβη+ϕ中,W1x应取( D )A .弯矩作用平面内最小受压纤维的毛截面模量B .弯矩作用平面外最小受压纤维的毛截面模量C .弯矩作用平面内最大受压纤维的毛截面模量D .弯矩作用平面外最大受压纤维的毛截面模量21.轴心受压杠设计公式AN ϕ≤f 中的ϕ为( A ) A .y kf σ B .R k γσ C .fk σ D .p k f σ 22.偏心受压杆计算公式中的塑性发展系数x γ和y γ只与下列哪种因素有关?( D ) A .回转半径I B .长细比λ C .荷载性质 D .截面形式 23.截面为两型钢组成的格构式钢柱,当偏心在虚轴上时,强度计算公式中的塑性发展系数γ取( A )。
A .大于1,与实腹式截面一样B .大于1,但小于实腹式截面的塑性发展系数C .等于1,因为不允许发展塑性D .等于1,这是偏于安全考虑24.轴心受压构件的整体稳定系数ϕ与( B )等因素有关。
A .构件截面类别、两端连接构造、长细比B .构件截面类别、钢号、长细比C ..构件截面类别、计算长度系数、长细比 D .构件截面类别、两个方向的长度、长细比25.轴心受压构件整体稳定性的计算公式的物理意义是( D )。
A .截面平均应力不超过钢材强度设计值B .截面最大应力不超过钢材强度设计值C .截面平均应力不超过构件欧拉临界应力设计值D .构件轴力设计值不超过构件稳定极限承载力设计值26.两端铰接的理想轴心受压构件,当构件为单轴对称截面形式时,在轴心压力作用下构件可能发生( B )。
A .弯曲屈曲和扭转屈曲B . 弯曲屈曲和弯扭屈曲C .扭转屈曲和弯扭屈曲D . 弯曲屈曲和侧扭屈曲27.双轴对称焊接组合工字形截面偏心受压柱,偏心荷载作用在腹板平面内。
若两个方向支撑情况相同,可能发生的失稳形式为( D )。
A .在弯矩作用平面内的弯曲失稳B .在弯矩作用平面外的弯扭失稳C .在弯矩作用平面外的弯曲失稳D .在弯矩作用平面内的弯曲失稳或弯矩作用平面外的弯扭失稳28.在计算工字形截面两端铰支轴心受压构件腹板的临界应力时,其支承条件为( A )A .四边简支B .三边简支,一边自由C .两边简支,两边自由D .悬臂29.保证焊接组合工字形截面轴心受压杆翼缘板局部稳定的宽厚比限制条件,是根据矩形板单向均匀受压确定的,其边界条件为( B )A .四边简支B .三边简支,一边自由C .两边简支,一边自由,一边弹性嵌固D .两边简支,一边自由,一边嵌固30.焊接组合工字形轴心受压柱的翼缘与腹板的焊缝承受( B )。
A .压力 B .压杆屈曲时的剪力C .同时承受压力与压杆屈曲时的剪力D .不受力31.钢结构实腹式压弯构件的设计一般应进行的计算内容为( D )。
A .强度、弯矩作用平面内的整体稳定性、局部稳定、变形B .弯矩作用平面内的整体稳定性、局部稳定、变形、长细比C .强度、变矩作用平面内及平面外的整体稳定性、局部稳定、变形D .强度、变矩作用平面内及平面外的整体稳定性、局部稳定、长细比32.为保证轴压钢柱腹板的局部稳定,应使其高厚比不大于某一限值,此限值( A ) A .与钢材的强度和柱的长细比均有关B .与钢材的强度有关,而与柱的长细比无关C .与钢材的强度无关,而与柱的长细比有关D .与钢材的强度和柱的长细比均无关33.实腹式偏心压杆在弯矩作用平面外的失稳是( A )A .弯扭屈曲B .弯曲屈曲C .扭转屈曲D .局部屈曲34.a 类截面的轴心压杆,其整体稳定系数值最高是由于( D )。
A .截面是轧制截面 B .截面的刚度最大C .初弯曲的影响最小D .残余应力的影响最小35.下列截面形式的轴心受压柱,可能发生弯扭失稳的是( D )A .H 型钢B .矩形钢管C .圆钢管D .T 形截面柱 36.当仅讨论截面形式对轴心受压杆的失稳影响时,一般来说,图示的四种截面中最易发生弯扭失稳的截面为( C )。
37.发生弯扭屈曲的理想轴心受压构件截面形式为( B )A .双轴对称工字形截面B .单角钢截面C .H 型钢截面D .箱形截面38.实腹式轴心压杆绕x 、y 轴的长细比分别为x λ、y λ,其稳定系数分别为y x ϕϕ,,若y x λλ=,则( D )。
A .y x ϕϕ>B .y x ϕϕ=C .y x ϕϕ<D .需根据稳定性分类判别39.确定轴心受压实腹柱腹板和翼缘宽厚比限值的原则是( B )A .等厚度原则B .等稳定原则C .等强度原则D .等刚度原则 40.为提高轴心受压构件的整体稳定,在杆件截面面积不变的情况下,杆件截面的形式应使其面积分布( B )A .尽可能集中于截面的形心处B .尽可能远离形心C .任意分布,无影响D .尽可能集中于截面的剪切中心41.钢结构设计规范规定容许长细比可以大于150的受压构件为( B )A .实腹柱B .格构柱的缀条C .桁架弦杆D .屋架支撑杆件42.实腹式组合工字形截面柱翼缘的宽厚比限值是( A )。
A .()y f 2351.010λ+ B .()y f 2355.025λ+ C .y f 235170 D .yf 23580 43.实腹式组合工字形截面柱腹板的宽厚比限值是( B )。
A .()y f 2351.010λ+ B .()y f 2355.025λ+ C .y f 235170 D .yf 23580 44.工字形轴心受压构件,翼缘的局部稳定条件为y f t b 235)1.010(1λ+≤,其中λ的含义为( A )。
A .构件最大长细比B .构件最小长细比C .最大长细比与最小长细比的平均值D .构件的换算长细比45.对于轴心压力作用下的双肢格构柱,在计算下列哪种情况下的稳定临界力时需要使用换算长细比,以考虑剪切变形的影响?( C )A .绕实轴的弯曲失稳B .绕实轴的弯扭失稳C .绕虚轴的弯曲失稳D .绕虚轴的弯扭失稳46.验算工字形组合截面轴心受压构件翼缘和腹板的局部稳定时,计算公式中的长细比为( C )。
