离散数学作业题
离散数学练习题(含答案)

离散数学试题第一部分选择题一、单项选择题1.下列是两个命题变元p,q的小项是( C )A.p∧┐p∧q B.┐p∨qC.┐p∧q D.┐p∨p∨q2.令p:今天下雪了,q:路滑,则命题“虽然今天下雪了,但是路不滑”可符号化为( D )A.p→┐q B.p∨┐qC.p∧q D.p∧┐q3.下列语句中是命题的只有( A )A.1+1=10 B.x+y=10C.sinx+siny<0 D.x mod 3=24.下列等值式不正确的是( C )A.┐(∀x)A⇔(∃x)┐AB.(∀x)(B→A(x))⇔B→(∀x)A(x)C.(∃x)(A(x)∧B(x))⇔(∃x)A(x)∧(∃x)B(x)D.(∀x)(∀y)(A(x)→B(y))⇔(∃x)A(x)→(∀y)B(y)5.谓词公式(∃x)P(x,y)∧(∀x)(Q(x,z)→(∃x)(∀y)R(x,y,z)中量词∀x的辖域是( C )A.(∀x)Q(x,z)→(∃x)(∀y)R(x,y,z))B.Q(x,z)→(∀y)R(x,y,z)C.Q(x,z)→(∃x)(∀y)R(x,y,z)D.Q(x,z)6.设A={a,b,c,d},A上的等价关系R={<a,b>,<b,a>,<c,d>,<d,c>}∪I A,则对应于R的A的划分是( D )A.{{a},{b,c},{d}} B.{{a,b},{c},{d}}C.{{a},{b},{c},{d}} D.{{a,b},{c,d}}7.设A={Ø},B=P(P(A)),以下正确的式子是( A )A.{Ø,{Ø}}∈B B.{{Ø,Ø}}∈BC.{{Ø},{{Ø}}}∈B D.{Ø,{{Ø}}}∈B8.设X,Y,Z是集合,一是集合相对补运算,下列等式不正确的是( A )A.(X-Y)-Z=X-(Y∩Z)B.(X-Y)-Z=(X-Z)-YC.(X-Y)-Z=(X-Z)-(Y-Z)D.(X-Y)-Z=X-(Y∪Z)9.在自然数集N上,下列定义的运算中不可结合的只有( D )A.a*b=min(a,b)B.a*b=a+bC.a*b=GCD(a,b)(a,b的最大公约数)02324# 离散数学试题第1 页共4页02324# 离散数学试题 第 2 页 共4页D .a*b=a(mod b)10.设R 和S 是集合A 上的关系,R ∩S 必为反对称关系的是( A ) A .当R 是偏序关系,S 是等价关系; B .当R 和S 都是自反关系; C .当R 和S 都是等价关系; D .当R 和S 都是传递关系11.设R 是A 上的二元关系,且R ·R ⊆R,可以肯定R 应是( D ) A .对称关系; B .全序关系; C .自反关系; D .传递关系第二部分 非选择题二、填空题1.设论域是{a,b,c},则(∀x)S(x)等价于命题公式 S(a)∧S(b)∧S(c) ;(x ∃)S(x)等价于命题公式 S(a)∨S(b) ∨S(c) 。
(完整版)离散数学题目及答案

数理逻辑习题判断题1.任何命题公式存在惟一的特异析取范式 ( √ ) 2. 公式)(q p p →⌝→是永真式 ( √ ) 3.命题公式p q p →∧)(是永真式 ( √ ) 4.命题公式r q p ∧⌝∧的成真赋值为010 ( × ) 5.))(()(B x A x B x xA →∃=→∀ ( √ )6.命题“如果1+2=3,则雪是黑的”是真命题 ( × ) 7.p q p p =∧∨)( ( √ )8.))()((x G x F x →∀是永真式 ( × ) 9.“我正在撒谎”是命题 ( × ) 10. )()(x xG x xF ∃→∀是永真式( √ )11.命题“如果1+2=0,则雪是黑的”是假命题 ( × ) 12.p q p p =∨∧)( ( √ )13.))()((x G x F x →∀是永假式 ( × )14.每个命题公式都有唯一的特异(主)合取范式 ( √ ) 15.若雪是黑色的:p ,则q →p 公式是永真式 ( √ ) 16.每个逻辑公式都有唯一的前束范式 ( × ) 17.q →p 公式的特异(主)析取式为q p ∨⌝ ( × ) 18.命题公式 )(r q p →∨⌝的成假赋值是110 ( √ ) 19.一阶逻辑公式)),()((y x G x F x →∀是闭式( × )单项选择题1. 下述不是命题的是( A )A.花儿真美啊! B.明天是阴天。
C.2是偶数。
D.铅球是方的。
2.谓词公式(∀y)(∀x)(P(x)→R(x,y))∧∃yQ(x,y)中变元y (B)A.是自由变元但不是约束变元B.是约束变元但不是自由变元C.既是自由变元又是约束变元D.既不是自由变元又不是约束变元3.下列命题公式为重言式的是( A )A.p→ (p∨q)B.(p∨┐p)→qC.q∧┐q D.p→┐q4.下列语句中不是..命题的只有(A )A.花儿为什么这样红?B.2+2=0C.飞碟来自地球外的星球。
离散数学考试题及详细参考答案

离散数学考试题(后附详细答案)一、命题符号化(共6小题,每小题3分,共计18分)1.用命题逻辑把下列命题符号化a)假如上午不下雨,我去看电影,否则就在家里读书或看报。
b)我今天进城,除非下雨。
c)仅当你走,我将留下。
2.用谓词逻辑把下列命题符号化a)有些实数不是有理数b)对于所有非零实数x,总存在y使得xy=1。
c) f 是从A到B的函数当且仅当对于每个a∈A存在唯一的b∈B,使得f(a)=b.二、简答题(共6道题,共32分)1.求命题公式(P→(Q→R)) (R→(Q→P))的主析取范式、主合取范式,并写出所有成真赋值。
(5分)2.设个体域为{1,2,3},求下列命题的真值(4分)a)x y(x+y=4)b)y x (x+y=4)3.求x(F(x)→G(x))→(xF(x)→xG(x))的前束范式。
(4分)4.判断下面命题的真假,并说明原因。
(每小题2分,共4分)a)(A B)-C=(A-B) (A-C)b)若f是从集合A到集合B的入射函数,则|A|≤|B|5.设A是有穷集,|A|=5,问(每小题2分,共4分)a)A上有多少种不同的等价关系?b)从A到A的不同双射函数有多少个?6.设有偏序集<A,≤>,其哈斯图如图1,求子集B={b,d,e}的最小元,最大元、极大元、极小元、上界集合、下界集合、上确界、下确界,(5分)f g图17.已知有限集S={a1,a2,…,a n},N为自然数集合,R为实数集合,求下列集合的基数S;P(S);N,N n;P(N);R,R×R,{o,1}N(写出即可)(6分)三、证明题(共3小题,共计40分)1.使用构造性证明,证明下面推理的有效性。
(每小题5分,共10分)a)A→(B∧C),(E→ F)→ C, B→(A∧ S) B→Eb)x(P(x)→ Q(x)), x(Q(x)∨R(x)),x R(x) x P(x)2.设R1是A上的等价关系,R2是B上的等价关系,A≠ 且B≠ ,关系R满足:<<x1,y1>,<x2,y2>>∈R,当且仅当< x1, x2>∈R1且<y1,y2>∈R2。
离散数学考试题及答案

离散数学考试题及答案一、选择题1. 关于图论的基本概念,以下哪个说法是正确的?A. 无向图中的边无方向性,有向图中的边有方向性。
B. 有向图中的边无方向性,无向图中的边有方向性。
C. 无向图和有向图都是由顶点和边组成的。
D. 无向图和有向图都只由边组成。
答案:A2. “若顶点集合为V,边集合为E,那么图G可以表示为G(V, E)”是关于图的哪个基本概念的描述?A. 图的顶点B. 图的边C. 图的邻接D. 图的表示方法答案:D3. 以下哪个命题是正确的?A. 若集合A和B互相包含,则A和B相等。
B. 若集合A和B相交为空集,则A和B相等。
C. 若集合A和B相等,则A和B互相包含。
D. 若集合A和B相等,则A和B相交为空集。
答案:C二、填空题1. 有一个集合A = {1, 2, 3, 4},则集合A的幂集的元素个数为__________。
答案:162. 设A = {a, b, c},B = {c, d, e},则集合A和B的笛卡尔积为__________。
答案:{(a, c), (a, d), (a, e), (b, c), (b, d), (b, e), (c, c), (c, d), (c, e)}3. 若p为真命题,q、r为假命题,则合取范式(p ∨ q ∨ r)的值为__________。
答案:真三、计算题1. 计算集合A = {1, 2, 3, 4}和集合B = {3, 4, 5, 6}的交集、并集和差集。
答案:交集:{3, 4}并集:{1, 2, 3, 4, 5, 6}差集:{1, 2}2. 计算下列命题的真值:(~p ∨ q) ∧ (p ∨ ~q),其中p为真命题,q为假命题。
答案:真四、证明题证明:对于任意集合A和B,如果A和B互相包含,则A和B相等。
证明过程:假设A和B互相包含,即A包含于B且B包含于A。
设x为集合A中的任意元素,则x也必然存在于集合B中,即x属于B。
同理,对于集合B中的任意元素y,y也属于集合A。
离散数学习题集(十五套含答案)
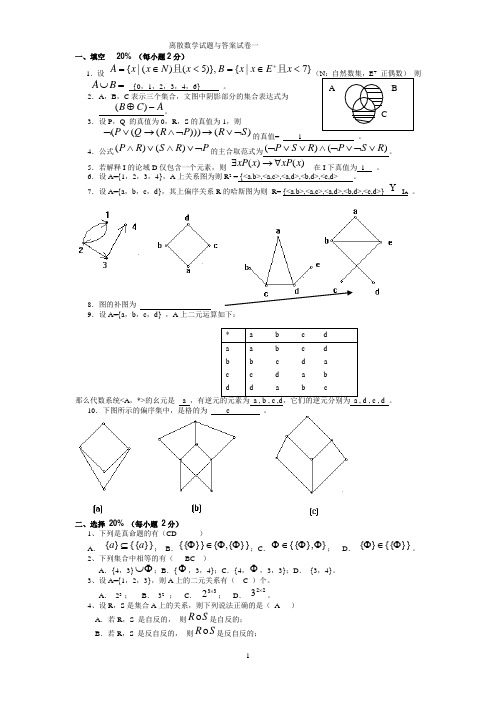
离散数学试题与答案试卷一一、填空20% (每小题2分)1.设}7|{)},5()(|{<∈=<∈=+xExxBxNxxA且且(+=⋃BA{0,1,2,3,4,6} 。
2.A,B,C表示三个集合,文图中阴影部分的集合表达式为。
3R,S的真值为1,则)()))(((SRPRQP⌝∨→⌝∧→∨⌝的真值= 1 。
4.公式PRSRP⌝∨∧∨∧)()(的主合取范式为)()(RSPRSP∨⌝∨⌝∧∨∨⌝。
5.若解释I的论域D仅包含一个元素,则)()(xxPxxP∀→∃在I下真值为1 。
6.设A={1,2,3,4},A上关系图为则R2 = {<a.b>,<a,c>,<a,d>,<b,d>,<c,d> 。
7.设A={a,b,c,d},其上偏序关系R的哈斯图为则R= {<a.b>,<a,c>,<a,d>,<b,d>,<c,d>} I A。
8.图的补图为9.设A={a,b,c,d} ,A上二元运算如下:那么代数系统<A,*>的幺元是 a ,有逆元的元素为a , b , c ,d,它们的逆元分别为 a , d , c , d 。
10.下图所示的偏序集中,是格的为 c 。
二、选择20% (每小题2分)1、下列是真命题的有(CD)A.}}{{}{aa⊆;B.}}{,{}}{{ΦΦ∈Φ;C.}},{{ΦΦ∈Φ;D.}}{{}{Φ∈Φ。
2、下列集合中相等的有(BC )A.{4,3}Φ⋃;B.{Φ,3,4};C.{4,Φ,3,3};D.{3,4}。
3、设A={1,2,3},则A上的二元关系有( C )个。
A.23 ;B.32 ;C.332⨯;D.223⨯。
4、设R,S是集合A上的关系,则下列说法正确的是(A )A.若R,S 是自反的,则SR 是自反的;B.若R,S 是反自反的,则SR 是反自反的;C .若R ,S 是对称的, 则S R是对称的;D .若R ,S 是传递的, 则S R 是传递的。
离散数学考试题及答案

离散数学考试题及答案一、选择题(每题5分,共20分)1. 下列哪个选项不是离散数学的研究对象?A. 图论B. 组合数学C. 微积分D. 逻辑学答案:C2. 在逻辑学中,下列哪个命题是真命题?A. 如果今天是周一,那么明天是周二。
B. 如果今天是周一,那么明天是周三。
C. 如果今天是周一,那么明天是周四。
D. 如果今天是周一,那么明天是周五。
答案:A3. 在集合论中,下列哪个符号表示集合的并集?A. ∩B. ∪C. ⊆D. ⊂答案:B4. 在图论中,下列哪个术语描述的是图中的顶点集合?A. 边B. 路径C. 子图D. 顶点答案:D二、填空题(每题5分,共20分)1. 如果一个集合A包含5个元素,那么它的子集个数是______。
答案:322. 在逻辑学中,如果命题P和命题Q都是真命题,那么复合命题“P且Q”的真值是______。
答案:真3. 在图论中,如果一个图的顶点数为n,那么它的最大边数是______。
答案:n(n-1)/24. 如果一个二叉树的深度为3,那么它最多包含______个节点。
答案:7三、简答题(每题10分,共30分)1. 请简述什么是图的连通性,并给出一个例子。
答案:图的连通性是指在图中任意两个顶点之间都存在一条路径。
例如,在一个完全图K3中,任意两个顶点之间都可以通过一条边直接连接,因此它是连通的。
2. 解释什么是逻辑蕴含,并给出一个例子。
答案:逻辑蕴含是指如果一个命题P为真,则另一个命题Q也必须为真。
例如,命题P:“如果今天是周一”,命题Q:“明天是周二”。
如果今天是周一,那么根据逻辑蕴含,明天必须是周二。
3. 请描述什么是二叉搜索树,并给出它的一个性质。
答案:二叉搜索树是一种特殊的二叉树,其中每个节点的左子树只包含小于当前节点的数,右子树只包含大于当前节点的数。
它的一个性质是中序遍历可以得到一个有序序列。
四、计算题(每题15分,共30分)1. 给定一个集合A={1, 2, 3, 4, 5},请计算它的幂集,并列出所有元素。
苏XI友离散数学作业(13篇)

作业6
补充作业:用等值演算证明下列等值式. (1)∃x∃y¬ (F(x)∧¬ G(y))∀xF(x)→∃yG(y). 证.∃x∃y¬ (F(x)∧¬ G(y))
∃x∃y(¬ F(x)∨G(y))或 ∃x(¬ F(x)∨∃yG(y)) ∃x∃y(F(x)→G(y)) ∃x¬ F(x)∨∃yG(y) ∃x(F(x)→∃yG(y)) ¬ ∀xF(x)∨∃yG(y) ∀xF(x)→∃yG(y). ∀xF(x)→∃yG(y)
2020
感谢 观看
*北京林业大学信息学院 苏喜友
作业6
P55-2.15 求下列各式的前束范式, 要求使用自 由变项换名规则.
(2)∃x(F(x)∧∀yG(x,y,z))→∃zH(x,y,z) 解.∃x(F(x)∧∀yG(x,y,z))→∃zH(x,y,z)
∃x(F(x)∧∀yG(x,y,u))→∃zH(v,w,z) ∃x∀y(F(x)∧G(x,y,u))→∃zH(v,w,z) ∀x∃y((F(x)∧G(x,y,u))→∃zH(v,w,z)) ∀x∃y∃z((F(x)∧G(x,y,u))→H(v,w,z)).
作业1
P33-1.7 (7)设A=(p∨¬ p)→((q∧¬ q)∧¬ r)
p q r ¬ p ¬ q ¬ r p∨¬ p q∧¬ q (q∧¬ q)∧¬ r A
000 1 1 1 1
0
0
0
001 1 1 0 1
0
0
0
010 1 0 1 1
0
0
0
011 1 0 0 1
0
0
0
100 0 1 1 1
0
*北京林业大学信息学院 苏喜友
作业5
(5)任何金属都可以溶解在某种液体中. 设M(x):x是金属, L(x):x是液体, R(x,y):x 溶解在y中. 符号化为: ∀x(M(x)→∃y(L(y)∧R(x,y))).
离散数学试题及答案解析

离散数学试题及答案解析一、选择题1. 在集合{1,2,3,4}中,含有3个元素的子集有多少个?A. 4B. 8C. 16D. 32答案:B解析:含有3个元素的子集可以通过组合数公式C(n, k) = n! / [k!(n-k)!]来计算,其中n为集合的元素个数,k为子集中的元素个数。
在本题中,n=4,k=3,所以C(4, 3) = 4! / [3!(4-3)!] = 4。
2. 下列哪个命题是真命题?A. 所有偶数都是整数。
B. 所有整数都是偶数。
C. 所有整数都是奇数。
D. 所有奇数都是整数。
答案:A解析:偶数是指能被2整除的整数,因此所有偶数都是整数,选项A是真命题。
选项B、C和D都是错误的,因为并非所有整数都是偶数或奇数。
二、填空题1. 逻辑运算符“非”(NOT)的真值表是:当输入为真时,输出为______;当输入为假时,输出为真。
答案:假解析:逻辑运算符“非”(NOT)是一元运算符,它将输入的真值取反。
如果输入为真,则输出为假;如果输入为假,则输出为真。
2. 命题逻辑中,合取词“与”(AND)的真值表是:当两个命题都为真时,输出为真;否则输出为______。
答案:假解析:合取词“与”(AND)是二元运算符,只有当两个命题都为真时,输出才为真;如果其中一个或两个命题为假,则输出为假。
三、简答题1. 解释什么是等价关系,并给出一个例子。
答案:等价关系是定义在集合上的一个二元关系,它满足自反性、对称性和传递性。
例如,考虑整数集合上的“同余”关系。
对于任意整数a,b,如果a和b除以同一个正整数n后余数相同,则称a和b模n同余。
这个关系是自反的(a同余a),对称的(如果a同余b,则b同余a),并且是传递的(如果a同余b且b同余c,则a同余c)。
2. 什么是图的连通性?一个图是连通的需要满足什么条件?答案:图的连通性是指在无向图中,任意两个顶点之间都存在一条路径。
一个图是连通的需要满足以下条件:图中的任意两个顶点v和w,都可以通过图中的边相互到达。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
离散数学作业题
第2章集合、关系与映射
1.A⊆B,A∈B能否同时成立,说明原因
求集合A={a,{a}}的幂集
2.证明:若B⊆C,则P(B)⊆ P(C)
3.如果A∪B=A∪C,是否有B=C?
如果A⊕B=A⊕C,是否有B=C?
4.试求1到10000之间不能被4,5或6整除的整数个数.
5.列出所有从A={a,b,c}到B={s}的关系,并指出集合A上的恒等关系和从A到B的全
域关系.
6.给出A上的关系及其关系图和矩阵表示.{<x,y>|0≤x-y<3} A={0,1,2,3,4}
7.已知S={a,b}. R⊆ ={〈x,y〉|x,y∈A∧x⊆y∧A为集合族ρ(S)}.试写出关系R⊆.
8.已知:A={a,b,c}, R={〈a,b〉,〈a,c〉,〈b,c〉}该关系具有什么性质?
(自反,反自反,对称,反对称,传递性)
9.设A={a,b,c},R={〈a,b〉,〈a,c〉} 计算:r(R),sr(R),tr(R),str(R).
10.设A是含有4个元素的集合,试求:
(1)在A上可以定义多少种对称关系?
(2)在A上可以定义多少种既是自反的,又是对称的关系?
(3)在A上可以定义多少种既不是自反的,也不是反自反的二元关系?
11.设集合A={0,1,2,3,4}. R={<x,y>|x+y=4,x,y∈A} ,S={<x,y>|y-x=1,x,y∈A}.
试求:R◦S,R◦R,(R◦S)◦R,R◦(S◦R).
12.证明:R是A上的传递关系⇔R◦R⊆R.
13.A={1,2,3,4,5},R={<x,y>|x,y∈A∧x-y可被2整除},试问R是否是A上的等价关系?
如果是,求出R的各等价类.
14.A={1,2,3,4,5},A上的划分∏={{1,2},{3,4},{5}},给出由∏所诱导出的A上的等价关系
R的集合表达式.
15.试给出一个单射但非满射的函数.(对某一集合而言)
16.设f:N→N×N,f(n)=<n,n+1>,则:
(1)说明f是否为单射和满射,并说明理由.
(2) f的反函数是否存在?并说明理由.
(3)求ranf.
17.已知如果从无限集合A到集合B存在单射f,则B也是无限集合。
设X是无限集合,集合Y≠φ,证明:X与Y的笛卡儿积X×Y是无限集合。
第六章代数结构
P247 习题六:4(1)(3)、6、16、21
1.以下集合和运算是否构成代数系统?如果构成,说明该系统是否满足结合律、交换律?
求出该运算的幺元、零元和所有可逆元素的逆元.
1)P(B)关于对称差运算⊕,其中P(B)为幂集.
2)A={a,b,c},*运算如下表所示:
2.设集合A={a,b},那么(1)在A上可以定义多少不同的二元运算?(2)在A上可以
定义多少不同的具有交换律的二元运算?
3.设A={1,2},B是A上的等价关系的集合.
1)列出B的元素.
2)给出代数系统V=<B,∩>的运算表.
3)求出V的幺元、零元和所有可逆元素的逆元.
4)说明V是否为半群、独异点和群?
4.设A={a,b,c},构造A上的二元运算*,使得a*b=c,c*b=b,且*运算满足幂等律、交换
律.
1)给出关于*运算的一个运算表.
2)*运算是否满足结合律,为什么?
5.设<R,*>是一个代数系统。
*是R上的一个二元运算,使得对于R(实数集合)中的任意元素a,b都有a*b=a+b+a·b (·和+为数集上的乘法和加法).
证明::<R,*> 是独异点.
6.如果<S,*>是半群,且*是可交换的.
证明:如果S中有元素a,b,使得a*a=a和b*b=b,则(a*b)*(a*b)=a*b.
7.设<G,·,–1,e>是一个群,则∀a,b,c∈S。
试证明:群G中具有消去律,即成立: 如果
a·b=a·c ,b·a=c·a 那么b=c.
8.设<G,*>是群,a∈G .
现定义一种新的二元运算⊙:x⊙y=x*a*y,∀x,y∈G .
证明:<G,⊙>也是群.
9.试写出模6加法群<Z6,+6>的每个子群及其相应的左陪集.
10.设A={1,2,5,10,11,22,55,110}.
1)A关于整除关系是否构成偏序集?
2)如果构成偏序集合,画出其对应的哈斯图.
3)如果构成偏序集,该偏序集合构成哪种格?(分配格、有界格、有补格、布尔格). 第七题图论
1.是否存在7阶无向简单图G,其度序列为1、3、3、4、6、6、7.给出相应证明.
2.求下图的补图.(无答案)
3. 1)试画一个具有5个顶点的自补图
2)是否存在具有6个顶点的自补图,试说明理由。
4. 设图G为n(n>2且为奇数)阶无向简单图,证明:G与G的补图中奇度顶点个数相等.
5. 无向图G中只有2个奇度顶点u和v,u与v是否一定连通.给出说明或证明。
6.图G如下图所示:
1)写出上图的一个生成子图.(不唯一)
2)δ(G),κ(G),λ(G).
7. 在什么条件下无向完全图K n为欧拉图?
8. 证明:有割边的图不是欧拉图.
9.证明:有割边的图不是哈密尔顿图.
10.树T有2个4度顶点,3个3度顶点,其余顶点全为树叶,问T有几片树叶?
11.给出全部互不同构的4阶简单无向图的平面图形。
12.如果G是平面图, 有n个顶点、m条边、f个面,G有k个连通分支。
试利用欧拉公式证明::n-m+f=k+1.。
