西南大学2020秋季初等数论【0346】
2020年自考《初等数论》专业考试题库及答案

2020年⾃考《初等数论》专业考试题库及答案2020年⾃考《初等数论》专业考试题库及答案⼀填空题(每空2分)1.写出30以内的所有素数 2,3,5,7,11,13,17,19,23,29 .2.,(,)(,)(,)a b a b a b a b =设是任意两个不为零的整数,则 1 . 3.若,a b 是⾮零整数,则a 与b 互素的充要条件是存在整数,x y ,适1ax by +=4.写出180的标准分解式是 22235?? ,其正约数个数有 (2+1)(2+1)(1+1)=18个.5.,1,2,,a b a b L 设与是正整数则在中能被整除的整数恰有 []ab个.6.设,a b 是⾮零整数,c 是整数,⽅程ax by c +=有整数解(,x y )的充要条件是 (,)|a b c7. 若整数集合A 是模m 的完全剩余系,则A 中含有 m 个整数.8.?(3)= 2 ;?(4)= 2 .9.当p 素数时,(1)()p ?= 1p - ;(2)()k p ?= 1k k p p -- . 10.(),(,)1,1m m a m a ?=-≡设是正整数则 0 (mod ).m 11.,,p p a a a -≡设是素数则对于任意的整数有 0 (mod ).p 12.已知235(mod7)x +≡,则x ≡ 1 (mod 7).13.同余⽅程22(mod 7)x ≡的解是 4(mod7) . 14.同余⽅程2310120(mod 9)x x ++≡的解是 .X=6. . 15.(,)1n p =若,n p 是模的⼆次剩余的充要条件是 -121(mod ).p n p ≡ . 16.(,)1n p =若,n p 是模的⼆次⾮剩余的充要条件是 -121(mod ).p np ≡- .17.3()=5 -1 ; 4()=5 1 .18.,p 设是奇素数则2()p=218(1).p --.19.,p 设是奇素数则1()p = 1 ;-1()p= -12(-1).p .20. 5()=9 1 ; 2()=45-1 .⼆判断题(判断下列结论是否成⽴,每题2分). 1. ||,|a b a c x y Z a bx cy ?∈+且对任意的有.成⽴2. (,)(,),[,][,]a b a c a b a c ==若则.不成⽴3. 23|,|a b a b 若则.不成⽴4.(mod ),0,(mod ).a b m k k N ak bk mk ≡>∈?≡成⽴5.(mod )(mod ).ac bc m a b m ≡?≡不成⽴6. 22(mod ),(mod )(mod )a b m a b m a b m ≡≡≡-若则或⾄少有⼀个成⽴. 不成⽴ 7. 222(mod ),(mod )a b m a b m ≡≡若则.不成⽴8. 若x 通过模m 的完全剩余系,则x b +(b 是整数)通过模m 的完全剩余系. 成⽴ 9. 1212{,,,}{,,,}.m m a a a b b b L L 若与都是模m 的完全剩余系不成⽴1122{,,,}.m m a b a b a b m +++L 则也是模的完全剩余系不成⽴10.若(,)1a m =,x 通过模m 的简化剩余系,则ax b +也通过模m 的简化剩余系. 不成⽴ 11.12121212,,(,)1,()()().m m N m m m m m m ∈==若则成⽴12. 同余⽅程24330(mod15)x x -+≡和同余⽅程2412120(mod15)x x +-≡是同解的. 成⽴13. (mod ).ax b m ax my b ≡+=同余⽅程等价于不定⽅程成⽴14. 2,(mod ),() 1.am x a m m≡=当是奇素数时若有解则成⽴15. 2,()1,(mod ).a m x a m m=≡当不是奇素数时若则⽅程⼀定有解不成⽴三计算题1. (1859,1573)-求.(6分)解:1.(1859,1573)(1859,1573)(286,1573)(286,15732865)(286,143)(0,143)143-===-?===2.求 [-36,108,204].(8分)解:22232232.[36,108,204][36,108,204],3623,10823,2042317,[36,108,204]23171836.-==?=?=??∴=??=Q3. 求(125,17),以及x ,y ,使得125x +17y =(125,17).(10分)解:3.651,16-56-(17-26)36-173(125-177)-173125-2217.1253-17221,3,-22.x y =+==?=?=??=??∴??===由等式起逐步回代得4. 求整数x ,y ,使得1387x -162y =(1387,162).(10分)解:4.9421,19-429-4(11-9)59-4115(20-11)-411520-911520-9(71320)322097132(91-71)97132914171329141(16291)73914116273(13878162)41162731387625162.1=?+=?=?=??=??=??=??-?=?-?=?-?=?-?=?-?-=?-?=?-?-?=?-?∴由等式起逐步回代得38773162625 1.-=5. 12!.分解为质因数乘积(8分)6. ,10|199!k k 求最⼤的正整数使.(8分)7. [1+L 求(10分) 8. 81743.x y +=求⽅程的整数解(6分)9.求⽅程19 x +20y=1909的正整数数解。
初等数论Z_华中师范大学20年春季考题库及答案共2个文档这是其中一个

A. x≡25(mod47)
B. x≡29(mod47)
C. x≡35(mod47)
D. x≡37(mod47)
[答案]:A
[一级属性]:
[二级属性]:
[难度]:
[公开度]:
3.如果n是一个自然数,那么n(n+1)是()
A.奇数
B.偶数
C.奇数或偶数
D. 3
[答案]:A
[一级属性]:
[二级属性]:
[难度]:
[公开度]:
18.取1元、2元、5元的硬币共10枚,付出18元,有()种不同的付法
A. 1
B. 2
C. 3
D. 4
[答案]:C
[一级属性]:
[二级属性]:
[难度]:
[公开度]:
19.如果a≡b(mod q),c≡d(mod q),则有()
A. a+c≡bd(mod q)
[二级属性]:
[难度]:
[公开度]:
10.所有不超过156的正整数中,7的倍数有()个
A. 20
B. 21
C. 22
D. 23
[答案]:C
[一级属性]:
[二级属性]:
[难度]:
[公开度]:
11.设n,m为整数,如果3|n,3|m,则9()nm
A.整除
B.不整除
C.等于
D.小于
[答案]:A
[一级属性]:
[二级属性]:
[难度]:
[公开度]:
3. 24871与3468的最大公因数是()
A. 11
B. 13
C. 3
D. 4
[答案:D
[一级属性]:
2020年秋学期西南大学[0346]《初等数论》作业3答案
![2020年秋学期西南大学[0346]《初等数论》作业3答案](https://img.taocdn.com/s3/m/6115dc68b14e852459fb5781.png)
填空题答案
1.7除29的商是 4 。
2.12除26的余数是 2 。
3.5的正因数是 1, 5 。
4.{4.5}= 0.5 。
5.[8.3] +[-8.3] = -1 。
6.30的最小质因数是 2 。
7.在所有质数中,是偶数的是 2 。
8.在所有质数中,最小的奇质数是 3 。
9.大于4小于16的素数有___5,7,11,13__ ____。
10.不定方程c by ax =+有整数解的充分必要条件是 (a ,b )|c 。
11.模5的最小非负完全剩余系是 0,1,2,3,4 。
12.模4的绝对最小完全剩余系是 -1,0,1,2 。
13.5555的个位数是 5 。
14.77的个位数是_______ 3 ________。
15.316的十进位表示中的个位数字是 1 。
16.66的个位数是 6 。
17.710被11除的余数是 1 。
18.(1516,600)= 4 。
19.6的所有正因数的和是 12 _。
20.24与60的最大公因数是 12 。
21.35的最小质因数是 5 。
22.46的个位数是 6 。
23.8的所有正因数的和是 15 _。
24.18的标准分解式为 23218⨯= 。
25.20的欧拉函数值)20(ϕ= 8 。
西南大学专业
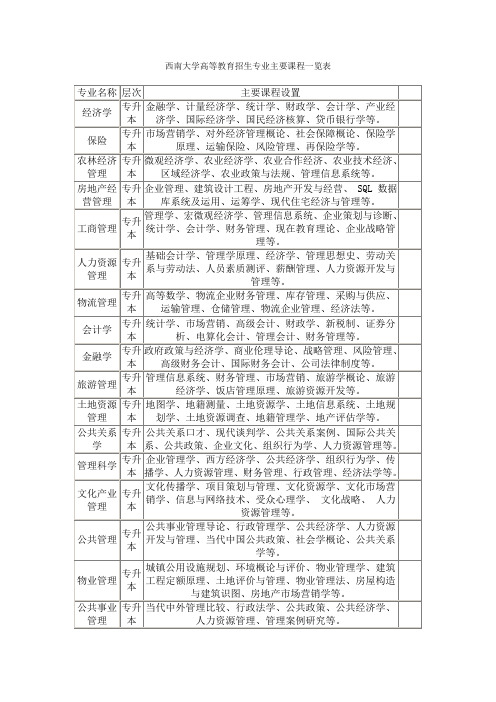
专升本
视唱练耳、歌曲作法、中国音乐史、欧洲音乐史、曲式学概论、复调常识、钢琴、声乐、专业论文写作等。
汉语言文学
高起本
中国现代文学、中国当代文学、中国古典文学、外国文学、中学语文教学法、书法、古代散文诗歌研究、西方现代派文学、新文学思潮与流派等。
计算机科学技术
高起本
电路原理、模拟电子技术、数字逻辑、数字分析、计算机系统结构、计算机网络、高级语言、汇编语言、数字结构、系统分析与控制、信号处理原理、通信原理概论等。
房地产经营管理
专升本
企业管理、建筑设计工程、房地产开发与经营、SQL数据库系统及运用、运筹学、现代住宅经济与管理等。
工商管理
专升本
管理学、宏微观经济学、管理信息系统、企业策划与诊断、统计学、会计学、财务管理、现在教育理论、企业战略管理等。
人力资源管理
专升本
基础会计学、管理学原理、经济学、管理思想史、劳动关系与劳动法、人员素质测评、薪酬管理、人力资源开发与管理等。
农学
专升本
植物生理学、遗传学、农业试验设计、粮食作物学、经济作物学、作物育种学、耕作与生态学、农业企业经营管理等。
动物医学
专升本
动物解剖与组织胚胎学、动物生理学、动物生物化学、兽医药理学、畜禽病理学、兽医微生物学与免疫学、兽医内科诊断学、畜禽流行病学、兽医卫生检验等。
动物科学
专升本
动物生理与生化学、动物遗传学、家畜育种学、动物营养学、饲料与饲养学、动物繁殖学、家畜环境卫生学、动物生产学、草地学等。
管理学原理、区域经济学、房地产开发、房屋建筑学、房地产估价、房地产经济学、物业管理概伦、房地产项目管理、房地产营销学等。
金融学
高起本
经济学、会计学、企业组织与环境、商务交流、财务管理、数量方法、管理会计、财务报表分析、组织行为学、电子商务概论、政府政策与经济学等。
2015秋季西南大学初等数论大作业答案

因为p、p+1、p+2除以3余数不同,p、p+2都不被3整除,所以p+1被3整除.
于是6是p+1的因数.
\
6.叙述孙子定理的内容。
11.孙子定理的内容为:设 是k个两两互质的正整数,
(1)
设 ,
则同余式组(1)的解是
(2)
其中 是满足 的任一个整数,i=1,2,…,k。
三、计算题(每小题8分,共40分)
1.求210与55的最大公因数。
答:210=2x3x5x7 ,55=5x11 210与55的最大公因数是5.
1.叙述整数a被整数b整除的概念。
答:设a,b是任意两个整数,其中b≠0,如果存在一个整数q使得等式a=bq成立,我们就称b整除a或a被b整除,记做b|a
2.叙述质数的概念,并写出小于14的所有质数。
答一个大于1的整数,如果它的正因数只有1和它本身,就叫作质数(或素数)。14的所有质数2,3,5,7, 11,13.
性质3①若a1=b1(mod m),a2=b2(mod m),则a1+ a2 =b1+ b2( (mod m)
②若a+b≡c(mod m),则a≡c-b(mod m)
5. 196是否是3的倍数,为什么?
答:196不是3的倍数。因为由定义可知设a,b是任意两个整数,其中b≠0,如果存在一个整数q使得等式a=bq成立,则将a叫做b的倍数。所以a=196,b=3,不存在一个整数q使得等式a=bq成立,所以196不是3的倍数。
西南大学网络与继续教育学院课程考试答题卷
学号:1513150663001姓名:陈琛层次:专科起点本科
类别:网教专业:数学与应用数学(数学教育)2015年11月西南大学网络教育鹰潭职业技术学院学习中心
奥鹏2020年6月福师《初等数论》在线作业一_3.doc

1.9x+11y=100的正整数解的个数是()A.0B.1C.2D.无穷【参考答案】: B2.题见图片A.AB.BC.CD.D【参考答案】: B3.题见图片A.AB.BC.CD.D【参考答案】: C4.被3除余1,被5除余4,被11除余5的最小正整数一定处于()的区间A.[10,20]B.[20,30]C.[30,40]D.[40,50]【参考答案】: D5.100!的末尾0的个数是()A.20B.21C.24D.25【参考答案】: C6.p为素数是2^(2^p)+1为素数的()A.充分条件B.必要条件C.充要条件D.既非充分也非必要条件【参考答案】: B7.。
A.AB.BC.CD.D【参考答案】: A8.整数202()A.能够写成两数平方和B.能够写成两数平方差C.都可以D.都不能【参考答案】: A9.题见图片A.AB.BC.CD.D10.题见图片A.AB.BC.CD.D 【参考答案】: B11.题见图片A.AB.BC.CD.D 【参考答案】: B12.。
A.AB.BC.CD.D13.题见图片A.AB.BC.CD.D【参考答案】: B14.100!最高能被45的()次幂整除A.20B.23C.24D.48【参考答案】: C15.题见下图A.AB.BC.CD.D【参考答案】: A16.题见图片A.AB.BC.CD.D【参考答案】: B17.a,b大于1且互素,则不定方程ax-by=ab的正整数解的个数是()A.0B.1C.2D.无穷【参考答案】: D18.。
A.AB.BC.CD.D【参考答案】: A19.题见图片A.AB.BC.CD.D 【参考答案】: B20.题见图片A.AB.BC.CD.D 【参考答案】: B21.题见图片A.AB.BC.CD.D 【参考答案】: B22.。
A.AB.BC.CD.D 【参考答案】: D23.。
A.AB.BC.CD.D 【参考答案】: A24.。
A.AB.BC.CD.D 【参考答案】: A25.题见图片A.AB.BC.CD.D 【参考答案】: B26.题面见图片A.错误B.正确【参考答案】: A27.题面见图片A.错误B.正确【参考答案】: B28.题面见图片A.错误B.正确【参考答案】: A29.题见图片A.错误B.正确【参考答案】: B 30.题见图片A.错误B.正确【参考答案】: B 31.题见图片A.错误B.正确【参考答案】: B 32.题见图片A.错误B.正确【参考答案】: B 33.题见图片A.错误B.正确【参考答案】: B34.题面见图片A.错误B.正确【参考答案】: B 35.题见图片A.错误B.正确【参考答案】: B 36.题见下图A.错误B.正确【参考答案】: A37.题面见图片A.错误B.正确【参考答案】: A 38.题见图片A.错误B.正确【参考答案】: B 39.题见下图A.错误B.正确【参考答案】: A40.题面见图片A.错误B.正确【参考答案】: B 41.题见图片A.错误B.正确【参考答案】: B42.题面见图片A.错误B.正确【参考答案】: B 43.题面见图片A.错误B.正确【参考答案】: AA.错误B.正确【参考答案】: B 45.题见下图A.错误B.正确【参考答案】: A 46.题见图片A.错误B.正确【参考答案】: B 47.题见图片A.错误B.正确【参考答案】: B48.题面见图片A.错误B.正确【参考答案】: AA.错误B.正确【参考答案】: A 50.题见下图A.错误B.正确【参考答案】: A。
2016年初等数论第四次作业答案

2016年西南大学初等数论第四次作业证明题1. 设n 是整数,证明6 | n (n + 1)(2n + 1)。
证明:n (n + 1)(2n + 1) = n (n + 1)(n – 1) + n (n + 1)(n + 2)。
n (n + 1)(n – 1)是三个连续整数的积,n (n + 1)(n + 2)也是三个连续整数的积, 而三个连续整数的积可被6整除,所以6 | n (n + 1)(n – 1),6 | n (n + 1)(n + 2)。
由整出的性质可得6 | n (n + 1)(2n + 1)。
2. 设n 是整数,证明:n n -3|6。
证明:)1)(1(3+-=-n n n n n 。
由于)1)(1(+-n n n 是3个连续整数的积,所以n n -3|3。
由于)1(-n n 是2个连续整数的积,所以n n -3|2。
又(2,3)= 1,所以n n -3|6。
3. 设x ,y 均为整数。
证明:若y x 2|7+,则y x 610|7+。
证明:)2(37610y x x y x ++=+,因为y x 2|7+,所以)2(3|7y x +, 因为7|7,所以7|7x ,从而)2(37|7y x x ++,所以y x 610|7+4. 设x ,y 均为整数。
证明:若y x 9|5+,则y x 78|5+。
证明:y y x y x 65)9(878-+=+。
因为y x 9|5+,所以)9(8|5y x +。
又因为5|65,所以5|65y 。
从而y y x 65)9(8|5-+,所以y x 78|5+。
5.设x 是实数,n 是正整数,证明:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡n x n x ][。
证明:设⎥⎦⎤⎢⎣⎡=n x a ,则1+<≤a n x a ,所以)1(+<≤a n x na 。
因为na 与n (a +1)都是整数,所以)1(][+<≤a n x na , 于是1][+<≤a n x a ,从而a n x =⎥⎦⎤⎢⎣⎡][,所以 ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡n x n x ][。
电大《初等数论》2020-2021期末试题及答案

A.一2,一l,0,1,2
B.一5,一4,一3,一2,一l
C.1,2,3,4,5
D.0,ห้องสมุดไป่ตู้,2,3,4
5.如果( ),则不定方程口ax+by=c有解.
A.(a,b)|c B.c|(a,b)
C.a|cD.(a,b)|a
6.整数637693能被( )整除.
A.3B.5
2.求解不定方程4x+12y=8.
解:因为(4,12)=418,所以有解化简x+3y=2,则有x=-l,y=l通解为x=一l+3t,y= l一t
3.解同余式12x+4≡o(mod7).
解:因为(12,7)=1|4,所以有解,而且解的个数为1……
变形l2x一7y=一4…
·简单计算x≡2(mod7).
4.解同余式z2≡2(mod23)
C.7 D.9
二、填空题(每题4分,共24分)
1.X=[x]+
2.同余式111x≡75(mod321)有解,而且解的个数.
3.在176与545之间有——是l7的倍数.
4.如果ab>0,则[a,b](a,b)=.
5.a,b的最小公倍数是它们公倍数的.
6.如果(a,6)=1,那么(ab,a+b)=.
三、计算题(共32分)
(供参考)
一、单项选择题(每题4分。共24分)
1.B 2.D 3.B 4.A 5.D 6.A
二、填空题(每题4分。共24分)
1.{X)
2.3
3.12
4.Ab
5.因数
6.1
三、计算题(每题8分。共32分)
1.求(336,221,391)=?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学期:2020年秋季
课程名称【编号】:初等数论【0346】A卷
考试类别:大作业 满分:100分Βιβλιοθήκη 每题分值20分,选做5个题。
1.简述题:叙述整除的概念,并判断6是否整除24,8是否整除42。
答:整除就是若整数“a” 除以大于0的整数“b”,商为整数,且余数为零。 我们就说a能被b整除(或说b能整除a),记作b|a,读作“b整除a”或“a能被b整除”.注意a or b作除数的其一为0则不叫整除。
答:在数论,对正整数n,欧拉函数是小于或等于n的正整数中与n互质的数的数目(因此φ(1)=1)。此函数以其首名研究者欧拉命名(Euler's totient function),它又称为Euler's totient function、φ函数、欧拉商数等。例如φ(8)=4,因为1,3,5,7均和8互质。从欧拉函数引伸出来在环论方面的事实和拉格朗日定理构成了欧拉定理的证明。
可得出φ(5)=1,φ(6)=3.
4.计算题:求220的标准分解式。
答:220=2*2*5*11
5.计算题:求3201除以8的余数。
6.计算题:求不定方程 的一切整数解。
答:不定方程ax+by=c的一组特解是x0,y0,(a,b)是a,b的最大公约数,那么方程的一切整数解是:
x=x0-b/(a,b)t,y=y0+a/(a,b)t,t是整数。
用在这个题上,先找到方程的一组特解: x0=2,y0=1
又因(3,5)=1,则可得x=2+5t,y=1+3t(t为整数)
7.计算题:解同余式 。
8.证明题:证明一切奇质数都可以表成 的形式(其中m是正整数)。
答:两个整数除了1以外没有其他的公约数了,这两个整数称为互质的整数.例如:8与15的公约数只有一个1,没有其它的公约数了,所以8与15就是两个互质的整数.又如:8与12的公约数除了1之外,还有一个公约数4,所以8与12就不是两个互质的整数.因此可以判断12和25是互质。
3.简述题:叙述欧拉函数 的概念,并求欧拉函数值 和 。
整除的性质:(1)如果a与b都能被c整除,那么a+b与a-b也能被c整除;(2)如果a能被b整除,c是任意整数,那么积ac也能被b整除;(3)如果a同时被b与c整除,并且b与c互质,那么a一定能被积bc整除.反过来也成立.因此得出,6可以整除24,但是8不能整除42.
2.简述题:叙述两个整数互质的概念,并判断12与25是否互质。
