北京科技大学自动控制理论习题集
北京科技大学第1-8章作业答案(必做题)

(b)
解:求反馈通道的传函
R(s)
C (s)
G1 ( s )
G2 ( s )
H1 (s) 1 H1 (s) H 2 (s)
G1 ( s)G2 ( s) 1 H1 ( s) H 2 ( s) G1 ( s) C ( s) G2 ( s) H1 ( s) R( s ) 1 G ( s) 1 G1 ( s) H1 ( s) H1 ( s) H 2 ( s) 1 1 H1 ( s) H 2 ( s)
2 1 (0) sc(0) 3c(0) R ( s ) c 2 2 s 3s 2 s 3s 2 2 1 2 R( s) 2 ( s 3) 零初态响应C1(s) 零输入响应C2(s) s 3s 2 s 3s 2
所以零初态响应:
2 1 1 2 1 C1 ( s) 2 , c1 (t ) 1 2et e 2t s 3s 2 s s s 1 s 2
零输入响应:
1 2 1 C2 ( s ) 2 ( s 3) , c2 (t ) 2e t e 2t s 3s 2 s 1 s 2
系统的输出响应: c(t ) c (t ) c (t ) 1 4et 2e2t 1 2
2-4 如图,已知G(s)和H(s)两方框相对应的微分方程分 别是: dc(t ) 6 10c(t ) 20e(t ) dt db(t ) 20 5b(t ) 10c(t ) dt
E (s) 1 10 R( s) 1 G (s) H (s) 1 10 20 10 6s 10 20s 5 10(6 s 10)(20s 5) 10(12s 2 23s 5) 2 120s 230s 250 12s 2 23s 25
北科大自动控制理论试题B及答案
1. 试在图 5 上作出系统的开环对数渐近幅频曲线及相频曲线。
1 s (0.1s � 1) 2
负反馈系统的开环传递函数: G ( s ) H ( s ) �
试在图 4 上作开环增益 K(由 0→∞)变动下系统的根轨迹,并确定保证系统闭环稳定时 K 值的允许变化范围。
K (0.2s � 1) 。 s ( s � 1) 2
姓名: 题号 得分
得 分 评卷人 一、填空题(每空 2 分,共 16 分) 1. 2. 3.
已知某单位反馈系统的开环传递函数为 G( s) � σ%及 t s。
16 ,试求单位阶跃响应的性能指标 s � 6s
2
班级: 一 二
得 分
评卷人 三、分析题(共 20 分)
自动控制通常可分为:开环控制、 连续系统稳定的充要条件是 任何系统的时间响应由 态响应两部分组成。 和稳
及 。
三种控制模式。
1.已知系统输入信号 r (t ) � t � 1(t ) ,输出信号 c(t ) � t � T (1 � e 递函数 G ( s )。
�t / T
), (t≥0) 。试求其传
4.
描述如图所示电路的输出 uc(t)、输入 ur(t)的微 分方程为 。
ur(t)
R
i(t)
C
uc(t)
��
E ( s) C ( s) C ( s ) 1 � K 0 K1 K 4 �� �� � N (s) N ( s) R ( s ) K 0 K1 K 2
1 � K 0 K1 K 4 K 0 K1 K 2 G1 � (1 � K 0 K1 K 4 � K1 K 2 K 3 G1 � K 0 K1 K 2 K 5 G1 ) K 0 K1 K 2
北京科技大学自动控制理论复习

推论3:如果当时间趋于无穷时,线性定常系统的阶 跃响应函数趋于某一个常数,则该线性定常系统稳定。
劳 斯 稳 定 判 据
2019/4/8
系统渐进稳定的必要条件是特征方程的系数均大于零。 如果劳斯表中第一列的系数均为正值,则其特征方程式 的根都在S的左半平面,相应的系统是稳定的。 ③如果劳斯表中第一列系数的符号有变化,则符号的变化 次数等于该特征方程式的根在S的右半平面上的个数,相 应的系统为不稳定。
线性系统稳定性分析的理论框架
稳定性分析 解析 方法 SISO的代数 分析方法 Routh判据 Houwitz判据 1892年俄国数学 家李雅普诺夫
根据SISO闭环特 征方程的系数判 定系统的稳定性
2019/4/8
北京科技大学自动化学院控制系
25
由稳定性定义可知:
1)线性系统的稳定性取决于系统自身的固 有特征(结构、参数),与系统的输入 信号无关。
2019/4/8 北京科技大学自动化学院控制系 19
0
收敛
稳定 临界稳定 不稳定
有阻尼 无阻尼 负阻尼
0 等幅振荡 0 发散 对于 0 有: 0 1 振荡收敛
1 1
欠阻尼
临界阻尼
虽是单调的 但介于振荡与不振荡之间 单调收敛
过阻尼
对于 0 有:
L1 ——信号流图中所有不同回环的传输之和;
L2 ——信号流图中每两个互不接触回环的传输乘积之
和; …… …… Lm ——m个互不接触回环的传输乘积之和;
k ——称为第k条通路特征式的余因子,是在Δ中除去
第k条前向通路相接触的各回环传输(即将其置 零)。
2019/4/8
北京科技大学自动化学院控制系
北京科技大学第1-8章作业答案(必做题)

第二章作业
2-1:试求图中以电枢电压ua为输入量,以电动机转角 θ为输出量的微分方程形式和传递函数。
解 Q m (t) &(t) 系统运动方程为:
d 3 (t)
d 2 (t)
d (t)
La Jm dt3 (La fm Ra Jm ) dt 2 (Ra fm CmCe ) dt
Cmua (t)
s2C(s) sc(0) c&(0) 3sC(s) c(0) 2C(s) 2R(s)
C(s)
s2
2 3s
2
R(s)
s2
1 3s
2
c&(0)
sc(0)
3c(0)
s2
2 3s
2
R(s)
s2
1 3s
2
(s
3)
零初态响应C1(s)
零输入响应C2(s)
阶跃输入 r(t) 1(t) 时, R(s) 1
y0.25 y 12.1137y
2-3
设系统传递函数为:C ( s) R(s)
s2
2 3s
2
且初始条件 c(0) 1,c&(0) 0 。
试求阶跃输入r(t)=1(t)时,系统的输出响应
c(t)。
解:系统的传递函数:
C(s) R(s)
s2
2 3s
2
初始条件: c(0) 1,c&(0) 0
微分方程: c&&(t) 3c&(t) 2c(t) 2r(t) 拉氏变换可得:
系统方块图如图所示:
1-2图是电炉温度控制系统原理示意图。试分析系统保持 电炉温度恒定的工作过程,指出系统的被控对象、被控 量以及各部件的作用,最后画出系统方块图。
北京科技大学自动控制原理课后习题答案
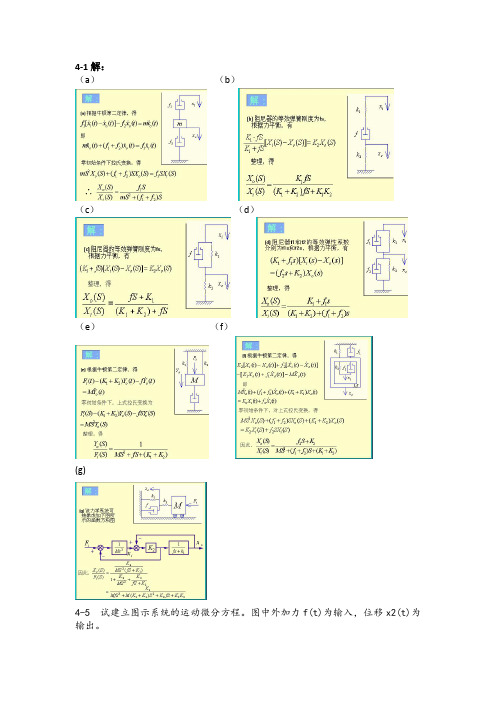
4-1解:(a)(b)(c)(d)(e)(f)(g)4-5试建立图示系统的运动微分方程。
图中外加力f(t)为输入,位移x2(t)为输出。
解:⎪⎪⎩⎪⎪⎨⎧=--⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛----2222222221321212131111)(dt x d m x K dt dx B dt dxdt dx B dt x d m dt dx dt dx B dt dx B x K t f dt t df B x K K dt dx B K B K B K B K dt x d B B B B B B K m K m dt x d B m B m B m B m dt x d m m )()()()(322123212312122232312112213233212312142421=++++++++++++++解:对图示阻容网络,根据复阻抗的概念,有:)()(212s U Z Z Z s U i o +=22222211sC C sR sC R Z +=+=4-6对于图4.64所示系统,试求:1、从作用力f1(t)到位移x2(t)的传递函数2、从作用力f2(t)到位移x1(t)的传递函数3、从作用力f1(t)到位移x1(t)的传递函数4、从作用力f2(t)到位移x2(t)的传递函数(b)5-1温度计的传递函数为1/(Ts+1),现用该温度计测量一容器内水的温度,发现需要1min 的时间才能指示出实际水温98%的数值,求此温度计的时间常数T 。
若给容器加热,使水温以10C/min 的速度变化,问此温度计的稳态指示误差是多少?解:温度计的单位阶跃响应为:T t o e t x /1)(--=由题意:()T o o e x x /601)()(98.0--∞=∞5-7对图示系统,要使系统的最大超调量等于0.2,峰值时间等于1s,试确定增益K和Kh 的数值,并确定此时系统的上升时间tr和调整时间ts。
5-10某单位反馈系统如图所示,试求在单位阶跃、单位速度和单位加速度输入信号作用下的稳态误差。
(完整版)自动控制理论试题及答案

二000年下半年高等教育自学考试全国统一命题考试自动控制理论试题(电力系统及其自动化专业·本科)本试题分两部分,第一部分为选择题,1页至2页,第二部分为非选择题,2页至8页,共8页,共8页;选择题20分,非选择题80分,满分100分。
考试时间150分钟。
第一部分 选择题一、单项选择题(本大题共15小题,前10小题每题1分,后5小题每题2分,共20分)在每小题列出的四个选项中有一个选项是符合题目要求的,请将正确选项前的字母填在题后的括号内。
1.实际生产过程的控制系统大部分是 【 】A.一阶系统B.二阶系统 C.低阶系统 D.高阶系统2.若开环传递函数G(s)H(s)不存在复数极点和零点,则 【 】A. 没有出射角和入射角 B. 有出射角和入射角C. 有出射角无入射角落D. 无出射角有入射角3.若开环传递函数为()1)(+=Ts s K s G , 此时相位裕量和K的关系是 【 】 A. 随K 增加而增大 B.随K 增大而减小C.以上都不是D.与K 值无关4.超前校正装置的最大超前相角 【 】 A. 11sin 1+--ββ B. 11sin 1-+-ββ C. 11cos 1+--ββ D.11cos 1-+-ββ 5.对于同一系统的状态变量和状态空间描述具有 【 】 A. 状态变量具有唯一性,状态空间描述具有非唯一性B. 状态变量具有非唯一性,状态空间描述具有唯一性C. 状态变量具有非唯一性,状态空间描述也具有非唯一性D. 状态变量具有唯一性,状态空间描述也具有唯一性6.在工程问题中,常用______数学模型来表达实际的系统。
【 】A. 精确的 B. 复杂的 C. 简化的 D. 类似的7. 正弦输入函数r(t)的数学表达式是 【 】A.t t r ωsin )(=rB. )sin()(θω+=t t rC.)sin()(θω+=t A t rD.)cos()(θω+t A t r8.二阶振荡环节的对数幅频特性的高频段的渐近线斜率为_______dB/dec 。
《自动控制理论》作业集参考答案(专本科函授)第一部分.

此为第一部分如合适,请再下第二部分1-6解 控制系统的任务是使摄像机自动跟踪光点显示器指示的方向。
当摄像机方向角与光点显示器指示的方向一致时,12θθ=,自整角机输出0=e ,交流放大器输出电压0=u ,电动机静止,摄像机保持原来的协调方向。
当光点显示器转过一个角度,12θθ≠时,自整角机输出与失谐角21θθθ-=∆成比例的电压信号(其大小、极性反映了失谐角的幅值和方向),经电位器后变成e ,经放大器放大后驱动伺服电动机旋转,并通过减速器带动摄像机跟踪光点显示器的指向,使偏差减小,直到摄像机与光点显示器指向重新达到一致时为止。
测速发电机测量电动机转速,进行速度反馈,用以改善系统性能。
系统中,摄像机是被控对象,摄像机的方向角2θ是被控量,给定量是光点显示器指示的方向角1θ。
系统方框图如图解1-6所示。
参 考 答 案第一章1-1解 (1)负反馈连接方式为:d a ↔,c b ↔; (2)系统方框图如图解1-1 所示。
1-3解 加热炉采用电加热方式运行,加热器所产生的热量与调压器电压c u 的平方成正比,c u 增高,炉温就上升,c u 的高低由调压器滑动触点的位置所控制,该触点由可逆转的直流电动机驱动。
炉子的实际温度用热电偶测量,输出电压f u 。
f u 作为系统的反馈电压与给定电压r u 进行比较,得出偏差电压e u ,经电压放大器、功率放大器放大成a u 后,作为控制电动机的电枢电压。
在正常情况下,炉温等于某个期望值T °C ,热电偶的输出电压f u 正好等于给定电压r u 。
此时,0=-=f r e u u u ,故01==a u u ,可逆电动机不转动,调压器的滑动触点停留在某个合适的位置上,使c u 保持一定的数值。
这时,炉子散失的热量正好等于从加热器吸取的热量,形成稳定的热平衡状态,温度保持恒定。
当炉膛温度T °C 由于某种原因突然下降(例如炉门打开造成的热量流失),则出现以下的控制过程:控制的结果是使炉膛温度回升,直至T °C 的实际值等于期望值为止。
北京科技大学《自动控制原理》复习

ci
s ir1 pi
ci
lim (s
s pi
pi )G(s)
i r 1,, n
c1i
1
d i1
(i
1)!
lim
s p1
dt
i1
(s
p1)r G(s)
i 1, , r.
p1
•
x
1
0
1 p1
0
p r 1
0
x
1
u
1
pn 1
y c11 c1r cr1 cn x
电位器
G(s) K
测速电机 G(s) Ks
电加热炉 单容水槽 双容水槽
G(s) K Ts 1
G(s) K Ts 1
G(s) K e s (有纯延迟)
Ts 1
(也可有延迟,略) K
G(s) T1T2s2 (T1 T2 )s 1
• 比例环节
• 一阶惯性环节 • 积分环节 • 微分环节、一阶微分环节 • 二阶振荡环节 • 二阶微分环节 • 延迟/时滞环节
5、高阶系统的时域分析
主导极点:在高阶系统中某一极点或一对共轭复数极点距虚轴的距 离是其它极点距虚轴距离的1/5或更小,并且附近没有闭环零点,称 该极点(对)为该高阶系统的主导极点。
①用主导极点来估计高阶系统的性能指标 ②导出高阶系统单位阶跃响应的近似表达式
偶极子: 指相距很近的一对零、极点。
6、线性系统状态方程的解 状态转移矩阵性质:
sa
(s a)2 2
控制系统的数学描述
定义: 单输入单输出线性定常动态对象的传递函数G(S)是零初值下
该对象的输出量的拉普拉斯变换Y(S)与输入量的拉普拉斯变换U(S)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自动控制理论习题集北京科技大学自动化学院控制系2014.4目录第一章 (1)第二章 (4)第三章 (14)第四章 (24)第五章 (28)第六章 (35)第七章 (40)第八章 (41)《自动控制理论习题集》第一章1、试述开环控制系统的主要优缺点。
2、题图1为液位自动控制系统示意图。
在任何情况下,希望液面高度c维持不变,试说明系统工作原理,并画出系统原理方框图。
题图1 液位自动控制系统示意图3、如题图2(a)、(b)所示两水位控制系统,要求(1)画出方块图(包括给定输入量和扰动输入量);(2)分析工作原理,讨论误差和扰动的关系。
题图24、如题图3所示炉温控制系统,要求:(1)指出系统输出量、给定输入量、扰动输入量、被控对象和自动控制器的各组成部分并画出方块图;(2)说明该系统是怎样得到消除或减少偏差的。
5、题图4是液位自动控制系统原理示意图。
在任意情况下,希望液面高度c维持不变,试说明系统工作原理并画出系统方块图。
题图3题图4 液位自动控制系统6、题图5是仓库大门自动控制系统原理示意图。
试说明系统自动控制大门开闭的工作原理并画出系统方块图。
题图5 仓库大门自动开闭控制系统7、说明负反馈的工作原理及其在自动控制系统中的应用。
8、开环控制系统和闭环控制系统各有什么优缺点?9、对自动控制系统基本的性能要求是什么?最主要的要求是什么?10、题图6所示为温度控制系统的原理图。
指出系统的输入量和被控量,并画出系统框图。
题图6 温度控制系统的原理图11、自动控制系统主要组成部分是什么?各个组成部分有什么功能?12、如题图7是液位自动控制系统原理示意图。
在任意情况下,希望液面高度c维持不变,试说明系统工作原理并画出系统方块图。
题图713、如题图8是电炉温度控制系统原理示意图。
试分析系统保持电炉温度恒定的工作过程,指出系统的被控对象、被控量以及各部件的作用,最后画出系统方块图。
题图8第二章1、试简化题图1中所示系统的结构图,并求传递函数C(s)/R(s)。
题图1 系统结构图2、已知单摆系统的运动如题图2所示。
(1) 写出运动方程式;(2) 求取线性化方程。
题图2 单摆系统运动示意图3、RC无源网络电路图如题图3所示,试采用复数阻抗法画出系统结构图,并求传递函数Uc(s)/Ur(s)。
题图3 RC无源网络4、有源网络如题图4所示,试用复阻抗法求网络传递函数,并根据求得的结果,直接用于题图5所示PI调节器,写出传递函数。
5、求下列微分方程的时域解x (t )。
已知3)0(,0)0(==xx 。
06322=++x dtdxdt x d6、已知系统结构图如题图6所示,试用化简法求传递函数C (s )/R (s )。
7、已知系统结构图如题图7所示,试用化简法求传递函数C (s )/R (s )。
8、已知机械系统如题图8(a )所示,电气系统如题图8(b )所示,试画出两系统结构图,并求出传递函数,证明它们是相似系统。
9、RC 网络如题图9所示,其中u 1为网络输入量,u 2为网络输出量。
题图4 有源网络题图5 PI 调节器题图6 系统结构图题图7 系统结构图题图8 系统结构图(a )机械系统(b )电气系统(1)画出网络结构图; (2)求传递函数U 2(s )/ U 1(s )。
10、已知系统的信号流图如题图10所示,试求传递函数C (s )/ R (s )。
题图10 信号流图11、求函数f(t)的拉普拉斯变换:300()0tt f t tet -<⎧=⎨≥⎩12、求下列函数的拉普拉斯变换:00()sin()0t f t t t ωθ<⎧=⎨+≥⎩其中,为常数。
13、已知2323()(1)s s F s s ++=+,用部分分式展开法求其反变换。
14、 求下列函数的拉氏变换:0.400()cos120tt f t e t t -<⎧=⎨≥⎩15、解下列微分方程:θ题图9 RC 网络16、试写出题图11所示的有源网络的传递函数U2(s)/ U1(s)。
题图11有源网络17、分析题图12所示质体、弹簧、阻尼系统的受力情况,画出系统结构图,写出外力f 与质体位移y 之间的数学表达式。
题图1218、题图13所示一个转速控制系统,输入量是电压V ,输出量是负载的转速,画出系统的结构图,并写出其输入输出间的数学表达式。
题图13 转速控制系统19、交流伺服电动机的原理线路和转矩-转速特性曲线如题图14所示。
图中,u 为控制电压.T 为电动机的输出转矩。
N 为电动机的转矩。
由图可T 与n 、u 呈非线性。
设在某平衡状态附近用增量化表示的转矩与转速、控制电压关系方程为,kn 、kc 为与平衡状态有关的值,可由转矩-转速特性曲线求得。
设折合到电动机的总转动惯量为J ,粘滞摩擦系数为f ,略去其他负载力矩,试写出交流伺服电动机的方程式 并求输入为uc ,输出为转角θ和转速为n 时交流伺服电动机的传递函数 。
)0(3)0(0372='==+'+''x x x xx题图14 交流伺服电动机的原理线路和转矩-转速特性曲线20、已知一系统由如下方程组组成,试绘制系统框图,求出闭环传递函数。
21、系统的微分方程组如下:其中K0,K1,K2,T均为正常数。
试建立系统结构图,并求传递函数C(s)/R(s),C(s)/N1(s)及C(s)/N2(s)。
22、试简化题图15中系统结构图,并求传递函数C(s)/R(s)。
题图1523、试用梅逊公式求解题图16所示系统的传递函数C(s)/R(s)。
题图1624、试求题图17所示结构图C(s)/R(s)。
题图1725、已知系统结构图如题图18所示,试写出系统在输入R(s)及扰动N(s)同时作用下输出C(s)的表达式。
题图1826、已知系统结构如题图19所示,试将其转换成信号流图,并求出C(s)/R(s)。
题图1927、系统的信号流图如题图20所示,试求C(s)/R(s)。
题图2028、题图21是一个模拟调节器的电路示意图。
(a)写出输入ur与输出uc之间的微分方程;(b)建立该调节器的结构图;(c)求闭环传递函数Uc(s)/Ur(s)。
题图2129、某弹簧的力-位移特性曲线如题图22所示。
在仅存在小扰动的情况下,当工作点分别为x0 =-1.2、0、2.5时,试计算弹簧在工作点附近的弹性系数。
题图22 弹簧的力-位移特性曲线30、试求题图23所示结构图的传递函数C(s)/R(s)。
题图2331、已知系统结构图如题图24所示,求传递函数C1(s)/R1(s),C2(s)/R1(s),C1(s)/R2(s),C2(s)/R2(s)。
题图2432、放大器可能存在死区,其工作特性曲线如题图25所示。
在近似线性工作区,可以用3次函数y = ax3来近似描述放大器的输入-输出特性。
当工作点为x =0.6时,试选择a的合适取值,并确定放大器的线性近似模型。
题图2533、设弹簧特性由下式描述:F=12. 651.1y,其中,F是弹簧力;y是变形位移。
若弹簧在形变位移0.25附近作微小变化,试推导F∆的线性化方程。
34、设系统传递函数为:2()2 ()32 C sR s s s=++且初始条件(0)1(0)0c c=-=,。
试求阶跃输入r(t)=1(t)时,系统的输出响应c(t)。
35、如题图26,已知G(s)和H(s)两方框相对应的微分方程分别是:()610()20()dc t c t e t dt +=;()205()10()db t b t c t dt +=且初始条件均为零,试求传递函数C(s)/R(s)及E(s)/R(s)。
题图2636、已知控制系统结构图如题图27所示。
试通过结构图等效变换求系统传递函数C(s)/R(s)。
题图2737、简化系统结构图如题图28并求传递函数C(s)/R(s)和 C(s)/N(s) 。
题图2838、试用梅森增益公式求图中各系统信号流图的传递函数C(s)/R(s)。
题图29(a )题图29(b )39、系统动态特性由下列微分方程描述,列写其相应的状态空间表达式。
5732y y y y u u +++=+40、已知系统的传递函数:列写其相应的状态空间表达式。
10(1)()(1)(3)s G s s s s -=++41、写如下传递函数的状态空间表达式的约当标准型:25()65G s s s =++42、系统状态空间表达式为:()0100()23011132()001x t x uy t x⎛⎫⎛⎫ ⎪ ⎪=--+ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭=1)画出系统的模拟结构图。
2)求系统的传递函数。
第三章1、设某高阶系统可用下列一阶微分方程近似描述:()()()()Tc t c t r t r t τ+=+其中 10T τ>->。
试证明系统的动态性能指标为2、设系统的微分方程如下:(1) 0.2()2()c t r t =(2) 0.04()0.24()()()c t c t c t r t ++=求系统的单位脉冲响应和单位阶跃响应。
已知全部初始条件为零。
3、已知系统的脉冲响应,试求系统闭环传递函数()s Φ()()()1.251()0.01252()510sin 445tk t e k t t t -==++4、设二阶系统的单位阶跃响应为1.2()1012.5sin(1.653.1)th t e t -=-+ 试求系统的超调量 δ%、峰值时间 t p 和调节时间t s 。
5、如题图1是简化的飞行控制系统结构图,试选择参数 k l 和k t ,使系统的6n ω=,1ξ= 。
题图16、下列矩阵是否满足状态转移矩阵的条件如果满足,试求与之对应的A 阵。
22222211(1)(1)(),20222(2)()2t t t t t t t tt t e t e e e e e t e e e e ----------⎛⎫- ⎪Φ= ⎪⎝⎭⎛⎫--Φ= ⎪--⎝⎭[0.693ln ]2.2[3ln]d r s T t T Tt T T t T Tττ-=+=-=+7、用拉氏反变换法求e At 。
010001254A ⎛⎫ ⎪= ⎪ ⎪-⎝⎭8、求下列状态空间表达式的解。
输入u(t)是单位阶跃。
()()0101001,0110x x ux y x⎧⎛⎫⎛⎫=+⎛⎫⎪ ⎪ ⎪=⎝⎭⎝⎭⎨ ⎪⎝⎭⎪=⎩9、已知单位反馈系统的开环传递函数:50()(0.11)(5)G s s s s =++试求输入分别为r(t)=2t 和r(t)=2+2t+t2时,系统的稳态误差。
10、已知单位反馈系统的开环传递函数:2()(4200)KG s s s s =++ 试求位置误差系数Kp ,速度误差系数Kv ,加速度误差系数Ka 。
