实验7线性回归
你应该要掌握的7种回归分析方法

你应该要掌握的7种回归分析⽅法你应该要掌握的7种回归分析⽅法标签:机器学习回归分析2015-08-24 11:29 4749⼈阅读评论(0) 收藏举报分类:机器学习(5)⽬录(?)[+]转载:原⽂链接:7 Types of Regression Techniques you should know!(译者/刘帝伟审校/刘翔宇、朱正贵责编/周建丁)什么是回归分析?回归分析是⼀种预测性的建模技术,它研究的是因变量(⽬标)和⾃变量(预测器)之间的关系。
这种技术通常⽤于预测分析,时间序列模型以及发现变量之间的因果关系。
例如,司机的鲁莽驾驶与道路交通事故数量之间的关系,最好的研究⽅法就是回归。
回归分析是建模和分析数据的重要⼯具。
在这⾥,我们使⽤曲线/线来拟合这些数据点,在这种⽅式下,从曲线或线到数据点的距离差异最⼩。
我会在接下来的部分详细解释这⼀点。
我们为什么使⽤回归分析?如上所述,回归分析估计了两个或多个变量之间的关系。
下⾯,让我们举⼀个简单的例⼦来理解它:⽐如说,在当前的经济条件下,你要估计⼀家公司的销售额增长情况。
现在,你有公司最新的数据,这些数据显⽰出销售额增长⼤约是经济增长的2.5倍。
那么使⽤回归分析,我们就可以根据当前和过去的信息来预测未来公司的销售情况。
使⽤回归分析的好处良多。
具体如下:1.它表明⾃变量和因变量之间的显著关系;2.它表明多个⾃变量对⼀个因变量的影响强度。
回归分析也允许我们去⽐较那些衡量不同尺度的变量之间的相互影响,如价格变动与促销活动数量之间联系。
这些有利于帮助市场研究⼈员,数据分析⼈员以及数据科学家排除并估计出⼀组最佳的变量,⽤来构建预测模型。
我们有多少种回归技术?有各种各样的回归技术⽤于预测。
这些技术主要有三个度量(⾃变量的个数,因变量的类型以及回归线的形状)。
我们将在下⾯的部分详细讨论它们。
对于那些有创意的⼈,如果你觉得有必要使⽤上⾯这些参数的⼀个组合,你甚⾄可以创造出⼀个没有被使⽤过的回归模型。
专题01 线性回归方程(解析版)

【解析】解: x 0 1 2 3 3 , y m 3 5.5 7 m 15.5 ,
4
2
4
4
这组数据的样本中心点是 ( 3 , m 15.5) , 24
关于 y 与 x 的线性回归方程 yˆ 2.1x 0.85 ,
m 15.5 2.1 3 0.85 ,解得 m 0.5 ,
x (次数 / 分
20
30
40
50
60
钟)
y( C)
25
27.5
29
32.5
36
A. 33 C
B. 34 C
C. 35 C
【解析】解:由题意,得 x 20 30 40 50 60 40 , 5
y 25 27.5 29 32.5 36 30 , 5
则 k y 0.25x 30 0.25 40 20 ;
故答案为:10.
例 7.已知一组数据点:
x
x1
x2
x8
y
y1
y2
y8
8
用最小二乘法得到其线性回归方程为 yˆ 2x 4 ,若数据 x1 , x2 , , x8 的平均数为 1,则 yi i 1
16 .
3
原创精品资源学科网独家享有版权,侵权必究!
【解析】解:由题意, x 1 ,设样本点的中心为 (1, y) , 又线性回归方程为 yˆ 2x 4 ,则 y 2 1 4 2 ,
购买一台乙款垃圾处理机器节约政府支持的垃圾处理费用 Y (单位:万元)的分布列为:
Y
30
20
70
120
P
0.3
0.4
0.2
0.1
E(Y ) 30 0.3 20 0.4 70 0.2 120 0.1 25 (万元)
2024-2025学年高二数学选择性必修第一册(配北师大版)课件第7章本章总结提升

0.24
0.22
0.15
技术人员选择模型 Y= ^
1
^
+ 2
作为 Y 与 X 的回归方程类型,令
1
2
ui= ,vi= .
^
^
(1)由最小二乘法得到线性回归方程 V=U+,求 Y 关于 X 的回归方程.
(2)利用(1)得出的结果,计算当单位面积播种数X为何值时,单位面积的总产
量W=XY的预测值最大?(计算结果精确到0.01)
10
∑ -10
=1
10
2
∑ 2 -10
≈
2 321-10×50×4
2
35 642-10×50
=
321
10 642
=1
∴V 关于 U 的回归方程是 V=0.03U+2.5;
则 Y 关于 X 的回归方程是 Y=
1
2.5+0.03
2.
^
≈0.03, =2.5.
(2)利用(1)得到的结果,
当且仅当
0.2
X= ,即定价为
5
-5
(X-0.2)=6-5
0.2
+
≤6-10 0.2 ≈1.5,
0.45 万元/吨时,等号成立,
所以每月的利润为30×1.5=45.00(万元),
所以预计定价为0.45万元/吨时,该产品一天的利润最大,此时的月利润为
45.00万元.
变式训练3为提高某作物产量,种植基地对单位面积播种数X(单位:棵/m2)
系数加以说明(结果保留2位小数).
解 由题可知, =
1
×(8+11+14+20+23+26)=17,
线性回归例子

考虑一座山在点(x,y)的高度是H(x,y)。 回归系数 是未知参数,通常用最大似然估计的方法获得。
P logistic回归—实例(1)
ln O () d ln d(s ) x x x 方向导数:如果函数z f (x,y)在点P (x,y)是可微分的,那么函0 数在该点1 沿1 任一方向l2 的方2 向导数都存在n ,且n 有
饮酒(x=1),患病概率和未患病概率分别为
患病(y=1) 55 74 此函数具有狭窄弯曲的山谷,最小值就在这些山谷之中,并且谷底很平。
一套200平方米的房子价格
129
未患病(y=0) 靠近极小值时速度减慢。
饮酒的患病率和Odds分别为
104663
212555
317218
合计 104718 212629 317347 多分类Logistic回归模型
以x1的回归系数 1 为例
一个暴露因素:暴露为1,非暴露为0。
ln O ()d ld n 1 P s(P ) 0 1x 1 2x2
除x1,固定其它自变量
1
2
1
1
2
其最小l值o在g(1,1i)处s,t数i值c为回0。 归—实例(1)
可能会'之字型'地下降。
优化过程是之字形的向极小值点靠近,速度非常缓慢。
在这一点的梯度是在该点坡度(或者说斜度)最陡的方向。
P越大,则Odds越大;
Odds=
(Odds为优势)
患病(Y=1)的概率为
梯度下降回归-----缺陷
回归系数 是未知参数,通常用最大似然估计的方法获得。
logistic回归—实例(1)
饮酒的患病率和Odds分别为
P 115 05 4718Od1d1 P s1P 115 05 4663
7种回归方法!请务必掌握!

7种回归⽅法!请务必掌握!7 种回归⽅法!请务必掌握!线性回归和逻辑回归通常是⼈们学习预测模型的第⼀个算法。
由于这⼆者的知名度很⼤,许多分析⼈员以为它们就是回归的唯⼀形式了。
⽽了解更多的学者会知道它们是所有回归模型的主要两种形式。
事实是有很多种回归形式,每种回归都有其特定的适⽤场合。
在这篇⽂章中,我将以简单的形式介绍 7 中最常见的回归模型。
通过这篇⽂章,我希望能够帮助⼤家对回归有更⼴泛和全⾯的认识,⽽不是仅仅知道使⽤线性回归和逻辑回归来解决实际问题。
本⽂将主要介绍以下⼏个⽅⾯:1. 什么是回归分析?2. 为什么使⽤回归分析?3. 有哪些回归类型?线性回归(Linear Regression)逻辑回归(Logistic Regression)多项式回归(Polynomial Regression)逐步回归(Stepwise Regression)岭回归(Ridge Regression)套索回归(Lasso Regression)弹性回归(ElasticNet Regression)4. 如何选择合适的回归模型?1什么是回归分析?回归分析是⼀种预测建模技术的⽅法,研究因变量(⽬标)和⾃变量(预测器)之前的关系。
这⼀技术被⽤在预测、时间序列模型和寻找变量之间因果关系。
例如研究驾驶员鲁莽驾驶与交通事故发⽣频率之间的关系,就可以通过回归分析来解决。
回归分析是进⾏数据建模、分析的重要⼯具。
下⾯这张图反映的是使⽤⼀条曲线来拟合离散数据点。
其中,所有离散数据点与拟合曲线对应位置的差值之和是被最⼩化了的,更多细节我们会慢慢介绍。
2为什么使⽤回归分析?如上⾯所说,回归分析能估计两个或者多个变量之间的关系。
下⾯我们通过⼀个简单的例⼦来理解:⽐如说,你想根据当前的经济状况来估计⼀家公司的销售额增长。
你有最近的公司数据,数据表明销售增长⼤约是经济增长的 2.5 倍。
利⽤这种洞察⼒,我们就可以根据当前和过去的信息预测公司未来的销售情况。
回归分析课件-第七章

第七章 多元线性回归模型的有偏估计
性质7.4的证明
并且
ˆ k trCov ˆ k E ˆ k MSE
2
i 1
p
i
i
k
2
k
2
i 1
p
i2
i
k
2
ˆ g1 k g 2 k ˆ g k
1949 年-1959 年法国进口总额与相关变量的数据 x1 149.3 171.5 175.5 180.8 190.7 202.1 202.1 212.4 226.1 231.9 239.0 x2 4.2 4.1 3.1 3.1 1.1 2.2 2.1 5.6 5.0 5.1 0.7 x3 108.1 114.8 123.2 126.9 132.1 137.7 146.0 154.1 162.3 164.3 167.6
第七章 多元线性回归模型的有偏估计
LS 估计的性能效果与设计矩阵 X 有关,当
R X X 接近是一个奇异阵时,即呈现所谓
的“病态”时,LS 估计的性能变坏。
上海财经大学 统计与管理学院 2
第七章 多元线性回归模型的有偏估计
例 7.2
表 7.1 是 Malinvand 于 1966 年提出的研究法国经济
上海财经大学 统计与管理学院 6
第七章 多元线性回归模型的有偏估计
将 x3 看作因变量, x1 自作解释变量,那么 x3 关于 x1 的一元线性回归方 程为
x3 60258 0.686x1 ,
这说明当 x1 变化时, x3 不可能保持一个常数,因此对回归系数的解释 就复杂了,不能仅从其符号上作解释, x1 与 x3 之间存在着多重共线性 关系,
EViews计量经济学实验报告-简单线性回归模型分析
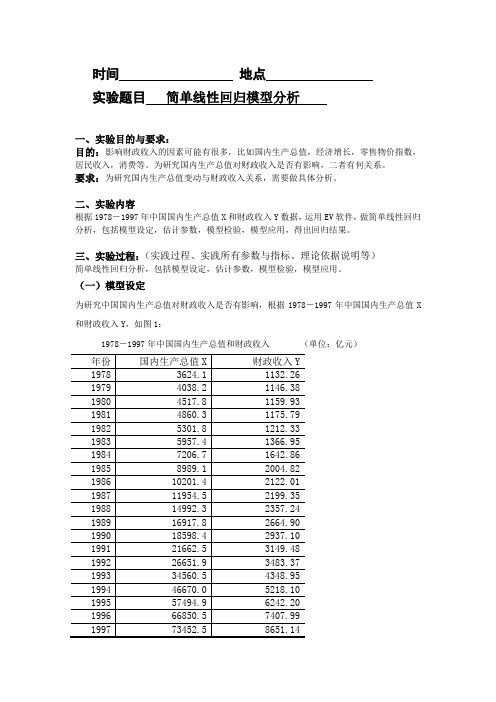
时间地点实验题目简单线性回归模型分析一、实验目的与要求:目的:影响财政收入的因素可能有很多,比如国内生产总值,经济增长,零售物价指数,居民收入,消费等。
为研究国内生产总值对财政收入是否有影响,二者有何关系。
要求:为研究国内生产总值变动与财政收入关系,需要做具体分析。
二、实验内容根据1978-1997年中国国内生产总值X和财政收入Y数据,运用EV软件,做简单线性回归分析,包括模型设定,估计参数,模型检验,模型应用,得出回归结果。
三、实验过程:(实践过程、实践所有参数与指标、理论依据说明等)简单线性回归分析,包括模型设定,估计参数,模型检验,模型应用。
(一)模型设定为研究中国国内生产总值对财政收入是否有影响,根据1978-1997年中国国内生产总值X 和财政收入Y,如图1:1978-1997年中国国内生产总值和财政收入(单位:亿元)根据以上数据,作财政收入Y 和国内生产总值X 的散点图,如图2:从散点图可以看出,财政收入Y 和国内生产总值X 大体呈现为线性关系,所以建立的计量经济模型为以下线性模型:01i i i Y X u ββ=++(二)估计参数1、双击“Eviews ”,进入主页。
输入数据:点击主菜单中的File/Open /EV Workfile —Excel —GDP.xls;2、在EV 主页界面点击“Quick ”菜单,点击“Estimate Equation ”,出现“Equation Specification ”对话框,选择OLS 估计,输入“y c x ”,点击“OK ”。
即出现回归结果图3:图3. 回归结果Dependent Variable: Y Method: Least Squares Date: 10/10/10 Time: 02:02 Sample: 1978 1997 Included observations: 20Variable Coefficient Std. Error t-Statistic Prob. C 857.8375 67.12578 12.77955 0.0000 X0.1000360.00217246.049100.0000R-squared 0.991583 Mean dependent var 3081.158 Adjusted R-squared 0.991115 S.D. dependent var 2212.591 S.E. of regression 208.5553 Akaike info criterion 13.61293 Sum squared resid 782915.7 Schwarz criterion 13.71250 Log likelihood -134.1293 F-statistic 2120.520 Durbin-Watson stat0.864032 Prob(F-statistic)0.000000参数估计结果为:i Y = 857.8375 + 0.100036i X(67.12578) (0.002172)t =(12.77955) (46.04910)2r =0.991583 F=2120.520 S.E.=208.5553 DW=0.8640323、在“Equation ”框中,点击“Resids ”,出现回归结果的图形(图4):剩余值(Residual )、实际值(Actual )、拟合值(Fitted ).(三)模型检验1、 经济意义检验回归模型为:Y = 857.8375 + 0.100036*X (其中Y 为财政收入,i X 为国内生产总值;)所估计的参数2ˆ =0.100036,说明国内生产总值每增加1亿元,财政收入平均增加0.100036亿元。
第七章回归分析

第七章回归分析本章介绍用于回归分析的常用SAS过程,包括一般回归分析过程REG、建立二次响应曲面回归模型过程RSREG、逐步回归分析过程STEPWISE、非线性回归分析过程NLIN等。
§7.1 一般回归分析过程 REG7.1.1 概述REG过程是一个通用回归过程,用最小二乘法估计线性回归模型。
此过程可以有多个模型(MODEL)语句,输入数据可以是原始样本数据,也可以是相关阵,可打印模型中的参数估计值、预测值、残差及置信区间等,并可作线性假设检验。
7.1.2 过程说明可用下列语句调用REG过程:PROC REG 选项;LABEL:MODEL 因变量表=回归变量表/选项;OUTPUT OUT=数据集关键字=名称表;BY 变量表;(1)PROC REG 选项;常用的选项有:DATA=数据集指定要分析的数据集,缺省时为最新建立的数据集。
ALL 要求各种输出项。
SIMPLE 为每个变量打印简单统计量。
NOPRINT 抑制正常的打印输出。
CORR 打印模型中所有变量的相关阵。
USSCP 为所用变量打印平方和及叉积阵。
(2)LABEL :MODEL 因变量=回归变量/选项;LABEL是模型标号,可省略。
如果使用多个模型,则可给予模型标号名称,便于区别。
常用的选项有:NOPRINT 抑制回归分析结果的打印输出。
NOINT 抑制模型中常数项的出现,缺省时模型中包括常数项。
I 打印X'X的逆矩阵。
XPX 打印X'X阵。
ALL 要求各项输出。
P 打印观测值号、实测值、预测值及残差。
R 要求残差分析。
包括预测值及残差的标准误,学生化残差及COOK'S统计量D。
CLM 打印每个观测值的因变量期望值的95%可信上下限,给出参数估计的变异范围,而不是预测区间。
CLI 要求为每一个观测值打印95%可信度的上下限。
DW 要求计算DURBIN-WASTON统计量,可检验误差是否有一阶自相关。
第七章 回归分析174 PARTIAL 要求打印每个回归变量的偏回归影响图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验编号: 07 四川师大SPSS实验报告 2017 年 4 月 24 日
计算机科学学院2015级5班实验名称:线性回归
姓名:唐雪梅学号: 2015110538 指导老师:__朱桂琼___ 实验成绩:_ __
实验七线性回归
一.实验目的及要求
1.了解SPSS 特点结构操作
2.利用SPSS进行简单数据统计
二.实验内容
(1)消费者品牌偏好分析:通过品牌使用时间和价格敏感度了解消费者的品牌偏好。
某彩妆系列产品公司进行了一项关于消费者品牌偏好态度的分析,调研人员收集了有关的调研数据,用11点标尺度量态度(1=非常不喜欢该品牌,11=非常喜欢该品牌)对于价格敏感度的度量也用11点标尺(1=对价格完全不敏
思考题:
(1)消费者对品牌的使用时间以及对其价格的敏感度对消费者的品牌偏好有何种影响?它们之间是一种什么样的关系?
(2)如果有影响,品牌偏好与使用时间之间的关系能否用一个模型表示出来?
(2)销售额和员工数量的关系:
随着公司的持续发展,常常有滑入无效率困境的危险,假定某公司的销售开始滑坡,但公司还是不停地招聘新人,公司有某个10年的关于销售额和员
(1)以销售额为自变量,员工数为因变量画出散点图,并建立一个回归模型,通过员工的数量来预测销售额。
(2)解释回归系数的实际意义。
(3)根据分析的结果回答:如果这个趋势继续下去,你对公司的管理层有何建议?你认为管理层应该关注什么?
(3)制度变迁是经济增长的源头,根据研究衡量制度变迁有两个变量:非国有化率和国家财政收入占GDP的比重。
自1998年以来中国的经济增长率一直未突破9%的状态,因此以9%为分界点,将经济增长定义为1(经济增长大于等于9%)或0(经济增长小于9%),
三、实验主要流程、基本操作或核心代码、算法片段(该部分如不够填写,请另加附页)实验一:多元线性回归分析
1.建立数据库
2.分析步骤:分析——回归——线性
3.结果
结论:在对编号为1的模型进行线性回归分析时所采用的方法是全部引入法:输入,此处无被剔出的变量
结论:R Square=0.966,接近于1,说明模型的拟合优度很高,方程拟合很好。
结论:sig=0<0.01,该模型具有显著性意义
系数a
模型
非标准化系数标准系数
t Sig.
B 标准误差试用版
1 (常量) .376 .629 .598 .565
使用时间.516 .060 .819 8.550 .000
价格敏感.235 .085 .266 2.772 .022
a. 因变量: 品牌偏好
拟合结果:y=0.516x1+0.235x2+0.376
Sig.取值大于0.05,没有理由拒绝原假设,即回归系数与零无显著性差异,模型中不存在共线性问题。
结论:特征根均不等于0,则不存在共线性问题,条件指数均小于30,本例中模型不存在共线性的问题。
(1)研究品牌偏好与使用时间之间的关系模型
B)原假设:回归系数与零无显著性差异
C)线性回归分析:
单击分析→回归→线性→打开线性回归主对话框;在弹出的线性回归对话框中,选择变量“品牌偏好(Y)”,添加到因变量框中;选择变量“使用时间(X1)”添加到自变量框中,单机统计量,选中估计、模型拟合度和DW 三个选项。
结果分析:R Square=0.936,接近于1,说明模型的拟合优度很高,方程拟合很好。
DW=2.783,说明残差是负自相关的,表明所假设的模型合理的。
拟合结果:y=0.59x+1.079
残差Mean=0,表明这些数据中无离群值,且数据的标准差也比较小,可以认为模型是合理的
实验二:回归分析
原假设:回归系数与零无显著性差异
1.建立数据库
2.散点图建立:图形——旧对话框——散点\点状——散点图
从图中看出销售额与员工数为非线性关系
(4)回归分析:
A)操作流程:
单击分析→回归→曲线估计→打开曲线估计主对话框;在弹出的曲线估计对话框中,选择变量“员工数”,添加到因变量框中;选择
变量“销售额”添加到自变量框中。
结论:从表中数据可以看出,三次方程的R Square=0.935最接近1,所以员工数和销售呈三次方的关系。
实验三:二维Logistic回归分析
(1)录入实验数据:
(2)二维Logistic回归分析:
1)原假设:回归系数与0无显著性差异
2)操作流程:选择菜单分析→回归→二维Logistic;然后选择Y变量使之添加到因变量框中,选择x1和x2变量,使它们分别进入协变量框中
3)结果分析:
其中常数项包括在模型中,初始-2LL为15.278,迭代结束于第三步,因为此时参数估计与其在上一步的变化已经小于0.001
分类结果表说明Step0的拟合效果。
可以看出对于y=1,有100%的准确性,对于y=0,有0%准确性,总共有66.7%的准确性
似然比卡方检验的观测值等于0.039,概率p值等于0.981。
显著性水平均大于0.05,所以可以拒绝原假设,即认为所有回归系数不同时为0,解释变量的全体与Logit P之间的线性关系显著,采用该模型合理。
模型拟合优度,给出了-2对数似然值较大,说明拟合优度并不理想,Cox和Shell 值以及Nagelkerke值较小,也说明拟合程度较低。
与前一步相比较,预测的准确率不变,模型的总体预测精度也不变。
Sig的值大于0.05,没有理由拒绝原假设,即认为该回归系数与0无显著性差异,它与Logit P的线性关系不是显著的,所以该模型是不可用的,应该重新建模。
四、实验结果的分析与评价(该部分如不够填写,请另加附页)
1.线性回归分析步骤
(1)确定回归方程中的解释变量(自变量)和被解释变量(因变量)。
(2)确定回归模型:通过观察散点图确定应通过哪种数学模型来概括回归线。
(3)建立回归方程:在一定的统计拟合准则下估计出模型中的各个参数,得到一个确定的回归方程
(4)对回归方程进行各种检验:检验回归方程是否真实地反映了事物总体间的统计关系以及回归方程能否用于预测等
(5)利用回归方程进行预测:根据回归方程对事物的未来发展趋势进行预测
2.一元线性回归操作
1.单击Analyze→Regression→Linear→打开Linear Regression主对话框
2.在弹出的LinearRegression对话框中,选择变量“气压”,添加到Dependent框中,表
示因变量;选择变量“沸点”,添加到Independent框中,表示自变量。
3.多元线性回归操作
Analyze→Regression→Linear命令,打开Linear Regression 对话框
选择解释变量Y进入Dependent框
将X1,X2和X5直接纳入模型
X3和X4通过逐步法。
而X6直接不予考虑
选择被解释变量X1,X2和X5进入Independent(s)框
在Method框中选择Enter(默认)表示所选变量强行进入回归方程
单击Next
选择被解释变量X3、X4进入Independent(s)框
在Method框中选择Stepwise对所选变量进行逐步筛选策略
在Linear Regression对话框中单击Statistics按钮
选中Estimates 和Model fit 复选框
选中Collinearity diagnostics复选框
单击OK按钮
4. 二维Logistic回归的SPSS操作
选择菜单Analyze →Regression→Binary Logistic
选择y变量使之添加到Dependent框中,选择x1变量、x2、x3,使它们分别进入Covariates 框中,表示其为自变量
单击Logistic Regression对话框中的Options按钮,选择所有选项,但保留各选项中的缺省值单击Continue按钮,返回上一个对话框,单击OK按钮
注:实验成绩等级分为(90-100分)优,(80-89分)良,(70-79分)中,(60-69分)及格,(59分)不及格。
