计量经济学 简单线性回归 实验报告.doc
计量经济学实验报告
计量经济学实验报告：马艺菡学号：4班级：9141070302任课教师：静文实验题目简单线性回归模型分析一实验目的与要求目的：影响财政收入的因素可能有很多，比如国生产总值，经济增长，零售物价指数，居民收入，消费等。
为研究国生产总值对财政收入是否有影响，二者有何关系。
要求：为研究国生产总值变动与财政收入关系，需要做具体分析。
二实验容根据1978-1997年中国国生产总值X和财政收入Y数据，运用EV软件，做简单线性回归分析，包括模型设定，模型检验，模型检验，得出回归结果。
三实验过程：（实践过程，实践所有参数与指标，理论依据说明等）简单线性回归分析，包括模型设定，估计参数，模型检验，模型应用。
（一）模型设定为研究中国国生产总值对财政收入是否有影响，根据1978-1997年中国国生产总值X和财政收入Y，如图11978-1997年中国国生产总值和财政收入（单位：亿元）1996 66850.5 7407.991997 73452.5 8651.14根据以上数据作财政收入Y 和国生产总值X的散点图，如图2从散点图可以看出，财政收入Y和国生产总值X大体呈现为线性关系，所以建立的计量经济模型为以下线性模型：（二）估计参数1、双击“Eviews”，进入主页。
输入数据：点击主菜单中的File/Open/EV Workfile—Excel—GDP.xls;2、在EV主页界面点击“Quick”菜单，点击“Estimate Equation”,出现“Equation Specification”对话框，选择OLS估计，输入““y c x”,点击“OK”。
即出现回归结果图3；参数估计结果为：Y=857.8375+0.100036iX（67.12578）（0.002172）t=（12.77955）（46.04910）2r=0.991583F=2120.520S.E.=208.5553DW=0.864 0323、在“Equation”框中，点击“Resids”,出现回归结果的图形（图4）:剩余值（Residual）、实际值(actual),拟合值（fitted）4、.（三）模型检验1.经济意义检验回归模型为：Y=857.8375+0.100036*X（其中Y为财政收入，iX为国生产总值；）所估计的参数=0.100036，说明国生产总值每增加1亿元，财政收入平均增加0.100036亿元。
计量经济学Eviews简单线性回归模型的建立与分析应用实验报告
实验一：简单线性回归模型的建立与分析应用【实验目的】1、熟悉计量经济学软件包EViews的界面和基本操作；2、掌握计量经济学分析实际经济问题的具体步骤；3、掌握简单线性回归模型的参数估计、统计检验、预测的基本操作方法；4、理解简单线性回归模型中参数估计值的经济意义。
【实验类型】综合型【实验软硬件要求】计量经济学软件包EViews、微型计算机【实验内容】为研究深圳市地方预算内财政收入（Y）与地区生产总值（X）的关系，建立简单线性回归模型，现根据深圳市统计局网站的相关信息，得到统计数据如下表：请按照下列步骤完成实验一，每个步骤要写出操作过程：（1）打开EViews，新建适当的工作文件夹；打开Eviews后，依次点击File－New－Workfile，新建一个时间序列数据（Dated-regular frequencied）类型的文件，频率选择年度（Annual），键入起止日期1990-2008（如图一），点击ok，新建工作文件夹完成（如图二）（图一）（图二）（2）在工作文件夹中新建变量X和Y，并输入数据；依次点击Objects－New Object，对象类型选择序列（Series），并输入序列名Y（如图三），点击OK，重复以上操作，新建系列对象X。
新建系列对象完成后如（图四）按住ctrl并同时选定X和Y，用鼠标右击选择open—as group，点击Edit ＋/－开始编辑，输入数据，数据输入完毕再点击Edit＋/－一次。
数据输入后如（图五）。
（图三）（图四）（图五）（3）生成X和Y的自然对数序列，保存在工作文件夹中，命名为lnX和lnY；依次点击Objects－Generate Sereies，出现Generate Series by Equation 窗口，在Enter equation窗口中输入公式：lnY=log(Y)点击ok，重复以上操作，输入：lnX=log(X) 创建序列lnX。
（如图六）（图六）（4）求X和Y的描述统计量的值，写出操作过程并画出相应表格；依次点击Quick－Group Statistics—Descriptive Statistics－Common sample，打开Series List窗口，输入x y，点击ok，输出结果（如图七）（图七）（5）作出X和Y的散点图，写出操作过程并画出相应图像，并判断模型是否接近于线性形式；依次点击Quick－Graph，打开Graph Options窗口，在Specific 中选择Scatter(散点图) （如图八）点击OK，得到散点图（如图九）（图八）由散点图可以看出模型接近线性形式（图九）（6） 用OLS 法对模型i i i u X Y ++=21ββ做参数估计，将估计结果保存在工作文件夹中，命名为eq01，写出操作过程和回归分析报告，并解释斜率的经济含义；在窗口空白处输入：ls y c x ，回车，得到结果如图回归分析报告：根据输出结果可得Ŷi = 26.02096 + 0.088820Xi (14.80278) (0.004356) t= (1.757843) (20.38986) R 2 = 0.960716 F=415.7464 D.W=0.626334 n=19 斜率的经济含义:斜率为0.088820，表示地区生产总值每增加1亿元，地方预算内财政收入平均来说增加0.088820亿元（7） 用OLS 法对模型i i i u X Y ++=ln ln 21ββ做参数估计，将估计结果保存在工作文件夹中，命名为eq02，写出操作过程和回归分析报告，并解释斜率 的经济含义；在主窗口空白处输入：ls lny c lnx ，回车，结果如图回归分析报告：根据输出结果可得lny = -1.272730 + 0.873867lnx(0.238775) (0.032394) t= (-5.330249) (26.9761) R 2 = 0.977172 F=727.7097 D.W= 0.811127 n=19 斜率的经济含义:斜率为0.873867，表示地区生产总值每增加1亿元，地方预算内财政收入平均来说增加0.0873867亿元（8） 将保存工作文件夹保存在桌面，文件名为test1.wfl ；依次点击File-Save As 将文件保存在桌面，命名为test1.wfl （9） 对eq01的估计结果做经济意义检验和统计检验（05.0=α），估计的效果如何？经济意义检验：x 的系数β2的估计值为0.088820，说明地区生产总值每增加1亿元，地方预算内财政收入平均来说增加0.088820亿元，该值处于（0,1）符合预期。
3 计量经济学上机实验报告-简单线性回归
实验一 简单线性回归一、 实验名称：简单线性回归 二、实验目的掌握一元线性回归模型的估计与应用，熟悉EViews 的基本操作,并且给案例做一元回归并做预测。
三、实验中所需要掌握的知识点掌握一元回归及其预测四、实验前预备的情况说明（包括上机步骤、实验所涉及的基本原理知识的复习理解、 对实验结果的预期解释等）(1)最小二乘法估计的原理 (2) t 检验 (3)拟合优度检验(4)点预测和区间预测五、上机实验内容（填写本次上机的情况）1．上机步骤⑴统计结果，如图1所示，Y ,X 的均值分别为3081.158和22225.13，Y,X 的标准差为2212.591,和22024.6图1(2) 设定模型为 12i i i Y X u ββ=++，经运算的 Equation 界面如图2图3由图2的数据得：；2．上机结果（1）回归估计结果为：Dependent Variable: Y Method: Least SquaresDate: 04/09/14 Time: 18:53 Sample (adjusted): 1978 1997Included observations: 20 after adjustmentsVariable CoefficientStd. Errort-Statistic Prob. X 0.100036 0.002172 46.04910 0.0000 C857.837567.1257812.77955 0.0000R-squared 0.991583 Mean dependent var 3081.158 Adjusted R-squared 0.991115 S.D. dependent var 2212.591 S.E. of regression 208.5553 Akaike info criterion 13.61293 Sum squared resid 782915.7 Schwarz criterion 13.71250 Log likelihood -134.1293 F-statistic2120.520 Durbin-Watson stat0.864032 Prob(F-statistic)0.000000因此得到回归模型为： Y=857.8375+0.100036X斜率系数的经济意义为：GDP 增加1亿元，财政收入增加0.1亿元。
计量经济学实验报告(多元线性回归 自相关 )
计量经济学实验报告(多元线性回归自相关 )1. 背景计量经济学是一门关于经济现象的定量分析方法研究的学科。
它的发展使得我们可以对经济现象进行更加准确的分析和预测，并对社会发展提供有利的政策建议。
本文通过对多元线性回归模型和自相关模型的实验研究，来讨论模型的建立与评价。
2. 多元线性回归模型在多元线性回归模型中，我们可以通过各个自变量对因变量进行预测和解释。
例如，我们可以通过考虑家庭收入、年龄和教育程度等自变量，来预测某个家庭的消费水平。
多元线性回归模型的一般形式为：$y_i=\beta_0+\beta_1 x_{i1}+\beta_2 x_{i2}+...+\beta_k x_{ik}+\epsilon_i$在建立模型之前，我们需要对因变量和自变量进行观测和测算。
例如，我们可以通过调查一定数量的家庭，获得他们的收入、年龄、教育程度和消费水平等数据。
接下来，我们可以通过多元线性回归模型，对家庭消费水平进行预测和解释。
在实际的研究中，我们需要对多元线性回归模型进行评价。
其中一个重要的评价指标是 $R^2$ 值，它表示自变量对因变量的解释程度。
$R^2$ 值越高，说明多元线性回归模型的拟合程度越好。
3. 自相关模型在多元线性回归模型中，我们假设各个误差项之间相互独立，即不存在自相关性。
但实际上，各个误差项之间可能会互相影响，产生自相关性。
例如，在一个气温预测模型中，过去的温度对当前的温度有所影响，说明当前的误差项和过去的误差项之间存在相关性。
我们可以通过自相关函数来研究误差项之间的相关性。
自相关函数表示当前误差项和过去 $l$ 期的误差项之间的相关性。
其中，$l$ 称为阶数。
自相关函数的一般形式为：$\rho_l={\frac{\sum_{t=l+1}^{T}(y_t-\bar{y})(y_{t-l}-\bar{y})}{\sum_{t=1}^{T}(y_t-\bar{y})^2}}$在自相关模型中，我们通过对误差项进行差分或滞后变量，来消除误差项之间的自相关性。
计量经济学实验报告(范例)
在“Objects”菜单中点击“New Objects”，在“New Objects”对话框中选“Group”，并在“Name for Objects”上定义文件名，点击“OK”出现数据编辑窗口。
1．学会OLS方法的估计过程
2．掌握了模型的估计和检验方法
3．深入了解了消费函数的计量结果，扩大了思路。
一、研究目的和意义
我们研究的对象是各地区居民消费的差异。居民消费可分为城市居民消费和农村居民消费，由于各地区的城市与农村人口比例及经济结构有较大差异，最具有直接对比可比性的是城市居民消费。而且，由于各地区人口和经济总量不同，只能用“城市居民每人每年的平均消费支出”来比较，而这正是可从统计年鉴中获得数据的变量。所以模型的被解释变量Y选定为“城市居民每人每年的平均消费支出”。
若要将工作文件存盘，点击窗口上方“Save”，在“SaveAs”对话框中给定路径和文件名，再点击“ok”，文件即被保存。
2、输入数据
在数据编辑窗口中，首先按上行键“↑”，这时对应的“obs”字样的空格会自动上跳，在对应列的第二个“obs”有边框的空格键入变量名，如“Y”，再按下行键“↓”，对因变量名下的列出现“NA”字样，即可依顺序输入响应的数据。其他变量的数据也可用类似方法输入。
Annual (年度) Weekly (周数据)
Quartrly (季度) Daily (5 day week ) (每周5天日数据)
Semi Annual (半年) Daily (7 day week ) (每周7天日数据)
计量经济学实验一一元线性回归完成版
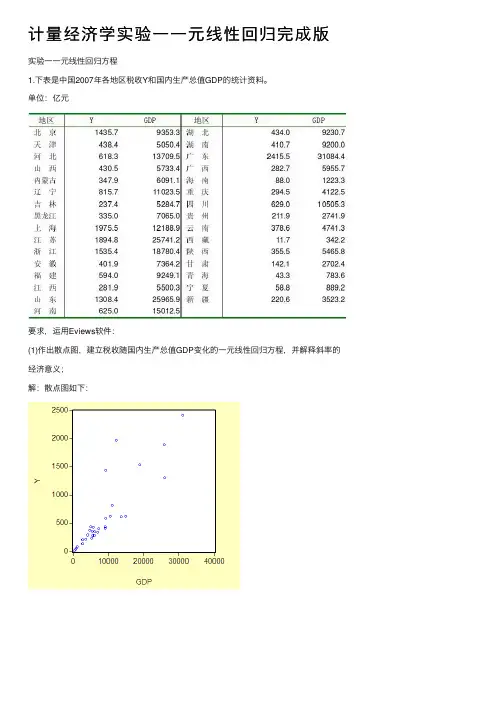
计量经济学实验⼀⼀元线性回归完成版实验⼀⼀元线性回归⽅程1.下表是中国2007年各地区税收Y和国内⽣产总值GDP的统计资料。
单位：亿元要求，运⽤Eviews软件：(1)作出散点图，建⽴税收随国内⽣产总值GDP变化的⼀元线性回归⽅程，并解释斜率的经济意义；解：散点图如下：得到估计⽅程为：0.07104710.62963=-y x这个估计结果表明，GDP 每增长1亿元，各地区税收将增加0.071047亿元。
(2) 对所建⽴的回归⽅程进⾏检验；解：从回归的估计的结果来看，模型拟合得较好。
可决系数20.7603R =，表明各地区税收变化的76.03%可由GDP 的变化来解释。
从斜率项的t 检验值看，⼤于5%显著性⽔平下⾃由度为229n -=的临界值0.025(29) 2.05t =，且该斜率满⾜0<0.071047<1，表明2007年，GDP 每增长1亿元，各地区税收将增加0.071047亿元。
(3) 若2008年某地区国内⽣产总值为8500亿元，求该地区税收收⼊的预测值及预测区间。
解：由上述回归⽅程可得地区税收收⼊的预测值：0.0710********.62963593.3Y =-= 下⾯给出税收收⼊95%置信度的预测区间：由于国内⽣产总值X 的样本均值与样本房差为()8891.126()57823134E X Var X ==于是，在95%的置信度下，0()E Y 的预测区间为593.3 2.045±593.3113.4761=±或(479.8239,706.7761)当GDP 为8500亿元时地区的税收收⼊的个值预测值仍为593.3。
同样的，在95%的置信度下，该地区的税收收⼊的预测区间为593.3 2.045593.3641.0421±=±或（-47.7,1234.3）。
资料来源:《深圳统计年鉴2002》，中国统计出版社解：(1)建⽴深圳地⽅预算内财政收⼊对GDP 的回归模型；得到回归⽅程：?0.134582 3.611151yx =-(2)估计所建⽴模型的参数，解释斜率系数的经济意义；X 的系数为0.314582，常数项为-3.611151。
计量经济学实验报告完整版范文
评语
教师
评语
成绩
辽宁工程技术大学上机实验报告
实验名称
计量经济学多元线性回归模型
院系
工商管理
专业
金融
班级
09-2
姓名
于佳琦
学号
日期
6.15
实验
目的
简述本次实验目的：熟悉多元线性回归模型中的解释变量的引入
掌握对计算机过的统计分析和经济分析
实验
பைடு நூலகம்准备
你为本次实验做了哪些准备：了解多元线性回归模型参数的OLS估计，统计检验，点预测以及区间估计，非线性回归的参数估计，受约束回归检验
实验
进度
本次共有3个练习，完成3个。
实验
总结
日
本次实验的收获、体会、经验、问题和教训：在简单线性回归的基础上引入了多元线性回归模型，操作也较之前更加复杂，最大的障碍在于多重共线性模型数据更多，输入时容易出错，而且软件非汉化版本，很多时候不了解数据的含义，操作也不是很熟练，一般思路是，先用OLS方法进行估计，建立模型，然后进行对模型的检验，理论相对简单，可是检验过程十分复杂，如果不用例题做实验，单纯找数据进行分析，总会有遗忘的影响因素，而导致结果的偏差，所以在选择分析对象的影响因素时考虑周全尤为重要。
实验
进度
本次共有1个练习，完成1个。
实验
总结
日
本次实验的收获、体会、经验、问题和教训：初步投身于计量经济学，通过利用Eviews软件将所学到的计量知识进行实践，让我加深了对理论的理解和掌握，直观而充分地体会到老师课堂讲授内容的精华之所在。在实验过程中我们提高了手动操作软件、数量化分析与解决问题的能力，还可以培养我在处理实验经济问题的严谨的科学的态度，并且避免了课堂知识与实际应用的脱节。虽然在实验过程中出现了很多错误，但这些经验却锤炼了我们发现问题的眼光，丰富了我们分析问题的思路。通过这次实验让我受益匪浅。
实验报告简单线性回归分析
西南科技大学Southwest University of Science and Technology经济管理学院计量经济学实验报告——多元线性回归的检验专业班级：姓名: 学号: 任课教师: 成绩:简单线性回归模型的处理实验目的：掌握多元回归参数的估计和检验的处理方法。
实验要求：学会建立模型，估计模型中的未知参数等。
试验用软件：Eviews实验原理：线性回归模型的最小二乘估计、回归系数的估计和检验。
实验内容：1、实验用样本数据：运用Eviews软件，建立1990-2001年中国国内生产总值X和深圳市收入Y的回归模型，做简单线性回归分析，并对回归结果进行检验。
以研究我国国内生产总值对深圳市收入的影响。
经过简单的回归分析后得出表EQ1：Depe ndent Variable: Y Method: Least Squares Date: 11/27/11 Time: 14:02 Sample: 1990 2001 In cluded observati ons: 12 VariableCoefficientStd. Error t-Statistic Prob.C -3.611151 4.161790 -0.867692 0.4059 X0.134582 0.003867 34.80013 0.0000 R-squared0.991810 Mean depe ndent var 119.8793 Adjusted R-squared 0.990991 S.D. dependent var 79.361247.02733 S.E. of regressi on7.532484 Akaike infocriteri on8Sum squared resid 567.3831 Schwarz criteri on 7.1081561211.0490.00000Log likelihood-40.16403F-statisticDurbin-Wats on stat 2.051640 Prob(F-statistic)其中拟合优度为：0.991810有很强的线性关系2、实验步骤: 1、 回归分析:(1) 在 Objects 菜单中点击 New objects ，在 New objects 选择 Group ，并以GROUP01定义文件名，点击 OK 出现数据编辑窗口，， 按顺序键入数据。
计量经济学-线性回归分析
4.写出模型的形式并对其进行解释和分析；
5.对模型进行参数检验、拟合优度检验及正态性检验；
6.利用模型进行预测。
（包括实验实施步骤、使用方法及相关命令、数据记录和处理等）
答：1.建立Work file
（工作文件）
数据输入：建立新数据文件
2.在EViews命令框中直接输入“dataXY”回车；
4.(1).参数估计结果如下：
Y282.2434+0.7585113X说明城市居民人均年可支配收入每相差一元，可导致居
民消费相差0.758511元
se=(287.2649) (0.036928)
t=(0.982520) (20.54026)
p=(0.3340)(0.0000) df=29
R-squared=0.93568
6.利用模型进行预测如下。
地区
城市居民人均年消费支出丫/元
城市居民人均年可支配收入X/兀
全国
6029.88
7702.8
黑龙江
4462.08
6100.56
上海
10464.00
13249.80
实 验 结 果 和 分 析
从图中我们可以看出实验结果由于全国各个地区经济发展速度不 同，居民消费有着明显差异。为了分析影响各地区居民消费支出有明显 差异的最主要因素，并分析影响因素与消费水平的数量关系，我们可以 建立相应的计量经济模型去研究。
Log likelihood-229.692206Hannan-Quinn criter.14.97804
F-statistic421.902301Durbin-Watson stat1.4814386
计量经济学实验报告一元线性回归模型实验
2013－2014第1学期计量经济学实验报告实验（一）：一元线性回归模型实验学号姓名：专业：国际经济与贸易选课班级：实验日期：2013年12月2日实验地点：K306实验名称：一元线性回归模型实验【教学目标】《计量经济学》是实践性很强的学科，各种模型的估计通过借助计算机能很方便地实现，上机实习操作是《计量经济学》教学过程重要环节。
目的是使学生们能够很好地将书本中的理论应用到实践中，提高学生动手能力，掌握专业计量经济学软件EViews的基本操作与应用。
利用Eviews做一元线性回归模型参数的OLS估计、统计检验、点预测和区间预测。
【实验目的】使学生掌握1.Eviews基本操作：（1）数据的输入、编辑与序列生成；（2）散点图分析与描述统计分析；（3）数据文件的存贮、调用与转换。
2. 利用Eviews做一元线性回归模型参数的OLS估计、统计检验、点预测和区间预测【实验内容】1.Eviews基本操作：（1）数据的输入、编辑与序列生成；（2）散点图分析与描述统计分析；（3）数据文件的存贮、调用与转换；2. 利用Eviews做一元线性回归模型参数的OLS估计、统计检验、点预测和区间预测。
实验内容以下面1、2题为例进行操作。
1、为了研究深圳地方预算中财政收入与国内生产总值关系，运用以下数据：(1)建立深圳的预算内财政收入对GDP的回归；(2)估计模型的参数，解释斜率系数的意义；(3)对回归结果进行检验；(4)若2002年的国内生产总值为3600亿元，试确定2002年财政收入的预测值和预α=)。
测区间(0.052、在《华尔街日报1999年年鉴》（The Wall Street Journal Almanac 1999）上，公布有美国各航空公司业绩的统计数据。
航班正点准时到达的正点率和此公司每10万名乘客中投诉1(1)做出上表数据的散点图(2)依据散点图，说明二变量之间存在什么关系？(3)描述投诉率是如何根据航班正点率变化，并求回归方程。
计量经济学报告
《计量经济学》实验报告目录简单线性回归模型案例 (1)多元线性回归模型案例 (4)多重线性案例 (7)异方差性案例 (10)自相关案例 (15)分布滞后模型与自回归模型案例 (19)虚拟变量回归案例 (24)1简单线性回归模型案例1、问题提出居民消费在社会经济的持续发展中有着重要的作用。
影响居民计算机拥有量的因素有多种，但从理论和经验分析，最主要的影响因素应是居民收入水平。
从理论上说居民收入水平越高，居民计算机拥有量越多。
所以我们设定“城镇居民家庭平均每百户计算机拥有量（台）”为被解释变量，“城镇居民平均每人全年家庭总收入（元）”为解释变量。
2、X 和Y 的散点图及分析图表2-1：各地区城镇居民每百户计算机拥有量与人均总收入的散点图分析：从散点图可以看出各地区城镇居民计算机拥有量随着人均总收入水平的提高而增加，近似于线性关系，为分析中国各地区城镇居民每百户计算机拥有量随人均总收入变动的数量规律性，可以考虑建立如下简单线性回归模型：t t u X Y ++=21ββt3、估计参数图表2-2：回归结果可用规范的形式将参数估计和检验的结果写为315836.1438320.0002873.09580.112====+=∧n F R Y (11.9826)(2.1267)t 24)(0.000 (5.6228) X tt 4、对数据X 和Y 的统计结果的描述图表2-3：X 和Y 的描述统计结果5、模型检验（1）经济意义检验所估计的参数∧1β=11.9580，∧2β=0.002 873，说明城镇居民家庭人均总收入每增加1元，平均说来城镇居民每百户计算机拥有量将增加0.002 873台，这与预期的经济意义相符。
（2）拟合优度和统计检验由拟合优度R 2=0.831996可知，所建立的模型对样本数据的拟合度较高。
对回归参数的显著性检验——t 检验：对β1建立下列假设条件：原假设H 0：β1=0 备择假设H 1：β1≠0取α=0.05，β1服从t~（29），P 值检验的结果是0.0421< 0.05，所以应该拒绝原假设β1=0，接受备择假设β1≠0，说明β1对被解释变量有显著性影响。
EViews计量经济学实验报告-简单线性回归模型分析
时间地点实验题目简单线性回归模型分析一、实验目的与要求：目的：影响财政收入的因素可能有很多，比如国内生产总值，经济增长，零售物价指数，居民收入，消费等。
为研究国内生产总值对财政收入是否有影响，二者有何关系。
要求：为研究国内生产总值变动与财政收入关系，需要做具体分析。
二、实验内容根据1978－1997年中国国内生产总值X和财政收入Y数据，运用EV软件，做简单线性回归分析，包括模型设定，估计参数，模型检验，模型应用，得出回归结果。
三、实验过程：（实践过程、实践所有参数与指标、理论依据说明等）简单线性回归分析，包括模型设定，估计参数，模型检验，模型应用。
（一）模型设定为研究中国国内生产总值对财政收入是否有影响，根据1978－1997年中国国内生产总值X 和财政收入Y，如图1：1978－1997年中国国内生产总值和财政收入（单位：亿元）根据以上数据，作财政收入Y 和国内生产总值X 的散点图，如图2：从散点图可以看出，财政收入Y 和国内生产总值X 大体呈现为线性关系，所以建立的计量经济模型为以下线性模型：01i i i Y X u ββ=++（二）估计参数1、双击“Eviews ”，进入主页。
输入数据：点击主菜单中的File/Open /EV Workfile —Excel —GDP.xls;2、在EV 主页界面点击“Quick ”菜单，点击“Estimate Equation ”,出现“Equation Specification ”对话框，选择OLS 估计，输入“y c x ”,点击“OK ”。
即出现回归结果图3：图3. 回归结果Dependent Variable: Y Method: Least Squares Date: 10/10/10 Time: 02:02 Sample: 1978 1997 Included observations: 20Variable Coefficient Std. Error t-Statistic Prob. C 857.8375 67.12578 12.77955 0.0000 X0.1000360.00217246.049100.0000R-squared 0.991583 Mean dependent var 3081.158 Adjusted R-squared 0.991115 S.D. dependent var 2212.591 S.E. of regression 208.5553 Akaike info criterion 13.61293 Sum squared resid 782915.7 Schwarz criterion 13.71250 Log likelihood -134.1293 F-statistic 2120.520 Durbin-Watson stat0.864032 Prob(F-statistic)0.000000参数估计结果为：i Y = 857.8375 + 0.100036i X（67.12578） （0.002172）t =（12.77955） （46.04910）2r =0.991583 F=2120.520 S.E.=208.5553 DW=0.8640323、在“Equation ”框中，点击“Resids ”,出现回归结果的图形（图4）:剩余值（Residual ）、实际值（Actual ）、拟合值（Fitted ）.（三）模型检验1、 经济意义检验回归模型为：Y = 857.8375 + 0.100036*X （其中Y 为财政收入，i X 为国内生产总值；）所估计的参数2ˆ =0.100036，说明国内生产总值每增加1亿元，财政收入平均增加0.100036亿元。
计量经济学实验报告回归分析
计量经济学实验报告回归分析计量经济学实验报告：回归分析一、实验目的本实验旨在通过运用计量经济学方法，对收集到的数据进行分析，研究自变量与因变量之间的关系，并估计回归模型中的参数。
通过回归分析，我们可以深入了解变量之间的关系，为预测和决策提供依据。
二、实验原理回归分析是一种常用的统计方法，用于研究自变量与因变量之间的线性或非线性关系。
在回归分析中，我们通过最小二乘法等估计方法，得到回归模型中未知参数的估计值。
根据估计的参数，我们可以对因变量进行预测，并分析自变量对因变量的影响程度。
三、实验步骤1.数据收集：收集包含自变量与因变量的数据集。
数据可以来自数据库、调查、实验等。
2.数据预处理：对收集到的数据进行清洗、整理和格式化，以确保数据的质量和适用性。
3.模型选择：根据问题的特点和数据的特性，选择合适的回归模型。
常见的回归模型包括线性回归模型、多元回归模型、岭回归模型等。
4.模型估计：运用最小二乘法等估计方法，对选择的回归模型进行估计，得到模型中未知参数的估计值。
5.模型检验：对估计后的模型进行检验，以确保模型的适用性和可靠性。
常见的检验方法包括残差分析、拟合优度检验等。
6.预测与分析：根据估计的模型参数，对因变量进行预测，并分析自变量对因变量的影响程度。
四、实验结果与分析1.数据收集与预处理本次实验选取了某网站的销售数据作为样本，数据包含了商品价格、销量、评价等指标。
在数据预处理阶段，我们剔除了缺失值和异常值，以确保数据的完整性和准确性。
2.模型选择与估计考虑到商品价格和销量之间的关系可能存在非线性关系，我们选择了多元回归模型进行建模。
采用最小二乘法进行模型估计，得到的估计结果如下：销量 = 100000 + 10000 * 价格 + 5000 * 评价 + 随机扰动项3.模型检验对估计后的模型进行残差分析，发现残差分布较为均匀，且均在合理范围内。
同时，拟合优度检验也表明模型对数据的拟合程度较高。
计量经济学实验报告2
Variable
Coefficient Std. Error t-Statistic Prob.
CS
1.278874 0.017267 74.06285 0.0000
-
C
2.68073 11.61500 -1.952710 0.0617
R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Durbin-Watson stat
DF= 28
DW =0.942712 F =1802.255
模型2：Yˆ ˆ1 ˆ2 X
SEˆ1 SEˆ2
t1 t2
R 2 =0.995282 SE =35.66468
DF=28 DW =1.561721
F =5022.505
模型3：Y1 t2
（三）回归分析
1、【模型设定】
（1）作因果关系检验（辅助“模型设定”） 分别对上述三组变量作因果关系检验（3组检验结果），并根据因果关系检验的结果， 作简单描述及分析。 因果关系检验结果表：（请对同一个模型的滞后期从2-5多试几次，并选定最终的结果。）
Pairwise Granger Causality Tests Date: 03/22/12 Time: 15:19 Sample: 1978 2005 Lags: 4
模型一：模型可决系数（判定系数） R2 ＝0.985779，表明拟合程度很好。
模型3： 1 ：-0.993108
2 ：2.980308
3、模型检验
（1）经济检验 根据模型参数的估计值，联系实际和相关经济理论，对各回归模型进行经济检验。
并解释参数值的经济意义。 模型一：财政收入CS对国内生产总值GDPS的回归系数0.080296，符合经济理论，即财政 收入的变化引起国内生产总值变化。 模型二：财政支出CZ对财政收入CS的回归系数1.278874，说明财政支出CZ中还有不被财政收入
计量经济学Eviews简单线性回归模型的建立与分析应用实验报告
实验一：简单线性回归模型的建立与分析应用【实验目的】1、熟悉计量经济学软件包EViews的界面和基本操作；2、掌握计量经济学分析实际经济问题的具体步骤；3、掌握简单线性回归模型的参数估计、统计检验、预测的基本操作方法；4、理解简单线性回归模型中参数估计值的经济意义。
【实验类型】综合型【实验软硬件要求】计量经济学软件包EViews、微型计算机【实验内容】为研究深圳市地方预算内财政收入（Y）与地区生产总值（X）的关系，建立简单线性回归模型，现根据深圳市统计局网站的相关信息，得到统计数据如下表：请按照下列步骤完成实验一，每个步骤要写出操作过程：（1）打开EViews，新建适当的工作文件夹；打开Eviews后，依次点击File－New－Workfile，新建一个时间序列数据（Dated-regular frequencied）类型的文件，频率选择年度（Annual），键入起止日期1990-2008（如图一），点击ok，新建工作文件夹完成（如图二）（图一）（图二）（2）在工作文件夹中新建变量X和Y，并输入数据；依次点击Objects－New Object，对象类型选择序列（Series），并输入序列名Y（如图三），点击OK，重复以上操作，新建系列对象X。
新建系列对象完成后如（图四）按住ctrl并同时选定X和Y，用鼠标右击选择open—as group，点击Edit ＋/－开始编辑，输入数据，数据输入完毕再点击Edit＋/－一次。
数据输入后如（图五）。
（图三）（图四）（图五）（3）生成X和Y的自然对数序列，保存在工作文件夹中，命名为lnX和lnY；依次点击Objects－Generate Sereies，出现Generate Series by Equation 窗口，在Enter equation窗口中输入公式：lnY=log(Y)点击ok，重复以上操作，输入：lnX=log(X) 创建序列lnX。
（如图六）（图六）（4）求X和Y的描述统计量的值，写出操作过程并画出相应表格；依次点击Quick－Group Statistics—Descriptive Statistics－Common sample，打开Series List窗口，输入x y，点击ok，输出结果（如图七）（图七）（5）作出X和Y的散点图，写出操作过程并画出相应图像，并判断模型是否接近于线性形式；依次点击Quick－Graph，打开Graph Options窗口，在Specific 中选择Scatter(散点图) （如图八）点击OK，得到散点图（如图九）（图八）由散点图可以看出模型接近线性形式（图九）（6） 用OLS 法对模型i i i u X Y ++=21ββ做参数估计，将估计结果保存在工作文件夹中，命名为eq01，写出操作过程和回归分析报告，并解释斜率的经济含义；在窗口空白处输入：ls y c x ，回车，得到结果如图回归分析报告：根据输出结果可得Ŷi = 26.02096 + 0.088820Xi (14.80278) (0.004356) t= (1.757843) (20.38986) R 2 = 0.960716 F=415.7464 D.W=0.626334 n=19 斜率的经济含义:斜率为0.088820，表示地区生产总值每增加1亿元，地方预算内财政收入平均来说增加0.088820亿元（7） 用OLS 法对模型i i i u X Y ++=ln ln 21ββ做参数估计，将估计结果保存在工作文件夹中，命名为eq02，写出操作过程和回归分析报告，并解释斜率 的经济含义；在主窗口空白处输入：ls lny c lnx ，回车，结果如图回归分析报告：根据输出结果可得lny = -1.272730 + 0.873867lnx(0.238775) (0.032394) t= (-5.330249) (26.9761) R 2 = 0.977172 F=727.7097 D.W= 0.811127 n=19 斜率的经济含义:斜率为0.873867，表示地区生产总值每增加1亿元，地方预算内财政收入平均来说增加0.0873867亿元（8） 将保存工作文件夹保存在桌面，文件名为test1.wfl ；依次点击File-Save As 将文件保存在桌面，命名为test1.wfl （9） 对eq01的估计结果做经济意义检验和统计检验（05.0=α），估计的效果如何？经济意义检验：x 的系数β2的估计值为0.088820，说明地区生产总值每增加1亿元，地方预算内财政收入平均来说增加0.088820亿元，该值处于（0,1）符合预期。
计量经济学实验报告剖析
实验报告金融系投资学专业14 级 2 班实验人吴儒君实验地点：实训楼B305 实验日期：2016/11/1学号20141206022026实验题目：线性回归模型实验类型：基本操作实验目的：熟悉Eviews软件的基本操作，实现用软件对简单线性模型进行参数估计，并对模型加以检验，对被解释变量进行预测，并分析所估计模型的经济意义和作用。
实验内容：一、为了研究浙江省财政预算收入与全省生产总值的关系，由浙江省统计年鉴得到下表（P57，练习题2.2，表2.8）的数据，要求：（1）建立浙江省财政预算收入与全省生产总值的计量经济模型，估计模型的参数，检验模型的显著性，用规范的形式写出估计检验结果，并解释所估计参数的经济意义。
（2）如果2011年，全省生产总值为32000亿元，比上年增长9.0%，利用计量经济模型对浙江省2011年的财政预算收入做出点预测和区间预测。
实验步骤：1.根据题目输入数据，建立工作文件：如图2.作X与Y的散点图，点击View/Graph/Scatter,在Fit lines中选择Regression line/ok生成图片：从散点图可以看出每年财政预算总收入随全省生产总值的增加而增加。
3.估计参数：在EViews命令框中直接键入 LS Y C X按回车键得回归结果实验结果：1. 检验结果为：2. 经济意义检验：所估计的参数 说明全省生产总值每增加1亿元，平均来说财政预算总收入增加0.176124亿元。
这与预期的经济意义相符。
3. 拟合优度和统计检验：如上图可以看出本题中可决系数为0.983702说明模型的拟合优度较好。
4. 对回归系数的t 检验：针对,取，查t 分布表得自由度为n-2=33-2=31的临界值因为()31)1(t 025.0^t >β，()3125639.43)2(t 025.0^t >=β 所以应拒绝 。
对斜率系数的显著性检验表明，全省生产总值对财政预算总收入有显著性影响。
计量经济学实验简单线性回归模型
计量经济学实验简单线性回归模型引言计量经济学是经济学中的一个分支，致力于通过经验分析和实证方法来研究经济问题。
实验是计量经济学中的重要方法之一，能够帮助我们理解和解释经济现象。
简单线性回归模型是实验中常用的工具之一，它能够通过建立两个变量之间的数学关系，预测一个变量对另一个变量的影响。
本文将介绍计量经济学实验中的简单线性回归模型及其应用。
简单线性回归模型模型定义简单线性回归模型是一种用于描述自变量（X）与因变量（Y）之间关系的线性模型。
其数学表达式为：Y = β0 + β1X + ε其中，Y表示因变量，X表示自变量，β0和β1为未知参数，ε表示误差项。
参数估计在实际应用中，我们需要通过数据来估计模型中的参数。
最常用的估计方法是最小二乘法（OLS）。
最小二乘法的目标是通过最小化观测值与拟合值之间的平方差来估计参数。
具体而言，我们需要求解以下两个方程来得到参数的估计值：∂(Y - β0 - β1X)^2 / ∂β0 = 0∂(Y - β0 - β1X)^2 / ∂β1 = 0解释变量与被解释变量在简单线性回归模型中，解释变量（X）用来解释或预测被解释变量（Y）。
例如，我们可以使用房屋的面积（X）来预测房屋的价格（Y）。
在实验中，我们可以根据收集到的数据来建立回归模型，并利用该模型进行预测和分析。
应用实例数据收集为了说明简单线性回归模型的应用，我们假设收集了一些关于学生学习时间与考试成绩的数据。
下面是收集到的数据：学习时间（小时）考试成绩（百分制）2 723 784 805 856 88模型建立根据收集到的数据，我们可以建立简单线性回归模型来分析学生学习时间与考试成绩之间的关系。
首先，我们需要确定自变量和因变量的符号。
在这个例子中，我们可以将学习时间作为自变量（X），考试成绩作为因变量（Y）。
然后，我们使用最小二乘法来估计模型中的参数。
通过计算，可以得到如下参数估计值：β0 = 69.85β1 = 2.95最终的回归方程为：Y = 69.85 + 2.95X预测与分析通过建立的回归模型，我们可以进行预测和分析。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验报告
1.实验目的
随着中国经济的发展，居民的常住收入水平不断提高，粮食销售量也不断增长。
研究粮食年销售量与人均收入之间的关系，对于探讨粮食年销售量的增长的规律性有重要的意义。
2.模型设定
为了分析粮食年销售量与人均收入之间的关系,选择“粮食年销售量”为被解释变量（用Y表示），选择“人均收入”为解释变量（用X表示）。
本次实验报告数据取自某市从1974年到1987年的数据（教材书上101页表3.11），数据如下图所示：
为分析粮食年销售量与人均收入的关系，做下图所谓的散点图:
粮食年销售量与人均收入的散点图
从散点图可以看出粮食年销售量与人均收入大体呈现为线性关系，可以建立如下简单现行回归模型：
3.估计参数
假定所建模型及其中的随机扰动项 i μ满足各项古典假定，可以
用OLS 法估计其参数。
通过利用EViews 对以上数据作简单线性回归分析，得出回归结果如下表所示：
t t t X Y μββ++=21
可用规范的形式将参数估计和检验的结果写为：
=t Y ^
99.61349+0.08147 t X
（6.431242）（0.10738） t= (15.48900) (7.587119)
2R =0.827498 F=57.56437 n=14
4.模型检验
（1）.经济意义检验
所估计的参数1^β=99.61349，2^β=0.08147，说明人均收入每增加1元，平均说来可导致粮食年销售量提高0.08147元。
这与经济学中边际消费倾向的意义相符。
（2）.拟合优度和统计检验
拟合优度的度量：由回归结果表可以看出，本实验中可决系数为0.827498，说明所建模型整体上对样本数据拟合一般偏好。
对回归系数的t 检验：针对0H :1β=0 和0H :2β=0，由回归结果表
中还可以看出，估计的回归系数1^β的标准误差和t 值分别为：SE(1^β)=6.431242,t(1^β)=15.48900;
2^β的标准误差和
t 值分别为：SE(2^β)=0.10738,t(2^β)=7.587119.取a=0.05，查t 分布表自由度为
n-2=14-2=12的临界值025.0t （12）=2.179.因为t(1^β)=15.48900>025.0t （12）=2.179, 所以应拒绝0H :1β=0;因为t(2^
β)=7.587119>025.0t （12）=2.179.
所以应拒绝0H :2β=0。
这表明，人均收入对粮食年销售量确有显著影
响。
实验报告（多元线性回归）
1.实验目的
随着经济的发展，人民的生活水平不断得到提高，粮食年销售量也随着增加，以某市为例，该市1974年的粮食年销售98.45万吨，而到了1987年，粮食年销售量已增加到了178.69万吨，为1974年的1.815倍。
因此研究粮食年销售量增长的主要原因，对于分析粮食年销售量未来的增长趋势，有很重要的经济意义，从而需要建立计量经济模型。
2.模型设定
为了全面反映该市粮食年销售量增长的全貌，选择“粮食年销售量”为被解释变量（用Y表示），选择“常住人口”、“人均收入”、“肉销售量”、“蛋销售量”、“鱼虾销售量”作为解释变量，分别用X2、X3、X4、X5、X6表示。
本次实验数据取自某市从1974年到1987年的数据（教材书101页表3.11），数据如下图所示：
为分析被解释变量与各个解释变量之间的关系，作相关线性图形如下图所示：
从上图可以看出被解释变量和各个解释变量之间大体呈现线性关系，因此可以建立线性回归模型如下：
3. 参数估计
假定所建模型及其中的随机扰动项 i μ满足各项古典假定，可以
用OLS 法估计其参数。
通过利用EViews 对以上数据作多元线性回归分析，得出回归结果如下表所示：
t t t t t t t X X X X X Y μββββββ++++++=66554433221
根据以上表中数据，模型估计的结果为：
65432^491407.4453715.3677595.2073672.012532.0491789.3X X X X X Y t -++++-= (30.00475) (0.059135) (0.037876) (1.257299) (2.450799) (2.214785) t=(-0.116375) (2.119221) (1.945119) (2.129640) (1.409220) (-2.027920) 2R =0.970442 _
2R =0.951968 F=52.53043 df=14-6=8 4. 模型检验
（1） 经济意义检验
模型估计结果说明，在假定其他变量不变的情况下，当常住人口每增加1万人，平均说来粮食年销售量会增加0.12532万吨；在假定其他变量不变的情况下，当人均收入每增加1元，平均说来粮食年销售量会增加0.073672万吨；在假定其他变量不变的情况下，当肉销售量每增加1万吨，平均说来粮食年销售量会增加2.677595万吨；在假定其他变量不变的情况下，当蛋销售量每增加1万吨，平均说来粮食年销售量会增加3.453715万吨；在假定其他变量不变的情况下，
当鱼虾销售量每增加1万吨，平均说来粮食年销售量会减少4.491407万吨。
这与理论分析和经验判断相一致。
（2） 统计检验
A ． 拟合优度：由回归结果表可知2R =0.970442 ，修正的可决系数为
_
2R =0.951968。
这说明模型对样本的拟合很好。
B ． F 检验：针对0H :2β=3β=4β=5β=6β=0，给定显著性水平a=0.05，
在F 分布中查出自由度为k-1=5和n-k=14-6=8的临界值)8,5(αF =3.69.由回归结果表可知F=52.53043,由于
F=52.53043>)8,5(αF =3.69,应拒
绝原假设0H :2β=3β=4β=5β=6β=0，说明回归方程显著，即“常住人口”、
“人均收入”、“肉销售量”、“蛋销售量”、“鱼虾销售量”等变量联合起来确实对“粮食年销售量”有显著影响。
C ． t 检验：分别针对0H ：j β=0（j=1，2，3，4，5，6），给定显著性
水平a=0.05，查t 分布表的自由度为n-k=8的临界值)(2/k n t -α=2.306.由回归结果表中数据可知，与^1β、^2β、^3β、^4β、^5β、^6β对应的t 统计量分别为-0.116375、2.119221、1.945119、
2.129640、1.409220、-2.027920，其绝对值均小于)(2/k n t -α=2.306，说明显著性水平a=0.05的条件下，分别都应当拒绝0H ：j β=0（j=1，2，3，4，5，6）也就是说在其他解释变量不变的情况下，“常住人口”、“人均收入”、“肉销售量”、“蛋销售量”、“鱼虾销售量”分别对被解释变量都没有显著影响。