数学史作业题7
09数学史作业题5+何柯+0929010032

09数学史作业题5一、选择题1.欧洲中世纪漫长的黑暗时期过后,第一位有影响的数学家是( A )。
A.斐波那契B.卡尔丹C.塔塔利亚D.费罗2.首先获得一元三次方程一般解法的数学家是( B )。
A.塔塔利亚 B.卡尔丹C.费罗 D.费拉里3.射影几何产生于文艺复兴时期的( D )A.音乐演奏B.服装设计C.雕刻艺术D.绘画艺术4.首先解决了一元四次方程一般解法的是数学家( C )A.塔塔利亚B.卡尔丹C.费拉里D.费罗二、填空题1.数学家_______斐波那契___在他的代表作《算经》中叙述了著名的“兔子问题”。
2.斐波那契数列的第一项是________1____,第七项是____13________。
3.首先将三次方程一般解法公开的是意大利数学家_____卡尔丹________。
三、简答题1.简述三次方程求根问题的解决过程,及其在数学发展史上的重大意义。
答:三次方程最早都是以实际問題出现的。
在古巴比伦人遺留下来的楔形文字小片中有相当于下列的三次方程問題: 12x~3+x~2=1+45/60(当时巴比伦使用六十进位制)。
但是在三四千年以前,巴比伦人怎样解这类三次方程問題,現在还不知道,不过不会有普遍解法是可以肯定的。
刁藩都(Diophantos,第三世紀人)是古代希腊著名的代数学家,在他的数学名著《算术》中研究了許多方程問題,其中有一个問題相当于下面的三次方程: x~3+8x-(5x~2+1)=x。
意义:,利用函数关系把几何图形变成代数问题来解决,2.简述对数计算方法的发明过程及其意义。
答:16、17世纪之交,随着天文、航海、工程、贸易以及军事的发展,改进数字计算方法成了当务之急。
苏格兰数学家纳皮尔(J.Napier,1550—1617)正是在研究天文学的过程中,为了简化其中的计算而发明了对数.意义:对数的发明是数学史上的重大事件,天文学界更是以近乎狂喜的心情迎接这一发明。
恩格斯曾经把对数的发明和解析几何的创始、微积分的建立称为17世纪数学的三大成就,伽利略也说过:”给我空间、时间及对数,我就可以创造一个宇宙。
七桥问题

笔画成。
回头来看七桥问题
由图可见,这个图形有 四个奇结点,所以,它 不能被一笔画。
转换一下图:
1 2 3 4
现在看完了七桥问题,来看看“八桥问题”吧
2
1
一 条 线 代 表 一 座 桥, 现 在 有 八 座 桥。
这个图形有两个奇结点, 所以可以一笔画。
七桥问题是一个几何问题,图中 什么都可以变,唯独点线之间的相 关位置,或相互连结的情况不能变。 欧拉认为对这类问题的研究,属于 一门新的几何学分支,他称之为” 位置几何学”。后来,这门数学分 支被正式命名为“拓扑学”(图 论)。现在,拓扑学已成为20世纪 最丰富多彩的一门数学分支。
18世纪著名古典数学问题之 一。在哥尼斯堡的一个公园 里,有七座桥将普雷格尔河 中两个岛及岛与河岸连接起 来(如图)。问是否可能从 这四块陆地中任一块出发, 恰好通过每座桥一次,再回 到起点?欧拉于1736年研究 并解决了此问题,他把问题 归结 “一笔画”问题,证明 上述走法是不可能的。
但是,为什么不可以呢?
“内部”与“外部”
一条头尾相连且自身不相 交的封闭曲线,把橡皮膜分 成两个部分。如果我们把其 中有限的部分称为闭曲线的 “内部”,那么另一部分便 是闭曲线的“外部”。从闭 曲线的内部走到闭曲线的外 部,不可能不通过该闭曲线。 因此,无论你怎样拉扯橡皮 膜,只要不切割、不撕裂、 不折叠、不穿孔,那么闭曲 线的内部和外部总是保持不 变的!
由左图可知,这个图形 有两个奇结点。
12ຫໍສະໝຸດ 简单的一笔画问题3
这个图形就不可以一笔 为什么呢 画。 仔细观察,这个图形有 四个奇结点; 所以不能一笔画。 没有奇数个奇结点的图 形。
人教版初一数学(七年级)课程讲义第一章:有理数的意义(解析版)

人教版初一数学(七年级)课程讲义第一章:有理数的意义(解析版)【例题1】体育课上,华英学校对九年级男生进行了引体向上测试,以能做7个为标准,超过的次数记为正数,不足的次数记为负数,其中8名男生的成绩如下:2,-1,0,3,-2,-3,1,0(1) 这8名男生有百分之几达到标准?(2) 他们共做了多少引体向上?【答案】(1)62.5%;(2)56个【解析】(1)由题意可知:正数或0表示达标,而正数或0的个数共有5个,所以百分率为:; 答:这8名男生有62.5%达到标准.(2)(7+2)+(7-1)+7+(7+3)+(7-2)+(7-3)+(7+1)+7=56(个)答:他们共做了引体向上56个.讲解用时:3分钟解题思路:解题时要注意对正负数的意义准确理解教学建议:一定要先引导学生弄清“基准”是什么.难度: 3 适应场景:当堂练习 例题来源:无 年份:2019【练习1.1】中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数.如果收入100元记作+100元.那么﹣80元表示( )A .支出20元B .收入20元C .支出80元D .收入80元【答案】C5100%62.5%8⨯=【解析】解:根据题意,收入100元记作+100元,则﹣80表示支出80元.故选:C.讲解用时:2分钟解题思路:在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.教学建议:解题关键是引导学生理解“正”和“负”的相对性,确定一对具有相反意义的量.难度: 3 适应场景:当堂例题例题来源:无年份:2019【例题2】如图所示是几位同学所画的数轴,其中正确的是 ( )A.(1)(2)(3) B.(2)(3)(4) C.只有(2) D.(1)(2)(3)(4) 【答案】C【解析】对数轴的三要素掌握不清.(1)中忽略了单位长度,相邻两整点之间的距离不一致;(3)中负有理数的标记有错误;(4)图中漏画了表示方向的箭头.讲解用时:3分钟解题思路:数轴是一条直线,可以向两端无限延伸;数轴的三要素:原点、正方向、单位长度缺一不可.教学建议:对学生强调数轴的三要素难度: 3 适应场景:当堂例题例题来源:无年份:2019【练习2.1】填空:(1)数轴上离原点5个单位长度的点表示的数是________;(2)从数轴上观察,-3与3之间的整数有________个.【答案】±5;5个.【解析】画出数轴,即可观察出离原点5个单位长度的点表示的数是±5,同时可以数出-3与3之间的整数有5个讲解用时:2分钟解题思路:准确画出数轴,即可得出答案教学建议:熟练掌握数轴的画法及数轴的三要素难度: 3 适应场景:当堂练习 例题来源:无 年份:2019【例题3】如图,数轴上有A ,B ,C ,D 四个点,其中表示2的相反数的点是( )A .点AB .点BC .点CD .点D【答案】A【解析】解:∵表示2的相反数的点,到原点的距离与2这点到原点的距离相等,并且与2分别位于原点的左右两侧,∴在A ,B ,C ,D 这四个点中满足以上条件的是A .故选A .讲解用时:3分钟解题思路:考查相反数的定义:只有符号不同的两个数互为相反数.根据定义,结合数轴进行分析.教学建议:引导学生观察总结互为相反数的两个数在数轴上的位置特点:分别位于原点的左右两侧,并且到原点的距离相等.难度: 3 适应场景:当堂练习 例题来源:无 年份:2019【练习3.1】51-的相反数是( ) A .5 B .51 C .51-D.-5 【答案】B【解析】根据相反数的概念:只有符号不同的两个数互为相反数即可得出答案为B讲解用时:3分钟解题思路:解决这类问题的关键是抓住互为相反数的特征“只有符号不同”,所以只要将原数的符号变为相反的符号,即可求出其相反数.教学建议:熟练掌握相反数的定义.难度: 3 适应场景:当堂例题 例题来源:无年份:2019 【例题4】当a≠0时,请解答下列问题:(1)求a a的值;(2)若b≠0,且0=+b b a a ,求ab ab的值.【答案】 (1)1±;(2)1-.【解析】解:(1)当a >0时,a a=1;当a <0时,a a=﹣1;(2)∵0=+b ba a,∴a ,b 异号,当a >0,b <0时,ab ab=﹣1;当a <0,b >0时,ab ab=﹣1;讲解用时:3分钟解题思路:(1)利用绝对值的代数意义化简即可求出值;(2)根据有理数的乘法法则和绝对值的代数意义化简即可求出值;教学建议:利用绝对值的代数意义化简是解本题的关键. 难度: 3 适应场景:当堂例题 例题来源:无 年份:2019【练习4.1】计算:已知|x|=32,|y|=21,且x <y <0,求6÷(x ﹣y )的值.【答案】﹣36.【解析】解:∵|x|=32,|y|=21,且x <y <0,∴x=﹣32,y=﹣21,∴6÷(x ﹣y )=6÷(﹣32+21) =﹣36.讲解用时:4分钟解题思路:直接利用绝对值的性质结合有理数混合运算法则计算得出答案. 教学建议:利用绝对值的性质和有理数混合运算,正确得出x ,y 的值是解题关键.难度: 3 适应场景:当堂练习 例题来源:无 年份:2019【例题5】如图,数轴上的三点A ,B ,C 分别表示有理数a,b,c ,化简|a ﹣b|﹣|a+c|+|b ﹣c|.【答案】2c【解析】解:由数轴得,c>0,a<b<0,因而a﹣b<0,a+c<0,b﹣c<0.∴原式=b﹣a+a+c+c﹣b=2c.讲解用时:3分钟解题思路:由数轴可知:c>0,a<b<0,所以可知:a﹣b<0,a+c<0,b﹣c <0.根据负数的绝对值是它的相反数可求值.教学建议:此题主要是考查学生对数轴和绝对值的理解,要求学生要对这些概念性的东西牢固掌握.难度: 3 适应场景:当堂例题例题来源:无年份:2019【练习5.1】已知|a﹣1|=9,|b+2|=6,且a+b<0,求a﹣b的值.【答案】0或﹣12.【解析】解:∵|a﹣1|=9,|b+2|=6,∴a=﹣8或10,b=﹣8或4,∵a+b<0,∴a=﹣8,b=﹣8或4,当a=﹣8,b=﹣8时,a﹣b=﹣8﹣(﹣8)=0,当a=﹣8,b=4时,a﹣b=﹣8﹣4=﹣12.综上所述,a﹣b的值为0或﹣12.讲解用时:3分钟解题思路:本题考查了垂线段,利用垂线段最短是解题关键.教学建议:引导学生掌握绝对值的性质,熟记运算法则和性质并判断出a、b的对应情况是解题的关键.难度: 3 适应场景:当堂练习例题来源:无年份:2019【例题6】有理数a、b、c在数轴上的位置如图:(1)判断正负,用“>”或“<”填空:b﹣c0,a+b0,c﹣a0.(2)化简:|b﹣c|+|a+b|﹣|c﹣a|.【答案】(1)<,<,>;(2)﹣2b.【解析】解:(1)由图可知,a<0,b>0,c>0且|b|<|a|<|c|,所以,b﹣c<0,a+b<0,c﹣a>0;故答案为:<,<,>;(2)|b﹣c|+|a+b|﹣|c﹣a|=(c﹣b)+(﹣a﹣b)﹣(c﹣a)=c﹣b﹣a﹣b﹣c+a=﹣2b.讲解用时:3分钟解题思路:(1)根据数轴判断出a、b、c的正负情况,然后分别判断即可;(2)去掉绝对值号,然后合并同类项即可.教学建议:必须让学生熟记三种位置角的形状.难度: 3 适应场景:当堂例题例题来源:无年份:2019【练习6.1】已知a、b、c都是负数,且0-+-+-=,则x + y + z______0.(填x a y b z c“>”、“<”、“=”).【答案】<【解析】利用绝对值的非负性,可得出x=a,y=b,z=c,则x+y+z=a+b+c<0讲解用时:4分钟解题思路:本题考查了绝对值的性质,准确识图观察出a、b、c的正负情况是解题的关键.教学建议:利用绝对值的非负性去掉绝对值符号是解此题的关键.难度: 3 适应场景:当堂练习例题来源:无年份:2019【例题7】已知:a=3,|b|=2,求(a+b)3的值.【答案】125或1.【解析】解:∵|b|=2,∴b=±2,当b=2时,(a+b)3=(3+2)3=125;当b=﹣2时,(a+b)3=(3﹣2)3=1,综上所述,(a+b)3的值为125或1.讲解用时:3分钟解题思路:利用绝对值的代数意义求出b的值,代入原式计算即可求出值.教学建议:熟练掌握绝对值的代数意义是解本题的关键.难度: 3 适应场景:当堂例题例题来源:无年份:2019【练习7.1】数学实验室:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.利用数形结合思想回答下列问题:①数轴上表示2和5两点之间的距离是,数轴上表示1和﹣3的两点之间的距离是.②数轴上表示x和﹣2的两点之间的距离表示为|.数轴上表示x和5的两点之间的距离表示为.③若x表示一个有理数,则|x﹣1|+|x+3|的最小值=.④若x表示一个有理数,且|x+3|+|x﹣2|=5,则满足条件的所有整数x的是.⑤若x表示一个有理数,当x为,式子|x+2|+|x﹣3|+|x﹣5|有最小值为.若﹣1<x<4,化简|x+1|+|4﹣x|.【答案】① 3,4;②|x+2|,|5﹣x|;③4;④﹣3或﹣2或﹣1或0或1或2;⑤3,7;【解析】解:①数轴上表示2和5两点之间的距离是5﹣2=3,数轴上表示1和﹣3的两点之间的距离是1﹣(﹣3)=4,故答案为:3,4;②数轴上表示x和﹣2的两点之间的距离表示为|x﹣(﹣2)|=|x+2|,数轴上表示x和5的两点之间的距离表示为|5﹣x|,故答案为:|x+2|,|5﹣x|;③当x<﹣3时,|x﹣1|+|x+3|=1﹣x﹣x﹣3=﹣2x﹣2,当﹣3≤x≤1时,|x﹣1|+|x+3|=1﹣x+x+3=4,当x>1时,|x﹣1|+|x+3|=x﹣1+x+3=2x+2,在数轴上|x﹣1|+|x+3|的几何意义是:表示有理数x的点到﹣3及到1的距离之和,所以当﹣3≤x≤1时,它的最小值为4,故答案为:4;④当x<﹣3时,|x+3|+|x﹣2|=﹣x﹣3+2﹣x=﹣2x﹣1=5,解得:x=﹣3,此时不符合x<﹣3,舍去;当﹣3≤x≤2时,|x+3|+|x﹣2|=x+3+2﹣x=5,此时x=﹣3或x=﹣2或0或1或2;当x>2时,|x+3|+|x﹣2|=x+3+x﹣2=2x+1=5,解得:x=2,此时不符合x>2,舍去;当x=0时,|x+3|+|x﹣2|=5;当x=1时,|x+3|+|x﹣2|=5;当x=﹣1时,|x+3|+|x﹣2|=5;故答案为:﹣3或﹣2或﹣1或0或1或2;⑤∵设y=|x+2|+|x﹣3|+|x﹣5|,i、当x≥5时,y=x+2+x﹣3+x﹣5=3x﹣6,∴当x=5时,y最小为:3x﹣6=3×5﹣6=9;ii、当3≤x<5时,y=x+2+x﹣3+5﹣x=x+4,∴当x=3时,y最小为7;iii、当﹣2≤x<3时,y=x+2+3﹣x+5﹣x=10﹣x,∴此时y最小接近7;iiii、当x<﹣2时,y=﹣x﹣2+3﹣x+5﹣x=6﹣x,∴此时y最小接近8;∴y的最小值为7.故答案为:3,7.讲解用时:4分钟解题思路:①②在数轴上A、B两点之间的距离AB=|a﹣b|,依此即可求解;④根据绝对值的性质去掉绝对值号,然后计算即可得解;③首先将原式变形为y=|x﹣1|+|x+3|,然后分别从当x≥1时,当﹣3≤x<1时,当x<﹣3时去分析,根据一次函数的增减性,即可求得y的最小值;④当x<﹣3时,当﹣3≤x≤2时,当x>2时,当x=﹣1,当x=1,当x=0去分析,根据一次函数的增减性,即可求得答案;⑤当x≥5时,当3≤x<5时,当﹣2≤x<3时,当x<﹣2时去分析,根据一次函数的增减性,即可求得y的最小值.教学建议:本题考查了数轴,绝对值的性质,读懂题目信息,理解数轴上两点间的距离的表示是解题的关键.注意分类思想的运用.难度: 3 适应场景:当堂练习例题来源:无年份:2019课后作业【作业1】下列说法正确的是()A. 一个数的绝对值一定比0大B. 一个数的相反数一定比它本身小C. 绝对值等于它本身的数一定是正数D. 最小的正整数是1【答案】D【解析】A、一个数的绝对值一定比0大,有可能等于0,故此选项错误;B、一个数的相反数一定比它本身小,负数的相反数,比它本身大,故此选项错误;C、绝对值等于它本身的数一定是正数,0的绝对值也等于其本身,故此选项错误;D、最小的正整数是1,正确.讲解用时:4分钟难度: 2 适应场景:练习题例题来源:无年份:2019【作业2】一只可爱的小虫从点O出发在一条直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,小虫爬行的各段路程(单位:cm)依次记为:+5,-3,+10,-8,-6,+12,-10,在爬行过程中,如果小虫每爬行1cm就奖励2粒芝麻,那么小虫一共可以得到多少粒芝麻?【答案】108【解析】小虫爬行的总路程为:|+5|+|-3|+|+10|+|-8|+|-6|+|+12|+|-10|=5+3+10+8+6+12+10=54(cm) .小虫得到的芝麻数为54×2=108(粒) .讲解用时:4分钟难度: 4 适应场景:练习题例题来源:无年份:2019【作业3】同学们都知道,|5﹣(﹣2)|表示5与﹣2之差的绝对值,实际上也可理解为5与﹣2两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数3的点与表示有理数的点之间的距离.试探索:(1)求|5﹣(﹣2)|=.(2)若|x﹣3|=|x+1|,则x=.【答案】(1)7;(2)1.【解析】解:(1)|5﹣(﹣2)|=|5+2|=7,故答案为:7;(2)由题意得:x﹣3+x+1=0,解得:x=1,故答案为:1;讲解用时:5分钟难度: 3 适应场景:练习题例题来源:无年份:2019。
七桥问题和一笔画

③但凡图形中有2个以上奇点旳,不能完毕一 笔画。
用你发觉旳规律,说一说七桥问题旳答案?
因为七桥问题中旳四个点都是奇点,所以能 够判断它是无法一笔画出来旳 ,也就是说 根本不存在能不反复走遍七座桥旳路线!
● 点A、B体现岛 点C。D体现岸
▎线体现桥
问题分析
问题旳答案怎样呢?让我们先来了解三个新概念。
①有奇数条边相连旳点叫奇点。如:
●
●
●
②有偶数条边相连旳点叫偶点。如:
●
●
●
③一笔画指:1、下笔后笔尖不能离开纸。 2、每条线都只能画一次而不能反复。
活动探究
下图形中。请找出每个图旳奇点个数,偶点个数。试一试哪些能够一笔画出,请填表,从中 你能发觉什么规律?
课堂练习
1、 一辆洒水车要给某城市旳街道洒水,街道地图如下:你能否设计一条洒水车洒水旳路 线,使洒水车不反复地走过全部旳街道,再回到出发点?
小广场
超市 菜市场
文具店 电器城
服装城
课堂练习
2、 下图是一种公园旳平面图,能不能使游 人走遍每一条路不反复?入口和出口又应设 在哪儿?
E ●
●G F ● D●
这就是数学史上著名旳七桥问题,你乐意试一试吗?
问题情景
18世纪时风景秀丽旳小城哥尼斯堡中有一 条河,河旳中间有两个小岛,河旳两岸与两 岛之间共建有七座桥(如图),当初小城旳 居民中流传着一道难题:一种人怎样才干不 反复地走过全部七座桥,再回到出发点?
问题分析
数学家欧拉懂得了七桥问题他用四个点A、B、 C、D分别体现小岛和岸,用七条线段体现七 座桥(如图)于是问题就成为怎样“一笔画”出 图中旳图形?
1.2.1有理数的概念+1.2.2数轴+1.2.3相反数(课件)人教版(2024)七年级上册

分数集合
-8-
任务五:课堂小结,形成体系
回顾数的产生和发展历程,引入负数后我们对数的认识已扩大到有理数范围。
相反意义的量
正数和负数 0
有理数
1.你对有理数有哪些认识?你会对有理数分类吗?
2.0是有理数吗?0有什么特殊之处?
3.你还有什么疑问吗?
-9-
布置作业: 1.教材P16 习题1.2,第1题 2.阅读教材P18 -P19: “图说数学史——慢慢长路识负数”, 写写你的感想。
-29-
任务五:尝试练习,巩固内化 解答:教材P12练习1、2、3、4
-30-
任务六:课堂小结,形成体系
1.反思与交流: (1)只有符号不同的两个数互为相反数。你是如何理解“只有”两个字的? (2)说说你对相反数的其它认识? (3)你还有疑问吗?
2.知识结构
相反意义的量
正数和负数 0
有理数
数 与 点 的 对 应
-17-
任务三:认识数轴,体验数轴的作用。 2.请画一条数轴。
提醒:规定了原点、正方向和单位长度的直线叫数轴。
数轴三要素: 原点、
正方向、 单位长度。
-18-
任务三:认识数轴,体验数轴的作用。
3.(教材P10例2)画出数轴,并在数轴上表示下列各数:
3 , -4 , 4 ,0.5 , 5 ,-1 2
-27-
任务四:求有理数的相反数 1.解答:(教材P12例3) (1)分别写出 -7 和 4 的相反数;
3 (2)a的相反数是2.4,写出a的值。
2.解答:写出下列各数的相反数
-7的相反数是7, 不能写出-7=7
归纳: (1)a和-a只有符号不同, a和-a互为相反数。其中,a表示任意一个有理数,可以 是正有理数、负有理数,也可以是0.
数学文化作业答案(全正确答案)

1数学的研究对象是()A、B、C、D、2一门学科,成功运用()才能走向成熟。
D、3研究对象不是物质或者物质运动形态的科学是()C、4数学素养对于文科生并不重要正确答案:×5通俗地说数学素养就是有条理地理性思维,周密地思考,求证,简洁,清晰,准确地表达。
正确答案:√6一个人不识字可以生活,不识数同样可以生活正确答案:×7数学文化中的文化是指狭义的文化正确答案:×8在我国数学文化最早是哪一年提出的?A、9数学文化这个词最早出现于:B、10数学文化这门课2002年被评为国家精品课程。
正确答案:×11“数学文化”中的文化是指广义文化。
正确答案:√12下列不属于开设数学文化课,学生收获的是:B、13以下不属于数学文化的侠义意思的是:A、B、C、D、14数学是和其他的自然学科在同一个层次上的科学。
正确答案:×15数学的研究可以用到不同的自然科学。
正确答案:√16对数学文化中文化一词的界定,更倾向于广义的解释。
()正确答案:×17数学文化的研究对象是人。
正确答案:√18大学生素质文化教育这个词是何时提出来的D、19何时首推建立32个“国家大学生素质文化教育基地”C、20数学文化一词在中国最早何时出现?A、1数学素养不包括()A、B、C、D、2数学素养不是与生俱来的,是在学习和实践中培养的正确答案:√3数学训练能提高一个人的A、B、C、D、4企业招考员工的题和数学推理往往有关正确答案:√5下面哪一项不是通过学习数学文化得到的?A、B、C、D、6数学素养的高低决定一个人工作的成效正确答案:√7数学不仅是一些知识还是一种素质(素养)。
正确答案:√8专业“数学素养”有几点?()B、9以下不是开数学文化课的指导思想的的是:C、10用数学方法可以解决实际生活中的问题。
正确答案:√11数学文化是以浅显数学知识为载体,讲述数学的思想、精神、方法、观点的一门课程。
正确答案:√12目前社会并不重视数学素养。
[资料]中国数学史
![[资料]中国数学史](https://img.taocdn.com/s3/m/7fbd24c532d4b14e852458fb770bf78a65293a1c.png)
中国数学史中国数学史1. 中国数学从公元前后至公元 14 世纪,先后经历了三次发展高潮,即 ___________ 、魏晋南北朝时期以及宋元时期,其中 ___________ 时期达到了中国古典数学发展的顶峰。
3.1 《周髀算经》与《九章算术》 1. 《史记》“夏本纪”记载说:夏禹治水,“左规矩,右准绳”,这里的规是指 ________ ,矩则是指 _____________ 。
2 “一尺之棰,日取其半,万世不竭”出自我国古代名著 ( ) 。
A. 《考工记》B. 《墨经》C. 《史记》D. 《庄子》3. 在现存的中国古代数学著作中,《 ________ 》是最早的一部。
卷上叙述的关于荣方与陈子的对话,包含了 ________ 的一般形式。
4 中国历史上最早叙述勾股定理的著作是《 ______ 》,中国历史上最早完成勾股定理证明的数学家是三国时期的 ______ 。
5 《九章算术》是从先秦至 ___________ 的长时期里经众多学者编撰、修改而成的一部数学著作。
6 、“九数”是指:方田、粟米、差分、少广、商功、均输、方程、赢不足、旁要。
7 、《九章算术》就是从九数发展来的。
8 《九章算术》 " 方田 " 、 " 商功 " 、 " 勾股 " 三章处理几何问题。
其中 " 方田 " 章讨论 _________ , " 勾股 " 章则是关于_________ 。
9 《九章算术》的“少广”章主要讨论()。
A. 比例术B. 面积术C. 体积术D. 开方术10 《九章算术》内容丰富,全书共有 ________ 章,大约有 ________ 个问题。
11. 世界上讲述方程最早的著作是 ( )A. 中国的《九章算术》B. 阿拉伯花拉子米的《代数学》C. 卡尔丹的《大法》D. 牛顿的《普遍算术》12 《九章算术》中 " 方程术 " 的关键算法是 "__________" ,实质上这就是我们今天所使用的解线性联立方程组的___________ 。
七桥问题在生活中的应用应用
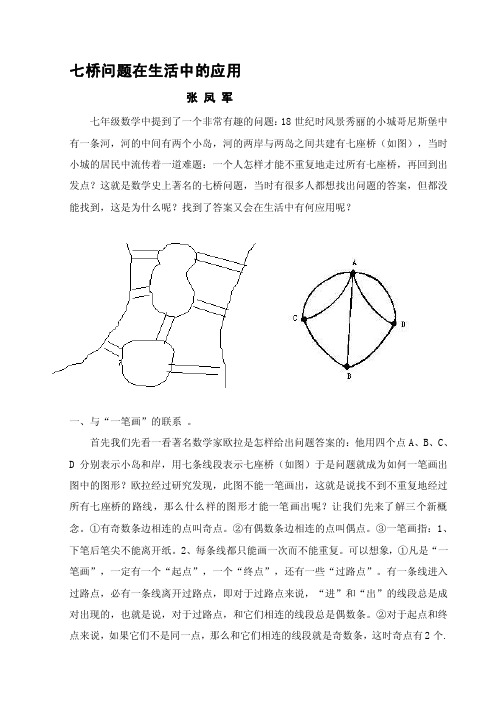
七桥问题在生活中的应用张凤军七年级数学中提到了一个非常有趣的问题:18世纪时风景秀丽的小城哥尼斯堡中有一条河,河的中间有两个小岛,河的两岸与两岛之间共建有七座桥(如图),当时小城的居民中流传着一道难题:一个人怎样才能不重复地走过所有七座桥,再回到出发点?这就是数学史上著名的七桥问题,当时有很多人都想找出问题的答案,但都没能找到,这是为什么呢?找到了答案又会在生活中有何应用呢?一、与“一笔画”的联系。
首先我们先看一看著名数学家欧拉是怎样给出问题答案的:他用四个点A、B、C、D分别表示小岛和岸,用七条线段表示七座桥(如图)于是问题就成为如何一笔画出图中的图形?欧拉经过研究发现,此图不能一笔画出,这就是说找不到不重复地经过所有七座桥的路线,那么什么样的图形才能一笔画出呢?让我们先来了解三个新概念。
①有奇数条边相连的点叫奇点。
②有偶数条边相连的点叫偶点。
③一笔画指:1、下笔后笔尖不能离开纸。
2、每条线都只能画一次而不能重复。
可以想象,①凡是“一笔画”,一定有一个“起点”,一个“终点”,还有一些“过路点”。
有一条线进入过路点,必有一条线离开过路点,即对于过路点来说,“进”和“出”的线段总是成对出现的,也就是说,对于过路点,和它们相连的线段总是偶数条。
②对于起点和终点来说,如果它们不是同一点,那么和它们相连的线段就是奇数条,这时奇点有2个.如果起点和终点是同一点,那么就没有奇点,即奇点个数为0.简单说:能够一笔画的图形奇点的个数只能是0或2,而七桥问题中不符合一笔画的条件,也就无法不重复的经过所有七座桥,通过上面的分析,我们今后能很快看出哪些图形可以一笔画,那些不能。
二、知识的拓宽与应用1.在七桥问题中,如果允许再架一座桥,能否不重复地一次走遍这八座桥?这座桥应架在哪里?请你试一试!2.一辆洒水车要给某城市的街道洒水,街道地图如下图(左):你能否设计一条洒水车洒水的路线,使洒水车不重复地走过所有的街道,再回到出发点?3.下图(右)是一个公园的平面图,能不能使游人走遍每一条路不重复?入口和出口又应设在哪儿?用概率判断游戏的公平性大北中学 张凤军我们在生活中常做一些游戏,但游戏规则的制定必须对双方都是公平的,这个游戏才能进行,否则就会有一方因为游戏不公平而退出游戏,那么如何判断游戏规则是否公平呢?学习了初中数学中《用列举法求概率》一节内容,问题便迎刃而解了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.证明了π的超越性,从而确立了化圆为方不可能性的数学家是( )
A.旺泽尔B.牛顿C.伽罗瓦D.林德曼
6.在射影几何的诞生过程中,对于透视画法所产生的问题从数学上直接给予解答的第一个人是( )
A.达·芬奇;B.笛卡儿;C.德沙格;D.牛顿
7.对于透视法所产生的问题从数学上直接给予解答的第一个人是( )。
17.德沙格和帕斯卡等是____________的开创者。
18.最先建立“非欧几何”理论的数学家是________,给出“非欧几何”这一名称的数学家是________。
19.”非欧几何”理论的建立源于对欧几里得几何体系中__________的证明,最先建立“非欧几何”理论的数学家是__________。
A.达·芬奇B.笛卡儿C.帕斯卡D.德沙格
8.最早提出对数方法的是英国数学家( )
A.纳皮尔B.布里格斯C.斯蒂弗尔D.比尔吉
9.对数方法的发明者是数学家( )。
A.拉普拉斯B.布里格斯C.纳皮尔D.帕斯卡
10.集合论的创立者是( )
A.希尔伯特B.戴德金C.庞加莱D.康托尔
二、填空题
11.十九世纪解决了代数方程可解性问题的两位年轻数学家分别是挪威人___________和法国人___________。
11数学史作业题7一、选源自题1.最先建立“非欧几何”理论的数学家是( )。
A.高斯B.罗巴契夫斯基C.波约D.黎曼
2.提出“集合论悖论”的数学家是( )。
A.康托尔B.罗素C.庞加莱D.希尔伯特
3.提出“集合论悖论”的数学家罗素是( )
A.英国数学家;B.法国数学家;C.德国数学家;D.巴西数学家
4.1900年,德国数学家希尔伯特在巴黎国际数学家大会上提出的著名数学问题共有( )。
12.除了__________籍数学家欧拉外,在18世纪推进微积分及其应用的欧陆数学家中,首先应该提到__________国学派,其代表人物有克莱洛、达郎贝尔、拉格朗日、蒙日、拉普拉斯等。
13.在微积分的应用中,于十八世纪形成并成长起来的新数学分支主要包括______________、偏微分方程、____________________和微分几何等。
23.简述康托尔生活在哪个世纪、所在国家及在数学上的主要成就。
20.罗巴契夫斯基所建立的“非欧几何”假定过直线外一点,______直线与已知直线平行,而且在该几何体系中,三角形内角和______两直角。
三、简答题
21、在牛顿、莱布尼茨之前有许多数学家曾对微积分的创立作出过重要贡献,请列举其中的两位,并指出他们的主要贡献。
22.写出在分析严格化过程中作出最主要贡献的两位数学家及其主要成就。
14.十八世纪对微分几何理论的建立和发展作出了重要贡献的数学家是克莱洛、_____________以及_____________。
15.微分几何诞生于________世纪,对微分几何理论的建立和发展作出了重要贡献的数学家是克莱洛、欧拉以及________。
16.法国几何学家庞斯列对射影几何的发展作出了杰出的贡献,在他的研究中,有两个基本原理扮演了重要角色。首先是_________,另一个是______。
