《材料力学》第6章-简单超静定问题-习题解
第6章简单的超静定问题

材料力学 任课教师:金晓勤
21
φ
代入变形几何条件得:
φ1 φ2
T1l T1l Tl GI P1 GI P 2 GI P 2
I P1T 32 T1 T2 I P1 I P 2 D 4 d 4 D 4 d 4 1 1 2 2 32 32 1004 904 2 1.165kNm 4 4 4 4 100 90 90 80
代入数据,得
FW 0.717 F Fst 0.283F
根据角钢许用应力,确定F
F
st
0.283F st Ast
F 698kN
根据木柱许用应力,确定F
0.717 F W W AW
许可载荷
F 1046kN
250 250
F 698kN
材料力学
将平衡方程与补充方程联立,求解,可得:
RA RB P RAl1 RB l2 E A E A 0 2 2 1 1
P RA E2 A2l1 1 E1 A1l2
P RB E1 A1l2 1 E2 A2l1
材料力学 任课教师:金晓勤
9
例题 木制短柱的4个角用4个40mm×40mm×4mm的等边角钢加固, 已知角钢的许用应力[σst]=160MPa,Est=200GPa;木材的许 用应力[σW]=12MPa,EW=10GPa,求许可载荷F。 F 解: 平衡方程: F FW Fst 变形协调关系: l st l w (1)
b
⑶物理方程
FN 1l1 FN 1l l1 E1 A1 E1 A1 cos FN 2l2 FN 2l l2 E2 A2 E2 A2
《材料力学》第6章-简单超静定问题-习题解
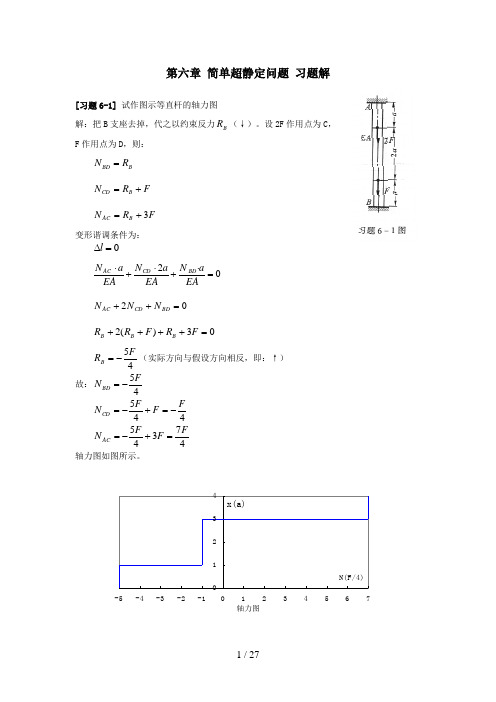
轴力图1234-5-4-3-2-11234567N(F/4)x(a)第六章 简单超静定问题 习题解[习题6-1] 试作图示等直杆的轴力图解:把B 支座去掉,代之以约束反力B R (↓)。
设2F 作用点为C , F 作用点为D ,则:B BD R N = F R N B CD += F R N B AC 3+=变形谐调条件为:0=∆l02=⋅+⋅+⋅EA aN EA a N EA a N BD CD AC 02=++BD CD AC N N N03)(2=++++F R F R R B B B45FR B -=(实际方向与假设方向相反,即:↑) 故:45FN BD-= 445F F F N CD -=+-=47345FF F N AC=+-= 轴力图如图所示。
[习题6-2] 图示支架承受荷载kN F 10=,1,2,3各杆由同一种材料制成,其横截面面积分别为21100mm A =,22150mm A =,23200mm A =。
试求各杆的轴力。
解:以节点A 为研究对象,其受力图如图所示。
∑=0X030cos 30cos 01032=-+-N N N0332132=-+-N N N 0332132=+-N N N (1)∑=0Y030sin 30sin 0103=-+F N N2013=+N N (2)变形谐调条件:设A 节点的水平位移为x δ,竖向位移为y δ,则由变形协调图(b )可知:00130cos 30sin x y l δδ+=∆x l δ=∆200330cos 30sin x y l δδ-=∆03130cos 2x l l δ=∆-∆2313l l l ∆=∆-∆设l l l ==31,则l l 232=223311233EA l N EA lN EA l N ⋅⋅=- 22331123A N A N A N =- 15023200100231⨯=-N N N23122N N N =-21322N N N -= (3)(1)、(2)、(3)联立解得:kN N 45.81=;kN N 68.22=;kN N 54.111=(方向如图所示,为压力,故应写作:kN N 54.111-=)。
6-简单超静定问题

FN 1l FN 3l cos EA cos EA FN 1 FN 3 cos 2
5、求解方程组得
FN 1 FN 2
F cos 2 1 2 cos 3
FN 3
F 1 2 cos 3
目 录
二、装配应力
构件的加工误差是难以避免的。对静定结构,加工误 差只是引起结构几何形状的微小变化,而不会在构件内引 起应力。但对静不定结构,加工误差就要在构件内引起应 力。这种由于装配而引起的应力称为装配应力。 装配应力是结构构件在载荷作用之前已具有的应力, 因而是一种初应力。
超静定结构中才有温度应力。
目 录
解题思路: 平衡方程:RA = RB 变形几何关系: 物理关系:
(t 时)
lT lF
lT l t
RB L
RB l lF EA
EA Lt
补充方程:
联立求解: RA RB EAt
EAt t Et A
目 录
一静定问题及超静定问题三基本静定系或相当系统是一个静定结构该结构上作用有荷载和多余约束力61超静定问题及其解法61超静定问题及其解法二多余约束及多余约束力在静定结构的基础上增加的约束
第六章
简单的超静定问题
§6–1 概述
§6–2 §6–3 §6–4 拉压超静定问题 扭转超静定问题 简单超静定梁
目的与要求:
M
max
WZ
32 M
d
max 3
76.4MPa
目 录
例题
结构如图示,设梁AB和CD的弯曲刚度EIz相同. 拉杆BC的拉压刚度EA为已知,求拉杆BC的轴力.
a
C
将杆CB移除,则AB,CD均为静定结构, 杆CB的未知轴力FN作用在AB,CD梁上。为1 D 次超静定。
材料力学——6简单的超静定问题

M
(x)
X
1
x
X1x, P(x
x l ), 2
l 2
x
l 2
B
l 0
M
(x)M EI
( x)dx
0
如果B处支撑为弹簧 (弹簧系数K) ?
例 P
A
l
l
2
2
BA
P
B
l
l
2
2
X1
解
M
(x)
X1
x
X1x, P(x
x l ), 2
l 2
x
静定基
l 2
x
B
l 0
M (x)M EI
(x)dx
X1 K
求解 线性方程
未知力
以一例说明解法
q
12 3
X1 X2 X3
• 静定基(含未知数)
1 0, 2 0, 3 0
• 位移协调条件
建立方程的过程
以1为例说明
X1 X2 X3
1
M (x)M1(x) dx EI
(M X1 M X2 M X3 M q )M1(x) dx EI
M X1M1 dx M X2 M1(x) dx M X3 M1(x) dx M qM1(x) dx
A
P0 =1 B
M (x) x
解: 协调条件——D截面转
角为零
A
静定基
D
/2
0
M
( )M
EI
()Rd
0
DX
P 2
二、装配应力
1、静定问题无装配应力
B
C
2、静不定问题存在装配应力
1
2
A
下图,3号杆的尺寸误差为,
材料力学-第六章 简单的超静定问题

变形协调条件:
l1 l 3 cos
F N1
F N3
F N2
l3
l1
A
A
l2
例2.图示AB为刚性梁,1、2两杆的抗拉(压)
刚度均为EA,制造时1杆比原长l短,将1杆装
到横梁后,求两杆内力。
解: 装配后各杆变形 1杆伸长 l1 2杆缩短 l 2 变形协调条件
A
1
l1
4、联解方程
FN 1 F E3 A3 2 cos 2 E1 A 1 cos
FN 3
F E1 A 3 1 1 2 cos E3 A3
●装配应力的计算
装配应力:超静定结构中由于加工误差, 装 配产生的应力。 平衡方程:
FN 1 FN 2
1
3 2
A
l
FN 3 ( FN1 FN 2 ) cos
2、AC和BC材料相同,面积不同,外力作用在 连接界面处,在外力不变的情况下,要使AC上 轴力增加,错误的方法有( )。 A、 增加AC的横截面积 B、 减小BC的横截面积 C、 增加AC的长度 D、 增加BC的长度
A l1 C F B l2
3、AB为等截面杆,横截面面积为A,外力F作 用在中间,则AC和BC上应力分别( )。
2
l 2
B
2( l1 ) l 2
解: 分析AB
A
aF 1 2aF 2 0
F1l 物理方程 l1 EA 变形协调条件
FA
F1
F2
B
F2 l l 2 (缩短) EA
2( l1 ) l 2
4EA 2EA F1 (拉力) F2 (压力) 5l 5l
材料力学教学课件 第六章 简单的超静定问题

FN a EA
2qa 3 A FN 2 3a A I Z
FN a 3 FN a q2a FN 2a 8EI Z 3EI Z 3EI Z EA
4
例题 6.10
当系统的温度升高时,下列结构中的____ A 不会 产生温度应力.
A
B
C
D
例题 6.11
所有超静定结构,都是在静定结构上再加一个或几个约束,这些约束对 于特定的工程要求是必要的,但对于保证结构平衡却是多余的,故称为多余 约束。未知力个数与平衡方程数之差,称为超静定次数。
对超静定问题,可综合运用平衡条件、变形的几何相容条件和力与变形 间的物理关系等三个方面来求解。
6-2.拉压超静定问题
例题:求图 ( a ) 所示等直杆 AB 上下端的约束力,并求 C 截面的位移。 杆的拉压刚度为EA。
解: 1、有两个未知约束力FA , FB (见 图a ) , 但只有一个独立的平衡方程, 故为一次超静定问题。
FA +FB - F = 0
2、取固定端B 为“多余”约束。相应 它应满足相容条件 的静定杆如图 (b)。 ΔBF + ΔBB = 0,参见图(c) (d)。 3、补充方程为
A. 有弯矩,无剪力;
q
B
B. 有剪力,无弯矩;
C. 既有弯矩又有剪力; D. 既无弯矩又无剪力;
A
L2
C
L2
例题 6.13
等直梁受载如图所示.若从截面C截开选取基本结 构,则_____. A
A. 多余约束力为FC,变形协调条件为ωC=0; B. 多余约束力为FC,变形协调条件为θC=0; C. 多余约束力为MC,变形协调条件为ωC=0; D. 多余约束力为MC,变形协调条件为θC=0;
孙训方材料力学06简单的超静定问题

B
DC
1
3
2
A
F
10
材料力学
第六章 简单的超静定问题
解:(1)判断超静定次数 结构为一次超静定。
(2)列平衡方程
Fx 0 FN1 FN2
Fy 0
FN1 cos FN2 cos FN3 F 0
B
D
1
3 2
l2 C
l1 A
A
B
F (6)联立平衡方程与补充方程求解
FN1 FN2 FN3 F 0 2aFN1 aFN2 0 FN1 FN3 2FN2
FN1 F / 6 FN2 F / 3 FN3 5F / 6
材料力学
Ⅱ. 装配应力
B
杆系装配好后,各杆将处于
材料力学
【例】 图示等直杆 AB 的两端分别与刚性支承连结。设两 支承的距离(即杆长)为 l,杆的横截面面积为 A,材料的弹
性模量为 E,线膨胀系数为 。试求温度升高 T 时杆内的
温度应力。
A
B
l
材料力学 A
解: 这是一次超静定问题
l
变形相容条件:杆的长度不变
A
Δl 0
杆的变形为两部分:
q B
l/2
FC
l
基本静定系 或相当系统
材料力学
第六章 简单的超静定问题
求解超静定问题的步骤
(1) 判断超静定次数:去掉多余约束,画上相应约束反力 —建立基本静定系。
(2) 列平衡方程: 在已知主动力,未知约束反力及多余约束 反力共同作用下;
(3) 列几何方程:根据变形相容条件; (4) 列物理方程:变形与力的关系; (5) 组成补充方程:物理方程代入几何方程即得。
材料力学简单的超静定问题

§6-4 简单超静定梁
1.基本概念: 超静定梁:支反力数目大于有效平衡方程数目的梁 多余约束:从维持平衡角度而言,多余的约束 超静定次数:多余约束或多余支反力的数目。 相当系统:用多余约束力代替多余约束的静定系统 2.求解方法: 解除多余约束,建立相当系统——比较变形,列变 形协调条件——由物理关系建立补充方程——利用 静力平衡条件求其他约束反力。
1Δ2l3cos
②
(3)代入物理关系,建立补充方程
1
N1 1 E1 A1
N1
E1 A1 cos
③
3
N3 E3 A3
13
2
A
2
1
3
A
§6-2 拉压超静定问题
(2)建立变形协调方程:如图三杆铰结, 画A节点位移图,列出变形相容条件。要 1 注意所设的变形性质必须与受力分析所 中设定的力的性质一致。由对称性知
C
(b)
F
B
F C
B
C
(c)
FBy
(c)
FBy FF
BB B
(d) (d) B
F CC C
C
(d) FBy
F(2a)2
1F 43a
(w B)F
(9a2a)
6EI
3EI
(wB)FBy
8FBya3 3EI
所以
14Fa3 8FBya3 0 3EI 3EI
FBy
7 4
F
4)由整体平衡条件求其他约束反力
M AF 2(a), F Ay 4 3F ( )
FCFFB 408.75
4.875kN
M C0 , M C2 F 4 F B 0
MC 4FB 2F
48.75240115kN.m
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 简单超静定问题 习题解[习题6-1] 试作图示等直杆的轴力图解:把B 支座去掉,代之以约束反力B R (↓)。
设2F 作用点为C , F 作用点为D ,则:B BD R N = F R N B CD += F R N B AC 3+=变形谐调条件为:0=∆l02=⋅+⋅+⋅EA aN EA a N EA a N BD CD AC 02=++BD CD AC N N N03)(2=++++F R F R R B B B45FR B -=(实际方向与假设方向相反,即:↑) 故:45FN BD-= 445F F F N CD -=+-=47345FF F N AC=+-= 轴力图如图所示。
[习题6-2] 图示支架承受荷载kN F 10=,1,2,3各杆由同一种材料制成,其横截面面积分别为21100mm A =,22150mm A =,23200mm A =。
试求各杆的轴力。
解:以节点A 为研究对象,其受力图如图所示。
∑=0X030cos 30cos 01032=-+-N N N0332132=-+-N N N 0332132=+-N N N (1)∑=0Y030sin 30sin 0103=-+F N N2013=+N N (2)变形谐调条件:设A 节点的水平位移为x δ,竖向位移为y δ,则由变形协调图(b )可知:00130cos 30sin x y l δδ+=∆x l δ=∆200330cos 30sin x y l δδ-=∆03130cos 2x l l δ=∆-∆2313l l l ∆=∆-∆设l l l ==31,则l l 232=223311233EA l N EA lN EA l N ⋅⋅=- 22331123A N A N A N =- 15023200100231⨯=-N N N23122N N N =-21322N N N -= (3)(1)、(2)、(3)联立解得:kN N 45.81=;kN N 68.22=;kN N 54.111=(方向如图所示,为压力,故应写作:kN N 54.111-=)。
[习题6-3] 一刚性板由四根支柱支撑,四根支柱的长度和截面都相同,如图所示。
如果荷载F 作用在A 点,试求这四根支柱各受多少力。
解:以刚性板为研究对象,则四根柱子对它对作用力均铅垂向上。
分别用4321,,,N N N N 表示。
由其平衡条件可列三个方程:0=∑Z04321=-+++F N N N N F N N N N =+++4321 (1)0=∑xM0222242=-⋅a N a N 42N N = (2)0=∑yM0222231=⋅-⋅+⋅a N e F a N aFeN N 231-=- (3)由变形协调条件建立补充方程EAN EA l N EA l N 2312=+2312N N N =+。
(4)(1)、(2)、(3)、(4)联立,解得:442F N N == F a e N )241(1-=F ae N )241(3+=[习题6-4] 刚性杆AB 的左端铰支,两根长度相等、横截面面积相同的钢杆CD 和EF 使该刚性杆处于水平位置,如所示。
如已知kN F 50=,两根钢杆的横截面面积21000mm A =,试求两杆的轴力和应力。
解:以AB 杆为研究对象,则:0=∑AM0350221=⨯-⋅+⋅a a N a N 150221=+N N (1)变形协调条件:122l l ∆=∆EAlN EA l N 122= 122N N = (2)(1)、(2)联立,解得:kN N 301= kN N 602=MPa mm NA N 30100030000211===σ MPa mm NA N 60100060000222===σ[习题6-5] 图示刚性梁受均布荷载作用,梁在A 端铰支,在B 点和C 点由两根钢杆BD 和CE 支承。
已知钢杆BD 和CE 的横截面面积22200mm A =和21400mm A =,钢杆的许用应力MPa 170][=σ,试校核该钢杆的强度。
解:以AB 杆为研究对象,则:0=∑AM023)330(3121=⨯⨯-⨯+⨯N N 135321=+N N (1)变形协调条件:3121=∆∆l l 123l l ∆=∆112238.1EA lN EA l N ⨯=⋅40032008.112N N =⋅ 212.1N N = (2)(1)、(2)联立,解得:kN N 571.381=(压);kN N 143.322=(拉)故可记作:kN N 571.381-=;kN N 143.322= 强度校核: MPa MPa mmNA N 170][4275.9640038571||||2111=<===σσ,符合强度条件。
MPa MPa mm N A N 170][715.160200321432122=<===σσ,符合强度条件。
[习题6-6] 试求图示结构的许可荷载[F]。
已知杆AD ,CE ,BF 的横截面面积均为A ,杆材料的许用应力为][σ,梁AB 可视为刚体。
解:以AB 杆为研究对象,则:∑=0Y0321=-++F N N NF N N N =++321 (1)∑=0AM0232=⋅-⋅+⋅a F a N a N F N N =+322 (2)变形协调条件: 2132l l l ∆+∆=∆EAlN EA l N EA l N 21322+=⋅ 2134N N N += (3)(1)(2)(3)联立,解得: 5221F N N ==;53FN = 强度条件: ][5221σσσ≤==AFA A F ][5.22][5σσ=≤][53σσ≤=AF][5σA F ≤故:A F ][5.2][σ=[习题6-7] 横截面积为mm mm 250250⨯的短木柱,用四根mm mm mm 54040⨯⨯的等边角钢加固,并承受压力F ,如图所示。
已知角钢的许用应力MPa s 160][=σ,弹性模量GPa E s 200=;木材的许用应力MPa w 12][=σ,弹性模量GPa E w 10=。
试求短木柱的许可荷载[F]。
解:(1)木柱与角钢的轴力由盖板的静力平衡条件:(1)由木柱与角钢间的变形相容条件,有(2)由物理关系:(3)式(3)代入式(2),得(4)解得:代入式(1),得:(2)许可载荷 由角钢强度条件由木柱强度条件:故许可载荷为:[习题6-8] 水平刚性横梁AB 上部由于某1杆和2杆悬挂,下部由铰支座C 支承,如图所示。
由于制造误差,杆1和长度短了mm 5.1=δ。
已知两杆的材料和横截面面积均相同,且GPa E E 20021==,A A A ==21。
试求装配后两杆的应力。
解:以AB 梁为研究对象,则:0=∑CM0145sin 2021=⨯+⋅-N N2142N N =…………(1) 变形协调条件: 11AA l -=∆δ1222BB l =∆2111212l l BB AA ∆∆-==δ 2122l l ∆=∆-δEAl N EA l N 22221⋅=-δEAlN EA l N 214=-δ………...(2) (1)、(2)联立,解得:l EA N )162(21+=δ;lEA N )162(42+=δMPa mm mm MPa l E 242.161500)162(5.1102002)162(231=⨯+⨯⨯⨯=+=δσMPa mmmm MPa lE 939.451500)162(5.1102004)162(432=⨯+⨯⨯⨯=+=δσ[习题6-9] 图示阶梯状杆,其上端固定,下端与支座距离mm 1=δ。
已知上、下两段杆的横截面面积分别为2600mm 和2300mm ,材料的弹性模量GPa E 210=。
试作图示荷载作用下杆的轴力图。
解:设装配后,支座B 的反力为B R (↓),则: B BC R N =40+=B CD R N (D 为60kN 集中力的作用点)100+=B AD R N变形协调条件:δ=∑=ni il1m R R m m kN m kN R B B B 36666262610110600102102.1)100(10600102104.2)40(10300/102102.1----⨯=⨯⨯⨯⋅++⨯⨯⨯⋅++⨯⨯⨯⋅1261202.1964.24.2=++++B B B R R R906-=B R)(15kN R B -=。
故:[习题6-10] 两端固定的阶梯状杆如图所示。
已知AC 段和BD 段的横截面面积为A ,CD 段的横截面面积为2A ;杆的弹性模量为GPa E 210=,线膨胀系数106)(1012--⨯=C l α。
试求当温度升高C 030后,该杆各部分产生的应力。
解:变形协调条件:0=∆l0=∆+∆t N l l04)2(22=⋅∆⋅++a t A E aN EA Na l α 043=⋅∆⋅+a t EANal α 043=⋅∆⋅+t EANl α )(100800/1021030)(101234342260106kN A Am m kN C c tEA N l -=⋅⨯⨯⨯⨯⨯-=∆-=--α MPa kPa ANBD AC 8.100)(100800-=-===σσ MPa kPa ANCD 4.50)(504002-=-==σ[习题6-11] 图示为一两端固定的阶梯状圆轴,在截面突变处承受外力偶矩e M 。
若212d d =,试求固定端的支反力偶矩A M 和B M ,并作扭矩图。
解:把B 支座去掉,代之以约束反力偶 ,其矩为B M ,转向为逆时针方向,则:B BC M T = e B CA M M T -=变形协调条件:A 、B 为两固定端支座,不允许其发生转动,故:0=+=CB AC AB ϕϕϕ02)(21=+-P B P e B GI aM GI a M M0221=+-P BP e B I M I M M式中,241414111632116)2(321321P P I d d d I =⋅===πππ,故: 021622=+-P B P e B I M I M M0216=+-B eB M M M33eB M M =333233ee e A M M M M -=-=(顺时针方向转动) 33eB BC M M T == 3332ee B CA M M M T -=-=AB 轴的轴力图如下:和截面C 的扭转角。
解:把B 支座去掉,代之以约束反力力偶,其矩为B M ,逆时针方向 转动。
,则:B CB M T = e B CA M M T -=变形协调条件:A 、B 为两固定端支座,不允许其发生转动,故:0=+=CB AC AB ϕϕϕ015.0)(=⋅+⋅-P B P e B GI M GI M M02=+-B e B M M M3eB M M =,故:)(267.138.33m kN M M T e B CB ⋅==== )(533.238.3232m kN M M M T e e B CA ⋅-=⨯-=-=-= C 截面左侧的最大切应力: PCACA W T =max,τ 式中,抗扭截面模量)(423906014.3161161333mm d W P =⨯⨯==π MPa mmmmN W T P CA CA8.594239010533.2||36max,=⋅⨯==τ C 截面右侧的最大切应力: PCBCB W T =max,τ MPa mmmm N W T P CB CB9.294239010267.1||36max,=⋅⨯==τ C 截面的转角: PCBCB BC C GI l T ==ϕϕ 式中,444412717006014.3321321mm mm d I P =⨯⨯==π 04236714.0)(01245.01271700/1080100010267.1==⨯⨯⨯⋅⨯===rad mm mm N mm mm N GI l T P CB CB BCC ϕϕ[习题6-13] 一空心圆管套在实心圆杆B 的一端,如图所示。
