材料力学 简单的超静定问题答案
关于超静定问题
题八图
五、刚架受力及尺寸如图所示，各段EI均为常数。试用力法正则方程求A、B处支座反力并画刚架的弯矩图。（20分）（2009北科大）
六、（20分）如下图所示刚架，AB、BC杆在同一平面内，且均为直径为d的实心圆截面杆，材料为Q235钢，已知G＝0.4E。试求C点的支反力。（2007西南交大）
题六图
三、平面直角曲拐ABC和CD杆均为圆截面，材料相同，已知： ， 。试求CD杆的内力。（20分）（2009吉大）
Hale Waihona Puke 题三图8、（20分）平面刚架的约束及尺寸如图所示，AB、BC、CD各杆的弯曲刚度EI相等，长度均为a。在D处有一水平载荷F的作用。求D点的水平位移 。（2009燕山大学）
题4图
1、图示结构，杆1与杆2的抗拉刚度均为EA，梁AB为刚性杆。在载荷F的作用下，求两杆的轴力。（20分）（湖南大学2008）
二、（15分）钢杆CD、EF的长度及横截面面积分别相同。结构未受力时，钢性杆AB处于水平位置。已知，钢杆横截面面积为A且P、A、E、l、a为已知。求B点的铅垂位移。（2005西南交大）
1、一不变形的刚性梁AB搁于三个相同的弹簧上，在梁上的D处作用一个力F，如图所示。设已知弹簧刚度k（ ）。试求三个弹簧各受力多少？（20分）（湖南大学2009）
三、（20分）结构受力如图所示，ABC梁和CD杆的材料相同，且EI＝EAL2，材料的线膨胀系数为α，均布载荷集度为q，若CD杆温度升高ΔT度时，试求CD杆的内力。（2008吉大）
图18
2、ABC为刚性杆，杆①、②长为a，且EI相同，线膨胀系数为 。现①杆升温Δt，求两杆内力。（15分）（2008北工大）
超静定结构习题答案
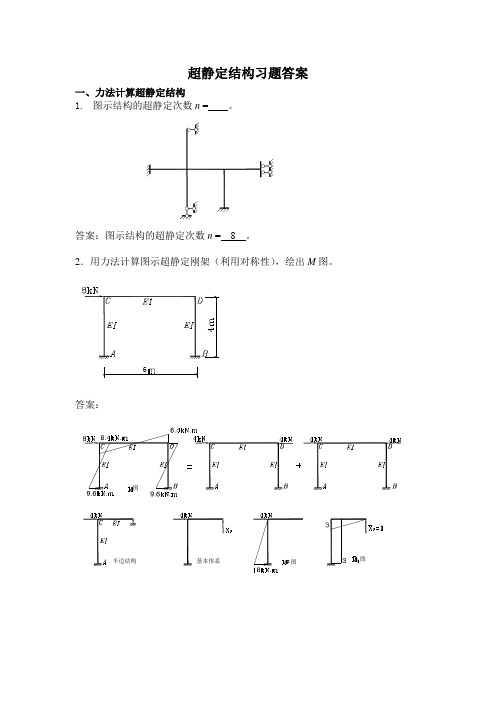
超静定结构习题答案一、力法计算超静定结构1. 图示结构的超静定次数n = 。
答案：图示结构的超静定次数n = 8 。
2．用力法计算图示超静定刚架（利用对称性），绘出M 图。
答案：kN13.296]341621[145]4333323321[1011111111=-=⨯⨯⨯-=∆=⨯⨯+⨯⨯⨯⨯==∆+X EIEI EI EI X P P δδ 3. 图(b )为 图(a ) 结构的力法基本体系，试求典型方程中的系 数 δ11和 自 由 项 ∆1P 。
X lq(b)q答案：q⎪⎭ ⎝-===ϕδl l EIl l X C 4341111作M 图 1X M M =二、位移法1.求图示结构位移法典型方程的系数 r11 和 自 由 项 R P1 ，（ 括号内 数表示相对 线刚度）。
m答案r11 = 17RP1 = 322.图示结构位移法典型方程的系数r22 和自由项 R P1 分 别 是 ⎽⎽⎽⎽ ，⎽⎽⎽⎽⎽ 。
（ 括 号 内 数 表 示 相 对 线 刚 度 ）22答案r22= 4.5RP1= -83. 计算图示结构位移法典型方程中的系 数 r r1122, 。
答案 :r EI 110375=.r EI 2235=.4.计算图示结构的位移法典型方程的全部自由项。
答案 ：R P 10=R P 280=-k N三、力矩分配法1.用力矩分配法作图示连续梁的弯矩图（分配两轮）。
答案：2.用力矩分配法作图示连续梁的弯矩图（分配两轮）。
答案：。
材料力学-第六章 简单的超静定问题
变形协调条件：
l1 l 3 cos
F N1
F N3
F N2
l3
l1
A
A
l2
例2.图示AB为刚性梁，1、2两杆的抗拉（压）
刚度均为EA，制造时1杆比原长l短，将1杆装
到横梁后，求两杆内力。
解: 装配后各杆变形 1杆伸长 l1 2杆缩短 l 2 变形协调条件
A
1
l1
4、联解方程
FN 1 F E3 A3 2 cos 2 E1 A 1 cos
FN 3
F E1 A 3 1 1 2 cos E3 A3
●装配应力的计算
装配应力：超静定结构中由于加工误差， 装 配产生的应力。 平衡方程：
FN 1 FN 2
1
3 2
A
l
FN 3 ( FN1 FN 2 ) cos
2、AC和BC材料相同，面积不同，外力作用在 连接界面处，在外力不变的情况下，要使AC上 轴力增加，错误的方法有（ ）。 A、 增加AC的横截面积 B、 减小BC的横截面积 C、 增加AC的长度 D、 增加BC的长度
A l1 C F B l2
3、AB为等截面杆，横截面面积为A，外力F作 用在中间，则AC和BC上应力分别（ ）。
2
l 2
B
2( l1 ) l 2
解: 分析AB
A
aF 1 2aF 2 0
F1l 物理方程 l1 EA 变形协调条件
FA
F1
F2
B
F2 l l 2 (缩短) EA
2( l1 ) l 2
4EA 2EA F1 (拉力) F2 (压力) 5l 5l
材料力学 简单的超静定问题答案
解：取消A端的多余约束，以代之，则（伸长），在外力作用下杆产生缩短变形。
因为固定端不能移动，故变形协调条件为：故故返回6-2 图示支架承受荷载各杆由同一材料制成，其横截面面积分别为，和。
试求各杆的轴力。
解：设想在荷载F作用下由于各杆的变形，节点A移至。
此时各杆的变形及如图所示。
现求它们之间的几何关系表达式以便建立求内力的补充方程。
即：亦即：将，，代入，得：即：亦即：（1）此即补充方程。
与上述变形对应的内力如图所示。
根据节点A的平衡条件有：；亦即：（2）；，亦即：（3）联解（1）、（2）、（3）三式得：（拉）（拉）（压）返回6-3 一刚性板由四根支柱支撑，四根支柱的长度和截面都相同，如图所示。
如果荷载F作用在A点，试求这四根支柱各受力多少。
解：因为2，4两根支柱对称，所以，在F力作用下：变形协调条件：补充方程：求解上述三个方程得：返回6-4 刚性杆AB的左端铰支，两根长度相等、横截面面积相同的钢杆CD和EF 使该刚性杆处于水平位置，如图所示。
如已知，两根钢杆的横截面面积，试求两杆的轴力和应力。
解：，（1）又由变形几何关系得知：，（2）联解式（1），（2），得，故，返回6-5(6-7) 横截面为250mm×250mm的短木柱，用四根40mm×40mm×5mm的等边角钢加固，并承受压力F，如图所示。
已知角钢的许用应力，弹性模量；木材的许用应力，弹性模量。
试求短木柱的许可荷载。
解：（1）木柱与角钢的轴力由盖板的静力平衡条件：（1）由木柱与角钢间的变形相容条件，有（2）由物理关系：（3）式（3）代入式（2），得（4）解得：代入式（1），得：（2）许可载荷由角钢强度条件由木柱强度条件：故许可载荷为：返回6-6(6-9) 图示阶梯状杆，其上端固定，下端与支座距离。
已知上、下两段杆的横截面面积分别为和，材料的弹性模量。
试作图示荷载作用下杆的轴力图。
解：变形协调条件故故，返回6-7(6-10) 两端固定的阶梯状杆如图所示。
材料力学土木类第六章简单的超静定问题
第6章 简单的超静定问题
静定结构: 仅靠静力平衡方程就可以求出结构的约束反力或内力
超静定结构(静不定结构): 静力学平衡方程不能求解 超静定结构的未知力的数目多于独立的平衡方程的数目；两者的差值称为超静定的次数
分析：画出受力及变形简图
写出独立平衡方程
一次超静定问题。
l
变形协调条件：原杆两端各自与刚性板固结在一起，故内、外杆的扭转变形相同。即变形协调条件为
代入物理关系(胡克定理)，与平衡方程联立，即可求得Ma和Mb。
并可进一步求得杆中切应力如图（内、外两杆材料不同），一般在两杆交界处的切应力是不同的。
按叠加原理：
BB、BM分别为MB、Me引起的在杆端B的扭转角。
线弹性时，物理关系(胡克定理)为
代入上式可解得
MA可平衡方程求得 。
例 图示一长为l 的组合杆，由不同材料的实心圆截面杆和空心圆截面杆套在一起而组成，内、外两杆均在线弹性范围内工作，其扭转刚度分别为GaIpa和GbIpb。当组合杆的两端面各自固结于刚性板上，并在刚性板处受一对扭转力偶矩Me作用时，试求分别作用在内、外杆上的扭转力偶矩。
根据分离体的平衡条件，建立独立的平衡方程；
建立变形协调条件，求补充方程
利用胡克定律，得到补充方程；
联立求解
归纳起来，求解超静定问题的步骤是：
例 一平行杆系，三杆的横截面面积、长度和弹性模量均分别相同，用A、l、E 表示。设AC为一刚性横梁，试求在荷载F 作用下各杆的轴力
解: (1)受力分析--平衡方程
例 设l，2，3杆用铰连接如图，1、2两杆的长度、横截面面积和材料均相同，即l1=l2=l，A1=A2 =A ， E1= E2=E；3杆长度为l3 ，横截面面积为A3，弹性模量为E3 ,试求各杆的轴力。
材料力学第5版(孙训方编)
FAy
F
(b)
5. 将上述二个补充方程与由平衡条件ΣMA=0所得平衡方程
FN1a FN3
1 2
a
FN
2
(2a)
F
(3a)
0
联立求解得
FN3
3 2F 110 2
，FN1
2FN3
6 2F 110 2
，FN2
4FN3
12 2F 110 2
17
第六章 简单的超静定问题
Ⅱ. 装配应力和温度应力 (1) 装配应力
所以这仍然是一次超静定问题。
23
第六章 简单的超静定问题
2. 变形相容条件(图c)为 l1 l3 e
这里的l3是指杆3在装配后的缩短值，不带负号。 3. 利用物理关系得补充方程：
FN1l FN3l e EA E3 A3
24
第六章 简单的超静定问题
4. 将补充方程与平衡方程联立求解得：
FN1 FN2
MA
Me
MB
Me
Mea l
M eb l
34
第六章 简单的超静定问题 (a)
4. 杆的AC段横截面上的扭矩为
TAC
M A
M eb l
从而有
C
TAC a GI p
M eab lGI p
35
第六章 简单的超静定问题
例题6-6 由半径为a的铜杆和外半径为b的钢管经紧 配合而成的组合杆，受扭转力偶矩Me作用，如图a。试求 铜杆和钢管横截面上的扭矩Ta和Tb，并绘出它们横截面上 切应力沿半径的变化情况。
而杆1和杆2中的装配内力利用图b中右侧的图可知为
FN1
FN 2
FN3
2 c os
2
孙训方材料力学06简单的超静定问题
B
DC
1
3
2
A
F
10
材料力学
第六章 简单的超静定问题
解：（1）判断超静定次数 结构为一次超静定。
（2）列平衡方程
Fx 0 FN1 FN2
Fy 0
FN1 cos FN2 cos FN3 F 0
B
D
1
3 2
l2 C
l1 A
A
B
F （6）联立平衡方程与补充方程求解
FN1 FN2 FN3 F 0 2aFN1 aFN2 0 FN1 FN3 2FN2
FN1 F / 6 FN2 F / 3 FN3 5F / 6
材料力学
Ⅱ. 装配应力
B
杆系装配好后，各杆将处于
材料力学
【例】 图示等直杆 AB 的两端分别与刚性支承连结。设两 支承的距离(即杆长)为 l，杆的横截面面积为 A，材料的弹
性模量为 E，线膨胀系数为 。试求温度升高 T 时杆内的
温度应力。
A
B
l
材料力学 A
解: 这是一次超静定问题
l
变形相容条件：杆的长度不变
A
Δl 0
杆的变形为两部分：
q B
l/2
FC
l
基本静定系 或相当系统
材料力学
第六章 简单的超静定问题
求解超静定问题的步骤
(1) 判断超静定次数：去掉多余约束，画上相应约束反力 —建立基本静定系。
(2) 列平衡方程: 在已知主动力，未知约束反力及多余约束 反力共同作用下；
(3) 列几何方程：根据变形相容条件； (4) 列物理方程：变形与力的关系； (5) 组成补充方程：物理方程代入几何方程即得。
孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-简单的超静定问题(圣才出品)
8 / 42
圣才电子书 十万种考研考证电子书、题库视频学习平台
Δl1＝FN1l1/EA1＝FN1l/（EA1cos30°） Δl2＝FN2l2/EA2＝FN2l/（EA2） Δl3＝FN3l3/EA3＝FN3l/（EA3cos30°） 代入式③可得补充方程： FN1l/（EA1sin30°·cos30°）＝2FN2l/（EA2tan30°）＋FN3l/（EA3sin30°·cos30°）④ （3）求解 联立式①②④，可得各杆轴力：FN1＝8.45kN，FN2＝2.68kN，FN3＝11.55kN。
9 / 42
圣才电子书 十万种考研考证电子书、题库视频学习平台
MB = 0
FN2 Leabharlann 2 2a+
FN4
2 2
a
+
FN3
2a − F ( 2 a + e) = 0 2
②
根据结构的对称性可得 FN2＝FN4③
（2）补充方程
如刚性板的位移图所示，根据几何关系可得：Δl1＋Δl3＝2Δl2④
由结构对称可知 Δl2＝Δl4，其中，由胡克定律可得各杆伸长量：
Δl1＝FN1l/EA，Δl2＝FN2l/EA，Δl3＝FN3l/EA
代入式④，整理可得补充方程：FN1＋FN3＝2FN2⑤
（3）求解
联立式①②③⑤，解得各杆轴力：
FN1
=
(1 4
−
e )F(压) 2a
FN2
=
FN4
=
F 4
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
6-1试作图示等直杆的轴力图。
解：取消A端的多余约束，以代之，则（伸长），在外力作用下杆产生缩短变形。
因为固定端不能移动，故变形协调条件为：
故
故
返回
6-2图示支架承受荷载各杆由同一材料制成，其横截面面积分
别为，和。
试求各杆的轴力。
解：设想在荷载F作用下由于各杆的变形，节点A移至。
此时各杆的变形及如图所示。
现求它们之
间的几何关系表达式以便建立求内力的补充方程。
即：
亦即：
将，，代入，
得：
即：
亦即：
（1）
此即补充方程。
与上述变形对应的内力如图所示。
根据节点A的平衡条件有：
；
亦
即：
（2）
；，
亦
即：
（3）
联解（1）、（2）、（3）三式得：
（拉）
（拉）
（压）
返回
6-3 一刚性板由四根支柱支撑，四根支柱的长度和截面都相同，如图所示。
如果荷载F作用在A点，试求这四根支柱各受力多少。
解：因为2，4两根支柱对称，所以，在F力作用下：
变形协调条件：
补充方程：
求解上述三个方程得：
返回
6-4 刚性杆AB的左端铰支，两根长度相等、横截面面积相同的钢杆CD和EF 使该刚性杆处于水平位置，如图所示。
如已知，两根钢杆的横截面面
积，试求两杆的轴力和应力。
解：，
（1）
又由变形几何关系得知：
，
（2）
联解式（1），（2），得，
故，
返回
6-5(6-7) 横截面为250mm×250mm的短木柱，用四根40mm×40mm×5mm的等边角钢加固，并承受压力F，如图所示。
已知角钢的许用应力，弹性模量；木材的许用应力，弹性模量。
试求短木柱的许可荷载。
解：（1）木柱与角钢的轴力由盖板的静力平衡条件：
（1）由木柱与角钢间的变形相容条件，有
（2）
由物理关系：
（3）
式（3）代入式（2），得
（4）
解得：
代入式（1），得：
（2）许可载荷
由角钢强度条件
由木柱强度条件：
故许可载荷为：
返回
6-6(6-9)图示阶梯状杆，其上端固定，下端与支座距离。
已知上、下两段杆的横截面面积分别为和，材料的弹性模量。
试作图示荷载作用下杆的轴力图。
解：变形协调条件
故
故，
返回
6-7(6-10)两端固定的阶梯状杆如图所示。
已知AC段和BD段的横截面面积为A，CD段的横截面面积为2A；杆材料的弹性模量为，线膨胀系数℃-1。
试求当温度升高℃后，该杆各部分产生的应力。
解：设轴力为，总伸长为零，故
==
返回
6-8(6-11)图示为一两端固定的阶梯状圆轴，在截面突变处承受外力偶矩。
若，试求固定端的支反力偶矩，并作扭矩图。
解：解除B端多余约束，则变形协调条件为
即
故：
即：
解得：
由于
故
返回
6-9(6-13)一空心圆管A套在实心圆杆B的一端，如图所示。
两杆在同一横
截面处各有一直径相同的贯穿孔，但两孔的中心线构成一个角。
现在杆B上施加外力偶使杆B扭转，以使两孔对准，并穿过孔装上销钉。
在装上销钉后卸
除施加在杆B上的外力偶。
试问管A和杆B横截面上的扭矩为多大？已知管A
和杆B的极惯性矩分别为；两杆的材料相同，其切变模量为G。
解：解除Ⅱ端约束，则Ⅱ端相对于截面C转了角，（因为事先将杆B的C端扭了一个角），故变形协调条件为=0
故：
故：
故连接处截面C，相对于固定端Ⅱ的扭转角为：
=
而连接处截面C，相对于固定端I的扭转角为：
=
应变能
=
=
返回
6-10(6-15)试求图示各超静定梁的支反力。
解（a）：原梁AB是超静定的，当去掉多余的约束
铰支座B时，得到可静定求解的基本系统（图i）
去掉多余约束而代之以反力，并根据原来约束条件，令B点的挠度，则得
到原超静定梁的相当系统（图ii）。
利用的位移条件，得补充方程：
由此得：
由静力平衡，求得支反力，为：
剪力图、弯矩图分别如图（iii），（iv）所示。
梁的挠曲线形状如图（v）所示。
这里遵循这样几个原则：
（1）固定端截面挠度，转角均为零；
（2）铰支座处截面挠度为零；
（3）正弯矩时，挠曲线下凹，负弯矩时，挠曲线上凸；
（4）弯矩为零的截面，是挠曲线的拐点位置。
（b）解：由相当系统（图ii）中的位移条件，得补充方程式：
因此得支反力：
根据静力平衡，求得支反力：
,
剪力图、弯矩图，挠曲线图分别如图（iii）、（iv）、
（v）所示。
（c）解：由于结构、荷载对称，因此得支反力
；
应用相当系统的位移条件，得补充方程式：
注意到，于是得：
=
剪力图、弯矩图、挠曲线分别如图（iii）、（iv）、
（v）所示。
其中：
若截面的弯矩为零，则有：
整理：
解得：或。
返回
6-11(6-16)荷载F作用在梁AB及CD的连接处，试求每根梁在连接处所受的力。
已知其跨长比和刚度比分别为
解：令梁在连接处受力为，则梁AB、CD受力如图（b）所示。
梁AB 截面B的挠度为：
梁CD 截面C的挠度为：
由于在铅垂方向截面B与C连成一体，因此有。
将有关式子代入得：
变换成：
即：
解得每个梁在连接处受力：
返回
6-12(6-18)图示结构中梁AB和梁CD的尺寸及材料均相同，已知EI为常量。
试绘出梁CD的剪力图和弯矩图。
解：由EF为刚性杆得
即
图（b）：由对称性，
剪力图如图（c）所示，
弯矩图如图（d）所示，
返回
6-13(6-21)梁AB的两端均为固定端，当其左端转动了一个微小角度时，试确定梁的约束反力。
解：当去掉梁的A端约束时，得一悬臂梁的基本系统（图a）。
对去掉的约束代之以反力和，并限定A截面的位移：。
这样得到原结构
的相当系统（图b）。
利用位移条件，，与附录（Ⅳ）得补充式方程如下：
（1）
（2）
由式（1）、（2）联解，得：
从静力平衡，进而求得反力是：。