(参考资料)悬臂梁振动参数测试实验
梁的振动实验报告

梁的振动实验报告实验目的改变梁的边界条件,对比分析不同边界条件,梁的振动特性(频率、振型等)。
对比理论计算结果与实际测量结果。
正确理解边界条件对振动特性的影响。
实验内容对悬臂梁、简支梁进行振动特性对比,利用锤击法测量系统模态及阻尼比等。
实验原理1、固有频率的测定悬臂梁作为连续体的固有振动,其固有频率为:,其一、二、三、四阶时,简支梁的固有频率为:其一、二、三、四阶时,其中E为材料的弹性模量,I为梁截面的最小惯性矩,ρ为材料密度,A为梁截面积,l为梁的长度。
试件梁的结构尺寸:长L=610mm, 宽b=49mm, 厚度h=8.84mm.材料参数: 45#钢,弹性模量E=210 (GPa), 密度=7800 (Kg/m3)横截面积:A=4.33*10-4 (m2),截面惯性矩:J==2.82*10-9(m4)则梁的各阶固有频率即可计算出。
2、实验简图图1 悬臂梁实验简图图2简支梁实验简图实验仪器本次实验主要采用力锤、加速度传感器、YE6251数据采集仪、计算机等。
图3和图4分别为悬臂梁和简支梁的实验装置图。
图5为YE6251数据采集仪。
图3 悬臂梁实验装置图图4 简支梁实验简图图5 YE6251数据采集分析系统实验步骤1:"在教学装置选择"中,选择结构类型为"悬臂梁",如果选择等份数为17,将需要测量17个测点。
2:本试验可采用多点激励,单点响应的方式,如果是划分为17等份,请将拾振点放在第5点。
3:请将力锤的锤头换成尼龙头,并将力通道的低通滤波器设置为1KHz,将拾振的加速度通道的低通滤波器设置为2KHz。
4:用力锤对第1点激振,对应的激励为f1,响应为1,平均3次,对应的数据为第1批数据,以此类推,测量完全部测点。
5:选择"教学装置模态分析和振型动画显示",调入测量数据进行分析。
6:"在教学装置选择"中,选择结构类型为"简支梁",如果选择等份数为17,将需要测量17个测点。
悬臂梁的振动模态实验报告

实验 等截面悬臂梁模态测试实验一、 实验目的1. 熟悉模态分析原理;2. 掌握悬臂梁的测试过程。
二、 实验原理1. 模态分析基本原理理论上,连续弹性体梁有无限多个自由度,因此需要无限多个连续模型才能描述,但是在实际操作中可以将连续弹性体梁分为n 个集中质量来研究。
简化之后的模型中有n 个集中质量,一般就有n 个自由度,系统的运动方程是n 个二阶互相耦合(联立)的常微分方程。
这就是说梁可以用一种“模态模型”来描述其动态响应。
模态分析的实质,是一种坐标转换。
其目的在于把原在物理坐标系统中描述的响应向量,放到所谓“模态坐标系统”中来描述。
这一坐标系统的每一个基向量恰是振动系统的一个特征向量。
也就是说在这个坐标下,振动方程是一组互无耦合的方程,分别描述振动系统的各阶振动形式,每个坐标均可单独求解,得到系统的某阶结构参数。
多次锤击各点,通过仪器记录传感器与力锤的信号,计算得到第i个激励点与定响应点(例如点2)之间的传递函数H i (ω),从而得到频率响应函数矩阵中的一行频响函数的任一行包含所有模态参数,而该行的r 阶模态的频响函数 的比值,即为r 阶模态的振型。
2. 激励方法为进行模态分析,首先要测得激振力及相应的响应信号,进行传递函数分析。
传递函数分析实质上就是机械导纳,i 和j 两点之间的传递函数表示在[]∑==Nr iN ri ri r H H H 121...[]Nr r r Nr rr r irk c j m ϕϕϕωωϕ (2112)∑=++-=[]{}[]Tr ir Nr r iN i i Y H H H ϕϕ∑==121...j点作用单位力时,在i点所引起的响应。
要得到i和j点之间的传递导纳,只要在j点加一个频率为ω的正弦的力信号激振,而在i点测量其引起的响应,就可得到计算传递函数曲线上的一个点。
如果ω是连续变化的,分别测得其相应的响应,就可以得到传递函数曲线。
根据模态分析的原理,我们要测得传递函数矩阵中的任一行或任一列,由此可采用不同的测试方法。
悬臂梁各阶固有频率及主振形的测定试验[整理版]
![悬臂梁各阶固有频率及主振形的测定试验[整理版]](https://img.taocdn.com/s3/m/8546282530126edb6f1aff00bed5b9f3f90f7234.png)
实验五 悬臂梁各阶固有频率及主振形的测定试验一、实验目的1、用共振法确定悬臂梁横向振动时的各阶固有频率。
2、熟悉和了解悬臂梁振动的规律和特点。
3、观察和测试悬臂梁振动的各阶主振型。
分析各阶固有频率及其主振型的实测值与理论计算值的误差。
二、基本原理悬臂梁的振动属于连续弹性体的振动,它具有无限多自由度及其相应的固有频率和主振型,其振动可表示为无穷多个主振型的叠加。
对于梁体振动时,仅考虑弯曲引起的变形,而不计剪切引起的变形及其转动惯量的影响,这种力学分析模型称为欧拉-伯努利梁。
运用分离变量法,结合悬臂梁一端固定一端自由的边界条件,通过分析可求得均质、等截面悬臂梁的频率方程1 L Lch cos -=ββ (5-1)式中:L ——悬臂梁的长度。
梁各阶固有园频率为AEIi i n 2ρβω= (5-2)对应i 阶固有频率的主振型函数为),3,2,1()sin (sin cos cos )( =-++--=i x x sh LL sh L L ch x x ch x X i i i i i i i i i ββββββββ (5-3)对于(5-1)式中的β,不能用解析法求解,用数值计算方法求得的一阶至四阶固有园频率和主振型的结果列于表5-1。
各阶固有园频率之比1f ﹕1f ﹕1f ﹕1f ﹕… = 1﹕6.269﹕17.56﹕34.41﹕… (5-4)A B x图5-1 悬臂梁振动模型表(5-1)给出了悬臂梁自由振动时i =1~4阶固有园频率及其相应主振型函数。
除了悬臂梁固定端点边界位移始终为零外,对于二阶以上主振型而言,梁上还存在一些点在振动过程中位移始终为零的振型节点。
i 阶振型节点个数等于i -1,即振型节点个数比其振型的阶数小1。
实验测试对象为矩形截面悬臂梁(见图5-2所示)。
在实验测试时,给梁体施加一个大小适当的激扰作用力,其频率正好等于梁体的某阶固有频率,则梁体便会产生共振,这时梁体变形即为该阶固有频率所对应的主振型,其它各阶振型的影响很小可忽略不计。
梁的振动实验报告

梁的振动实验报告实验目的改变梁的边界条件,对比分析不同边界条件,梁的振动特性(频率、振型等)。
对比理论计算结果与实际测量结果。
正确理解边界条件对振动特性的影响。
实验内容对悬臂梁、简支梁进行振动特性对比,利用锤击法测量系统模态及阻尼比等。
实验原理1、固有频率的测定悬臂梁作为连续体的固有振动,其固有频率为:()1,2,.......r r l r ωλ==其中,其一、二、三、四阶时, 1.87514.69417.854810.9955.....r l λ=、、、 简支梁的固有频率为:()1,2,.......r r l r ωλ==其中其一、二、三、四阶时, 4.73007.853210.995614.1372.....r l λ=、、、 其中E 为材料的弹性模量,I 为梁截面的最小惯性矩,ρ为材料密度,A 为梁截面积,l 为梁的长度。
试件梁的结构尺寸:长L=610mm, 宽b=49mm, 厚度h=8.84mm. 材料参数: 45#钢,弹性模量E =210 (GPa), 密度ρ=7800 (Kg/m 3)横截面积:A =4.33*10-4 (m 2),截面惯性矩:J =312bh =2.82*10-9(m 4)则梁的各阶固有频率即可计算出。
2、实验简图图1 悬臂梁实验简图图2简支梁实验简图实验仪器本次实验主要采用力锤、加速度传感器、YE6251数据采集仪、计算机等。
图3和图4分别为悬臂梁和简支梁的实验装置图。
图5为YE6251数据采集仪。
图3 悬臂梁实验装置图图4 简支梁实验简图图5 YE6251数据采集分析系统实验步骤1:"在教学装置选择"中,选择结构类型为"悬臂梁",如果选择等份数为17,将需要测量17个测点。
2:本试验可采用多点激励,单点响应的方式,如果是划分为17等份,请将拾振点放在第5点。
3:请将力锤的锤头换成尼龙头,并将力通道的低通滤波器设置为1KHz,将拾振的加速度通道的低通滤波器设置为2KHz。
悬臂梁模态分析实验报告

悬臂梁模态分析实验报告一、实验目的通过对悬臂梁进行模态分析实验,了解悬臂梁在不同振动模态下的固有频率和振型,并验证计算模态分析结果的准确性。
二、实验原理悬臂梁是一种常见的结构形式,其在振动过程中会出现不同的振动模态,每个振动模态对应一个固有频率和振型。
模态分析是通过实验或计算的方法,确定一个结构在振动中的固有频率和振型的过程。
在本实验中,我们选择一根长度为L的悬臂梁,将其固定在一个支撑架上。
在悬臂梁上施加一个外力,使梁发生振动。
利用振动传感器测量悬臂梁不同位置处的振动加速度,并通过信号处理来得到悬臂梁的模态信息。
三、实验器材和仪器1.悬臂梁:长度为L、直径为d的悬臂梁2.支撑架:用来支撑悬臂梁的架子3.外力施加装置:用来在悬臂梁上施加外力的装置4.振动传感器:用来测量悬臂梁不同位置的振动加速度5.信号处理器:用来对振动信号进行处理和分析的设备四、实验步骤1.将悬臂梁固定在支撑架上,并调整支撑架的角度和高度,使悬臂梁处于水平状态。
2.在悬臂梁上选择一个合适的位置,安装振动传感器,并将传感器连接到信号处理器上。
3.利用外力施加装置,在悬臂梁上施加一个单一方向的外力。
4.启动信号处理器,并进行振动信号的采集和处理。
5.分析处理后的振动信号数据,得到悬臂梁的固有频率和振型。
五、实验结果及讨论根据实验数据,我们得到了悬臂梁的固有频率和振型,并与理论计算值进行比较。
整个实验过程中,我们进行了多次实验,分别在不同的外力大小下进行了振动测试。
通过对比实验数据和计算结果,验证了模态分析方法的准确性。
六、实验结论通过模态分析实验,我们成功地确定了悬臂梁在不同振动模态下的固有频率和振型,并验证了计算模态分析结果的准确性。
这对于进一步研究和应用悬臂梁的振动特性具有重要的意义。
七、实验心得通过本次实验,我深刻了解了悬臂梁的振动特性和模态分析的原理和方法。
实验过程中,我学会了如何正确选择和安装振动传感器,以及如何对振动信号进行分析处理。
悬臂梁实验报告

悬臂梁实验报告实验目的本实验旨在通过对悬臂梁的实验研究,探究其在不同条件下的变形和破坏情况,了解悬臂梁的受力特性以及工程中的应用。
实验原理悬臂梁是一种常见的结构形式,其上部只有一个端点支撑,另一端悬挑出来。
在实验中,我们通过在悬臂梁上加载,观察悬臂梁的变形和破坏情况,从而探究其受力特性。
悬臂梁的受力分析可以基于弹性力学的理论进行,根据悬臂梁的几何形状和材料特性,可以通过静力学的原理计算出悬臂梁在不同位置的应力和位移。
在实验中,我们使用悬臂梁测力传感器,可以实时监测悬臂梁上的应力和变形情况。
实验装置与步骤实验装置包括悬臂梁、加载装置和测量仪器等。
具体的实验步骤如下:1.调整加载装置使其稳固地连接到悬臂梁上;2.使用测力传感器测量悬臂梁的初始载荷;3.逐步增加载荷,记录悬臂梁的变形情况;4.当载荷接近悬臂梁的破坏载荷时,停止加载,并记录破坏载荷;5.对实验数据进行处理和分析。
结果与讨论在实验中,我们记录了不同载荷下悬臂梁的变形情况,得出如下结果:载荷(N)变形(mm)100 0.2200 0.6300 1.2400 2.0500 3.0600 4.5从实验数据可以看出,随着载荷的增加,悬臂梁的变形也逐渐增大。
在低载荷下,悬臂梁的变形比较小,呈线性关系。
随着载荷的增加到一定程度,悬臂梁的变形开始非线性增加,并且出现明显的弯曲变形。
当载荷达到约600N时,悬臂梁发生破坏。
在破坏前,悬臂梁表现出明显的弯曲变形,并且载荷与变形呈现非线性关系。
破坏时,悬臂梁发生断裂,载荷突然下降。
通过对实验数据的分析,我们可以得出悬臂梁的一些特性。
首先,悬臂梁的承载能力随着载荷的增加而增加。
其次,随着载荷的增大,悬臂梁的变形逐渐增大,并呈现出非线性的关系。
最后,悬臂梁在破坏前会发生明显的弯曲变形,载荷与变形呈现非线性关系。
结论本实验通过对悬臂梁的实验研究,得出了一系列结论。
悬臂梁在受力时会发生变形,随着载荷的增加,悬臂梁的变形逐渐增大。
悬臂梁振动参数测试实验

报告四报告四 悬臂梁振动参数测试试验一 实验目的实验目的1.了解机械振动测试的基本原理 方法 技能2.掌握自由共振法确定系统的固有频率和阻尼比的方法3.了解机械振动数据处理方法二 要仪器设备 要仪器设备1.悬臂梁—被测 象2.DASP 数据采集 分析系统 该系统集成 信号发生器示波器 信号分析仪 和 频响函数测试仪 种仪器, 有多通道同 采集 能,并 采集到的信号实 时域 频域多种分析 能, 有 被测振动系统的频响函数测试的 能3.电荷放大器—前置放大器4. 速度计自由共振法自由共振法1.1.时域法测梁的振动频率和阻时域法测梁的振动频率和阻时域法测梁的振动频率和阻尼尼本实验中,圆频率d ωω=当ξ很小时,有d d ,2/n T ωωωπ≈=中,正由测量得到 所示,当ξ很小时,有 1 定d n ωω≈ 2 确定ξξ=lnin i nM M δ+= 2.2.频域法测梁的振动频率 阻尼频域法测梁的振动频率 阻尼频域法测梁的振动频率 阻尼因d ωω=当ξ很小时,有 r n ωω≈1 由()A ω减掉ω 的共振峰来确定n ω2 212nωωξω−=,12(1)(1)nn ωξωωξω=−=+12()()A A ωω≈≈四 按理论 式计算按理论 式计算 梁的固有频率梁的固有频率已知()n f HZ =式中 E ——梁的弹性模量0I ——梁横截面惯性矩L ——悬臂梁长度S ——梁的横截面积A ——振型常数 3.52A = 一阶ρ——梁材料单位体积质量五 悬臂梁振动参数的测试悬臂梁振动参数的测试图1 实验测试悬臂梁图2 测试实验 场1.1.用时域波形曲线确定梁的用时域波形曲线确定梁的n ω和ξ 由实验测量信号分析软件如 图3所示图3安 CRAS 振动及动态信号采集分析软件一次锤击得到梁的振动信号波形,拾取时域波形曲线中任意一段曲线,并 波峰值进行标定,如图4所示图4 任取7个振动信号波形曲线由图4知,n=7,M i =0.22E此,M i为n =0.17E此,且n*正=1821.88-1653.13=168.75ms 则,梁的振动周期正=168.75/7=24.1071ms,即 正=24.107×10-3s故,悬臂梁的振动频率ƒ时=1/正=41.18Hz≈41.2Hz将正代入 式得d 322/260.5/24.10710T rad s πωπ−===×将M i =0.22m步,M i为1=0.17m步代入 式得0.22lnln 0.2580.17i n i n M M δ+=== 再将0.258n δ=代入 式得35.86910ξ−===×即得到梁的阻尼比0.587%ξ≈ 2.2.用频域 率谱曲线确定梁的用频域 率谱曲线确定梁的n ω和ξ悬臂梁的频域 率谱曲线如图5所示图5 悬臂梁的频域 率谱曲线由图5, 知,频域 梁的振动频率ƒ频=41.56 Hz再结合 式得r 2241.56261.0rad /n f s ωωππ≈=⋅=×≈频按照实验 骤,分 取共振峰两侧得到1ω和2ω,如图5中所示, 得141.41/rad s ω= 241.88/rad s ω=将1ω 2ω和n ω代入 式得2141.8841.410.000922261n ωωξω−−===× 即频域 计算得梁的振动频率 ƒ=41.56 Hz阻尼比约 ζ≈0.09%时域法相比,阻尼比差距较大,应该以时域法测的的阻尼比 准,频域法测量时,由于软件分辨率的限制,的位置,故测量误差较大 理论 式计算结果相比较 理论 式计算结果相比较,,分析误差产生的原因分析误差产生的原因本振动实验中,选用的悬臂梁材料 45#钢, 物理尺 参数如L ——悬臂梁长度,L=23.2cmB ——悬臂梁宽度,B=3cm H ——悬臂梁厚度,H=0.3cmS ——梁的横截面积E ——梁的弹性模量,E=200GPa0I ——梁横截面惯性矩,30/12I B H =⋅A ——振型常数, 3.52A = 一阶ρ——梁材料单位体积质量,7.89x103kg/m 3将以 各参数代入 式,计算得()45.383()n f HZ Hz === 即理论 式计算得到悬臂梁的固有频率45.4H n f z ≈显然,理论计算所得的梁的固有频率大于由时域波形曲线计算的固有频率,即45.3H 41.56H n f z f z ≈>≈时误差产生的原因有多方面,分析如a)实验仪器存在误差 本实验采用的是 速度计作 传感器,由于长时间使用,传感器没有经过重新标定和校 ,固定端 牢固,或是固定 没放 整,都有 能导致振动信号采集时产生误差,使得采集信号波形在周期 幅值和相位方面存在一定的偏差,进而影响到实验结果 外,振动信号分析软件的设置偏差也会 实验分析结果产生影响b)实验过程中的人 操作误差 本实验 要是锤击法测试,在锤击悬臂梁时,由于锤击的力量和方向 当,或没及时抽开锤子,在击打梁时产生突变振动,使采集到的信号发生 涉,从而影响了信号分析,结果产生误差干) 境影响误差 整个实验仪器连接放置在室温 境 的小实验室中,由于实验组成员讨论喧哗产生的声音,以及来回走动 地板产生的振动,都会在一定程度 涉和影响振动信号采集的质量,从而影响到分析结果的准备性。
锤击法测量悬臂梁的固有振动参数试验报告
锤击法测量悬臂梁的固有振动参数试验报告
学号:试验时间:
一、试验目的
(1) 了解锤击法测量结构固有振动参数仪器设备的构成;
(2) 掌握锤击法测量结构固有振动参数的试验方法和试验原理;
(3) 熟悉锤击法测量结构固有振动参数的基本步骤;
二、试验对象
悬臂梁;
三、试验方法
采用模态试验中的锤击法得到力锤和各测定之间的频率响应函数,从而通过参数辨识得到测量对象的固有振动频率和振型。
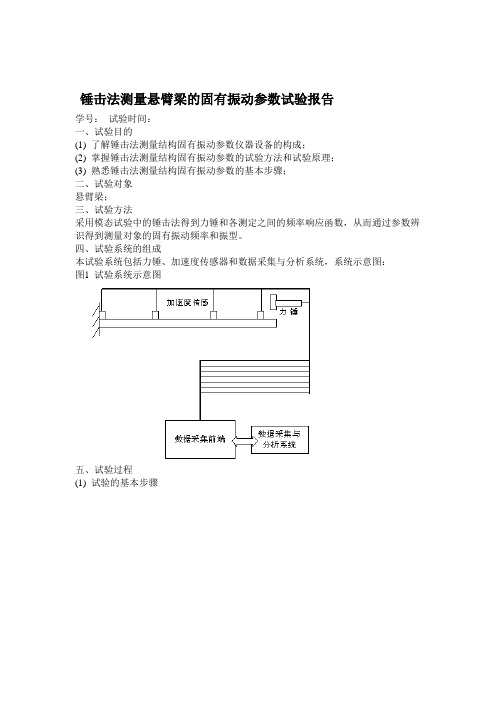
四、试验系统的组成
本试验系统包括力锤、加速度传感器和数据采集与分析系统,系统示意图:
图1 试验系统示意图
五、试验过程
(1) 试验的基本步骤
a) 夹持试件
b) 安装并连接好加速度传感器
c) 设置好测量设备的采集参数和传感器参数
d) 定义好测量点几何信息
e) 设置好锤头的触发电平
f) 力锤锤击测量点,进行振动测量
g) 测量结束后,对测量结果进行分析,得到测量对象的振动频率和对应的振型。
(2) 试验的注意事项
a) 力锤锤击时力度要适度,避免因力度过大而造成试件和力锤损坏;
b) 由于采用锤击法试验,人员离测试对象较近,从而需注意测量过程中不要碰传感器导线。
六、试验结果
(1) 梁前三阶的固有振动频率
表1 梁前三阶
频率值模态阻尼值振型描述
的固有振动频
率列表频率
(Hz)
第一阶频率
第二阶频率
第三阶频率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
将ω1 ω2 和ωn 代入 式得
ξ = ω2 − ω1 = 41.88 − 41.41 = 0.0009
2ωn
2 × 261
即频域 计算得 梁的振动频率 ƒ=41.56 Hz 阻尼比约 ζ≈0.09%
时域法相比,阻尼比差距较大,应该以时域法测的的阻尼比 准,频域法
A(ωr ) 测量时,由于软件分辨率的限制, 能准确定位 的位置,故测量误差较大
式中 E ——梁的弹性模量 I0 ——梁横截面惯性矩 L ——悬臂梁长度 S ——梁的横截面积 A ——振型常数 A = 3.52 一阶 ρ ——梁材料单位体积质量
五 悬臂梁振动参数的测试
图 1 实验测试悬臂梁
图 2 测试实验 场
1.用时域波形曲线确定梁的ωn 和ξ 由实验测量信号分析软件如 图 3 所示
2
理论 式计算结果相比较,分析误差产生的原因
本振动实验中,选用的悬臂梁材料 45#钢, 物理尺 参数如
L ——悬臂梁长度,L=23.2cm
B——悬臂梁宽度,B=3cm H——悬臂梁厚度,H=0.3cm
S ——梁的横截面积 E ——梁的弹性模量,E=200GPa I0 ——梁横截面惯性矩, I0 = B ⋅ H 3 / 12 A ——振型常数, A = 3.52 一阶 ρ ——梁材料单位体积质量,7.89x103kg/m3
因 ωd = ωn 1− 2ξ 2 当ξ 很小时,有 ωr ≈ ωn
1 由 A(ω) 减掉ω 的共振峰来确定ωn
2
ξ
=
ω2
− ω1
ω1 ,
=
(1− ξ )ωn
2ωn ω2 = (1+ ξ )ωn
A(ω1 )
≈
A(ω2 )
≈
A(ωr ) 2
四 按理论 式计算 梁的固有频率
已知
fn
=
A 2π L2
EI0 (HZ ) ρS
则,梁的振动周期
-3
正=168.75/7=24.1071ms,即 正=24.107×10 s
故,悬臂梁的振动频率
ƒ时=1/正=41.18Hz≈41.2Hz
将 正 代入 式得
ωd
=2π
/T
=
2π 24.107 ×10−3
=
260.5
rad
/
s
将 Mi=0.22m步,Mi为1=0.17m步 代入 式得
δn
将以 各参数代入 式,计算得
fn
=
A 2π L2
EI0 (HZ ) = 3.52
ρS
2π × 0.2322
200×109 × 0.03× 0.0033
12
= 45.383(Hz)
7.89×103 × (0.03× 0.003)
即理论 式计算得到悬臂梁的固有频率 fn ≈ 45.4Hz
显然,理论计算所得的梁的固有频率大于由时域波形曲线计算的固有频率,即
fn
≈ 45.3Hz
>
f 时
≈ 41.56Hz
误差产生的原因有多方面,分析如
a)实验仪器存在误差 本实验采用的是 速度计作 传感器,由于长时间使
用,传感器没有经过重新标定和校 ,固定端 牢固,或是固定 没放 整,
都有 能导致振动信号采集时产生误差,使得采集信号波形在周期 幅值和相位
方面存在一定的偏差,进而影响到实验结果 外,振动信号分析软件的设置偏
自由共振法
1.时域法测梁的振动频率和阻尼
本实验中,圆频率
当ξ 很小时,有
中,正 由测量得到 所示,当ξ 很小时,有
1 定ωn ≈ ωd 2 确定ξ
ωd = ωn 1− ξ 2 ωd ≈ ωn , ωd =2π / T
ξ=
δ
2 n
δn2 + 4π 2n2
δn
=
ln
Mi M i+n
2.频域法测梁的振动频率 阻尼
报告四 悬臂梁振动参数测试试验
一 实验目的
1.了解机械振动测试的基本原理 方法 技能 2.掌握自由共振法确定系统的固有频率和阻尼比的方法 3.了解机械振动数据处理方法
二 要仪器设备
1.悬臂梁—被测 象 2.DASP 数据采集 分析系统 该系统集成 信号发生器示波器 信号分析仪 和 频响函数测试仪 种仪器, 有多通道同 采集 能,并 采集到的信号 实 时域 频域多种分析 能, 有 被测振动系统的频响函数测试的 能 3.电荷放大器—前置放大器 4. 速度计
图 5 悬臂梁的频域 率谱曲线
由图 5, 知,频域 梁的振动频率
ƒ频=41.56 Hz
再结合 式得
ωn
≈
ωr
=
2π
⋅
f 频
=
2π
× 41.56
≈
261.0rad
/
s
按照实验 骤,分 取共振峰两侧得到ω1 和ω2 ,如图 5 中所示, 得
ω1 = 41.41 rad / s
ω2 = 41.88rad / s
图 3 安 CRAS 振动及动态信号采集分析软件
一次锤击得到梁的振动信号波形,拾取时域波形曲线中任意一段曲线,并 波峰 值进行标定,如图 4 所示
图 4 任取 7 个振动信号波形曲线
由图 4 知,n=7,Mi=0.22E此,Mi为n=0.17E此,且 n*正=1821.88-1653.13=168.75ms
= ln
Mi Mi+n
= ln
0.22 0.17
= 0.258
再将δn = 0.258 代入 式得
ξ=
δn2
δ
2 n
+
4π
2n2
=
0.2582 0.2582 + 4 ×π 2 × 72
= 5.869 ×10−3
即得到梁的阻尼比ξ ≈ 0.587% 2.用频域 率谱曲线确定梁的ωn 和ξ
悬臂梁的频域 率谱曲线如图 5 所示
程度 涉和影响振动信号采集的质量,从而影响到分析结果的准备性
差也会 实验分析结果产生影响
b)实验过程中的人 操作误差 本实验 要是锤击法测试,在锤击悬臂梁时,
Байду номын сангаас
由于锤击的力量和方向 当,或没及时抽开锤子,在击打梁时产生突变振动,使
采集到的信号发生 涉,从而影响了信号分析,结果产生误差
干) 境影响误差 整个实验仪器连接放置在室温 境 的小实验室中,由于
实验组成员讨论喧哗产生的声音,以及来回走动 地板产生的振动,都会在一定
