LL_1_预测分析器的构造

合集下载

LL(1)语法分析程序实验报告

LL1实验报告1.设计原理所谓LL（1）分析法，就是指从左到右扫描输入串（源程序），同时采用最左推导，且对每次直接推导只需向前看一个输入符号，便可确定当前所应当选择的规则。

实现LL（1）分析的程序又称为LL（1）分析程序或LL1（1）分析器。

我们知道一个文法要能进行LL（1）分析，那么这个文法应该满足：无二义性，无左递归，无左公因子。

当文法满足条件后，再分别构造文法每个非终结符的FIRST和FOLLOW 集合，然后根据FIRST和FOLLOW集合构造LL（1）分析表，最后利用分析表，根据LL(1)语法分析构造一个分析器。

LL（1）的语法分析程序包含了三个部分，总控程序，预测分析表函数，先进先出的语法分析栈，本程序也是采用了同样的方法进行语法分析，该程序是采用了C++语言来编写，其逻辑结构图如下：LL（1）预测分析程序的总控程序在任何时候都是按STACK栈顶符号X和当前的输入符号a做哪种过程的。

对于任何（X，a），总控程序每次都执行下述三种可能的动作之一：（１）若X = a =‘#’，则宣布分析成功，停止分析过程。

（２）若X = a ‘#’，则把X从STACK栈顶弹出，让a指向下一个输入符号。

（３）若X是一个非终结符，则查看预测分析表M。

若M[A，a]中存放着关于X的一个产生式，那么，首先把X弹出STACK栈顶，然后，把产生式的右部符号串按反序一一弹出STACK栈（若右部符号为ε，则不推什么东西进STACK栈）。

若M[A，a]中存放着“出错标志”，则调用出错诊断程序ERROR。

事实上，LL（1）的分析是根据文法构造的，它反映了相应文法所定义的语言的固定特征，因此在LL（1）分析器中，实际上是以LL（1）分析表代替相应方法来进行分析的。

2.分析LL ( 1) 分析表是一个二维表，它的表列符号是当前符号，包括文法所有的终结和自定义。

的句子结束符号#，它的表行符号是可能在文法符号栈SYN中出现的所有符号，包括所有的非终结符，所有出现在产生式右侧且不在首位置的终结符，自定义的句子结束符号#表项。

编译原理笔记10 自上而下分析-预测分析程序与LL(1)文法

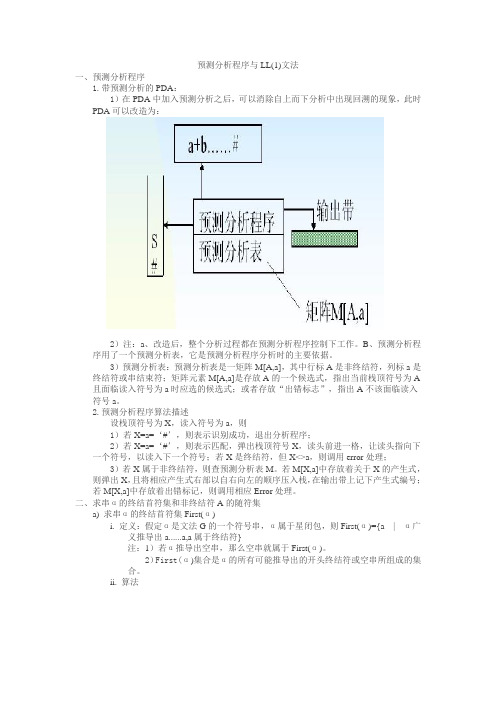
预测分析程序与LL(1)文法一、预测分析程序1.带预测分析的PDA：1）在PDA中加入预测分析之后，可以消除自上而下分析中出现回溯的现象，此时PDA可以改造为：2）注：a、改造后，整个分析过程都在预测分析程序控制下工作。

B、预测分析程序用了一个预测分析表，它是预测分析程序分析时的主要依据。

3）预测分析表：预测分析表是一矩阵M[A,a]，其中行标A是非终结符，列标a是终结符或串结束符；矩阵元素M[A,a]是存放A的一个候选式，指出当前栈顶符号为A 且面临读入符号为a时应选的候选式；或者存放“出错标志”，指出A不该面临读入符号a。

2.预测分析程序算法描述设栈顶符号为X，读入符号为a，则1）若X=a=‘#’，则表示识别成功，退出分析程序；2）若X=a=‘#’，则表示匹配，弹出栈顶符号X，读头前进一格，让读头指向下一个符号，以读入下一个符号；若X是终结符，但X<>a，则调用error处理；3）若X属于非终结符，则查预测分析表M。

若M[X,a]中存放着关于X的产生式，则弹出X，且将相应产生式右部以自右向左的顺序压入栈，在输出带上记下产生式编号；若M[X,a]中存放着出错标记，则调用相应Error处理。

二、求串α的终结首符集和非终结符A的随符集a) 求串α的终结首符集First(α)i. 定义：假定α是文法G的一个符号串，α属于星闭包，则First(α)={a | α广义推导出a......a,a属于终结符}注：1）若α推导出空串，那么空串就属于First(α)。

2）First(α)集合是α的所有可能推导出的开头终结符或空串所组成的集合。

ii. 算法具体步骤：b) 求非终结符A的随符集Follow(A)i. 定义：假定S是文法G的开始符号，对于G的任何非终结符A，定义：ii. 算法1. 对文法开始符号S，将‘#’加入到Follow(S)中；2. 若B->αAβ是文法G的一个产生式，则将First(β)-空串加入到Folow(A)中；3. 若B->αA是文法G的一个产生式，或B->αAβ是文法G的一个产生式，且β推导出空串，则将Follow(B)加入到Follow(A)中；注：这里的文法必须消除左递归且提取了左因子后的文法。

LL（1）分析法

LL（1）分析法LL（1）分析法⼜叫预测分析法，是⼀种不带回溯的⾮递归⾃顶向下的分析法。

LL（1）是不带回溯的⾮递归的分析法是因为，它每次都只有⼀个可⽤的产⽣式，所以是不带回溯和⾮递归的，当⽆法处理输⼊符号时，即出错。

第⼀个L表⽰是从左到右扫描输⼊串，第⼆个L表⽰推导过程中使⽤最左推导，（1）表明只需要向右看⼀个符号，就可以决定如何推导的（即知道⽤哪个产⽣式进⾏推导）。

什么是LL（1）分析法LL（1）分析法的原理是这样的，它的基本思想是根据输⼊串的当前输⼊符号来唯⼀确定选⽤哪个产⽣式来进⾏推导。

⽐如当前的⽂法符号是A，⾯临输⼊串的⾸个符号是a，存在若⼲个产⽣式，A→X1|X2|...|X k，如果a∈FIRST(X i)，那么肯定就是⽤A→X i这个产⽣式来进⾏推导。

⼜或者当前的⽂法符号是A，⾯临的输⼊串的⾸个符号是a，存在产⽣式A→X，若ϵ∈FIRST(X), 且a∈FOLLOW(A)，那么肯定是⽤产⽣式A=>ϵ进⾏推导。

即当然⽂法符号是没⽤的。

所以LL（1）⽂法要满⾜下⾯的条件，若存在A→X1|X2（1）FIRST(X1)⋂FIRST(X2)=ϕ。

即如果对于⽂法符号A，有两个产⽣式的FIRST交集不为空，那么就是⼆义的，就不是LL(1)⽂法（2）若ϵ∈FIRST(X2),则有FIRST(X1)⋂FOLLOW(X2)=ϕ，同样的，这样也是⼆义的。

对LL（1）⽂法构造LL（1）分析表根据上⾯的思想，我们可以预处理出⼀张LL（1）分析表，对于任意的⽂法符号S，⾯临输⼊符号a，该⽤哪个产⽣式。

⾸先，然后根据3条规则来构造LL（1）分析表（这⾥默认该⽂法是LL（1）⽂法）。

①对⽂法G[S]的每个产⽣式A→α执⾏②，③两步②对每个终结符a∈FIRST(α)，把A→α加⼊到表格中的[A,a] 这个格⼦。

即当⽂法符号A⾯临输⼊符号a时，应该使⽤产⽣式A→α③若ϵ∈FIRST(α)，则对所有的终结符b∈FOLLOW(A)，将A→ϵ加⼊到[A,b]这个格⼦。

LL(1)预测分析器的构造

给，【是指串中第ｊｊ】个字符。
（）２逐一扫描产生式右部，要处理如下两种隋况： ①若产生式的右部为空字符串或第一个字符为非终结符，
则将 ‘ 和终结符加入此非终结符的ＨＲＴ集合，出（）ｓ’ Ｓ跳２； ②若产生式右部为非终结符，则将【的ＨＲＴ集合加ｊ】Ｓ
的问题。下面就这两个问题提出解决的算法。
编辑软件，ＡｏｅＰｅｉｒ对屏幕录像和摄像机的录像进行合如ｄｂｒｍｅｅ院的《网页没计教程》课件就是一种有“ 动态电脑屏幕画面 ” 和 “ 教师讲课画面” 合成为画中画）ｉ（及“ 井课音频” 的流媒体课件。
参考文献：［１陈代武．流媒体课件制作中关键技术研究［计算机与现代化，１ａｌ
２００１９－１１７．０：
家里直观自主地学习，定能收到好的学习效果。没有上网的学
习者，以购买配套光盘进行学习。可
３２用于课堂教学．
在课堂教学中，公用的多媒体教室讲台上的电脑只安装了
上教学、课堂教学。
３１用于网上教学．
流媒体课件的最大优势是实时传输，能实现网上边下载边
播放。“ 动态屏幕捕获型” 流媒体课件在现代远程教育（电大，如
４结束语
通过所述屏幕录像方式可以将电脑屏幕的动态变化信息以文件的形式记录保存下来，制成流媒体课件，编特别适宜于
网络教育学院开办的远程教育）或校园网教学中大有用武之
地。若将一些应用软件的教学制成流媒体课件，学习者可以在

LL(1)预测分析程序设计与实现

ｍｇｂｓｄｏｅａｒｃｒ．ｅｕｔｓｏａｉｃｎｅｒｃｙｅａｔ（ｅａｓｔｅｔｈｔｒｍａｅｎｔｓｄｔｓｕｔｅＲｓｌｗｔｔｔｏｏｅｄ，ｘｃｙｕＩｅｎｅｅｈｅａｔｕｓｈｈｒｌｊｇｔｍｗｈａａ
．
２Ｌ（）Ｌ１预测分析方法的设计与实现
预测分析的核心是构造预测分析表，而预测分析表的构造基础是文法非终结符的候选首终结符集ＦｓＡ和后随符号集ＦｌｗＡ．以，ｒ（ｉｔ）ｏｌ（）所ｏ预测分析技术的实现可以划分为如下３步骤：个 ① 求文法非终结符的候选首终结符集和后随符号集；构造预测分析表根据输入符号和预测 ② ； ③ 分析表对句子进行分析．考虑到构造预测分析表的需要，对非终结符的每个候选式求出其对应的候选首终结符集，也
ｇｖｎｓｎｅｃｅｏｇｏａｇａｉｔｎｅｂｌｓｔｒｍｍａｒｎｔｅｅｎｒｏｏ．
ＫｙｗｒｓＬ１ｒｄｔｅａａｓ；ｏｐｅｒｃｌ；ｇａｍｒｅｔｃｅｏｄ：Ｌ（）ｐｅｃｖｎｌｉｃｍｉｒｉｉｅｒａ；ｓｎｎｅｉｉｙｓｌｐｎｐｓｍｅ
分析和ＬＲ分析方法．Ｌ１预测分析方法以其执Ｌ（）行效率高，便于维护的优点而被广泛采用… ．
・
收稿日期：０７６２２ｏ —０ —１基金项目：国防科工委纵向课题资助项目（１２０Ａ０）Ｈ００６０４．作者简介：（９９，，曹琼１一）女四川邻水人，７硕士，主要从事软件工程方面的研究．

编译原理实验二LL(1)语法分析实验报告

专题3_LL(1)语法分析设计原理与实现李若森 13281132 计科1301一、理论传授语法分析的设计方法和实现原理；LL(1) 分析表的构造；LL(1)分析过程；LL(1)分析器的构造。

二、目标任务实验项目实现LL(1)分析中控制程序（表驱动程序）；完成以下描述算术表达式的 LL(1)文法的LL(1)分析程序。

G[E]:E→TE’E’→ATE’|εT→FT’T’→MFT’|εF→(E)|iA→+|-M→*|/设计说明终结符号i为用户定义的简单变量，即标识符的定义。

加减乘除即运算符。

设计要求(1)输入串应是词法分析的输出二元式序列，即某算术表达式“专题 1”的输出结果，输出为输入串是否为该文法定义的算术表达式的判断结果；(2)LL(1)分析程序应能发现输入串出错；(3)设计两个测试用例（尽可能完备，正确和出错），并给出测试结果。

任务分析重点解决LL(1)表的构造和LL(1)分析器的实现。

三、实现过程实现LL(1)分析器a)将#号放在输入串S的尾部b)S中字符顺序入栈c)反复执行c)，任何时候按栈顶Xm和输入ai依据分析表，执行下述三个动作之一。

构造LL(1)分析表构造LL(1)分析表需要得到文法G[E]的FIRST集和FOLLOW集。

构造FIRST(α)构造FOLLOW(A)构造LL(1)分析表算法根据上述算法可得G[E]的LL(1)分析表，如表3-1所示：表3-1 LL(1)分析表主要数据结构pair<int, string>:用pair<int, string>来存储单个二元组。

该对照表由专题1定义。

map<string, int>:存储离散化后的终结符和非终结符。

vector<string>[][]:存储LL(1)分析表函数定义init:void init();功能：初始化LL(1)分析表，关键字及识别码对照表，离散化（非）终结符传入参数：（无）传出参数：（无）返回值：（无）Parse:bool Parse( const vector<PIS> &vec, int &ncol )；功能：进行该行的语法分析传入参数：vec:该行二元式序列传出参数：emsg:出错信息epos:出错标识符首字符所在位置返回值：是否成功解析。

智慧树答案编译原理知到课后答案章节测试2022年

第一章1.编译器(Compiler)能捕捉的错误都是静态错误(Static errors)。

答案:对2.编译器只能识别动态(Dynamic)语义，但不能识别静态(Static)语义。

答案:错3.对源程序进行编译正确处理顺序为（）答案:词法分析、语法分析、语义分析、代码生成4.编译器的各个阶段的产物分别是（）、中间代码和目标代码。

答案:记号序列、语法树、注释树5.（）执行翻译代码的功能，且立即执行源程序，而不产生中间代码。

答案:解释程序6.将编译程序分成若干个“遍”是为了____。

答案:利用有限的机器内存并提高机器的执行效率7.词法分析器用于识别_____。

答案:单词8.在编译器的功能模块中，扫描器的功能是（）。

答案:词法分析9.编译器进行的是（）答案:静态语义分析10.编译器中词法分析的输入和输出分别是（）答案:字符串、记号串第二章1.确定的自动机以及不确定的自动机都能正确地识别正规集。

答案:对2.正则文法、 DFA和正则表达式均可以用于描述高级程序设计语言的词法。

答案:对3.在有穷自动机中，两个状态是等价的条件是（）。

答案:A和B4.扫描器所完成的任务是从字符串形式的源程序中识别出一个个具有独立含义的最小语法单位即（）答案:单词5.设∑为{a，b}，则a，ba，{}，Ø都是∑上的正规式。

答案:对6.以下( )不是DFA的组成部分。

答案:初始状态集合7.在有穷自动机中，有穷自动机的状态s和t不等价，则称这两个状态是可区别的。

答案:对8.“由大写字母组成的、以Z开头并且不以Z结尾的字符串”的正则表达式是（）答案:Z [a-Z]*[A-Y]9.下面( )是词法分析的理论基础。

答案:有穷自动机第三章1.高级语言编译程序常用的语法分析方法中，递归下降分析法属于（）分析方法。

答案:自顶向下2.下面哪种分析方法是自顶向下分析（）。

答案:LL(1)3.推导是一个替换序列，每一步都是对（）进行替换，形成一个从单独的结构名开始，结束于一串记号符号的过程。

编译原理课程设计-LL1文法分析器设计C++语言实现

集美大学计算机工程学院编译原理课程设计报告选题名称:LL（1）文法分析院（系）:计算机工程学院专业:计算机科学与技术班级:计算1412指导教师:付永刚学年学期:2016 ~ 2017 学年第 2 学期2017 年06 月29 日摘要：选题要求：根据某一文法编制调试LL(1) 文法语法分分析程序，以便对任意输入的符号串进行分析。

本次课程设计的目的主要是加深对预测分析LL(1)文法语法分析法的理解。

具体如下：1、对语法规则有明确的定义；2、编写的分析程序能够对给定文法进行正确的语法分析；3、对输入给定的文法，手工计算FIRST、FOLLOW集合和select集合，应能判断识别是否为给定文法的句子，并给出推导过程。

4、对输入给定的文法，由程序自动构造FIRST、FOLLOW集合。

5、对于遇到的语法错误，能够做出简单的错误处理，给出简单的错误提示，保证顺利完成语法分析过程。

关键词：语法分析；FIRST集合；FOLLOW集合；分析表一、设计内容及要求(1) 基于PL/0语言，通过编程判断该文法是否为LL(1)文法；(2)计算出文法的First() Follow()(3)构造相应文法的预测分析表(4)对某个输入句子进行语法分析二、实现原理1．LL(1)文法LL(1)文法是一类可以进行确定的自顶向下语法分析的文法。

就是要求描述语言的文法是无左递归的和无回溯的。

根据LL(1)文法的定义，对于同一非终结符A的任意两个产生式A:=a和A:=b，都要满足：SELECT(A：=a )∩SELECT(A:=b)=Ø。

（1）文法的左递归当一个文法是左递归文法时，采用自顶向下分析法会使分析过程进入无穷循环之中。

所以采用自顶向下语法分析需要消除文法的左递归性。

文法的左递归是指若文法中对任一非终结符A有推导AÞA…，则称该文法是左递归的。

左递归又可以分为直接左递归和间接左递归。

●直接左递归若文法中的某一产生式形如A→Aα，α∈V*，则称该文法是直接左递归的。

编译原理LL(1)文法分析器实验(java)

编译原理LL(1)文法分析器实验本程序是基于已构建好的某一个语法的预测分析表来对用户的输入字符串进行分析，判断输入的字符串是否属于该文法的句子。

基本实现思想：接收用户输入的字符串（字符串以“#”表示结束）后，对用做分析栈的一维数组和存放分析表的二维数组进行初始化。

然后取出分析栈的栈顶字符，判断是否为终结符，若为终结符则判断是否为“#”且与当前输入符号一样，若是则语法分析结束，输入的字符串为文法的一个句子，否则出错若不为“#”且与当前输入符号一样则将栈顶符号出栈，当前输入符号从输入字符串中除去，进入下一个字符的分析。

若不为“#”且不与当前输入符号一样，则出错。

若栈顶符号为非终结符时，查看预测分析表，看栈顶符号和当前输入符号是否构成产生式，若产生式的右部为ε，则将栈顶符号出栈，取出栈顶符号进入下一个字符的分析。

若不为ε，将产生式的右部逆序的入栈，取出栈顶符号进入下一步分析。

程序流程图：本程序中使用以下文法作对用户输入的字符串进行分析：E→TE’E’→+TE’|εT→FT’T’→*FT’|εF→i|(E)该文法的预测分析表为：1、显示预测分析表，提示用户输入字符串2、输入的字符串为正确的句子：3、输入的字符串中包含了不属于终结符集的字符4、输入的字符串不是该文法能推导出来的句子程序代码：package ;import java.io.*;public class LL {String Vn[] = { "E", "E'", "T", "T'", "F" }; // 非终结符集String Vt[] = { "i", "+", "*", "(", ")", "#" }; // 终结符集String P[][] = new String[5][6]; // 预测分析表String fenxi[] ; // 分析栈int count = 1; // 步骤int count1 = 1;//’分析栈指针int count2 = 0, count3 = 0;//预测分析表指针String inputString = ""; // 输入的字符串boolean flag;public void setCount(int count, int count1, int count2, int count3){this.count = count;this.count1 = count1;this.count2 = count2;this.count3 = count3;flag = false;}public void setFenxi() { // 初始化分析栈fenxi = new String[20];fenxi[0] = "#";fenxi[1] = "E";}public void setP() { // 初始化预测分析表for (int i = 0; i < 5; i++) {for (int j = 0; j < 6; j++) {P[i][j] = "error";}}P[0][0] = "->TE'";P[0][3] = "->TE'";P[1][1] = "->+TE'";P[1][4] = "->ε";P[1][5] = "->ε";P[2][0] = "->FT'";P[2][3] = "->FT'";P[3][1] = "->ε";P[3][2] = "->*FT'";P[3][4] = "->ε";P[3][5] = "->ε";P[4][0] = "->i";P[4][3] = "->(E)";// 打印出预测分析表System.out.println(" 已构建好的预测分析表");System.out.println("----------------------------------------------------------------------");for (int i=0; i<6; i++) {System.out.print(" "+Vt[i]);}System.out.println();System.out.println("----------------------------------------------------------------------");for (int i=0; i<5; i++) {System.out.print(" "+Vn[i]+" ");for (int j=0; j<6; j++) {int l = 0;if (j>0) {l = 10-P[i][j-1].length();}for (int k=0; k<l; k++) {System.out.print(" ");}System.out.print(P[i][j]+" ");}System.out.println();}System.out.println("----------------------------------------------------------------------"); }public void setInputString(String input) {inputString = input;}public boolean judge() {String inputChar = inputString.substring(0, 1); // 当前输入字符boolean flage = false;if (count1 >= 0) {for (int i=0; i<6; i++) {if (fenxi[count1].equals(Vt[i])) { // 判断分析栈栈顶的字符是否为终结符flage = true;break;}}}if (flage) {// 为终结符时if (fenxi[count1].equals(inputChar)) {if (fenxi[count1].equals("#")&&inputString.length()==1) { // 栈顶符号为结束标志时// System.out.println("最后一个");String fenxizhan = "";for (int i=0; i<=P.length; i++) { // 拿到分析栈里的全部内容（滤去null）if (fenxi[i] == null) {break;} else {fenxizhan = fenxizhan + fenxi[i];}}// 输出当前分析栈情况，输入字符串，所用产生式或匹配System.out.print(" " + count);String countToString = Integer.toString(count);int farWay = 14 - countToString.length();for (int k=0; k<farWay; k++) {System.out.print(" ");}System.out.print(fenxizhan);farWay = 20 - fenxizhan.length();for (int k=0; k<farWay; k++) {System.out.print(" ");}System.out.print(inputString);farWay = 25 - inputString.length();for (int k=0; k<farWay; k++) {System.out.print(" ");}System.out.println("接受");flag = true;return true;} else {// 分析栈栈顶符号不为结束标志符号时String fenxizhan = "";for (int i=0; i<=P.length; i++) { // 拿到分析栈里的全部内容（滤去null）if (fenxi[i] == null) {break;} else {fenxizhan = fenxizhan + fenxi[i];}}// 输出当前分析栈情况，输入字符串，所用产生式或匹配System.out.print(" "+count);String countToString = Integer.toString(count);int farWay = 14 - countToString.length();for (int k=0; k<farWay; k++) {System.out.print(" ");}System.out.print(fenxizhan);farWay = 20 - fenxizhan.length();for (int k=0; k<farWay; k++) {System.out.print(" ");}System.out.print(inputString);farWay = 25 - inputString.length();for (int k=0; k<farWay; k++) {System.out.print(" ");}System.out.println("\"" + inputChar + "\"" + "匹配");// 将栈顶符号出栈，栈顶指针减一fenxi[count1] = null;count1 -= 1;if (inputString.length() > 1) { // 当当前输入字符串的长度大于1时，将当前输入字符从输入字符串中除去inputString = inputString.substring(1, inputString.length());} else { // 当前输入串长度为1时inputChar = inputString;}// System.out.println(" "+count+" "+fenxizhan+"// "+inputString +" "+P[count3][count2]);// System.out.println(count + inputChar + "匹配");count++;judge();}}else { // 判断与与输入符号是否一样为结束标志System.out.println(" 分析到第" + count + "步时出错！");flag = false;return false;}} else {// 非终结符时boolean fla = false;for (int i=0; i<6; i++) { // 查询当前输入符号位于终结符集的位置if (inputChar.equals(Vt[i])) {fla = true;count2 = i;break;}}if(!fla){System.out.println(" 分析到第" + count + "步时出错！");flag = false;return false;}for (int i=0; i<5; i++) { // 查询栈顶的符号位于非终结符集的位置if (fenxi[count1].equals(Vn[i])) {count3 = i;break;}}if (P[count3][count2] != "error") { // 栈顶的非终结符与输入的终结符存在产生式时String p = P[count3][count2];String s1 = p.substring(2, p.length()); // 获取对应的产生式if (s1.equals("ε")) { // 产生式推出“ε”时String fenxizhan = "";for (int i=0; i<=P.length; i++) {if (fenxi[i] == null) {break;} else {fenxizhan = fenxizhan + fenxi[i];}}// 输出当前分析栈情况，输入字符串，所用产生式或匹配System.out.print(" " + count);String countToString = Integer.toString(count);int farWay = 14 - countToString.length();for (int k=0; k<farWay; k++) {System.out.print(" ");}System.out.print(fenxizhan);farWay = 20 - fenxizhan.length();for (int k=0; k<farWay; k++) {System.out.print(" ");}System.out.print(inputString);farWay = 25 - inputString.length();for (int k=0; k<farWay; k++) {System.out.print(" ");}System.out.println(fenxi[count1] + P[count3][count2]);// 将栈顶符号出栈，栈顶指针指向下一个元素fenxi[count1] = null;count1 -= 1;count++;judge();} else { // 产生式不推出“ε”时int k = s1.length();String fenxizhan = "";for (int i=0; i<=P.length; i++) {if (fenxi[i] == null) {break;} else {fenxizhan = fenxizhan + fenxi[i];}}// 输出当前分析栈情况，输入字符串，所用产生式或匹配System.out.print(" "+count);String countToString = Integer.toString(count);int farWay = 14 - countToString.length();for (int o=0; o<farWay; o++) {System.out.print(" ");}System.out.print(fenxizhan);farWay = 20 - fenxizhan.length();for (int o=0; o<farWay; o++) {System.out.print(" ");}System.out.print(inputString);farWay = 25 - inputString.length();for (int o=0; o<farWay; o++) {System.out.print(" ");}System.out.println(fenxi[count1] + P[count3][count2]);for (int i=1; i<=k; i++) { // 将产生式右部的各个符号入栈String s2 = s1.substring(s1.length() - 1, s1.length());s1 = s1.substring(0, s1.length() - 1);if (s2.equals("'")) {s2 = s1.substring(s1.length() - 1, s1.length())+ s2;i++;s1 = s1.substring(0, s1.length() - 1);}fenxi[count1] = s2;if (i < k)count1++;// System.out.println("count1=" + count1);}// System.out.println(" "+count+" "+fenxizhan+"// "+inputString +" "+P[count3][count2]);count++;// System.out.println(count);judge();}} else {System.out.println(" 分析到第" + count + "步时出错！");flag = false;return false;}}return flag;}public static void main(String args[]) {LL l = new LL();l.setP();String input = "";boolean flag = true;while (flag) {try {InputStreamReader isr = new InputStreamReader(System.in);BufferedReader br = new BufferedReader(isr);System.out.println();System.out.print("请输入字符串(输入exit退出)：");input = br.readLine();} catch (Exception e) {e.printStackTrace();}if(input.equals("exit")){flag = false;}else{l.setInputString(input);l.setCount(1, 1, 0, 0);l.setFenxi();System.out.println();System.out.println("分析过程");System.out.println("----------------------------------------------------------------------");System.out.println(" 步骤| 分析栈| 剩余输入串| 所用产生式");System.out.println("----------------------------------------------------------------------");boolean b = l.judge();System.out.println("----------------------------------------------------------------------");if(b){System.out.println("您输入的字符串"+input+"是该文发的一个句子");}else{System.out.println("您输入的字符串"+input+"有词法错误！");}}}}}。

编译原理实验报告《LL(1)语法分析器构造》(推荐文档)

《LL（1）分析器的构造》实验报告一、实验名称LL(1)分析器的构造二、实验目的设计、编制、调试一个LL(1)语法分析器，利用语法分析器对符号串的识别，加深对语法分析原理的理解。

三、实验内容和要求设计并实现一个LL(1)语法分析器，实现对算术文法:G[E]:E->E+T|TT->T*F|FF->(E)|i所定义的符号串进行识别，例如符号串i+i*i为文法所定义的句子，符号串ii+++*i+不是文法所定义的句子。

实验要求:1、检测左递归，如果有则进行消除；2、求解FIRST集和FOLLOW集；3、构建LL(1)分析表；4、构建LL分析程序，对于用户输入的句子，能够利用所构造的分析程序进行分析，并显示出分析过程。

四、主要仪器设备硬件：微型计算机。

软件： Code blocks（也可以是其它集成开发环境）。

五、实验过程描述1、程序主要框架程序中编写了以下函数，各个函数实现的作用如下：void input_grammer(string *G);//输入文法Gvoid preprocess(string *G,string *P,string &U,string &u,int &n,int &t,int &k);//将文法G预处理得到产生式集合P，非终结符、终结符集合U、u，int eliminate_1(string *G,string *P,string U,string *GG);//消除文法G中所有直接左递归得到文法GGint* ifempty(string* P,string U,int k,int n);//判断各非终结符是否能推导为空string* FIRST_X(string* P,string U,string u,int* empty,int k,int n)；求所有非终结符的FIRST集string FIRST(string U,string u,string* first,string s)；//求符号串s=X1X2...Xn的FIRST集string** create_table(string *P,string U,string u,int n,int t,int k,string* first)；//构造分析表void analyse(string **table,string U,string u,int t,string s)；//分析符号串s2、编写的源程序#include<cstdio>#include<cstring>#include<iostream>using namespace std;void input_grammer(string *G)//输入文法G,n个非终结符{int i=0;//计数char ch='y';while(ch=='y'){cin>>G[i++];cout<<"继续输入?(y/n)\n";cin>>ch;}}void preprocess(string *G,string *P,string &U,string &u,int &n,int &t,int &k)//将文法G预处理产生式集合P，非终结符、终结符集合U、u，{int i,j,r,temp;//计数char C;//记录规则中（）后的符号int flag;//检测到（）n=t=k=0;for( i=0;i<50;i++) P[i]=" ";//字符串如果不初始化，在使用P[i][j]=a时将不能改变，可以用P[i].append(1,a)U=u=" ";//字符串如果不初始化，无法使用U[i]=a赋值，可以用U.append(1,a) for(n=0;!G[n].empty();n++){ U[n]=G[n][0];}//非终结符集合，n为非终结符个数for(i=0;i<n;i++){for(j=4;j<G[i].length();j++){if(U.find(G[i][j])==string::npos&&u.find(G[i][j])==string::npos)if(G[i][j]!='|'&&G[i][j]!='^')//if(G[i][j]!='('&&G[i][j]!=')'&&G[i][j]!='|'&&G[i][j]!='^')u[t++]=G[i][j];}}//终结符集合，t为终结符个数for(i=0;i<n;i++){flag=0;r=4;for(j=4;j<G[i].length();j++){P[k][0]=U[i];P[k][1]=':';P[k][2]=':';P[k][3]='=';/* if(G[i][j]=='('){ j++;flag=1;for(temp=j;G[i][temp]!=')';temp++);C=G[i][temp+1];//C记录（）后跟的字符，将C添加到（）中所有字符串后面}if(G[i][j]==')') {j++;flag=0;}*/if(G[i][j]=='|'){//if(flag==1) P[k][r++]=C;k++;j++;P[k][0]=U[i];P[k][1]=':';P[k][2]=':';P[k][3]='=';r=4;P[k][r++]=G[i][j];}else{P[k][r++]=G[i][j];}}k++;}//获得产生式集合P，k为产生式个数}int eliminate_1(string *G,string *P,string U,string *GG)//消除文法G1中所有直接左递归得到文法G2，要能够消除含有多个左递归的情况）{string arfa,beta;//所有形如A::=Aα|β中的α、β连接起来形成的字符串arfa、betaint i,j,temp,m=0;//计数int flag=0;//flag=1表示文法有左递归int flagg=0;//flagg=1表示某条规则有左递归char C='A';//由于消除左递归新增的非终结符，从A开始增加，只要不在原来问法的非终结符中即可加入for(i=0;i<20&&U[i]!=' ';i++){ flagg=0;arfa=beta="";for(j=0;j<100&&P[j][0]!=' ';j++){if(P[j][0]==U[i]){if(P[j][4]==U[i])//产生式j有左递归{flagg=1;for(temp=5;P[j][temp]!=' ';temp++) arfa.append(1,P[j][temp]);if(P[j+1][4]==U[i]) arfa.append("|");//不止一个产生式含有左递归}else{for(temp=4;P[j][temp]!=' ';temp++) beta.append(1,P[j][temp]);if(P[j+1][0]==U[i]&&P[j+1][4]!=U[i]) beta.append("|");}}}if(flagg==0)//对于不含左递归的文法规则不重写{GG[m]=G[i]; m++;}else{flag=1;//文法存在左递归GG[m].append(1,U[i]);GG[m].append("::=");if(beta.find('|')!=string::npos) GG[m].append("("+beta+")");else GG[m].append(beta);while(U.find(C)!=string::npos){C++;}GG[m].append(1,C);m++;GG[m].append(1,C);GG[m].append("::=");if(arfa.find('|')!=string::npos) GG[m].append("("+arfa+")");else GG[m].append(arfa);GG[m].append(1,C);GG[m].append("|^");m++;C++;}//A::=Aα|β改写成A::=βA‘，A’=αA'|β，}return flag;}int* ifempty(string* P,string U,int k,int n){int* empty=new int [n];//指示非终结符能否推导到空串int i,j,r;for(r=0;r<n;r++) empty[r]=0;//默认所有非终结符都不能推导到空int flag=1;//1表示empty数组有修改int step=100;//假设一条规则最大推导步数为100步while(step--){for(i=0;i<k;i++){r=U.find(P[i][0]);if(P[i][4]=='^') empty[r]=1;//直接推导到空else{for(j=4;P[i][j]!=' ';j++){if(U.find(P[i][j])!=string::npos){if(empty[U.find(P[i][j])]==0) break;}else break;}if(P[i][j]==' ') empty[r]=1;//多步推导到空else flag=0;}}}return empty;}string* FIRST_X(string* P,string U,string u,int* empty,int k,int n){int i,j,r,s,tmp;string* first=new string[n];char a;int step=100;//最大推导步数while(step--){// cout<<"step"<<100-step<<endl;for(i=0;i<k;i++){//cout<<P[i]<<endl;r=U.find(P[i][0]);if(P[i][4]=='^'&&first[r].find('^')==string::npos) first[r].append(1,'^');//规则右部首符号为空else{for(j=4;P[i][j]!=' ';j++){a=P[i][j];if(u.find(a)!=string::npos&&first[r].find(a)==string::npos)//规则右部首符号是终结符{first[r].append(1,a);break;//添加并结束}if(U.find(P[i][j])!=string::npos)//规则右部首符号是非终结符,形如X：：=Y1Y2...Yk{s=U.find(P[i][j]);//cout<<P[i][j]<<":\n";for(tmp=0;first[s][tmp]!='\0';tmp++){a=first[s][tmp];if(a!='^'&&first[r].find(a)==string::npos)//将FIRST[Y1]中的非空符加入first[r].append(1,a);}}if(!empty[s]) break;//若Y1不能推导到空，结束}if(P[i][j]==' ')if(first[r].find('^')==string::npos)first[r].append(1,'^');//若Y1、Y2...Yk都能推导到空，则加入空符号}}}return first;}string FIRST(string U,string u,string* first,string s)//求符号串s=X1X2...Xn的FIRST集{int i,j,r;char a;string fir;for(i=0;i<s.length();i++){if(s[i]=='^') fir.append(1,'^');if(u.find(s[i])!=string::npos&&fir.find(s[i])==string::npos){ fir.append(1,s[i]);break;}//X1是终结符，添加并结束循环if(U.find(s[i])!=string::npos)//X1是非终结符{r=U.find(s[i]);for(j=0;first[r][j]!='\0';j++){a=first[r][j];if(a!='^'&&fir.find(a)==string::npos)//将FIRST(X1)中的非空符号加入fir.append(1,a);}if(first[r].find('^')==string::npos) break;//若X1不可推导到空，循环停止}if(i==s.length())//若X1-Xk都可推导到空if(fir.find(s[i])==string::npos) //fir中还未加入空符号fir.append(1,'^');}return fir;}string** create_table(string *P,string U,string u,int n,int t,int k,string* first)//构造分析表，P为文法G的产生式构成的集合{int i,j,p,q;string arfa;//记录规则右部string fir,follow;string FOLLOW[5]={")#",")#","+)#","+)#","+*)#"};string **table=new string*[n];for(i=0;i<n;i++) table[i]=new string[t+1];for(i=0;i<n;i++)for(j=0;j<t+1;j++)table[i][j]=" ";//table存储分析表的元素，“ ”表示error for(i=0;i<k;i++){arfa=P[i];arfa.erase(0,4);//删除前4个字符，如：E::=E+T,则arfa="E+T"fir=FIRST(U,u,first,arfa);for(j=0;j<t;j++){p=U.find(P[i][0]);if(fir.find(u[j])!=string::npos){q=j;table[p][q]=P[i];}//对first（）中的每一终结符置相应的规则}if(fir.find('^')!=string::npos){follow=FOLLOW[p];//对规则左部求follow()for(j=0;j<t;j++){if((q=follow.find(u[j]))!=string::npos){q=j;table[p][q]=P[i];}//对follow（）中的每一终结符置相应的规则}table[p][t]=P[i];//对#所在元素置相应规则}}return table;}void analyse(string **table,string U,string u,int t,string s)//分析符号串s{string stack;//分析栈string ss=s;//记录原符号串char x;//栈顶符号char a;//下一个要输入的字符int flag=0;//匹配成功标志int i=0,j=0,step=1;//符号栈计数、输入串计数、步骤数int p,q,r;string temp;for(i=0;!s[i];i++){if(u.find(s[i])==string::npos)//出现非法的符号cout<<s<<"不是该文法的句子\n";return;}s.append(1,'#');stack.append(1,'#');//’#’进入分析栈stack.append(1,U[0]);i++;//文法开始符进入分析栈a=s[0];//cout<<stack<<endl;cout<<"步骤分析栈余留输入串所用产生式\n";while(!flag){// cout<<"步骤分析栈余留输入串所用产生式\n"cout<<step<<" "<<stack<<" "<<s<<" ";x=stack[i];stack.erase(i,1);i--;//取栈顶符号x,并从栈顶退出//cout<<x<<endl;if(u.find(x)!=string::npos)//x是终结符的情况{if(x==a){s.erase(0,1);a=s[0];//栈顶符号与当前输入符号匹配，则输入下一个符号cout<<" \n";//未使用产生式，输出空}else{cout<<"error\n";cout<<ss<<"不是该文法的句子\n";break;}}if(x=='#'){if(a=='#') {flag=1;cout<<"成功\n";}//栈顶和余留输入串都为#，匹配成功else{cout<<"error\n";cout<<ss<<"不是该文法的句子\n";break;}}if(U.find(x)!=string::npos)//x是非终结符的情况{p=U.find(x);q=u.find(a);if(a=='#') q=t;temp=table[p][q];cout<<temp<<endl;//输出使用的产生式if(temp[0]!=' ')//分析表中对应项不为error{r=9;while(temp[r]==' ') r--;while(r>3){if(temp[r]!='^'){stack.append(1,temp[r]);//将X::=x1x2...的规则右部各符号压栈i++;}r--;}}else{cout<<"error\n";cout<<ss<<"不是该文法的句子\n";break;}}step++;}if(flag) cout<<endl<<ss<<"是该文法的句子\n";}int main(){int i,j;string *G=new string[50];//文法Gstring *P=new string[50];//产生式集合Pstring U,u;//文法G非终结符集合U，终结符集合uint n,t,k;//非终结符、终结符个数,产生式数string *GG=new string[50];//消除左递归后的文法GGstring *PP=new string[50];//文法GG的产生式集合PPstring UU,uu;//文法GG非终结符集合U，终结符集合uint nn,tt,kk;//消除左递归后的非终结符、终结符个数,产生式数string** table;//分析表cout<<" 欢迎使用LL(1)语法分析器!\n\n\n";cout<<"请输入文法（同一左部的规则在同一行输入，例如：E::=E+T|T；用^表示空串）\n";input_grammer(G);preprocess(G,P,U,u,n,t,k);cout<<"\n该文法有"<<n<<"个非终结符：\n";for(i=0;i<n;i++) cout<<U[i];cout<<endl;cout<<"该文法有"<<t<<"个终结符：\n";for(i=0;i<t;i++) cout<<u[i];cout<<"\n\n 左递归检测与消除\n\n";if(eliminate_1(G,P,U,GG)){preprocess(GG,PP,UU,uu,nn,tt,kk);cout<<"该文法存在左递归！\n\n消除左递归后的文法:\n\n"; for(i=0;i<nn;i++) cout<<GG[i]<<endl;cout<<endl;cout<<"新文法有"<<nn<<"个非终结符：\n";for(i=0;i<nn;i++) cout<<UU[i];cout<<endl;cout<<"新文法有"<<tt<<"个终结符：\n";for(i=0;i<tt;i++) cout<<uu[i];cout<<endl;//cout<<"新文法有"<<kk<<"个产生式：\n";//for(i=0;i<kk;i++) cout<<PP[i]<<endl;}else{cout<<"该文法不存在左递归\n";GG=G;PP=P;UU=U;uu=u;nn=n;tt=t;kk=k;}cout<<" 求解FIRST集\n\n";int *empty=ifempty(PP,UU,kk,nn);string* first=FIRST_X(PP,UU,uu,empty,kk,nn);for(i=0;i<nn;i++)cout<<"FIRST("<<UU[i]<<"): "<<first[i]<<endl;cout<<" 求解FOLLOW集\n\n";for(i=0;i<nn;i++)cout<<"FOLLOW("<<UU[i]<<"): "<<FOLLOW[i]<<endl; cout<<"\n\n 构造文法分析表\n\n"; table=create_table(PP,UU,uu,nn,tt,kk,first);cout<<" ";for(i=0;i<tt;i++) cout<<" "<<uu[i]<<" ";cout<<"# "<<endl;for( i=0;i<nn;i++){cout<<UU[i]<<" ";for(j=0;j<t+1;j++)cout<<table[i][j];cout<<endl;}cout<<"\n\n 分析符号串\n\n";cout<<"请输入要分析的符号串\n";cin>>s;analyse(table,UU,uu,tt,s);return 0;}3、程序演示结果（1）输入文法（2）消除左递归（3）求解FIRST和FOLLOW集（4）构造分析表（5）分析符号串匹配成功的情况：匹配失败的情况五、思考和体会1、编写的LL(1)语法分析器应该具有智能性，可以由用户输入任意文法，不需要指定终结符个数和非终结符个数。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

２ＬＬ（１）预测分析器的构造
２．１预测分析器的工作流程ＬＬ（１）预测分析器的总控程序利用栈顶元素和当前输入符
号对输入串进行预测分析，而预测的信息则存放在分析表的相应入口里。分析表可用一个矩阵Ｍ表示。矩阵的元素Ｍ［Ａ，ａ］中的下标Ａ表示非终结符，ａ为终结符或句子括号“ ＃”。矩阵元素Ｍ［Ａ，ａ］中存放着一条关于Ａ的产生式，即当用非终结符Ａ向下推导，遇到输入符ａ时所应采取的候选产生式，当元素内容无产生式时，则表明用Ａ为左部向下推导时遇到了不该出现的符号，此时应转向出错处理。分析程序的工作流程如图１所示。
图１预测分析程序的工作流程图２．２类定义
ｃｌａｓｓＰｒｅｃｅｐｔ／／定义产生式类｛ｐｕｂｌｉｃ：
Ｐｒｅｃｅｐｔ（ｖｏｉｄ）；Ｐｒｅｃｅｐｔ（ｓｔｒｉｎｇｌｅｆｔ，ｓｔｒｉｎｇｒｉｇｈｔ）；￣Ｐｒｅｃｅｐｔ（ｖｏｉｄ）；ｓｔｒｉｎｇＧｅｔＬｅｆｔ（）；／／截取产生式中“ →”的左边字符ｓｔｒｉｎｇＧｅｔＲｉｇｈｔ（）；／／截取产生式中“ →”的右边字符ｐｒｉｖａｔｅ：ｓｔｒｉｎｇｓｔｒＬｅｆｔ；／／存放“ →”的左边字符ｓｔｒｉｎｇｓｔｒＲｉｇｈｔ；／／存放“ →”的右边字符ｐｕｂｌｉｃ：ｖｏｉｄＣｌｅａｒ（ｖｏｉｄ）；／／将所有产生式清空｝；ｃｌａｓｓＳｅｔ／／定义集合类｛ｐｕｂｌｉｃ：Ｓｅｔ（ｖｏｉｄ）；￣Ｓｅｔ（ｖｏｉｄ）；Ｓｅｔ（ｃｏｎｓｔＳｅｔ＆ｓｅｔ）；／／构造函数Ｓｅｔ（ｃｈａｒｃＣｈａｒ）；／／构造函数ｂｏｏｌＩｎｓｅｒｔ（ｃｈａｒｃＩｎｓｅｒｔ）；／／在原来的集合中插入一个字符ｂｏｏｌＤｅｌｅｔｅ（ｃｈａｒｃＤｅｌｅｔｅ）；／／在原来的集合中删除一个字符ｂｏｏｌＦｉｎｄ（ｃｈａｒｃＦｉｎｄ）；／／在集合中查找字符ｃＦｉｎｄｉｎｔＦｉｎｄＰｏｓ（ｃｈａｒｃＦｉｎｄ）；／／在集合中查找字符ｃＦｉｎｄ的位置ｉｎｔＡｄｄ（ｃｏｎｓｔＳｅｔ＆ｓｅｔ）；／／添加集合ｓｅｔｉｎｔＳｕｂ（ｃｏｎｓｔＳｅｔ＆ｓｅｔ）；／／删除集合ｓｅｔｉｎｔＳｉｚｅ（）ｃｏｎｓｔ；／／求集合的大小Ｓｅｔｏｐｅｒａｔｏｒ＋（ｃｏｎｓｔＳｅｔ＆ｓｅｔ）；／／合并两个集合Ｓｅｔｏｐｅｒａｔｏｒ－（ｃｏｎｓｔＳｅｔ＆ｓｅｔ）；
计算机时代２００８年第３期
·６３·
ＬＬ（１）预测分析器的构造
褚亚飞
（浙江海洋学院高职杭州分院，浙江杭州３１１２５８）
摘要：着重分析了编译原理课程中的ＬＬ（１）预测分析器的设计算法。对于给定的代码，求出ＦＩＲＳＴ、ＦＯＬＬＯＷ和ＳＥＬＥＣＴ集，构造相应的ＬＬ（１）预测分析器，给出预测分析表，并对求解ＦＩＲＳＴ集和ＦＯＬＬＯＷ集中存在的环问题提出了解决算法。关键词：ＦＩＲＳＴ；ＦＯＬＬＯＷ；ＳＥＬＥＣＴ；ＬＬ（１）；算法
４结束语
通过所述屏幕录像方式可以将电脑屏幕的动态变化信息以文件的形式记录保存下来，编制成流媒体课件，特别适宜于网上进行应用软件教学。它建构出直观生动的学习情境，避免了教学中出现“ 只可意会不可言传”的尴尬局面，丰富了教学信息资源，增大了教学信息容量，减轻了教师的劳动强度，取得了良好的教学效果，具有广阔的应用前景。参考文献：［１］陈代武．流媒体课件制作中关键技术研究［Ｊ］．计算机与现代化，
计算机时代２００８年第３期
·６５·
／／在集合中删掉集合ｓｅｔ中的字符ｃｏｎｓｔＳｅｔｏｐｅｒａｔｏｒ＝（ｃｏｎｓｔＳｅｔ＆ｓｅｔ）；／／对集合进行赋值ｃｈａｒＧｅｔＡｔ（ｉｎｔｉＰｏｓ）；／／取集合中第ｉＰｏｓ个字符ｂｏｏｌＩｓＥｍｐｔｙ（）；／／判断集合是否为空ｐｒｉｖａｔｅ：ｖｅｃｔｏｒ＜ｃｈａｒ＞ＳｅｔＣｏｎｔｅｎｔ；
１ＦＩＲＳＴ，ＦＯＬＬＯＷ，ＳＥＬＥＣＴ集的算法设计
１．１求解ＦＩＲＳＴ集合的算法 ⑴ 逐一扫描代码中的产生式，将产生式右部的字符串赋
给 γ， γ［ｊ］是指 γ 串中第ｊ个字符。 ⑵ 逐一扫描产生式右部，要处理如下两种情况： ①若产生式的右部为空字符串或第一个字符为非终结符，
一个字符），则继续，求得所有的非终结符的ＦＩＲＳＴ
集合，跳出⑴。所求得的ＦＩＲＳＴ集合中还可能存在环的问题（形如产生式
Ｘ→Ｘ…（Ｘ∈Ｖｎ）或者求非终结符的ＦＩＲＳＴ集合需要先求代码中其他非终结符的ＦＩＲＳＴ集合的两种情况）和存在重复终结符的问题。下面就这两个问题提出解决的算法。
０引言
学好编译原理对计算机专业的学生至关重要。随着计算机科学的迅速发展，程序设计语言也有了飞速的发展，语言的功能、结构均有了本质的改变。相对而言，编译原理课程的教学却大大落后于实际需要，仍然停留在以理论教学为主的状态。编译原理作为计算机专业学生的必修课，较其他专业课程而言，显得过于枯燥、抽象和难于理解，由此出现学生学习积极性不高、兴趣不浓、掌握不透等现象。本分析器以给出解答过程和答案为主要内容，以简单清晰的界面给出问题的具体解答过程，给学习者一个直观的认识，使他们了解编译原理工作的过程，进而提高对编译原理的兴趣。
２００７．１０：９￣１１
▲ ［２］李志河．多媒体课件制作技术［Ｍ］．清华大学出版社，２００５．ＣＥ
·６４·
ＣｏｍｐｕｔｅｒＥｒａＮｏ．３２００８
解决“ 环”的算法 ⑴ 将代码中的所有非终结符按预处理的结果顺序处理。 ⑵ 三种扫描方式： ①按顺序扫描ＦＩＲＳＴ集合（Ｘ１，Ｘ２， …，Ｘｎ），若该非终结符Ｘｊ需由另一个非终结符的Ｘｉ求得，那么若Ｘｉ排在Ｘｊ前面，则将Ｘｉ代入Ｘｊ中； ②逐一扫描按顺序排列的ＦＩＲＳＴ集合（Ｘ１，Ｘ２， …，Ｘｎ），若非终结符的ＦＩＲＳＴ集合中含有它本身，则删除等式右部的该非终结符； ③从序号最大的非终结符的ＦＩＲＳＴ集开始，逐一扫描按顺序排列的ＦＩＲＳＴ集合（Ｘ１，Ｘ２， …，Ｘｎ），若该非终结符Ｘｊ需由另一个非终结符的Ｘｉ求得，那么若Ｘｉ排在Ｘｊ后面，则将该Ｘｉ回代入Ｘｊ中，调用第②步。 ⑶ 若所有非终结符的ＦＩＲＳＴ集中都已经为终结符，则 “ 环”问题已经解决。解决终结符的重复存在问题的算法 ①用“ 起泡法 ”对ＦＩＲＳＴ集合里的终结符进行判断并将重复的终结符删除； ②将‘ ε’字符加入可以推出空的非终结符ＦＩＲＳＴ集合中，并将不能推出空的非终结符的ＦＩＲＳＴ集合中的‘ ε’字符全部删除。１．２求解ＦＯＬＬＯＷ集合的算法 ⑴ 逐一扫描代码中的产生式，将产生式右部赋给 γ 串， γ［ｊ］表示 γ 串中的第ｊ个字符。 ⑵ 逐一扫描产生式的右部，若 γ［ｊ］为非终结符Ｘ，找出 γ［ｊ］后继的第一个字符 γ［ｋ］。 ① 若 γ［ｋ］为终结符，则将该终结符加入到ＦＯＬＬＯＷ集合，结束，跳出⑵； ②若 γ［ｋ］为非终结符，则ＦＩＲＳＴ集合‘－ ε’，执行⑶。 ⑶ 逐一扫描Ｘ后的字符串，分为下面两种情况：ａ．若非终结符 γ［ｋ］能推出空字符串，则ｋ＋＋，继续执行①、 ②两步；ｂ．若非终结符 γ［ｋ］为产生式最后一个字符，则将该产生式的左部非终结符的ＦＯＬＬＯＷ集合加入该非终结符的ＦＯＬ－ＬＯＷ集合。 ⑷ 若扫描完全部的产生式，则求得所有非终结符的ＦＯＬＬＯＷ集合。在计算ＦＯＬＬＯＷ集中也存在“ 环”和重复的终结符的问题，解决的办法与ＦＩＲＳＴ集的相同。１．３求ＳＥＬＬＥＣＴ集合对代码中的任意产生式Ａ→ａ，Ａ∈ＶＮ，ａ∈Ｖ＊，求ＳＥＬＥＣＴ集。可按下列算法：ＩＦ（ａ不能推出 ε）ＳＥＬＥＣＴ（Ａ→ａ）＝ＦＩＲＳＴ（ａ）ＥＬＳＥＳＥＬＥＣＴ（Ａ→ａ）＝ＦＩＲＳＴ（ａ）∪ＦＯＬＬＯＷ（Ａ）
则将‘ ε’和终结符加入此非终结符的ＦＩＲＳＴ集合，跳出⑵； ②若产生式右部为非终结符，则将 γ［ｊ］的ＦＩＲＳＴ集合加
入该非终结符的ＦＩＲＳＴ集合。ａ．若 γ［ｊ］不能推出空字符串，则结束，跳出⑵；ｂ．若ｊ＜＝γ 串的长度（即该非终结符 γ［ｊ］不是产生式最后
３“ 动态屏幕捕获型”流媒体课件的应用
“ 动态屏幕捕获型”流媒体课件的应用非常广泛，可用于网上教学、课堂教学。３．１用于网上教学
流媒体课件的最大优势是实时传输，能实现网上边下载边播放“。动态屏幕捕获型”流媒体课件在现代远程教育（如电大、网络教育学院开办的远程教育）或校园网教学中大有用武之地。若将一些应用软件的教学制成流媒体课件，学习者可以在家里直观自主地学习，定能收到好的学习效果。没有上网的学习者，可以购买配套光盘进行学习。３．２用于课堂教学